Abstract
First-order theorem provers are commonly utilised as backends to proof assistants. In order to improve efficiency, it is desirable that such provers can carry out some higher-order reasoning. In his 1991 paper, Dougherty proposed a combinatory unification algorithm for higher-order logic. The algorithm removes the need to deal with \(\lambda \)-binders and \(\alpha \)-renaming, making it attractive to implement in first-order provers. However, since publication it has garnered little interest due to a number of characteristics that make it unsuitable for a practical implementation. It fails to terminate on many trivial instances and requires polymorphism. We present a restricted version of Dougherty’s algorithm that is incomplete, terminating and does not require polymorphism. Further, we describe its implementation in the Vampire theorem prover, including a novel use of a substitution tree as a filtering index for higher-order unification. Finally, we analyse the performance of the algorithm on two benchmark sets and show that it is competitive.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
Note that the definition of higher-order subterm here is different to its usage in [3].
- 2.
- 3.
Some of these problems are marked as being solvable by Satallax on the TPTP website. However, the CASC-2018 version of Satallax that we used in our tests was unable to find a proof.
- 4.
This problem can be solved by the new version of E, Ehoh developed by Vukmirović et al. [32].
References
Baader, F., Nipkow, T.: Term Rewriting and All That. Cambridge University Press, Cambridge (1999)
Beeson, M.: Lambda logic. In: Basin, D., Rusinowitch, M. (eds.) IJCAR 2004. LNCS (LNAI), vol. 3097, pp. 460–474. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-25984-8_34
Bentkamp, A., Blanchette, J.C., Cruanes, S., Waldmann, U.: Superposition for lambda-free higher-order logic. In: Galmiche, D., Schulz, S., Sebastiani, R. (eds.) IJCAR 2018. LNCS (LNAI), vol. 10900, pp. 28–46. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-94205-6_3
Bentkamp, A., Blanchette, J.C., Tourret, S., Vukmirović, P., Waldmann, U.: Superposition with lambdas (2019, submitted for publication)
Bhayat, A., Reger, G.: Set of support for higher-order reasoning. In: PAAR 2018. CEUR Workshop Proceedings, vol. 2162, pp. 2–16 (2018)
Brown, C.E.: Satallax: an automatic higher-order prover. In: Gramlich, B., Miller, D., Sattler, U. (eds.) IJCAR 2012. LNCS (LNAI), vol. 7364, pp. 111–117. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-31365-3_11
Burel, G.: Embedding deduction modulo into a prover. In: Dawar, A., Veith, H. (eds.) CSL 2010. LNCS, vol. 6247, pp. 155–169. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-15205-4_15
Cruanes, S.: Superposition with structural induction. In: Dixon, C., Finger, M. (eds.) FroCoS 2017. LNCS (LNAI), vol. 10483, pp. 172–188. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-66167-4_10
Czajka, Ł., Kaliszyk, C.: Hammer for coq: automation for dependent type theory. J. Autom. Reason. 61(1), 423–453 (2018)
de Moura, F.L.C., Ayala-Rincón, M., Kamareddine, F.: Higher-order unification: a structural relation between Huet’s method and the one based on explicit substitutions. J. Appl. Logic 6(1), 72–108 (2008)
Dougherty, D.J.: Higher-order unification via combinators. Theor. Comput. Sci. 114(2), 273–298 (1993)
Dowek, G.: Higher order unification via explicit substitutions. Inf. Comput. 157(1–2), 183–235 (2000)
Dowek, G., Hardin, T., Kirchner, C.: Theorem proving modulo. J. Autom. Reason. 31(1), 33–72 (2003)
Graf, P.: Substitution tree indexing. In: Hsiang, J. (ed.) RTA 1995. LNCS, vol. 914, pp. 117–131. Springer, Heidelberg (1995). https://doi.org/10.1007/3-540-59200-8_52
Hoder, K., Voronkov, A.: Comparing unification algorithms in first-order theorem proving. In: Mertsching, B., Hund, M., Aziz, Z. (eds.) KI 2009. LNCS (LNAI), vol. 5803, pp. 435–443. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-04617-9_55
Huet, G.: A unification algorithm for typed \(\lambda \)-calculus. Theor. Comput. Sci. TCS 1(1), 27–57 (1975)
Kovács, L., Voronkov, A.: First-order theorem proving and Vampire. In: Sharygina, N., Veith, H. (eds.) CAV 2013. LNCS, vol. 8044, pp. 1–35. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-39799-8_1
Levy, J.: Decidable and undecidable second-order unification problems. In: Nipkow, T. (ed.) RTA 1998. LNCS, vol. 1379, pp. 47–60. Springer, Heidelberg (1998). https://doi.org/10.1007/BFb0052360
Libal, T., Miller, D.: Functions-as-constructors higher-order unification. In: 1st International Conference on Formal Structures for Computation and Deduction (FSCD 2016). Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik (2016)
Libal, T., Steen, A.: Towards a substitution tree based index for higher-order resolution theorem provers. In: PAAR 2016. CEUR Workshop Proceedings, vol. 1635 (2016)
Meng, J., Paulson, L.C.: Translating higher-order clauses to first-order clauses. J. Autom. Reason. 40(1), 35–60 (2008)
Miller, D.: Unification of simply typed lambda-terms as logic programming. In: Logic Programming Conference, pp. 255–269. MIT Press (1991)
Paulson, L.C., Blanchette, J.C.: Three years of experience with sledgehammer, a practical link between automatic and interactive theorem provers. In: IWIL 2010, vol. 2, pp. 1–11 (2010)
Pientka, B.: Higher-order term indexing using substitution trees. ACM Trans. Comput. Logic 11(1), 6:1–6:40 (2009)
Prehofer, C.: Decidable higher-order unification problems. In: Bundy, A. (ed.) CADE 1994. LNCS, vol. 814, pp. 635–649. Springer, Heidelberg (1994). https://doi.org/10.1007/3-540-58156-1_46
Schmidt-Schauß, M., Schulz, K.U.: Decidability of bounded higher-order unification. J. Symb. Comput. 40(2), 905–954 (2005)
Snyder, W., Gallier, J.: Higher-order unification revisited: complete sets of transformations. J. Symb. Comput. 8(1–2), 101–140 (1989)
Steen, A.: Extensional Paramodulation for Higher-Order Logic and its Effective Implementation Leo-III. Ph.D. thesis, Freie Universität Berlin (2018)
Steen, A., Benzmüller, C.: The higher-order prover Leo-III. In: Galmiche, D., Schulz, S., Sebastiani, R. (eds.) IJCAR 2018. LNCS (LNAI), vol. 10900, pp. 108–116. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-94205-6_8
Stump, A., Sutcliffe, G., Tinelli, C.: StarExec: a cross-community infrastructure for logic solving. In: Demri, S., Kapur, D., Weidenbach, C. (eds.) IJCAR 2014. LNCS (LNAI), vol. 8562, pp. 367–373. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-08587-6_28
Sutcliffe, G.: The TPTP problem library and associated infrastructure, from CNF to TH0, TPTP v6.4.0. J. Autom. Reason. 59(4), 483–502 (2017)
Vukmirović, P., Blanchette, J.C., Cruanes, S., Schulz, S.: Extending a brainiac prover to lambda-free higher-order logic. In: Vojnar, T., Zhang, L. (eds.) TACAS 2019. LNCS, vol. 11427, pp. 192–210. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17462-0_11
Acknowledgements
Thanks to Jasmin Blanchette, Alexander Bentkamp, Simon Cruanes and Petar Vukmirović for many discussions on aspects of this research. A big thanks to the Matryoshka team as a whole for sharing their benchmarks. We would also like to thank Andrei Voronkov, Michael Rawson, Alexander Steen, the maintainers of StarExec and the anonymous paper reviewers. Special thanks to Martin Riener for proof-reading the paper. The first author thanks the family of James Elson for funding his research.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
A Restricted Combinatory Unification Is Terminating
A Restricted Combinatory Unification Is Terminating
We prove the termination of an algorithm identical to RCU, except that reductions can be performed at all positions. That RCU is terminating follows immediately. A straight-forward corollary of this is that RCU is incomplete.
Lemma 6
For any (finite) system \(\mathcal {S}\), if there exists an infinite RCU computation path on \(\mathcal {S}\), then there exists a system \(\mathcal {S}'\) such that \(\mathcal {S} \Longrightarrow ^* \mathcal {S}'\) and there exists an infinite computation path on \(\mathcal {S}'\) that does not include the Eliminate or Split transforms.
Proof
Both Eliminate and Split reduce the number of unsolved variables in \(\mathcal {S}\). As \(\mathcal {S}\) is finite, it can only contain a finite number of unsolved variables. A case analysis of the other rules shows that either they reduce the number of unsolved variables or leave it unchanged. Thus Split and Eliminate can only be carried out a finite number of times. \(\square \)
Based on Lemma 6, to prove that RCU is terminating, it suffices to prove that RCU without the eliminate and split transforms is terminating. Call the resulting set of transformation rules RCU−. Next a result analogous to Lemma 6 is proved with respect to the HeadNarrow transformation.
Definition 4
(Size). The size of a type \(\sigma \) is defined inductively as follows:
-
\(\sigma \) is atomic, the \(size(\sigma ) = 0\)
-
\(\sigma = \alpha \rightarrow \beta \), then \(size(\sigma ) = size(\alpha ) + size(\beta ) + 1\)
For a term t, its type is denoted by \(\tau (t)\)
Intuitively, \(size(\sigma )\) is the number of ‘\(\rightarrow \)’s in \(\sigma \).
Lemma 7
For any (finite) system \(\mathcal {S}\), if there exists an infinite RCU− computation path on \(\mathcal {S}\), then there exists a system \(\mathcal {S}'\) such that \(\mathcal {S} \Longrightarrow ^* \mathcal {S}'\) and there exists an infinite computation path on \(\mathcal {S}'\) that does not include the head narrow transform.
Proof
Consider the following measure on systems:
Where the pairs are compared lexicographically and \(\# \mathcal {S}\) denotes the number of  variables in \(\mathcal {S}\) or equivalently, the cardinality of
variables in \(\mathcal {S}\) or equivalently, the cardinality of  . The transformation rules of RCU−, other than head narrow, keep this measure constant or reduce it. HeadNarrow reduces the measure, so there can only be a finite number of applications of head narrow. The former claim is demonstrated for a number of HeadNarrow steps:
. The transformation rules of RCU−, other than head narrow, keep this measure constant or reduce it. HeadNarrow reduces the measure, so there can only be a finite number of applications of head narrow. The former claim is demonstrated for a number of HeadNarrow steps:
-
1.
KX-narrow. For a variable X to be eligible for a KX-narrow step, it must have type \(\alpha \rightarrow \beta \). It is replaced by a term \(\varvec{\mathsf {K}}_{\beta \rightarrow \alpha \rightarrow \beta } X'_{\beta }\). Clearly \(size(\tau (X')) < size(\tau (X))\) and so the first item of the measure is reduced.
-
2.
BX-narrow. For a variable X to be eligible for a BX-narrow step, it must have type \((\alpha \rightarrow \beta ) \rightarrow \alpha \rightarrow \gamma \). It is replaced by a term \(\varvec{\mathsf {B}}_{(\beta \rightarrow \gamma ) \rightarrow (\alpha \rightarrow \beta ) \rightarrow \alpha \rightarrow \gamma } X'_{\beta \rightarrow \gamma }\). Again \(size(\tau (X')) < size(\tau (X))\) and so the first item of the measure is reduced.
-
3.
CX-narrow. In this case, the size of the type of the variable being narrowed is not reduced. For a variable X to be eligible for a CX-narrow step, it must have type \(\alpha \rightarrow \beta \rightarrow \gamma \). It is replaced by a term \(\varvec{\mathsf {C}}_{(\beta \rightarrow \alpha \rightarrow \gamma ) \rightarrow \alpha \rightarrow \beta \rightarrow \gamma } X'_{\beta \rightarrow \alpha \rightarrow \gamma }\). Here \(size(\tau (X')) = size(\tau (X))\). However, each CX-narrow step replaces a
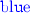 variable with a
variable with a  variable and therefore the second item of the measure is reduced. \(\square \)
variable and therefore the second item of the measure is reduced. \(\square \)
Based on Lemma 7 to prove that RCU− is terminating, it suffices to prove that RCU− without the HeadNarrow transformation is terminating. This is precisely Dougherty’s VT transformations which he has proven to be terminating in [11]. Therefore we have:
Theorem 2
Every sequence of RCU transformations terminates.
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Bhayat, A., Reger, G. (2019). Restricted Combinatory Unification. In: Fontaine, P. (eds) Automated Deduction – CADE 27. CADE 2019. Lecture Notes in Computer Science(), vol 11716. Springer, Cham. https://doi.org/10.1007/978-3-030-29436-6_5
Download citation
DOI: https://doi.org/10.1007/978-3-030-29436-6_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-29435-9
Online ISBN: 978-3-030-29436-6
eBook Packages: Computer ScienceComputer Science (R0)


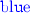 variable with a
variable with a  variable and therefore the second item of the measure is reduced.
variable and therefore the second item of the measure is reduced.