Abstract
This chapter is devoted to the basic parallel computing laws.
This chapter is devoted to the basic parallel computing laws.
3.1 The RAM and PRAM Models
A computing system model called the random access machine (RAM) [10, 45] is widely used for the analysis of program performance. We list here the main properties of the RAM.
The system running in the RAM model consists of a processor, a memory access device (a system bus), and a memory consisting of a finite number of cells (Fig. 3.1). The processor executes successively the instructions of a program Π; in doing so, it executes arithmetic and logical operations and reads and writes data to and from the memory. It is postulated that each instruction is executed in a fixed interval of time.
A random access operation of the processor consists of three stages:
-
1.
Reading of data from the memory into one of its registers r i, where \({1\leqslant i\leqslant N}\).
-
2.
Executing an arithmetic or logical operation on the contents of its registers.
-
3.
Writing of data from a register r j, where \(1\leqslant j\leqslant N\), into some memory cell.
It is assumed that the execution of the three above steps takes time Θ(1). (The function Θ(f(n)) is used for estimation of the execution time of an algorithm as a function of the size n of its input data [13, 22]. Thus, for example, Θ(n 2) indicates a quadratic dependence, Θ(log2n) indicates a logarithmic dependence, and Θ(1) indicates the absence of a dependence on the input data size. The estimation of the execution time of algorithms is described in more detail in Appendix A.)
One of the most widely used models of parallel computer systems is the parallel random access machine (PRAM ) [45, 59]. The PRAM combines p processors, a shared memory, and a control device that transmits instructions from a program Π to the processors (Fig. 3.2).
An important feature of the PRAM is the limited access time of any of the system’s processors to a random memory cell. As in the case of the RAM , a step of an algorithm corresponds to three processor operations:
-
1.
Reading by a processor P i from the j-th memory cell.
-
2.
Executing an arithmetic or logical operation by processor P i on the contents of its registers.
-
3.
Writing of data into the k-th memory cell.
We emphasize once again that a step of an algorithm is executed in time Θ(1).
Simultaneous access of two or more processors to the same memory cell leads to access conflicts . These are subdivided into read and write conflicts .
If multiple processors attempt to read data from one cell, then two options for further operations are possible:
-
1.
Exclusive read (ER). Only one processor is allowed to read at a given time, otherwise an error occurs in the program.
-
2.
Concurrent read (CR). The number of processors accessing the same memory cell is not limited.
If more than one processor attempts to write data to one address, then two options exist:
-
1.
Exclusive write (EW). Only one processor is allowed to write to a given cell at a particular moment in time.
-
2.
Concurrent write (CW). Multiple processors have simultaneous access to a single memory cell.
The following are the options for what rule a processor (or processors) follows to write a record in the latter case [37, 45, 59]:
-
Record of a general value. All processors ready to make a record in a single memory cell must record the same value for all of them, otherwise the recording instruction is considered to be erroneous.
-
Random choice. The processor that executes the recording operation is chosen randomly.
-
Prioritized recording. Each of the competing processors is assigned a certain priority, such as the value of its computation, and only the value that comes from the processor with the highest or lowest priority (as determined in advance) is retained.
-
Mixed choice. All processors provide values for the recording, from which by some operation a result (e.g., the sum of the values or the maximum value) is created, which is then recorded.
The classification of PRAM models by conflict resolution method is shown in Fig. 3.3. EREW systems have significant limitations imposed on the work that they can do with memory cells. On the other hand, and CREW , ERCW , and CRCW systems with a large number of processors are difficult to construct for technical reasons, since the number of cores that can simultaneously access a certain memory segment is limited. However, there is an important and somewhat unexpected result that makes it possible to simulate the work of a CRCW machine on a system built in accordance with the EREW principle [71].
Emulation Theorem
Let there be an algorithm for a CRCW machine that solves a certain problem with a parameter of size N in time T(N), using p processors. Then there exists an algorithm for the same problem on an EREW system with p processors which can be executed in time O(T(N)log2N). (The size of the memory of the PRAM must be increased by O(p) times.)
Unlike the case for the RAM model, the main measure of the complexity of algorithms for multiprocessor computer systems is the execution time of the algorithm. We introduce the following notation: T 1(N) is the time required by a sequential algorithm to solve a problem, the complexity of which is estimated by the parameter N; and T p(N) is the time required by a parallel algorithm on a machine with p processors, where p > 1. Since it follows from the definition of the RAM that each operation requires a certain time, the value of T 1(N) is proportional to the number of computational operations in the algorithm used.
Note that the minimum execution time of an algorithm is observed in the case p →∞. A hypothetical computer system with an infinitely large number of available processors is called a paracomputer . The asymptotic complexity of an algorithm for a paracomputer is denoted by T ∞(N).
Note
Brief information about methods of mathematical estimation of the properties of algorithms is provided in Appendix A.
In the analysis of parallel algorithms, the concepts of speedup , efficiency, and cost are widely used. First of all, we need to pay attention to how quickly the problem can be solved by comparison with solution on a single-processor machine.
The speedup, S p(N), obtained by using a parallel algorithm on a machine with p processors is given by
This is a measure of the productivity gain compared with the best sequential algorithm. The greater the speedup, the greater the difference in the problem-solving time between a system with a single processor and a multiprocessor system.
The efficiency, E p(N), of the use of the processors by a particular parallel algorithm is
The cost, C p(N), is measured as the product of the time for the parallel solution to the problem and the number of processors used: C p(N) = pT p(N). A cost-optimal algorithm is characterized by a cost that is proportional to the complexity of the best sequential algorithm, and in this case
Example 3.1
The running time of a sequential version of some algorithm \(\mathcal {A}\) is T 1(N) = 2Nlog2(N) τ, where N is the input data size and τ is the execution time for one computing operation. Assuming that the algorithms allows maximal parallelization, i.e., the running time on a computing system with p processors is T p(N) = T 1(N)∕p, calculate the running time of algorithm \(\mathcal {A}\) in the case N = 64, p = 8.
Solution
The problem is solved by direct substitution of the given data into the relation  :
:
Using the numerical values, we obtain
\(\square \)
The limiting values of the speedup and efficiency , as follows directly from their definitions, are S p = p and E p = 1. The maximum possible value of S p is achieved when it is possible to uniformly distribute the computation across all processors and no additional operations are required to provide communication between the processors during the running of the program and to combine the results. Increasing the speedup by increasing the number of processors will reduce the value of E p, and vice versa. Maximum efficiency is achieved by using only a single processor (p = 1).
We will not discuss here the superlinear speedup effects that may arise in models other than the PRAM for several reasons [81]:
-
the sequential algorithm used for comparison in those models is not optimal;
-
the multiprocessor system architecture has specific features;
-
the algorithm is nondeterministic;
-
there are significant differences in the volume of available main memory when the sequential algorithm is required to access a relatively “slow” peripheral memory, and the parallel algorithm uses only “fast” memory.
Many of the algorithms described below require the presence of a sufficiently large number of processors. Fortunately, this does not limit their practical application, since for any algorithm in the PRAM model there is the possibility of modification of it for a system with a smaller number of processors. The latter statement is called Brent’sFootnote 1 lemma [9, 13, 43].
Brent’s Lemma
Let a parallel algorithm \(\mathcal {A}\) to solve some problem be executed on a RAM in a time T 1, and on a paracomputer in a time T ∞. Then there exists an algorithm \(\mathcal {A}'\) for the solution of the given problem such that on a PRAM with p processors it is executed in a time T(p), where \(T(p)\leqslant T_\infty +{(T_1-T_\infty )}/{p}\).
The proof of Brent’s lemma is given in the solution to Problem 3.8.
Any parallel program has a sequential part which is made up of input/output operations, synchronization, etc. Assume that, in comparison with the sequential method of solution, the following are true:
-
1.
When the problem is divided into independent subproblems, the time required for interprocessor communication and union of the results is negligibly small.
-
2.
The running time of the parallel part of the program decreases in proportion to the number of computational nodes.
Under these assumptions, an estimate of the value of S p is known.
Amdahl’s Law
Let f be the proportion of sequential calculations in an algorithm \(\mathcal {A}\). Then the speedup when \(\mathcal {A}\)is run on a system of p processors satisfies the inequality
To prove this, we calculate the time required for executing the algorithm on a multiprocessor. This time consists of the time for sequential operations, fT 1, and the time for operations that can be parallelized, and is equal to T p = fT 1 + ((1 − f)∕p)T 1. Therefore, the upper limit on the speedup can be represented as
which proves Amdahl’s law .
The inequality \(S_p\leqslant \left ( S_p \right )_{\text{max}}\) shows that the existence of sequential computations that cannot be parallelized imposes a restriction on S p. Even when a paracomputer is used, the speedup cannot exceed the value S ∞ = 1∕f.
Figure 3.4 shows the dependence of S p on the number of processors p for typical values of the parameter f in computing tasks.
It is found empirically that, for a wide class of computing tasks, the proportion of sequential computations decreases with increasing size of the input data of the task. Therefore, in practice, the speedup can be increased by increasing the computational complexity of the task being performed.
Despite the fact that the PRAM model is in widespread use, we should not forget its limitations. In particular, the possibility of different data transfer rates for different processors in specific computer system architectures is completely ignored.
Let us consider an example that illustrates Amdahl’s law .
Example 3.2
Suppose that a researcher needs to solve a resource-intensive computing problem \(\mathcal {Z}\). A sequential version of a program that solves the problem \(\mathcal {Z}\) is executed in time T 1. A parallel version of the program contains a fraction f of sequential computations, 0 < f < 1. A third-party organization provides access to a computing system consisting of p processors (1 < p < 512), and the cost of access to the system is \(w_p(t)=\alpha \ln p + \beta t^{\gamma }\), where α, β, γ are constants, and t is the time that the system works on the researcher’s problem. How many processes should be used in order to minimize the cost of working on the problem \(\mathcal {Z}\)? Let us perform computations for the following values of the parameters:
Solution
According to Amdahl’s law, the speedup when using a computing system consisting of p processors is equal to
hence, the time required to work on the parallel version of the problem \(\mathcal {Z}\) will be
According to the statement of the problem, the cost function w p(t) depends on the number of separate computational nodes and on the time required to work on the problem: \(w_p(t)=\alpha \ln p+\beta t^{\gamma }\). By substituting the above value of T p, we determine the following function for the cost depending on the parameter p:
Now, we investigate the function w p for the presence of a minimum in the interval (1, 512). As is well known from any course in mathematical analysis, the minimum points should be sought from among the roots of the equation dw p∕dp = 0. By direct differentiation, we obtain

Because the equation dw p∕dp = 0 cannot be solved analytically, numerical methods must be used. We can show that there is only one minimum for p ∈ (1, 512). We can find its abscissa by a bisection method (see Problem 3.9).
A program in the language C that performs a computation of the minimum of the cost function is shown in Listing 3.1.
Listing 3.1
1 #include <stdio.h>
2 #include <stdlib.h>
3 #include <math.h>
4
5 #define PMIN 1.0 // PMIN and PMAX
6 #define PMAX 512.0 // are endpoints
7 // of the interval
8 #define EPS 1.0e-14 // zero of function
9 // determination accuracy
10
11 double f,T1,alpha,beta,gamma; // cost function
12 // parameters
13
14 double fprime(double p) // derivative
15 // of cost function
16 {
17 double temp = pow(f+(1-f)/p,gamma-1.0);
18 return alpha/p - \
19 beta*gamma*pow(T1,gamma)*(1-f)*temp/(p*p);
20 }
21
22 double bisection(double func(double), \
23 double x1, double x2,\
24 const double epsilon)
25 {
26 double xmid;
27 while ( fabs(x2 - x1) > epsilon )
28 {
29 xmid = (x1 + x2) / 2;
30 if (func(x2) * func(xmid) < 0.0)
31 x1 = xmid;
32 else
33 x2 = xmid;
34 }
35 return (x1 + x2) / 2;
36 }
37
38 int main(void)
39 {
40 int pz; // zero of function fprime(p)
41 FILE * fp;
42
43 if ((fp = fopen( "input.txt", "r")) == NULL)
44 {
45 perror( "\nError opening file " \
46 "\"input.txt\"");
47 exit(EXIT_FAILURE);
48 }
49 fscanf(fp, "%lf %lf %lf %lf %lf", \
50 &f,&T1,&alpha,&beta,&gamma);
51 fclose(fp);
52
53 pz = \
54 (int)round(bisection(fprime,PMIN,PMAX,EPS));
55 if ( pz<PMIN || pz>PMAX )
56 {
57 perror( "\nError determining zero " \
58 "of function fprime(p)");
59 exit(EXIT_FAILURE);
60 }
61 if ((fp = fopen( "output.txt", "w")) == NULL)
62 {
63 perror( "\nError opening file " \
64 "\"output.txt\"");
65 exit(EXIT_FAILURE);
66 }
67 else
68 if (fprintf(fp, "%d",pz)<=0)
69 // fprintf returns the number of written
70 // characters
71 {
72 perror( "\nError writing to file " \
73 "\"output.txt\"");
74 fclose(fp);
75 exit(EXIT_FAILURE);
76 }
77 fclose(fp);
78 printf( "The answer is written to file " \
79 "\"output.txt\"");
80 return 0;
81 }
The program reads the parameters f, T 1, α, β, γ from a text file input.txt. The function bisection( ) realizes the binary division algorithm and finds a zero of the function func( ) in the interval (x 1, x 2) with an accuracy of epsilon. Into the file output.txt, after execution of the program, the number 64 will be written; i.e., with a number of processors p = 64, the cost function with the parameters listed in the example will be minimized. \(\square \)
Note
Notice the method of organizing the data streams in the program when the data are read from a text file, for example input.txt, and when the result of the program is put into a text file, for example output.txt (or into several files, where necessary). The method described is generally accepted for high-performance computations since it is convenient when working with remote computational resources. Moreover, when a program is used as part of a suite of programs, storing the results of the computation in a file allows one, when necessary, to visualize the data and to pass them as input data to another program for processing.
3.2 The “Operations–Operands” Graph
Let us recall some definitions from graph theory that we require for the following presentation [2, 6].
A directed graph, or digraph, is a pair D = (V, E), where V is a finite set of vertices and E is a relation on V . The elements of the set E are called directed edges or arcs . An arc that connects a pair (u, v) of vertices u and v of a digraph D is denoted by uv.
A path of length n in a digraph is a sequence of vertices v 0, v 1, …, v n, each pair v i−1v i (i = 1, …, n) of which forms an arc. A sequence of vertices v 0, v 1, …, v n where the first vertex v 0 coincides with the last one, i.e., v 0 = v n, and where there are no other repeated vertices forms a circuit .
The outdegree of a vertex v of a digraph D is the number of arcs d +(v) of the digraph going out from v, and the indegree of that vertex is the number of arcs d −(v) going into it.
For example, for the directed graph D with five vertices a, b, c, d, and e whose diagram is presented in Fig. 3.5, the following relations are fulfilled:
The structure of an algorithm for solving a problem may be graphically represented as a directed graph called an “operations–operands” graph. It is an acyclic digraph. We denote it by D = (V, E), where V is a set of vertices representing the operations performed in the algorithm, and E is a set of edges. An edge v iv j ∈ E if and only if the operation numbered j uses the result of the operation numbered i. Vertices \(v^{(\text{in})}_k\), where \(k\in \mathbb {N}\), with indegree \(\forall k\;d^-(v^{(\text{in})}_k)=0\) are used for data input operations, and vertices \(v^{(\text{out})}_l\), \(l\in \mathbb {N}\), with outdegree \(\forall l\;d^+(v^{(\text{out})}_l)=0\) correspond to output operations (Fig. 3.6).
If we assume that the computations at each vertex of the digraph D using a RAM take a constant time τ, the algorithm execution time on a paracomputer is equal to
where C (i, j) is the path \(v^{(\text{in})}_i\), …, \(v^{(\text{out})}_j\), and the maximum is taken with respect to all possible pairs (i, j). In other words, the time T ∞ is proportional to the number of vertices in the maximal path connecting vertices \(v^{(\text{in})}_i\) and \(v^{(\text{out})}_j\) for all i and j.
3.3 Bernstein’s Conditions
In most programming languages, as is well known, the program code consists of a sequence of statements . One of the principal tasks that arises when working with parallel computing systems is the investigation of the possibility of independent execution of statements using the resources of parallelism.
We refer to two statements u and v as independent or commutative if after permutation of them in the program code the program output remains unchanged for any input data [19, 20]. The sufficient conditions for independence of program code sections are known as Bernstein’s Footnote 2 conditions.
Suppose that statements u and v perform data reading and writing at known addresses in the random access memory of a computing system. Let R(u) be the set of memory cells (more precisely, memory cell addresses) from which information is read during execution of the statement u. Further, let W(u) be the set of memory cells (more precisely, memory cell addresses) into which data are written. R(u) and W(u) are often called the input object set and the output object set, respectively, of statement u [54].
Bernstein’s Conditions [7, 19]
Two statements u and v are independent and their order does not influence the program output if the following equalities are fulfilled:
-
1.
\(W(u)\cap W(v) = \varnothing \).
-
2.
\(W(u)\cap R(v) = \varnothing \).
-
3.
\(R(u)\cap W(v) = \varnothing \).
The above equalities are sufficient but not necessary conditions for the commutativity of two statements (see Problem 3.13).
If, for two statements u and v, at least one of the equalities in Bernstein’s conditions is violated, the notation  is used. In this case it is said that u and v have a dependency relationship
.
is used. In this case it is said that u and v have a dependency relationship
.
Note that the equalities 1–3 forming Bernstein’s conditions are fulfilled independently from each other. In this connection, special notation for violation of each of these equalities is used [54]:
-
1.
If the first condition is violated and \(W(u)\cap W(v) \neq \varnothing \), then it is said that between statements u and v there exists an output dependency ,
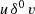 .
. -
2.
If the second condition is violated and \(W(u)\cap R(v) \neq \varnothing \), then u and v are in a relationship of true or flow dependency ,
 .
. -
3.
If the third condition is violated and \(R(u)\cap W(v) \neq \varnothing \), then between statements u and v there exists an antidependency ,
 .
.
Using this notation, a dependency relationship can be presented symbolically in the form

Example 3.3
Investigate the possibility of parallelizing the following program code sections, for which Bernstein’s conditions are violated:
-
1.
o 1: x = y + 1; o 2: x = z * 2;
-
2.
p 1: x = y + 1; p 2: z = x * x;
-
3.
q 1: x = y + 1; q 2: y = z / 2;
Solution
-
1.
For this pair of statements, there exists an input data dependency \(W(o_1)\cap W(o_2)=\{\mathtt {x}\}\cap \{\mathtt {x}\}=\{\mathtt {x}\}\neq \varnothing \), i.e.,
 . Usually, input dependencies allow parallelizing after renaming of the variables. In our case, the following pair \((o^{\prime }_1,o^{\prime }_2)\) will satisfy Bernstein’s conditions:
. Usually, input dependencies allow parallelizing after renaming of the variables. In our case, the following pair \((o^{\prime }_1,o^{\prime }_2)\) will satisfy Bernstein’s conditions:\(o^{\prime }_1\): x1 = y + 1; \(o^{\prime }_2\): x2 = z * 2;
-
2.
Since for the pair (p 1, p 2) we have \(W(p_1)\cap R(p_2)=\{\mathtt {x}\}\cap \{\mathtt {x}\}=\{\mathtt {x}\}\neq \varnothing \), the program code contains a true dependency
 , and no parallelizing is possible in this case.
, and no parallelizing is possible in this case. -
3.
One and the same variable in the given code section is used first in q 1 and then in q 2: \(R(q_1)\cap W(q_2)=\{\mathtt {y}\}\cap \{\mathtt {y}\}=\{\mathtt {y}\}\neq \varnothing \). There exists an antidependency
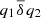 . The code section under consideration can be parallelized if we copy the value of the variable y into the local memories of the computational nodes, and only after that begin execution of the statements q
1 and q
2. \(\square \)
. The code section under consideration can be parallelized if we copy the value of the variable y into the local memories of the computational nodes, and only after that begin execution of the statements q
1 and q
2. \(\square \)
Analysis of Example 3.3 shows that dependencies of the type  and
and  appear not because the data are passed from one statement to another, but because the same memory area is used in several places. Output dependencies and antidependencies can often be eliminated by renaming some variables and, additionally, copying data [54].
appear not because the data are passed from one statement to another, but because the same memory area is used in several places. Output dependencies and antidependencies can often be eliminated by renaming some variables and, additionally, copying data [54].
Example 3.4
Enumerate the dependencies between the statements in the following program code section:
- o 1 ::
-
a = a + 2;
- o 2 ::
-
b = a + d / 2;
- o 3 ::
-
c = 2 * c;
- o 4 ::
-
a = a + c + 1;
Solution
We write out the output object sets W(o i) and input object sets R(o i) for i = 1, 2, 3, 4:
For each pair of statements (o i, o j), where i, j = 1, 2, 3, 4 and i < j, we construct the intersections W(o i) ∩ W(o j), W(o i) ∩ R(o j), and R(o i) ∩ W(o j). Those intersections that are not empty sets lead to dependencies between statements:

As a result, we obtain the following dependencies in the program code section considered:

\(\square \)
In parallel programming, Bernstein’s conditions are used to obtain a mathematically correct proof that after applying a parallelization procedure to a sequential program code the program output remains unchanged. Programs for numerical computation usually require only storing of the final answer; in other words, identity of the output files that are created is needed. However, as can be seen, the set of parallel program suites extends further than just numerical computation programs. There exist continuously functioning programs, for example operating systems, and in this connection a more detailed consideration of data change in the parallel system’s random access memory is needed. Not only the information at a fixed moment in time, but also data sets at previous moments in time are of great importance.
Let us introduce the notion of a memory content history —a time-ordered set of vectors made up of all the data in the computing system’s memory. Using this definition, we can formulate the statement permutation theorem, which is the mathematical basis for program code parallelization and optimization [19].
Statement Permutation Theorem
Let a computing device perform sequentially a program made up of an ordered collection of statements U = {u 1, u 2, …, u n}, where \(n\in \mathbb {N}\) is the number of statements, or the program size. We permute the components of the vector U in such a way that all dependent statements preserve their relative order, i.e.,
Then the memory content history of the computing system will not change as a result of this permutation.
The proof of this theorem is based on the method of mathematical induction (see Problem 3.15).
In practical applications, Bernstein’s conditions are relatively easily checked for computational operations with scalar values and arrays. Considerable difficulties in checking arise, however, if the program code uses operations with pointers . In the general case, there is no algorithm able to determine the possibility of parallel execution of two program code sections [7].
Theorem of Undecidability of the Possibility of Parallelism
There exists no algorithm that can determine the possibility of parallel execution of two arbitrary program code sections.
In order to prove the theorem, we use the method of “proof by contradiction.” Suppose that there exists an algorithm as described in the statement of the theorem. We can us show that it entails the solution of an arbitrary TuringFootnote 3 machine halting problem [61, 69].
Consider a Turing machine T, whose input tape stores a natural number N. We denote by N i the number formed by the i highest-order digits of the number N.
Let a program Π execute the following operations:
-
S1:
The value of N i is written at the address A. If the Turing machine T halts after N or fewer steps, then the value \(N_i^2\) is stored at the address A; otherwise, the value written in A is stored at the address Z 1.
-
S2:
The value written in A is stored at the address Z 2.
Let us analyze the operation of the program Π. If T does not halt for any input data N, then S
1 and S
2 can be executed in parallel. Otherwise, for some N, the value of \(N_i^2\) is stored at the address Z
2 during the operation S
2. Then S
1 and S
2 must be executed sequentially, since  .
.
We obtain the result that the problem of determining the possibility of parallel execution of the parts of code S 1 and S 2 is equivalent to the arbitrary Turing machine halting problem , but this problem, as is well known, is undecidable [61, 69]. Hence, the theorem of undecidability of the possibility of parallelism is proved.
The practical importance of Bernstein’s conditions is not limited to the field of parallel programming. One of the methods for program code optimization consists in changing the order of execution of some statements or code sections . For example, the use of data located as near as possible to the place of their description in the program increases the performance of the computing system owing to active use of cache memory . As is well known, when the central processor addresses random access memory, the request is first sent to cache memory . If the required data are available, the cache memory sends them quickly, to a processor register. Hence, a change in the order of execution of some statements can increase the speed of the computing system.
3.4 Test Questions
-
1.
Describe the RAM model.
-
2.
In what why is the PRAM model a generalization of the RAM model?
-
3.
Define the term “access conflict.”
-
4.
How is the PRAM model classified by conflict resolution method?
-
5.
Formulate the emulation theorem.
-
6.
What is the notion of a “paracomputer” introduced for?
-
7.
What values are used for the analysis of parallel algorithms?
-
8.
What are the limiting values of the speedup and efficiency equal to?
-
9.
Formulate Brent’s lemma.
-
10.
How is Amdahl’s law used for estimation of the speedup?
-
11.
What peculiarities of multiprocessor computing systems are not taken into account in the PRAM model?
-
12.
Describe the “operations–operands” graph.
-
13.
State Bernstein’s conditions.
-
14.
Describe clearly the role of the statement permutation theorem in parallel programming.
3.5 Problems
-
3.1.
The execution time of a sequential version of some algorithm \(\mathcal {A}\) is T 1(N) = 2Nlog2(N) τ, where N is the input data size and τ is the execution time of one computational operation. Supposing that the algorithm allows maximal parallelizing, i.e., the execution time on a computation system with p processors is T p(N) = T 1(N)∕p, calculate the execution time of the algorithm \(\mathcal {A}\) in the following cases:
-
(a)
N = 32, p = 4;
-
(b)
N = 32, p = 16.
-
(a)
-
3.2.
Solve the previous problem for an algorithm \(\mathcal {B}\) with an exponential asymptotic complexity T 1(N) = 2Nτ.
-
3.3.
Let the proportion of sequential computation in a program be f = 1∕10. Calculate the maximum speedup \(\left ( S_p \right )_{\text{max}}\) of the program on a computation system with p processors taking into account Amdahl’s law .
-
3.4.
Let the proportion of sequential computation in a program be f = 1∕100. Calculate the maximum speedup S ∞ of the program taking into account Amdahl’s law .
-
3.5.
Let the speedup for some parallel algorithm \(\mathcal {A}\) executed on a system with p processors be S p. Taking into account Amdahl’s law, calculate the speedup when the algorithm \(\mathcal {A}\) is executed on a system with p′ processors.
-
3.6.
Consider a computational algorithm \(\mathcal {A}\) consisting of two blocks \(\mathcal {A}_1\) and \(\mathcal {A}_2\), where the second block can start execution only after completion of the first. Let the proportions of sequential computation in \(\mathcal {A}_1\) and \(\mathcal {A}_2\) be f 1 and f 2, respectively, and let the execution time of \(\mathcal {A}_2\) in the sequential mode exceed the sequential execution time of \(\mathcal {A}_1\) by η times. Calculate the maximum speedup of the algorithm \(\mathcal {A}\) achievable on a computation system with p processors.
-
3.7.
Draw a graph of the maximum efficiency \(\left ( E_p \right )_{\text{max}}\) of use of the processors by a parallel algorithm as a function of the number of computational nodes p taking into account Amdahl’s law , if the proportion of sequential computation is equal to:
-
(a)
f = 1∕10;
-
(b)
f = 1∕50.
-
(a)
-
3.8.
* Prove Brent’s lemma .
-
3.9.
Give a detailed explanation of how a numerical solution of the equation dw p∕dp = 0 in Example 3.2 can be obtained.
-
3.10.
Suppose that a researcher needs to solve a resource-intensive computing problem \(\mathcal {Z}\). A sequential version of a program that solves the problem \(\mathcal {Z}\) is executed in time T 1. A parallel version contains a proportion f of sequential computation, 0 < f < 1. A third-party organization provides access to a computing system consisting of p processors (1 < p < 512), and the cost of access to the system is \(w_p(t)=\alpha \ln p + \beta t^{\gamma }\), where α, β, γ are constants and t is the time that the system works on the researcher’s problem. How many processors should be used in order to minimize the cost of working on the problem \(\mathcal {Z}\)? Perform calculations for the following values of the parameters:
-
(a)
f = 0.1, T 1 = 10.0, α = 1.70, β = 11.97, γ = 1.9;
-
(b)
f = 0.1, T 1 = 10.0, α = 2.73, β = 8.61, γ = 1.1;
-
(c)
f = 0.1, T 1 = 10.0, α = 2.17, β = 35.44, γ = 1.7.
-
(a)
-
3.11.
Solve Problem 3.10 for a cost function of the form w p(t) = αp + βt γ. Perform calculations for the following values of the parameters:
-
(a)
f = 0.1, T 1 = 10.0, α = 1.17, β = 3.84, γ = 1.9;
-
(b)
f = 0.1, T 1 = 10.0, α = 1.08, β = 9.31, γ = 1.9;
-
(c)
f = 0.1, T 1 = 10.0, α = 1.19, β = 35.90, γ = 1.8.
-
(a)
-
3.12.
Solve Problem 3.10 for a cost function of the form w p(t) = e αp + βt γ. Perform calculations for the following values of the parameters:
-
(a)
f = 0.1, T 1 = 10.0, α = 0.001, β = 10.62, γ = 1.9;
-
(b)
f = 0.1, T 1 = 10.0, α = 0.002, β = 2.70, γ = 1.8;
-
(c)
f = 0.1, T 1 = 10.0, α = 0.004, β = 4.40, γ = 1.1.
-
(a)
-
3.13.
Show that Bernstein’s conditions are not necessary conditions for the commutativity of two statements.
-
3.14.
List the dependencies between statements in the following program code section:
o 1: a = c - 1; o 2: b = a / 2 - 1; o 3: c = b + c / b; o 4: b = a * c + 1;
-
3.15.
* Prove the statement permutation theorem.
Notes
- 1.
Richard Peirce Brent (b. 1946), Australian mathematician and computer scientist.
- 2.
Gene Myron Amdahl (1922–2015), American computer scientist and computer technology expert.
- 3.
Arthur Jay Bernstein, an American researcher, is a specialist in the field of computing systems.
- 4.
Alan Mathison Turing (1912–1954), English mathematician and logician.
References
Anderson, J.A.: Discrete Mathematics with Combinatorics. Prentice Hall, Upper Saddle River (2003)
Bang-Jensen, J., Gutin, G.: Digraphs: Theory, Algorithms and Applications, 2nd edn. Springer Monographs in Mathematics. Springer, London (2008)
Bernstein, A.J.: Analysis of programs for parallel processing. IEEE Trans. Electromagn. Compat. EC-15(5), 757–763 (1966)
Brent, R.P.: The parallel evaluation of general arithmetic expressions. J. Assoc. Comput. Mach. 21(2), 201–206 (1974)
Breshears, C.: The Art of Concurrency. O’Reilly, Beijing (2009)
Cormen, T.H., Leiserson, C.E., Rivest, R.L., Stein, C.: Introduction to Algorithms, 3rd edn. MIT Press, Cambridge (2009)
Feautrier, P.: Bernstein’s conditions. In: Padua, D. (ed.) Encyclopedia of Parallel Computing. Springer Reference. Springer, Boston (2011)
Feautrier, P.: Dependences. In: Padua, D. (ed.) Encyclopedia of Parallel Computing. Springer Reference. Springer, Boston (2011)
Gonnet, G.H., Baeza-Yates, R.: Handbook of Algorithms and Data Structures: In Pascal and C, 2nd edn. International Computer Science Series. Addison-Wesley, Boston (1991)
Kruskal, C.P., Rudolph, L., Snir, M.: A complexity theory of efficient parallel algorithms. Theor. Comput. Sci. 71(1), 95–132 (1990)
McCool, M., Robison, A.D., Reinders, J.: Structured Parallel Programming: Patterns for Efficient Computation. Elsevier, Amsterdam (2012)
Miller, R., Boxer, L.: Algorithms Sequential and Parallel: A Unified Approach, 3rd edn. Cengage Learning, Boston (2013)
Padua, D.A., Wolfe, M.J.: Advanced compiler optimizations for supercomputers. Commun. ACM 29(12), 1184–1201 (1986)
Rauber, T., Rünger, G.: Parallel Programming for Multicore and Cluster Systems, 2nd edn. Springer, Berlin (2013)
Rosen, K.H., Michaels, J.G., Gross, J.L., et al. (eds.): Handbook of Discrete and Combinatorial Mathematics. Discrete Mathematics and Its Applications. CRC Press, Boca Raton (2000)
Shen, A., Vereshchagin, N.K.: Computable Functions. Student Mathematical Library, vol. 19. American Mathematical Society, Providence (2003)
Smith, J.R.: The Design and Analysis of Parallel Algorithms. Oxford University Press, New York (1993)
Wilkinson, B., Allen, M.: Parallel Programming Techniques and Applications Using Networked Workstations and Parallel Computers, 2nd edn. Pearson Prentice Hall, Upper Saddle River (2004)
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Kurgalin, S., Borzunov, S. (2019). Fundamentals of Parallel Computing. In: A Practical Approach to High-Performance Computing. Springer, Cham. https://doi.org/10.1007/978-3-030-27558-7_3
Download citation
DOI: https://doi.org/10.1007/978-3-030-27558-7_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-27557-0
Online ISBN: 978-3-030-27558-7
eBook Packages: Computer ScienceComputer Science (R0)








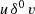 .
. .
. .
. . Usually, input dependencies allow parallelizing after renaming of the variables. In our case, the following pair
. Usually, input dependencies allow parallelizing after renaming of the variables. In our case, the following pair  , and no parallelizing is possible in this case.
, and no parallelizing is possible in this case.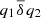 . The code section under consideration can be parallelized if we copy the value of the variable
. The code section under consideration can be parallelized if we copy the value of the variable