Abstract
We could start this section by considering directly the connecting vector and derive all the results. However the average – certainly the new – reader is not familiar with this concept and would possibly think that all is a matter of mathematical exercise. For this reason we shall start with the traditional velocity picture which is familiar to all and then we shall rederive the results using the connecting vector. Perhaps we should emphasize that in Special and especially in General Relativity the kinematics can be discussed only in the connecting vector approach.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
The assumption of nearness is necessary because otherwise there is no a linear connection between the velocities of the points P, Q. Here we have the first requirement for the definition of nearness.
- 2.
Note that we work on Newtonian Physics therefore time is absolute i.e. the same for all particles. This is not the case in relativistic theories.
- 3.
The replacement of d r with r means that we linearize the problem. That is relation (20.2) defines the d v P! The continua which satisfy this requirement are named Linear Continua. Not all continua are expected to be linear! In general we should write
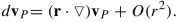
- 4.
It is easy to prove that \(\mathbf {(r\cdot \triangledown )(r}\cdot \triangledown )=\mathbf {(r\cdot \triangledown )}\) by writing \(\mathbf { (r\cdot \triangledown )=}\) \(x \frac {\partial }{\partial x}+y\frac {\partial }{\partial y}+z\frac {\partial }{ \partial z}.\) A shorter proof is the following. We write x μ ∂ μ for the term \(\mathbf {r\cdot \triangledown }\) and have:
$$\displaystyle \begin{aligned} (x^{\mu }\partial _{\mu })(x^{\nu }\partial _{\nu })v^{\rho }=(x^{\mu }\delta _{\mu }^{\nu }\partial _{\nu })v^{\rho }+x^{\mu }x^{\nu }\partial _{\mu }\partial _{\nu }v^{\rho }=(x^{\nu }\partial _{\nu })v^{\rho }+O(x^{\mu }x^{\nu }).\end{aligned} $$ - 5.
Nearness is understood as in the last section. That is, P is the origin of the coordinates and the position vector r Q of the point Q has components r Q = x i + y j+ z k where the quantities x, y, z are small in the sense that their mutual products can be neglected.
- 6.
Do not overlook the fact that we consider linear deformable bodies only!
- 7.
This condition defines the linear deformable body at the level of relative position vectors, thus completing the definition we gave previously in terms of the relative velocity.
- 8.
Note that we are dealing with Newtonian Kinematics therefore t is common for both points. In Relativity this is not possible!
- 9.
In the following we drop the index P from s P because P is arbitrary.
- 10.
We omit the term \(\frac {1}{2}\triangledown (\mathbf {r\cdot w}dt)\) because we are considering a rigid motion therefore the strain motion vanishes.
- 11.
The proof of this result is as follows. The term r ⋅ ( ω × r) =0 because r is normal to ( ω × r). From the identity of vector calculus
$$\displaystyle \begin{aligned} (\boldsymbol{A}\mathbf{\,\times\, B)\cdot }(\mathbf{C\times D)=\ }(\boldsymbol{A} \mathbf{\,\cdot\, C)\cdot }(\mathbf{B\cdot D)-}(\boldsymbol{A}\mathbf{\,\cdot\, D)\cdot }(\mathbf{B\cdot C)} \end{aligned}$$we have:
$$\displaystyle \begin{aligned} (\boldsymbol{\omega }\mathbf{\,\times\, r)\cdot }(\boldsymbol{\omega }\mathbf{ \,\times\, r)=\omega }^{2}r^{2}-(\boldsymbol{\omega }\cdot \mathbf{r)}^{2}=r^{2} \boldsymbol{\omega }^{2}(1-\cos ^{2}\theta )=\boldsymbol{\omega }^{2}r^{2}\sin ^{2}\theta .\end{aligned} $$ - 12.
A similar point of view seams to be taken in Cybernetics, although not justified so clearly. They say (see http://pespmc1.vub.ac.be/):
“Among the most elementary actions known to us are small displacements “in space”. We have put the quotes, because people have accustomed to imagine that some entity, called “space” exists as a primary reality, which creates the possibility of moving from one point of this space to another. Our analysis turns this notion topsy-turvy. Only actions constitute observable reality; space is nothing but a product of our imagination which we construct from small displacements, or shifts, of even smaller objects called points. If x is such a shift, then xx – the action x repeated twice – is a double shift, which we would call in our conventional wisdom a shift at the double distance in the same direction. On the other hand, we may want to represent a shift x as the result of another shift x’ repeated twice: x = x’x’. It so happens that we can make three different kinds of shifts, call them x, y, z, none of which can be reduced to a combination of the other two. At the same time any shift w can be reduced to a properly chosen combination of shifts x, y, z. So we say that our space has three dimensions.”
- 13.
The discussion is general and applies to linear spaces of any finite dimension.
- 14.
The formula \(t_{S}^{i}=\sigma _{ij}n^{j}\) is known as Cauchy stress formula.
- 15.
This is the experimental result of Pascal with perfect fluids.
- 16.
As we have said the strain is the “motion” of a Newtonian deformable body which remains after the global translation and the global rotation have been removed. Therefore under strain motion only the shape of the body changes. Because we have no rotation the stress tensor which produces the strain must be symmetric (otherwise it would produce couples, therefore rotation about the center of mass.)
- 17.
This observation takes us closely to the case of General Relativity.
- 18.
The principal directions of a positive definite metric for different real eigenvalues are normal (in the Euclidian sense) to each other.
- 19.
Or use the equation of the plane in vector form n ⋅ (r −r 0) = 0.
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Tsamparlis, M. (2019). The Physics of Newtonian Deformable Bodies: Newtonian Fluids. In: Special Relativity. Undergraduate Lecture Notes in Physics. Springer, Cham. https://doi.org/10.1007/978-3-030-27347-7_20
Download citation
DOI: https://doi.org/10.1007/978-3-030-27347-7_20
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-27346-0
Online ISBN: 978-3-030-27347-7
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)