Abstract
We address the problem of analyzing asynchronous event-driven programs, in which concurrent agents communicate via unbounded message queues. The safety verification problem for such programs is undecidable. We present in this paper a technique that combines queue-bounded exploration with a convergence test: if the sequence of certain abstractions of the reachable states, for increasing queue bounds k, converges, we can prove any property of the program that is preserved by the abstraction. If the abstract state space is finite, convergence is guaranteed; the challenge is to catch the point \(k_{\max }\) where it happens. We further demonstrate how simple invariants formulated over the concrete domain can be used to eliminate spurious abstract states, which otherwise prevent the sequence from converging. We have implemented our technique for the P programming language for event-driven programs. We show experimentally that the sequence of abstractions often converges fully automatically, in hard cases with minimal designer support in the form of sequentially provable invariants, and that this happens for a value of \(k_{\max }\) small enough to allow the method to succeed in practice.
Work supported by the US National Science Foundation under Grant No. 1253331, and by Microsoft Research India while hosting the second author for a sabbatical.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others

1 Introduction
Asynchronous event-driven (AED) programming refers to a style of programming multi-agent applications. The agents communicate shared work via messages. Each agent waits for a message to arrive, and then processes it, possibly sending messages to other agents, in order to collectively achieve a goal. This programming style is common for distributed systems as well as low-level designs such as device drivers [11]. Getting such applications right is an arduous task, due to the inherent concurrency: the programmer must defend against all possible interleavings of messages between agents. In response to this challenge, recent years have seen multiple approaches to verifying AED-like programs, e.g. by delaying send actions, or temporarily bounding their number (to keep queue sizes small) [7, 10], or by reasoning about a small number of representative execution schedules, to avoid interleaving explosion [5].
In this paper we consider the P language for AED programming [11]. A P program consists of multiple state machines running in parallel. Each machine has a local store, and a message queue through which it receives events from other machines. P allows the programmer to formulate safety specifications via a statement that asserts some predicate over the local state of a single machine. Verifying such reachability properties of course requires reasoning over global system behavior and is, for unbounded-queue P programs, undecidable [8].
The unboundedness of the reachable state space does not prevent the use of testing tools that try to explore as much of the state space as possible [3, 6, 11, 13] in the quest for bugs. Somewhat inspired by this kind of approach, the goal of this paper is a verification technique that can (sometimes) prove a safety property, despite exploring only a finite fraction of that space. Our approach is as follows. Assuming that the machines’ queues are the only source of unboundedness, we consider a bound k on the queue size, and exhaustively compute the reachable states  of the resulting finite-state problem, checking the local assertion \(\varPhi \) along the way. We then increase the queue bound until (an error is found, or) we reach some point
of the resulting finite-state problem, checking the local assertion \(\varPhi \) along the way. We then increase the queue bound until (an error is found, or) we reach some point
 of convergence: a point that allows us to conclude that increasing k further is not required to prove \(\varPhi \).
of convergence: a point that allows us to conclude that increasing k further is not required to prove \(\varPhi \).
What kind of “convergence” are we targeting? We design a sequence
 of abstractions of each reachability set over a finite abstract state space. Due to the monotonicity of sequence
of abstractions of each reachability set over a finite abstract state space. Due to the monotonicity of sequence
 , this ensures convergence, i.e. the existence of
, this ensures convergence, i.e. the existence of
 such that
such that
 for all
for all
 . Provided that an abstract state satisfies \(\varPhi \) exactly if all its concretizations do, we have: if all abstract states in
. Provided that an abstract state satisfies \(\varPhi \) exactly if all its concretizations do, we have: if all abstract states in
 comply with \(\varPhi \), then so do all reachable concrete states of P—we have proved the property.
comply with \(\varPhi \), then so do all reachable concrete states of P—we have proved the property.
We implement this strategy using an abstraction function
 with a finite co-domain that leaves the local state of a machine unchanged and maintains the first occurrence of each event in the queue; repeat occurrences are dropped. This abstraction preserves properties over the local state and the head of the queue, i.e. the visible (to the machine) part of the state space, which is typically sufficient to express reachability properties.
with a finite co-domain that leaves the local state of a machine unchanged and maintains the first occurrence of each event in the queue; repeat occurrences are dropped. This abstraction preserves properties over the local state and the head of the queue, i.e. the visible (to the machine) part of the state space, which is typically sufficient to express reachability properties.
The second major step in our approach is the detection of the point of convergence of
 : We show that, for the best abstract transformer
: We show that, for the best abstract transformer
 [9, 27, see Sect. 4.2], if
[9, 27, see Sect. 4.2], if
 , then
, then
 for all \(K \ge k\). In fact, we have a stronger result: under an easy-to-enforce condition, it suffices to consider abstract dequeue operations: all others, namely enqueue and local actions, never lead to abstract states in
for all \(K \ge k\). In fact, we have a stronger result: under an easy-to-enforce condition, it suffices to consider abstract dequeue operations: all others, namely enqueue and local actions, never lead to abstract states in
 . The best abstract transformer for dequeue actions is efficiently implementable for a given P program.
. The best abstract transformer for dequeue actions is efficiently implementable for a given P program.
It is of course possible that the convergence condition
 never holds (the problem is undecidable). This manifests in the presence of a spurious abstract state in the image produced by
never holds (the problem is undecidable). This manifests in the presence of a spurious abstract state in the image produced by
 , i.e. one whose concretization does not contain any reachable state. Our third contribution is a technique to assist users in eliminating such states, enhancing the chances for convergence. We have observed that spurious abstract states are often due to violations of simple machine invariants: invariants that do not depend on the behavior of other machines. By their nature, they can be proved using a cheap sequential analysis.
, i.e. one whose concretization does not contain any reachable state. Our third contribution is a technique to assist users in eliminating such states, enhancing the chances for convergence. We have observed that spurious abstract states are often due to violations of simple machine invariants: invariants that do not depend on the behavior of other machines. By their nature, they can be proved using a cheap sequential analysis.
We can eliminate an abstract state (e.g. produced by
 ) if all its concretizations violate a machine invariant. In this paper, we propose a domain-specific temporal logic to express invariants over machines with event queues and, more importantly, an algorithm that decides the above abstract queue invariant checking problem, by reducing it efficiently to a plain model checking problem. We have used this technique to ensure the convergence in “hard” cases that otherwise defy convergence of the abstract reachable states sequence.
) if all its concretizations violate a machine invariant. In this paper, we propose a domain-specific temporal logic to express invariants over machines with event queues and, more importantly, an algorithm that decides the above abstract queue invariant checking problem, by reducing it efficiently to a plain model checking problem. We have used this technique to ensure the convergence in “hard” cases that otherwise defy convergence of the abstract reachable states sequence.
We have implemented our technique for the P language and empirically evaluated it on an extensive set of benchmark programs. The experimental results support the following conclusions: (i) for our benchmark programs, the sequence of abstractions often converges fully automatically, in hard cases with minimal designer support in the form of separately dischargeable invariants; (ii) almost all examples converge at a small value of
 ; and (iii) the overhead our technique adds to the bounding technique is small: the bulk is spent on the exhaustive bounded exploration itself.
; and (iii) the overhead our technique adds to the bounding technique is small: the bulk is spent on the exhaustive bounded exploration itself.
Proofs and other supporting material can be found in the Appendix of [23].
2 Overview
We illustrate the main ideas of this paper using an example in the P language. A machine in a P program consists of multiple states. Each state defines an entry code block that is executed when the machine enters the state. The state also defines handlers for each event type e that it is prepared to receive. A handler can either be on e do foo (executing foo on receiving e), or ignore e (dequeuing and dropping e). A state can also have a defer e declaration; the semantics is that a machine dequeues the first non-deferred event in its queue. As a result, a queue in a P program is not strictly FIFO. This relaxation is an important feature of P that helps programmers express their logic compactly [11]. Figure 1 shows a P program named \( PiFl \), in which a
 (eventually) floods a
(eventually) floods a
 queue with
queue with
 events. This queue is the only source of unboundedness in \( PiFl \).
events. This queue is the only source of unboundedness in \( PiFl \).
A critical property for P programs is (bounded) responsiveness: the receiving machine must have a handler (e.g. on, defer, ignore) for every event arriving at the queue head; otherwise the event will come as a “surprise” and crash the machine. To prove responsiveness for \( PiFl \), we have to demonstrate (among others) that in state
 , the
, the
 event is never at the head of the Receiver’s queue. We cannot perform exhaustive model checking, since the set of reachable states is infinite. Instead, we will compute a conservative abstraction of this set that is precise enough to rule out
event is never at the head of the Receiver’s queue. We cannot perform exhaustive model checking, since the set of reachable states is infinite. Instead, we will compute a conservative abstraction of this set that is precise enough to rule out
 events at the queue head in this state.
events at the queue head in this state.
We first define a suitable abstraction function
 that collapses repeated occurrences of events to each event’s first occurrence. For instance, the queue
that collapses repeated occurrences of events to each event’s first occurrence. For instance, the queue

will be abstracted to
 . The finite number of possible abstract queues is \(1 + 3 + 3 \cdot 2 + 3 \cdot 2 \cdot 1 = 16\). The abstraction preserves the head of the queue. This and the machine state has enough information to check responsiveness.
. The finite number of possible abstract queues is \(1 + 3 + 3 \cdot 2 + 3 \cdot 2 \cdot 1 = 16\). The abstraction preserves the head of the queue. This and the machine state has enough information to check responsiveness.
We now generate the sequence
 of abstractions of the reachable states sets
of abstractions of the reachable states sets
 for queue size bounds \(k=0,1,2,\ldots \), by computing each finite set
for queue size bounds \(k=0,1,2,\ldots \), by computing each finite set
 , and then
, and then
 as
as
 . The obtained monotone sequence
. The obtained monotone sequence
 over a finite domain will eventually converge, but we must prove that it has. This is done by applying the best abstract transformer
over a finite domain will eventually converge, but we must prove that it has. This is done by applying the best abstract transformer
 , restricted to dequeue operations (defined in Sect. 4.2), to the current set
, restricted to dequeue operations (defined in Sect. 4.2), to the current set
 , and confirming that the result is contained in
, and confirming that the result is contained in
 .
.
As it turns out, the confirmation fails for the \( PiFl \) program: \(k=5\) marks the first time set
 repeats, i.e.
repeats, i.e.
 , so we are motivated to run the convergence test. Unfortunately we find a state
, so we are motivated to run the convergence test. Unfortunately we find a state
 , preventing convergence. Our approach now offers two remedies to this dilemma. One is to refine the queue abstraction. In our implementation, function
, preventing convergence. Our approach now offers two remedies to this dilemma. One is to refine the queue abstraction. In our implementation, function
 is really
is really
 , for a parameter p that denotes the size of the prefix of the queue that is kept unchanged by the abstraction. For example, for the queue from Eq. (1) we have
, for a parameter p that denotes the size of the prefix of the queue that is kept unchanged by the abstraction. For example, for the queue from Eq. (1) we have
 , where \(\mid \) separates the prefix from the “infinite tail” of the abstract queue. This (straightforward) refinement maintains finiteness of the abstraction and increases precision, by revealing that the queue starts with three
, where \(\mid \) separates the prefix from the “infinite tail” of the abstract queue. This (straightforward) refinement maintains finiteness of the abstraction and increases precision, by revealing that the queue starts with three  events. Re-running the analysis for the \( PiFl \) program with \(p=4\), at \(k=5\) we find
events. Re-running the analysis for the \( PiFl \) program with \(p=4\), at \(k=5\) we find
 , and the proof is complete.
, and the proof is complete.
The second remedy to the failed convergence test dilemma is more powerful but also less automatic. Let’s revert to prefix \(p=0\) and inspect the abstract state
 that foils the test. We find that it features a
that foils the test. We find that it features a
 event followed by a
event followed by a
 event in the
event in the
 queue. A simple static analysis of the
queue. A simple static analysis of the
 machine in isolation shows that it permits no path from the
machine in isolation shows that it permits no path from the
 to the
to the
 statement. The behavior of other machines is irrelevant for this invariant; we call it a machine invariant. We pass the invariant to our tool via the command line using the expression
statement. The behavior of other machines is irrelevant for this invariant; we call it a machine invariant. We pass the invariant to our tool via the command line using the expression

in a temporal-logic like notation called QuTL (Sect. 5.1), where  universally quantifies over all queue entries. Our tool includes a QuTL checker that determines that every concretization of \(\bar{s}\) violates property (2), concluding that \(\bar{s}\) is spurious and can be discarded. This turns out to be sufficient for convergence.
universally quantifies over all queue entries. Our tool includes a QuTL checker that determines that every concretization of \(\bar{s}\) violates property (2), concluding that \(\bar{s}\) is spurious and can be discarded. This turns out to be sufficient for convergence.
3 Queue-(Un)Bounded Reachability Analysis
Communicating Queue Systems. We consider P programs consisting of a fixed and known number n of machines communicating via event passing through unbounded FIFO queues.Footnote 1 For simplicity, we assume the machines are created at the start of the program; dynamic creation at a later time can be simulated by having the machine ignore all events until it receives a special creation event.
We model such a program as a communicating queue system (CQS). Formally, given \(n \in \mathbb N\), a CQS
 is a collection of n queue automata (QA)
is a collection of n queue automata (QA)
 ,
,
 . A QA consists of a finite queue alphabet \(\varSigma \) shared by all QA, a finite set
. A QA consists of a finite queue alphabet \(\varSigma \) shared by all QA, a finite set
 of local states, a finite set
of local states, a finite set
 of action labels, a finite set
of action labels, a finite set
 of transitions, and an initial local state
of transitions, and an initial local state
 . An action label
. An action label
 is of the form
is of the form
-
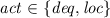 , denoting an action internal to
, denoting an action internal to
 (no other QA involved) that either dequeues an event (\( deq \)), or updates its local state (\( loc \)); or
(no other QA involved) that either dequeues an event (\( deq \)), or updates its local state (\( loc \)); or -
 , for
, for
 , denoting a transmission, where
, denoting a transmission, where
 (the sender) adds event
(the sender) adds event
 to the end of the queue of
to the end of the queue of
 (the receiver).
(the receiver).
The individual QA of a CQS model machines of a P program; hence we refer to QA states as machine states. A transmit action is the only communication mechanism among the QA.
Semantics. A machine state
 of a QA is of the form
of a QA is of the form
 ; state
; state
 is initial. We define machine transitions corresponding to internal actions as follows (transmit actions are defined later at the global level):
is initial. We define machine transitions corresponding to internal actions as follows (transmit actions are defined later at the global level):

A (global) state
 of a CQS is a tuple
of a CQS is a tuple
 where
where
 for
for
 . State
. State
 is initial. We extend the machine transition relation
is initial. We extend the machine transition relation
 to states as follows:
to states as follows:

if there exists  such that one of the following holds:
such that one of the following holds:
-
(internal)
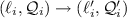 , and for all
, and for all
 ,
,
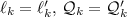 ;
; -
(transmission) there exists
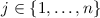 and
and
 such that:
such that:-
1.
 ;
; -
2.
 ;
; -
3.
 for all
for all
 ; and
; and -
4.
 for all
for all
 .
.
-
1.
The execution model of a CQS is strictly interleaving. That is, in each step, one of the two above transitions (internal) or (transmission) is performed for a nondeterministically chosen machine i.
Queue-Bounded and Queue-Unbounded Reachability. Given a CQS
 , a state
, a state
 , and a number k, the queue-bounded reachability problem (for
, and a number k, the queue-bounded reachability problem (for
 and k) determines whether
and k) determines whether
 is reachable under queue bound k, i.e. whether there exists a path
is reachable under queue bound k, i.e. whether there exists a path
 such that
such that
 , and for
, and for
 , all queues in state
, all queues in state
 have at most k events. Queue-bounded reachability for k is trivially decidable, by making enqueue actions for queues of size k blocking (the sender cannot continue), which results in a finite state space. We write
have at most k events. Queue-bounded reachability for k is trivially decidable, by making enqueue actions for queues of size k blocking (the sender cannot continue), which results in a finite state space. We write
 .
.
Queue-bounded reachability will be used in this paper as a tool for solving our actual problem of interest: Given a CQS
 and a state
and a state
 , the Queue-UnBounded reachability Analysis (QUBA) problem determines whether
, the Queue-UnBounded reachability Analysis (QUBA) problem determines whether
 is reachable, i.e. whether there exists a (queue-unbounded) path from
is reachable, i.e. whether there exists a (queue-unbounded) path from
 to
to
 . The QUBA problem is undecidable [8]. We write
. The QUBA problem is undecidable [8]. We write
 (
(
 ) for the set of reachable states.
) for the set of reachable states.
4 Convergence via Partial Abstract Transformers
In this section, we formalize our approach to detecting the convergence of a suitable sequence of observations about the states
 reachable under k-bounded semantics. We define the observations as abstractions of those states, resulting in sets
reachable under k-bounded semantics. We define the observations as abstractions of those states, resulting in sets
 . We then investigate the convergence of the sequence
. We then investigate the convergence of the sequence
 .
.
4.1 List Abstractions of Queues
Our abstraction function applies to queues, as defined below. Its action on machine and system states then follows from the hierarchical design of a CQS. Let  denote the number of events in
denote the number of events in  , and
, and
 the ith event in
the ith event in

 .
.
Definition 1
For a parameter \(p \in \mathbb N\), the list abstraction function
 is defined as follows:
is defined as follows:
-
1.
 .
. -
2.
For a non-empty queue
 ,
,  (3)
(3)
Intuitively,
 abstracts a queue by leaving its first p events unchanged (an idea also used in [16]). Starting from position p it keeps only the first occurrence of each event
abstracts a queue by leaving its first p events unchanged (an idea also used in [16]). Starting from position p it keeps only the first occurrence of each event
 in the queue, if any; repeat occurrences are dropped.Footnote 2 The preservation of existence and order of the first occurrences of all present events motivates the term list abstraction. An alternative is an abstraction that keeps only the set (not: list) of queue elements from position p, i.e. it ignores multiplicity and order. This is by definition less precise than the list abstraction and provided no efficiency advantages in our experiments. An abstraction that keeps only the queue head proved cheap but too imprecise.
in the queue, if any; repeat occurrences are dropped.Footnote 2 The preservation of existence and order of the first occurrences of all present events motivates the term list abstraction. An alternative is an abstraction that keeps only the set (not: list) of queue elements from position p, i.e. it ignores multiplicity and order. This is by definition less precise than the list abstraction and provided no efficiency advantages in our experiments. An abstraction that keeps only the queue head proved cheap but too imprecise.
The motivation for parameter p is that many protocols proceed in rounds of repeating communication patterns, involving a bounded number of message exchanges. If p exceeds that number, the list abstraction’s loss of information may be immaterial.
We write an abstract queue
 in the form
in the form
 s.t. \(p=| pref |\), and refer to \( pref \) as
s.t. \(p=| pref |\), and refer to \( pref \) as
 prefix (shared with
prefix (shared with
 ), and \( suff \) as
), and \( suff \) as
 suffix.
suffix.
Example 2
The queues
 are
are
 -equivalent:
-equivalent:
 .
.
We extend
 to act on a machine state via
to act on a machine state via
 , on a state via
, on a state via
 , and on a set of states pointwise via
, and on a set of states pointwise via
 .
.
Discussion. The abstract state space is finite since the queue prefix is of fixed size, and each event in the suffix is recorded at most once (the event alphabet is finite). The sets of reachable abstract states grow monotonously with increasing queue size bound k, since the sets of reachable concrete states do:

Finiteness and monotonicity guarantee convergence of the sequence of reachable abstract states.
We say the abstraction function
 respects a property of a state if, for any two
respects a property of a state if, for any two
 -equivalent states (see Example 2), the property holds for both or for neither. Function
-equivalent states (see Example 2), the property holds for both or for neither. Function
 respects properties that refer to the local-state part of a machine, and to the first \(p+1\) events of its queue (which are preserved by
respects properties that refer to the local-state part of a machine, and to the first \(p+1\) events of its queue (which are preserved by
 ). In addition, the property may look beyond the prefix and refer to the existence of events in the queue, but not their frequency or their order after the first occurrence.
). In addition, the property may look beyond the prefix and refer to the existence of events in the queue, but not their frequency or their order after the first occurrence.
The rich information preserved by the abstraction (despite being finite-state) especially pays off in connection with the defer feature in the P language, which allows machines to delay handling certain events at the head of a queue [11]. The machine identifies the first non-deferred event in the queue, a piece of information that is precisely preserved by the list abstraction (no matter what p).
Definition 3
Given an abstract queue
 , the concretization function
, the concretization function
 maps
maps
 to the language of the regular expression
to the language of the regular expression

i.e.
 .
.
As a special case,
 and so
and so
 for the empty queue. We extend
for the empty queue. We extend
 to act on abstract (machine or global) states in a way analogous to the extension of
to act on abstract (machine or global) states in a way analogous to the extension of
 , by moving it inside to the queues occurring in those states.
, by moving it inside to the queues occurring in those states.
4.2 Abstract Convergence Detection
Recall that finiteness and monotonicity of the sequence
 guarantee its convergence, so nothing seems more suggestive than to compute the limit. We summarize our overall procedure to do so in Algorithm 1. The procedure iteratively increases the queue bound k and computes the concrete and (per
guarantee its convergence, so nothing seems more suggestive than to compute the limit. We summarize our overall procedure to do so in Algorithm 1. The procedure iteratively increases the queue bound k and computes the concrete and (per
 -projection) the abstract reachability sets
-projection) the abstract reachability sets
 and
and
 . If, for some k, an error is detected, the procedure terminates (Lines 4–5; in practice implemented as an on-the-fly check).
. If, for some k, an error is detected, the procedure terminates (Lines 4–5; in practice implemented as an on-the-fly check).

The key of the algorithm is reflected in Lines 6–9 and is based on the following idea (all claims are proved as part of Theorem 4 below). If the computation of
 reveals no new abstract states in round k (Line 6; by monotonicity, “same size” implies “same sets”), we apply the best abstract transformer [9, 27]
reveals no new abstract states in round k (Line 6; by monotonicity, “same size” implies “same sets”), we apply the best abstract transformer [9, 27]
 to
to
 : if the result is contained in
: if the result is contained in
 , the abstract reachability sequence has converged. However, we can do better: we can restrict the successor function
, the abstract reachability sequence has converged. However, we can do better: we can restrict the successor function
 of the CQS to dequeue actions, denoted \( Im _{ deq }\) in Line 7. The ultimate reason is that firing a local or transmit action on two
of the CQS to dequeue actions, denoted \( Im _{ deq }\) in Line 7. The ultimate reason is that firing a local or transmit action on two
 -equivalent states r and s results again in
-equivalent states r and s results again in
 -equivalent states \(r'\) and \(s'\). This fact does not hold for dequeue actions: the successors \(r'\) and \(s'\) of dequeues depend on the abstracted parts of r and s, resp., which may differ and become “visible” during the dequeue (e.g. the event behind the queue head moves into the head position). Our main result therefore is: if
-equivalent states \(r'\) and \(s'\). This fact does not hold for dequeue actions: the successors \(r'\) and \(s'\) of dequeues depend on the abstracted parts of r and s, resp., which may differ and become “visible” during the dequeue (e.g. the event behind the queue head moves into the head position). Our main result therefore is: if
 and dequeue actions do not create new abstract states (Lines 7 and 8), sequence
and dequeue actions do not create new abstract states (Lines 7 and 8), sequence
 has converged:
has converged:
Theorem 4
If
 and
and
 , then for any \(K \ge k\),
, then for any \(K \ge k\),
 .
.
If the sequence of reachable abstract states has converged, then all reachable concrete states (any k) belong to
 (for the current k). Since the abstraction function
(for the current k). Since the abstraction function
 respects property \(\varPhi \), we know that if any reachable concrete state violated \(\varPhi \), so would any other concrete state that maps to the same abstraction. However, for each abstract state in
respects property \(\varPhi \), we know that if any reachable concrete state violated \(\varPhi \), so would any other concrete state that maps to the same abstraction. However, for each abstract state in
 , Line 4 has examined at least one state r in its concretization; a violation was not found. We conclude:
, Line 4 has examined at least one state r in its concretization; a violation was not found. We conclude:
Corollary 5
Line 9 of Algorithm 1 correctly asserts that no reachable concrete state of the given CQS violates \(\varPhi \).
The corollary (along with the earlier statement about Lines 4–5) confirms the partial correctness of Algorithm 1. The procedure is, however, necessarily incomplete: if no error is detected and the convergence condition in Line 8 never holds, the for loop will run forever.
We conclude this part with two comments. First, note that we do not compute the sets
 as reachability fixpoints in the abstract domain (i.e. the domain of
as reachability fixpoints in the abstract domain (i.e. the domain of
 ). Instead, we compute the concrete reachability sets first, and then obtain the
). Instead, we compute the concrete reachability sets first, and then obtain the
 via projection (Line 1). The reason is that the projection gives us the exact set of abstractions of reachable concrete states, while an abstract fixpoint likely overapproximates (for instance, the best abstract transformer from Line 7 does) and loses precision. Note that a primary motivation for computing abstract fixpoints, namely that the concrete fixpoint may not be computable, does not apply here: the concrete domains are finite, for each k.
via projection (Line 1). The reason is that the projection gives us the exact set of abstractions of reachable concrete states, while an abstract fixpoint likely overapproximates (for instance, the best abstract transformer from Line 7 does) and loses precision. Note that a primary motivation for computing abstract fixpoints, namely that the concrete fixpoint may not be computable, does not apply here: the concrete domains are finite, for each k.
Second, we observe that this projection technique comes with a cost: sequence
 may stutter at intermediate moments:
may stutter at intermediate moments:
 . The reason is that
. The reason is that
 is not obtained as a functional image of
is not obtained as a functional image of
 , but by projection from
, but by projection from
 . As a consequence, we cannot short-cut the convergence detection by just “waiting” for
. As a consequence, we cannot short-cut the convergence detection by just “waiting” for
 to stabilize, despite the finite domain.
to stabilize, despite the finite domain.
4.3 Computing Partial Best Abstract Transformers
Recall that in Line 7 we compute

The line applies the best abstract transformer, restricted to dequeue actions, to
 . This result cannot be computed as defined in (5), since
. This result cannot be computed as defined in (5), since
 is typically infinite. However,
is typically infinite. However,
 is finite, so we can iterative over
is finite, so we can iterative over
 , and little information is actually needed to determine the abstract successors of \(\bar{r}\). The “infinite fragment” of \(\bar{r}\) remains unchanged, which makes the action implementable.
, and little information is actually needed to determine the abstract successors of \(\bar{r}\). The “infinite fragment” of \(\bar{r}\) remains unchanged, which makes the action implementable.
Formally, let
 with
with
 . To apply a dequeue action to \(\bar{r}\), we first perform local-state updates on
. To apply a dequeue action to \(\bar{r}\), we first perform local-state updates on
 as required by the action, resulting in
as required by the action, resulting in
 . Now consider
. Now consider
 . The first suffix event,
. The first suffix event,
 , moves into the prefix due to the dequeue. We do not know whether there are later occurrences of
, moves into the prefix due to the dequeue. We do not know whether there are later occurrences of
 before or after the first suffix occurrences of
before or after the first suffix occurrences of
 . This information determines the possible abstract queues resulting from the dequeue. To compute the exact best abstract transformer, we enumerate these possibilities:
. This information determines the possible abstract queues resulting from the dequeue. To compute the exact best abstract transformer, we enumerate these possibilities:

The first case for
 applies if there are no occurrences of
applies if there are no occurrences of
 in the suffix after the dequeue. The remaining cases enumerate possible positions of the first occurrence of
in the suffix after the dequeue. The remaining cases enumerate possible positions of the first occurrence of
 (boxed, for readability) in the suffix after the dequeue. The cost of this enumeration is linear in the length of the suffix of the abstract queue.
(boxed, for readability) in the suffix after the dequeue. The cost of this enumeration is linear in the length of the suffix of the abstract queue.
Since our list abstraction maintains the first occurrence of each event, the semantics of defer (see the Discussion in Sect. 4.1) can be implemented abstractly without loss of information (not shown above, for simplicity).
5 Abstract Queue Invariant Checking
The abstract transformer function in Sect. 4 is used to decide whether sequence
 has converged. Being an overapproximation, the function may generate spurious states: they are not reachable, i.e. no concretization of them is. Unfortunate for us, spurious abstract states always prevent convergence.
has converged. Being an overapproximation, the function may generate spurious states: they are not reachable, i.e. no concretization of them is. Unfortunate for us, spurious abstract states always prevent convergence.
A key empirical observation is that concretizations of spurious abstract states often violate simple machine invariants, which can be proved from the perspective of a single machine, while collapsing all other machines into a nondeterministically behaving environment. Consider our example from Sect. 2 for \(p=0\). It fails to converge since Line 7 generates an abstract state \(\bar{s}\) that features a
 event followed by a
event followed by a
 event in the
event in the
 queue. A light-weight static analysis proves that the
queue. A light-weight static analysis proves that the
 machine permits no path from the
machine permits no path from the
 to the
to the
 statement. Since every concretization of \(\bar{s}\) features a
statement. Since every concretization of \(\bar{s}\) features a
 followed by a
followed by a
 event, the abstract state \(\bar{s}\) is spurious and can be eliminated.
event, the abstract state \(\bar{s}\) is spurious and can be eliminated.
Our tool assists users in discovering candidate machine invariants, by facilitating the inspection of states in
 (which foil the test in Line 8). We discharge such invariants separately, via a simple sequential model-check or static analysis. In the section we focus on the more interesting question of how to use them. Formally, suppose the P program comes with a queue invariant I, i.e. an invariant property of concrete queues. The abstract invariant checking problem is to decide, for a given abstract queue
(which foil the test in Line 8). We discharge such invariants separately, via a simple sequential model-check or static analysis. In the section we focus on the more interesting question of how to use them. Formally, suppose the P program comes with a queue invariant I, i.e. an invariant property of concrete queues. The abstract invariant checking problem is to decide, for a given abstract queue
 , whether every concretization of
, whether every concretization of
 violates I; in this case, and this case only, an abstract state containing
violates I; in this case, and this case only, an abstract state containing
 can be eliminated. In the following we define a language QuTL for specifying concrete queue invariants (5.1), and then show how checking an abstract queue against a QuTL invariant can be efficiently solved as a model checking problem (5.2).
can be eliminated. In the following we define a language QuTL for specifying concrete queue invariants (5.1), and then show how checking an abstract queue against a QuTL invariant can be efficiently solved as a model checking problem (5.2).
5.1 Queue Temporal Logic (QuTL)
Our logic to express invariant properties of queues is a form of first-order linear-time temporal logic. This choice is motivated by the logic’s ability to constrain the order (via temporal operators) and multiplicity of queue events, the latter via relational operators that express conditions on the number of event occurrences.
Queue Relational Expressions (QuRelE). These are of the form \(\#{e} \triangleright c\), where \(e \in \varSigma \) (queue alphabet), \(\triangleright \in \{<,\le ,=,\ge ,>\}\), and \(c \in \mathbb N\) is a literal natural number. The value of a QuRelE is defined as the Boolean

where \(|\cdot |\) denotes set cardinality and \(\triangleright \) is interpreted as the standard integer arithmetic relational operator. In the following we write
 (read: “
(read: “
 from i”) for the queue obtained from queue
from i”) for the queue obtained from queue
 by dropping the first i events.
by dropping the first i events.
Definition 6
(Syntax of QuTL). The following are QuTL formulas:
-
\( false \) and \( true \).
-
 , for
, for
 .
. -
E, for a queue relational expression E.
-
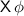 ,
,  ,
,  , for a QuTL formula \(\phi \).
, for a QuTL formula \(\phi \).
The set QuTL is the Boolean closure of the above set of formulas.
Definition 7
(Concrete semantics of QuTL). Concrete queue
 satisfies QuTL formula \(\phi \), written
satisfies QuTL formula \(\phi \), written
 , depending on the form of \(\phi \) as follows.
, depending on the form of \(\phi \) as follows.
-
 .
. -
for
 iff
iff
 and
and
 .
. -
for a queue relational expression E,
 iff \(V(E) = true \).
iff \(V(E) = true \). -
 iff
iff
 and
and
 .
. -
 iff there exists \(i \in \mathbb N\) such that
iff there exists \(i \in \mathbb N\) such that
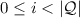 and
and
 .
. -
 iff for all \(i \in \mathbb N\) such that
iff for all \(i \in \mathbb N\) such that
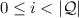 ,
,
 .
.
Satisfaction of Boolean combinations is defined as usual, e.g.
 iff
iff
 . No other pair
. No other pair
 satisfies
satisfies
 .
.
For instance, formula  is true exactly for queues containing at most 3
is true exactly for queues containing at most 3
 , and formula
, and formula  is true of
is true of
 iff
iff
 is empty or its final event (!) is
is empty or its final event (!) is
 . See App. B of [23] for more examples.
. See App. B of [23] for more examples.
Algorithmically checking whether a concrete queue
 satisfies a QuTL formula \(\phi \) is straightforward, since
satisfies a QuTL formula \(\phi \) is straightforward, since
 is of fixed size and straight-line. The situation is different with abstract queues. Our motivation here is to declare that an abstract queue
is of fixed size and straight-line. The situation is different with abstract queues. Our motivation here is to declare that an abstract queue
 violates a formula \(\phi \) if all its concretizations (Definition 3) do: under this condition, if \(\phi \) is an invariant, we know
violates a formula \(\phi \) if all its concretizations (Definition 3) do: under this condition, if \(\phi \) is an invariant, we know  is not reachable. Equivalently:
is not reachable. Equivalently:
Definition 8
(Abstract semantics of QuTL). Abstract queue
 satisfies QuTL formula \(\phi \), written
satisfies QuTL formula \(\phi \), written
 , if some concretization of
, if some concretization of
 satisfies \(\phi \):
satisfies \(\phi \):

For example, we have
 since for instance
since for instance
 satisfies the formula. See App. B of [23] for more examples.
satisfies the formula. See App. B of [23] for more examples.
5.2 Abstract QuTL Model Checking
A QuTL constraint is a QuTL formula without Boolean connectives. We first describe how to model check against QuTL constraints, and come back to Boolean connectives at the end of Sect. 5.2.
Model checking an abstract queue
 against a QuTL constraint \(\phi \), i.e. checking whether some concretization of
against a QuTL constraint \(\phi \), i.e. checking whether some concretization of
 satisfies \(\phi \), can be reduced to a standard model checking problem over a labeled transition system (LTS)
satisfies \(\phi \), can be reduced to a standard model checking problem over a labeled transition system (LTS)  with states
with states  , transitions
, transitions  , and a labeling function
, and a labeling function
 . The LTS characterizes the concretization
. The LTS characterizes the concretization  of
of
 , as illustrated in Fig. 2 using an example: the concretizations of
, as illustrated in Fig. 2 using an example: the concretizations of
 are formed from the regular-expression traces generated by paths of
are formed from the regular-expression traces generated by paths of
 LTS that end in the double-circled green state.
LTS that end in the double-circled green state.
The straightforward construction of the LTS
 is formalized in App. A.2 of [23]. Its size is linear in
is formalized in App. A.2 of [23]. Its size is linear in
 .
.
We call a path through
 complete if it ends in the right-most state \(s_z\) of
complete if it ends in the right-most state \(s_z\) of
 (green in Fig. 2). The labeling function extends to paths via
(green in Fig. 2). The labeling function extends to paths via
 . This gives rise to the following characterization of
. This gives rise to the following characterization of
 :
:
Lemma 9
Given abstract queue
 over alphabet \(\varSigma \), let
over alphabet \(\varSigma \), let  be its LTS.
be its LTS.

We say path
 satisfies \(\phi \), written
satisfies \(\phi \), written
 , if there exists
, if there exists
 s.t.
s.t.
 .
.
Corollary 10
Let
 and M as in Lemma 9, and \(\phi \) a QuTL constraint. Then the following are equivalent.
and M as in Lemma 9, and \(\phi \) a QuTL constraint. Then the following are equivalent.
-
1.
 .
. -
2.
There exists a complete path
 from \(s_0\) in
from \(s_0\) in  such that
such that
 .
.
Proof
immediate from Definition 8 and Lemma 9. \(\square \)
Given an abstract queue
 , its LTS
, its LTS
 , and a QuTL constraint \(\phi \), our abstract queue model checking algorithm is based on Corollary 10: we need to find a complete path from \(s_0\) in
, and a QuTL constraint \(\phi \), our abstract queue model checking algorithm is based on Corollary 10: we need to find a complete path from \(s_0\) in
 that satisfies \(\phi \). This is similar to standard model checking against existential temporal logics like ECTL, with two particularities:
that satisfies \(\phi \). This is similar to standard model checking against existential temporal logics like ECTL, with two particularities:
First, paths must be complete. This poses no difficulty, as completeness is suffix-closed: a path ends in \(s_z\) iff any suffix does. This implies that temporal reductions on QuTL constraints work like in standard temporal logics. For example: there exists a complete path
 from \(s_0\) in
from \(s_0\) in
 such that
such that
 iff there exists a complete path
iff there exists a complete path
 from some successor \(s_1\) of \(s_0\) such that
from some successor \(s_1\) of \(s_0\) such that
 .
.
Second, we have domain-specific atomic (non-temporal) propositions. These are accommodated as follows, for an arbitrary start state \(s \in S\):
-
 ):
):
this is true iff
 , as is immediate from the
, as is immediate from the
 case in Definition 7.
case in Definition 7. -
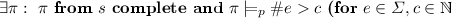 ): this is true iff
): this is true iff-
the number of states reachable from s labeled e is greater than c, or
-
there exists a state reachable from s labeled with e that has a self-loop.
The other relational expressions
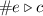 are checked similarly. \(\square \)
are checked similarly. \(\square \) -
Boolean Connectives. Let now \(\phi \) be a full-fledged QuTL formula. We first bring it into negation normal form, by pushing negations inside, exploiting the usual dualities
 , and
, and
 . The subset \(\triangleright \in \{<,\le ,\ge ,>\}\) of the queue relational expressions is semantically closed under negation; “\(\lnot {=}\)” is replaced by “\(> \vee<\)”. A path
. The subset \(\triangleright \in \{<,\le ,\ge ,>\}\) of the queue relational expressions is semantically closed under negation; “\(\lnot {=}\)” is replaced by “\(> \vee<\)”. A path
 from s satisfies
from s satisfies  (for
(for  ) iff
) iff
 this condition states that either \(L(s) = \varepsilon \), or there exists some label other than e in L(s), so the existential property \(\lnot e\) holds.
this condition states that either \(L(s) = \varepsilon \), or there exists some label other than e in L(s), so the existential property \(\lnot e\) holds.
Disjunctions are handled by distributing \(\models _{p}\) over them:
 iff
iff
 . What remains are conjunctions. The existential flavor of \(\models _{p}\) implies that \(\models _{p}\) does not distribute over them; see Ex. 13 in App. B.1 of [23]. Suppose we ignore this and replace a check of the form
. What remains are conjunctions. The existential flavor of \(\models _{p}\) implies that \(\models _{p}\) does not distribute over them; see Ex. 13 in App. B.1 of [23]. Suppose we ignore this and replace a check of the form
 by the weaker check
by the weaker check
 , which may produce false positives. Now consider how we use these results: if
, which may produce false positives. Now consider how we use these results: if
 holds, we decide to keep the state containing the abstract queue. False positives during abstract model checks therefore may create extra work, but do not introduce unsoundness. In summary, our abstract model checking algorithm soundly approximates conjunctions, but remains exact for the purely disjunctive fragment of QuTL.
holds, we decide to keep the state containing the abstract queue. False positives during abstract model checks therefore may create extra work, but do not introduce unsoundness. In summary, our abstract model checking algorithm soundly approximates conjunctions, but remains exact for the purely disjunctive fragment of QuTL.
 : property holds; p: minimum unabstracted prefix for required convergence; \(k_{\max }\): point of convergence or exposed bugs (– means divergence); Time: runtime (sec); Mem.: memory usage (Mb.).
: property holds; p: minimum unabstracted prefix for required convergence; \(k_{\max }\): point of convergence or exposed bugs (– means divergence); Time: runtime (sec); Mem.: memory usage (Mb.).6 Empirical Evaluation
We implemented the proposed approaches in C# atop the bounded model checker PTester [11], an analysis tool for P programs. PTester employs a bounded exploration strategy similar to Zing [4]. We denote by Pat the implementation of Algorithm 1, and by
 the version with queue invariants (“Pat+ Invariants”). A detailed introduction to tool design and implementation is available online [22].
the version with queue invariants (“Pat+ Invariants”). A detailed introduction to tool design and implementation is available online [22].
Experimental Goals. We evaluate the approaches against the following questions:
-
Q1. Is Pat effective: does it converge for many programs? for what values of k?
-
Q2. What is the impact of the QuTL invariant checking?
Experimental Setup. We collected a set of P programs (available online [22]); most have been used in previous publications:
-
1–5: protocols implemented in P: the German Cache Coherence protocol with different number of clients (1–2) [11], a buggy version of a token ring protocol [11], and a fixed version (3–4), and a failure detector protocol from [25] (5).
-
6–7: two device drivers where OSR is used for testing USB devices [10].
-
8–14: miscellaneous: 8–10 [25], 11 [15], 12 is the example from Sect. 2, 13–14 are the buggy and fixed versions of an Elevator controller [11].
We conduct two types of experiments: (i) we run Pat on each benchmark to empirically answer Q1; (ii) we run
 on the examples which fail to verify in (i) to answer Q2. All experiments are performed on a 2.80 GHz Intel(R) Core(TM) i7-7600 machine with 8 GB memory, running 64-bit Windows 10. The timeout is set to 3600 s (1h); the memory limit to 4 GB.
on the examples which fail to verify in (i) to answer Q2. All experiments are performed on a 2.80 GHz Intel(R) Core(TM) i7-7600 machine with 8 GB memory, running 64-bit Windows 10. The timeout is set to 3600 s (1h); the memory limit to 4 GB.
Results. Table 1 shows that Pat converges on almost all safe examples (and successfully exposes the bugs for unsafe ones). Second, in most cases, the \(k_{\max }\) where convergence was detected is small, 5 or less. This is what enables the use of this technique in practice: the exploration space grows fast with k, so early convergence is critical. Note that \(k_{\max }\) is guaranteed to be the smallest value for which the respective example converges. If convergent, the verification succeeded fully automatically: the queue abstraction prefix parameter p is incremented in a loop whenever the current value of p caused a spurious abstract state.
The German protocol does not converge in reasonable time. In this case, we request minimal manual assistance from the designer. Our tool inspects spurious abstract states, compares them to actually reached abstract states, and suggests candidate invariants to exclude them. We describe the process of invariant discovery, and why and how they are easy to prove, in [22].
The following table shows the invariants that make the German protocol converge, and the resulting times and memory consumption.
Program | p | \(k_{\max }\) | Time | Mem. | Invariant |
|---|---|---|---|---|---|
German-1 | 0 | 4 | 15.65 | 45.65 | Server: \(\#{ req\_excl } \le 1 \wedge \#{req\_share} \le 1\) |
German-2 | 0 | 4 | 629.43 | 284.75 | Client: \(\#{ ask\_excl } \le 1 \wedge \#{ ask\_share } \le 1\) |
The invariant states that there is always at most one exclusive request and at most one shared request in the Server or Client machine’s queue.
Performance Evaluation. We finally consider the following question: To perform full verification, how much overhead does Pat incur compared to PTester? We iteratively run PTester with a queue bound from 1 up to \(k_{\max }\) (from Table 1).

The figure on the right compares the running times of Pat and PTester. We observe that the difference is small, in all cases, suggesting that turning PTester into a full verifier comes with little extra cost. Therefore, as for improving Pat’s scalability, the focus should be on the efficiency of the
 computation (Line 3 in Algorithm 1). Techniques that lend themselves here are partial order reduction [2, 28] or symmetry reduction [29]. Note that our proposed approach is orthogonal to how these sets are computed.
computation (Line 3 in Algorithm 1). Techniques that lend themselves here are partial order reduction [2, 28] or symmetry reduction [29]. Note that our proposed approach is orthogonal to how these sets are computed.
7 Related Work
Automatic verification for asynchronous event-driven programs communicating via unbounded FIFO queues is undecidable [8], even when the agents are finite-state machines. To sidestep the undecidability, various remedies are proposed. One is to underapproximate program behaviors using various bounding techniques; examples include depth- [17] and context-bounded analysis [19, 20, 26], delay-bounding [13], bounded asynchrony [15], preemption-bounding [24], and phase-bounded analysis [3, 6]. It has been shown that most of these bounding techniques admit a decidable model checking problem [19, 20, 26] and thus have been successfully used in practice for finding bugs.
Gall et al. proposed an abstract interpretation of FIFO queues in terms of regular languages [16]. While our works share some basic insights about taming queues, the differences are fundamental: our abstract domain is finite, guaranteeing convergence of our sequence. In [16] the abstract domain is infinite; they propose a widening operator for fixpoint computation. More critically, we use the abstract domain only for convergence detection; the set of reachable states returned is in the end exact. As a result, we can prove and refute properties but may not terminate; [16] is inexact and cannot refute but always returns.
Several partial verification approaches for asynchronous message-passing programs have been presented recently [5, 7, 10]. In [5], Bakst et al. propose canonical sequentialization, which avoids exploring all interleavings by sequentializing concurrent programs. Desai et al. [10] propose an alternative way, namely by prioritizing receive actions over send actions. The approach is complete in the sense that it is able to construct almost-synchronous invariants that cover all reachable local states and hence suffice to prove local assertions. Similarly, Bouajjani et al. [7] propose an iterative analysis that bounds send actions in each interaction phase. It approaches the completeness by checking a program’s synchronizability under the bounds. Similar to our work, the above three works are sound but incomplete. An experimental comparison against the techniques reported in [7, 10] fails due to the unavailability of a tool that implements them. While tools implementing these techniques are not available [7, 10], a comparison based on what is reported in the papers suggests that our approach is competitive in both performance and precision.
Our approach can be categorized as a cutoff detection technique [1, 12, 14, 28]. Cutoffs are, however, typically determined statically, often leaving them too large for practical verification. Aiming at minimal cutoffs, our work is closer in nature to earlier dynamic strategies [18, 21], which targeted different forms of concurrent programs. The generator technique proposed in [21] is unlikely to work for P programs, due to the large local state space of machines.
8 Conclusion
We have presented a method to verify safety properties of asynchronous event-driven programs of agents communicating via unbounded queues. Our approach is sound but incomplete: it can both prove (or, by encountering bugs, disprove) such properties but may not terminate. We empirically evaluate our method on a collection of P programs. Our experimental results showcase our method can successfully prove the correctness of programs; such proof is achieved with little extra resource costs compared to plain state exploration. Future work includes an extension to P programs with other sources of unboundedness than the queue length (e.g. messages with integer payloads).
Notes
- 1.
The P language permits unbounded machine creation, a feature that we do not allow here and that is not used in any of the benchmarks we are aware of.
- 2.
Note that the head of the queue is always preserved by
 , even for \(p=0\).
, even for \(p=0\).
References
Abdulla, A.P., Haziza, F., Holík, L.: All for the price of few (parameterized verification through view abstraction). In: VMCAI, pp. 476–495 (2013)
Abdulla, P., Aronis, S., Jonsson, B., Sagonas, K.: Optimal dynamic partial order reduction. In: POPL, pp. 373–384 (2014)
Abdulla, P.A., Atig, M.F., Cederberg, J.: Analysis of message passing programs using SMT-solvers. In: Van Hung, D., Ogawa, M. (eds.) ATVA 2013. LNCS, vol. 8172, pp. 272–286. Springer, Cham (2013). https://doi.org/10.1007/978-3-319-02444-8_20
Andrews, T., Qadeer, S., Rajamani, S.K., Rehof, J., Xie, Y.: Zing: a model checker for concurrent software. In: Alur, R., Peled, D.A. (eds.) CAV 2004. LNCS, vol. 3114, pp. 484–487. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-27813-9_42
Bakst, A., Gleissenthall, K.v., Kici, R.G., Jhala, R.: Verifying distributed programs via canonical sequentialization. PACMPL 1(OOPSLA), 110:1–110:27 (2017)
Bouajjani, A., Emmi, M.: Bounded phase analysis of message-passing programs. Int. J. Softw. Tools Technol. Transf. 16(2), 127–146 (2014)
Bouajjani, A., Enea, C., Ji, K., Qadeer, S.: On the completeness of verifying message passing programs under bounded asynchrony. In: Chockler, H., Weissenbacher, G. (eds.) CAV 2018. LNCS, vol. 10982, pp. 372–391. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96142-2_23
Brand, D., Zafiropulo, P.: On communicating finite-state machines. J. ACM 30(2), 323–342 (1983)
Cousot, P., Cousot, R.: Systematic design of program analysis frameworks. In: POPL, pp. 269–282 (1979)
Desai, A., Garg, P., Madhusudan, P.: Natural proofs for asynchronous programs using almost-synchronous reductions. In: OOPSLA, pp. 709–725 (2014)
Desai, A., Gupta, V., Jackson, E., Qadeer, S., Rajamani, S., Zufferey, D.: P: safe asynchronous event-driven programming. In: PLDI, pp. 321–332 (2013)
Emerson, E.A., Kahlon, V.: Reducing model checking of the many to the few. In: McAllester, D. (ed.) CADE 2000. LNCS (LNAI), vol. 1831, pp. 236–254. Springer, Heidelberg (2000). https://doi.org/10.1007/10721959_19
Emmi, M., Qadeer, S., Rakamarić, Z.: Delay-bounded scheduling. In: POPL, pp. 411–422 (2011)
Farzan, A., Kincaid, Z., Podelski, A.: Proof spaces for unbounded parallelism. In: POPL, pp. 407–420 (2015)
Fisher, J., Henzinger, T.A., Mateescu, M., Piterman, N.: Bounded asynchrony: concurrency for modeling cell-cell interactions. In: Fisher, J. (ed.) FMSB 2008. LNCS, vol. 5054, pp. 17–32. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-68413-8_2
Le Gall, T., Jeannet, B., Jéron, T.: Verification of communication protocols using abstract interpretation of FIFO queues. In: Johnson, M., Vene, V. (eds.) AMAST 2006. LNCS, vol. 4019, pp. 204–219. Springer, Heidelberg (2006). https://doi.org/10.1007/11784180_17
Godefroid, P.: Model checking for programming languages using VeriSoft. In: POPL, pp. 174–186 (1997)
Kaiser, A., Kroening, D., Wahl, T.: Dynamic cutoff detection in parameterized concurrent programs. In: Touili, T., Cook, B., Jackson, P. (eds.) CAV 2010. LNCS, vol. 6174, pp. 645–659. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14295-6_55
La Torre, S., Parthasarathy, M., Parlato, G.: Analyzing recursive programs using a fixed-point calculus. In: PLDI, pp. 211–222 (2009)
Lal, A., Reps, T.: Reducing concurrent analysis under a context bound to sequential analysis. Form. Methods Syst. Des. 35(1), 73–97 (2009)
Liu, P., Wahl, T.: CUBA: interprocedural context-unbounded analysis of concurrent programs. In: PLDI, pp. 105–119 (2018)
Liu, P., Wahl, T., Lal, A.: (2019). www.khoury.northeastern.edu/home/lpzun/quba
Liu, P., Wahl, T., Lal, A.: Verifying asynchronous event-driven programs using partial abstract transformers (extended manuscript). CoRR abs/1905.09996 (2019)
Musuvathi, M., Qadeer, S.: Iterative context bounding for systematic testing of multithreaded programs. In: PLDI, pp. 446–455 (2007)
P-GitHub: The P programming langugage (2019). https://github.com/p-org/P
Qadeer, S., Rehof, J.: Context-bounded model checking of concurrent software. In: Halbwachs, N., Zuck, L.D. (eds.) TACAS 2005. LNCS, vol. 3440, pp. 93–107. Springer, Heidelberg (2005). https://doi.org/10.1007/978-3-540-31980-1_7
Reps, T., Sagiv, M., Yorsh, G.: Symbolic implementation of the best transformer. In: Steffen, B., Levi, G. (eds.) VMCAI 2004. LNCS, vol. 2937, pp. 252–266. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24622-0_21
Sousa, M., Rodríguez, C., D’Silva, V., Kroening, D.: Abstract interpretation with unfoldings. In: Majumdar, R., Kunčak, V. (eds.) CAV 2017. LNCS, vol. 10427, pp. 197–216. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63390-9_11
Wahl, T., Donaldson, A.: Replication and abstraction: symmetry in automated formal verification. Symmetry 2(2), 799–847 (2010)
Acknowledgments
We thank Dr. Vijay D’Silva (Google, Inc.), for enlightening discussions about partial abstract transformers.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2019 The Author(s)
About this paper
Cite this paper
Liu, P., Wahl, T., Lal, A. (2019). Verifying Asynchronous Event-Driven Programs Using Partial Abstract Transformers. In: Dillig, I., Tasiran, S. (eds) Computer Aided Verification. CAV 2019. Lecture Notes in Computer Science(), vol 11562. Springer, Cham. https://doi.org/10.1007/978-3-030-25543-5_22
Download citation
DOI: https://doi.org/10.1007/978-3-030-25543-5_22
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-25542-8
Online ISBN: 978-3-030-25543-5
eBook Packages: Computer ScienceComputer Science (R0)






 -Flood scenario. The
-Flood scenario. The
 and the
and the
 communicate via events of types
communicate via events of types
 , and
, and
 . After sending some
. After sending some
 events and one
events and one
 , the
, the
 floods the
floods the
 with
with
 . The
. The
 initially
initially  . Upon receiving
. Upon receiving
 it enters a state in which it
it enters a state in which it  .
.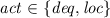 , denoting an action internal to
, denoting an action internal to
 (no other QA involved) that either dequeues an event (
(no other QA involved) that either dequeues an event ( , for
, for
 , denoting a transmission, where
, denoting a transmission, where
 (the sender) adds event
(the sender) adds event
 to the end of the queue of
to the end of the queue of
 (the receiver).
(the receiver).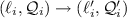 , and for all
, and for all
 ,
,
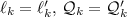 ;
;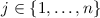 and
and
 such that:
such that: ;
; ;
; for all
for all
 ; and
; and for all
for all
 .
. .
. ,
, 
 , for
, for
 .
.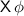 ,
,  ,
,  , for a QuTL formula
, for a QuTL formula  .
. iff
iff
 and
and
 .
. iff
iff  iff
iff
 and
and
 .
. iff there exists
iff there exists 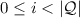 and
and
 .
. iff for all
iff for all 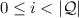 ,
,
 .
.
 (
( , resp. (Color figure online)
, resp. (Color figure online) .
. from
from  such that
such that
 .
. ):
):
 , as is immediate from the
, as is immediate from the
 case in Definition
case in Definition 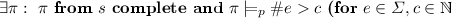 ): this is true iff
): this is true iff are checked similarly.
are checked similarly.  , even for
, even for