Abstract
The verification of asynchronous fault-tolerant distributed systems is challenging due to unboundedly many interleavings and network failures (e.g., processes crash or message loss). We propose a method that reduces the verification of asynchronous fault-tolerant protocols to the verification of round-based synchronous ones. Synchronous protocols are easier to verify due to fewer interleavings, bounded message buffers etc. We implemented our reduction method and applied it to several state machine replication and consensus algorithms. The resulting synchronous protocols are verified using existing deductive verification methods.
Supported by: Austrian Science Fund (FWF) via NFN RiSE (S11405) and project PRAVDA (P27722); WWTF grant APALACHE (ICT15-103); French National Research Agency ANR project SAFTA (12744-ANR-17-CE25-0008-01).
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Fault tolerance protocols provide dependable services on top of unreliable computers and networks. One distinguishes asynchronous vs. synchronous protocols based on the semantics of parallel composition. Asynchronous protocols are crucial parts of many distributed systems for their better performance when compared against the synchronous ones. However, their correctness is very hard to obtain, due to the challenges of concurrency, faults, buffered message queues, and message loss and re-ordering at the network [5, 19, 21, 26, 31, 35, 37, 42]. In contrast, reasoning about synchronous round-based semantics is simpler, as one only has to consider specific global states at round boundaries [1, 8, 10, 11, 13, 17, 29, 32, 40].
The question we address is how to connect both worlds, in order to exploit the advantage of verification in synchronous semantics when reasoning about asynchronous protocols. We consider asynchronous protocols that work in unreliable networks, which may lose and reorder messages, and where processes may crash. We focus on a class of protocols that solve state machine replication.
Due to the absence of a global clock, fault tolerance protocols implement an abstract notion of time to coordinate. The local state of a process maintains the value of the abstract time (potentially implicit), and a process timestamps the messages it sends accordingly. Synchronous algorithms do not need to implement an abstract notion of time: it is embedded in the definition of any synchronous computational model [9, 15, 18, 28], and it is called the round number. The key insight of our results is the existence of a correspondence between values of the abstract clock in the asynchronous systems and round numbers in the synchronous ones. Using this correspondence, we make explicit the “hidden” round-based synchronous structure of an asynchronous algorithm.
We discuss our approach using a leader election algorithm. We consider n of processes, which periodically elect collectively a new leader. These periods are called ballots, and in each ballot at most one leader should be elected. The protocol in Fig. 3 solves leader election. In a ballot, a process that wants to become leader proposes itself by sending a message containing its identifier me to all, and it is elected if (1) a majority of processes receive its message, (2) these receivers send a message of leadership acknowledgment to the entire network, and (3) at least one processes receives leadership acknowledgments for its leader estimate from a majority of processes. Figure 1(b) sketches an execution where process P3 fails to be elected in ballot 1 because the network drops all the messages sent by P3 marked with a cross. All processes timeout and there is no leader elected in ballot 1. In the second ballot, P2 tries to become leader, the network delivers all messages between P1 and P2 in time, the two processes form a majority, and P2 is elected leader of ballot 2.
The protocol is defined by the asynchronous parallel composition of n copies of the code in Fig. 3. Each process executes a loop, where each iteration defines the executors behavior in a ballot. The variable ballot encodes the ballot number. The function coord() provides a local estimate whether a process should try to become leader. Multiple processes may be selected by coord() as leader candidates, resulting in a race which is won by a process that is acknowledged by a majority (more than \(n/2\) processes). Depending on the result of coord(), a process may take the leader branch on the left or the follower branch on the right. On the leader branch, a message is prepared and sent, at line 7. The message contains the ballot number, the label NewBallot, the leaders identity. On the other branch, a follower waits for a message from a process, which proposes itself for the current ballot number of the follower. This waiting is implemented by a loop, which terminates either on timeout or when a message is received. Next, the followers, which received a message, and the leader candidates send their leader estimate to all at lines 12 and 41, where the message contains the ballots number, the label AckBallot, and the leaders identity. If a processes receives more than \(n/2\) messages labeled with AckBallot and its current ballot, it checks using \(\mathtt {all\_same(mbox,leader)}\) in lines 22 and 49, whether a majority of processes acknowledges the leadership of its estimate. In this case, it adds this information to the array log (which stores the locally elected leader of each ballot, if any) and outputs it, before it empties its mailbox and continues with the next iteration.
Figure 1(a) shows another execution of this protocol. Again, P3 sends NewBallot messages for ballot 1 to all processes. P3’s NewBallot messages are delayed, and P2 times out in ballot 1, moving to ballot 2 where it is a leader candidate. The messages sent in ballot 2 are exchanged like in Fig. 1(b). Contrary to Fig. 1(b), while exchanging ballot 2 messages, the network delivers to P2, P3’s NewBallot message from ballot 1. However, P2 ignores it, because of the receive statement in line 14 that only accepts messages for greater or equal (ballot, label) pairs. The message from ballot 1 arrived too “late” because P2 already is in ballot 2. Thus, the messages from ballot 1 have the same effect as if they were dropped, as in Fig. 1(b). The executions are equivalent from the local perspective of the processes: By applying a “rubber band transformation” [30], one can reorder transitions, while maintaining the local control flow and the send/receive causality.
Another case of equivalent executions is given in Fig. 2. While P1 and P2 made progress, P3 was disconnected. In Fig. 2(a), while P3 is waiting for ballot 1 messages, the networks delivers a message for ballot 20. P3 receives this message in line 29 and updates ballot in line 35. P3 thus “jumps forward in time”, acknowledging P2’s leadership in ballot 20. In Fig. 2(b), P3’s timeout expires in all ballots from 1 to 19, without P3 receiving any messages. Thus, it does not change its local state (except the ballot number) in these ballots. For P3, these two executions are stutter equivalent. Reducing verification to verification of executions as the ones to the right —i.e., synchronous executions —reduces the number of interleavings and drastically simplifies verification. In the following we discuss conditions on the code that allow such a reduction.
Communication Closure. In our example, the variables ballot and label encode abstract time: Let b and \(\ell \) be their assigned values. Then abstract time ranges over \(\mathcal {T} = \{(b,\ell ):b\in \mathbb {N}, \ell \in \{\texttt {NewBallot},\texttt {AckBallot}\}\}\). We fix NewBallot to be less than AckBallot, and consider the lexicographical order over \(\mathcal {T}\). The sequence of \((b,\ell )\) induced by an execution at a process is monotonically increasing; thus \((b,\ell )\) encodes a notion of time. A protocol is communication-closed if (i) each process sends only messages timestamped with the current time, and (ii) each process receives only messages timestamped with the current or a higher time value. For such protocols we show in Sect. 5 that for each asynchronous execution, there is an equivalent (processes go through the same sequence of local states) synchronous one. We use ideas from [17], but we allow reacting to future messages, which is a more permissive form of communication closure. This is essential for jumping forward, and thus for liveness in fault tolerance protocols.
The challenge is to check communication closure at the code level. For this, we rely on user-provided “tag” annotations that specify the variables and the message fields representing local time and timestamps. A system of assertions formalizes that the user-provided annotations encode time and that the protocol is communication-closed w.r.t. this definition of time. In the example, the user provides \((\texttt {ballot}, \texttt {label})\) for local time and msg->bal and msg->lab for timestamps. In Fig. 3, we give example assertions that we add for the send and receive conditions (i) and (ii). These assertions only consider the local state, i.e., we do not need to capture the states of other processes or the message pool. We check the assertions with the static verifier Verifast [22].
Synchronous Semantics. Central to our approach is re-writing communication-closed asynchronous protocol into synchronous ones. To formalize synchronous semantics we introduce multi Heard-Of protocols, mHO for short. An mHO computation is structured into a sequence of mHO-rounds that execute synchronously. Figure 4 is an example of an mHO protocol. It has two mHO-rounds: \(\mathtt {NewBallot}\) and \(\mathtt {AckBallot}\). Within a round, SEND functions, resp. UPDATE functions, are executed synchronously across all processes. The round number r is initially 0 and it is incremented after each execution of an mHO-round. The interesting feature, which models faults and timeouts, are the heard-of sets \( HO \) [9]. For each round r and each process p, the set \( HO (p,r)\) contains the set of processes from which p hears of in round r, i.e., whose messages are in the mailbox set taken as parameter by UPDATE (mbox). If the message from q to p is lost in round r, then \(q \not \in HO (p,r)\). Figures 1(b) and 2(b) are examples of executions of the protocol in Fig. 4. We extend the HO model [9] by allowing composition of multiple protocols. Verification in synchronous semantics, and thus in mHO, is simpler due to the round structure, which entails (i) no interleavings, (ii) no message buffers, and (iii) simpler invariants at the round boundaries.
Rewriting to mHO. We introduce a procedure that takes as input the asynchronous protocol together with tag annotations that have been checked, and produces the protocol rewritten in mHO, e.g., Fig. 3 is rewritten into Fig. 4. The rewriting is based on the idea of matching abstract time (ballot, label) to mHO round numbers r. Roughly, mHO-round NewBallot is obtained by combining the code of the first box on each path in Fig. 3 (the red boxes) and AckBallot is obtained my combining the second box on each path (the blue ones) as follows. The three message reception loops (the code in the boxes with highlighted background) are removed, because receptions are implicit in mHO; they correspond to a non-deterministic parameter of the UPDATE function. For each round, we record the context in which it is executed, e.g., the lower box for the follower is executed only if a NewBallot message was received (more details in Sect. 6).
Verification. The specification of the running example is that if two processes find the leader election for a ballot b successful (i.e., there is log entry for b), then they agree on the leader. In general, to prove the specification, we need invariants that quantify over the ballot number b. As processes decide asynchronously, the proof of ballot 1, for some process p, must refer to the first entry of log of processes that might already be in ballot 400. As discussed in [38], in general invariants need to capture the complete message history and the complete local state of processes. The proof of the same property for the synchronous protocol requires no such invariant. Due to communication closure, no messages need to be maintained after a round terminated, that is, there is no message pool. The rewritten synchronous code has a simpler correctness proof, independent of the chosen verification method. One could use model checking [1, 29, 39, 40], theorem prover approaches [8, 11], or deductive verification [14] for synchronous systems.
For several protocols, we formalize their specification in Consensus Logic [13], we have computed the equivalent mHO protocol, and proved it correct using the existing deductive verification engine from [13].
2 Asynchronous Protocols
All processes execute the same code, written in the core language in Fig. 5. The communication between processes is done via typed messages. Message payloads, denoted \(\mathtt {M} \), are wrappers of primitive or composite type. We denote by \(\mathcal {M}\) the set of message types. Wrappers are used to distinguish payload types. Send instructions take as input an object of some payload type and the receivers identity or \(\star \) corresponding to a send to all. Receives statements are non-blocking, and return an object of payload type or \(\texttt {NULL}\). Receive statements are parameterized by conditions (i.e., pointers to function) on the values in the received messages (e.g., timestamp). At most one message is received at a time. If no message has been delivered or satisfies the condition, receive returns \(\texttt {NULL}\). In Fig. 3, we give the definition of the function \(\mathtt {eq}\), used to filter messages acknowledging the leadership of a process. The followers use also \(\mathtt {geq}\) that checks if the received message is timestamped with a value higher or equal to the local time. We assume that each loop contains at least one send or receive statement. The iterative sequential computations are done in local functions, i.e.,
 . The instructions in() and out() are used to communicate with an external environment.
. The instructions in() and out() are used to communicate with an external environment.
The semantics of a protocol \(\mathcal {P}\) is the asynchronous parallel composition of n copies of the same code, one copy per process, where n is a parameter. Formally, the state of a protocol \(\mathcal {P} \) is a tuple  where: \(s \in [P \rightarrow (\mathtt {Vars} \cup \{{\texttt {pc}}\}) \rightarrow \mathcal {D} ]\) is a valuation in some data domain \(\mathcal {D} \) of the variables in \(\mathcal {P}\), where \(\texttt {pc}\) is represents the current control location, where \(\mathtt {Loc} \) is the set of all protocol locations, and \(msg\subseteq \bigcup _{\mathtt {M} \in \mathcal {M}}(P\times \mathcal {D}(\mathtt {M})\times P)\) is the multiset of messages in transit (the network may lose and reorder messages). Given a process \(p\in P\), s(p) is the local state of p, which is a valuation of p’s local variables, i.e., \(s(p)\in \mathtt {Vars} _p\cup \{\texttt {pc}_p\} \rightarrow \mathcal {D}\). The state of a crashed process is a wildcard state that matches any state. The messages sent by a process are added to the global pool of messages msg, and a receive statement removes a messages from the pool. The interface operations in and out do not modify the local state of a process. An execution is an infinite sequence s0 A0 s1 A1 . . . such that \(\forall i \ge 0\), si is a protocol state, \(Ai \in A\) is a local statement, whose execution creates a transition of the form
where: \(s \in [P \rightarrow (\mathtt {Vars} \cup \{{\texttt {pc}}\}) \rightarrow \mathcal {D} ]\) is a valuation in some data domain \(\mathcal {D} \) of the variables in \(\mathcal {P}\), where \(\texttt {pc}\) is represents the current control location, where \(\mathtt {Loc} \) is the set of all protocol locations, and \(msg\subseteq \bigcup _{\mathtt {M} \in \mathcal {M}}(P\times \mathcal {D}(\mathtt {M})\times P)\) is the multiset of messages in transit (the network may lose and reorder messages). Given a process \(p\in P\), s(p) is the local state of p, which is a valuation of p’s local variables, i.e., \(s(p)\in \mathtt {Vars} _p\cup \{\texttt {pc}_p\} \rightarrow \mathcal {D}\). The state of a crashed process is a wildcard state that matches any state. The messages sent by a process are added to the global pool of messages msg, and a receive statement removes a messages from the pool. The interface operations in and out do not modify the local state of a process. An execution is an infinite sequence s0 A0 s1 A1 . . . such that \(\forall i \ge 0\), si is a protocol state, \(Ai \in A\) is a local statement, whose execution creates a transition of the form  where \(\{I,O\}\) are the observable events generated by the Ai (if any). We denote by \([\![{\mathcal {P}}]\!]\) the set of executions of the protocol \(\mathcal {P}\).
where \(\{I,O\}\) are the observable events generated by the Ai (if any). We denote by \([\![{\mathcal {P}}]\!]\) the set of executions of the protocol \(\mathcal {P}\).
3 Round-Based Model: mHO
Intra-procedural. mHO captures round-based distributed algorithms and is a reformulation of the model in [9]. All processes execute the same code and the computation is structured in rounds. We denote by P the set of processes and \(n=|P|\) is a parameter. The central concept is the \( HO \)-set, where \( HO (p,r)\) contains the processes from which process p has heard of —has received messages from —in round r; this models faults and timeouts.
Syntax. An mHO protocol consists of variable declarations, \(\mathtt {Vars} \) is the set of variables, an initialization method \(\texttt {init} \), and a non-empty sequence of rounds, called phase; cf. Fig. 6. A phase is a fixed-size array of rounds. Each round has a send and update method, parameterized by a type \(\mathtt {M} \) (denoted by round\(_{\mathtt {M}}\)) which represents the message payload. The method SEND has no side effects and returns the messages to be sent based on the local state of each sender; it returns a partial map from receivers to payloads. The method UPDATE takes as input the received messages and updates the local state of a process. It may communicate with an external client via \(\mathtt {in}\) and \(\mathtt {out}\). For data computations, UPDATE uses iterative control structures only indirectly via sequential functions, e.g., \(\mathtt {all\_same(mbox,leader)}\) in Fig. 3, which checks whether the payloads of all messages in \(\mathtt {mbox}\) are equal to the local leader estimate.
Semantics. The set of executions of a mHO protocol is defined by the execution in a loop, of SEND followed by UPDATE for each round in the phase array. The initial configuration is defined by init. There are three predefined execution counters: the phase number, which is increased after a phase has been executed, the step number which tracks which mHO-round is executed in the current phase, and the round number which counts the total number of rounds executed so far and is defined by the phase times the length of the phase array, plus the step.
A protocol state is a tuple  where: P is the set of processes, \(SU \in \{\textsc {Send}, \textsc {Update}\}\) indicates the next transition, \(s \in [P \rightarrow \mathtt {Vars} \rightarrow \mathcal {D}]\) stores the process local states, \(r \in \mathbb {N}\) is the round number, \(msg \subseteq 2^{(P,\mathcal {D}(\mathtt {M}),P)}\) stores the in-transit messages, where \(\mathtt {M} \) is the type of the message payload, \( HO \in [P \rightarrow 2^P]\) evaluates the \( HO \)-sets for the current round. After the initialization, an execution alternates Send and Update transitions. In the Send transition, all processes send messages, which are added to a pool of messages msg, without modifying the local states. The values of the HO sets are updated non-deterministically to be a subset of P. A message is lost if the sender’s identity does not belong to the HO set of the receiver. In an Update transition, UPDATE is applied at each process, taking as input the set of received messages by that process in that round. If the processes communicate with an external process, then UPDATE might produce observable events \(o_p\). These events correspond to calls to \(\mathtt {in}\), which returns an input value, and \(\mathtt {out}\) that sends the value given as parameter to the client. At the end of the round, msg is purged and r is incremented. Figure 1(b) shows an execution of the mHO algorithm in Fig. 4.
where: P is the set of processes, \(SU \in \{\textsc {Send}, \textsc {Update}\}\) indicates the next transition, \(s \in [P \rightarrow \mathtt {Vars} \rightarrow \mathcal {D}]\) stores the process local states, \(r \in \mathbb {N}\) is the round number, \(msg \subseteq 2^{(P,\mathcal {D}(\mathtt {M}),P)}\) stores the in-transit messages, where \(\mathtt {M} \) is the type of the message payload, \( HO \in [P \rightarrow 2^P]\) evaluates the \( HO \)-sets for the current round. After the initialization, an execution alternates Send and Update transitions. In the Send transition, all processes send messages, which are added to a pool of messages msg, without modifying the local states. The values of the HO sets are updated non-deterministically to be a subset of P. A message is lost if the sender’s identity does not belong to the HO set of the receiver. In an Update transition, UPDATE is applied at each process, taking as input the set of received messages by that process in that round. If the processes communicate with an external process, then UPDATE might produce observable events \(o_p\). These events correspond to calls to \(\mathtt {in}\), which returns an input value, and \(\mathtt {out}\) that sends the value given as parameter to the client. At the end of the round, msg is purged and r is incremented. Figure 1(b) shows an execution of the mHO algorithm in Fig. 4.
Inter-procedural. The model introduced so far allows to express one protocol, e.g., a leader election protocol (e.g., Fig. 4). However, realistic systems typically combine several protocols, e.g., we can transform Fig. 4 into a replicated state machine protocol, by allowing processes to enter an atomic broadcast protocol in every ballot where a leader is elected successfully. Figure 7 sketches such an execution, where in the update of round AckBallot, a subprotocol is called; its execution is sketched with thicker edges. In the subprotocol, the leader broadcasts client requests in a loop until it loses its quorum. When a follower does not receive a message from the leader, it considers the leader crashed, and the control returns to the leader election protocol.
An inter-procedural mHO protocol differs from an intra-procedural one only in the UPDATE function: It may call another protocol and block until the call returns. An UPDATE may call at most one protocol on each path in its control flow (a sequence of calls can be implemented using multiple rounds). Thus, an inter-procedural mHO protocol is a collection of non-recursive mHO protocols, with a main protocol as entry point. Different protocols exchange messages of different types.
4 Formalizing Communication Closure Using Tags
We introduce synchronization tags which are program annotations that define communication-closed rounds within an asynchronous protocol.
Definition 1
(Tag annotation). For a protocol \(\mathcal {P} \), a tag annotation is a tuple \((\mathtt {SyncV},\mathtt {tags}, \mathtt {tagm}, \preceq ,\mathcal {D})\) where:
-
\(\mathcal {D} = (D_1, D_2, \ldots , D_{2m-1}, D_{2m})\), with \((D_i,\preceq _i, \bot _i)\) an ordered domain with a minimal element, denoted \(\bot _i\), for \(1 \le i \le 2m\). The cardinality of \(D_{2i}\) is bounded and all \(D_{2i}\) are pairwise disjoint, for \(i \in [1,m]\).
-
relation \(\preceq \) is the lexicographical order: the ith component is ordered by \( \preceq _i\),
-
\(\mathtt {SyncV} =(v_1,v_2,\ldots , v_{2m-1}, v_{2m})\) is a tuple of fresh variables,
-
\(\mathtt {tags}:\mathtt {Loc} \rightarrow [\mathtt {SyncV} \overset{ inj }{\rightharpoonup }\mathtt {Vars} ]\) annotates each control location with a partially defined injective function, that maps \(\mathtt {SyncV} \) over protocol variables,
-
\(\mathtt {tagm}:\mathcal {M} \rightarrow [\mathtt {SyncV} \overset{ inj }{\rightharpoonup } Fields ({\mathtt {M})}]\) annotates each message type \({\mathtt {M}}\in \mathcal {M}\) with a partially defined injective function, that maps \(\mathtt {SyncV} \) over the fields of \({\mathtt {M}}\).
The evaluation of a tag over \(\mathcal {P}\)’s semantics is denoted \(([\![\mathtt {tags} ]\!],[\![\mathtt {tagm} ]\!])\), where
-
\([\![\mathtt {tags} ]\!]:\Sigma \rightarrow [\mathtt {SyncV} \rightarrow \mathcal {D} ]\) is defined over the set of local process states \(\Sigma =\bigcup _{s\in [\![\mathcal {P} ]\!]}\bigcup _{p\in P}s(p)\), such that \([\![\mathtt {tags} ]\!]_s = (d_1,\ldots , d_{|\mathtt {SyncV} |})\) with
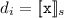 if
if 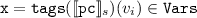 otherwise \(d_i = \bot _i\), where \(s\in \Sigma \),
otherwise \(d_i = \bot _i\), where \(s\in \Sigma \), 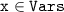 , \(v_i\) is the i\(^{th}\) component in \(\mathtt {SyncV} \), and \(\texttt {pc}\) is the program counter;
, \(v_i\) is the i\(^{th}\) component in \(\mathtt {SyncV} \), and \(\texttt {pc}\) is the program counter; -
\([\![\mathtt {tagm} ]\!]: \bigcup _{\mathtt {M} \in \mathcal {M}}\mathcal {D}(\mathtt {M}) \rightarrow [\mathtt {SyncV} \rightarrow \mathcal {D} \cup \bot ]\) is a function that for any message value \(m=(m_1,\ldots ,m_t)\), in the domain of some message type \({\mathtt {M}}\), associates a tuple \([\![\mathtt {tagm} ]\!]_{m:{\mathtt {M}}}=(d_1,\ldots ,d_{|\mathtt {SyncV} |})\) with \(d_i=m_j\) if \(j = \mathtt {tagm} ({\mathtt {M}})(v_i)\) otherwise \(d_i = \bot _i\), where \({v_i}\) is the i\(^{th}\) element in \(\mathtt {SyncV} \).
For every \(1\le i \le m\), \(v_{2i-1}\) is called a phase tag and \(v_{2i}\) is called step tag. Given an execution \(\pi \in [\![\mathcal {P} ]\!]\), a transition \(sAs'\) in \(\pi \) is tagged by \([\![\mathtt {tagm} ]\!]_m\) if
A is send(m) or \(m=recv(*cond)\), or A is tagged by \([\![\mathtt {tags} ]\!]_s'\) otherwise.
For Fig. 3, \(\mathtt {SyncV} =(v_1,v_2)\), and \(\mathtt {tags} \) matches \(v_1\) and \(v_2\) with ballot and label, resp., at all control locations, i.e., a process is in step \(\mathtt {NewBallot}\) of phase 3, when ballot = 3 and label = \(\mathtt {NewBallot}\). For the type \(\mathtt {msg}\), \(\mathtt {tagm} \) matches the field \(\mathtt {ballot}\) and \(\mathtt {lab}\) with \(v_1\) and \(v_2\), resp., i.e., a message \((3,\mathtt {NewBallot},5)\) is a phase 3 step \(\mathtt {NewBallot}\) message. To capture that messages of type \(\mathtt {A}\) are sent locally before messages of type \(\mathtt {B}\), the tagging function \(\mathtt {tagm} (\mathtt {B})\) should be defined on the same synchronization variables as \(\mathtt {tagm} (\mathtt {A})\).
Definition 2
(Synchronization tag). Given a protocol \(\mathcal {P} \), an annotation tag \((\mathtt {SyncV},\mathtt {tags},\mathtt {tagm},\mathcal {D}, \preceq )\) is called synchronization tag iff:
-
(I.)
for any local execution \(\pi =s_0 A_0 s_1 A_1 \ldots \in [\![\mathcal {P} ]\!]_{p}\) of a process p, the sequence \([\![\mathtt {tags} ]\!]_{s_0}[\![\mathtt {tags} ]\!]_{s_1}[\![\mathtt {tags} ]\!]_{s_2}\ldots \) is a monotonically increasing w.r.t. \(\preceq \).
Moreover \(\forall j, j' \in [1..m], j<j'.\) if \( [\![\mathtt {tags} ]\!]_{s_i}^{(2j-1,2j)} \ne [\![\mathtt {tags} ]\!]_{s_i+1}^{(2j-1,2j)}\) and \([\![\mathtt {tags} ]\!]_{s_i}^{(2j'-1,2j')} \ne [\![\mathtt {tags} ]\!]_{s_i+1}^{(2j'-1,2j')}\) then \( [\![\mathtt {tags} ]\!]_{s_i+1}^{(2j'-1,2j')} = (\bot _{2j'-1},\bot _{2j'})\) where \([\![\mathtt {tags} ]\!]_{s_i}^{(2j-1,2j)}\) is the projection of the tuple \([\![\mathtt {tags} ]\!]_{s_i}\) on the \(2j-1\) and 2j components,
-
(II.)
for any local execution \(\pi \in [\![\mathcal {P} ]\!]_{p}\), if \(s \overset{send(m,\_)}{\longrightarrow }s'\) is a transition of \(\pi \), with m a message value, then \([\![\mathtt {tags} ]\!]_s = [\![\mathtt {tagm} ]\!]_{m}\) and \([\![\mathtt {tags} ]\!]_s = [\![\mathtt {tags} ]\!]_{s'}\),
-
(III.)
for any local execution \(\pi \in [\![\mathcal {P} ]\!]_{p}\), if \(s \xrightarrow {{m= recv (cond)}} sr\) is a transition of \(\pi \), with m a value of some message type, then
-
if \(m\ne \texttt {NULL}\) then \([\![\mathtt {tags} ]\!]_s\preceq [\![\mathtt {tagm} ]\!]_{m}\), \([\![\mathtt {tags} ]\!]_s=[\![\mathtt {tags} ]\!]_{sr}\), and
-
if \(m=\texttt {NULL}\) then \(s=sr\),
-
-
(IV.)
for any local execution \(\pi \in [\![\mathcal {P} ]\!]_{p}\), if \(s\xrightarrow { stm } s'\) is a transition of \(\pi \) such that
-
\(s\ne s'\) and \(s\mid _{\mathtt {M},\mathtt {SyncV}} = s'\mid _{\mathtt {M},\mathtt {SyncV}}\), that is, s and s’ differ on the variables that are neither of some message type nor in the image of \(\mathtt {tags} \),
-
or \(\mathtt {stm}\) is a \(\mathtt {send, break, continue}\), or \(\mathtt {out()}\),
then for all message type variables \(\mathtt {m}\) in the protocol, \([\![\mathtt {tags} ]\!]_{s}=[\![\mathtt {tagm} ]\!]_{m}\), where m is the value in the state s of \(\mathtt {m}\), and for any \(\mathtt {Mbox}\) variables of type set of messages, \([\![\mathtt {tags} ]\!]_{s}=[\![\mathtt {tagm} ]\!]_{m}\) with \(m\in [\![\mathtt {Mbox}]\!]_s\),
-
-
(V.)
for any local execution \(\pi \in [\![\mathcal {P} ]\!]_{p}\), if \(s_1\xrightarrow { send(m,\_) } s_2\overset{ stm ^+}{\rightarrow }s_3\xrightarrow { send(m',\_) } s_4\) or \(s_1\xrightarrow { m=recv(*cond) } s_2\overset{ stm ^+}{\rightarrow }s_3\xrightarrow { send(m',\_) } s_4\) are sequences of transitions in \(\pi \), then \([\![\mathtt {tagm} ]\!]_m \prec [\![\mathtt {tagm} ]\!]_{m'}\), where \( stm \) is any statement except send or recv. Moreover, if \(s_1\xrightarrow { m=recv(*cond) } s_2\overset{ stm ^+}{\rightarrow }s_3\xrightarrow { m'=recv(*cond') }s_4\) in \(\pi \), then \(s_2\mid _{\mathtt {Vars} \setminus (\mathtt {M} \cup \mathtt {SyncV})} = s_3\mid _{\mathtt {Vars} \setminus (\mathtt {M} \cup \mathtt {SyncV})}\) or \([\![\mathtt {tags} ]\!]_{s_2} \prec [\![\mathtt {tags} ]\!]_{s_3}\).
A protocol \(\mathcal {P} \) is communication-closed, if there exists a synchronization tag for \(\mathcal {P} \).
Condition (I.) states that \(\mathtt {SyncV} \) is not decreased by any local statement (it is a notion of time). Further, one synchronization pair is modified at a time, except a reset (i.e., a pair is set to its minimal value) when the value of a preceding pair is updated. Checking this, translates into checking a transition invariant, stating that the value of the synchronization tuple \(\mathtt {SyncV} \) is increased by any assignment. To state this invariant we introduce “old synchronization variables” that maintain the value of the synchronization variables before the update.
Condition (II.) states that any message sent is tagged with a timestamp that equals the current local time. Checking it, reduces to an assert statement that expresses that for every \(v\in \mathtt {SyncV} \), \(\mathtt {tagm} (\mathtt {M})(v) = \mathtt {tags} (\mathtt {pc})(v)\), where \(\mathtt {M}\) is the type of the message m which is sent, and \(\mathtt {pc}\) is the program location of the send.
Condition (III.) states that any message received is tagged with a timestamp greater than or equal to the current time of the process. To check it, we need to consider the implementation of the functions passed as argument to a recv statement. These functions (e.g., eq and geq in Fig. 3) implement the filtering of the messages delivered by the network. We inline their code and prove Condition (III.) by comparing the tagged fields of message variables with the phase and step variables. In Fig. 3, \( \mathtt {assert\ m\rightarrow bal}==\mathtt {ballot\ \& \& \ m\rightarrow lab == label}\) after \(\mathtt {recv(eq(ballot,label))}\) checks this condition on the leader’s branch.
Condition (IV.) states that if the local state of a process changes (except changes of message type variables and synchronization variables), then all locally stored messages are timestamped with the current local time. That is, future messages cannot be “used” (no variable can be written, except message type variables) before the phase and step tags are updated to match the highest timestamp. To check it, we need to prove a stronger property than the one for (III.). At each control location that writes to either variables of primitive or composite type or mailbox variables, the values of the phase (and step) variables must be equal to the phase (and step) tagged fields of all allocated message type objects. In Fig. 3, the statement \(\mathtt {assert(equal(mbox, ballot,label))}\) checks this condition on the leader’s branch. It is a separation logic formula that uses the inductive list definition of \(\mathtt {mbox}\) which includes the content of the \(\mathtt {mbox}\).
The first four conditions imply that there is a global notion of time in the asynchronous protocol. However, this does not restrict the number of the messages exchanged between two processes with the same timestamp. mHO restricts the message exchange: for every time value (corresponding to a mHO-round), processes first send, then they receive messages, and then they perform a computation without receiving or sending more messages before time is increased. Condition (V.) ensures that the asynchronous protocol has this structure. We do a syntactic check of the code to ensure the code meets these restrictions.
Intuitively, each pair of synchronization variables identifies uniquely a mHO-protocol. To rewrite an asynchronous protocol into nested (inter-procedural) mHO-protocols, the tag of the inner protocol should include the tag of the outer one. The asynchronous code advances the time of one protocol at a time, that is, modifies one synchronization pair at a time. The only exception is when inner protocols terminate: in this case, the time of the outer protocol is advanced, while the time of the inner one is reset. Moreover, different protocols exchange different message types. To be able to order the messages exchanged by an inner protocol w.r.t. the messages exchanged by an outer protocol, the inner protocol messages should be tagged also with the synchronization variables identifying the outer one. This is actually happening in state machine replication algorithms, where the ballot (or view number), which is the tag of the outer leader election algorithm, tags also all the messages broadcast by the leader in the inner one.
5 Reducing Asynchronous Executions
We show that any execution of an asynchronous protocol that has a synchronization tag can be reduced to an indistinguishable mHO execution.
Definition 3
(Indistinguishability). Given two executions \(\pi \) and \(\pi '\) of a protocol \(\mathcal {P}\), we say a process p cannot distinguish locally between \(\pi \) and \(\pi '\) w.r.t. a set of variables W, denoted \(\pi \simeq _p^W\pi '\), if the projection of both executions on the sequence of states of p, restricted to the variables in W, agree up to finite stuttering, denoted, \(\pi \downharpoonright _{p,W} \equiv \pi '\downharpoonright _{p,W}\).
Two executions \(\pi \) and \(\pi '\) are indistinguishable w.r.t. a set of variables W, denoted \(\pi \simeq ^W\pi '\), iff no process can distinguish between them, i.e., \(\forall p.\ \pi \simeq _p^W\pi '\).
The reduction preserves so-called local properties [7], among which are consensus and state machine replication.
Definition 4
(Local properties). A property \(\phi \) is local if for any two executions a and b that are indistinguishable \(a\,\models \,\phi \) iff \(b\,\models \,\phi \).
Theorem 1
If there exists a synchronization tag \((\mathtt {SyncV},\mathtt {tags},\mathtt {tagm}, \mathcal {D},\preceq )\) for \(\mathcal {P} \), then \(\forall \textsf {ae}^{}\in [\![\mathcal {P} ]\!]\) there exists an mHO-execution \(\textsf {se}^{}\) that is indistinguishable w.r.t. all variables except for \(\mathtt {M} \) or \(\mathtt {Set}(\mathtt {M})\) variables, therefore \(\textsf {ae}^{}\) and \(\textsf {se}^{}\) satisfy the same local properties.
Proof Sketch. There are two cases to consider. Case (1): every receive transition \(s\xrightarrow { m=recv(*cond) } sr\) in \(\textsf {ae}^{}\) satisfies that \([\![\mathtt {tags} ]\!]_{sr} = [\![\mathtt {tagm} ]\!]_{m}\), i.e., all messages received are timestamped with the current local tag of the receiver. We use commutativity arguments to reorder transitions so that we obtain an indistinguishable asynchronous execution in which the transition tags are globally non-decreasing: The interesting case is if a send comes before a lower tagged receive in \(\textsf {ae}^{}\). Then the tags of the two transitions imply that the transitions concern different messages so that swapping them cannot violate send/receive causality.
We exploit that in the protocols we consider, no correct process locally keeps the tags unchanged forever (e.g., stays in a ballot forever) to arrive at an execution where the subsequence of transitions with the same tag is finite. Still, the resulting execution is not an mHO execution; e.g., for the same tag a receive may happen before a send on a different process. Condition (V.) ensures that mHO send-receive-update order is respected locally at each process. From this, together with the observation that sends are left movers, and updates are right movers, we obtain a global send-receive-update order which implies that the resulting execution is a mHO execution.
Case (2): there is a transition \(s\xrightarrow { m=recv(*cond) } sr\) in \(\textsf {ae}^{}\) such that \([\![\mathtt {tags} ]\!]_{sr} \prec [\![\mathtt {tagm} ]\!]_{m}\), that is, a process receives a message with tag \(k'\), higher than its state tag k. In mHO, a process only receives for its current round. To bring the asynchronous execution in such a form, we use Condition (IV.) and mHO semantics, where each process goes through all rounds. First, Condition (IV.) ensures that the process must update the tag variables to \(k'\) at some point t after receiving it, if it wants to use the content of the message. It ensures that the process stutters during the time instance between k and \(k'\), w.r.t. the values of the variables which are not of message type. That is, for the intermediate values of abstract time, between k and \(k'\), no messages are sent, received, and no computation is performed. We split \(\textsf {ae}^{}\) at point t and add empty send instructions, receive instructions, and instructions that increment the synchronization variables, until the tag reaches \(k'\). If we do this for each jump in \(\textsf {ae}^{}\), we arrive at an indistinguishable asynchronous execution that falls into the Case (1). \(\Box \)
6 Rewriting of Asynchronous to mHO
We introduce a rewriting algorithm that takes as input an asynchronous protocol \(\mathcal {P}\) annotated with a synchronization tag and produces a mHO protocol whose executions are indistinguishable from the executions of \(\mathcal {P}\).
Message Reception. mHO receives all messages of a round at once, while in the asynchronous code, messages are received one by one. By Condition (V.), receive steps that belong to the same round are separated only by instructions that store the messages in the mailbox. We consider that message reception is implemented in a simple while(true) loop (the most inner one); cf. filled boxes in Fig. 3. Conditions (III.) and (IV.) ensure that all messages received in a loop belong to one round (the current one or the one the code will jump to after exiting the reception loop). Thus, we replace a reception loop by havoc and assume statements that subsume the possible effects of the loop, satisfying all the conditions regarding synchronization tags found in the original receive statements.
Rewriting to an Intra-procedural
 . When the synchronization tag is defined over a pair of variables, the rewriting will produce an intra-procedural mHO protocol. Recall that the values of synchronization variables incarnate the round number, so that each update to a pair of synchronization variables marks the beginning of a new mHO round. The difficulty is that different execution prefixes may lead to the same values of the synchronization variables. To compute mHO-rounds, the algorithm exploits the position of the updates to the synchronization variables in the control flow graph (CFG). We consider different CFG patterns, from the simplest to the most complicated one.
. When the synchronization tag is defined over a pair of variables, the rewriting will produce an intra-procedural mHO protocol. Recall that the values of synchronization variables incarnate the round number, so that each update to a pair of synchronization variables marks the beginning of a new mHO round. The difficulty is that different execution prefixes may lead to the same values of the synchronization variables. To compute mHO-rounds, the algorithm exploits the position of the updates to the synchronization variables in the control flow graph (CFG). We consider different CFG patterns, from the simplest to the most complicated one.
Case 1: If the CFG is like in Fig. 8(a), i.e., it consists of one loop, where the phase tag \(\mathtt {ph}\) is incremented once at the beginning of each loop iteration, and for every value of the step tag \(\mathtt {st}\) there is exactly one assignment in the loop body (the same on all paths). In this case, the phase tag takes the same values as the loop iteration counter (maybe shifted with some initial value). Therefore, the loop body defines the code of an mHO-phase. It is easy to structure it into two mHO-rounds: the code of round A is the part of the CFG from the beginning of the loop’s body up to the second assignment of the \(\mathtt {st}\) variable, and round B is the rest of the code up to the end of the loop body.
Case 2: The CFG is like in Fig. 8(b). It differs from Case 1 in that the same value is assigned to \(\mathtt {st}\) in different branches. Each of this assignments marks the beginning of a mHO round B, which thus has multiple entry points. In mHO, a round only has one entry point. To simulate the multiple entry points in mHO, we store in auxiliary variables the values of the conditions along the paths that led to the entry point. In the figure, the code of round A is given by the red box, and the code of round B by the condition in the first blue box, expressed on the auxiliary variable, followed by the respective branches in the blue box.
In our example in Fig. 3, the assignment label = AckBallot appears in the leader and the follower branch. Followers send and receive AckBallot messages only if they have received a NewBallot. The rewrite introduces old_mbox1 in the mHO protocol in Fig. 4 to store this information. Also, we eliminate the variables \(\mathtt {ballot}\) and \(\mathtt {label}\); they are subsumed by the phase and round number of mHO.
Case 3: Let us assume that the CFG is like in Fig. 8(c). It differs from Case 1 because the phase tag \(\mathtt {ph}\) is assigned twice. We rewrite it into asynchronous code that falls into Case 1 or 2. The resulting CFG is sketched in Fig. 8(d), with only one assignment to \(\mathtt {ph}\) at the beginning of the loop.
If the second assignment changes the value of \(\mathtt {ph}\), then there is a jump. In case of a jump, the beginning of a new phase does not coincide with the first instruction of the loop. Thus there might be multiple entry points for a phase. We introduce (non-deterministic) branching in the control flow to capture different entry points: In case there is no jump, the green followed by the purple edge are executed within the same phase. In case of a jump, the rewritten code allows the green and the purple paths to be executed in different phases; first the green, and then the purple in a later phase. We add empty loops to simulate the phases that are jumped over. As a pure non-deterministic choice at the top of the loop would be too imprecise, we use the variable jump to make sure that the purple edge is executed only once prior to green edge. In case of multiple assignments, we perform this transformation iteratively for each assignment.
The protocol in Fig. 4 is obtained using two optimizations of the previous construction: First we do not need empty loops. They are subsumed by the mHO semantics as all local state changes are caused by some message reception. Thus, an empty loop is simulated by the execution of a phase with empty HO sets. Second, instead of adding \(\mathtt {jump}\) variables, we reuse the non-deterministic value of mbox. This is possible as the jump is preconditioned by a cardinality constraint on the mbox, and the green edge is empty (assignments to \(\mathtt {ballot}\) and \(\mathtt {label}\) correspond to ph++ and reception loops have been reduced to havoc statements).
Nesting. Cases 1–3 capture loops without nesting. Nested loops are rewritten into inter-procedural mHO protocols, using the structure of the tag annotations from Sect. 4. Each loop is rewritten into one protocol, starting with the most inner loop using the procedure above. For each outer loop, it first replaces the nested loop with a call to the computed mHO protocol, and then applies the same rewriting procedure. Interpreting each loop as a protocol is pessimistic, and our rewriting may generate deeper nesting than necessary. Inner loops appearing on different branches may belong to the same sub-protocol, so that these different loops exchange messages. If \(\mathtt {tags} \) associates different synchronization variables to different loops then the rewriting builds one (sub-)protocol for each loop. Otherwise, the rewriting merges the loops into one mHO protocol. To soundly merge several loops into the same mHO protocol, the rewrite algorithm identifies the context in which the inner loop is executed.
Theorem 2
Given an asynchronous protocol \(\mathcal {P} \) annotated with a synchronization tag \((\mathtt {SyncV},\mathtt {tags},\mathtt {tagm},\mathcal {D},\preceq )\), the rewriting returns an inter-procedural mHO protocol \(\mathcal {P} ^ \textsf {mHO} \) whose executions are indistinguishable from the executions of \(\mathcal {P} \).
7 Experimental Results
We implemented the rewriting procedure in a prototype tool ATHOS (https://github.com/alexandrumc/async-to-sync-translation). We applied it to several fault-tolerant distributed protocols. Figure 9 summarizes our results.
Verification of Synchronization Tags. The tool takes protocols in a C embedding of the language from Sect. 2 as input. We use a C embedding to be able to use Verifast [22] for checking the conditions in Sect. 4, i.e., the communication closure of an asynchronous protocol. Verifast is a deductive verification tool based on separation logic for sequential programs. Therefore, communication closure is specified in separation logic in our tool. To reason about sending and receiving messages, we inline every \(\mathtt {recv(*cond)}\) and use predefined specifications for send and recv. We consider only the prototype and the specification of these functions.
The user specifies in a configuration file the synchronization tag by (i) defining the number of (nested) protocols, (ii) for each protocol, the phase and step variables, and (iii) for each messages type the fields that encode the timestamp, i.e., the phase and step number. Figure 9 gives the names of phase and step variables of our benchmarks. For now, we manually insert the specification to be proven, i.e., the assert statements that capture Conditions (I.) to (V.) in Sect. 4. In Fig. 9, column Async gives the size in LoC of the input asynchronous protocol, +CC gives the size in LoC of the input annotated with the checks for communication closure (Conditions (I.) to (V.)) and their proofs.
Benchmarks. Our tool has rewritten several challenging benchmarks: the algorithm from [6, Fig. 6] solves consensus using a failure detector. The algorithm jumps to a specific decision round, if a special decision message is received. Multi-Paxos is the Paxos algorithm from [25] over sequences, without fast paths, where the classic path is repeated as long as the leader is stable. Roughly, it does a leader election similar to our running example (\(\mathtt {NewBallot}\) is Phase1a), except that the last all-to-all round is replaced by one back-and-forth communication between the leader and its quorum: the leader receives \(n/2\) acknowledgments that contain also the log of its followers (Phase1b). The leader computes the maximal log and sends it to all (Phase1aStart). In a subprotocol, a stable leader accepts client requests, and broadcasts them one by one to its followers. The broadcast is implemented by three rounds, Phase2aClassic, Phase2bClassic, Learn, and is repeated as long as the leader is stable. ViewChange is a leader election algorithm similar to the one in ViewStamped [34]. Normal-Op is the subprotocol used in ViewStamped to implement the broadcasting of new commands by a stable leader. The last column of Fig. 9 gives the size of the mHO protocol computed by the rewriting. The implementation uses pycparser [3], to obtain the abstract syntax tree of the input protocol.
Verification. We verified the safety specification (agreement) of the mHO counter-parts of the running example (Fig. 3), Normal-Op, and Multi-Paxos, by deductive verification: We encoded the specification of these algorithms, i.e., atomic broadcast, consensus, leader election, and the transition relation in Consensus Logic CL [13]. CL is a specification logic that allows us to express global properties of synchronous systems, and it contains expressions for processes, values, sets, cardinalities, and set comprehension. The verification conditions are soundly discarded by using an SMT solver. We used Z3 [33] in our experiments.
For Multi-Paxos we did a modular proof. First we prove the correctness of the sub-protocol Normal-Op which implements a loop of atomic broadcasts (executed in case of a stable leader). Then we prove the leader election outer loop correct, by replacing the subprotocol Normal-Op with its specification.
8 Related Work and Conclusions
Verification of asynchronous protocols received a lot of attention in the past years. Mechanized verification techniques like IronFleet [21] and Verdi [41] were the first to address verification of state machine replication. Later, Disel [38] proposes a logic to make the reasoning less protocol-specific, with the tradeoff of proofs that use the entire message history. At the other end of the spectrum, model checking based techniques [2, 4, 20, 23, 24] are fully automated but more restricted regarding the protocols they apply to. In between, semi-automated verification techniques based on deductive verification like natural proofs [12], Ivy [36], and PSync [14] try to minimize the user input for similar benchmarks.
We propose a technique that reduces the verification of an asynchronous protocol to a synchronous one, which simplifies the verification task no matter which method is chosen. We verified the resulting synchronous protocols with deductive verification based on [14]. Our technique uses the notion of communication closure [17], which we believe is the essence of any explicit or implicit synchrony in the system. We formalized a more general notion of communication closure that allows jumping over rounds, which is a catch-up mechanism essential to re-synchronize and ensure liveness. Previous reduction techniques focus on shared memory systems [16, 27], in contrast we focus on message passing concurrency.
The closest approaches are the results in [4, 24] and [2, 20], which also explore the synchrony of the system. Compared to these approaches, our technique allows more general behaviors, e.g., reasoning about stable leaders is possible because communication closure includes (for the first time) unbounded jumps. Also, we reduce to a stronger synchronous model, a round-based one instead of a peer to peer one, where interleavings w.r.t. actions of other rounds are removed.
As future work, we will address the relation between communication closure and specific network assumptions, e.g., FIFO channels, and a current limitation of communication closure which is reacting on messages from the past. For instance, recovery protocols react to such messages.
References
Aminof, B., Rubin, S., Stoilkovska, I., Widder, J., Zuleger, F.: Parameterized model checking of synchronous distributed algorithms by abstraction. In: Dillig, I., Palsberg, J. (eds.) VMCAI 2018. LNCS, vol. 10747, pp. 1–24. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-73721-8_1
Bakst, A., von Gleissenthall, K., Kici, R.G., Jhala, R.: Verifying distributed programs via canonical sequentialization. PACMPL 1(OOPSLA), 110:1–110:27 (2017)
Bendersky, E.: pycparser. https://github.com/eliben/pycparser. Accessed 7 Nov 2018
Bouajjani, A., Enea, C., Ji, K., Qadeer, S.: On the completeness of verifying message passing programs under bounded asynchrony. In: Chockler, H., Weissenbacher, G. (eds.) CAV 2018, Part II. LNCS, vol. 10982, pp. 372–391. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96142-2_23
Chandra, T.D., Griesemer, R., Redstone, J.: Paxos made live: an engineering perspective. In: PODC, pp. 398–407 (2007)
Chandra, T.D., Toueg, S.: Unreliable failure detectors for reliable distributed systems. J. ACM 43(2), 225–267 (1996)
Chaouch-Saad, M., Charron-Bost, B., Merz, S.: A reduction theorem for the verification of round-based distributed algorithms. In: Bournez, O., Potapov, I. (eds.) RP 2009. LNCS, vol. 5797, pp. 93–106. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-04420-5_10
Charron-Bost, B., Debrat, H., Merz, S.: Formal verification of consensus algorithms tolerating malicious faults. In: Défago, X., Petit, F., Villain, V. (eds.) SSS 2011. LNCS, vol. 6976, pp. 120–134. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-24550-3_11
Charron-Bost, B., Schiper, A.: The heard-of model: computing in distributed systems with benign faults. Distrib. Comput. 22(1), 49–71 (2009)
Chou, C., Gafni, E.: Understanding and verifying distributed algorithms using stratified decomposition. In: PODC, pp. 44–65 (1988)
Debrat, H., Merz, S.: Verifying fault-tolerant distributed algorithms in the heard-of model. In: Archive of Formal Proofs 2012 (2012)
Desai, A., Garg, P., Madhusudan, P.: Natural proofs for asynchronous programs using almost-synchronous reductions. In: Proceedings of the 2014 ACM International Conference on Object Oriented Programming Systems Languages & Applications, OOPSLA 2014, Part of SPLASH 2014, Portland, OR, USA, 20–24 October 2014, pp. 709–725 (2014)
Drăgoi, C., Henzinger, T.A., Veith, H., Widder, J., Zufferey, D.: A logic-based framework for verifying consensus algorithms. In: McMillan, K.L., Rival, X. (eds.) VMCAI 2014. LNCS, vol. 8318, pp. 161–181. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54013-4_10
Drăgoi, C., Henzinger, T.A., Zufferey, D.: PSync: a partially synchronous language for fault-tolerant distributed algorithms. In: POPL, pp. 400–415 (2016)
Dwork, C., Lynch, N., Stockmeyer, L.: Consensus in the presence of partial synchrony. JACM 35(2), 288–323 (1988)
Elmas, T., Qadeer, S., Tasiran, S.: A calculus of atomic actions. In: Proceedings of the 36th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL 2009, Savannah, GA, USA, 21–23 January 2009, pp. 2–15 (2009)
Elrad, T., Francez, N.: Decomposition of distributed programs into communication-closed layers. Sci. Comput. Program. 2(3), 155–173 (1982)
Gafni, E.: Round-by-round fault detectors: unifying synchrony and asynchrony (extended abstract). In: PODC, pp. 143–152 (1998)
García-Pérez, Á., Gotsman, A., Meshman, Y., Sergey, I.: Paxos consensus, deconstructed and abstracted. In: Ahmed, A. (ed.) ESOP 2018. LNCS, vol. 10801, pp. 912–939. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-89884-1_32
von Gleissenthall, K., Gökhan Kici, R., Bakst, A., Stefan, D., Jhala, R.: Pretend synchrony: synchronous verification of asynchronous distributed programs. PACMPL 3(POPL), 59:1–59:30 (2019)
Hawblitzel, C., et al.: IronFleet: proving safety and liveness of practical distributed systems. Commun. ACM 60(7), 83–92 (2017)
Jacobs, B., Smans, J., Piessens, F.: A quick tour of the verifast program verifier. In: Ueda, K. (ed.) APLAS 2010. LNCS, vol. 6461, pp. 304–311. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-17164-2_21
Konnov, I.V., Lazic, M., Veith, H., Widder, J.: A short counterexample property for safety and liveness verification of fault-tolerant distributed algorithms. In: POPL, pp. 719–734 (2017)
Kragl, B., Qadeer, S., Henzinger, T.A.: Synchronizing the asynchronous. In: CONCUR, pp. 21:1–21:17 (2018)
Lamport, L.: Generalized consensus and paxos. Technical report, March 2005. https://www.microsoft.com/en-us/research/publication/generalized-consensus-and-paxos/
Lesani, M., Bell, C.J., Chlipala, A.: Chapar: certified causally consistent distributed key-value stores. In: POPL, pp. 357–370 (2016)
Lipton, R.J.: Reduction: a method of proving properties of parallel programs. Commun. ACM 18(12), 717–721 (1975)
Lynch, N.: Distributed Algorithms. Morgan Kaufman, San Francisco (1996)
Marić, O., Sprenger, C., Basin, D.: Cutoff bounds for consensus algorithms. In: Majumdar, R., Kunčak, V. (eds.) CAV 2017, Part II. LNCS, vol. 10427, pp. 217–237. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63390-9_12
Mattern, F.: On the relativistic structure of logical time in distributed systems. In: Parallel and Distributed Algorithms, pp. 215–226 (1989)
Moraru, I., Andersen, D.G., Kaminsky, M.: There is more consensus in Egalitarian parliaments. In: SOSP, pp. 358–372 (2013)
Moses, Y., Rajsbaum, S.: A layered analysis of consensus. SIAM J. Comput. 31(4), 989–1021 (2002)
de Moura, L., Bjørner, N.: Z3: an efficient SMT solver. In: Ramakrishnan, C.R., Rehof, J. (eds.) TACAS 2008. LNCS, vol. 4963, pp. 337–340. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78800-3_24
Oki, B.M., Liskov, B.: Viewstamped replication: a general primary copy. In: PODC, pp. 8–17 (1988)
Ongaro, D., Ousterhout, J.K.: In search of an understandable consensus algorithm. In: 2014 USENIX Annual Technical Conference, USENIX ATC 2014, pp. 305–319 (2014)
Padon, O., McMillan, K.L., Panda, A., Sagiv, M., Shoham, S.: Ivy: safety verification by interactive generalization. In: PLDI, pp. 614–630 (2016)
Rahli, V., Guaspari, D., Bickford, M., Constable, R.L.: Formal specification, verification, and implementation of fault-tolerant systems using EventML. ECEASST 72 (2015)
Sergey, I., Wilcox, J.R., Tatlock, Z.: Programming and proving with distributed protocols. PACMPL 2(POPL), 28:1–28:30 (2018)
Stoilkovska, I., Konnov, I., Widder, J., Zuleger, F.: Verifying safety of synchronous fault-tolerant algorithms by bounded model checking. In: Vojnar, T., Zhang, L. (eds.) TACAS 2019, Part II. LNCS, vol. 11428, pp. 357–374. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17465-1_20
Tsuchiya, T., Schiper, A.: Verification of consensus algorithms using satisfiability solving. Distrib. Comput. 23(5–6), 341–358 (2011)
Wilcox, J.R., et al.: Verdi: a framework for implementing and formally verifying distributed systems. In: PLDI, pp. 357–368 (2015)
Woos, D., Wilcox, J.R., Anton, S., Tatlock, Z., Ernst, M.D., Anderson, T.E.: Planning for change in a formal verification of the RAFT consensus protocol. In: CPP, pp. 154–165 (2016)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2019 The Author(s)
About this paper
Cite this paper
Damian, A., Drăgoi, C., Militaru, A., Widder, J. (2019). Communication-Closed Asynchronous Protocols. In: Dillig, I., Tasiran, S. (eds) Computer Aided Verification. CAV 2019. Lecture Notes in Computer Science(), vol 11562. Springer, Cham. https://doi.org/10.1007/978-3-030-25543-5_20
Download citation
DOI: https://doi.org/10.1007/978-3-030-25543-5_20
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-25542-8
Online ISBN: 978-3-030-25543-5
eBook Packages: Computer ScienceComputer Science (R0)












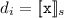 if
if 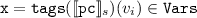 otherwise
otherwise 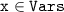 ,
, 
