Abstract
We present abstraction-refinement algorithms for model checking safety properties of timed automata. The abstraction domain we consider abstracts away zones by restricting the set of clock constraints that can be used to define them, while the refinement procedure computes the set of constraints that must be taken into consideration in the abstraction so as to exclude a given spurious counterexample. We implement this idea in two ways: an enumerative algorithm where a lazy abstraction approach is adopted, meaning that possibly different abstract domains are assigned to each exploration node; and a symbolic algorithm where the abstract transition system is encoded with Boolean formulas.
This work was funded by ANR project Ticktac (ANR-18-CE40-0015) and by ERC grant EQualIS (StG-308087).
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others

1 Introduction
Model checking [4, 10, 12, 26] is an automated technique for verifying that the set of behaviors of a computer system satisfies a given property. Model-checking algorithms explore finite-state automata (representing the system under study) in order to decide if the property holds; if not, the algorithm returns an explanation. These algorithms have been extended to verify real-time systems modelled as timed automata [2, 3], an extension of finite automata with clock variables to measure and constrain the amount of time elapsed between occurrences of transitions. The state-space exploration can be done by representing clock constraints efficiently using convex polyhedra called zones [8, 9]. Algorithms based on this data structure have been implemented in several tools such as Uppaal [7], and have been applied in various industrial cases.
The well-known issue in the applications of model checking is the state-space explosion problem: the size of the state space grows exponentially in the size of the description of the system. There are several sources for this explosion: the system might be made of the composition of several subsystems (such as a distributed system), it might contain several discrete variables (such as in a piece of software), or it might contain a number of real-valued clocks as in our case.
Numerous attempts have been made to circumvent this problem. Abstraction is a generic approach that consists in simplifying the model under study, so as to make it easier to verify [13]. Existential abstraction may only add extra behaviors, so that when a safety property holds in an abstracted model, it also holds in the original model; if on the other hand a safety property fails to hold, the model-checking algorithms return a witness trace exhibiting the non-safe behaviour: this either invalidates the property on the original model, if the trace exists in that model, or gives information about how to automatically refine the abstraction. This approach, named CEGAR (counter-example guided abstraction refinement) [11], was further developed and used, for instance, in software verification (BLAST [20], SLAM [5], ...).
The CEGAR approach has been adapted to timed automata, e.g. in [14, 18], but the abstractions considered there only consist in removing clocks and discrete variables, and adding them back during refinement. So for most well-designed models, one ends up adding all clocks and variables which renders the method useless. Two notable exceptions are [22], in which the zone extrapolation operators are dynamically adapted during the exploration, and [29], in which zones are refined when needed using interpolants. Both approaches define “exact” abstractions in the sense that they make sure that all traces discovered in the abstract model are feasible in the concrete model at any time.
In this work, we consider a more general setting and study predicate abstractions on clock variables. Just like in software model checking, we define abstract state spaces using these predicates, where the values of the clocks and their relations are approximately represented by these predicates. New predicates are generated if needed during the refinement step. We instantiate our approach by two algorithms. The first one is a zone-based enumerative algorithm inspired by the lazy abstraction in software model checking [19], where we assign a possibly different abstract domain to each node in the exploration. The second algorithm is based on binary decision diagrams (BDD): by exploiting the observation that a small number of predicates was often sufficient to prove safety properties, we use an efficient BDD encoding of zones similar to one introduced in early work [28].
Let us explain the abstract domains we consider. Assume there are two clock variables x and y. The abstraction we consider consists in restricting the clock constraints that can be used when defining zones. Assume that we only allow to compare x with 2 or 3; that y can only be compared with 2, and \(x-y\) can only be compared with \(-1\) or 2. Then any conjunction of constraints one might obtain in this manner will be delimited by the thick red lines in Fig. 1; one cannot define a finer region under this restriction. The figure shows the abstraction process: given a “concrete” zone, its abstraction is the smallest zone which is a superset and is definable under our restriction. For instance, the abstraction of \(1\le x,y\le 2\) is \(0\le x,y\le 2\wedge -1\le x-y\) (cf. Fig. 1a).
Related Works. We give more detail on zone abstractions in timed automata. Most efforts in the literature have been concentrated in designing zone abstraction operators that are exact in the sense that they preserve the reachability relation between the locations of a timed automaton; see [6]. The idea is to determine bounds on the constants to which a given clock can be compared to in a given part of the automaton, since the clock values do not matter outside these bounds. In [21, 22], the authors give an algorithm where these bounds are dynamically adapted during the exploration, which allows one to obtain coarser abstractions. In [29], the exploration tree contains pairs of zones: a concrete zone as in the usual algorithm, and a coarser abstract zone. The algorithm explores all branches using the coarser zone and immediately refines the abstract zone whenever an edge which is disabled in the concrete zone is enabled. In [17], a CEGAR loop was used to solve timed games by analyzing strategies computed for each abstract game. The abstraction consisted in collapsing locations.
Some works have adapted the abstraction-refinement paradigm to timed automata. In [14], the authors apply “localization reduction” to timed automata within an abstraction-refinement loop: they abstract away clocks and discrete variables, and only introduce them as they are needed to rule out spurious counterexamples. A more general but similar approach was developed in [18]. In [31], the authors adapt the trace abstraction refinement idea to timed automata where a finite automaton is maintained to rule out infeasible edge sequences.
The CEGAR approach was also used recently in the LinAIG framework for verifying linear hybrid automata [1]. In this work, the backward reachability algorithm exploits don’t-cares to reduce the size of the Boolean circuits representing the state space. The abstractions consist in enlarging the size of don’t-cares to reduce the number of linear predicates used in the representation.
2 Timed Automata and Zones
2.1 Timed Automata
Given a finite set of clocks \(\mathcal {C}\), we call valuations the elements of \(\mathbb {R}_{\ge 0}^\mathcal {C}\). For a clock valuation v, a subset \(R\subseteq \mathcal {C}\), and a non-negative real d, we denote with \(v[R \leftarrow d]\) the valuation w such that \(w(x) = v(x)\) for \(x \in \mathcal {C}\setminus R\) and \(w(x) = d\) for \(x \in R\), and with \(v+d\) the valuation \(w'\) such that \(w'(x)=v(x)+d\) for all \(x\in \mathcal {C}\). We extend these operations to sets of valuations in the obvious way. We write \(\mathbf {0}\) for the valuation that assigns 0 to every clock. An atomic guard is a formula of the form \(x \prec k\) or \(x-y \prec k\) with \(x,y \in \mathcal {C}\), \(k\in \mathbb {N}\), and  . A guard is a conjunction of atomic guards. A valuation v satisfies a guard g, denoted \(v \models g\), if all atomic guards hold true when each \(x\in \mathcal {C}\) is replaced with v(x). Let \([\![g ]\!] = \{ v \in \mathbb {R}_{\ge 0}^\mathcal {C}\mid v \models g\}\) denote the set of valuations satisfying g. We write \(\varPhi _\mathcal {C}\) for the set of guards built on \(\mathcal {C}\).
. A guard is a conjunction of atomic guards. A valuation v satisfies a guard g, denoted \(v \models g\), if all atomic guards hold true when each \(x\in \mathcal {C}\) is replaced with v(x). Let \([\![g ]\!] = \{ v \in \mathbb {R}_{\ge 0}^\mathcal {C}\mid v \models g\}\) denote the set of valuations satisfying g. We write \(\varPhi _\mathcal {C}\) for the set of guards built on \(\mathcal {C}\).
A timed automaton \(\mathcal {A}\) is a tuple  , where \(\mathcal {L}\) is a finite set of locations,
, where \(\mathcal {L}\) is a finite set of locations,  defines location invariants, \(\mathcal {C}\) is a finite set of clocks, \(E \subseteq \mathcal {L} \times \varPhi _\mathcal {C}\times 2^\mathcal {C}\times \mathcal {L}\) is a set of edges, and \(\ell _0\in \mathcal {L}\) is the initial location. An edge \(e = (\ell ,g,R,\ell ')\) is also written as \(\ell \xrightarrow {g, R} \ell '\). For any location \(\ell \), we let \(E(\ell )\) denote the set of edges leaving \(\ell \).
defines location invariants, \(\mathcal {C}\) is a finite set of clocks, \(E \subseteq \mathcal {L} \times \varPhi _\mathcal {C}\times 2^\mathcal {C}\times \mathcal {L}\) is a set of edges, and \(\ell _0\in \mathcal {L}\) is the initial location. An edge \(e = (\ell ,g,R,\ell ')\) is also written as \(\ell \xrightarrow {g, R} \ell '\). For any location \(\ell \), we let \(E(\ell )\) denote the set of edges leaving \(\ell \).
A configuration of \(\mathcal {A}\) is a pair \(q=(\ell ,v)\in \mathcal {L}\times \mathbb {R}_{\ge 0}^{\mathcal {C}}\) such that  . A run of \(\mathcal {A}\) is a sequence \(q_1e_1q_2e_2\ldots q_n\) where for all \(i\ge 1\), \(q_i=(\ell _i,v_i)\) is a configuration, and either \(e_i \in \mathbb {R}_{>0}\), in which case \(q_{i+1} = (\ell _i,v_i + e_i)\), or \(e_i =(\ell _i,g_i,R_i,\ell _{i+1})\in E\), in which case \(v_i \models g_i\) and \(q_{i+1} = (\ell _{i+1},v_i[R_i\leftarrow 0])\). A path is a sequence of edges with matching endpoint locations.
. A run of \(\mathcal {A}\) is a sequence \(q_1e_1q_2e_2\ldots q_n\) where for all \(i\ge 1\), \(q_i=(\ell _i,v_i)\) is a configuration, and either \(e_i \in \mathbb {R}_{>0}\), in which case \(q_{i+1} = (\ell _i,v_i + e_i)\), or \(e_i =(\ell _i,g_i,R_i,\ell _{i+1})\in E\), in which case \(v_i \models g_i\) and \(q_{i+1} = (\ell _{i+1},v_i[R_i\leftarrow 0])\). A path is a sequence of edges with matching endpoint locations.
2.2 Zones and DBMs
Several tools for timed automata implement algorithms based on zones, which are particular polyhedra definable with clock constraints. Formally, a zone Z is a subset of \(\mathbb {R}_{\ge 0}^{\mathcal {C}}\) definable by a guard in \(\varPhi _\mathcal {C}\).
We recall a few basic operations defined on zones. First, the intersection \(Z\cap Z'\) of two zones Z and \(Z'\) is clearly a zone. Given a zone Z, the set of time-successors of Z, defined as \(Z\mathord \uparrow = \{v+t \in \mathbb {R}_{\ge 0}^\mathcal {C}\mid t\in \mathbb {R}_{\ge 0},\ v \in Z\}\), is easily seen to be a zone; similarly for time-predecessors \(Z\mathord \downarrow = \{v \in \mathbb {R}_{\ge 0}^\mathcal {C}\mid \exists t \ge 0.\ {v + t \in Z}\}\). Given \(R\subseteq \mathcal {C}\), we let  be the zone \(\{v[R\leftarrow 0] \in \mathbb {R}_{\ge 0}^\mathcal {C}\mid v \in Z\}\), and
be the zone \(\{v[R\leftarrow 0] \in \mathbb {R}_{\ge 0}^\mathcal {C}\mid v \in Z\}\), and  .
.
Zones can be represented as difference-bound matrices (DBM) [8, 15]. Let \({\mathcal {C}_0}= \mathcal {C}\cup \{0\}\), where 0 is an extra symbol representing a special clock variable whose value is always 0. A DBM is a \(|{\mathcal {C}_0}| \times |{\mathcal {C}_0}| \)-matrix taking values in  . Intuitively, cell (x, y) of a DBM M stores a pair \((d,\prec )\) representing an upper bound on the difference \(x-y\). For any DBM M, we let \([\![M ]\!]\) denote the zone it defines.
. Intuitively, cell (x, y) of a DBM M stores a pair \((d,\prec )\) representing an upper bound on the difference \(x-y\). For any DBM M, we let \([\![M ]\!]\) denote the zone it defines.
While several DBMs can represent the same zone, each zone admits a canonical representation, which is obtained by storing the tightest clock constraints defining the zone. This canonical representation can be obtained by computing shortest paths in a graph where the vertices are clocks and the edges weighted by clock constraints, with natural addition and comparison of elements of  . This graph has a negative cycle if, and only if, the associated DBM represents the empty zone.
. This graph has a negative cycle if, and only if, the associated DBM represents the empty zone.
All the operations on zones can be performed efficiently (in \(O(|{\mathcal {C}_0}| ^3)\)) on their associated DBMs while maintaining reduced form. For instance, the intersection \(N=Z\cap Z'\) of two canonical DBMs Z and \(Z'\) can be obtained by first computing the DBM \(M=\min (Z,Z')\) such that \(M(x,y)=\min \{Z(x,y),Z'(x,y)\}\) for all \((x,y)\in {\mathcal {C}_0}^2\), and then turning M into canonical form. We refer to [8] for full details. By a slight abuse of notation, we use the same notations for DBMs as for zones, writing e.g. \(M'=M\mathord \uparrow \), where M and \(M'\) are reduced DBMs such that \([\![M' ]\!]=[\![M ]\!]\mathord \uparrow \). Given an edge \(e = (\ell ,g,R,\ell ')\), and a zone Z, we define  , and
, and  . For a path \(\rho =e_1e_2\ldots e_n\), we define
. For a path \(\rho =e_1e_2\ldots e_n\), we define  and
and  by iteratively applying
by iteratively applying  and
and  respectively.
respectively.
2.3 Clock-Predicate Abstraction and Interpolation
For all clocks x and y in \({\mathcal {C}_0}\), we consider a finite set  , and gather these in a table
, and gather these in a table  .
.  is the abstract domain which restricts zones to be defined only using constraints of the form \(x-y \prec k\) with
is the abstract domain which restricts zones to be defined only using constraints of the form \(x-y \prec k\) with  , as seen earlier. Let us call
, as seen earlier. Let us call  the concrete domain if
the concrete domain if  for all \(x,y \in {\mathcal {C}_0}\). A zone Z is
for all \(x,y \in {\mathcal {C}_0}\). A zone Z is  -definable if there exists a DBM D such that \(Z=[\![D ]\!]\) and
-definable if there exists a DBM D such that \(Z=[\![D ]\!]\) and  for all \(x,y\in {\mathcal {C}_0}\). Note that we do not require this witness DBM D to be reduced; the reduction of such a DBM might introduce additional values. We say that domain
for all \(x,y\in {\mathcal {C}_0}\). Note that we do not require this witness DBM D to be reduced; the reduction of such a DBM might introduce additional values. We say that domain  is a refinement of
is a refinement of  if for all \(x,y \in {\mathcal {C}_0}\), we have
if for all \(x,y \in {\mathcal {C}_0}\), we have  .
.
An abstract domain  induces an abstraction function
induces an abstraction function  where
where  is the smallest
is the smallest  -definable zone containing Z. For any reduced DBM D,
-definable zone containing Z. For any reduced DBM D,  can be computed by setting
can be computed by setting  (with \(\min \emptyset =(\infty ,<)\)).
(with \(\min \emptyset =(\infty ,<)\)).
An interpolant for a pair of zones \((Z_1,Z_2)\) with \(Z_1\cap Z_2 = \emptyset \) is a zone \(Z_3\) with \(Z_1 \subseteq Z_3\) and \(Z_3 \cap Z_2 = \emptyset \)Footnote 1 [29]. We use interpolants to refine our abstractions; in order not to add too many new constraints when refining, our aim is to find minimal interpolants: define the density of a DBM D as \(d(D) =\#\{(x,y) \in {\mathcal {C}_0}^2 \mid D(x,y)\not =(\infty ,<)\}\). Notice that while any pair of disjoint convex polyhedra can be separated by hyperplanes, not all pairs of disjoint zones admit interpolants of density 1; this is because not all (half-spaces delimited by) hyperplanes are zones. Still, we can bound the density of a minimal interpolant:
Lemma 1
For any pair of disjoint, non-empty zones (A, B), there exists an interpolant of density less than or equal to \(|{\mathcal {C}_0}|/2\).
By adapting the algorithm of [29] for computing interpolants, we can compute minimal interpolants efficiently:
Proposition 2
Computing a minimal interpolant can be performed in \(O(|\mathcal {C}| ^4)\).
3 Enumerative Algorithm
The first type of algorithm we present is a zone-based enumerative algorithm based on the clock-predicate abstractions. Let us first describe the overall algorithm in Algorithm 1, which is a typical abstraction-refinement loop. We then explain how the abstract reachability and refinement procedures are instantiated.

The initialization at line 1 chooses an abstract domain for the initial state, which can be either empty (thus the coarsest abstraction) or defined according to some heuristics. The algorithm maintains the
 and
and
 lists that are used in the forward exploration. As usual, the
lists that are used in the forward exploration. As usual, the
 list can be implemented as a stack, a queue, or another priority list that determines the search order. The algorithm also uses covering nodes. Indeed if there are two node n and \(n'\), with
list can be implemented as a stack, a queue, or another priority list that determines the search order. The algorithm also uses covering nodes. Indeed if there are two node n and \(n'\), with  ,
,  , \(n.\ell =n'.\ell \), and \(n'{.}z\subseteq n{.}Z\), then we know that every location reachable from \(n'\) is also reachable from n. Since we have already explored n and we generated its successors, there is no need to explore the successors of \(n'\). The algorithm explicitly creates an exploration tree: line 2 creates a node containing location \(\ell _0\), zone \(\mathbf {0}{\uparrow }\), and the abstract domain
, \(n.\ell =n'.\ell \), and \(n'{.}z\subseteq n{.}Z\), then we know that every location reachable from \(n'\) is also reachable from n. Since we have already explored n and we generated its successors, there is no need to explore the successors of \(n'\). The algorithm explicitly creates an exploration tree: line 2 creates a node containing location \(\ell _0\), zone \(\mathbf {0}{\uparrow }\), and the abstract domain  as the root of our tree, and adds this to the
as the root of our tree, and adds this to the
 list. More details on the tree are given in the next subsection. Procedure
list. More details on the tree are given in the next subsection. Procedure
 then looks for a trace to the target location \(\ell _T\). If such a trace exists, line 9 checks its feasibility. Here \(\pi \) is a sequence of node and edges of \(\mathcal {A}\). The feasibility check is done by computing predecessors with zones starting from the final state, without using the abstraction function. If the last zone intersects our initial zone, this means that the trace is feasible. More details are given in Sect. 3.2.
then looks for a trace to the target location \(\ell _T\). If such a trace exists, line 9 checks its feasibility. Here \(\pi \) is a sequence of node and edges of \(\mathcal {A}\). The feasibility check is done by computing predecessors with zones starting from the final state, without using the abstraction function. If the last zone intersects our initial zone, this means that the trace is feasible. More details are given in Sect. 3.2.
3.1 Abstract Forward Reachability:

We give a generic algorithm independently from the implementations of the abstraction functions and the refinement procedure.
Algorithm 2 describes the reachability procedure under a given abstract domain  . It is similar to the standard forward reachability algorithm using a
. It is similar to the standard forward reachability algorithm using a
 -list and a
-list and a
 -list. We explicitly create an exploration tree where the leaves are nodes in
-list. We explicitly create an exploration tree where the leaves are nodes in  , covered nodes, or nodes that have no non-empty successors. Each node n contains the fields \(\ell ,Z\) which are labels describing the current location and zone; field
, covered nodes, or nodes that have no non-empty successors. Each node n contains the fields \(\ell ,Z\) which are labels describing the current location and zone; field
 points to a node covering the current node (it is undefined if the current node is not (known to be) covered); field
points to a node covering the current node (it is undefined if the current node is not (known to be) covered); field
 points to the parent node in the tree (it is undefined for the root); and field
points to the parent node in the tree (it is undefined for the root); and field  is the abstract domain associated with the node. Thus, the algorithm uses a possibly different abstract domain for each node in the exploration tree.
is the abstract domain associated with the node. Thus, the algorithm uses a possibly different abstract domain for each node in the exploration tree.
The difference of our algorithm w.r.t. the standard reachability can be seen at lines 8 and 11. At line 8, we apply the abstraction function to the zone taken from the
 -list before adding it to the
-list before adding it to the
 -list. The abstraction function \(\alpha \) is a function of a zone Z and a node n. This allows one to define variants with different dependencies; for instance, \(\alpha \) might depend on the abstract domain \(n.\) at the current node, but it can also use other information available in n or on the path ending in n. For now, it is best to think of
-list. The abstraction function \(\alpha \) is a function of a zone Z and a node n. This allows one to define variants with different dependencies; for instance, \(\alpha \) might depend on the abstract domain \(n.\) at the current node, but it can also use other information available in n or on the path ending in n. For now, it is best to think of  . At line 11, the function
. At line 11, the function
 chooses an abstract domain for the node \(n'\). The domain could be chosen global for all nodes, or local to each node. A good trade-off, which we used in our experiments, is to have domains associated with locations of the timed automaton.
chooses an abstract domain for the node \(n'\). The domain could be chosen global for all nodes, or local to each node. A good trade-off, which we used in our experiments, is to have domains associated with locations of the timed automaton.
Remark 1
Note that we use the abstraction function when the node is inserted in the
 list. This is because we want the node to contain the smallest zone possible when we test whether the node is covered. We only need to use the abstracted zone when we compute its successor and when we test whether the node is covering. This allows us to store a unique zone.
list. This is because we want the node to contain the smallest zone possible when we test whether the node is covered. We only need to use the abstracted zone when we compute its successor and when we test whether the node is covering. This allows us to store a unique zone.
As a first step towards proving correctness of our algorithm, we show that the following property is preserved by Algorithm
 :
:

Lemma 3
Algorithm
 preserves Property (1).
preserves Property (1).
Note that although we use inclusion in Property (1),
 would actually preserve equality of zones, but we will not always have equality before running
would actually preserve equality of zones, but we will not always have equality before running
 . This is because
. This is because
 might change the zones of some nodes without updating the zones of all their descendants.
might change the zones of some nodes without updating the zones of all their descendants.
3.2 Refinement:

We now describe our refinement procedure
 . Let us now assume that
. Let us now assume that
 returns \(\pi = A_1 \xrightarrow []{\sigma _1} A_2 \xrightarrow {\sigma _2} \ldots \xrightarrow {\sigma _{k-1}} A_k\), and write
returns \(\pi = A_1 \xrightarrow []{\sigma _1} A_2 \xrightarrow {\sigma _2} \ldots \xrightarrow {\sigma _{k-1}} A_k\), and write  for the domain associated with each \(A_i\). We write \(C_1\) for the initial concrete zone, and for \(i< k\), we define
for the domain associated with each \(A_i\). We write \(C_1\) for the initial concrete zone, and for \(i< k\), we define  . We also note \(Z_k=A_k\) and for \(i<k\),
. We also note \(Z_k=A_k\) and for \(i<k\),  . Then \(\pi \) is not feasible if, and only if,
. Then \(\pi \) is not feasible if, and only if,  , or equivalently
, or equivalently  . Since for all \(i<k\), it holds \(C_i\subseteq A_{i+1}\), we have that \(\pi \) is not feasible if, and only if, \(\exists i\le k.\ C_i\cap Z_i=\emptyset \). We illustrate this on Fig. 2.
. Since for all \(i<k\), it holds \(C_i\subseteq A_{i+1}\), we have that \(\pi \) is not feasible if, and only if, \(\exists i\le k.\ C_i\cap Z_i=\emptyset \). We illustrate this on Fig. 2.
Let us assume that \(\pi \) is not feasible. Let us denote by \(i_0\) the maximal index such that \(C_{i_0}\cap Z_{i_0}=\emptyset \). This index also has the property that for all \(j < i_0\), we have \(Z_j=\emptyset \) and \(Z_{i_0}\ne \emptyset \). Once we have identified this trace as spurious by computing the \(Z_j\), we have two possibilities:
-
if
 : this means that we can reach \(A_k\) from
: this means that we can reach \(A_k\) from  but not from \(C_{i_0}\). In other words, our abstraction is too coarse and we must add some values to
but not from \(C_{i_0}\). In other words, our abstraction is too coarse and we must add some values to  so that
so that  . Those values are found by computing the interpolant of \(Z_{i_0}\) and \(C_{i_0}\)
. Those values are found by computing the interpolant of \(Z_{i_0}\) and \(C_{i_0}\) -
Otherwise it means that
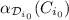 cannot reach \(A_k\) and the only reason the trace exists is because either
cannot reach \(A_k\) and the only reason the trace exists is because either  or \(A_{i_0 -1}\) has been modified at some point and \(A_{i_0}\) was not modified accordingly.
or \(A_{i_0 -1}\) has been modified at some point and \(A_{i_0}\) was not modified accordingly.
We can then update the values of \(C_i\) for \(i>i_0\) and repeat the process until we reach an index \(j_0\) such that \(C_{j_0}= \emptyset \). We then have modified the nodes \(n_{i_0},\ldots ,n_{j_0}\) and knowing that \(n_{j_0}{.}Z=\emptyset \), we can delete it and all of its descendants. Since some of the descendants of \(n_{i_0}\) have not been modified, this might cause some refinements of the first type in the future. In order to ensure termination, we sometimes have to cut a subtree from a node in \(n_{i_0},\ldots ,n_{j_0-1}\) and reinsert it in the
 list to restart the exploration from there. We call this action
list to restart the exploration from there. We call this action
 , and we can use several heuristics to decide when to use it. In the rest of this paper we will use the following heuristics: we perform
, and we can use several heuristics to decide when to use it. In the rest of this paper we will use the following heuristics: we perform
 on the first node of \(n_{i_0}...n_{j_0}\) that is covered by some other node. Since this node is covered, we know that we will not restart the exploration from this node, or that the node was covered by one of its descendant. If none of these nodes are covered, we delete \(n_{j_0}\) and its descendants. Other heuristics are possible, for instance applying
on the first node of \(n_{i_0}...n_{j_0}\) that is covered by some other node. Since this node is covered, we know that we will not restart the exploration from this node, or that the node was covered by one of its descendant. If none of these nodes are covered, we delete \(n_{j_0}\) and its descendants. Other heuristics are possible, for instance applying
 on \(n_{i_0}\). We found that the above heuristics was the most efficient in our experiments.
on \(n_{i_0}\). We found that the above heuristics was the most efficient in our experiments.
Lemma 4
Pick a node n, and let \(Y=n{.}Z\). Then after running
 , either node n is deleted, or it holds \(n{.}Z\subseteq Y\). In other words, the zone of a node can only be reduced by
, either node n is deleted, or it holds \(n{.}Z\subseteq Y\). In other words, the zone of a node can only be reduced by
 .
.
It follows that
 also preserves Property (1), so that:
also preserves Property (1), so that:
Lemma 5
Algorithm 1 satisfies Property (1).
We can then prove that our algorithm correctly decides the reachability problem and always terminates.
Theorem 6
Algorithm 1 terminates and is correct.
4 Symbolic Algorithm
4.1 Boolean Encoding of Zones
We now present a symbolic algorithm that represents abstract states using Boolean formulas. Let  , and
, and  be a set of variables. A Boolean formula f that uses variables from set
be a set of variables. A Boolean formula f that uses variables from set  will be written f(X) to make the dependency explicit; we sometimes write f(X, Y) in place of \(f(X\cup Y)\). Such a formula represents a set
will be written f(X) to make the dependency explicit; we sometimes write f(X, Y) in place of \(f(X\cup Y)\). Such a formula represents a set  . We consider primed versions of all variables; this will allow us to write formulas relating two valuations. For any subset
. We consider primed versions of all variables; this will allow us to write formulas relating two valuations. For any subset  , we define \(X' = \{p' \mid p \in X\}\).
, we define \(X' = \{p' \mid p \in X\}\).
A literal is either p or \(\lnot p\) for a variable p. Given a set X of variables, an X-minterm is the conjunction of literals where each variable of X appears exactly once. X-minterms can be seen as elements of \(\mathbb {B}^X\). Given a vector of Boolean formulas \(Y=(Y_x)_{x \in X}\), formula \(f[Y{/}X]\) is the substitution of X by Y in f, obtained by replacing each \(x \in X\) with the formula \(Y_x\). The positive cofactor of f(X) by x is \( \exists x.\ (x \wedge f(X))\), and its negative cofactor is \(\exists x.\ (\lnot x \wedge f(X))\).
Let us define a generic operator \(\texttt {post} \) that computes successors of a set S(X, Y) given a relation \(R(X,X')\) (here, Y designates any set of variables on which S might depend outside of X): \( \texttt {post} _R(S(X,Y)) = (\exists X. S(X,Y) \wedge R(X,X'))[X/X'] \). Similarly, we set \( \texttt {pre} _R(S(X,Y)) = (\exists X'. S(X,Y)[X'/X] \wedge R(X,X')) \), which computes the predecessors of S(X, Y) by the relation R [24].
Clock Predicate Abstraction. We fix a total order \(\mathrel {\triangleleft }\) on \({\mathcal {C}_0}\). In this section, abstract domains are defined as  , that is only for pairs \(x\mathrel {\triangleleft }y\). In fact, constraints of the form \(x-y \le k\) with \(x\mathrel {\triangleright }y\) are encoded using the negation of \(y-x<-k\) since \((x-y\le k) \Leftrightarrow \lnot (y-x <-k\)). We thus define
, that is only for pairs \(x\mathrel {\triangleleft }y\). In fact, constraints of the form \(x-y \le k\) with \(x\mathrel {\triangleright }y\) are encoded using the negation of \(y-x<-k\) since \((x-y\le k) \Leftrightarrow \lnot (y-x <-k\)). We thus define  for all \(x \mathrel {\triangleright }y\).
for all \(x \mathrel {\triangleright }y\).
For \(x,y \in {\mathcal {C}_0}\), let  denote the set of clock predicates associated to
denote the set of clock predicates associated to  :
:

Let  denote the set of all clock predicates associated with
denote the set of all clock predicates associated with  (we may omit the superscript
(we may omit the superscript  when it is clear). For all \((x,y) \in {\mathcal {C}_0}^2\) and
when it is clear). For all \((x,y) \in {\mathcal {C}_0}^2\) and  , we denote by \(p_{x-y\prec k} \) the literal \(P_{x-y\prec k} \) if \(x\mathrel {\triangleleft }y\), and \(\lnot P_{y-x \prec ^{-1} -k} \) otherwise (where
, we denote by \(p_{x-y\prec k} \) the literal \(P_{x-y\prec k} \) if \(x\mathrel {\triangleleft }y\), and \(\lnot P_{y-x \prec ^{-1} -k} \) otherwise (where  and
and  ). We also consider a set \(\mathcal {B}\) of Boolean variables used to encode locations. Overall, the state space is described using Boolean formulas on these two types of variables, so states are elements of
). We also consider a set \(\mathcal {B}\) of Boolean variables used to encode locations. Overall, the state space is described using Boolean formulas on these two types of variables, so states are elements of  .
.
Our Boolean encoding of clock constraints and semantic operations follow those of [28] for a concrete domain. We define these however for abstract domains, and show how successor computation and refinement operations can be performed.
Let us define the clock semantics of predicate \(P_{x-y\preceq k} \) as \([\![P_{x-y \preceq k} ]\!]_{{\mathcal {C}_0}} = \{\nu \in \mathbb {R}_{\ge 0}^{\mathcal {C}_0}\mid \nu (x) - \nu (y) \preceq k\}\). Since the set \(\mathcal {C}\) of clocks is fixed, we may omit the subscript and just write \([\![P_{x-y\preceq k} ]\!]\). We define the conjunction, disjunction, and negation as intersection, union, and complement, respectively. Given a  -minterm
-minterm  , we define
, we define  . Thus, negation of a predicate encodes its complement. For a Boolean formula
. Thus, negation of a predicate encodes its complement. For a Boolean formula  , we set
, we set  . Intuitively, the minterms of
. Intuitively, the minterms of  define smallest zones of \(\mathbb {R}_{\ge 0}^\mathcal {C}\) definable using
define smallest zones of \(\mathbb {R}_{\ge 0}^\mathcal {C}\) definable using  . A minterm
. A minterm  defines a pair
defines a pair  where l is encoded by
where l is encoded by  and
and  . A Boolean formula F on
. A Boolean formula F on  defines a set
defines a set  of such pairs. A minterm v is satisfiable if
of such pairs. A minterm v is satisfiable if  .
.
An abstract domain  induces an abstraction function
induces an abstraction function  with
with  , from the set of zones to the set of subsets of Boolean valuations on
, from the set of zones to the set of subsets of Boolean valuations on  . We define the concretization function as
. We define the concretization function as  . The pair
. The pair  is a Galois connection, and
is a Galois connection, and  is the most precise abstraction of Z in the domain induced by
is the most precise abstraction of Z in the domain induced by  . Notice that
. Notice that  is non-convex in general: for instance, if the clock predicates are \(x\le 2,y\le 2\), then the set defined by the constraint \(x=y\) maps to \((p_{x\le 2} \wedge p_{y\le 2}) \vee (\lnot p_{x\le 2} \wedge \lnot p_{y\le 2})\).
is non-convex in general: for instance, if the clock predicates are \(x\le 2,y\le 2\), then the set defined by the constraint \(x=y\) maps to \((p_{x\le 2} \wedge p_{y\le 2}) \vee (\lnot p_{x\le 2} \wedge \lnot p_{y\le 2})\).
4.2 Reduction and Successor Computation
We now define the reduction operation, which is similar to the reduction of DBMs. The idea is to eliminate unsatisfiable minterms from a given Boolean formula. For example, we would like to make sure that in all minterms, if \(p_{x-y\le 1}\) holds, then so does \(p_{x-y\le 2}\), when both are available predicates. Another issue is to eliminate minterms that are unsatisfiable due to triangle inequality. This is similar to the shortest path computation used to turn DBMs in canonical form.
Example 1
Given predicates  , the formula \(p_{x-y\le 1} \wedge p_{y-z\le 1} \) is not reduced since it contains the unsatisfiable minterm \(p_{x-y\le 1} \wedge p_{y-z\le 1} \wedge \lnot p_{x-z\le 2} \). However, the same formula is reduced if
, the formula \(p_{x-y\le 1} \wedge p_{y-z\le 1} \) is not reduced since it contains the unsatisfiable minterm \(p_{x-y\le 1} \wedge p_{y-z\le 1} \wedge \lnot p_{x-z\le 2} \). However, the same formula is reduced if  .
.
In this paper, we use limited reduction, since reductions are the most expensive operations in our algorithms. The following formula corresponds to 2-reduction, which intuitively amounts to applying shortest paths for paths of lengths 1 and 2:

Lemma 7
For all formulas  , we have
, we have  and all minterms of
and all minterms of  are 2-reduced.
are 2-reduced.
Since 2-reduction des not consider shortest paths of all lengths, there are, in general, 2-reduced unsatisfiable minterms. Nevertheless, any abstraction can be refined so that the updated 2-reduction eliminates a given unsatisfiable minterm:
Lemma 8
Let  be a minterm such that
be a minterm such that  and \([\![v ]\!] = \emptyset \). One can compute in polynomial time a refinement
and \([\![v ]\!] = \emptyset \). One can compute in polynomial time a refinement  such that
such that  .
.
We now explain how successor computation is realized in our encoding. For a guard g, assume we have computed an abstraction  in the present abstract domain. For each transition \(\sigma =(\ell _1,g,R,\ell _2)\), let us define the formula
in the present abstract domain. For each transition \(\sigma =(\ell _1,g,R,\ell _2)\), let us define the formula  . We show how each basic operation on zones can be computed in our BDD encoding. In our algorithm, all formulas
. We show how each basic operation on zones can be computed in our BDD encoding. In our algorithm, all formulas  representing sets of states are assumed to be reduced, that is,
representing sets of states are assumed to be reduced, that is,  .
.
The intersection operation is simply logical conjunction:
Lemma 9
For all reduced formulas  and
and  , we have
, we have  .
.
For the time successors, we define  where
where

Lemma 10
For any Boolean formula  ,
,  . Moreover, if
. Moreover, if  is the concrete domain and A is reduced, then this holds with equality.
is the concrete domain and A is reduced, then this holds with equality.
Following similar ideas, we handle clock resets by defining  , for a (complex) relation
, for a (complex) relation  to encode how predicates evolve (see the long version [27] of this article for more detailled explanations).
to encode how predicates evolve (see the long version [27] of this article for more detailled explanations).
We get:
Lemma 11
For any Boolean formula  , and any clock \(z\in \mathcal {C}\), we have
, and any clock \(z\in \mathcal {C}\), we have  . Moreover, if
. Moreover, if  is the concrete domain, and A is reduced, then the above holds with equality.
is the concrete domain, and A is reduced, then the above holds with equality.
4.3 Model-Checking Algorithm
Algorithm 3 shows how to check the reachability of a target location given an abstract domain. The list
 contains, at position i, the set of states that are reachable in i steps. The function
contains, at position i, the set of states that are reachable in i steps. The function  computes the disjunction of immediate successors by all edges. It consists in looping over all edges \(e=(l_1,g,R,l_2)\), and gathering the following image by e:
computes the disjunction of immediate successors by all edges. It consists in looping over all edges \(e=(l_1,g,R,l_2)\), and gathering the following image by e:

where \(R=\{r_1,\ldots ,r_k\}\). We thus use a partitioned transition relation and do not compute the monolithic transition relation.
When the target location is found to be reachable,
 (
(
 ) returns a trace reaching the target location. This is standard and can be done by computing backwards from the last element of
) returns a trace reaching the target location. This is standard and can be done by computing backwards from the last element of
 , by finding which edge can be applied to reach the current state. Since both reset and time successor operations are defined using relations, predecessors in our abstract system can be easily computed using the operator \(\texttt {pre} _R\). As it is standard, we omit the precise definition of this function (the reader can refer to the implementation) but assume that it returns a trace of the form \( A_1 \xrightarrow []{\sigma _1} A_2 \xrightarrow {\sigma _2} \ldots \xrightarrow {\sigma _{n-1}} A_n, \) where the
, by finding which edge can be applied to reach the current state. Since both reset and time successor operations are defined using relations, predecessors in our abstract system can be easily computed using the operator \(\texttt {pre} _R\). As it is standard, we omit the precise definition of this function (the reader can refer to the implementation) but assume that it returns a trace of the form \( A_1 \xrightarrow []{\sigma _1} A_2 \xrightarrow {\sigma _2} \ldots \xrightarrow {\sigma _{n-1}} A_n, \) where the  are minterms and the \(\sigma _i\) belong to the trace alphabet \(\varSigma = \{\text {up}, r_\emptyset \} \cup \{r(x)\}_{x \in \mathcal {C}}\), with the following meaning:
are minterms and the \(\sigma _i\) belong to the trace alphabet \(\varSigma = \{\text {up}, r_\emptyset \} \cup \{r(x)\}_{x \in \mathcal {C}}\), with the following meaning:
-
if \(A_i\xrightarrow {\text {up}} A_{i+1}\) then
 ;
; -
if \(A_i \xrightarrow {r_\emptyset } A_{i+1}\) then \(A_{i+1} = A_i\);
-
if \(A_i \xrightarrow {r(x)} A_{i+1}\) then
 .
.
The feasibility of such a trace is easily checked using DBMs.

The overall algorithm then follows a classical CEGAR scheme. We initialize  by adding the clock constraints that appear syntactically in \(\mathcal {A}\), which is often a good heuristic. We run the reachability check of Algorithm 3. If no trace is found, then the target location is not reachable. If a trace is found, then we check for feasibility. If it is feasible, then the counterexample is confirmed. Otherwise, the trace is spurious and we run the refinement procedure described in the next subsection, and repeat the analysis.
by adding the clock constraints that appear syntactically in \(\mathcal {A}\), which is often a good heuristic. We run the reachability check of Algorithm 3. If no trace is found, then the target location is not reachable. If a trace is found, then we check for feasibility. If it is feasible, then the counterexample is confirmed. Otherwise, the trace is spurious and we run the refinement procedure described in the next subsection, and repeat the analysis.
4.4 Abstraction Refinement
Since we initialize  with all clock constraints appearing in guards, we can assume that all guards are represented exactly in the considered abstractions. Note that the algorithm can be easily extended to the general case; but this simplifies the presentation.
with all clock constraints appearing in guards, we can assume that all guards are represented exactly in the considered abstractions. Note that the algorithm can be easily extended to the general case; but this simplifies the presentation.
The abstract transition relation we use is not the most precise abstraction of the concrete transition relation. Therefore, it is possible to have abstract transitions \(A_1 \xrightarrow {a} A_2\) for some action a while no concrete transition exists between \([\![A_1 ]\!]\) and \([\![A_2 ]\!]\). This requires care and is not a direct application of the standard refinement technique from [11]. A second difficulty is due to incomplete reduction of the predicates using  . In fact, some reachable states in our abstract model will be unsatisfiable. Let us explain how we refine the abstraction in each of these cases.
. In fact, some reachable states in our abstract model will be unsatisfiable. Let us explain how we refine the abstraction in each of these cases.
Consider an algorithm  which returns an interpolant of given zones \(Z_1,Z_2\). In what follows, by the refinement of
which returns an interpolant of given zones \(Z_1,Z_2\). In what follows, by the refinement of  by
by  , we mean the domain obtained by adding
, we mean the domain obtained by adding  to
to  for all constraints \(x-y\prec k\) of
for all constraints \(x-y\prec k\) of  . Observe that
. Observe that  in this case.
in this case.
We define concrete successor and predecessor operations for the actions in \(\varSigma \). For each \(a \in \varSigma \), let  denote the concrete predecessor operation on zones defined straightforwardly, and similarly for
denote the concrete predecessor operation on zones defined straightforwardly, and similarly for  .
.
Consider domain  and the induced abstraction function
and the induced abstraction function  . Assume that we are given a spurious trace \(\pi =A_1 \xrightarrow []{\sigma _1} A_2 \xrightarrow {\sigma _1} \ldots \xrightarrow {\sigma _{n-1}} A_n\). Let \(B_1\ldots B_n\) be the sequence of concrete states visited along \(\pi \) in \(\mathcal {A}\), that is, \(B_1\) is the concrete initial state, and for all \(2\le i \le n\), let
. Assume that we are given a spurious trace \(\pi =A_1 \xrightarrow []{\sigma _1} A_2 \xrightarrow {\sigma _1} \ldots \xrightarrow {\sigma _{n-1}} A_n\). Let \(B_1\ldots B_n\) be the sequence of concrete states visited along \(\pi \) in \(\mathcal {A}\), that is, \(B_1\) is the concrete initial state, and for all \(2\le i \le n\), let  . This sequence can be computed using DBMs.
. This sequence can be computed using DBMs.
The trace is realizable if \(B_n \ne \emptyset \), in which case the counterexample is confirmed. Otherwise it is spurious. We show how to refine the abstraction to eliminate a spurious trace \(\pi \).
Let \(i_0\) be the maximal index such that \(B_{i_0} \ne \emptyset \). There are three possible reasons explaining why \(B_{i_0+1}\) is empty:
-
1.
first, if the abstract successor \(A_{i_0+1}\) is unsatisfiable, that is, if it contains contradictory predicates; in this case, \([\![A_{i_0+1} ]\!] = \emptyset \), and the abstraction is refined by Lemma 8 to eliminate this case by strengthening
 .
. -
2.
if there are predecessors of \(A_{i_0+1}\) inside \(A_{i_0}\) but none of them are in \(B_{i_0}\), i.e.,
 ; in this case, we refine the domain by separating these predecessors from the rest of \(A_{i_0}\) using
; in this case, we refine the domain by separating these predecessors from the rest of \(A_{i_0}\) using  , as in [11].
, as in [11]. -
3.
otherwise, there are no predecessors of \(A_{i_0+1}\) inside \(A_{i_0}\): we refine the abstraction according to the type of the transition from step \(i_0\) to \(i_0+1\):
-
(a)
if \(\pi _{i_0}=\text {up}\): refine
 by
by 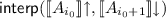 .
. -
(b)
if \(\pi _{i_0}=r(x)\): refine
 by
by 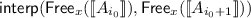 .
.
-
(a)
Note that the case \(\pi _{i_0}=r_\emptyset \) is not possible since this induces the identity function both in the abstract and concrete systems.
Given abstraction  and spurious trace \(\pi \), let
and spurious trace \(\pi \), let  denote the refined abstraction
denote the refined abstraction  obtained as described above.
obtained as described above.
The following two lemmas justify the two subcases of the third case above. They prove that the detected spurious transition disappears after refinement. The reset and up operations depend on the abstraction, so we make this dependence explicit below by using superscripts, as in  and
and  , in order to distinguish the operations before and after a refinement.
, in order to distinguish the operations before and after a refinement.
Lemma 12
Consider  with \([\![A_1 ]\!]\mathord \uparrow \cap [\![A_2 ]\!] = \emptyset \). Then \([\![A_{1} ]\!]\mathord \uparrow \cap [\![A_{2} ]\!]\mathord \downarrow = \emptyset \). Moreover, if \(\alpha '\) is obtained by refinement of \(\alpha \) by
with \([\![A_1 ]\!]\mathord \uparrow \cap [\![A_2 ]\!] = \emptyset \). Then \([\![A_{1} ]\!]\mathord \uparrow \cap [\![A_{2} ]\!]\mathord \downarrow = \emptyset \). Moreover, if \(\alpha '\) is obtained by refinement of \(\alpha \) by  , then for all
, then for all  , \([\![A_1' ]\!] \subseteq [\![A_1 ]\!]\) implies \([\![A_2' ]\!] \cap [\![A_2 ]\!] = \emptyset \).
, \([\![A_1' ]\!] \subseteq [\![A_1 ]\!]\) implies \([\![A_2' ]\!] \cap [\![A_2 ]\!] = \emptyset \).

Lemma 13
Consider \(x \in \mathcal {C}\), and  such that \([\![A_1 ]\!][x\leftarrow 0] \cap [\![A_2 ]\!] = \emptyset \). Then
such that \([\![A_1 ]\!][x\leftarrow 0] \cap [\![A_2 ]\!] = \emptyset \). Then  . Moreover, if \(\alpha '\) is obtained by refinement of \(\alpha \) by
. Moreover, if \(\alpha '\) is obtained by refinement of \(\alpha \) by  , then for all
, then for all  with \([\![A_1' ]\!] \subseteq [\![A_1 ]\!]\), we have \([\![A_2' ]\!] \cap [\![A_2 ]\!] = \emptyset \).
with \([\![A_1' ]\!] \subseteq [\![A_1 ]\!]\), we have \([\![A_2' ]\!] \cap [\![A_2 ]\!] = \emptyset \).
5 Experiments
We implemented both algorithms. The symbolic version was implemented in OCaml using the CUDD libraryFootnote 2; the explicit version was implemented in C++ within an existing model checker using Uppaal DBM library. Both prototypes take as input networks of timed automata with invariants, discrete variables, urgent and committed locations. The presented algorithms are adapted to these features without difficulty.
We evaluated our algorithms on three classes of benchmarks we believe are significant. We compare the performance of the algorithm with that of Uppaal [7] which is based on zones, as well as the BDD-based model checker engine of PAT [25]. We were unable to compare with RED [30] which is not maintained anymore and not open source, and with which we failed to obtain correct results. The tool used in [16] was not available either. We thus only provide a comparison here with two well-maintained tools.
Two of our benchmarks are variants of schedulability-analysis problems where task execution times depend on the internal states of executed processes, so that an analysis of the state space is necessary to obtain a precise answer.
Monoprocess Scheduling Analysis. In this variant, a single process sequentially executes tasks on a single machine, and the execution time of each cycle depends on the state of the process. The goal is to determine a bound on the maximum execution time of a single cycle. This depends on the semantics of the process since the bound depends on the reachable states.
More precisely, we built a set of benchmarks where the processes are defined by synchronous circuit models taken from the Synthesis Competition (http://www.syntcomp.org). We assume that each latch of the circuit is associated with a resource, and changing the state of the resource takes some amount of time. So a subset of the latches have clocks associated with them, which measure the time elapsed since the latest value change (latest moment when the value changed from 0 to 1, or from 1 to 0). We provide two time positive bounds \(\ell _0\) and \(\ell _1\) for each latch, which determine the execution time as follows: if the value of latch \(\ell \) changes from 0 to 1 (resp. from 1 to 0), then the execution time of the present cycle cannot be less than \(\ell _1\) (resp. \(\ell _0\)). The execution time of the step is then the minimum that satisfies these constraints.
Multi-process Stateful Scheduling Analysis. In this variant, three processes are scheduled on two machines with a round-robin policy. Processes schedule tasks one after the other without any delay. As in the previous benchmarks, a process executing a task (on any machine) corresponds to a step of the synchronous circuit model. Each task is described by a tuple \((C_1,C_2,D)\) which defines the minimum and maximum execution times, and the relative deadline. When a task finishes, the next task arrives immediately. The values in the tuple depend on the state of the process. The goal is to check the absence of any deadline miss. Processes are also instantiated with AIG circuits from http://www.syntcomp.org.
Asynchronous Computation. We consider an asynchronous network of “threshold gates”, defined as follows: each gate is characterized by a tuple \((n,\theta ,[l,u])\) where n is the number of inputs, \(0\le \theta \le n\) is the threshold, and \(l\le u\) are lower and upper bounds on activation time. Each gate has an output which is initially undefined. The gate becomes active during the time period [l, u]. During this time, if all inputs are defined, and if at least \(\theta \) of the inputs have value 1, then it sets its output to 1. At the end of the time period, it becomes deactivated and the output becomes undefined again, until the next period, which starts l time units after the deactivation. The goal is to check whether the given gate can output 1 within a given time bound T.
Results. Figure 3 displays the results of our experiments. All algorithms were given 8 GB of memory and a timeout of 30 min, and the experiments were run on laptop with an Intel i7@3.2 Ghz processor running Linux. The symbolic algorithm performs best among all on the monoprocess and multiprocess scheduling benchmarks. Uppaal is the second best, but does not solve as many benchmarks as our algorithm. Our enumerative algorithm quickly fails on these benchmarks, often running out of memory. On asynchronous computation benchmarks, our enumerative algorithm performs remarkably well, beating all other algorithms. We ran our tools on the CSMA/CD benchmarks (with 3 to 12 processes); Uppaal performs the best but our enumerative algorithm is slightly behind. The symbolic algorithm does not scale, while PAT fails to terminate in all cases.
The tool used for the symbolic algorithm is open source and can be found at https://github.com/osankur/symrob along with all the benchmarks.
6 Conclusion and Future Work
There are several ways to improve the algorithm. Since the choice of interpolants determines the abstraction function and the number of refinements, we assumed that taking the minimal interpolant should be preferable as it should keep the abstractions as coarse as possible. But it might be better to predict which interpolant is the most adapted for the rest of the computation in order to limit future refinements. The number of refinement also depends on the search order, and although it has already been studied in [23], it could be interesting to study it in this case. Generally speaking, it is worth noting that we currently cannot predict which (variant of) our algorithms is better suited for which model.
Several extensions of our algorithms could be developed, e.g. combining our algorithms with other methods based on finer abstractions as in [22], integrating predicate abstraction on discrete variables, or developing SAT-based versions of our algorithms.
Notes
- 1.
It is sometimes also required that the interpolant only involves clocks that have non-trivial constraints in both \(Z_1\) and \(Z_2\). We do not impose this requirement in our definition, but it will hold true in the interpolants computed by our algorithm.
- 2.
References
Althaus, E., et al.: Verification of linear hybrid systems with large discrete statespaces using counterexample-guided abstraction refinement. Sci. Comput. Program. 1(48), 123–160 (2017)
Alur, R., Courcoubetis, C., Dill, D.L.: Model-checking in dense real-time. Inf. Comput. 104(1), 2–34 (1993)
Alur, R., Dill, D.: Automata for modeling real-time systems. In: Paterson, M.S. (ed.) ICALP 1990. LNCS, vol. 443, pp. 322–335. Springer, Heidelberg (1990). https://doi.org/10.1007/BFb0032042
Baier, Ch., Katoen, J.-P.: Principles of Model-Checking. MIT Press, Cambridge (2008)
Ball, T., Rajamani, S.K.: The SLAM toolkit. In: Berry, G., Comon, H., Finkel, A. (eds.) CAV 2001. LNCS, vol. 2102, pp. 260–264. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44585-4_25
Behrmann, G., Bouyer, P., Larsen, K.G., Pelánek, R.: Lower and upper bounds in zone based abstractions of timed automata. In: Jensen, K., Podelski, A. (eds.) TACAS 2004. LNCS, vol. 2988, pp. 312–326. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24730-2_25
Behrmann, G.: Uppaal 4.0. In: Proceedings of the 3rd International Conference on Quantitative Evaluation of Systems (QEST 2006), pp. 125–126. IEEE Computer Society Press, September 2006
Bengtsson, J., Yi, W.: Timed automata: semantics, algorithms and tools. In: Desel, J., Reisig, W., Rozenberg, G. (eds.) ACPN 2003. LNCS, vol. 3098, pp. 87–124. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-27755-2_3
Berthomieu, B., Menasche, M.: An enumerative approach for analyzing time Petri nets. In: Mason, R.E.A. (eds.) Information Processing–Proceedings of the 9th IFIP World Computer Congress (WCC 1983), pp. 41–46. North-Holland/IFIP, September 1983
Clarke, E.M., Emerson, E.A.: Design and synthesis of synchronization skeletons using branching time temporal logic. In: Kozen, D. (ed.) Logic of Programs 1981. LNCS, vol. 131, pp. 52–71. Springer, Heidelberg (1982). https://doi.org/10.1007/BFb0025774
Clarke, E.M., Grumberg, O., Jha, S., Lu, Y., Veith, H.: Counterexample-guided abstraction refinement for symbolic model checking. J. ACM 50(5), 752–794 (2003)
Clarke, E.M., Grumberg, O., Peled, D.A.: Model Checking. MIT Press, Cambridge (2000)
Cousot, P., Cousot, R.: Abstract interpretation: a unified lattice model for static analysis of programs by construction or approximation of fixpoints. In: Conference Record of the 4th ACM Symposium on Principles of Programming Languages (POPL 1977), pp. 238–252. ACM Press, January 1977
Dierks, H., Kupferschmid, S., Larsen, K.G.: Automatic abstraction refinement for timed automata. In: Raskin, J.-F., Thiagarajan, P.S. (eds.) FORMATS 2007. LNCS, vol. 4763, pp. 114–129. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-75454-1_10
Dill, D.L.: Timing assumptions and verification of finite-state concurrent systems. In: Sifakis, J. (ed.) CAV 1989. LNCS, vol. 407, pp. 197–212. Springer, Heidelberg (1990). https://doi.org/10.1007/3-540-52148-8_17
Ehlers, R., Fass, D., Gerke, M., Peter, H.-J.: Fully symbolic timed model checking using constraint matrix diagrams. In: Proceedings of the 31st IEEE Symposium on Real-Time Systems (RTSS 2010), pp. 360–371. IEEE Computer Society Press, November 2010
Ehlers, R., Mattmüller, R., Peter, H.-J.: Combining symbolic representations for solving timed games. In: Chatterjee, K., Henzinger, T.A. (eds.) FORMATS 2010. LNCS, vol. 6246, pp. 107–121. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-15297-9_10
He, F., Zhu, H., Hung, W.N.N., Song, X., Gu, M.: Compositional abstraction refinement for timed systems. In: 2010 4th IEEE International Symposium on Theoretical Aspects of Software Engineering, pp. 168–176, August 2010
Henzinger, T.A., Jhala, R., Majumdar, R., Sutre, G.: Lazy abstraction. In: Conference Record of the 29th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages (POPL 2002). ACM Press, January 2002. ACM SIGPLAN Notices 37(1), 58–70
Henzinger, T.A., Jhala, R., Majumdar, R., Sutre, G.: Software verification with BLAST. In: Ball, T., Rajamani, S.K. (eds.) SPIN 2003. LNCS, vol. 2648, pp. 235–239. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-44829-2_17
Herbreteau, F., Kini, D., Srivathsan, B., Walukiewicz, I.: Using non-convex approximations for efficient analysis of timed automata. In: Chakraborty, S., Kumar, A. (eds.) Proceedings of the 31st Conference on Foundations of Software Technology and Theoretical Computer Science (FSTTCS 2011), volume 13 of Leibniz International Proceedings in Informatics, pp. 78–89. Leibniz-Zentrumfür Informatik, December 2011
Herbreteau, F., Srivathsan, B., Walukiewicz, I.: Lazy abstractions for timed automata. In: Sharygina, N., Veith, H. (eds.) CAV 2013. LNCS, vol. 8044, pp. 990–1005. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-39799-8_71
Herbreteau, F., Tran, T.-T.: Improving search order for reachability testing in timed automata. In: Sankaranarayanan, S., Vicario, E. (eds.) FORMATS 2015. LNCS, vol. 9268, pp. 124–139. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-22975-1_9
McMillan, K.L.: Symbolic model checking—an approach to the state explosion problem. Ph.D. thesis, Carnegie Mellon University, Pittsburgh, Pennsylvania, USA (1993)
Nguyen, T.K., Sun, J., Liu, Y., Dong, J.S., Liu, Y.: Improved BDD-based discrete analysis of timed systems. In: Giannakopoulou, D., Méry, D. (eds.) FM 2012. LNCS, vol. 7436, pp. 326–340. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32759-9_28
Pnueli, A.: The temporal logic of programs. In: Proceedings of the 18th Annual Symposium on Foundations of Computer Science (FOCS 1977), pp. 46–57. IEEE Computer Society Press, October–November 1977
Roussanaly, V., Sankur, O., Markey, N.: Abstraction refinement algorithms for timed automata. Technical report arXiv:1905.07365 arXiv, May 2019
Seshia, S.A., Bryant, R.E.: Unbounded, fully symbolic model checking of timed automata using boolean methods. In: Hun Jr., W.A., Somenzi, F. (eds.) CAV 2003. LNCS, vol. 2725, pp. 154–166. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-45069-6_16
Tóth, T., Majzik, I.: Lazy reachability checking for timed automata using interpolants. In: Abate, A., Geeraerts, G. (eds.) FORMATS 2017. LNCS, vol. 10419, pp. 264–280. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-65765-3_15
Wang, F.: Symbolic verification of complex real-time systems with clock-restriction diagram. In: Kim, M., Chin, B., Kang, S., Lee, D. (eds.) Proceedings of the 21st IFIP TC6/WG6.1 International Conference on Formal Techniques for Networked and Distributed Systems (FORTE 2001), volume 197 of IFIP Conference Proceedings, pp. 235–250. Chapman & Hall, August 2001
Wang, W., Jiao, L.: Trace abstraction refinement for timed automata. In: Cassez, F., Raskin, J.-F. (eds.) ATVA 2014. LNCS, vol. 8837, pp. 396–410. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-11936-6_28
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2019 The Author(s)
About this paper
Cite this paper
Roussanaly, V., Sankur, O., Markey, N. (2019). Abstraction Refinement Algorithms for Timed Automata. In: Dillig, I., Tasiran, S. (eds) Computer Aided Verification. CAV 2019. Lecture Notes in Computer Science(), vol 11561. Springer, Cham. https://doi.org/10.1007/978-3-030-25540-4_2
Download citation
DOI: https://doi.org/10.1007/978-3-030-25540-4_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-25539-8
Online ISBN: 978-3-030-25540-4
eBook Packages: Computer ScienceComputer Science (R0)









 : this means that we can reach
: this means that we can reach  but not from
but not from  so that
so that  . Those values are found by computing the interpolant of
. Those values are found by computing the interpolant of 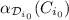 cannot reach
cannot reach  or
or  ;
; .
. .
. ; in this case, we refine the domain by separating these predecessors from the rest of
; in this case, we refine the domain by separating these predecessors from the rest of  , as in [
, as in [ by
by 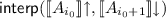 .
. by
by 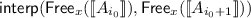 .
.