Abstract
What conception of negation a dialetheist might have, in holding that a statement and its negation can both be true, has been the subject to considerable debate. Several of the issues in play in this area—such as the unique characterization of negation, and the interplay between contrariety and subcontrariety—are broached here by considering some positions taken on them by Graham Priest and assorted critics (in particular, Hartley Slater and Jean-Yves Béziau). Some of the more intricate points, as well as detailed discussions of commentators (including those just mentioned as well as Heinrich Wansing) on Priest are handled in explicitly labelled Digressions and in two Appendices.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
- 2.
More explicitly, what is at issue here is non-trivialist dialetheism, since if trivialism—the view that all statements are true—were correct then there would be no equally pressing need to curtail the inference from contradictions to arbitrary statements. Priest’s spelling of dialetheism with the ‘e’ before the ‘-ism’ is employed here and in dialetheist; but I will follow Priest’s etymological critics in writing dialethic rather than dialetheic, though more for reasons of euphony than historical fidelity.
- 3.
- 4.
- 5.
Slater replies to this response in Slater (2007b).
- 6.
This point about da Costa’s logics was made by Priest and Routley in their (1989), as is quoted by Slater in (1995) with a view that Priest is vulnerable to the same criticism as he and Routley had levelled against da Costa. According to Béziau (2002, p. 473, n. 6), ‘Later on Priest recognized that we should rather consider erroneous his original argument against da Costa’s negation than to think that Slater’s generalized argument is right.’ This is not easily reconciled with the fact that the passage quoted from Priest with its remarks about da Costa above appeared in a publication dated 5 years later than that in which Béziau makes this remark.
- 7.
- 8.
Béziau (2002), using ‘LNC’ as Priest does and ‘EC’ (‘ex contradictione’) for the principle that (for all A, B): \(A, \lnot A \vdash B\), writes (p. 477): ‘In fact the question is still open to know if we can find an intuitive interpretation of an operator which obeys EC but not LNC or obeys LNC and not EC.’ It is not clear what ‘intuitive’ means here, but the Verum interpretation satisfies LNC without satisfying EC, and a ‘Falsum’ interpretation satisfies EC without satisfying LNC.
- 9.
This point is also made near the top of p. 89 in Wansing’s note (2006), whose subtitle coincides with my title.
- 10.
- 11.
The notion of a consequence relation is assumed to be familiar; see, for example, p. 15 of Shoesmith and Smiley (1978).
- 12.
Some may feel that more needs to be said about subcontrariety and contrariety than is said by these formulations, so as to make the two relations mutually exclusive. This issue is discussed in Appendix 1 at the end of the paper; in fact, Priest himself takes this alternative line (the ‘say more’ line, as it is called in that Appendix). In the meantime, we assume they overlap, and that their intersection is the relation of being contradictories.
- 13.
It may be that Restall and Priest both accept that some of what the present author thinks of as non-logical theories, such naive semantics or naive set theory, are themselves to be thought of as part of the logic. For example, Priest’s concern with getting a non-conservative extension (in fact, of nonconservativity in the most extreme form: triviality) by the joint imposition of two sets of principles when either set taken separately gives a conservative extension—for an uncontroversially ‘purely logical’ example of which, see p. 568 of Humberstone (2011a)—involves a rule governing a nullary connective together with an instance of the T-schema at Priest (2006b), p. 90, treats the two as being on a par in this respect. The principle governing the new connective, \(*\) is that we should have \(A \leftrightarrow * \vdash B\), concerning which Priest says: “Triviality then follows from the instance of the T-schema \(T \langle * \rangle \, \leftrightarrow \, *\).” (As it happens the appeal to the T-schema is not in this case needed, since we can simply substitute \(*\) itself for A in the condition \(A \leftrightarrow * \vdash B\). But the way Priest cites the T-schema, perhaps not noticing the redundancy of the current appeal to it, suggests that it is being treated as a logical principle just like the unfortunate \(*\) principle.) A warning about the word ‘spread’ in this connection: it is used quite differently in, for example, Sylvan and Urbas (1993) and (especially) Sect. 4 of Brady (2004), where the principle—rejection of which characterized paraconsistency—that contradictions have all statements as consequences, variously known elsewhere as Explosion, Ex Falso Quodlibet, Ex Contradictione Quodlibet (see Footnote 8), is referred to as the ‘Spread Law’. On Restall’s usage, the spread is from one contradiction to further contradictions, but not to triviality. Restall is sympathetic to the paraconsistent part of the story, which allows for this ‘but not to triviality’, though not to the dialetheist part, which would have us assenting to the contradictions in question.
- 14.
Closely related lines of thought can be found in more recent discussions, such as those of Asmus (2012) and Martin (2015). A related argument couched in possible worlds terms rather than in modal terms appeared in Lewis (1986), p. 7, note 3; of course Lewis had no sympathy for either the weaker or the prima facie stronger form of dialetheism, and was for this debate on the other side—doing the staring—of the famous incredulous stare: see Lewis (2004). (Priest describes a reaction of Stewart Shapiro’s in these terms in Sect. 17.8 of Priest 2006a.) There is a corresponding issue about trivialism—of whether a weak modal form can be prevented from spreading to an outbreak of trivialism simpliciter, discussed, for example, in Humberstone (2011b).
- 15.
Priest (2006b), p. 98.
- 16.
On p. 81: ‘In this section, I have talked of truth. I have said nothing about truth-in-an-interpretation, as required, for example, for a model-theoretic account of validity. It is important to distinguish these two notions, for they are often confused. The first is a property (or at least a monadic predicate); the second is a (set-theoretic) relation. It is natural enough to suppose that truth is at least coextensive with truth-in-\(\mathcal {I}\), where \(\mathcal {I}\) is someone’s privileged interpretation (set). And this may provide a constraint on the notion of truth-in-an-interpretation. But it, even together with an account of truth, is hardly sufficient to determine a theory of truth-in-an-interpretation. It does not even determine, for example, how to conceptualize an interpretation.’
- 17.
A smattering of discussions, listed chronologically: Dummett (1991) (especially, pp. 26–29, 33–37, 55–60 and 66), Humberstone (1996a), Brady and Rush (2009) (especially, Sect. 5), and Williamson (2017). Dummett’s reply to Priest’s rhetorical question, ‘Is it to be supposed that their account of this behaviour is to be given in a way that they take to be incorrect?’ is that the discussion should make use of only of principles accepted by both parties to such debates. This is admittedly going to make communication difficult in the present instance. Priest accepts the inference from ‘It is impossible that A’ to ‘It is impossible that A and not-B’, but not the further inference to ‘Necessarily, if A then B’. One may then suggest (oversimplifying here for the sake of a structural point) that an argument be defined as valid* in non-conditional terms, as one concerning which it is impossible that the premisses are true and the conclusion not be, rather than as one concerning which it is necessary that if the premisses are true then the conclusion is. Now an argument with contradictory premisses is valid*, but from the validity* of an argument and the truth of its premisses, the truth of the conclusion does not follow, by Priest’s lights.
- 18.
Littmann and Simmons voice similar misgivings at p. 318 of Littmann and Simmons (2004).
- 19.
It is introduced on p. 83 of Priest (2006b) thus: ‘As we observed in 4.4, the fact that \(\lnot \Diamond (\alpha \wedge \lnot \alpha )\) holds does not rule out \(\alpha \wedge \lnot \alpha \) holding too. This does not mean that \(\lnot \) is not a contradictory-forming operator. It just means that there is more to negation than one might have thought. Let us call this more, for want of a better phrase, its surplus content. The classical view is to the effect that negation does not have surplus content: any such content would turn into the total content of everything since \(\alpha \wedge \lnot \alpha \vdash \beta \). But the classical view has been called into question by dialetheists’. I cannot understand this explanation of what surplus content is supposed to mean. Interestingly, as Sam Butchart pointed out to me, the phrase does not appear in the source text for Chap. 4, namely Priest (1999). Similarly, the phrase appears seven times in Chap. 5 of Priest (2006b), though not at all in the source material (Priest 1990). The first of these occurrences are on the opening page (p. 88) of the chapter: ‘In the last chapter I argued for a certain account of negation. The account, whilst respecting traditional features of the notion of negation, such as its being a contradictory-forming operator, nonetheless allowed for contradictions to be true without triviality—that is, as I put it there, for negation to have surplus content’. Again, the metaphor seems to be the wrong way round: if the surplus content comprised the unwanted consequences of a negated statement when taken together with the statement negated, it would be lacking rather than having surplus content that was desirable in negation treated paraconsistently. (Yablo 2014, Sect. 6.1, employs the phrase surplus content when paraphrasing the argument of Popper and Miller 1983 against inductive probability, but this seems to be an unrelated use of the same terminology.)
- 20.
This issue arises in the context of dialogue with a dialetheist with whom you have a difference of opinion but who, disconcertingly, agrees with everything you say. It is given some attention in Ripley (2011) and, briefly, at the end of Horn and Wansing (2016), which provides a useful survey of several aspects of negation (though see also Wansing 2001 for some more technical material). Further references and discussion can be found in Priest (2006a), p. 291ff.
- 21.
However, the use of matrix methodology should in no way be thought of as buying into the idea of functional completeness as a desideratum. This will frequently take us outside of what should be expressible given the particular motivations in play. See the Digression at the end of this section for illustration of this issue.
- 22.
It is not just over the issue of the vertical spread of contradictions that Priest seems to be following a motto: when the going gets tough, go homophonic. Note 30 of Chap. 5 of Priest (2006b), dealing with a suggestion of A. Everett by objecting to contraction for ‘if...then ...’ in the metalanguage, is somewhat alarming. As Priest says there, he had treated the matter in somewhat similar terms in Priest (1996), where it is conditional proof that is called into question. But here we are discussing a Kripke style model theory with an accessibility relation which is supposed to be handling the non-classical conditional connective, so one does not expect to be debarred from reasoning entirely classically about what is true at which points in the models.
- 23.
As a referee reminds me, one can then take an interest in a restricted notion of functional completeness: definability of all the functions meeting whatever restrictions are considered desirable; cf. Wansing (1993) and references therein for deployment of a similar idea outside of the narrower confines of matrix semantics.
- 24.
- 25.
Other standard notational liberties are also taken, writing such things as ‘\(\Gamma , A\Vdash B, C\)’ for ‘\(\Gamma \cup \{A\}\Vdash \{B, C\}\)’.
- 26.
Restall (2004) makes a similar use of empty right-hand sides with \(A \wedge \lnot A \Vdash \varnothing \) as a version of the Law of Non-Contradiction, though he writes \(\vdash \) rather than \(\Vdash \) (and \(\sim \) rather than \(\lnot \): this applies for the passage about to be quoted), and does not use the terminology of consequence relations in the constrained way it is being used here (see Footnote 11), saying on p. 74, for example, that according to classical logic understood as classical propositional consequence we have LEM in the form ‘\(A \vdash B \vee \lnot B\)’, and that ‘endorsing classical logic very nearly assures that we are committed to each instance of \(B \vee \lnot B\)’. The insistence on the ‘A’ of the left and of the italicized phrase here will come as quite a surprise to many readers. Restall goes on to say that ‘the situation with the law of non-contradiction is completely dual’, giving this as \(A \wedge \lnot A \vdash B\). But what we have with consequence relations sensu stricto is precisely an asymmetrical arrangement not answering at all well to the demands of duality: there must be exactly one formula on the right of the \(\vdash \) but there can be fewer or more on the left. This underlies the ‘Carnapian phenomena’ to be recalled presently; they were first isolated in Carnap (1943), especially, Sects. 15–18
- 27.
- 28.
See Rauszer (1980); while Rauszer writes the dual negation by horizontally inverting the standard negation symbol, here a vertically inverted form has been chosen.
- 29.
In fact, as is also well known, ‘
 ’ forms the strongest subcontrary of what it applies to: \(\vdash _\mathsf{HB}A \vee B\) implies
’ forms the strongest subcontrary of what it applies to: \(\vdash _\mathsf{HB}A \vee B\) implies 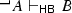 for arbitrary A, B. Further information may be found in 8.11 and 8.22 of my (Humberstone 2011a). To the list of references supplied at p. 1250 of Humberstone (2011a) should be added Priest (2009), in which Priest discusses the relation between dual intuitionistic negation and da Costa’s negation. Discussion of contrariety and contradictoriness connected with another optional extra from the negation menu for intuitionistic logic—strong negation (‘constructible falsity’)—is provided in Wansing (2001, 2006).
for arbitrary A, B. Further information may be found in 8.11 and 8.22 of my (Humberstone 2011a). To the list of references supplied at p. 1250 of Humberstone (2011a) should be added Priest (2009), in which Priest discusses the relation between dual intuitionistic negation and da Costa’s negation. Discussion of contrariety and contradictoriness connected with another optional extra from the negation menu for intuitionistic logic—strong negation (‘constructible falsity’)—is provided in Wansing (2001, 2006). - 30.
I may be misinterpreting Béziau here, since editorial remarks at p. 57 of Béziau et al. (2007) clearly show familiarity with Wójcicki’s observation (announced initially in 1970). (For certain fragments, one does have the definability of the corresponding classical fragment in the intuitionistic consequence relation, as C. A. Meredith famously showed in the case of the implicational fragment. But since the current topic is negation, it can hardly be any such positive fragment that Béziau has in mind.) A second point: the contrariety claim for intuitionistic negation Béziau describes as an erroneous conclusion someone might reach by means of an argument similar to Slater’s. Even if Béziau is wrong about the erroneousness of the conclusion, there is a good point here: why didn’t Slater complain as loudly that intuitionistic negation doesn’t deserve the name, on the grounds that it does not form contradictories because it fails to deliver subcontraries?
- 31.
- 32.
In Humberstone (1996b) binary operations are considered which are—as it is put there—Galois dual to familiar sentence connectives in the way in which conjunctive combination is to conjunction.
- 33.
These are essentially familiar to philosophers as supervaluations over V, except that like all valuations here, they are bivalent and assign F to all formulas not verified by every \(v \in V\) (rather than just those falsified by every \(v \in V\)).
- 34.
A roundabout conditional way—already mentioned (apropos of subcontrariety according to a consequence relation in general) under (ii) in the opening paragraph of the Digression in Sect. 15.3—which would amount to this for a \(\vdash \) which is not \(\vee \)-classical would be to say that for any set \(\Gamma \) and formula C, if \(\Gamma , A \vdash C\) and \(\Gamma , B \vdash C\), we have \(\Gamma \vdash C\).
- 35.
Essentially this is what Béziau suggests in the Remark, just alluded to, in the middle of p. 23 of Béziau (2006). This Remark is appended to a Theorem, the key part of which we may extract here as follows: if \(\vdash \) is a consequence relation on some language with 1-ary \(\#\) as one of its connective and \(\vdash \) is determined by at least one class V of valuations with the property that for no \(v \in V\) and formula A, do we have \(v(A) = v(\#A) = T\)—never mind whether \(\vdash \) is also determined by other classes of valuations (such as the class of all valuations consistent with \(\vdash \)) which do not share this feature with V—then for all formulas A, B, we have \(A, \#A \vdash B\). This observation is more or less immediate from the definitions of the terms deployed in it: if \(A, \#\!A \nvdash B\) and \(\vdash \) is determined by V, then there must be \(v \in V\) with \(v(A) = v(\#\!A) = T\) (and also \(v(B) = F\)), so V is not as advertised (A and \(\#A\) are not ‘contraries over V’, being both verified on v). Short of paraconsistently homophonic maneuvering in the metalogic, this result is not negotiable, and as Béziau notes, this can be regarded as a way of presenting Slater’s point. Here I have extracted the contrariety condition from Béziau’s formulation, which incorporates also subcontrariety, and amounts to this: if \(\vdash \) is determined by some class of valuations V such that \(v(A) \ne v(\#A)\) for all formulas A and all \(v \in V\) then \(\#\) satisfies the condition already mentioned—that \(A, \#\!A \vdash B\)—as well as the ‘subcontrariety’ condition: whenever \(\Gamma , A \vdash B\) and also \(\Gamma , \#\!A \vdash B\), we have \(\Gamma \vdash B\). In other words, reading \(\#\) as \(\lnot \), \(\vdash \) is \(\lnot \)-classical, as it is put in Humberstone (2011a) (though Béziau uses a Tarski-style characterization of \(\lnot \)-classicality which is more economical but less transparent); the condition that (for all A) \(v(A) \ne v(\lnot A)\) for \(v \in V\) is the condition that V contains only \(\lnot \)-Boolean valuations. Incidentally, these formulations with the explicit existential quantification—\(\vdash \) determined by some V such that ...—are fine in the converse direction. (The ‘absent converse’ mentioned in Béziau’s Remark is to the converse of a formulation to the effect that where a class of valuations V determines \(\vdash \), if V contains only \(\lnot \)-Boolean valuations then \(\vdash \) is \(\lnot \)-classical.)
- 36.
Here I have been interpreting the passage quoted from Priest above as saying, incorrectly, LDN is derivable from LEM and LNC. A more generous—if somewhat vaguer—reading, suggested to me by Sam Butchart, is also possible: after mentioning LEM and LNC, what Priest says about LDN is that it is ‘simply derivable’: he does not explicitly say, as my interpretation presumes, that it is ‘simply derivable from these two principles’.
- 37.
We do not even need to appeal to the commutativity of \(\wedge \) and \(\vee \) which underlies the remark about the contradictoriness relation being symmetric, since these connectives are out of the picture.
- 38.
More specifically: as the absolutely free algebra of its signature, with compounding via the primitive connectives as the fundamental operations.
- 39.
Priest uses a variant on the last notation in Priest (1979), with t, p (for paradoxical) and f for \(\varvec{t}\), \(\varvec{b}\) and \(\varvec{f}\). In Priest (2006a) he uses the \(\{1\}, \{1, 0\}, \{0\}\) notation. In numerous other places, including material added in the section edition of Priest (2006a) (e.g. p. 288f.), as well as (2014), Priest prefers not to use sets of classical truth values at all but to avoid functions which would assign such sets of values in favour of relations relating formulas (potentially plurally) to the elements of those sets. This ‘preference for the plural’ extends well beyond the present manifestation of it: see Priest (1995).
- 40.
In fact, finding more emphasis in Kleene on the underlying algebra, in Humberstone (2011a) I described the LP matrix and the familiar (‘strong’) Kleene matrix both as Kleene matrices and called them \(\mathbf{K}_1\) and \(\mathbf{K}_{1,2}\) respectively, the subscripts reflecting which of the three elements denoted by 1, 2, and 3, were taken as designated.
- 41.
Recall that we are setting aside as dialectically unhelpful the vertically homophonic move considered in Sect. 15.2: oh but they are mutually exclusive—it just happens that despite being mutually exclusive truth and falsity can both apply to the same thing.
- 42.
The definition of Cn in the quotation should be understood as prefaced by “for all \(h \in \mathbf{P}\)”. This formulation involves a consequence operation instead of a consequence relation. For the latter purposes ‘\(A \in Cn (\Gamma )\)’ would be written as ‘\(\Gamma \vdash _\mathsf{LP} A\)’.
- 43.
Does explaining negation as forming the weakest statement incompatible with a given statement (Berto 2006, p. 253) help with any of this? (Note that this characterization coincides with that of intuitionistic negation as forming the weakest contrary of a statement; compare dual intuitionistic negation—see Footnote 29 and the text to which it is appended, as well as the passage quoted at the start of Sect. 15.5, below—as forming a statement’s strongest subcontrary. In the classical setting, the strongest subcontrary coincides with the weakest contrary, so there is nothing to choose between the two formulations.)
- 44.
In fact, the original passage contained at this point the phrase ‘salva provabilitate’, but as an astute referee observes, there is no such phrase. I apologize profusely to readers of other publications of mine featuring this piece of confused pseudo-Latin.
- 45.
This terminology at least once enjoyed considerable currency—as in Meyer and Martin (1986).
- 46.
This is a standard way of turning the Anderson–Belnap binary FDE-relation into a consequence relation; see Pynko (1995), p. 445, where the corresponding consequence operation is defined.
- 47.
For more discussion of the concepts issues involved here, see Sect. 4.3 of Humberstone (2011a).
- 48.
Béziau (2002), p. 477: ‘In Priest’s logic LP and in da Costa and D’Ottaviano’s logic J3, the formulas \(p \vee \lnot p\) and \(q \vee \lnot q\) are logically equivalent but not their negations and here again no philosophical justification for this failure has been presented’. This seems a bit harsh in the case of Priest, since the equivalence in the former case is a by-product of the decision to smooth gaps out of the picture to concentrate in gluts, and the latter brings with it the distinction between those contradictions which embody the gluts and those which are simply false. (In the quotation just given, I have changed the notion to match that in use here.)
- 49.
In fact, it is the use of non-normal worlds in models for properly quasi-normal modal logics in Chap. III of Segerberg (1971) that is closer in spirit, and it is the distinguished worlds rather than normal worlds there that are pertinent. (These enter into the definition of validity as the worlds unfalsifiability at which is significant, rather than entering into the inductive definition of truth at a world.) The use of ‘non-normal’ in the text echoes Priest (1992), though unless I misunderstand it, I am disagreeing with the parenthetical remark in the following passage from p. 301 of that paper: ‘These constructions ensure that normal worlds are complete and consistent, respectively. (Note how these issues can be handled separately on this construction, in a way that they cannot be, using the * operator.)’
- 50.
For this solution, I am indebted to Sam Butchart.
- 51.
See Humberstone (2011a) p. 599f.
- 52.
More informatively: the above (\(\vee \) Left) and \(\vee \)-Elimination preserve the property of holding on any given matrix evaluation, where a sequent
 holds on h iff it is not the case that h(C) is designated for each \(C \in \Gamma \) while h(A) is undesignated.
holds on h iff it is not the case that h(C) is designated for each \(C \in \Gamma \) while h(A) is undesignated. - 53.
This example is given to illustrate the same point in the Digression on p. 1192f. of Humberstone (2011a).
- 54.
One of the referees of the present paper expressed surprise at this formulation of minimal logic, wondering what it was really sound and complete, suggesting that a word is in order on the semantics in play. Using suitably adapted Kripke semantics for Johansson’s logic (as in Segerberg 1968 or Sect. 2.3 of Odintsov 2008) the idea is to define a sequent
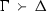 of Set-Fmla\(_0\) to be valid just in case in every model, at every point x in the model, with Q for its set of queer or non-normal elements (at precisely which elements f is true, in any modal), if all formulas in \(\Gamma \) are true at x in the model then either \(\Delta = \{D\}\) for some formula and D is true at x, or \(\Delta = \varnothing \) and \(x \in Q\). The valid sequents are then easily seen to coincide with those provable in the present proof system.
of Set-Fmla\(_0\) to be valid just in case in every model, at every point x in the model, with Q for its set of queer or non-normal elements (at precisely which elements f is true, in any modal), if all formulas in \(\Gamma \) are true at x in the model then either \(\Delta = \{D\}\) for some formula and D is true at x, or \(\Delta = \varnothing \) and \(x \in Q\). The valid sequents are then easily seen to coincide with those provable in the present proof system. - 55.
- 56.
See my (Humberstone 2011a), p. 151, for detailed bibliographical references and further discussion. Those references can be supplemented by mention of at least one new recruit: Restall (in preparation).
- 57.
I was certainly aware of the negation case in 1974 and on noticing it mentioned it to as many of my fellow graduate students at Oxford as would stand still long enough. The point is implicit in the restriction on the rule called RAA\(_{\lnot }\) on p. 174 of Humberstone (1979), which prevents the intuitionistic style negation in play there from collapsing into the simultaneously present classical style negation. (This was alluded to at the end of the Digression with which Sect. 15.2 concluded. A more sophisticated venture with a similar motivation can be found in Lucio 2000.) The material in Sect. 4.3 of Humberstone (2011a), incidentally, was originally presented at a splendid AAL conference in Perth in 1983, organized by Priest.
- 58.
There are several other aspects of the passage just quoted which might merit further attention than can be given to them here. For instance, the claim that ‘Classical and intuitionist negations have different truth conditions’ makes one wonder what semantic account is in play supplying truth condition to the classical negation of a statement and the intuitionistic negation of that same statement; it’s not as though there is even, in the intuitionistic case a single option as to how to do the (heterophonic, model-theoretic) semantics: do we use the Kripke semantics, the Beth semantics, or something else again? What are ‘the’ truth conditions for intuitionistic disjunctions, for instance, (\(\vee \) receiving a different treatment in Beth and Kripke)?
- 59.
Here we understand the rules as applying in a substitution-invariant way over the combined language, not subject to such restrictions as were alluded to in Footnote 57.
- 60.
This last means that \(\lnot \) and \(\sim \) both have to satisfy the following identities here stated in a neutral notation, with −: \(-(x \wedge -y) \approx -x \vee y\), \(-(x \vee y) \approx -x \wedge -y\), and \(--x \approx x\). Cf. the ‘double Ockham algebras’ of Fang (2008). Ockham algebras are distributive lattices expanded by a 1-ary operation obeying the De Morgan identities, construed narrowly so to exclude the involution condition (i.e. the identity \(--x \approx x\)). Hence the present terminology of double De Morgan algebras—or more accurately double De Morgan lattices. (See Footnote 61.)
- 61.
In the literature the appellation ‘De Morgan algebra’ is typically now reserved for the bounded version of a De Morgan lattice. The older terminology of quasi-Boolean algebras seems to have fallen out of use. (‘Bounded’ here means having the bounds in the signature, thereby restricting the options for homomorphisms and subalgebras; of course, all finite De Morgan lattices are de facto bounded in the sense of having top and bottom elements.) The numbers of quasi-varieties of De Morgan lattices and of De Morgan algebras are very different, as is reported in the middle of p. 321 of Rivieccio (2012).
- 62.
It may be tempting to connect this with the idea that of LEM ‘as a (possibly correct) substantive metaphysical principle not appropriately built into one’s account of the logic of the connectives concerned’, as it was put in the opening paragraph of Humberstone and Lock (1986).
- 63.
See p. 328 of Rivieccio (2012), where Font (1997) is observed not to have taken the necessary steps. The same point underlies Rivieccio’s observation on the preceding page, that where \(\vdash '\) is the smallest consequence relation \(\vdash \) extending \(\vdash _\mathsf{FDE}\) such that \(A \wedge \lnot A \vdash B\) for all A, B, we do not have \(\lnot p \wedge (p \vee q)\vdash ' q\). The observation hangs on the absence of the qualification ‘\(\vee \)-classical’ in characterizing \(\vdash '\). (Rivieccio calls \(\vdash _\mathsf{FDE}\) ‘\(\vdash _{\mathcal {B}}\)’, in honour of Belnap.)
- 64.
And where, in fact, the ‘say less’ interpretation is explicitly labelled as such, though the phrase ‘say more’ for the alternative does not explicitly appear.
- 65.
- 66.
The claim about something being provable is something of an oversimplification. If we have an \(\vee \)-classical consequence relation \(\vdash \) then the subcontrariety of A, B does find expression in the provability of their disjunction, but the ‘purified’ form of this condition given in (ii) of the Digression in Section is a conditional rather than an unconditional \(\vdash \)-condition, and even in the unconditional case—as we see from considering contrariety, the provability is a matter of provability of sequents rather than just formulas. If we were thinking of the purified version of subcontrariety for Set-Set sequents we do of course have the unconditional demand that
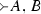 should be provable—formulated as the condition ‘\(\Vdash A, B\)’ on generalized consequence relations at the start of Sect. 15.3.
should be provable—formulated as the condition ‘\(\Vdash A, B\)’ on generalized consequence relations at the start of Sect. 15.3. - 67.
Here I am, in the usual ‘say less’ manner, taking contradictory to mean subcontrary and contrary, and in calling the formulations just cited equivalent am assuming the meta-logical analogue of the equivalence of \(p \wedge \lnot q\) with \(p \wedge \lnot (p \wedge q)\)—an equivalence which does not hold for LP or FDE, leaving someone with Priest’s inclinations (both logical and methodological) with the option, if they wanted to exploit it, of distinguishing two separate notions of mere contrariety and also of mere subcontrariety.
- 68.
While finishing off the present contribution, I became increasingly curious about this. Unfortunately, by the time I tried to contact Slater for an answer to the question (May 2016), I heard from a relative fielding his correspondence the sad news that it was too late: Hartley had suddenly fallen victim to an incapacitating and inoperable brain tumour.
- 69.
To see this, suppose that neither A nor B is tautologous and write A and B in the equivalent form of formulas \(A' \,=\,p_1 \leftrightarrow p_2 \leftrightarrow \cdots \leftrightarrow p_m\) (parentheses omitted because of associativity) and \(B'\,=\,q_1 \leftrightarrow q_2 \leftrightarrow \cdots \leftrightarrow q_n\), in which each sentence letter (the \(p_i\) and \(q_i\)) that occurs occurs exactly once. (We delete any letters occurring in pairs until only one occurrence remains, knowing that one occurrence must remain or the formula would have been tautologous: shades of Leśniewski here.) Noting that any such formula is false on any \(\leftrightarrow \)-Boolean valuation in which exactly one of its sentence letters is false (indeed any odd number of those sentence letters), consider two cases: (i) for some i, j, \(p_i\, = \,q_j\); and (ii) no \(p_i\) coincides with any \(q_j\). In case (i), pick one shared sentence letter (a \(p_i\) which coincides with some \(q_j\), that is) and consider a Boolean valuation assigning F to that sentence letter and T to all the others: each of \(A', B'\), and hence of A, B, is false on this valuation, contradicting the assumption of subcontrariety. For case (ii), pick any one of the variables \(p_i\) occurring in \(A'\) and one \(q_j\) occurring in \(B'\) and again assign the selected variables the value F while assigning T to all the other variables; as before, we get a Boolean valuation falsifying both \(A'\) and \(B'\).
- 70.
On the reasonable assumption that the intersection of any two logical relations is a logical relation, (2) can equivalently be formulated as (2\('\)): for any (coercive) binary logical relation S such that S(A, B), we have \(R \subseteq S\).
- 71.
- 72.
We recall also from Footnote 29 that Wansing discusses numerous proposed negation connectives—such as that associated with constructible falsity—in Wansing (2006) and their status as contrary and contradictory-forming operators, though here we consider only standard (‘Heyting’) intuitionistic negation. Later chapters of Odintsov (2008) also treat these Nelson style systems in some detail.
- 73.
From the perspective of the methodogical desideratum (‘purity’) we are putting on hold for this Appendix, Wansing’s formulations in (a) and (b) are preferable, in that fewer object language connectives are involved.
- 74.
Spelling this out in more detail, we may say that A, B are Wansing subcontraries according to a consequence relation \(\vdash \) when the following condition is satisfied: for any \(A', B'\) if \(A', A \vdash C\) and \(B', B \vdash C\) for all C, then \(A', B' \vdash C\) for all C. Specializing to \(\vdash \,= \,\vdash _\mathsf{IL}\), this relation holds between formulas A and B iff \(\vdash _\mathsf{IL} \lnot (\lnot A \wedge \lnot B\)).
- 75.
\(((A \rightarrow B) \rightarrow B)\) has \(\lnot A \rightarrow B\) as an intuitionistic consequence, though in general not conversely, and adding the converse in its general form would classicize \(\vdash _\mathsf{IL}\).
- 76.
By contrast, there seems no such uniquely salient non-classical analogue of exclusive disjunction in FDE, where the two pre-eminent candidates have their own merits: the strong exclusive disjunction of p with q, \((p \wedge \lnot q) \vee (\lnot p \wedge q)\), on the one hand, and the weak exclusive disjunction on the other \((p \vee q) \wedge (\lnot p \vee \lnot q)\). See p. 29 of Humberstone (2014). The two are equivalent in LP, as are the stronger and weaker FDE equivalence connectives contrasted there (originally in both cases, in fact, by A. J. Dale).
References
Asmus, C. (2012). Paraconsistency on the rocks of dialetheism. Logique et Analyse, 55, 3–21.
Berto, F. (2006). Characterizing negation to face dialetheism. Logique et Analyse, 49, 241–261.
Béziau, J.-Y. (1996). Review of B. H. Slater (1995), Mathematical Reviews, MR1338752 (96e:03035) 1996. (Revised version on MathSciNet, 2007.)
Béziau, J.-Y. (2002). Are paraconsistent negations negations? In W. A. Carnielli, M. E. Coniglio, & I. M. L. D’Ottaviano (Eds.), Paraconsistency: The logical way to the inconsistent (pp. 465–486). New York: Marcel Dekker.
Béziau, J.-Y. (2006). Paraconsistent logic! (A Reply to Slater). Sorites, 17, 17–25.
Béziau, J.-Y. (2016). Disentangling contradiction from contrariety via incompatibility. Logica Universalis, 10, 157–170.
Béziau, J.-Y., He, H., Costa-Leite, A., Zhong, Y., & Ma, Y. (Eds.). (2007). Handbook of the second world congress and school on universal logic UNILOG’07 (August 16–22 2007). China: Xi’an.
Blamey, S. (2002). Partial logic. In D. Gabbay & F. Guenthner (Eds.), Handbook of philosophical logic, Vol. III: Alternatives to classical logic (pp. 1–70). Dordrecht: Reidel. Reprinted in Gabbay & Guenthner (Eds.), Handbook of philosophical logic (2nd ed., Vol. 5, pp. 261–354).
Blamey, S., & Humberstone, L. (1991). A perspective on modal sequent logic. Publications of the Research Institute for Mathematical Sciences, Kyoto University, 27, 763–782.
Brady, R. (2004). On the formalization of the law of non-contradiction (pp. 41–48) in Priest (2004).
Brady, R., & Rush, P. (2009). Four basic logical issues. Review of Symbolic Logic, 2, 488–508.
Brown, B. (1999). Yes, Virginia, there really are paraconsistent logics. Journal of Philosophical Logic, 28, 489–500.
Bull, R. A. (1962). The implicational fragment of Dummett’s LC. Journal of Symbolic Logic, 27, 189–194.
Buss, S. R. (1998). An introduction to proof theory. In Buss (Ed.). Handbook of proof theory (pp. 1–70). Amsterdam: Elsevier.
Carnap, R. (1943). Formalization of logic, first publ. 1943, reprinted as Volume II within Introduction to semantics and formalization of logic, 1961. Cambridge, MA: Harvard University Press.
Chellas, B. (1980). Modal logic: An introduction. Cambridge: Cambridge University Press. Reprinted (with corrections) 1988 and subsequently.
Cresswell, M. J. (2008). Does every proposition have a unique contradictory? Analysis, 68, 112–114.
Curry, H. B. (1957). A theory of formal deducibility. Notre Dame, Indiana: Notre Dame University Press.
Denyer, N. (1989). Dialetheism and trivialization. Mind, 98, 259–263.
Dummett, M. (1959a). Truth. Proceedings of the Aristotelian Society, 59, 141–162.
Dummett, M. (1959b). A propositional calculus with denumerable matrix. Journal of Symbolic Logic, 24, 97–106.
Dummett, M. (1991). The logical basis of metaphysics. Cambridge, MA: Harvard University Press.
Dunn, J. M. (1976). Intuitive semantics for first-degree entailments and “Coupled Trees”. Philosophical Studies, 29, 149–168.
Fang, J. (2008). Commuting double Ockham algebras. Science in China Series A: Mathematics, 51, 185–194.
Font, J. M. (1997). Belnap’s four-valued logic and De Morgan lattices. Logic Journal of the IGPL, 5, 413–440.
Girard, P., & Weber, Z. (2015). Bad worlds. Thought, 4, 93–101.
Harris, J. H. (1982). What’s so logical about the “Logical” axioms? Studia Logica, 41, 159–171.
Horn, L. (1989). A natural history of negation. Chicago: University of Chicago Press.
Horn, L., & Wansing, H. (2016). Negation. In E. N. Zalta (Ed.), Stanford encyclopedia of philosophy (Spring 2016 ed.). http://plato.stanford.edu/archives/spr2016/entries/negation/.
Humberstone, L. (1979). Interval semantics for tense logic: Some remarks. Journal of Philosophical Logic, 8, 171–196.
Humberstone, L. (1987). Operational semantics for positive R. Notre Dame Journal of Formal Logic, 29, 61–80.
Humberstone, L. (1992). Review of Priest, Routley and Norman (Priest 1989) (and of J. M. Dunn and A. Gupta (eds.), Truth or Consequences (Kluwer: 1990)). Australasian Journal of Philosophy, 70, 362–366.
Humberstone, L. (1996a). Homophony, validity, modality. In B. J. Copeland (Ed.), Logic and reality: Essays on the legacy of A. N. Prior (pp. 215–236). Oxford: Clarendon Press.
Humberstone, L. (1996b). Classes of valuations closed under operations Galois-Dual to boolean sentence connectives. Publications of the Research Institute for Mathematical Sciences, Kyoto University, 32, 9–84.
Humberstone, L. (1998). Many-valued logics, philosophical issues. In E. Craig (Ed.), Routledge encyclopedia of philosophy (Vol. 6, pp. 84–91). London: Routledge.
Humberstone, L. (2001). The pleasures of anticipation: Enriching intuitionistic logic. Journal of Philosophical Logic, 30, 395–438.
Humberstone, L. (2002). Implicational converses. Logique et Analyse, 45, 61–79.
Humberstone, L. (2003). Note on contraries and subcontraries. Noûs, 37, 690–705.
Humberstone, L. (2005a). Contrariety and subcontrariety: The anatomy of negation (with Special Reference to an Example of J.-Y. Béziau). Theoria, 71, 241–262.
Humberstone, L. (2005b). Modality. In F. C. Jackson & M. Smith (Eds.), The Oxford handbook of contemporary philosophy, Chapter 20 (pp. 534–614). Oxford and New York: Oxford University Press.
Humberstone, L. (2005c). Logical discrimination. In J.-Y. Béziau (Ed.), Logica universalis: Towards a general theory of logic (pp. 207–228). Birkhäuser: Basel.
Humberstone, L. (2011a). The connectives. Cambridge MA: MIT Press.
Humberstone, L. (2011b). Variation on a trivialist argument of Paul Kabay. Journal of Logic, Language and Information, 20, 115–132.
Humberstone, L. (2013a). Inverse images of box formulas in modal logic. Studia Logica, 101, 1031–1060.
Humberstone, L. (2013b). Logical relations. Philosophical Perspectives, 27, 176–230.
Humberstone, L. (2014). Power matrices and Dunn-Belnap semantics: Reflections on a remark of Graham Priest. Australasian Journal of Logic, 11, 14–45.
Humberstone, L. (2015). Sentence connectives in formal logic. In E. N. Zalta (Ed.), Stanford encyclopedia of philosophy (Fall 2015 ed.). http://plato.stanford.edu/archives/fall2015/entries/connectives-logic/.
Humberstone, L. (2016). Philosophical applications of modal logic. London: College Publications.
Humberstone, L. (2019). Supervenience, dependence, disjunction. Logic and Logical Philosophy, 28, 3–135.
Humberstone, L., & Lock, A. (1986). Semicomplemented lattices and the finite model property. Zeitschr. für math. Logik und Grundlagen der Math., 32, 431–437.
Kripke, S. A. (1965). Semantical analysis of modal logic II. Non-normal modal propositional calculi. In J. W. Addison, L. Henkin, & A. Tarski (Eds.), The theory of models (pp. 206–220). Amsterdam: North-Holland.
Lewis, D. (1986). On the plurality of worlds. Oxford: Blackwell.
Lewis, D. (2004) Letters to Beall and Priest (pp. 176–177) in Priest (2004).
Littmann, G., & Simmons, K. (2004). A critique of dialetheism (pp. 314–335) in Priest (2004).
Lucio, P. (2000). Structured sequent calculi for combining intuitionistic and classical first-order logic. In H. Kirchner & C. Ringeissen (Eds.), Frontiers of Combining Systems: Third International Workshop, FroCoS 2000, LNAI #1794 (pp. 88–104). Berlin: Springer.
Marcos, J. (2007). Ineffable inconsistencies. In J.-Y. Béziau, W. Carnielli, & D. Gabbay (Eds.), Handbook of paraconsistency (pp. 341–352). London: College Publications.
Martin, B. (2015). Dialetheism and the impossibility of the world. Australasian Journal of Philosophy, 93, 61–75.
Meyer, R. K. (1985). Proving semantic completeness “Relevantly” for R. Logic Research Paper #23 of the Logic Group. Department of Philosophy, RSSS, Australian National University.
Meyer, R. K., & Martin, E. P. (1986). Logic on the Australian plan. Journal of Philosophical Logic, 15, 305–332.
Odintsov, S. P. (2008). Constructive negations and paraconsistency. Dordrecht: Springer.
Oller, C. A. (2014). Is classical negation a contradictory-forming operator? Notae Philosophicae Scientiae Formalis, 3, 1–7.
Oller, C. A. (2016). Contradictoriness, paraconsistent negation and non-intended models of classical logic. In H. Andreas & P. Verdée (Eds.), Logical studies of paraconsistent reasoning in science and mathematics (pp. 103–109). Cham (Switzerland): Springer.
Paoli, F. (2003). Quine and Slater on paraconsistency and deviance. Journal of Philosophical Logic, 32, 531–548.
Popper, K., & Miller, D. (1983). A proof of the impossibility of inductive probability. (Letters to) Nature, 302, 687–688.
Priest, G. (1979). The logic of paradox. Journal of Philosophical Logic, 8, 219–241.
Priest, G. (1989). Denyer’s \$ not backed by sterling arguments. Mind, 98, 265–268.
Priest, G. (1990). Boolean negation and all that. Journal of Philosophical Logic, 19, 201–215.
Priest, G. (1992). What is a non-normal world? Logique et Analyse, 35, 291–302.
Priest, G. (1995). Multiple denotation, ambiguity, and the strange case of the missing amoeba. Logique et Analyse, 38, 361–373.
Priest, G. (1996). Everett’s trilogy. Mind, 105, 631–47.
Priest, G. (1998). What is so bad about contradictions? Journal of Philosophy, 95, 410–426. (Appearing with minor changes as ‘What’s So Bad About Contradictions?’ as pp. 24–38 in Priest et al. (2004).
Priest, G. (1999). What not? A defence of dialetheic theory of negation. In D. Gabbay & H. Wansing (Eds.), What is negation? (pp. 101–120). Dordrecht: Kluwer.
Priest, G. (2002). Paraconsistent logic. In D. Gabbay & F. Guenthner (Eds.), Handbook of philosophical logic (2nd ed., Vol. 6, pp. 287–393). Dordrecht: Kluwer.
Priest, G. (2006a). In contradiction: A study of the transconsistent (2nd ed.). Oxford: Clarendon Press. (First edn. Martinus Nijhoff, The Hague 1987).
Priest, G. (2006b). Doubt truth to be a liar. Oxford: Oxford University Press.
Priest, G. (2007). Reply to Slater. In J.-Y. Béziau, W. Carnielli, & D. Gabbay (Eds.), Handbook of paraconsistency (pp. 467–474). London: College Publications.
Priest, G. (2009). Dualising intuitionistic negation. Principia, 13, 165–184.
Priest, G. (2010). The logic of the catuskoti. Comparative Philosophy, 1, 24–54.
Priest, G. (2014). Plurivalent logics. Australasian Journal of Logic, 11, 2–13.
Priest, G. (2015). None of the above: The catuṣkoṭi in Indian Buddhist logic. In J.-Y. Béziau, M. Chakraborty, & S. Dutta (Eds.), New directions in paraconsistent logic (pp. 517–527). Springer.
Priest, G., Beall, J. C., & Armour-Garb, B. (Eds.). (2004). The law of non-contradiction: New philosophical essays. Oxford: Oxford University Press.
Priest, G., & Routley, R. (1989). Systems of paraconsistent logic (pp. 151–186) in Priest (1989).
Priest, G., Routley, R., & Norman, J. (Eds.). (1989). Paraconsistent logic: Essays on the inconsistent. Munich: Philosophia.
Pynko, A. J. (1995). Characterizing Belnap’s logic via De Morgan’s laws. Mathematical Logic Quarterly, 41, 442–454.
Rauszer, C. (1980). An algebraic and Kripke-style approach to a certain extension of intuitionistic logic. Dissertationes mathematicae, 167
Restall, G. (1997). Paraconsistent logics!. Bulletin of the Section of Logic, 26, 156–173.
Restall, G. (2004). Laws of non-contradiction, laws of the excluded middle, and logics (pp. 73–84) in Priest (2004).
Restall, G. Generality and existence I: Quantification and free logic. in preparation.
Rivieccio, U. (2012). An infinity of super-Belnap logics. Journal of Applied Non-Classical Logics, 22, 319–335.
Ripley, D. (2011). Negation, denial, and rejection. Philosophy Compass, 6, 622–629.
Routley, R., & Routley, V. (1972). Semantics of first degree entailment. Noûs, 6, 335–359.
Segerberg, K. (1968). Propositional logics related to Heyting’s and Johansson’s. Theoria, 34, 26–61.
Segerberg, K. (1971). An essay in classical modal logic. Uppsala: Filosofiska Studier.
Shoesmith, D. J., & Smiley, T. J. (1978). Multiple-conclusion logic. Cambridge: Cambridge University Press.
Slater, B. H. (1995). Paraconsistent logics? Journal of Philosophical Logic, 24, 451–454.
Slater, B. H. (2007a). Dialetheias are mental confusions. In J.-Y. Béziau, W. Carnielli, & D. Gabbay (Eds.), Handbook of paraconsistency (pp. 459–466). London: College Publications.
Slater, B. H. (2007b). Response to Priest. In J.-Y. Béziau, W. Carnielli, & D. Gabbay (Eds.), Handbook of paraconsistency (pp. 475–476). London: College Publications.
Sylvan, R., & Urbas, I. (1993). Paraconsistent classical logic. Logique et Analyse, 36, 3–24.
Wansing, H. (1993). Functional completeness for subsystems of intuitionistic propositional logic. Journal of Philosophical Logic, 22, 303–321.
Wansing, H. (1998). Displaying modal logic. Dordrecht: Kluwer.
Wansing, H. (2001). Negation. In L. Goble (Ed.), The Blackwell guide to philosophical logic (pp. 415–436). Basil Blackwell.
Wansing, H. (2006). Contradiction and contrariety: Priest on negation. In J. Malinowski & A. Pietruszczak (Eds.), Essays in logic and ontology (pp. 81–93). Amsterdam: Rodopi.
Williamson, T. (2017). Dummett on the relation between logics and metalogics. In M. Frauchiger (Ed.), Truth, meaning, justification, and reality: Themes from Dummett (pp. 153–176). Berlin: De Gruyter.
Wójcicki, R. (1988). Theory of logical calculi. Dordrecht: Kluwer.
Yablo, S. (2014). Aboutness. Princeton: Princeton University Press.
Acknowledgements
I am greatly indebted to Sam Butchart for helpful observations and suggestions which have improved this paper, to two referees for the detection and correction of numerous errors, and to Heinrich Wansing for additional assistance.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
Appendix 1: Subcontraries and Mere Subcontraries
For the general point to be discussed here, the title could equally well have been (or included) ‘Contraries and Mere Contraries’, but that chosen reflects more specifically some aspects of the discussion of Slater (1995). Let us recall that there are two understandings of the terminology of contraries and subcontraries, distinguished as the ‘say less’ and ‘say more’ interpretations in Humberstone (2003), where numerous textual references and some further discussion may be found.Footnote 64 On the ‘say less’ approach, the most influential advocate for which was perhaps E. J. Lemmon,Footnote 65 semantically formulated, contraries/subcontraries are defined to be incapable of joint truth/falsity, or modulating to a consequence relation relativity, to be contraries/subcontraries relative to \(\vdash \) when \(\vdash \) is determined by some class of (bivalent) valuations no element of which verifies/falsifies both. This is the usage that has been followed in the present paper.
The ‘say more’ interpretation, understandably, says more, adding a requirement that the class of valuations in question should also provide at least one verifying both of the subcontraries (respectively, falsifying both of them) for them to deserve that description. Both are perfectly legitimate things to mean by the terminology, but the smoothest discussion of the issues with which we have been concerned takes the ‘say less’ approach. Contrariety and subcontrariety are then what are called coercive logical relations in Humberstone (2013b), by contrast with, for example, consistency, understood as the relation holding between A and B precisely when they are not contraries, is what is there called a permissive logical relation. The coercive relations are defined by a requirement—and here we put it syntactically—that something should be provable in the logic to which they are relativized, whereas the permissive relations such as consistency and independence are those obtaining in virtue of something’s not being provable in the logic in question.Footnote 66 (In terms of quantification over valuations in a determining class, the coercive relations involve universal quantification and the permissive relations involve existential quantifications.) Contrariety on and subcontrariety on the ‘say more’ approach are mixed coercive and permissive logical relations, like the relation of unilateral implication (holding between A and B according to \(\vdash \) when \(A \vdash B\) and \(B \nvdash A\)), and having selected the ‘say less’ option, we can still make a concession to the alternative option by calling contraries which are not also subcontraries, mere contraries, and subcontraries which are not also contraries mere subcontraries.
Note that the definitions are just given of mere contrariety and mere subcontrariety could equivalently have been put in the following way: mere contraries are contraries which are not contradictories, and mere subcontraries are subcontraries which are not contradictories.Footnote 67 For this reason, it does not matter whether Slater’s objection is put by saying, on the one hand, that LP’s negation turns a formula into a subcontrary but not (in the general case) into one which is a contradictory, or, on the other hand, that the LP’s negation turns a formula into a mere subcontrary, so nothing hangs in this debate on whether Slater had the ‘say less’ or the ‘say more’ understanding of the word subcontrary in mind. Béziau seems to think otherwise, and himself favours the ‘say more’ reading, as is also clear from Béziau (2016). This may be part of why he thinks that Slater’s discussion is confused, since he attributes this interpretation to Slater also (see the Digression below) and it is perhaps also connected with his claim—quoted in the Digression in Sect. 15.3—that intuitionistic negation is not a contrary-forming operator. To illustrate in the latter case, for some choices of A, A and \(\lnot A\) will not be mere contraries, in the sense that they are contraries without being subcontraries: for example, take A as \(p \wedge \lnot p\). We resume the present discussion after an optional explanation of Béziau’s grounds for attributing the ‘say more’ interpretation to Slater. (Appendix 2 addresses Heinrich Wansing’s similar claim that negation in intuitionistic logic does not form what we are calling mere contraries.)
Digression. On the ‘say more’ interpretation, subcontraries and contradictories are mutually exclusive relations. Slater (1995) has the example of coming to call red things blue not amounting to changing their colour but only our terminology for attributing colours to them. This is meant to be analogous to coming to calling subcontraries contradictories not actually making them contradictories, so in view of the mutual exclusivity of red and blue as standardly understood, Béziau concludes that Slater assumes as standard an understanding of subcontrary and contradictory one which makes them likewise mutually exclusive, as the ‘say more’ interpretation does. But this may be a purely incidental feature of the example. Here is Béziau making a case for his reading of Slater, from p. 19 of Béziau (2006), beginning with a characterization of the ‘say less’ option:
In this case, confusing subcontraries with contradictories would not be the same as switching red with blue, or cats with dogs, but rather would amount of confusing dogs with canines. Let us call global confusion this kind of error by contrast to the first one that we can call switching confusion. As Slater claims through his red and blue example that paraconsistent logicians are making a switching confusion rather than a global one, it seems implicit that he doesn’t consider that all contradictories are subcontraries, neither do we here.
As I say, the fact that blue and red were chosen may just be for dramatic effect. In any case, although Slater did envisage a switch, calling red things blue and blue things red, the point of the example would have survived if red things came to be called blue but the blue things continued to be called blue. And this would have been more plausible since no party to the present debate could be described as calling contradictories subcontraries in the way that Slater accuses Priest of calling subcontraries contradictories. (The opening sentence of Béziau 1996 seems to offer such a description but this seems to be a matter of not being completely familiar with the ‘calling Xs Ys’ construction in English.) Despite its having (if I am right) no bearing on the merits of Slater’s objection to dialetheism, it would have been interesting to know whether in writing Slater (1995) he had in mind the ‘say less’ or the ‘say more’ interpretation.Footnote 68 End of Digression.
The use of the word ‘mere’ above is a special ad hoc technicalization of the ordinary use. In the everyday sense the dual intuitionistic negation of a formula is not a ‘mere’ subcontrary, if that means there is nothing more informative to be said on the matter, since (as recalled more than once already) it specifically forms the strongest subcontrary of the formula in question (and similarly in the case of intuitionistic negation proper and mere contrariety, interchanging ‘contrary’ and ‘subcontrary’ and ‘weakest’ and ‘strongest’). And in the case of intuitionistic logic itself, we note that there is always something stronger to be said than merely that two formulas are subcontraries, since by the Disjunction Property, one will be provable outright. Really this would be better described as the Subcontrariety Property, since the issue arises in \(\vee \)-free fragments of the logic (as was noted for LC in the Digression in Sect. 15.3): whenever formulas A, B are subcontraries in the sense there defined according to the fragment-specific consequence relation in question, one or other of them is a consequence of \(\varnothing \). Indeed one can supply such an example for a fragment of classical logic too, taking the \(\{\leftrightarrow \}\)-fragment of \(\vdash _\mathsf{CL}\): whenever A and B, constructed using only \(\leftrightarrow \) from sentence letters, are subcontraries, at least one of A or B is a classical tautology.Footnote 69 Unlike the intuitionistic case, the Subcontrariety Property for the equivalential fragment of classical logic does not extend to the obvious ternary (or more) generalization of the relation of subcontrariety: for example, p, q and \(p \leftrightarrow q\) are ‘ternary subcontraries’ (no Boolean valuation falsifying all of them), no one of which is tautologous. (However, the result does extend to allowing dependence on assumptions: If \(\Gamma \vdash _\mathsf{CL} A \vee B\) and the only connective appearing in \(\Gamma \,\cup \,\{A, B\}\), is \(\leftrightarrow \), then either \(\Gamma \vdash _\mathsf{CL} A\) or \(\Gamma \vdash _\mathsf{CL} B\). A proof of this, which requires some apparatus going beyond that deployed for the \(\Gamma = \varnothing \) case treated in Footnote 69, can be found in Humberstone 2019; see Proposition 1.4(ii) there.)
An attempt at precisifying something like the ‘mereness’ idea for coercive binary logical relations is set out in pp. 200–204 of my (Humberstone 2013b), which involves passage from such a relation, R, to the relation \(\mu (R)\) of standing minimally in the relation R, with \(\mu (R)\) defined to hold between A and B when (1) R(A, B) and (2) there is no (coercive) binary logical relation \(S \,\subsetneq R\) such that S(A, B).Footnote 70 Thus if R is the relation of subcontrariety, its minimization \(\mu (R)\), unlike R itself, never holds between contraries A and B, since if the relation of being contradictories held between them, that would then be a proper subrelation S of R for which S(A, B), violating (2). The discussion of logical relations in Humberstone (2013b) has many features oriented specifically to the setting of classical logic but we can apply this idea to the Disjunction Property, to revert to this slightly misleading label, along with the name \(R^{\vee }\) for the relation of subcontrariety, now to be understood as ‘according to the consequence relation of intuitionistic logic’. As observed in the previous paragraph, in this setting subcontrariety is a somewhat degenerate affair, in that there is always something much more informative that can be said, since one or other of the relata is outright (intuitionistically) provable. In terms of the present apparatus this amounts to: \(\mu (R^{\vee })\, = \, \varnothing \). The reason is as follows. Writing  (respectively,
(respectively,  ) for the relation holding between any two formulas the first (respectively, the second) of which is IL-provable, the Disjunction Property means that
) for the relation holding between any two formulas the first (respectively, the second) of which is IL-provable, the Disjunction Property means that  , so whenever \(R^{\vee }(A, B)\) there is a proper subrelation of \(R^{\vee }\), whether it be
, so whenever \(R^{\vee }(A, B)\) there is a proper subrelation of \(R^{\vee }\), whether it be  or
or  (or indeed their intersection) which relates A and B; thus we can never have \(\mu (R^{\vee })(A, B)\). This example shows that being ‘minimal subcontraries’ does not coincide with being ‘mere subcontraries’ as defined above, since, for example, p and \(q \rightarrow q\) are mere subcontraries (subcontraries which are not contraries—equivalently, contraries which are not contradictories) but not minimal subcontraries (since they stand in the relation
(or indeed their intersection) which relates A and B; thus we can never have \(\mu (R^{\vee })(A, B)\). This example shows that being ‘minimal subcontraries’ does not coincide with being ‘mere subcontraries’ as defined above, since, for example, p and \(q \rightarrow q\) are mere subcontraries (subcontraries which are not contraries—equivalently, contraries which are not contradictories) but not minimal subcontraries (since they stand in the relation  ). Note that the present example can be understood with either classical or intuitionistic logic as the background setting—the Disjunction Property is not required. (For the intuitionistic case the appropriateness of our official definition of subcontrariety will not be taken for granted in Appendix 2 below.)
). Note that the present example can be understood with either classical or intuitionistic logic as the background setting—the Disjunction Property is not required. (For the intuitionistic case the appropriateness of our official definition of subcontrariety will not be taken for granted in Appendix 2 below.)
Finally, let us note that if one applies the ‘mere’ modifier in connection with contrary or subcontrary-forming operators, an ambiguity arises, as we illustrate in the contrariety case. A 1-ary operator \(\#\) may be called a mere contrary-forming operator in order to convey that for every formula A, \(\#A\) and A are mere contraries (contraries which are not contradictories). On the other hand one may by this same phrase intend to convey that \(\#\) is a contrary-forming but not a contradictory-forming operator: in other words while for every formula A and \(\#A\) are contraries, it is not the case that for every formula A, A and \(\#A\) are contradictories. (To get back to the first—stronger—sense, replace this last every by any.) It is in this second sense that intuitionistic negation is a mere contrary-forming operator: see the example just before the Digression above. In Appendix 2 we look at the claim that (pace Priest among others), intuitionistic negation forms contradictories. These clarificatory remarks also apply if instead of taking a contrary-forming (or subcontrary-forming or contradictory) operator to be—as we have been presuming—a 1-place primitive or derived connective, but any function from formulas to formulas. In any extension of the normal modal logic KD (sometimes called D), for instance,Otherwise the intuitionist \(\Box p\) and \(\Box \lnot p\) we can ask whether these are contraries, and answer affirmatively. (The ‘say more’ advocate will have to hedge here and say, for example, that they are contraries in KD but not in its extension KD!,Footnote 71 where they are contradictories.) First, we can consider a (partial) function f which assigns to each formula \(\Box A\) the formula \(\Box \lnot A\). This, in the extended sense of the phrase, would then count as a contradictory-forming (better: contradictory-yielding) operator, but it is what Humberstone (2011a) calls a non-connectival operation on formulas, in that there is no KD-definable connective \(\#\) for which \(\#\Box A\) is KD-provably equivalent to \(\Box \lnot A\). Indeed with A as, e.g. p, \(\Box \lnot A\) is a paradigm case of contrariety from the modal square of opposition in some sense in which another mere contrary for all that has been said in this paper, namely \(\lnot (\Box p \vee \Box \lnot p)\), is not: see Sect. 3 of my (Humberstone 2005b), for this and references to the work of Robert Blanché, who saw in this last formula together with \(\Box p\) and \(\Box \lnot p\) a triangle of formulas all mutually contrary in the only sense (as Blanché felt) there is. What is involved here (further elaborated in Humberstone 2005b) may be connected with what Horn (1989) calls polar contrariety; the issue (as with the corresponding issue for subcontraries) has been kept out of sight in the present paper as not being of special significance in connection with Priest’s discussion of negation and the reactions of commentators to that discussion. However, Horn does have a useful discussion, with historical references, to the main subject—‘say less’ versus ‘say more’—on p. 36f. of Horn (1989).
Appendix 2: Wansing on Priest on Negation
At the end of the Digression in Sect. 15.3 it was mentioned that Wansing does not share Priest’s view that intuitionistic negation forms mere contraries, preferring to describe it as genuinely contradictory-forming. Here we examine his reasons. For conformity with the rest of the notation used above, ‘\(\alpha \)’ is replaced by ‘A’ and to avoid a conflict with the ‘(1), (2)’ of Sect. 15.1, that numbering has been replaced by ‘(i), (ii)’ in the following (somewhat ellipsed) quotation from p. 92f. of Wansing (2006), though the unparenthesized ‘1, 2’ remain as in Wansing (2006). The references to Priest are to (1999), which this passage begins by summarizing—essentially the same as the material from Priest (2007), p. 467 (and Chap. 4 of Priest 2006b):
The set \(\{A, \lnot A\}\) thus forms a contradictory pair if the LNC and the LEM are provable:
\((i)\,\vdash \lnot (A \wedge \lnot A)\) and \(\vdash A \vee \lnot A\).
A reformulated statement of the contradictoriness of \(\{A, \lnot A\}\) corresponding to the reading Priest attributes to traditional logic and common sense is:
1. A and \(\lnot A\) cannot both be true.
2. One of A and \(\lnot A\) must be true.
On another reading, \(\{A, \lnot A\}\) is a contradictory pair if
1. Necessarily, if A is true, then \(\lnot A\) is false.
2. A and \(\lnot A\) cannot both be false.
If the Deduction Theorem is assumed (to avoid using implication), this reading gives
\((ii)\,A \vdash \lnot \lnot A\) and \(\vdash \lnot (\lnot A \wedge \lnot \lnot A)\).
If the contradictoriness of \(\{A, \lnot A\}\) is expressed by (i), intuitionistic negation fails to be contradictory-forming, and if the contradictoriness of \(\{A, \lnot A\}\) is expressed by (ii), intuitionistic negation does give rise to contradictions. As Priest (1999, p. 107) observes, in order to consider the truth conditions of negated statements, we ‘need a definition of falsity. Let us define “A is false” to mean that \(\lnot A\) is true. (...) And the present definition is one that all parties can agree upon, classical, intuitionist and paraconsistent’. Since Priest regards intuitionistic negation to be not a contradictory-forming connective but a contrary-forming one, his explanation cannot mean that A is false iff its contradictory is true. Otherwise, the intuitionist as Priest conceives of him or her should not agree upon the definition of falsity. Thus, the notion of falsity in a logic \(\Lambda \) is expressed by the negation operation used in \(\Lambda \) (assuming that \(\Lambda \) comprises only one ‘official’ negation and taking into account that this may not be a contradictory-forming connective and hence not a negation in Priest’s sense). The question thus is: When is \(\{A, \lnot A\}\) a contradictory pair?
Now, none of this—Priest’s discussion or Wansing’s development of it—is really methodologically optimal, as Section 1 of the present paper has tried to make clear. The question that should be asked is not what makes \(\{A, \lnot A\}\) a contradictory pair, but what makes \(\{A, B\}\) in general to a contradictory pair, or more simply put, what it is for A and B to be contradictories. One then applies the general ruling to the special case in which B is \(\lnot A\). The most plausible general proposal to see as implicit in the above passage arises by putting ‘B’ in place of all of its occurrences of ‘\(\lnot A\)’. A further moral of the discussion of the present paper is that by taking the ‘say more’ approach Priest and Wansing make it hard to describe the separate ingredients of their differing proposals permitted on the ‘say less’ approach with the simple vocabulary of contrariety and subcontrariety. (Wansing goes on to consider contrariety specifically in Sect. 3 of Wansing (2006) but this concerns the mixed coercive–permissive relation of mere contrariety rather than just the ‘incompatibility’ conception of contrariety of the ‘say less’ approach.) The first and second conjuncts of (i) are Priest’s chosen ways of formulating the contrariety and subcontrariety conditions on A and B for the case of \(B\, =\, \lnot A\), whereas the first and second conjuncts of (ii) are Wansing’s preferred formulations of the same two conditions. Moving to the general level, then, we may say that Wansing’s preference for the contrariety and subcontrariety conditions for A, B according to a consequence relation \(\vdash \) is given by:
Wansing contraries iff \(A \vdash \lnot B\); Wansing subcontraries iff \(\vdash \lnot (\lnot A \wedge \lnot B)\);
Priest contraries iff \(\vdash \lnot (A \wedge B\)); Priest subcontraries iff \(\vdash A \vee B\).
Some criticisms made in Sect. 15.1 of Priest’s discussion applies to Wansing’s also: to bring to bear a criterion of contrariety or subcontrariety (or the two of them together, for contradictoriness) on the question of whether something and its negation stand in the chosen relation, the clean approach would formulate the various criteria without deploying that very connective in the formulation, and in fact we went on to prefer formulations purified not only of \(\lnot \) but also of \(\wedge \) and \(\vee \). (For example, for \(\vdash \) with \(\vee \) in its language the Priest subcontrariety condition will not deliver the intended results unless \(A \vee B\)’s consequences are the common consequences of A and B, since \(\vdash \) may fail to be \(\vee \)-classical.) But Wansing here is not defending Priest’s approach, so much as looking for ‘Priest-style’ criteria that might be preferable, and, let us recall, specifically noting that his preferred criteria rule that according to the consequence relation \(\vdash _\mathsf{IL}\) of intuitionistic logic, since for any formula A, A and \(\lnot A\) are Wansing contradictories in the sense of being both Wansing contraries and Wansing subcontraries, even though they are not Priest contradictories because they are not in general Priest subcontraries.Footnote 72) (As we noted in Appendix 1, intuitionistic subcontrariety à la Priest—purged of any ‘say more’ trappings—is something of a degenerate relation because of the Disjunction Property.) Note that, by contrast with the case of subcontrariety, Wansing contrariety and Priest contrariety coincide for \(\vdash \,=\, \vdash _\mathsf{IL}\) and we use the terminology of Wansing contrariety for these equivalent formulations below (so that we can use ‘Wansing contradictories’ for pairs that are both Wansing contraries and Wansing subcontraries).Footnote 73
Wansing does not say a lot in favour of his subcontrariety condition, which would of course coincide with the disjunctive version against the background of \(\vdash _\mathsf{CL}\) rather than \(\vdash _\mathsf{IL}\), though certainly it looks like a more direct transcription of—‘2’ under (i) in the quoted passage—‘A and \(\lnot A\) cannot both be false’—once \(\lnot \) is connected, in the manner Priest suggests, with falsity. Whatever one wants to call it, there is a perfectly good logical relation here, holding—to purify the characterization—between A and B (according to \(\vdash \)) when the weakest contraries (according to \(\vdash \)) of A and B are themselves contraries. (Here we rely on the purified—and rather paraconsistency-unfriendly) characterization of contrariety given at the start of the Digression in Sect. 15.3.Footnote 74) There are many families of discernible logical relations of interest each collapsing to a single familiar relation in the setting of \(\vdash _\mathsf{CL}\), though leading separate lives in the more discriminating habitat of \(\vdash _\mathsf{IL}\), such as the relation of what in Humberstone (2011a), e.g. Remark 4.22.10 on p. 555, is called pseudo-subcontrariety, holding between A and B in that order when \(A \rightarrow B \vdash B\). (Formulation purifying away the \(\rightarrow \) to get the intended general effect: whenever for all \(\Gamma \) if \(\Gamma , A \vdash B\) then \(\Gamma \vdash B\).) Intuitionistically (i.e. taking \(\vdash \) as \(\vdash _\mathsf{IL}\)) this relation is not symmetric, so the ‘in that order’ is essential. On the other hand any talk of subcontraries with or without the ‘pseudo’ prefix, is inclined to suggest symmetry because of the wording ‘A and B are subcontraries’, so in Humberstone (2001) when A and B stand in this relation we say A anticipates B (according to \(\vdash \)); this paper looks into several aspects of this relation (see also Humberstone 2011a, p. 625f. for an update). Alternatively, one could symmetrize pseudo-subcontrariety by taking the intersection of the relation with its converse, which amounts to requiring the provability of
well known as the definiens in a definition of \(A \vee B\) in the intermediate logic LC, mentioned already in the Digression in Sect. 15.3, though for this point one really must give the fundamental reference, Dummett (1959b). According to Proposition 1.1 in Humberstone (2002) two formulas A and B are implicit implicational converses in intuitionistic logic, in the sense that there are formulas \(C \rightarrow D\) and \(D \rightarrow C\) respectively equivalent to A and B, if and only if the conjunction inset above is intuitionistically provable. (Alternatively put: iff A and B are mutual pseudo-subcontraries according to \(\vdash _\mathsf{IL}\); for \(\vdash _\mathsf{CL}\) we can just say ‘are subcontraries’—i.e. replace the above formula with \(A \vee B\), which indeed we can already say at the level of the intermediate \(\vdash _\mathsf{LC}\), in view of the above definability point.) But let us return to Wansing’s discussion of contradictoriness, to see him dismissing three other candidate characterizations (Wansing 2006, p. 83).
Among the various classically equivalent Priest-style formulations of Aristotle’s characterization of contradictoriness, there are three pairs of conditions that may be set aside:
- (a)
\(A \vdash \lnot \lnot A\), \(\lnot A \vdash \lnot A\)
(Necessarily, if A is true, then \(\lnot A\) is false. Necessarily, if A is false, then \(\lnot A\) is true.)
- (b)
\(\lnot A \vdash \lnot A\), \(\lnot \lnot A \vdash A\)
(Necessarily, if \(\lnot A\) is true, then A is false. Necessarily, if \(\lnot A\) is false, then A is true.)
- (c)
\(\vdash \lnot (A \wedge \lnot A),\quad \vdash \lnot (\lnot A \wedge \lnot \lnot A)\)
(A and \(\lnot A\) cannot both be true. A and \(\lnot A\) cannot both be false.)
In (a) and (b) the condition \(\lnot A \vdash \lnot A\) holds because of a general property of derivability. In (c), one condition is an instantiation of the other. We may ask whether or not the remaining classically valid and classically equivalent pairs of conditions, exhibiting in addition to \(\lnot \) at most \(\wedge \) and \(\vee \), hold in various non-classical propositional logics.
The reference to ‘the remaining classically valid and classically equivalent pairs of conditions’ is perhaps to those collected in a table on the following page of Wansing (2006), though it could be interpreted quite generally as referring to arbitrary further pairs of conditions. As before, abstracting from the above formulations to the underlying binary relations involved in A and B’s being contradictory according to the various proposals, we get general conditions on A and B which are all classically equivalent, which, for the special case on which the above passage concentrates in which B is \(\lnot A\), conditions are not just equivalent but classically valid (satisfied for arbitrary A, according to the consequence relation of classical logic, that is). And for a clearer focus on the issues, it pays to consider separately the contrariety and subcontrariety components in each case, and do so in the generalized setting—which is to say as conditions on arbitrary A and B, rather than just taking B as \(\lnot A\). This removes any inclination to think of the second condition for (c) as a redundant special case (substitution instance) of the first, since we now see that Table 1’s contrariety and subcontrariety conditions as independent (still reading \(\vdash \) as \(\vdash _\mathsf{IL}\)), and in particular we can have the contrariety condition satisfied for a particular A, B while the subcontrariety condition is not. For example, take \(A\, =\, p\) and \(B\, = \, \lnot p \wedge q\). Thus, in the terminology introduced above, these formulas are (intuitionistically) Wansing contraries but not Wansing subcontraries. (Conversely, keeping A as here and changing \(\wedge \) to \(\vee \) in B gives us a pair of Wansing subcontraries—though not Priest subcontraries, for the reason given in Appendix 1—which are not Wansing contraries.)
Table 15.1 separates out the general components in play in the passage from Wansing (2006) last quoted. Let us consider the various conditions with special reference to the choice of \(\vdash \) as \(\vdash _\mathsf{IL}\), so as to connect with Wansing’s proposal that \(\lnot \) is a contradictory-forming operator in intuitionistic logic. The first point that jumps out is that the three contrariety conditions are all equivalent, in the sense that for any A, B, any one of these conditions is satisfied (with \(\vdash \) as \(\vdash _\mathsf{IL}\)) if and only if any other is satisfied. We noted this already before in connection with the contrariety conditions for (a) and (c), temporarily baptized Wansing contrariety and Priest contrariety, so Wansing’s own favoured proposal, combining Wansing contrariety with Wansing subcontrariety (the subcontrariety condition for (c) in Table 15.1) is in fact equivalent, in the intuitionistic case, to proposal (c), which Wansing writes ‘may be set aside’. for the reason that ‘in (c), one condition is an instantiation of the other’. Wansing was there, of course, looking at the special case in which B was \(\lnot A\), but we can see in Table 15.1 that the same holds in the general case: the subcontrariety condition is the special case or ‘subschema’—though of course in this case not generally provable—of the contrariety condition, in that every instance of the former is an instance of the latter (though not conversely). But this is not an objection to the characterization of contrariety and subcontrariety in this way, since we would simply be saying that formulas are subcontraries (according to \(\vdash _\mathsf{IL}\)) iff their negations are contraries—an entirely familiar state of affairs: think of the Square of Opposition. In the present case we can equally say, as we can there, that on proposal (c) formulas are contraries iff their negations are subcontraries, since the outer negations allow for double negation replacements—or indeed any classically sanctioned (propositional) replacements which would otherwise raise an intuitionist’s eyebrow—in their scopes (by Glivenko).
That same consideration reminds us that while Wansing’s conception of contrariety coincides with the Priest’s conception, his subcontrariety condition differs from Priest’s disjunctive conception—a point in its favour in view of the degenerate nature of the latter, even though it is Priest’s rather than Wansing’s notion that amounts in the present setting to subcontrariety according to the consequence relation \(\vdash _\mathsf{IL}\), as this was given above in ‘connective-free’ terms (last recalled in Footnote 34). Wansing’s version can be thought of as replacing the reference to \(A \vee B\) in Priest’s with its double negation—intuitionistically equivalent to \(\lnot (\lnot A \wedge \lnot B)\). (Of course, the positions are here described in ‘say less’ terminology rather than that Priest and Wansing themselves officially adopt.) There is no need to exclude it on the grounds that the subcontrariety half follows from the contrariety half of the condition, since, as we have seen, this is not so in general for the two forms as defining as binary relations, neither of the binary contrariety and subcontrariety relations given in (c) of Table 15.1 is included in the other. And this is just as well, since it coincides with what Wansing wants to say in the intuitionistic case.
The subcontrariety conditions recorded for (a) and (b) are not, by contrast with the corresponding contrariety conditions, equivalent to each other (taking \(\vdash \) as \(\vdash _\mathsf{IL}\)), and are evidently close relatives of the pseudo-subcontrariety conditions mentioned above.Footnote 75 There is no reason why they should not be given consideration as subcontrariety-like conditions, preferably (again) in a form purified at least of the presence of \(\lnot \). This multiplicity of options arises for the same reason as we noted in Sect. 15.4 that when the true and the false no longer partition the field, ‘what might otherwise be taken to be mere reformulations now emerge as non-equivalent possibilities’. In the case of subcontrariety in IL the situation is even more complicated, since we don’t just have to distinguish ‘at least one of A, B is true’ (the \(A \vee B\) version of subcontrariey) from ‘not both A, B are false’ (the Wansing version, under (c) in Table 15.1), but we have also these further options (using \((A \rightarrow B) \rightarrow B\), \(\lnot A \rightarrow B\), etc., once we are considering, as with Wansing subcontrariety, departures from the abstract characterization mentioned in Footnote 34 and earlier). These are, of course, repercussions of the generally greater discriminatory power of deductively weaker logics—the subject of Humberstone (2005c)—though Humberstone (2011a) does suggest some guidance in looking for the most direct intuitionistic analogues of classical connectives in the shape of their topoboolean incarnations in the Kripke semantics (making the intuitionistic compound true at a point in a model if the corresponding classical compound is true at all accessible points, that is). See, for example, p. 786ff. of Humberstone (2011a), where this is applied in the case of exclusive disjunction (\({\veebar }\), say), a particularly significant connective for the present discussion since the Lemmon-style logical relation (along the lines of \(R^{\vee }\) in Appendix 1) \(R^{{\veebar }}\), induced by this connective in the classical setting is the relation of being contradictories.Footnote 76
We conclude with some general remarks on the subject of Wansing contradictories (in intuitionistic logic). Let us denote the set of Wansing contradictories of a formula A by WCtd(A), recalling here the precise definition:
As one expects, the relation here is symmetric: for any A, B, \(A \in \textit{WCtd}(B)\) if and only if \(B \in \textit{WCtd}(A)\). Another expectation—cf. the title of Cresswell (2008)—might be that contradictories are unique, i.e. that for any A, all formulas in WCtd(A) are (IL-)equivalent, but it is easy to see that this expectation is not fulfilled for Wansing contradictories, since, for example, WCtd(\(\lnot p\)) contains both p and \(\lnot \lnot p\). A certain interest accordingly attaches to the question of how much variation one might expect to find within WCtd(A) for a given A.
For example, one can ask whether there is in general for any given formula, strongest or weakest Wansing contradictories in intuitionistic logic, and for assistance in pursuing that question, make the observation that the set of Wansing contradictories of a formula WCtd(A), coincides with the set of formulas which are classically equivalent to \(\lnot A\). If A is, for example, \({\lnot p \vee q}\) WCtd(A) contains \(\lnot (\lnot p \vee q)\), \(p \wedge \lnot q\), and (infinitely) many other non-IL-equivalent formulas. Relatedly, one could explore the inverse image under \(\lnot \) of a formula C in intuitionistic logic, where this is understood along the same lines as the corresponding notion in (classically based) modal logic, for which (Humberstone 2013a) introduces the notation, for a monomodal logic S, ‘\(\Box ^{-1}[C]^{S}\)’ to denote the set \(\{B\text {: } \vdash _{S} \Box B \leftrightarrow C\}\), called the inverse image under \(\Box \) of the formula C, according to S. For present purposes, one would be interested in the set \(\lnot ^{-1}[C]^{\textit{IL}}\), comprising those formulas whose negations are intuitionistically equivalent to C. This will be empty if C has no equivalent with \(\lnot \) as main connective, but in the simple case of \(C = \lnot p\) contains not only p and \(\lnot \lnot p\), already mentioned, but also such things as \(p \wedge (q \vee \lnot q)\), not equivalent to either of them. More generally a little calculation reveals that for any formula B:
We see that there is no IL-strongest formula in general in such a set, since given any formula B not containing the sentence letters \(q_1,\dots q_n,\ldots \) the sequence:
contains ever stronger formulas, as long as B is IL-consistent. There is a similar sequence of ever weaker formulas to establish the dual claim, obtainable from the above sequence by replacing all occurrences of \(\wedge \) with \(\rightarrow \) (and replacing the proviso on B with: ‘as long as B is not IL-provable’). To tie this up with our discussion of Wansing contradictories, and clarify the recent use of the word ‘relatedly’, note that for any formula C,
and thus
Such a characterization tells immediately, for example, that the set of Wansing contradictories of any given formula is closed under \(\wedge \) and \(\vee \). But with this we conclude our reflections on (some of the strands in) Wansing’s discussion of Priest on negation.
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Humberstone, L. (2019). Priest on Negation. In: Başkent, C., Ferguson, T. (eds) Graham Priest on Dialetheism and Paraconsistency. Outstanding Contributions to Logic, vol 18. Springer, Cham. https://doi.org/10.1007/978-3-030-25365-3_15
Download citation
DOI: https://doi.org/10.1007/978-3-030-25365-3_15
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-25364-6
Online ISBN: 978-3-030-25365-3
eBook Packages: Religion and PhilosophyPhilosophy and Religion (R0)


 ’ forms the strongest subcontrary of what it applies to:
’ forms the strongest subcontrary of what it applies to: 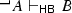 for arbitrary A, B. Further information may be found in 8.11 and 8.22 of my (Humberstone
for arbitrary A, B. Further information may be found in 8.11 and 8.22 of my (Humberstone  holds on h iff it is not the case that h(C) is designated for each
holds on h iff it is not the case that h(C) is designated for each 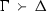 of
of 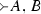 should be provable—formulated as the condition ‘
should be provable—formulated as the condition ‘