Abstract
Expressions in specification and programming languages often extend algebraic terms by additional term formation rules and enlarged evaluation domains. For use in different contexts, the semantics of these expressions must allow for interface modification, that is, evaluation must be compatible with signature translation and with variable renaming. This work introduces term charters as an abstract framework for terms and expressions following the slogan “evaluation is invariant under change of notation”. Several examples illustrate the use of term charters. Different term charter representations are discussed and morphisms between term charters are defined. Finally, the relation of term charters with institutions in general and with context institutions in particular is demonstrated.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Algebraic signatures are customarily connected with a fixed grammar for term construction as well as a canonical accompanying procedure for term evaluation; what may vary is the term representation when using different names for function symbols. More often than not, expressions of specification or programming languages build on algebraic signatures and evaluation, but exceed the boundaries of such a tightly connected syntactical and semantical scheme. For instance, the “Object Constraint Language” (OCL [10]) is mainly based on order-sorted algebra with function symbols like  and append giving rise to expressions like
and append giving rise to expressions like  and
and  as well as their usual evaluation.
as well as their usual evaluation.
The OCL grammar, however, also offers a general iteration construct  for applying the expression e over the successive elements of the sequence c using the iterator i and accumulating the partial results in a initialised by \(e_0\). Here, e has to be evaluated multiple times for different valuations of its bound variables i and a. This would be at least cumbersome to comprise into order-sorted terms using a different function symbol for every possible iteration expression. Alternatively, full higher-order algebras [14] could be employed, which yet would seem rather generous for such a small excursion. A more direct solution is to use a special evaluation rule for the iteration construct with only one local auxiliary semantic function of higher order.
for applying the expression e over the successive elements of the sequence c using the iterator i and accumulating the partial results in a initialised by \(e_0\). Here, e has to be evaluated multiple times for different valuations of its bound variables i and a. This would be at least cumbersome to comprise into order-sorted terms using a different function symbol for every possible iteration expression. Alternatively, full higher-order algebras [14] could be employed, which yet would seem rather generous for such a small excursion. A more direct solution is to use a special evaluation rule for the iteration construct with only one local auxiliary semantic function of higher order.
Another set of language features of the OCL that stretches order-sorted algebras is \({\texttt {undef}}\) representing undefinedness, its corresponding undefinedness test  , and the conditional
, and the conditional  that is only strict in its first argument. A change to the setting of partial algebras [14] could be considered, but also sticking with order-sortedness and just extending the value domains of the algebras by a semantic value \(\dagger \) and providing a special evaluation rule for the conditional presents a viable alternative.
that is only strict in its first argument. A change to the setting of partial algebras [14] could be considered, but also sticking with order-sortedness and just extending the value domains of the algebras by a semantic value \(\dagger \) and providing a special evaluation rule for the conditional presents a viable alternative.
These examples suggest that it is sometimes necessary to consider special expression construction and evaluation rules added to algebraic languages. In order to be applicable in varying contexts and to allow for different representations of the underlying algebraic signature, evaluation still has to be compatible with changes to the interface of expressions, i.e., the function symbols and the free variables. In the following, we discuss a notion of evaluation for generalised terms in an abstract framework that we call term charter. It captures the fundamental properties of evaluation w.r.t. variables, signatures, variable renamings, and signature translations along the slogan “evaluation is invariant under change of notation”. Using this as a guideline, the present account of term charters provides a simplification and rational reconstruction of our previous rendition in [6].
We first review the motivational OCL examples and the principal evaluation properties more precisely in Sect. 2, though starting, for simplicity, from many-sorted algebras. Based on indexed categories [15, 17], we then present term charters in Sect. 3. Term charters are built over term charter domains consisting of values and variables, structures, and the underlying values of structures, all indexed over signatures. A term charter itself consists of a term constructor, a variable embedding, and evaluation maps for terms over a signature and variables using valuations; the interaction of these ingredients is regulated by three axioms for variable evaluation, variable renaming, and signature translations such that indeed evaluation is invariant under change of notation. We also discuss two more compact alternative presentations of term charters using comma categories [8] and the Grothendieck construction [17] in Sect. 4. The latter lets us directly construct an institution [3, 5] from a term charter as shown in Sect. 5; again, this new construction simplifies [6]. The generation of an institution conveniently embeds term charters into the landscape of logical systems. What is more, the induced institution is closely related to the notion of context institutions by Pawłowski [12], which has been introduced in a similar effort to capture open formulæ over variables in institutions. We finally discuss different notions of morphisms between term charter domains and term charters in Sect. 6. We conclude in Sect. 7 with some application scenarios of term charters to OCL. Mainly for fixing notation, some categorical prerequisites are briefly summarised in Appendix A.
2 Extending Algebraic Term Evaluation
The evaluation of terms over a many-sorted signature \(\varSigma = (S, F)\) of sorts and function symbols directly follows term formation. Given S-sorted variables \(X = (X_s)_{s \in S}\), the family of terms  over \(\varSigma \) and X is inductively defined by
over \(\varSigma \) and X is inductively defined by
-
 if \(x \in X_s\);
if \(x \in X_s\); -
 if
if 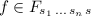 and
and  for \(1 \le i \le n\).
for \(1 \le i \le n\).
For a \(\varSigma \)-structure \(M = (S^M, F^M)\) and a valuation  from the variables X to the underlying sets
from the variables X to the underlying sets  of the structure, term evaluation
of the structure, term evaluation  is inductively defined in correspondence with term formation of the grammar:
is inductively defined in correspondence with term formation of the grammar:
-
\(\mathopen \llbracket x\mathclose \rrbracket ^{\text {m}}_{(\varSigma , X)} (M, \beta )_s = \beta _s(x)\) for \(x \in X_s\), and
-
 for \(f \in F_{s_1\,\ldots \,s_n\,s}\) and
for \(f \in F_{s_1\,\ldots \,s_n\,s}\) and  for \(1 \le i \le n\).
for \(1 \le i \le n\).
If, however, other term formation rules are considered that transcend the boundaries of the compliance of the function symbols f with the interpreting functions \(f^M\) or that require values besides the sorted universes \(s^M\) of the structure M for evaluation, recourse to an extended notion of structures has to be taken.
Example 1
Consider the many-sorted signature \(\varSigma ^{\circ }_{} = (S, F)\) showing as sorts S,  for the booleans,
for the booleans,  for the integers, and, for every sort \(s \in S\),
for the integers, and, for every sort \(s \in S\),  for the (finite) lists, together with some function symbols F like
for the (finite) lists, together with some function symbols F like  for zero and
for zero and  for addition; and the \(\varSigma ^{\circ }_{}\)-structure \(M^{\circ }_{} = (S^{M^{\circ }_{}}, F^{M^{\circ }_{}})\) interpreting these sorts and function symbols of \(\varSigma ^{\circ }_{}\) in the standard way, such that, in particular,
for addition; and the \(\varSigma ^{\circ }_{}\)-structure \(M^{\circ }_{} = (S^{M^{\circ }_{}}, F^{M^{\circ }_{}})\) interpreting these sorts and function symbols of \(\varSigma ^{\circ }_{}\) in the standard way, such that, in particular,  ,
,  ,
,  ,
,  , and
, and  . Besides the usual term formation rules from the variables and the function symbols above, we want to include an OCL-like iteration construct
. Besides the usual term formation rules from the variables and the function symbols above, we want to include an OCL-like iteration construct

in the grammar of iteration terms  : Starting with the accumulator variable a of sort \(s'\) initialised with the evaluated term
: Starting with the accumulator variable a of sort \(s'\) initialised with the evaluated term  , each entry in the evaluated term
, each entry in the evaluated term  is successively assigned to the iterator variable i of sort s updating the accumulator a with the result of evaluating the term
is successively assigned to the iterator variable i of sort s updating the accumulator a with the result of evaluating the term  , which thus may contain i and a as fresh local variables, and finally, the last value of a is returned; such that, e.g., evaluation of
, which thus may contain i and a as fresh local variables, and finally, the last value of a is returned; such that, e.g., evaluation of  yields 6. Evaluation of iterations could rely on an extended \(\varSigma ^{\circ }_{}\) with function symbols
yields 6. Evaluation of iterations could rely on an extended \(\varSigma ^{\circ }_{}\) with function symbols  for every possible iteration expression (and a correspondingly extended \(M^{\circ }_{}\)), or an embedding of the whole language into higher-order algebra. As a more moderate alternative, the evaluation of iterations can also be directly expressed using \(M^{\circ }_{}\) based on an intermediate, ad hoc higher-order function \( it ^{M^{\circ }_{}}\):
for every possible iteration expression (and a correspondingly extended \(M^{\circ }_{}\)), or an embedding of the whole language into higher-order algebra. As a more moderate alternative, the evaluation of iterations can also be directly expressed using \(M^{\circ }_{}\) based on an intermediate, ad hoc higher-order function \( it ^{M^{\circ }_{}}\):

where  , like Haskell’s foldr, is defined by \( it ^{M^{\circ }_{}}(\varepsilon , v_a, h) = v_a\) and \( it ^{M^{\circ }_{}}(v_i {:}{:} \ell , v_a, h) = it ^{M^{\circ }_{}}(\ell , h(v_i, v_a), h)\).
, like Haskell’s foldr, is defined by \( it ^{M^{\circ }_{}}(\varepsilon , v_a, h) = v_a\) and \( it ^{M^{\circ }_{}}(v_i {:}{:} \ell , v_a, h) = it ^{M^{\circ }_{}}(\ell , h(v_i, v_a), h)\).
In order to obtain a proper evaluation, the basic properties of algebraic term evaluation w.r.t. the interface of terms must be retained also for extended term formation rules and structures, i.e., compatibility with variable renamings and signature translations has to be ensured. For the many-sorted case a variable renaming \(\xi = (\xi _s : X_{1, s} \rightarrow X_{2, s})_{s \in S} : X_1 \rightarrow X_2\) induces a term renaming  , which usually is denoted again by \(\xi \); then for each
, which usually is denoted again by \(\xi \); then for each  a “renaming lemma” holds:
a “renaming lemma” holds:

Moreover, a signature translation \(\sigma = (\sigma _{\mathrm {S}} : S \rightarrow S', \sigma _{\mathrm {F}} : F \rightarrow F') : \varSigma = (S, F) \rightarrow \varSigma ' = (S', F')\) and the corresponding reducts of variables \(X' | \sigma = (X'_{\sigma _{\mathrm {S}}(s)})_{s \in S}\) and terms  induce a term translation
induce a term translation  inductively defined by
inductively defined by
-
 for
for  ;
; -
 for \(f \in F_{s_1\,\ldots \,s_n\,s}\) and
for \(f \in F_{s_1\,\ldots \,s_n\,s}\) and  for \(1 \le i \le n\).
for \(1 \le i \le n\).
Then, for the \(\sigma \)-reduct of structures  and valuations \(\beta ' | \sigma = (\beta '_{\sigma _{\mathrm {S}}(s)})_{s \in S}\), and abbreviating
and valuations \(\beta ' | \sigma = (\beta '_{\sigma _{\mathrm {S}}(s)})_{s \in S}\), and abbreviating  by just \(\sigma \), a “translation lemma” for each
by just \(\sigma \), a “translation lemma” for each  holds:
holds:

These properties (R\(_\mathrm{m}\)), (T\(_\mathrm{m}\)) can be straight forwardly transferred to properties (\(\text {R}_\mathrm{it}\)), (\(\text {T}_\mathrm{it}\)) for the evaluation of iterations in Example 1: The signatures and structures are taken to be restricted to the forms of \(\varSigma ^{\circ }_{}\) and \(M^{\circ }_{}\) such that signature translations preserve  , etc., and
, etc., and  and
and  are defined to preserve the grammar also of
are defined to preserve the grammar also of  such that, in particular, the additional clause for variable renamings becomes
such that, in particular, the additional clause for variable renamings becomes

Name capturing of the bound variables i and a is avoided due to the explicit provision of fresh variables in \(X \uplus \{ i : s, a : s' \}\) and the corresponding extension of \(\xi \).
Example 2
Again inspired by the OCL, consider the addition of a term former undef denoting undefinedness over the signature \(\varSigma ^{\circ }_{}\) and the \(\varSigma ^{\circ }_{}\)-structure \(M^{\circ }_{}\) from above. The predefined function symbols are to be interpreted strictly, i.e., if any of the argument terms of a function symbol is undefined, the overall result shall be undefined. Additionally, we want to include the non-strict term former  for testing for undefinedness, and the conditional
for testing for undefinedness, and the conditional  which is only strict in its first argument. Here, a first option is to change the interpreting structure \(M^{\circ }_{}\) into a partial algebra. As an alternative to such a pervasive adaptation, we may also opt for just including a semantic value \(\dagger \) into the underlying sets of \(M^{\circ }_{}\) by defining
which is only strict in its first argument. Here, a first option is to change the interpreting structure \(M^{\circ }_{}\) into a partial algebra. As an alternative to such a pervasive adaptation, we may also opt for just including a semantic value \(\dagger \) into the underlying sets of \(M^{\circ }_{}\) by defining  . The valuations then are of the form
. The valuations then are of the form  and the evaluation becomes
and the evaluation becomes  defined by
defined by

The corresponding properties (R\(_\mathrm{u}\)) and (T\(_\mathrm{u}\)), where  and
and  now also preserve undef, isUndef(), and the conditional, can be proved by induction on term formation.
now also preserve undef, isUndef(), and the conditional, can be proved by induction on term formation.
3 Term Charter Domains and Term Charters
We present an abstract framework capturing the basic properties of term evaluation over structures, where the terms are formed according to a grammar and the structures can consist of extended algebras. Signatures, values and variables, structures, and underlying values are comprised into a term charter domain; the grammar of term formation, variable renaming, variable embedding, and the evaluation proper is collected into a term charter over such a domain requiring conditions for variable embedding and invariance under renaming and translation. We use indexed categories [15, 17] (see Appendix A.1) as a foundation for the abstract framework, since they provide a close match with the algebraic signatures as indexes also used in institutions [14]. We show that term structure constructors induce term charters. Additionally, we discuss a different form for term translation and a notion of substitutions in term charters. Term charters have already been introduced in [6]. The presentation there, however, employed the technical means of Grothendieck categories throughout, thereby somewhat obscuring the relation of term charters with generalised evaluation.
3.1 Term Charter Domains
A term charter domain  is given by a category
is given by a category  of signatures, an indexed category
of signatures, an indexed category  of value variables, an indexed category
of value variables, an indexed category  of structures, and an underlying indexed functor
of structures, and an underlying indexed functor  .
.
We use the terminology of “value variables”, since  plays the rôle of both. In fact, variables in
plays the rôle of both. In fact, variables in  can only be assigned values in
can only be assigned values in  , not, e.g., sets of values or functions.
, not, e.g., sets of values or functions.
Example 3
(1) A term charter domain  for many-sorted algebras can be obtained as follows (order-sorted or higher-order algebras can be handled similarly): The signature category
for many-sorted algebras can be obtained as follows (order-sorted or higher-order algebras can be handled similarly): The signature category  comprises the many-sorted signatures \(\varSigma = (S, F)\) and the signature morphisms \(\sigma = (\sigma _{\mathrm {S}}, \sigma _{\mathrm {F}}) : \varSigma \rightarrow \varSigma '\). The category
comprises the many-sorted signatures \(\varSigma = (S, F)\) and the signature morphisms \(\sigma = (\sigma _{\mathrm {S}}, \sigma _{\mathrm {F}}) : \varSigma \rightarrow \varSigma '\). The category  of \(\varSigma \)-value variables comprises the set families \(X = (X_s)_{s \in S}\) and the renamings \(\xi = (\xi _s : X_{1, s} \rightarrow X_{2, s})_{s \in S} : X_1 \rightarrow X_2\); the reduct functor
of \(\varSigma \)-value variables comprises the set families \(X = (X_s)_{s \in S}\) and the renamings \(\xi = (\xi _s : X_{1, s} \rightarrow X_{2, s})_{s \in S} : X_1 \rightarrow X_2\); the reduct functor  yields
yields  and
and  . The category
. The category  of \(\varSigma \)-structures comprises the many-sorted structures
of \(\varSigma \)-structures comprises the many-sorted structures  and the homomorphisms \(\mu = (\mu _s : s^{M_1} \rightarrow s^{M_2})_{s \in S} : M_1 \rightarrow M_2\) with
and the homomorphisms \(\mu = (\mu _s : s^{M_1} \rightarrow s^{M_2})_{s \in S} : M_1 \rightarrow M_2\) with  for \(f \in F\); the reduct functor
for \(f \in F\); the reduct functor  yields
yields  and
and  . Finally, define
. Finally, define  and
and  for the underlying value variables and renamings, such that indeed
for the underlying value variables and renamings, such that indeed  .
.
(2) For iterate in Example 1, the term charter domain  is obtained by restricting
is obtained by restricting  :
:  shows all signatures with predefined sorts Bool, Int,
shows all signatures with predefined sorts Bool, Int,  and function symbols 0, \(\mathtt{+}\), etc., as well as all signature morphisms preserving these predefined symbols;
and function symbols 0, \(\mathtt{+}\), etc., as well as all signature morphisms preserving these predefined symbols;  is only defined on
is only defined on  ; the structures in
; the structures in  are those with standard interpretations of the predefined symbols; and the underlying functor
are those with standard interpretations of the predefined symbols; and the underlying functor  operates only on
operates only on  .
.
(3) For the undefinedness extension in Ex. 2, the term charter domain  is defined using the indexed endo-functor
is defined using the indexed endo-functor  with
with  and
and  for a Kleisli construction [1]: The objects of
for a Kleisli construction [1]: The objects of  and
and  coincide, but a morphism
coincide, but a morphism  of
of  is given by the
is given by the  -morphism
-morphism  ; the
; the  -identities \(1_{X} : X \rightarrow X\) are the inclusions
-identities \(1_{X} : X \rightarrow X\) are the inclusions  , the composition
, the composition  of
of  and
and  is
is  . The underlying functor
. The underlying functor  is chosen as
is chosen as  and
and  .
.
3.2 Term Charters
Let  be a term charter domain. Let
be a term charter domain. Let  be a lax indexed functor, where the functors
be a lax indexed functor, where the functors  for each
for each  construct terms and rename terms along value variable renamings, and the natural transformations
construct terms and rename terms along value variable renamings, and the natural transformations  for each
for each  translate terms along signature morphisms. Let furthermore
translate terms along signature morphisms. Let furthermore  be a lax indexed natural transformation, where the natural transformations
be a lax indexed natural transformation, where the natural transformations  for each
for each  embed value variables into terms. Finally, for each
embed value variables into terms. Finally, for each  ,
,  , and
, and  , let
, let

be a function extending a value variable valuation \(\beta \) into a term valuation  . Then
. Then  is a term charter over
is a term charter over  if the following variable condition (V), renaming condition (R), and translation condition (T) are satisfied:
if the following variable condition (V), renaming condition (R), and translation condition (T) are satisfied:

for all  ,
,  , i.e., the term valuation over a value variable valuation indeed extends the value variable valuation;
, i.e., the term valuation over a value variable valuation indeed extends the value variable valuation;

for all  ,
,  ,
,  , i.e., the “renaming lemma” holds; and
, i.e., the “renaming lemma” holds; and

for all  ,
,  , i.e., the “translation lemma” holds.
, i.e., the “translation lemma” holds.
This notion of term charters in fact directly translates the properties of concrete evaluation as discussed in Sect. 2 into an abstract framework: Assume that for each  there is a faithful functor
there is a faithful functor  , i.e., each
, i.e., each  is a concrete category. Writing X for \(\mathcal {U}_{\varSigma }(X)\) when
is a concrete category. Writing X for \(\mathcal {U}_{\varSigma }(X)\) when  , \(\xi \) for \(\mathcal {U}_{\varSigma }(\xi )\) when
, \(\xi \) for \(\mathcal {U}_{\varSigma }(\xi )\) when  ,
,  for both
for both  and
and  ,
,  for
for  , \(\xi (t)\) for
, \(\xi (t)\) for  , and \(\sigma (t)\) for
, and \(\sigma (t)\) for  , the conditions become
, the conditions become
-
(V)
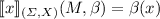 ;
; -
(R)
 ;
; -
(T)
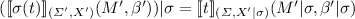 .
.
Example 4
(1) For many-sorted algebras as described in Sect. 2,  with
with  and
and  forms a
forms a  -term charter. Note that indeed
-term charter. Note that indeed  .
.
(2) For the iteration extension in Example 1,  with
with

 , and
, and  constitutes an
constitutes an  -term charter, as the instantiated properties (V\(_\mathrm{it}\)), (R\(_\mathrm{it}\)), and (T\(_\mathrm{it}\)) hold by induction on term construction.
-term charter, as the instantiated properties (V\(_\mathrm{it}\)), (R\(_\mathrm{it}\)), and (T\(_\mathrm{it}\)) hold by induction on term construction.
(3) Similarly, for the undefinedness extension in Example 2,  with
with  and
and  constitutes an
constitutes an  -term charter.
-term charter.
Since  is a lax indexed functor, the renaming condition (R) and the translation condition (T) can be equivalently combined into a single context condition on term charters for expressing that “evaluation is invariant under change of notation”:
is a lax indexed functor, the renaming condition (R) and the translation condition (T) can be equivalently combined into a single context condition on term charters for expressing that “evaluation is invariant under change of notation”:

for all  ,
,  , and
, and  , where
, where  .
.
3.3 Obtaining a Term Charter from a Term Structure Constructor
In the many-sorted case, the terms themselves form an algebra. In particular, for each  , there is a functor
, there is a functor  that is left adjoint to the underlying functor
that is left adjoint to the underlying functor  with a unit natural transformation
with a unit natural transformation  and a unique lifting
and a unique lifting  in
in  for each
for each  in
in  . This adjunction, where
. This adjunction, where  is a term structure constructor, can equivalently be used to obtain the many-sorted term charter of Example 4.
is a term structure constructor, can equivalently be used to obtain the many-sorted term charter of Example 4.
Indeed, for a term charter domain  , let
, let  be an
be an  -wise adjunction for the family of functors
-wise adjunction for the family of functors  , the family of natural transformations
, the family of natural transformations  , and the liftings
, and the liftings  for each
for each  and
and  . Then, for each
. Then, for each  , there is a natural transformation
, there is a natural transformation  defined by
defined by  such that
such that  becomes a lax indexed functor, for which
becomes a lax indexed functor, for which

is satisfied for  . In order to construct a term charter
. In order to construct a term charter  , define the term constructor
, define the term constructor  by
by  ,
,  and the evaluation morphisms as
and the evaluation morphisms as  . The embedding
. The embedding  forms a lax indexed natural transformation, since
forms a lax indexed natural transformation, since  . Term charter requirements (V) and (C) hold by expanding the definitions and using (\(*\)).
. Term charter requirements (V) and (C) hold by expanding the definitions and using (\(*\)).
3.4 Term Translations and Substitutions in Term Charters
The term translation  along a signature translation \(\sigma : \varSigma = (S, F) \rightarrow \varSigma ' = (S', F')\) used by the many-sorted term charter operates on the terms over the \(\sigma \)-reduct of the value variables
along a signature translation \(\sigma : \varSigma = (S, F) \rightarrow \varSigma ' = (S', F')\) used by the many-sorted term charter operates on the terms over the \(\sigma \)-reduct of the value variables  . It may seem more natural (and is indeed assumed in context institutions, see Sect. 5.2) to have a term translation work on terms over an
. It may seem more natural (and is indeed assumed in context institutions, see Sect. 5.2) to have a term translation work on terms over an  . This can be achieved via a map
. This can be achieved via a map  when defining
when defining  and setting
and setting  for the canonical injection
for the canonical injection  with
with  . In particular, the functor
. In particular, the functor  with
with  is left adjoint to the reduct functor
is left adjoint to the reduct functor  (cf. [2, Prop. 2.1]). Hence, both translation approaches are equivalent.
(cf. [2, Prop. 2.1]). Hence, both translation approaches are equivalent.
For the general case of a term charter  over a term charter domain
over a term charter domain  with adjunctions
with adjunctions  for each signature morphism \(\sigma \), we obtain natural transformations
for each signature morphism \(\sigma \), we obtain natural transformations  such that the translation condition (T) becomes
such that the translation condition (T) becomes

Moreover, term construction for many-sorted algebras is idempotent up to isomorphism, i.e., it holds that  ; this, in fact, applies to the iteration and the undefinedness extensions as well. In particular, for a term substitution
; this, in fact, applies to the iteration and the undefinedness extensions as well. In particular, for a term substitution  assigning the value variables in
assigning the value variables in  full terms over
full terms over  and not only value variables, the “substitution lemma”
and not only value variables, the “substitution lemma”

holds for all  and
and  , where
, where  is abbreviated by \(\theta \).
is abbreviated by \(\theta \).
The idempotency property may also be obtained for a general term charter  when requiring that there is a lax natural transformation
when requiring that there is a lax natural transformation  for flattening nested term constructions such that
for flattening nested term constructions such that  is an indexed monad [11]. A substitution condition on the term charter can then be expressed as
is an indexed monad [11]. A substitution condition on the term charter can then be expressed as

for all  ,
,  .
.
4 Alternative Term Charter Definitions
As demonstrated in Sect. 3.3, the evaluation maps  of a term charter
of a term charter  resemble the liftings
resemble the liftings  of an adjunction
of an adjunction  with
with  ; the palpable difference is that, for
; the palpable difference is that, for  ,
,  whereas
whereas  . The situation of a term charter is thus asymmetric, and
. The situation of a term charter is thus asymmetric, and  only affects the first parameter of the hom-functor
only affects the first parameter of the hom-functor  . Lawvere [7] (see [8, Exc. IV.1.2]) observed that the symmetric constellation of an adjunction \((\eta , \kappa ) : F \dashv G\) between the functors \(F : C \rightarrow D\) and \(G : D \rightarrow C\) can be equivalently expressed by an isomorphism
. Lawvere [7] (see [8, Exc. IV.1.2]) observed that the symmetric constellation of an adjunction \((\eta , \kappa ) : F \dashv G\) between the functors \(F : C \rightarrow D\) and \(G : D \rightarrow C\) can be equivalently expressed by an isomorphism  of comma categories such that the following diagram commutes, with \(\pi _i\) the projections:
of comma categories such that the following diagram commutes, with \(\pi _i\) the projections:

We transfer this observation to term charters in Sect. 4.1 where we capture the evaluation maps into a single indexed functor  and thus obtain a quite succinct characterisation using indexed comma categories (briefly summarised in Appendix A.2).
and thus obtain a quite succinct characterisation using indexed comma categories (briefly summarised in Appendix A.2).
On the other hand, the interface of a term in a term charter is given by its signature \(\varSigma \) and its value variables X; see condition (C). It thus seems natural to combine these two into a single entity  and to consider terms to be constructed over the combined interface. This is afforded by an application of the Grothendieck construction (briefly recapitulated in Appendix A.3) turning the indexed category
and to consider terms to be constructed over the combined interface. This is afforded by an application of the Grothendieck construction (briefly recapitulated in Appendix A.3) turning the indexed category  into a flat category
into a flat category  with objects
with objects  . The structures M and the valuations \(\beta \) also belong together, and can be combined into
. The structures M and the valuations \(\beta \) also belong together, and can be combined into  with objects \((M, \beta )\). In Sect. 4.2 we thus again obtain a more compact equivalent presentation of term charters where the evaluation maps can be comprised into a single indexed functor
with objects \((M, \beta )\). In Sect. 4.2 we thus again obtain a more compact equivalent presentation of term charters where the evaluation maps can be comprised into a single indexed functor  .
.
4.1 Characterising Term Charters with Comma Categories
Let  be a term charter domain. Let
be a term charter domain. Let  be a lax indexed functor,
be a lax indexed functor,  a lax indexed natural transformation, and
a lax indexed natural transformation, and  an
an  -indexed functor. Then
-indexed functor. Then  is a term charter over
is a term charter over  if, and only if, the following diagram commutes:
if, and only if, the following diagram commutes:

where the  -indexed functor
-indexed functor  is given by
is given by  and
and  .
.
Indeed,  yields that
yields that  holds. Thus,
holds. Thus,  induces the family of functions
induces the family of functions  which, for each
which, for each  and
and  , forms a natural transformation in
, forms a natural transformation in  , such that the renaming condition (R) holds. Furthermore,
, such that the renaming condition (R) holds. Furthermore,  yields the variable condition (V). Finally, by the indexedness of
yields the variable condition (V). Finally, by the indexedness of  it holds that
it holds that  , which is the translation condition (T), as
, which is the translation condition (T), as

4.2 Characterising Term Charters with Grothendieck Categories
Using the Grothendieck construction for a term charter domain  we obtain the
we obtain the  -indexed category
-indexed category  such that
such that  and
and  . A term charter
. A term charter  over the term charter domain
over the term charter domain  then yields a
then yields a  -indexed functor
-indexed functor  with
with  and
and  such that indeed for
such that indeed for 

Furthermore, it holds that  , since
, since

Conversely, given an  -indexed functor
-indexed functor  (i.e., (C) holds), which satisfies
(i.e., (C) holds), which satisfies  (i.e., (V) holds), we can reconstruct the evaluation morphisms by setting
(i.e., (V) holds), we can reconstruct the evaluation morphisms by setting  for
for  . Indeed, we obtain
. Indeed, we obtain  since
since  .
.
Summarising, a term charter is equivalently given by a lax indexed functor  , a lax indexed natural transformation
, a lax indexed natural transformation  , and a
, and a  -indexed functor
-indexed functor  such that the following diagram commutes:
such that the following diagram commutes:

We write  for
for  when
when  .
.
5 Constructing Institutions from a Term Charter
Institutions [3, 5] provide an abstract framework for studying logical systems. Term charters concentrate on the evaluation of terms yielding values rather than the satisfaction of formulæ. Still, as shown in Sect. 5.1, if there is a notion of truth values in the structures of a term charter domain, an institution can be derived from a term charter, thus embedding term charters into the landscape of logical systems. This construction resembles the generation of an institution from a charter [4], which has been the original reason for the choice of the name “term charters” in [6]. It turns out that also a context institution can be obtained, as introduced by Pawłowski [12] for capturing open formulæ in the framework of institutions; after summarising the definition of context institutions, we demonstrate their relationship with term charters in Sect. 5.2.
5.1 Institutions
An institution  is given by a category
is given by a category  of signatures; an indexed category
of signatures; an indexed category  of structures; a sentence functor
of structures; a sentence functor  ; and a family
; and a family  of satisfaction relations, such that for all
of satisfaction relations, such that for all  ,
,  , and
, and  the satisfaction condition holds:
the satisfaction condition holds:

For constructing an institution from a term charter  over a term charter domain
over a term charter domain  we assume that
we assume that  is logical via a family of functors
is logical via a family of functors  yielding formulœ and being equipped with truth values
yielding formulœ and being equipped with truth values  for each
for each  and
and  such that
such that  and
and  for all
for all  in
in  and
and  .
.
Example 5
(1) For the term charter domain  , we may base the formulæ on equations between value variables, representing
, we may base the formulæ on equations between value variables, representing  as the pair \((x_1, x_2)\):
as the pair \((x_1, x_2)\):  ,
,  , and
, and  . In fact, this construction can be applied to all term charters domains with a concrete category of value variables.
. In fact, this construction can be applied to all term charters domains with a concrete category of value variables.
(2) For the term charter domain  , every signature
, every signature  shows the predefined sort Bool that is interpreted by
shows the predefined sort Bool that is interpreted by  in every structure
in every structure  . Thus we can choose
. Thus we can choose  and
and  .
.
(3) For the term charter domain  , we may again choose
, we may again choose  , although now also the value
, although now also the value  for undefinedness will be contained. We may also again set
for undefinedness will be contained. We may also again set  since
since  .
.
Based on Sect. 4.2 we obtain an institution  over
over  and
and  (where the superscript
(where the superscript  abbreviates
abbreviates  ) as follows: The category of signatures
) as follows: The category of signatures  is defined to be
is defined to be  ; the indexed category
; the indexed category  of structures is defined to be
of structures is defined to be  ; the sentence functor
; the sentence functor  is defined as
is defined as  and
and  ; the family of satisfaction relations
; the family of satisfaction relations  is defined by
is defined by

For the satisfaction condition it suffices to prove that

which follows from the term charter requirement (C).
5.2 Context Institutions
Context institutions [12] have been introduced to capture open formulæ in institutions. A context institution, like an ordinary institution, shows a category  of signatures and an indexed category of structures
of signatures and an indexed category of structures  . Instead of the sentences, however, formulæ are built by a family of functors
. Instead of the sentences, however, formulæ are built by a family of functors  over a family of context categories
over a family of context categories  that allow to incorporate variables. Contexts are translated, i.e., variables are renamed, by a family of functors
that allow to incorporate variables. Contexts are translated, i.e., variables are renamed, by a family of functors  , and formulæ are translated along a context translation by a family of natural transformations
, and formulæ are translated along a context translation by a family of natural transformations  . Valuations are given by a family of functors
. Valuations are given by a family of functors  together with a family of natural transformations
together with a family of natural transformations  constructing adjoint valuations along signature morphisms, and, for each
constructing adjoint valuations along signature morphisms, and, for each  , families of natural transformations
, families of natural transformations  translating valuations along context translations, such that the coherence condition for
translating valuations along context translations, such that the coherence condition for  ,
,  , and
, and  is satisfied:
is satisfied:
-
(1)

Finally, context institutions show for all  ,
,  , and
, and  satisfaction relations
satisfaction relations  for which the substitution condition (2) and the satisfaction condition (3) have to be satisfied:
for which the substitution condition (2) and the satisfaction condition (3) have to be satisfied:
-
(2)

for all  ,
,  ,
,  ;
;
-
(3)

for all  ,
,  ,
,  .
.
Summarising, a context institution can be represented as the tuple  . In fact, this account (besides calling the valuations
. In fact, this account (besides calling the valuations  instead of \( Val \)) omits some parts of the original definition in [12] that has been formulated somewhat more concretely: For contexts and formulæ categories with an inclusion system are used and it is required that an indexed set of carriers can be computed from a structure as well as a sorted set of variables from a context. Then, the valuations can be represented as a concrete hom-set and the adjoint valuations can be derived.
instead of \( Val \)) omits some parts of the original definition in [12] that has been formulated somewhat more concretely: For contexts and formulæ categories with an inclusion system are used and it is required that an indexed set of carriers can be computed from a structure as well as a sorted set of variables from a context. Then, the valuations can be represented as a concrete hom-set and the adjoint valuations can be derived.
Let  be a term charter over a logical term charter domain
be a term charter over a logical term charter domain  with formulæ functor
with formulæ functor  , as above. For obtaining a context institution
, as above. For obtaining a context institution  from
from  it is straightforward to choose
it is straightforward to choose  and
and  , as well as
, as well as  ,
,  , and
, and  for each
for each  , as the value variables correspond to the notion of context. However, the context translation functors
, as the value variables correspond to the notion of context. However, the context translation functors  along \(\sigma : \varSigma \rightarrow \varSigma '\) have to be defined as going in the opposite direction than
along \(\sigma : \varSigma \rightarrow \varSigma '\) have to be defined as going in the opposite direction than  . We thus have to require that there is an adjunction
. We thus have to require that there is an adjunction  , as discussed in Sect. 3.4, and then can define
, as discussed in Sect. 3.4, and then can define  and
and  with
with  ; for each \(\sigma : \varSigma \rightarrow \varSigma \) in
; for each \(\sigma : \varSigma \rightarrow \varSigma \) in  define
define  , and for each \(\xi : X_1 \rightarrow X_2\) in
, and for each \(\xi : X_1 \rightarrow X_2\) in  define
define  . The coherence condition (1) then reads
. The coherence condition (1) then reads

which is evident by the naturality of \(\eta _{\sigma }\). For the satisfaction relations we finally can define

the substitution condition (2) and the satisfaction condition (3) then become

and follow from the conditions (R) and (\(\text {T}_{\dashv }\)) of term charters.
6 Morphisms for Term Charter Domains and Term Charters
For institutions there are four basic types of relationships, the institution (co-)morphisms and the institution forward (co-)morphisms [14]. For example, an institution morphism expresses a kind of projection from a “richer” source to a “poorer” target logic, or, conversely, how the “richer” logic is built over the “poorer” logic. Formally, an institution morphism  consists of a functor
consists of a functor  , an indexed functor
, an indexed functor  , and a natural transformation
, and a natural transformation  , such that for all
, such that for all  ,
,  , and
, and  the following satisfaction condition holds:
the following satisfaction condition holds:

In fact, the sentence translation  may be split off, yielding an institution semi-morphism
may be split off, yielding an institution semi-morphism  ; an institution forward morphism then just reverses the direction of the sentence translation. Similarly, an institution semi-co-morphism has components
; an institution forward morphism then just reverses the direction of the sentence translation. Similarly, an institution semi-co-morphism has components  and
and  ; it can be extended into an institution (forward) co-morphism with a sentence translation going in the opposite (the same) direction as the structure translation.
; it can be extended into an institution (forward) co-morphism with a sentence translation going in the opposite (the same) direction as the structure translation.
For term charters and their term charter domains, a similar family of relationships arises, where the notions of semi-(co-)morphisms applies to term charter domains and the extension to (forward) (co-)morphisms to term charters. We concentrate on projecting from a more complex evaluation framework to a simpler one and show that its definition gives rise to an institution morphism on the institutions constructed in Sect. 5.1.
A term charter domain morphism  is given by a functor
is given by a functor  and indexed functors
and indexed functors  and
and  such that
such that  .
.
Example 6
There is a term charter domain morphism  :
:  is the injection of
is the injection of  into
into  , and also
, and also  and
and  just inject the value variables and structures, respectively.
just inject the value variables and structures, respectively.
Let now  and
and  be term charters over the term charter domains
be term charters over the term charter domains  and
and  , respectively, and let
, respectively, and let  be a term charter domain morphism. A
be a term charter domain morphism. A  -term charter morphism
-term charter morphism  is given by a lax natural transformation
is given by a lax natural transformation  such that for all
such that for all  ,
,  , and
, and  it holds that
it holds that

Example 7
There is a  -term charter morphism
-term charter morphism  where
where  is the embedding of many-sorted terms into iteration terms. The relation guarantees that both evaluations coincide on many-sorted terms.
is the embedding of many-sorted terms into iteration terms. The relation guarantees that both evaluations coincide on many-sorted terms.
For the Grothendieck representation of term charters in Sect. 4.2,  induces an indexed functor
induces an indexed functor  with
with  . Condition (\(\text {m}_1\)) for
. Condition (\(\text {m}_1\)) for  then is
then is  and condition \(\text {m}_2\) is
and condition \(\text {m}_2\) is  .
.
In order to compare this definition of a  -term charter morphism
-term charter morphism  with institution morphisms, let the term charter domains
with institution morphisms, let the term charter domains  and
and  be logical with formulæ functors
be logical with formulæ functors  and
and  such that
such that  and
and  . We obtain an institution morphism
. We obtain an institution morphism  for
for  and
and  constructed over
constructed over  and
and  as in Sect. 5.1 with
as in Sect. 5.1 with  ,
,  , and
, and  : Using the abbreviations
: Using the abbreviations  ,
,  ,
,  , and
, and  , the satisfaction condition
, the satisfaction condition

for  follows from the observation that
follows from the observation that

To achieve further accordance with institutions, a \(\mathsf {d}\)-term charter forward morphism must reverse the direction of the term translation. A term charter domain co-morphism  must reverse the direction of the value variables and structures translation, and then can again be extended to a
must reverse the direction of the value variables and structures translation, and then can again be extended to a  -term charter (forward) co-morphism with term translation in the opposite (the same) direction as structure translation. As for institutions, these morphisms provide for embeddings, projections, and encodings of term charters.
-term charter (forward) co-morphism with term translation in the opposite (the same) direction as structure translation. As for institutions, these morphisms provide for embeddings, projections, and encodings of term charters.
7 Conclusions
We have presented term charter domains and term charters as a framework for general term evaluation such that evaluation is compatible with variable renamings and signature translations. This account simplifies our previous definition in [6] and puts term charters in a more general perspective. Term charter domains and term charters arrange values and variables, structures, term construction and term evaluation, all indexed over signatures, such that “evaluation is invariant under change of notation”. Term structure constructors give rise to term charters and also substitutions can be captured in term charters. We have re-presented term charters using comma and Grothendieck categories to highlight the interface character of signatures and variables. We have demonstrated a tight connection with institutions in general and context institutions in particular; along the lines of institution (semi-)morphisms we have introduced term charter (domain) morphisms.
The use of indexed categories should be complemented by fibrations [1] which may lead to another compact presentation of term charters. From the viewpoint of institutions, on the one hand substitutions in term charters should be connected with the notion of generalised substitutions [3, 16] and generalised terms in 2-institutions [2]. On the other hand, an alignment with parchments [4], that focus on directly establishing the satisfaction relation rather than on term evaluations, could be based on the requirement of formulæ and truth values as above which are used for constructing an institution from a term charter. This also applies to Mayoh’s galleries [9] (similar to generalized institutions [4]) and Poigné’s foundations [13] which are based on the overall extension of functions or frames instead of values of terms.
Our original motivation for [6] has been to “institutionalise” OCL by combining small, well-understood expression language fragments, all captured as term charters, into a bigger whole using a sequencing operator and co-limits. For this purpose, the term charter (domain) morphisms now provide a basis for term charter combinations also over heterogeneous term charter domains. What is most notably missing for an OCL-institution is the possibility to handle pre-/post-condition specifications. For the evaluation of the OCL expression for the post-condition, a pre- and a post-state must be present, which necessitates a construction on term charters or a suitable extension such that two structures can be accessed simultaneously.
References
Borceux, F.: Handbook of Categorical Algebra: Vol. 2, Categories and Structures. Cambridge University Press, Cambridge (1994)
Climent Vidal, J., Soliveres Tur, J.: A 2-categorial generalization of the concept of institution. Stud. Logica 95, 301–344 (2010)
Diaconescu, R.: Institution-independent Model Theory. SUL. Birkhäuser, Basel (2008). https://doi.org/10.1007/978-3-7643-8708-2
Goguen, J.A., Burstall, R.M.: A study in the foundations of programming methodology: specifications, institutions, charters and parchments. In: Pitt, D., Abramsky, S., Poigné, A., Rydeheard, D. (eds.) Category Theory and Computer Programming. LNCS, vol. 240, pp. 313–333. Springer, Heidelberg (1986). https://doi.org/10.1007/3-540-17162-2_131
Goguen, J.A., Burstall, R.M.: Institutions: abstract model theory for specification and programming. J. ACM 39, 95–146 (1992)
Knapp, A., Cengarle, M.V.: Institutions for OCL-like expression languages. In: De Nicola, R., Hennicker, R. (eds.) Software, Services, and Systems. LNCS, vol. 8950, pp. 193–214. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-15545-6_14
Lawvere, F.W.: Functorial semantics of algebraic theories. Ph.D. thesis, Columbia University (1963)
Mac Lane, S.: Categories for the Working Mathematician. GTM, vol. 5. Springer, New York (1978). https://doi.org/10.1007/978-1-4757-4721-8
Mayoh, B.H.: Galleries and institutions. Technical report DAIMI PB - 191, Aarhus University (1985)
Object management group: object constraint language. Standard formal/2014-02-03, OMG (2014). http://www.omg.org/spec/OCL/2.4
Paré, R., Schumacher, D.: Abstract families and the adjoint functor theorems. Indexed Categories and Their Applications. LNM, vol. 661, pp. 1–125. Springer, Heidelberg (1978). https://doi.org/10.1007/BFb0061361
Pawłowski, W.: Context institutions. In: Haveraaen, M., Owe, O., Dahl, O.-J. (eds.) ADT/COMPASS -1995. LNCS, vol. 1130, pp. 436–457. Springer, Heidelberg (1996). https://doi.org/10.1007/3-540-61629-2_57
Poigné, A.: Foundations are rich institutions, but institutions are poor foundations. In: Ehrig, H., Herrlich, H., Kreowski, H.-J., Preuß, G. (eds.) Categorical Methods in Computer Science with Aspects from Topology. LNCS, vol. 393, pp. 82–101. Springer, Heidelberg (1989). https://doi.org/10.1007/3-540-51722-7_6
Sannella, D., Tarlecki, A.: Foundations of Algebraic Specification and Formal Software Development. EATCS. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-17336-3
Tarlecki, A., Burstall, R.M., Goguen, J.A.: Some fundamental algebraic tools for the semantics of computation, Part 3: indexed categories. Theoret. Comput. Sci. 91, 239–264 (1991)
Ţuţu, I., Fiadeiro, J.: From conventional to institution-independent logic programming. J. Log. Comput. 27(6), 1679–1716 (2015)
Wolter, U., Martini, A.: Shedding new light in the world of logical systems. In: Moggi, E., Rosolini, G. (eds.) CTCS 1997. LNCS, vol. 1290, pp. 159–176. Springer, Heidelberg (1997). https://doi.org/10.1007/BFb0026987
Acknowledgements
We have profited much from discussions with Till Mossakowski, Rolf Hennicker, and Daniel Calegari. We thank the anonymous referees for their insightful comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
A Categorical Terminology
A Categorical Terminology
We briefly summarise the categorical terminology used in the main text; for indexed categories our account is based on [3, 14, 15, 17], for comma categories on [8], and for Grothendieck categories on [17]. We write \(\mathpunct {\overset{{\scriptscriptstyle *}}{,}}\) for the horizontal composition of natural transformations when using diagrammatic notation.
1.1 A.1 Indexed Categories
An indexed category N over an index category I is a functor \(N : {I}^{\mathrm {op}} \rightarrow \mathrm {Cat}\).
A lax indexed functor \(F : M \mathrel {\ddot{ \rightarrow }}N\) between the I-indexed categories M and N is given by families of functors \((F_i : M(i) \rightarrow N(i))_{i \in |I|}\) and natural transformations  with
with  such that
such that  for all \(u_1 \in I(i_1, i_2)\), \(u_2 \in I(i_2, i_3)\). The composition
for all \(u_1 \in I(i_1, i_2)\), \(u_2 \in I(i_2, i_3)\). The composition  of
of  and
and  for the I-indexed categories L, M, N is given by \((F ; G)_i = F_i ; G_i\) for \(i \in |I|\) and
for the I-indexed categories L, M, N is given by \((F ; G)_i = F_i ; G_i\) for \(i \in |I|\) and  for \(u \in I(i_1, i_2)\). An indexed functor
for \(u \in I(i_1, i_2)\). An indexed functor  is a lax indexed functor
is a lax indexed functor  with
with  for all \(u \in I(i_1, i_2)\), i.e., a natural transformation from M to N.
for all \(u \in I(i_1, i_2)\), i.e., a natural transformation from M to N.
For M, N I-indexed categories and  lax indexed functors, a lax indexed natural transformation
lax indexed functors, a lax indexed natural transformation  is given by a family of natural transformations
is given by a family of natural transformations  such that
such that  for \(u \in I(i_1, i_2)\). If F and G are both indexed functors,
for \(u \in I(i_1, i_2)\). If F and G are both indexed functors,  is also called an indexed natural transformation; it then has to hold that
is also called an indexed natural transformation; it then has to hold that  for all \(u \in I(i_1, i_2)\).
for all \(u \in I(i_1, i_2)\).
1.2 A.2 Comma Categories
Given two functors \(F_1 : A_1 \rightarrow C\) and \(F_2 : A_2 \rightarrow C\), the comma category  has as objects the triples \((X_1, f, X_2)\) with \(X_1 \in |A_1|\), \(X_2 \in |A_2|\), and \(f : F_1(X_1) \rightarrow F_2(X_2)\) in C; and as morphisms from \((X_{11}, f_1, X_{21})\) to \((X_{12}, f_2, X_{22})\) the pairs \((x_1, x_2)\) with \(x_1 : X_{11} \rightarrow X_{12}\) in \(A_1\) and \(x_2 : X_{21} \rightarrow X_{22}\) in \(A_2\) such that \(f_1; F_2(x_2) = F_1(x_1); f_2\). It is equipped with the projection functors
has as objects the triples \((X_1, f, X_2)\) with \(X_1 \in |A_1|\), \(X_2 \in |A_2|\), and \(f : F_1(X_1) \rightarrow F_2(X_2)\) in C; and as morphisms from \((X_{11}, f_1, X_{21})\) to \((X_{12}, f_2, X_{22})\) the pairs \((x_1, x_2)\) with \(x_1 : X_{11} \rightarrow X_{12}\) in \(A_1\) and \(x_2 : X_{21} \rightarrow X_{22}\) in \(A_2\) such that \(f_1; F_2(x_2) = F_1(x_1); f_2\). It is equipped with the projection functors  defined by \(\pi _i(X_1, f, X_2) = X_i\) and \(\pi _i(x_1, x_2) = x_i\) for \(i \in \{ 1, 2 \}\).
defined by \(\pi _i(X_1, f, X_2) = X_i\) and \(\pi _i(x_1, x_2) = x_i\) for \(i \in \{ 1, 2 \}\).
For the functors \(F_1, G_1 : A_1 \rightarrow C\) and \(F_2, G_2 : A_2 \rightarrow C\) consider the functor  with \(H(X_1, f, X_2) = (X_1, f^H, X_2)\) and \(H(x_1, x_2) = (x_1, x_2)\). Then \((F_1(x_1); f_2)^H = G_1(x_1); f_2^H\) and \((f_1; F_2(x_2))^H = f_1^H; G_2(x_2)\) for all \(X_i \in |A_i|\), \(x_i \in A_i(X_{i1}, X_{i2})\), \(f_1 : F_1(X_1) \rightarrow F_2(X_{21})\), and \(f_2 : F_1(X_{12}) \rightarrow F_2(X_2)\). Thus, H induces natural transformations
with \(H(X_1, f, X_2) = (X_1, f^H, X_2)\) and \(H(x_1, x_2) = (x_1, x_2)\). Then \((F_1(x_1); f_2)^H = G_1(x_1); f_2^H\) and \((f_1; F_2(x_2))^H = f_1^H; G_2(x_2)\) for all \(X_i \in |A_i|\), \(x_i \in A_i(X_{i1}, X_{i2})\), \(f_1 : F_1(X_1) \rightarrow F_2(X_{21})\), and \(f_2 : F_1(X_{12}) \rightarrow F_2(X_2)\). Thus, H induces natural transformations

Conversely, a bi-natural transformation  induces the functor
induces the functor  given by \(\eta (X_1, f, X_2) = (X_1, \eta (X_1, X_2)(f),X_2)\) and \(\eta (x_1, x_2) = (x_1, x_2)\).
given by \(\eta (X_1, f, X_2) = (X_1, \eta (X_1, X_2)(f),X_2)\) and \(\eta (x_1, x_2) = (x_1, x_2)\).
The indexed comma category  for a lax indexed functor
for a lax indexed functor  and an indexed functor \(G : M_2 \mathrel {\dot{ \rightarrow }}N\) over I-indexed categories \(M_1\), \(M_2\), and N is defined at \(i \in |I|\) as the comma category
and an indexed functor \(G : M_2 \mathrel {\dot{ \rightarrow }}N\) over I-indexed categories \(M_1\), \(M_2\), and N is defined at \(i \in |I|\) as the comma category  , and at \(u \in I(i_1, i_2)\) as the functor
, and at \(u \in I(i_1, i_2)\) as the functor  given by
given by

1.3 A.3 Grothendieck Categories
The (contravariant) Grothendieck category  over an I-indexed category N has as objects the pairs
over an I-indexed category N has as objects the pairs  with \(i \in |I|\) and \(O \in |N(i)|\); and as morphisms from
with \(i \in |I|\) and \(O \in |N(i)|\); and as morphisms from  to
to  the pairs
the pairs  with \(u \in I(i_1, i_2)\) and \(o \in N(i_1)(O_1, N(u)(O_2))\) where the composition of
with \(u \in I(i_1, i_2)\) and \(o \in N(i_1)(O_1, N(u)(O_2))\) where the composition of  and
and  is
is  . The projection functor \(\pi _N\) from
. The projection functor \(\pi _N\) from  to I is defined by
to I is defined by  and
and  .
.
The Grothendieck functor  over a lax indexed functor
over a lax indexed functor  for I-indexed categories M and N is defined by
for I-indexed categories M and N is defined by  for each
for each  ; and
; and  with \(F_u(o) = F_{i_1}(o); F_u(O_2) : F_{i_1}(O_1) \rightarrow N(u)(F_{i_2}(O_2))\) for each
with \(F_u(o) = F_{i_1}(o); F_u(O_2) : F_{i_1}(O_1) \rightarrow N(u)(F_{i_2}(O_2))\) for each  in
in  .
.
A lax indexed natural transformation \(\eta : F \mathrel {\dot{ \rightarrow }}G\) induces the Grothendieck natural transformation  defined by
defined by  .
.
For a lax indexed functor  and an indexed functor \(G : M_2 \mathrel {\dot{ \rightarrow }}N\) over I-indexed categories \(M_1\), \(M_2\), and N define the indexed category
and an indexed functor \(G : M_2 \mathrel {\dot{ \rightarrow }}N\) over I-indexed categories \(M_1\), \(M_2\), and N define the indexed category  on objects by
on objects by  , where we abbreviate an object \((F_i(O_1), p, O_2)\) of this comma category to \((O_2, p)\) and a morphism
, where we abbreviate an object \((F_i(O_1), p, O_2)\) of this comma category to \((O_2, p)\) and a morphism  to \(o_2\), and on morphisms by
to \(o_2\), and on morphisms by 
 with
with  and
and  .
.
A lax indexed natural transformation  then induces the indexed functor
then induces the indexed functor  defined by
defined by  and
and  .
.
Rights and permissions
Copyright information
© 2019 IFIP International Federation for Information Processing
About this paper
Cite this paper
Knapp, A., Cengarle, M.V. (2019). Term Charters. In: Fiadeiro, J., Țuțu, I. (eds) Recent Trends in Algebraic Development Techniques. WADT 2018. Lecture Notes in Computer Science(), vol 11563. Springer, Cham. https://doi.org/10.1007/978-3-030-23220-7_7
Download citation
DOI: https://doi.org/10.1007/978-3-030-23220-7_7
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-23219-1
Online ISBN: 978-3-030-23220-7
eBook Packages: Computer ScienceComputer Science (R0)





 if
if  if
if 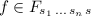 and
and  for
for  for
for  for
for  for
for  ;
; for
for  for
for 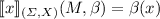 ;
; ;
;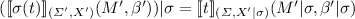 .
.


