Abstract
There are countless sources of data available to governments, companies, and citizens, which can be combined for good or evil. We analyse the concepts of combining data from common sources and linking data from different sources. We model the data and its information content to be found in a single source by an ordered partial monoid, and the transfer of information between sources by different types of morphisms. To capture the linkage between a family of sources, we use a form of Grothendieck construction to create an ordered partial monoid that brings together the global data of the family in a single structure. We apply our approach to database theory and axiomatic structures in approximate reasoning. Thus, ordered partial monoids provide a foundation for the algebraic study for information gathering in its most primitive form.
This research was supported by the EPSRC project Data Release—Trust, Identity, Privacy and Security (EP/N028139/1 and EP/N027825/1).
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
There are countless public and private sources of data that can be linked and analysed for all sorts of reasons, and with all sorts of consequences. The extraordinary variety of what may be considered data—i.e., data that is informative in some way—is a challenge to attempts to discover general principles and techniques for understanding linkage. Motivated by movements for data sharing we try to uncover general structures common to disparate situations.
1.1 Motivation: Exploiting Open Datasets
The vast stores of data built up by governments, agencies, institutions and companies in the course of their operations hold information of value in diverse and unexpected situations. Some governments have launched initiatives to encourage bodies to share their data with other organizations and the public. The released open data is intended to improve transparency, allowing accountability and engagement with decision making. A systematic review is [2].
For example, in the UK, there are several national and local registers and a plethora of statistical data that are now widely shared. A simple example of the commercial use of open datasets are web services for selling and letting properties such as Zoopla. In addition to traditional information about a property, official financial data about local house sales and crime statistics are provided.
The UK’s Open Data Initiative demonstrates the ambition to publish internal government data as open datasets. There are many patterns of data sharing, of which three are particularly important: (i) making data public—data release into the wild; (ii) data sharing by contract with a data analysis organization; and (iii) data sharing with delegation to a new data controller for further onward sharing. However, data custodians have a legal duty, and a social duty of care, to ensure that privacy is not breached by the release of open data sets.
The technical question arises: What information is revealed by, or can be inferred from, the data? Naturally, prior to its release, a data set can be filtered and anonymised but (i) anonymization is difficult and often flawed; and (ii) data from various other sources can be combined with a given data set to reveal much more. There are many data sources to call upon, and many unknown unintended consequences in making data publicly available.
An early example is Sweeney’s finding [23] that \(97\%\) of voters in Cambridge, Massachusetts, USA, can be uniquely identified by birth dates and postcodes; these can be further linked with a hospital discharge database to discover individuals’ medical history—e.g., of the governor of Massachusetts at that time [24].
Lately, Narayanan and Shmatikov [17] devised an algorithm exploiting sparsity to combine datasets. As a case study they analysed the Netflix prize dataset and found ‘\(84\%\) of (Netflix) subscribers present in the dataset can be uniquely identified if the adversary knows six out of eight movies outside the top 500’ that the subscriber rated. Such source of film ratings may come from social engineering or the Internet Movie Database (IMDb). In response to these privacy concerns, Netflix decided to withdraw the datasets. Unfortunately, they are still available to download using BitTorrent or https://archive.org.
1.2 Algebraic Models of Combination and Linkage
In this paper we take a fresh look at the challenge of combining data sets and linking pieces of data. Our aim is to develop abstract tools to analyse formally the general nature of data sharing, and technical issues of policy specification and compliance. To this end, we seek algebras of data representations, whose operations combine two or more pieces of data from the same source to form data with higher information content. These data representation algebras are to be defined axiomatically. In its simplest form—that presented here—such an algebra is an ordered structure with a partial commutative binary operation \(\oplus \) and an identity element 0, namely, an ordered partial commutative monoid. The operation \(\oplus \) combines data from the same source. Morphisms between such monoids model the transfer of data between sources—a process we call linkage. We create an ordered partial commutative monoid that brings together all the data from a family of sources using a simplified Grothendieck construction. We show that our monoid theory of linkage applies to databases and approximate reasoning.
A complete set of proofs can be found at arXiv:1810.08096.
2 Algebras for Data Combination
2.1 Information Ordering
Data itself is often hierarchical or due to uncertainty becomes so. In this paper, when we reason about data, we implicitly work on a set with an ordering that measures specificity, knowledge, or informativeness. Ideas of information ordering are nothing new, as they appear to be well-known to different communities working on uncertainty reasoning [11, Section 2.7], multi-valued logic [3], program semantics [20], formal concept analysis [6, Chapter 3], and (implicitly) anonymization techniques [16, 26], to name but a few.
Definition 2.1
Given a set X, an information order \(\preceq \) on X is a preorder, i.e. (i) \(x \preceq x\) and (ii) \(x \preceq y \preceq z\) implies \(x \preceq z\). An information space is merely a preordered set \((X, \preceq )\).
To illustrate the use of preordered sets in the context of data release and privacy, we discuss in some detail the use of postcodes to identify locations.
Example 2.2
The taxonomic hierarchy of British postal codes mostly consists of 6 to 8 alphanumeric characters in a format detailed below. Each postcode is divided into the outward code and the inward code by a single space ‘␣’. Each component is formed of two further parts and each part covers a smaller area. For example, SA2␣8PP is the full postcode of the Singleton Campus of Swansea University and it is understood as follows:

Let the set of all full postcodes be denoted by \(\mathbf {Post}_{\mathrm {UK}}\).
For simplicity, a partial postcode refers to a code, where less significant parts might be missing, ordered by prefix order including the empty string ‘\(\epsilon \)’ as a special postcode indicating everywhere. For example, SA stands for Swansea and SA2 for a district in Swansea, and we have partial postcodes

note that \(\texttt {???\textvisiblespace 8PP}\) is not a partial postcode. Let us denote the set of all partial postcodes by \(\mathbf {PPost}_{\mathrm {UK}}\).
Each full postcode is incomparable with another, as each of them stands for a disjoint set of postal addresses. On the contrary, the set of partial postcodes possesses the prefix order \(\preceq \) for the hierarchy. Every partial postcode P can be realised as a set of full postcodes by

For instance, an empty string \(\epsilon \) is realised by \(\mathbf {Post}_{\mathrm {UK}}\), as it contains no information apart from being a postcode. Each full postcode P in \(\mathbf {Post}_{\mathrm {UK}}\) is realised by the singleton set \(\{ P \}\). Note that \(\llbracket {P}\rrbracket \)’s are always non-empty. \(\square \)
The reader may find our definition of information space intriguing. For example, why is this only a preordered set instead of a partially ordered set? Indeed, as we can observe from the above example, there are two possible representations of partial knowledge for postcode:
-
(i)
\(\mathbb {P}^+(\mathbf {Post}_{\mathrm {UK}})\)—the non-empty powerset of full postcodes, or
-
(ii)
\(\mathbf {PPost}_{\mathrm {UK}}\)—the set of partial postcodes determined by its format.
The first (i) can be called the possible world representation [11, Section 2.1]. It is well-understood in the community of knowledge representation. It is more expressive and general than (ii). Every taxonomic hierarchy of a set of entities can be realised by a possible world interpretation, as each classification level defines a partition of all the entities. The reverse inclusion order ‘\(\supseteq \)’ reflects the information order of taxonomic hierarchy, i.e. P is of higher hierarchy than Q only if \(\llbracket {P}\rrbracket \subseteq \llbracket {Q}\rrbracket \) and ‘\(\supseteq \)’ is surely a partial order. We return to this general points in Sect. 3.2.
On the other hand, the second kind of representations is often what we have in the first place or what we would like to use in data release. The information order \(\preceq \) requires some effort to decide, but generally it is clear from the context. However, we may have two different representations for the very same set of entities. If a weight is attached to the data in question, then the second representation is more manageable than the first:
Example 2.3
Consider a version due to a privacy concern.Footnote 1 Both kinds of representations build a frequency distribution, and some probabilities can be calculated based on the information order over postcodes, say, \(\Pr [\mathtt {SA2} \preceq X]\).
In Kolmogorov’s probability theory, the first step is to find out a sample space \(\varOmega \) and a \(\sigma \)-algebra \(\varSigma \), and the typical choice is \(\varOmega = \mathbf {Post}_{\mathrm {UK}}\) and \(\varSigma = \mathbb {P}(\mathbf {Post}_{\mathrm {UK}})\). The probability measure for the original dataset (Fig. 1a) is clear. But, it is tricky to define faithfully a probability measure for the sanitised dataset (Fig. 1b), since it requires to assign a probability to each full postcode with the prefix SA1␣3. The convention is to apply the principle of indifference—each postcode of \(\llbracket {\texttt {SA1\textvisiblespace 3}}\rrbracket \) has the same probability 1/k where k is the possibly unknown number of postcodes in \(\llbracket {\texttt {SA1\textvisiblespace 3}}\rrbracket \). Even if k is known, the presumed probability 1/k is an over-approximation of the given information.
On the other hand, no matter what probability is assigned to subsets of full postcodes, the probability of \(\Pr [ \mathtt {SA2} \preceq X ]\) is always the sum
without knowing any further information. The expressiveness is limited if we confine ourselves to probabilities of partial postcodes only, since partial postcodes are not closed under Boolean connectives contrary to the subset representation. Yet this limitation enables us to represent the exact information of data. \(\square \)
Another problem of the possible world representation arises if the information order is by nature not anti-symmetric. It is intuitive to see that Fig. 1a is more informative than Fig. 1b. There are at least three applicable orderings over subsets P, Q of elements in an information space X, which are
The ordering can model a number of processes or situations. \(P \preceq ^\flat Q\) models that everything in P has a more informative datum in Q. So Q is an enrichment of P. Conversely, \(P \preceq ^\sharp Q\) models that everything in Q has a less informative datum in P, so P is an adulteration of Q.
Each of the orderings plays a role in various contexts, such as non-deterministic computation [9] and relative likelihood [11, Section 2.7]. These orderings are preorders but not anti-symmetric in general.
Example 2.4
Ignoring user ID and repetitions, we have two sets representing the information in Fig. 1:

The set \(P_1\) is more informative than \(P_2\) with respect to \(\preceq ^\flat \), \(\preceq ^\sharp \), and \(\preceq ^\natural \). \(\square \)
Even further, the standard equality ‘\(=\)’ on the data in X is irrelevant from the information-theoretic perspective, as we only care about the information content of data. For example, any subset P of an information space \((X, \preceq )\) is indistinguishable from but fails to be equal to its convex hullFootnote 2  , i.e.
, i.e.
So, we introduce:
Definition 2.5
Given an information order \(\preceq \) on a set X, define an equivalence relation by
and x is said to be equivalent to y. Each element in the same equivalence class is of the same information content.
From a mathematical viewpoint, each element x is a representative of the information class [x]. Every representative of the same class embodies the same amount of information with respect to the information order \(\preceq \). Computing and deciding the information class could be costly and conceptually gain little, so it is easier to work and present our latter formulations with representatives directly.
Remark 2.6
From this, we can argue further that ‘\(\cong \)’ is the right notion of equality where the strict equality ‘\(=\)’ plays no role at all in an ordered setting. Indeed, the convention is to consider the quotient \((X/{\cong }, {\preceq }/{\cong })\) as the poset of information and \([x] = [y]\) is equivalent to \(x \cong y\), but this convention makes notations rather heavy.
So the point is that only the preorder \(\preceq \) for information matters and it fails to be a partial order in general.
2.2 Ordered Partial Commutative Monoids
To combine and link data across various domains yields data that is presumably more informative than the separate pieces of information alone. In this section, we introduce an algebraic operation over an information space for combining data. Central to our investigation is the concept of ordered partial commutative monoids. Whilst monoids of many kinds, e.g., ordered commutative monoids [8] and partial commutative monoids [7, 27], have been discovered and developed in many application areas, surprisingly we have not found a monoid combining both—ordering and partiality. A possible exception we found is monoids viewed as a degenerated class of partial monoidal categories defined in [5].
Definition 2.7
An ordered partial commutative monoid \({(M, \preceq , \oplus , 0)}\) consists of (i) a preordered set \((M, \preceq )\), (ii) a constant \(0 \in M\), and (iii) a partial binary operation \(\oplus :M \times M \rightharpoonup M\), i.e. \(x \oplus y\) may not be defined. For brevity, ‘\(x \perp y\)’ stands for ‘\(x \oplus y\)’ is defined. Further, \((M, \preceq , \oplus , 0)\) satisfies the properties below.
-
(OPCM1) \(0 \oplus x \cong x\).
-
(OPCM2) \(y \perp x\) and \(x \oplus y \cong y \oplus x\) if \(x \perp y\).
-
(OPCM3) \(x \perp y\), \((x \oplus y) \perp z\), and \(x \oplus (y \oplus z) \cong (x \oplus y) \oplus z\) if \(y \perp z\) and \(x \perp (y \oplus z)\).
-
(OPCM4) \(x_{1} \oplus y \preceq x_{2} \oplus y\) if \(x_{i} \perp y\) for \(i = 1, 2\) and \(x_{1}\preceq x_{2}\).
An ordered partial commutative monoid is written as OPCM for short. An (unordered) partial commutative monoid \((M, \oplus , 0)\), PCM for short, is an OPCM with the discrete ordering \(x \preceq y \iff x = y\). An ordered commutative monoid is an OPCM with the binary operation \(\oplus \) being total.
The element \(x \oplus y\) denotes data that represents a combination of the information of x and y. The constant 0 stands for some vacuous information so that \(x \oplus 0\) is always defined and equivalent to x. Partiality enables us to encapsulate consistency or other premises. That is, x may contradict y so that no viable information can be derived; see Example 2.13.
Referring to Remark 2.6, the following fact shows that the use of ‘\(\cong \)’ is equivalent to the standard equality ‘\(=\)’ in the partially ordered quotient:
Proposition 2.8
Let \((M, \preceq , \oplus , 0)\) be an OPCM. Then,
-
(i)
the relation defined by \([x] \le [y] \iff x \preceq y\) on the quotient set
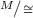 is a partial order and \([x] = [y] \iff x \cong y\);
is a partial order and \([x] = [y] \iff x \cong y\); -
(ii)
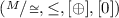 with \([x] \mathbin {[\oplus ]} [y]\) defined as \([x \oplus y]\) is an OPCM.
with \([x] \mathbin {[\oplus ]} [y]\) defined as \([x \oplus y]\) is an OPCM.
The algebraic structure of a PCM also gives rise to a natural ordering between information purely determined by the combination \(\oplus \).
Definition 2.9
The algebraic ordering on an OPCM is defined by
Proposition 2.10
Every PCM \((M, \oplus , 0)\) with algebraic ordering \(\sqsubseteq \) is an
-
(i)
OPCM which satisfies
-
(ii)
\(0 \sqsubseteq x\), and that
-
(iii)
if \((x, y) \sqsubseteq (x', y')\), \(x' \perp y'\), \(x \perp x\), then \(x \oplus y \sqsubseteq x' \oplus y'\).
The algebraic ordering of an OPCM \((M, \preceq , \oplus , 0)\) is compatible with the information ordering if the identity 0 is the \(\preceq \)-least informative element:
Proposition 2.11
Let \((M, \preceq , \oplus , 0)\) be an OPCM such that \(0 \preceq x\). Then,
-
(i)
\(x \sqsubseteq y \implies x \preceq y\);
-
(ii)
\(x, y \preceq x \oplus y\) whenever \(x \perp y\).
Remark 2.12
The implication (i) in Proposition 2.11 along with (ii) in Proposition 2.10 suggests the hypothesis \(0 \preceq x\) is decisive, otherwise \(\oplus \) may not represent ‘combination of information’ but something else (cf. the semantics of Belnap’s 4-valued logic [1]). However, the property that \(0 \preceq x\) for all \(x \in M\) is not needed for our technical results.
Example 2.13
Consider the collection of all non-empty subsets of full postcodes \(\mathbb {P}^+(\mathbf {Post}_{\mathrm {UK}})\) equipped with the reverse inclusion order \(P_1 \preceq P_2\) iff \(P_2 \subseteq P_1\). The intersection \(\cap \) of subsets as a combination operation \(\oplus \), is a partial operation, since \(P_1 \cap P_2\) might be empty and \(\not \in \mathbb {P}^+(\mathbf {Post}_{\mathrm {UK}})\). Clearly, intersection is monotone with respect to the reverse inclusion order. Similarly, the set of partial postcodes equipped with the prefix ordering \(\preceq \) discussed in Example 2.2 has a simple OPCM structure: \(x \oplus y\) is defined as \(\max \{x, y\}\).
2.3 Homomorphisms
The internal structure of an OPCM models data and information of a single source. So the external interaction between OPCMs models a comparison, combination, interpretation, or linkage between sources. Various kinds of structure preserving maps between OPCMs arise naturally, e.g., order-preserving maps, \(\oplus \)-preserving maps, or both. We begin with the familiar one.
Definition 2.14
A homomorphism \(M \xrightarrow {f} N\) of OPCMs is a function satisfying
-
(HOM1) \(x \preceq _M y \implies fx \preceq _N fy\)
-
(HOM2) \(f(0_M) \cong 0_N\)
-
(HOM3) \(x \perp y \implies f(x \oplus _M y) \cong fx \oplus _N fy\)
The collection of OPCMs with their homomorphisms forms a category \(\mathbf {PCM}_\preceq \).
An ‘interpretation’ of information in a different domain of discourse or context, is a typical example of a homomorphism. The trivial map \(f:M \rightarrow N\) defined by \(f(x) = 0\) is a homomorphism that destroys all the information in M. The set of partial postcodes per se is merely a set of strings following a specific format, so it makes little sense to say how rare a postcode P is among other postcodes; it becomes meaningful when it refers to certain geographic area, population, or other associated information.
Example 2.15
Let \(\mathbf {Pop}_{\mathrm {UK}}\) denote the UK population. Assume that (i) everyone (of interest) is registered with exactly one postcode for their main residence, and (ii) each postcode is associated with someone. The assumption amounts to a surjective function \(f:\mathbf {Pop}_{\mathrm {UK}}\rightarrow \mathbf {Post}_{\mathrm {UK}}\).
Consider the possible world representation for \(\mathbf {Pop}_{\mathrm {UK}}\). Each set S of postcodes then can be interpreted as the set  of population officially registered in the area specified by P. The mapping \(\llbracket {-}\rrbracket :\mathbb {P}^+\mathbf {Post}_{\mathrm {UK}}\rightarrow \mathbb {P}^+\mathbf {Pop}_{\mathrm {UK}}\) is clearly homomorphic w.r.t. the OPCM discussed in Example 2.13, since
of population officially registered in the area specified by P. The mapping \(\llbracket {-}\rrbracket :\mathbb {P}^+\mathbf {Post}_{\mathrm {UK}}\rightarrow \mathbb {P}^+\mathbf {Pop}_{\mathrm {UK}}\) is clearly homomorphic w.r.t. the OPCM discussed in Example 2.13, since
-
(i)
it is monotone, as \(\llbracket {S_1}\rrbracket \supseteq \llbracket {S_2}\rrbracket \) if \(S_1 \supseteq S_2\);
-
(ii)
it preserves the identity, as \(f^{-1}(\mathbf {Post}_{\mathrm {UK}}) = \mathbf {Pop}_{\mathrm {UK}}\);
-
(iii)
and moreover \(\llbracket {S_1 \cap S_2}\rrbracket = \llbracket {S_1}\rrbracket \cap \llbracket {S_2}\rrbracket \) as \(f^{-1}\) preserves intersection.
\(\square \)
Besides concrete homomorphisms, one has the following standard notions: isomorphism, monomorphism, embedding, epimorphism, and so on, following the doctrine of category theory. Among them, the product of two OPCMs can be understood as pairs of independent sources of information.
Definition 2.16
The product monoid \(M_1 \times M_2\) of \(M_i = (M_i, \preceq _i, \oplus _i, 0_i)\) for \(i = 1, 2\) is the cartesian product equipped with
-
(i)
the pointwise ordering \((x_1, x_2) \preceq (y_1, y_2) \iff x_1 \preceq _1 y_1 \wedge x_2 \preceq _2 y_2\),
-
(ii)
 , and
, and -
(iii)
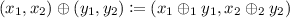 if \(x_1 \perp y_1\) and \(x_2 \perp y_2\).
if \(x_1 \perp y_1\) and \(x_2 \perp y_2\).
The universal property for product shows that \(M_1 \times M_2\) consists of pairs of independent pieces of information from \(M_1\) and \(M_2\):
Proposition 2.17
For any OPCM N and any pair of homomorphisms \(f_i:N \rightarrow M_i\) for \(i = 1, 2\), there exists a unique homomorphism \(h:N \rightarrow M_1 \times M_2\) such that \(\pi _i \circ h = f_i\), where \(\pi _i\) is the i-th projection homomorphism.
Other useful notions are embedding and isomorphism.
Definition 2.18
A homomorphism \(e:M \rightarrowtail N\) is an order-embedding if it not only preserves but also reflects the ordering: \(e(x) \preceq e(y) \iff x \preceq y\). An isomorphism is a bijective order-embedding.
3 Further Examples
3.1 Flat Algebras
The most simple OPCM is perhaps a set X equipped with an additional element \(\bot \) denoting unknown and \(x \le y\) iff \(x = \bot \) or \(x = y\) with  . In spite of its simplicity, it has been elaborated further in relational database theory [4, Chapter 8].
. In spite of its simplicity, it has been elaborated further in relational database theory [4, Chapter 8].
3.2 Possibilities over a Set
We have used a possible world representation discussing postcodes (Sect. 2.2). In this section, we study its general properties. As the reader may have observed from our examples about non-empty subsets of full postcodes, the argument is completely generic and can be applied to any non-empty set X. In short, we have the following generalisation of Example 2.13:
Proposition 3.1
For any non-empty set X, the non-empty powerset \(\mathbb {P}^+X\) with the reverse inclusion and intersection forms an OPCM \((\mathbb {P}^+X, \supseteq , \cap , X)\).
In general, the set X represents some elementary form of atomic information such as codes, labels, tags or facts from which is made. The data in the source is a non-empty subset S of X containing a set of possible choices from X.
3.3 Possibilities over an OPCM
It is often the case that only pieces of information shared by a group of people is known instead of each individual’s. As each piece of information in our algebraic theory is an element of some OPCM, we proceed with non-empty subsets of an OPCM which is in turn another OPCM.
The starting point is the observation that a mere intersection of two subsets of an OPCM \((M, \preceq , \oplus , 0)\) would exclude combinable but not exactly the same information. Note that we can reformulate intersection in a rather silly way as
We can utilise ‘\(\oplus \)’ and define a combination of two subsets of OPCM by

consisting of refined information only. How about the information order between subsets? It turns out that only one of the orderings for powersets introduced in Sect. 2.1,
is a sensible preorder with respect to the definition of \(P\oplus Q\).
Theorem 3.2
Let \((M, \preceq , \oplus , 0)\) be an OPCM such that M is \(\oplus \)-downward closed, i.e. if \(x \preceq x'\) and \(x' \perp y\) then \(x \perp y\). For non-empty subsets P and Q,

Then,
-
(i)
\(\mathbb {P}^+M = (\mathbb {P}^+M, \preceq ^\sharp , \varvec{\oplus }, \{0\})\) is also an OPCM;
-
(ii)
\(\{0\} \preceq ^\sharp P\) for any P if \(0 \preceq x\) for any \(x \in M\).
4 Data Linkage
A domain of discourse can have a number of data sources so that the same piece of information can be understood in various contexts differently. How do we know that the original information remains intact?
4.1 Change of Domain
A homomorphism \(f:M \rightarrow N\) qualifies as a mapping changing domains from M to N but it can lose data, e.g. the trivial map \(f(x) = 0\) destroys all data. One way to avoid this problem is to use homomorphisms with a restriction map \(f^*:N \rightarrow M\) satisfying a ‘preservation condition’ \(x \preceq f^* f(x)\) for \(x \in M\).
Definition 4.1
A homomorphism \(f:M \rightarrow N\) is a change of domain if f is a lower adjoint,Footnote 3 i.e. there exists an order-preserving map \(f^*:N \rightarrow M\) such that
Our formal definition requires that an extension f with its restriction \(f^*\) forms a Galois connection [6].
Every Galois connection \((f, f^*)\) gives rise to a closure operator—a monotone function \(f^* \circ f\) satisfying (i) \(x \preceq f^*f(x)\) and (ii) \(f^*f(f^*f x)\preceq f^* fx\). Intuitively, the information represented by \(f^*f(x)\) is at least as informative as x.
The class of changes of domain is closed under composition. It is not hard to see that the composite \(k\circ f\) of two lower adjoints is again a lower adjoint, because \(k \circ f\) is homomorphic and by definition
Trivially, an identity function \( id \) is itself a change of domain. Therefore, the class of OPCMs and changes of domain forms a subcategory of \(\mathbf {PCM}_\preceq \).
Example 4.2
The homomorphism \(\llbracket {-}\rrbracket :\mathbb {P}^+\mathbf {Post}_{\mathrm {UK}}\rightarrow \mathbb {P}^+\mathbf {Pop}_{\mathrm {UK}}\) discussed in Example 2.15 is indeed a change of domain. The restriction from \(\mathbb {P}^+\mathbf {Pop}_{\mathrm {UK}}\) to \(\mathbb {P}^+\mathbf {Post}_{\mathrm {UK}}\) is given by mapping a set of population to the set of their registered postcodes. The existence of this restriction follows from the assumption that everyone of interest signs a register with a full postcode. Formally, the restriction is the forward-image function of the surjection \(f:\mathbf {Pop}_{\mathrm {UK}}\rightarrow \mathbf {Post}_{\mathrm {UK}}\) given by our assumption, so
for any non-empty \(S \subseteq \mathbf {Post}_{\mathrm {UK}}\) and \(A \subseteq \mathbf {Pop}_{\mathrm {UK}}\).
Given a change of domain \(f:M \rightarrow N\), there are two different ways to combine \(x \in M\) with \(y \in N\). Their relationship can be stated as follows:
Proposition 4.3
Given a change of domain \(f:M \rightarrow N\), the following
always holds for any \(x \in M\) and \(y \in N\).
Armed with these notions, we now formally define ‘linkage’ as follows.
Definition 4.4
A linking passage \((f_i, g_i)_{i = 1, 2}\) of \(M_1\) and \(M_2\) is a commutative diagram of changes of domain up to equivalence:

i.e. the equation \(f_1 \circ g_1(k) \cong f_2 \circ g_2(k)\) for any \(k \in K\). Given a linking passage as above, elements \(x_i \in M_i\) can be linked as \(\bigoplus _{i} f_ix_i\) in N.
In the context of information, the OPCM K above is some common domain of discourse between \(M_1\) and \(M_2\); N is some domain at least including \(M_1\) and \(M_2\).
Given a linking passage of \(M_1\) and \(M_2\), there are two ways transferring information from \(M_1\) to \(M_2\)—one through the larger domain N and the other through their common domain K. The former route intuitively preserves more information than the other, and this intuition can be justified as follows.
Proposition 4.5
Given a linking passage \((f_i, g_i)_{i = 1, 2}\) and for any \(x \in M_1\), the inequation \(g_2 (g_1^*(x)) \preceq f_2^* (f_1(x))\) holds. Diagrammatically,

Example 4.6
Assume that \(M_1 = \mathbb {P}^+(X \times Y)\) and \(M_2 = \mathbb {P}^+(Y \times Z)\). Then,

is a linking passage where \(f_1, f_2, g_1, g_2\) are preimage functions of corresponding projections. Moreover, the subset \(f_1(U) \cap f_2(V)\) is equal to
for any non-empty \(U \subseteq X \times Y\) and \(V \subseteq Y \times Z\), which is the natural join in relational database theory. For a plausible example in practice, consider \(U \subseteq \mathbf {Pop}_{\mathrm {UK}}\times \mathbf {Addr}_{\mathrm {UK}}\) a non-empty set of suspects with their hiding places and \(V \subseteq \mathbf {Addr}_{\mathrm {UK}}\times \mathbf {Pop}_{\mathrm {UK}}\) a non-empty set of house addresses and their owners. The combined information \(f_1(U) \cap f_2(V)\) may represent triplets of suspects, addresses, and house owners who possibly provide shelters to suspects.
Local Computation Scheme. In practice, each datum \(x_i\) about the attribute i is collected from various data sources \(M_i\). To combine all \(x_i\)’s, we can combine them in a common domain M and then restrict the combined information to a smaller domain N of interest, i.e.
represented symbolically. The computation is usually costly, however. One interesting observation stated as the combination axiom from [13] in a similar form is that the above information can be computed locally without the need of extending everything to M if inequalities in Propositions 4.3 and 4.5 are in fact equivalences for the involved changes of domains. This observation would be useful for developing an efficient computation algorithm, however, which is beyond the scope of this paper.
4.2 Possibilities over a Set
A surjective function \(X \twoheadrightarrow Y\) gives rise to a change of domain from \(\mathbb {P}^+Y\) to \(\mathbb {P}^+X\). The surjectivity requirement is essential to ensure that a non-empty subset \(S \subseteq Y\) is mapped to a non-empty subset \(f^{-1}(S) \subseteq X\).
Proposition 4.7
For any surjective function \(f:X \twoheadrightarrow Y\), there is a Galois connection
where the preimage function \(f^{-1}\) is a homomorphism from \(\mathbb {P}^+ Y\) to \(\mathbb {P}^+X\) and the forward-image function \(f[{-}]:\mathbb {P}^+ X \rightarrow \mathbb {P}^+Y\) is monotonic.
It is straightforward to see that the inequality of Proposition 4.3 is an equality for any change of domain given by a surjective function. That is,
for any U and V by simple calculations.
Proposition 4.8
Suppose that there are \(f_i:X_i \twoheadrightarrow Z\) and \(g_i:Y \twoheadrightarrow X_i\) for \(i = 1, 2\) with \(g_1 \circ f_1 = g_2 \circ f_2\). Then, \((g_i^{-1}, f_i^{-1})\) is a linking passage, i.e.

If a linking passage is created by functions \(g_i:Y \rightarrow X_i\), then non-empty subsets \(U_i \subseteq X_i\) can be linked as a subset of Y
Example 4.9
Let A be a set of attributes and for each \(a \in A\) a set \(\varPhi _a\) of values for the attribute i. For example, i can be g for ‘gender’, p for ‘British postcode’, s for ‘salary’, etc., then \(\varPhi _g\) could be the two-element set  , \(\varPhi _p = \mathbf {Post}_{\mathrm {UK}}\) the set of all full British postcodes, and \(\varPhi _s = \mathbb {N}\) the set of natural numbers. Given any two sets \(I, J \subseteq A\) of attributes, we have a commutative diagram
, \(\varPhi _p = \mathbf {Post}_{\mathrm {UK}}\) the set of all full British postcodes, and \(\varPhi _s = \mathbb {N}\) the set of natural numbers. Given any two sets \(I, J \subseteq A\) of attributes, we have a commutative diagram

where \(g_i\) and \(f_i\) are all projections.
5 Data Sources and Linkage
So far, an OPCM M is an abstract collection of data from a data source for a single domain of discourse that can be combined and compared. A model of data linkage requires a family of PCMs \((M_i, \preceq _i, \oplus _i, 0_i)\), for \(i \in I\), and ways to move among various sources and domains. Further, the nature of sources and domains induces a structure to the index set I, typically an ordering \(\preceq \), that reflects the relationship between sources and domains such as \(i \preceq j\). With these components, we will model and illustrate data linkage using a form of Grothendieck construction for I-indexed OPCMs.
We will develop the theory in two steps and compare our construction with axiomatic frameworks in the community of approximate reasoning such as ordered valuation algebras [10] and information algebras [13, 14].
5.1 Grothendieck Construction for Preordered Sets
Let I be a preordered set and P an I-indexed family of preordered sets \(P_i\) for \(i \in I\) together with order-preserving functions \(P^i_j:P_i \rightarrow P_j\) whenever \(i \preceq j\) satisfying
-
(i)
\(P^i_i \cong id _{P_i} :P_i \rightarrow P_i\) is the identity function, and
-
(ii)
\(P^j_k \circ P^i_j \cong P^i_k :P_i \rightarrow P_k\)
where \(P^j_k \circ P^i_j \cong P^i_k\) means \(P^j_k \circ P^i_j(x) \cong P^i_k(x)\) for every x and similarly for \(P^i_i \cong id \). Note that P is a pseudo-functor. If the above equations hold strictly, then P is a (proper) functor.
Definition 5.1
The Grothendieck completion of P consists of

with a relation defined by
The ordering appears natural in our context: \(P^i_j\) is typically a change of domain, and \(P^i_j(x)\) is merely an extension of x and \((i, x) \preceq (j, y)\) if and only if j is a larger domain of discourse than i and the extended form of x is still less informative than y.
Proposition 5.2
The following statements are true:
-
(i)
The above Grothendieck completion \(\int P\) is a preordered set.
-
(ii)
If \((I, \le )\) and every \((P_i, \le )\) is partially ordered, then so is \((\int P, \preceq )\).
-
(iii)
The projection \(p:\int P \rightarrow (I, \preceq )\) is functorial.
-
(iv)
p is an opfibration. That is, for every \((i, x) \in \int P\), j with \(i \preceq j\) there exists (j, y) such that \((i, x) \preceq (j, y)\) and moreover for any (k, z) with \((i, x) \preceq (k, z)\) and \(j \preceq k\) it is also true that \((j, y) \preceq (k, z)\).
-
(v)
If each \(P^i_j\) has a right adjoint, then p is an bifibration, i.e. \(p^\mathrm {op}:(\int P, \succeq ) \rightarrow (I, \succeq )\) is also an opfibration.
Remark 5.3
The construction presented here is a form of Grothendieck construction. The full construction works no only for preordered sets but also categories and beyond. See, e.g., [12], for details.
5.2 Grothendieck Construction for OPCMs
In this section, we extend the Grothendieck construction to OPCMs indexed by a \(\vee \)-semilattice \((L, \preceq )\), where L is partially ordered with a least element denoted by \(\bot \) and for every pair (i, j) of elements there is a least upper bound \(i \vee j\). Given a (pseudo-)functor from \((L, \le )\) to \(\mathbf {PCM}_\preceq \) we extend the local combination operations \(\oplus _i\) for each \(i \in L\) to a global combination operation \(\boxplus \) for \(\int M\).
To simplify our discussion, we confine ourselves to functors instead of pseudofunctors. Indeed, all of our discussion and examples in the remaining section do not require this generality.
Theorem 5.4
Let \((L, \le )\) be a bounded \(\vee \)-semilattice and \(M:(L, \le ) \rightarrow \mathbf {PCM}_\preceq \) a functor. Then, the Grothendieck completion \((\int M, \preceq )\) can be equipped with an OPCM given by

where \(k = i \vee j\) and \((i, x) \boxplus (j, y)\) is defined if \(M^i_k(x) \oplus M^j_k(y)\) is defined.
The above construction is a slight modification of a form of Grothedieck construction for monoidal categories, see [22] for details.
5.3 Example: Natural Join for Relational Dataset
Before we show our general result of ordered valuation algebras, we proceed with our simplest example—the possibility representation. The linkage operation \(\boxplus \) derived from Theorem 5.4 is the natural join in relational database theory [4].
First of all, we assume that there is a set \(\mathfrak {A}\) of known attribute names and a set \(\varPhi _a\) of values for each attribute \(a \in \mathfrak {A}\). For example, \(\mathfrak {A}\) may consist of tags for UK postcode, personal information, medical conditions, and so on. By abuse of notation, we denote by \(\varPhi _A\) for \(A \subseteq \mathfrak {A}\) the cartesian product  . Whenever \(A \subseteq B\), we have projections \(p_{B, A}\) from \(\varPhi _B\) to \(\varPhi _A\) which sends \((x_b)_{b \in B}\) to \((x_a)_{a \in A}\). A functor P from the powerset \(\mathbb {P}(\mathfrak {A}, \subseteq )\) to \(\mathbf {PCM}_\preceq \) is defined by
. Whenever \(A \subseteq B\), we have projections \(p_{B, A}\) from \(\varPhi _B\) to \(\varPhi _A\) which sends \((x_b)_{b \in B}\) to \((x_a)_{a \in A}\). A functor P from the powerset \(\mathbb {P}(\mathfrak {A}, \subseteq )\) to \(\mathbf {PCM}_\preceq \) is defined by
In our interpretation, any set \(S \in \mathbb {P}^+\varPhi _A\) is a set of possibilities where only one of them is true, so having more elements in S means less specific information. If \(A \subseteq B\), then \(p_{B, A}^{-1}(S)\) is merely the set S padded with all combinations, i.e. \(S \times \prod _{b \in B - A} \varPhi _b\). So, \(p_{B, A}^{-1}(S)\) contains no information about attributes \(B - A\).
Therefore the ordering on the Grothendieck completion \(\int \varPhi \)
simply means that (A, S) is less informative than (B, T) if (B, T) contains more attributes and is more specific on those already known in A.
By Theorem 5.4, the derived operation \(\boxplus \) is given as \((A, S) \boxplus (B, T) = (A \cup B, S \bowtie T)\) for \(A, B \subseteq \mathfrak {A}\), \(S \in \mathbb {P}^+(\varPhi _A)\), and \(T \in \mathbb {P}^+(\varPhi _B)\) where
which is by definition the natural join in relational database theory.
5.4 Ordered Valuation Algebras
It is observed in the community of approximate reasoning that with two algebraic operations of combination and marginalization a number of approximating inference techniques can be formalized under reasonable assumptions. The axiomatic approach is pursued by Shenoy and Shafer [21], Shenoy and Kohlas [15], Haenni [10], etc. In this section, we show that a variant of their axiomatic frameworks can be derived by our Grothendieck construction for ordered (total) commutative monoids, clarifying the relationship between our approach and theirs.
The following concept is derived from [10]:
Definition 5.5
A (stable) ordered valuation algebra is a two-sorted algebra \((\varPhi , \le , D)\), consisting of a partially ordered set \((\varPhi , \le )\) of valuations and a bounded lattice D of domains with operations
-
(i)
\(\otimes :\varPhi \times \varPhi \rightarrow \varPhi \) called combination,
-
(ii)
\(d:\varPhi \rightarrow D\) such that \(d(\varphi )\) is called the domain of \(\varphi \),
-
(iii)
\((-)^{\downarrow -}:\varPhi \times D \rightharpoonup \varPhi \) called focusing where \(\varphi ^{\downarrow x}\) is defined for \(x \le d(\varphi )\),
-
(iv)
and \(e:D \rightarrow \varPhi \) such that \(e_x\) is (called) an identity element
satisfying conditions below. In the following context, \(\varPhi _x = \{\, \varphi \in \varPhi \mid d(\varphi ) = x \,\}\).
-
(i)
\((\varPhi , \otimes )\) is a commutative semigroup.
-
(ii)
Comparable valuations are of the same domain: \(\varphi \le \psi \) implies \(d(\varphi ) = d(\psi )\).
-
(iii)
Identity element: \(d(e_x) = x\), \(e_x \otimes e_y = e_{x \vee y}\), and \(\varphi \otimes e_x = \varphi \) for \(\varphi \in \varPhi _x\).
-
(iv)
Stability of identity under focusing: \(e_y^{\downarrow x} = e_x\) for \(x \le y\).
-
(v)
Labelling: \(d(\varphi \otimes \psi ) = d(\varphi ) \vee d(\psi )\) and \(\varphi ^{{\downarrow } x} \in \varPhi _x\) if \(x \le d(\varphi )\).
-
(vi)
Transitivity of focusing \((\varphi ^{\downarrow y})^{\downarrow x} = \varphi ^{{\downarrow } x}\) for \(x \le y \le d(\varphi )\).
-
(vii)
Distributivity of focusing over combination: \((\varphi \otimes \psi )^{\downarrow d(\varphi )} = \varphi \otimes \psi ^{{\downarrow } d(\varphi ) \wedge d(\psi )}\).
-
(viii)
Combination preserves ordering: \(\varphi _1 \otimes \varphi _2 \le \psi _1 \otimes \psi _2\) whenever \(\varphi _i \le \psi _i\).
-
(ix)
Focusing preserves ordering: \(\varphi ^{\downarrow x} \le \psi ^{\downarrow x}\) for any \(x \le d(\varphi ) = d(\psi )\) and \(\varphi \le \psi \).
The focusing operation \(\downarrow \) formalises marginalization in probability theory and projection in relational database theory. The intuitive meaning of every other operation is self-evident. In addition to the focusing operation, a vacuous extension operation, coined in [13], \(({-})^{\uparrow y}:\varPhi _x \rightarrow \varPhi _y\) can be defined for every \(y \ge x\) via

We will see that \(\downarrow \) and \(\uparrow \) form a Galois connection under mild conditions.
Remark 5.6
The original formulation in [10] imposes additional requirements. For example, D is only a powerset instead of a lattice and \(\varPhi _x\) also requires a null (or, absorbing) element which in [10] represents a special inconsistent information. For the sake of brevity, we refrain to discuss these conditions. More variants of (unordered) valuation algebras can be found in [13, 18].
Proposition 5.7
Let \((\varPhi , \le , D; \otimes , d, \downarrow , e)\) be an ordered valuation algebra. Then, the following statements hold:
-
(i)
\((\varPhi _x, \le , \otimes , e_x)\) is an ordered commutative monoid.
-
(ii)
For any \(x \le y\), the vacuous extension operation \((-)^{\uparrow y}\) is an order-preserving monoid homomorphism from \(\varPhi _x\) to \(\varPhi _y\).
-
(iii)
\((\varPhi , \le , D; \otimes , d, \downarrow , e)\) gives rise to a functor from D to the category of ordered commutative monoids.
As we intend to view ordered valuation algebras as Grothendieck completions of families of commutative monoids, an obvious discrepancy is that \(\varphi \) and \(\psi \) are comparable only if \(d(\varphi ) = d(\psi )\) in ordered valuation algebras while elements \((x, \varphi )\) and \((y, \psi )\) in \(\int P\) are comparable even if domains x and y are different. This can be readily mitigated by extending \(\le \) canonically:
Proposition 5.8
The ordered algebraic structure \((\varPhi , \le ', D; \otimes , d, \downarrow , e)\) satisfies the conditionsFootnote 4 of ordered valuation algebra except that \(\varphi \le \psi \) implies \(d(\varphi )= d(\psi )\).
By applying the Grothendieck construction (Theorem 5.4) to the D-indexed family of ordered commutative monoids \(\varPhi _x\) (Proposition 5.7), we have a partially ordered set \((\int \varPhi , \preceq )\). The mapping \((x, \varphi ) \mapsto \varphi \) is evidently bijective since \(d(\varphi ) = x\), and \((x, \varphi ) \preceq (y, \psi ) \iff \varphi \le ' \psi \) by definition. That is, the bijection \((x, \varphi ) \mapsto \varphi \) is an order isomorphism between \((\int \varPhi , \preceq )\) and \((\varPhi , \le ')\).
It is clear that the domain operation \(d:\varPhi \rightarrow D\) is the projection \(p:\int \varPhi \rightarrow D\) through the isomorphism, i.e. \(p(x, \varphi ) = d(\varphi )\). Similarly, \(e_x \in \varPhi _x\) is unique for each x, so it defines \(e:D \rightarrow \int \varPhi \).
As for the combination operations \(\otimes \) and \(\boxtimes \), note that \(\boxtimes \) is given by
where \(z = x \vee y\) and \(\varphi ^{\uparrow z} \otimes \psi ^{\uparrow z} = \varphi \otimes \psi \) by an easy calculation. Henceforth, \(\otimes \) is the same as \(\boxtimes \) via the isomorphism.
It remains to derive the focusing operation from the Grothendieck construction. To this point, we need a regularity condition:
Lemma 5.9
For any ordered valuation algebra \(\varPhi = (\varPhi , \le , D; \otimes , d, \downarrow , e)\), the following statements are true:
-
(i)
\(\varphi ^{\uparrow y} \le \psi \) implies \(\varphi \le \psi ^{\downarrow x}\).
-
(ii)
If \(e_x \le \varphi \) for any \(\varphi \in \varPhi _x\) and \(\varPhi \) is regular, i.e. for any \(\varphi \) and \(x \le d(\varphi )\) there is \(\chi \in \varPhi _x\) such that \(\varphi ^{\downarrow x} \otimes \chi \otimes \varphi \le \varphi \), then \(\varphi \le \psi ^{\downarrow x}\) implies \(\varphi ^{\uparrow y} \le \psi \).
Remark 5.10
The condition(s) in Lemma 5.9 are studied in [18]. Idempotent valuation algebras are called information algebras by Kohlas [13].
Every adjoint is uniquely determined by the other adjoint, so in particular the focusing operation \(\downarrow \) is uniquely determined by the vacuous extension \(\uparrow \).
To sum up, we have shown that the combination operation \(\otimes \) of an ordered valuation algebra can be derived by the Grothendieck construction:
Theorem 5.11
Every regular ordered valuation algebra \((\varPhi , \le , D; \otimes , \downarrow , e)\) with \(e_x \le \varphi \) for any \(\varphi \in \varPhi _x\) is isomorphic to the Grothendieck completion \((\int \varPhi , \preceq , \boxtimes , 0)\) of the functor given by Proposition 5.7.
Remark 5.12
Both Theorems 5.4 and 5.11 justify our claim that data linkage is made of data combination and changes of domain. The Grothendieck construction is in fact an equivalence of categories so that a pseudo-functor from a preorder to monoidal structures is essentially an opfibration equipped with a global monoidal structure. For interested readers, see [22, Theorem 12.7].
6 Concluding Remarks
Ubiquitous computing has led to ubiquitous data. Technologies exist that explore information content by combining data in a dataset and, in particular, linking data from different datasets. Given the diversity of what passes for data—exact, approximate, erroneous, fictitious—a very abstract conceptual framework is needed to discover any general principles in today’s datafest.
We have presented an abstract algebraic framework based on axiomatic notions that model a data source, data representations and their combination ‘\(\oplus \)’, a measure of information content ‘\(\preceq \)’, and linkage between data sources. By stripping down intuitions we have found that ordered partial commutative monoids provide algebraic structures to be found at the heart of many quite disparate data sharing situations.
Our approach could be developed further using category-theoretic notions which have proved successful in database theory, see e.g., [19]. While databases provide useful examples for our theory, the exact connection remains unclear.
Our next steps are to map the scope of ordered partial commutative monoids by exploring new and various
-
(i)
types of data, especially those in approximate reasoning such as belief functions and those discussed in uncertainty reasoning [11], and so on;
-
(ii)
types of operations on and between our algebras.
Returning to our background motivation in the introduction, clearly more attention needs to be paid to the concept of data privacy and how linkage of data can lead to privacy breach, e.g., de-anonymization. This is the subject of ongoing investigations, cf. [25].
Interestingly, there does not seem to be much of a theory of ordered partial commutative monoids so that, too, is something to do.
Notes
- 1.
Some privacy protection models are achieved by generalisation and suppression of cell values, see [24] for example.
- 2.
See, e.g., [6, p. 63].
- 3.
Every adjoint is unique up to order isomorphism—that is, if g is an upper adjoint of f then \(f^*y \cong g y\) for any y, so we can say that a homomorphism f is a change of domain without referring to \(f^*\).
- 4.
The order-preservation property of focusing accordingly becomes ‘if \(\varphi \le \psi \) and \(x \le d(\varphi )\) then \(\varphi ^{\downarrow x} \le \psi ^{\downarrow x}\)’.
References
Arieli, O., Avron, A.: The value of the four values. Artif. Intell. 102(1), 97–141 (1998). https://doi.org/10.1016/S0004-3702(98)00032-0
Attard, J., Orlandi, F., Scerri, S., Auer, S.: A systematic review of open government data initiatives. Gov. Inform. Q. 32(4), 399–418 (2015). https://doi.org/10.1016/j.giq.2015.07.006
Belnap, N.D.: A useful four-valued logic. In: Dunn, J.M., Epstein, G. (eds.) Modern Uses of Multiple-Valued Logic. Episteme(A Series in the Foundational, Methodological, Philosophical, Psychological, Sociological, and Political Aspects of the Sciences, Pure and Applied), vol. 2, pp. 5–37. Springer, Dordrecht (1977). https://doi.org/10.1007/978-94-010-1161-7_2
Codd, E.F.: The Relational Model for Database Management: Version 2. Pearson, London (1990)
Coecke, B., Lal, R.: Causal categories: a backbone for a quantum-relativistic universe of interacting processes. In: Proceedings of QPL VII, pp. 17–26 (2010)
Davey, B.A., Priestley, H.A.: Introduction to Lattices and Order, 2nd edn. Cambridge University Press, Cambridge (2002)
Foulis, D.J., Bennett, M.K.: Effect algebras and unsharp quantum logics. Found. Phys. 24(10), 1331–1352 (1994). https://doi.org/10.1007/BF02283036
Fritz, T.: Resource convertibility and ordered commutative monoids. Math. Struct. Comp. Sci. 27(06), 850–938 (2017). https://doi.org/10.1017/S0960129515000444
Gunter, C.A.: The mixed powerdomain. Theor. Comput. Sci. 103(2), 311–334 (1992). https://doi.org/10.1016/0304-3975(92)90017-A
Haenni, R.: Ordered valuation algebras: a generic framework for approximating inference. Int. J. Approx. Reason. 37(1), 1–41 (2004). https://doi.org/10.1016/j.ijar.2003.10.009
Halpern, J.Y.: Reasoning About Uncertainty, 1st edn. The MIT Press, Cambridge (2003)
Jacobs, B.: Categorical Logic and Type Theory. North Holland, Amsterdam (1999)
Kohlas, J.: Discrete mathematics and theoretical computer science. Information Algebras. Generic Structures For Inference, vol. 1. Springer-Verlag, London (2003)
Kohlas, J., Pouly, M., Schneuwly, C.: Generic local computation. J. Comput. Syst. Sci. 78(1), 348–369 (2012). https://doi.org/10.1016/j.jcss.2011.05.012
Kohlas, J., Shenoy, P.P.: Computation in valuation algebras. In: Kohlas, J., Moral, S. (eds.) Handbook of Defeasible Reasoning and Uncertainty Management Systems. Handbook of Defeasible Reasoning and Uncertainty Management Systems, vol. 5, pp. 5–39. Springer, Dordrecht (2000)
Machanavajjhala, A., Kifer, D., Gehrke, J., Venkitasubramaniam, M.: \(l\)-diversity: Privacy beyond \(k\)-anonymity. ACM T. Knowl. Discov. D. 1(1), 3 (2007). https://doi.org/10.1145/1217299.1217302
Narayanan, A., Shmatikov, V.: Robust de-anonymization of large sparse datasets. In: 2008 IEEE Symposium on Security and Privacy, pp. 111–125. IEEE (2008). https://doi.org/10.1109/SP.2008.33
Pouly, M., Kohlas, J.: Generic Inference. Wiley, Hoboken, USA (2011)
Schultz, P., Spivak, D.I., Wisnesky, R.: Algebraic model management: a survey. In: James, P., Roggenbach, M. (eds.) WADT 2016. LNCS, vol. 10644, pp. 56–69. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-72044-9_5
Scott, D.S.: Data types as lattices. SIAM J. Comput. 5(3), 522–587 (1976). https://doi.org/10.1137/0205037
Shenoy, P.P., Shafer, G.: Studies in fuzziness and soft computing. In: Yager, R.R., Liu, L. (eds.) Axioms for Probability and Belief-Function Propagation. Classic Works of the Dempster-Shafer Theory of Belief Functions, pp. 499–528. Springer, Heidelberg (2008)
Shulman, M.: Framed bicategories and monoidal fibrations. Theory Appl. Categ. 20(18), 650–738 (2008)
Sweeney, L.: Weaving technology and policy together to maintain confidentiality. J. Law. Med. Ethics 25(2–3), 98–110 (1997). https://doi.org/10.1111/j.1748-720X.1997.tb01885.x
Sweeney, L.: \(k\)-anonymity: a model for protecting privacy. Int. J. Uncertain. Fuzz. 10(05), 557–570 (2002). https://doi.org/10.1142/S0218488502001648
Wang, V., Tucker, J.V.: Surveillance and identity: conceptual framework and formal models. J. Cybersecurity 3(3), 145–158 (2017). https://doi.org/10.1093/cybsec/tyx010
Wang, Y., Huang, Z., Mitra, S., Dullerud, G.E.: Entropy-minimizing mechanism for differential privacy of discrete-time linear feedback systems. In: 53rd IEEE Conference on Decision and Control, pp. 2130–2135. IEEE (2014). https://doi.org/10.1109/CDC.2014.7039713
Wehrung, F.: Refinement Monoids, Equidecomposability Types, and Boolean Inverse Semigroups. LNM, vol. 2188. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-61599-8
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 IFIP International Federation for Information Processing
About this paper
Cite this paper
Chen, LT., Roggenbach, M., Tucker, J.V. (2019). An Algebraic Theory for Data Linkage. In: Fiadeiro, J., Țuțu, I. (eds) Recent Trends in Algebraic Development Techniques. WADT 2018. Lecture Notes in Computer Science(), vol 11563. Springer, Cham. https://doi.org/10.1007/978-3-030-23220-7_3
Download citation
DOI: https://doi.org/10.1007/978-3-030-23220-7_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-23219-1
Online ISBN: 978-3-030-23220-7
eBook Packages: Computer ScienceComputer Science (R0)






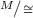 is a partial order and
is a partial order and 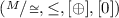 with
with  , and
, and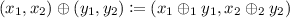 if
if 