Abstract
Sacks proved that every admissible countable ordinal is the first admissible ordinal relatively to a real. We give an algorithmic proof of this result for constructibly countable admissibles. Our study is completed by an algorithmic approach to a generalization of Sacks’ theorem due to Jensen, that finds a real relatively to which a countable sequence of admissibles, having a compatible structure, constitutes the sequence of the first admissibles. Our approach deeply involves infinite time Turing machines. We also present different considerations on the constructible ranks of the reals involved in coding ordinals.
The research for this paper has been done thanks to the support of the Agence nationale de la recherche through the RaCAF ANR-15-CE40-0016-01 grant.
The authors would like to thank the anonymous referees for their constructive comments which helped a lot to improve the manuscript.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
Let \(\beta > \alpha \) be countable ordinals such that there is an elementary embedding \(j : L_\beta \rightarrow L_{\omega _2}\) with critical point
 . For every
. For every 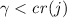 , \(L_{\omega _2} \models \) “\(\text {No new reals appear between ranks }\omega _1\) and \(\omega _1+\gamma \).” No new reals thus appear between
, \(L_{\omega _2} \models \) “\(\text {No new reals appear between ranks }\omega _1\) and \(\omega _1+\gamma \).” No new reals thus appear between 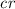 (j) and
(j) and 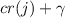 , by elementarity and absoluteness. Cf. [31, 2, 3, 28].
, by elementarity and absoluteness. Cf. [31, 2, 3, 28]. - 2.
\(E_\alpha \) is an arithmetical copy of \(L_\alpha \) if there is one-one function f from \(L_\alpha \) to \(\omega \) (and onto the field of \(E_\alpha \)) such that \(\forall x, y \in L_\alpha \), \( x\in y \iff \langle f(x), f(y) \rangle \in E_\alpha \).
- 3.
There exists \(\alpha \) such that \(L_\alpha \prec L_{\omega _1}\), \(\alpha \) is thus not definable in \(L_{\omega _1}\). There is a countable \(\upsilon > \alpha \) such that \(L_\upsilon \prec L_{\omega _1}\), and \(\alpha \) is already not definable in \(L_\upsilon \).
- 4.
\(\upsilon _0\) is clearly \(\leqslant \) the least such \(\eta \), \(\eta _0\), since whenever one has \(L_\alpha \prec L_\beta \), \(\alpha \) is not definable in \(L_\beta \). Now, suppose that \(\upsilon _0 < \eta _0\), in other words, for all \(\delta < \upsilon _0\), \(L_\delta \not \prec L_{\upsilon _0}\). Now, by Löwenheim-Skolem there is a countable elementary submodel of \(L_{\upsilon _0}\). Take the \(\subseteq \)-least such model M. By the Condensation Lemma, there is an \(\alpha <\upsilon _0\) and an isomorphism j such that the Mostowski collapse of M is isomorphic to \(L_\alpha \) via j. j cannot be trivial as this would mean that \(L_\alpha \prec L_\delta \), although \(\delta < \upsilon _0\) and \(\upsilon _0\) is the least such ordinal. We can thus consider \(\kappa \), the critical point\(^{1}\) of j. Since \(L_\alpha \cong M \prec L_{\upsilon _0}\), \(L_\kappa \prec L_{j(\kappa )}\). But then \(\kappa \) cannot be definable in \(L_{j(\kappa )}\), and thus \(\upsilon _0 \leqslant j(\kappa )\). But \(j(\kappa )<\upsilon _0\), contradiction.
- 5.
Consider \(\kappa = \aleph _\alpha \). \(\kappa \) is definable as the greatest cardinal in \(L_{\kappa ^+}\). (Here \(\kappa ^+\) denotes the least ordinal of cardinality greater than \(\kappa \).) And thus \(\alpha \) is also definable in \(L_{\kappa ^+}\). Löwenheim-Skolem’s theorem, in conjunction with Mostowski’s lemma and the Condensation Lemma, provides the countable \(\beta \) such that \(\alpha \) is definable in \(L_\beta \).
- 6.
- 7.
Any countable \(\tau \) such that \(L_\tau \prec L_{\omega _1}\) is such an upper bound: if \(\alpha \) is definable at \(\beta \), take \(\delta \) above \(\tau \) and \(\beta \) such that \(L_\delta \prec L_{\omega _1}\). We then have \(L_\tau \prec L_\delta \prec L_{\omega _1}\). \(\alpha \) is thus definable at \(\delta \), since \(\delta \) is above \(\beta \), and also at \(\tau \). \(\tau \) is therefore above \(\alpha \) and any other definable ordinal. In fact, the least non-memorable ordinal \(\tau _0\) is the least ordinal \(\tau \) with uncountably many elementary extensions \(L_\tau \prec L_\gamma \). (Cf. footnote 6).
- 8.
We use Barwise’s convention for admissibles: \(\tau _0=\omega \), \(\tau _1=\omega _1^{{\mathrm{CK}}}\), ..., \(\tau _\alpha \) is the \(\alpha \)-th admissible. Note that there exist admissibles \(\alpha \) such that \(\alpha =\tau _\alpha \). Such is the case for \(\lambda _\infty \), but it is not the first one.
- 9.
The infinite join, \(\bigoplus _i r_i\), of the \(r_i\)’s is defined as \(\left\{ \langle i,j\rangle : j \in r_i \right\} \).
- 10.
An ordinal \(\alpha \) is admissible relative to a set of ordinals A if \(\langle L_\alpha \left[ A\right] ; A \cap \alpha \rangle \) is an admissible structure.
- 11.
Recall that \(Y \leqslant _h X\) if Y is hyperarithmetic in X, that is if Y is ITTM-computable in some bounded recursive ordinal length of time (\(<\omega _1^{{\mathrm{CK}},X}\)).
- 12.
This hypothesis carries the ideas of progressivity of the sequence and indiscernibility by first order properties: in the list of admissibles \(\langle \tau _\beta : \beta < \lambda _\infty \rangle \), the sequence of indices that correspond to the considered sequence does not contain too much information in itself.
References
Barwise, J.: Admissible Sets and Structures: An Approach to Definability Theory, Perspectives in Mathematical Logic, vol. 7. Springer, Heidelberg (1975)
Boolos, G.S.: The hierarchy of constructible sets of integers. Ph.D. thesis, Massachusetts Institute of Technology, Cambridge, Mass. (1966)
Boolos, G.S., Putnam, H.: Degrees of unsolvability of constructible sets of integers. J. Symb. Log. 33, 497–513 (1968)
Boyd, R., Hensel, G., Putnam, H.: A recursion-theoretic characterization of the ramified analytical hierarchy. Trans. Am. Math. Soc. 141, 37–62 (1969)
Carl, M.: Ordinal Computability. De Gruyter Series in Logic and Its Applications, vol. 9. De Gruyter, July 2019
Carl, M., Durand, B., Lafitte, G., Ouazzani, S.: Admissibles in gaps. In: Kari et al. [24], pp. 175–186
Chong, C.T.: A recursion-theoretic characterization of constructible reals. Bull. Lond. Math. Soc. 9, 241–244 (1977)
Chong, C.T., Yu, L.: Recursion theory. De Gruyter Series in Logic and Its Applications, vol. 8. De Gruyter (2015)
David, R.: A functorial \(\varPi ^1_2\) singleton. Adv. Math. 74, 258–268 (1989)
Devlin, K.: Constructibility. Springer, Heidelberg (1984)
Durand, B., Lafitte, G.: A constructive Swiss knife for infinite time Turing machines (2016)
Friedman, H.: Minimality in the \({\varDelta }^1_2\)-degrees. Fundamenta Mathematicae 81(3), 183–192 (1974)
Friedman, H., Jensen, R.: Note on admissible ordinals. In: Barwise, J. (ed.) The Syntax and Semantics of Infinitary Languages. LNM, vol. 72, pp. 77–79. Springer, Heidelberg (1968). https://doi.org/10.1007/BFb0079683
Friedman, S.D.: An introduction to the admissibility spectrum. In: Marcus, R.B., Dorn, G.J., Weingartner, P. (eds.) Logic, Methodology and Philosophy of Science VII, Proceedings of the Seventh International Congress of Logic, Methodology and Philosophy of Science (Salzburg, 1983). Studies in Logic and the Foundations of Mathematics, vol. 114, pp. 129–139. North-Holland (1986)
Friedman, S.D.: Strong coding. Ann. Pure Appl. Log. 35, 1–98 (1987)
Grilliot, T.: Omitting types: applications to recursion theory. J. Symb. Log. 37, 81–89 (1972)
Hamkins, J.D., Lewis, A.: Infinite time Turing machines. J. Symb. Log. 65(2), 567–604 (2000)
Hodes, H.T.: Jumping through the transfinite: the master code hierarchy of Turing degrees. J. Symb. Log. 45(2), 204–220 (1980)
Hodes, H.T.: Upper bounds on locally countable admissible initial segments of a Turing degree hierarchy. J. Symb. Log. 46, 753–760 (1981)
Hodes, H.T.: Jumping through the transfinite. Ph.D. thesis, Harvard University (1977)
Jech, T.: Set Theory: The Third Millennium Edition, Revised and Expanded. SMM. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-44761-X
Jensen, R.B.: The fine structure of the constructible hierarchy. Ann. Math. Log. 4, 229–308 (1972). Erratum, ibid. 4, 443 (1972)
Jensen, R.B.: Admissible sets, December 2010. https://www.mathematik.hu-berlin.de/~raesch/org/jensen.html. Handwritten notes (1969)
Kari, J., Manea, F., Petre, I. (eds.): CiE 2017. LNCS, vol. 10307. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-58741-7
Koepke, P.: Turing computations on ordinals. Bull. Symb. Log. 11, 377–397 (2005)
Koepke, P., Seyfferth, B.: Ordinal machines and admissible recursion theory. Ann. Pure Appl. Log. 160, 310–318 (2009)
Le Scornet, P.: Les machines de Turing en temps transfini. Rapport de stage, Ecole Normale Supérieure de Rennes, June 2017
Leeds, S., Putnam, H.: An intrinsic characterization of the hierarchy of constructible sets of integers. In: Gandy, R.O., Yates, C.M.E. (eds.) Logic Colloquium ’69 (Proceedings of the Summer School and Colloquium in Mathematical Logic, Manchester, August 1969), pp. 311–350. North-Holland (1971)
Lukas, J.D., Putnam, H.: Systems of notations and the ramified analytical hierarchy. J. Symb. Log. 39, 243–253 (1974)
Marek, W., Srebrny, M.: Gaps in the constructible universe. Ann. Math. Log. 6, 359–394 (1974)
Putnam, H.: A note on constructible sets of integers. Notre Dame J. Formal Log. 4(4), 270–273 (1963)
Sacks, G.E.: Forcing with perfect closed sets. In: Proceedings of the Symposia Pure Math, vol. XIII, pp. 331–355. American Mathematical Society (1971)
Sacks, G.E.: Countable admissible ordinals and hyperdegrees. Adv. Math. 19, 213–262 (1976)
Seyfferth, B.: Three models of ordinal computability. Ph.D. thesis, Rheinischen Friedrich-Wilhelms-Universitat Bonn (2012)
Simpson, S.G., Weitkamp, G.: High and low Kleene degrees of coanalytic sets. J. Symb. Log. 48(2), 356–368 (1983)
Welch, P.D.: Eventually infinite time Turing degrees: infinite time decidable reals. J. Symb. Log. 65(3), 1193–1203 (2000)
Welch, P.D.: Characteristics of discrete transfinite time Turing machine models: halting times, stabilization times, and normal form theorems. Theoret. Comput. Sci. 410, 426–442 (2009)
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Durand, B., Lafitte, G. (2019). An algorithmic approach to characterizations of admissibles. In: Manea, F., Martin, B., Paulusma, D., Primiero, G. (eds) Computing with Foresight and Industry. CiE 2019. Lecture Notes in Computer Science(), vol 11558. Springer, Cham. https://doi.org/10.1007/978-3-030-22996-2_16
Download citation
DOI: https://doi.org/10.1007/978-3-030-22996-2_16
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-22995-5
Online ISBN: 978-3-030-22996-2
eBook Packages: Computer ScienceComputer Science (R0)


 . For every
. For every 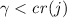 ,
, 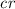 (j) and
(j) and 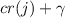 , by elementarity and absoluteness. Cf. [
, by elementarity and absoluteness. Cf. [