Abstract
Most current clustering based anomaly detection methods use scoring schema and thresholds to classify anomalies. These methods are often tailored to target specific data sets with “known” number of clusters. The paper provides a streaming clustering and anomaly detection algorithm that does not require strict arbitrary thresholds on the anomaly scores or knowledge of the number of clusters while performing probabilistic anomaly detection and clustering simultaneously. This ensures that the cluster formation is not impacted by the presence of anomalous data, thereby leading to more reliable definition of “normal vs abnormal” behavior. The motivations behind developing the INCAD model [17] and the path that leads to the streaming model are discussed.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
- Anomaly detection
- Bayesian non-parametric models
- Extreme value theory
- Clustering based anomaly detection
1 Introduction
Anomaly detection heavily depends on the definitions of expected and anomalous behaviors [14, 20, 22]. In most real systems, observed system behavior typically forms natural clusters whereas anomalous behavior either forms a small cluster or is weakly associated with the natural clusters. Under such assumptions, clustering based anomaly detection methods form a natural choice [7, 10, 18] but have several limitations.
Firstly, clustering based methods usually require baseline assumptions that are often conjectures and generalizing them is not always trivial. This leads to inaccurate choices for model parameters such as the number of clusters or the thresholds that are required to classify anomalies. Score based models have thresholds that are often based on data/user preference. Such assumptions result in models that are susceptible to modeler’s bias and possible over-fitting.
Secondly, setting the number of clusters has additional challenges when dealing with streaming data, where new behavior could emerge and form new clusters. Non-stationarity is inherent as data evolves over time. Moreover, the data distribution of a stream changes over time due to changes in environment, trends or other unforeseen factors [13, 21]. This leads to a phenomenon called concept drift, due to which an anomaly detection algorithm cannot assume any fixed distribution for data streams. Thus, there arises a need for a definition of an anomaly that is dynamically adapted.
Thirdly, when anomaly detection is performed post clustering [2, 12], the presence of anomalies gives a skewed (usually slight) definition of traditional/normal behavior. However, since the existence of anomalies impacts the clustering as well as the definition of the ‘normal’Footnote 1 behavior, it seems counter-intuitive to classify anomalies based on such definitionsFootnote 2. To avoid this, simultaneous clustering and anomaly detection needs to be performed.
In addition to the above challenges, extending these assumptions to the streaming context leads to a whole new set of challenges. Many supervised [8, 16] and unsupervised anomaly detection techniques [4, 8, 15, 18] are offline learning methods that require the full data set in advance for data mining which makes them unsuitable for real-time streaming data. Although supervised anomaly detection techniques may be effective in yielding good results, they are typically unsuitable for anomaly detection in streaming data [16]. We propose a method called Integrated Clustering and Anomaly Detection (INCAD), that couples Bayesian non-parametric modeling and extreme value theory to simultaneously perform clustering and anomaly detection. Table 1 summarizes the properties of INCAD vs other strategies for anomaly detection. The primary contributions of the paper are as follows:
-
1.
Generalized anomaly definition with adaptive interpretation. The model definition of an anomaly has dynamic interpretation allowing anomalous behaviors to evolve into normal behaviors and vice versa. This definition not only evolves the number of clusters with an incoming stream of data (using non-parametric mixture models) but also helps evolve the classification of anomalies.
-
2.
Combination of Bayesian non-parametric models and extreme value theory (EVT). The novelty of the INCAD approach lies in blending extreme value theory and Bayesian non-parametric models. Non-parametric mixture models [19], such as Dirichlet Process Mixture Models (DPMM) [3, 25, 28], allow the number of components to vary and evolve during inference. While there has been limited work that has explored DPMM for the task of anomaly detection [26, 29], they have not been shown to operate in a streaming mode or ignore online updates to the DPMM model. On the other hand, EVT gives the probability of a point being anomalous which has a more universal interpretation, in contrast to the scoring schema with user-defined thresholds. Although EVT’s definition of anomalies is more adaptable for streaming data sets [1, 11, 27], fitting an extreme value distribution (EVD) on a mixture of distributions or even multivariate distributions is challenging. This novel combination brings out the much-needed aspects in both the models.
-
3.
Extension to streaming settings. The model is non-exchangeable which is well suited to capture the effect of the order of data input and utilize this dependency to develop streaming adaptation.
-
4.
Ability to handle complex data generative models. The model can be generalized to multivariate distributions and complex mixture models.
2 Motivation
2.1 Assumptions on Anomalous Behavior
One of the key drivers in developing any model are the model assumptions. For INCAD model, we assume that the data has multiple “normal” as well as “anomalous” behaviors. These behaviors are dynamic with a tendency to evolve from “anomalous” to “normal” and vice versa. Each such behavior (normal/anomalous) forms a sub-population that can be represented using a cluster. These clusters are assumed to be generated from a family of distributions whose cluster proportions and cluster parameters are generated from a non-parametric distribution.
There are two distinct differences between normal and anomalous data that must be identified: (a) “Anomalous” instances are different from tail instances of “normal” behavior and need to be distinguished from them. They are assumed to be generated from distributions that are different from “normal” data. (b) The distributions for anomalous data result in relatively fewer instances in the observed set.
As mentioned earlier, clustering based anomaly detection methods could be good candidates for monitoring such systems, but require the ability to allow the clustering to evolve with the streaming data, i.e., new clusters form, old clusters grow or split. Furthermore, we need the model to distinguish between anomalies and extremal values of the “normal”.
Thus, non-parametric models that can accommodate infinite clusters are integrated with extreme value distributions that distinguish between anomalous and non-anomalous behaviors.
We now describe the two ingredients that go into our model namely, mixture models and extensions of EVT.
2.2 EVT and Generalized Pareto Distribution in Higher Dimensions
Estimation of parameters for extreme value distributions in higher dimensions is complex. To overcome this challenge, Clifton et al. [9] proposed an extended version of the generalized Pareto distribution that is applicable for different multi-model and multivariate distributions. For a given data \(X\in \mathbb {R}^n\) distributed as \(f_X:X\rightarrow {}Y\) where \(Y\in \mathbb {R}\) is the image of the pdf values of X, let \(Y\in [0,y_{max}]\) be the range of Y where \(y_{max}=sup(f_X)\). Let,
where \(f_Y^{-1}:Y\rightarrow {}X\) is the pre-image of \(f_X\) given by, \(f_Y^{-1}([0,y])=\{x|f_X(x)\in [0,y]\}\). Then \(G_Y\) is in the domain of attraction of generalized Pareto distribution (GPD) \(G^e_Y\) for \(y\in [0,u]\) as \(u\rightarrow {}0\) given by,
where, \(\nu , \beta \) and \(\xi \) are the location, scale and shape parameters of the GPD respectively.
2.3 Mixture Models
Mixture models assume that the data consists of sub-populations each generated from a different distribution. It can be used to study the properties of clusters using mixture distributions. In the classic version, when the number of clusters is known, finite mixture models are used with Dirichlet priors. However, when the number of latent clusters is unknown, one can extend finite mixture models to infinite mixture models like Dirichlet process mixture model (DPMM). In DPMM, the mixture distributions being sampled from a Dirichlet process (DP). DP can be viewed as a distribution over a family of distributions, that constitutes a base distribution \(G_0\) which is a prior over the cluster parameters \(\theta \) and positive scaling parameter \(\alpha _{DP}\). G is a Dirichlet process (denoted as \(G\sim DP(G_0,\alpha _{DP})\)) if G is a random distribution with same support as the base distribution \(G_0\) and for any measurable finite partition of the support \(A_1 \cup A_2 \cup \ldots \cup A_k\), we have \((G(A_1), G(A_2), \ldots , G(A_k)) \sim \) Dir(\(\alpha _{DP} G_0(A_1),\ldots ,\alpha _{DP} G_0(A_k)\)).
In order to learn the number of clusters from the data, Bayesian non-parametric (BNP) models are used. BNP models like DPMM assume an infinite number of clusters of which only a finite number are populated. It brings forth a finesse in choosing the number of clusters while assuming a prior on the cluster assignments of the data. The prior is given by the Chinese restaurant process(CRP) which is defined analogously to the seating of N customers who sequentially join tables in a Chinese restaurant. Here, the probability of the \(n^{th}\) customer joining an existing table is proportional to the table size while the probability the customer forms a new table is always proportional to parameter \(\alpha \), \(\forall n\in {1,2,..,N}\). This results in a distribution over the set of all partitions of integers 1, 2, .., N. More formally, the distribution can be represented using the following probability function:
where \(z_i\) is the cluster assignment of the \(i^{th}\) data point, \(n_k\) is the size of the \(k^{th}\) cluster, \(\alpha >0\) is the concentration parameter. Large \(\alpha \) values correspond to an increased tendency of data points to form new clustersFootnote 3.
3 Integrated Clustering and Anomaly Detection (INCAD)
The proposed INCAD model’s prior is essentially a modification of a Chinese Restaurant Process (CRP). The seating of a customer at the Chinese restaurant is dependent on an evaluation by a gatekeeper. The gatekeeper decides the ability of the customer to start a new table based on the customer’s features relative to existing patrons. If the gatekeeper believes the customer stands out, the customer is assigned a higher concentration parameter \( \alpha \) that bumps up their chances of getting a new table. The model was inspired by the work of Blei and Frazier [5] in their distance dependent CRP models. The integrated INCAD model defines a flexible concentration parameter \(\alpha \) for each data point. The probabilities are given by (Fig. 1):
where \(z,n,n_k\) are described earlier and \(\alpha _2=f(\alpha |x_n,\mathbf x ,\mathbf z )\) is a function of a base concentration parameter \(\alpha \). The function is chosen such that it is monotonic in \(p(x_n)\) where, p is the probability of \(x_i\) being in the tail of the mixture distribution. In this paper, f is given by,
where, \(\alpha ^*=\frac{100}{1-p_n}\) and
Traditional CRP not only mimics the partition structure of DPMM but also allows flexibility in partitioning differently for different data sets. However, CRP lacks the ability to distinguish anomalies from non-anomalous points. To set differential treatment for anomalous data, the CRP concentration parameter \(\alpha \) is modified to be sensitive to anomalous instances and nudge them to form individual clusters. The tail points are clustered using this updated concentration parameter \(\alpha _2\) which is designed to increase with increasing probability of a point being anomalous. This ensures that the probability of tail points forming individual clusters increases as they are further away from the rest of the data.
4 Choice of the Extreme Value Distribution
The choice for \(G^{EV}_0\), the base distribution for the anomalous cluster parameters, is the key for identifying anomalous instances. By choosing \(G^{EV}_0\) as the extreme value counterpart of \(G_0\), the model ensures that the anomalous clusters are statistically “far” from the normal clusters. However, as discussed earlier, not all distributions have a well-defined EVD counterpart. We first describe the inference strategy for the case where \(G^{EV}_0\) exists. We then adapt this strategy for the scenario where \(G^{EV}\) is not available.
4.1 Inference When \(G^{EV}_0\) Is Available
Inference for traditional DPMMs is computationally expensive, even when conjugate priors are used. MCMC based algorithms [24] and variational techniques [6] have been typically used for inference. Here we adopt the Gibbs sampling based MCMC method for conjugate priors (Algorithm 1 [24]). This algorithm can be thought of as an extension of a Gibbs sampling-based method for a fixed mixture model, such that the cluster indicator \(z_i\) can take values between 1 and \(K+1\), where K is the current number of clusters.
Gibbs Sampling. Though INCAD is based on DPMM, the model has an additional anomaly classification variable \(a_.\) that determines the estimation of the rest of the parameters. In the Gibbs sampling algorithm for INCAD, the data points \(\{x_i\}_{i=1}^N\) are observed and the number of clusters K, cluster indicators \(\{z_i\}_{i=1}^N\) and anomaly classifiers \(\{a_i\}_{i=1}^N\) are latent. Using Markov property and Bayes rule, we derive the posterior probabilities for \(z_i\ \forall i\in {1,2,\dots , N}\) as:
where \(\alpha ^*=\frac{100}{1- p_i}\), \(p_i\) is the probability of \(x_i\) being anomalous and K is the number of non-empty clusters. Thus, the posterior probability of forming a new cluster denoted by \(K+1\) is given by:
Similarly, the parameters for clusters \(k\in \{1,2,\dots ,K\}\) are sampled from:
where \(\varvec{x}_k=\{x_i|z_i=k\}\) is the set of all points in cluster k. Finally, to identify the anomaly classification of the data, the posterior probability of \(a_i\) is given by:
Similarly,
4.2 Inference When \(G^{EV}_0\) Is Not Available
The estimation of \(G^{EV}_0\) is required on two occasions. Firstly, while sampling the parameters of anomalous clusters when generating the data and estimating the posterior distribution. Secondly, to compute the probability of the point being anomalous when estimating the updated concentration parameter \(\alpha _2\). When estimating \(G_0^{EV}\) is not feasible, the following two modifications to the original model are proposed:
-
1.
Since an approximate \(G_0^{EV}\) distribution need not belong to the family of conjugate priors of F, we need a different approach to sample the parameters for anomalous clusters. Thus, we assume \(\theta ^a\sim G_0\) for sampling the parameters \(\{\theta ^a_k\}_{k=1}^\infty \) for anomalous clusters.
-
2.
To estimate the probability of a point being anomalous, use the approach described by Clifton et al. [9].
The pseudo-Gibbs sampling algorithm, presented in Algorithm 2, has been designed to address the cases when \(G^{EV}_0\) is not available. For such cases, the modified f is given by,
where \(ev\_prop\) determines the effect of a anomalous behavior on the concentration parameterFootnote 4. \(ev\_prop\) is solely used to speed up the convergence in the Gibbs sampling. Since the estimation of the \(G^{EV}\) distribution is not always possible, an alternate/pseudo Gibbs sampling algorithm has been presented in Algorithm 2.


4.3 Exchangeability
A model is said to be exchangeable when for any permutation S of \(\{1,2,...,n\}\), \(P(x_1,x_2,...x_n)=P(x_{S(1)},x_{S(2)},...x_{S(n)})\). Looking at the joint probability of the cluster assignments for the integrated model, we know,
Without loss of generality, let us assume there are K clusters. Let, for any \(k<K\), the joint probability of all the points in cluster k be given by
where \(N_k\) is the size of the cluster k, \(I_{k,i}\) is the index of the \(i^{th}\) instance joining the \(k^{th}\) cluster and \(p_{k,i}=p_{I_{k,i}}\). Thus, the joint probability for complete data is then given by
which is dependent on the order of the data. This shows that the model is not exchangeable unless \(\alpha =\alpha ^*\) or \(p_{k,n_k}=0\) or \(p_{k,n_k}=1\). These conditions effectively reduce the prior distribution to a traditional CRP model. Hence, it can be concluded that the INCAD model cannot be modified to be exchangeable.
Non-exchangeable Models in Streaming Settings. Though exchangeability is a reasonable assumption in many situations, the evolution of behavior over time is not captured by traditional exchangeable models. In particular for streaming settings, using non-exchangeable models captures the effect of the order of the data. In such settings, instances that are a result of new evolving behavior should be monitored (as anomalous) until the behavior becomes relatively prevalent. Similarly, relapse of outdated behaviors (either normal or anomalous) should also be subjected to critical evaluation due to extended lag observed between similar instances. Such order driven dependency can be well captured in non-exchangeable models making them ideal for studying streaming data.
4.4 Adaptability to Sequential Data
One of the best outcomes of having a non-exchangeable prior is its ability to capture the drift or evolution in the behavior(s) either locally or globally or a mixture of both. INCAD model serves as a perfect platform to detect these changes and delivers an adaptable classification and clustering. The model has a straightforward extension to sequential settings where the model evolves with every incoming instance. Rather than updating the model for entire data with each new update, the streaming INCAD model re-evaluates only the tail instances. This enables the model to identify the following evaluations in the data (Fig. 3):
-
1.
New trends that are classified as anomalous but can eventually grow to become normal.
-
2.
Previously normal behaviors that have vanished over time but have relapsed and hence become anomalous (eg. disease relapse post complete recovery).
The Gibbs sampling algorithm for the streaming INCAD model is given in Algorithm 3.

5 Results
In this section, we evaluate the proposed model using benchmark streaming datasets from NUMENTA. The streaming INCAD model’s anomaly detection is compared with SPOT algorithm developed by Siffer et al. [27]. The evolution of clustering and anomaly classification using the streaming INCAD model is visualized using simulated dataset. In addition, the effect of batch vs stream proportion on quality of performance is presented. For Gibbs sampling initialization, the data was assumed to follow a mixture of MVN distributions. 10 clusters were initially assumed with the same initial parameters. The cluster means were set to the sample mean and the covariance matrix as a multiple of the sample covariance matrix, using a scalar constant. The concentration parameter \(\alpha \) was always set to 1.
5.1 Simulated Data
For visualizing the model’s clustering and anomaly detection, a 2-dimensional data set of size 400 with 4 normal clusters and 23 anomalies sampled from a normal distribution centered at (0,0) and a large variance was generated for model evaluation. Small clusters and data outliers are regarded as true anomalies. Data from the first 3 normal clusters (300 data points) were first modeled using non-streaming INCAD. The final cluster and the anomalies were then used as updates for the streaming INCAD model. The evolution in the anomaly classification is presented in Fig. 2.
NUMENTA traffic data: (from left to right) Anomaly detection and clustering using streaming INCAD and anomaly detection using SPOT [27]
Anomaly detection on NUMENTA AWS cloud watch data using streaming INCAD (left) and SPOT [27] (right)
5.2 Model Evaluation on NUMENTA Data
Two data sets from NUMENTA [23] namely the real traffic data and the AWS cloud watch data were used as benchmarks for the streaming anomaly detection. The streaming INCAD model was compared with the SPOT algorithm developed by Siffer et al. [27]. Unlike SPOT algorithm, the streaming INCAD is capable of modeling data with more than one feature. Thus, the data instance, as well as the time of the instance, were used to develop the anomaly detection model. Since the true anomaly labels are not available, the model’s performance with respect to SPOT algorithm was evaluated based on the ability to identify erratic behaviors. The model results on the datasets using streaming INCAD and SPOT have been presented in Figs. 4 and 5.
6 Sensitivity to Batch Proportion
Streaming INCAD model re-evaluates the tail data at each update, the dependency of the model’s performance on the current state must be evaluated. Thus, various metrics were used to study the model’s sensitivity to the initial batch proportion. Figure 6 shows the effect of batch proportion on computational time and performance of anomaly detection. The simulated data defined in Sect. 5.1 was used for the sensitivity analysis. It can be seen that the computational time is optimal for \(25\%\) of data used in to run the non-streaming INCAD model. As anticipated, precision, accuracy, specificity, and f-measure for the anomaly detection were observed to plateau after a significant increase.
7 Conclusion and Future Work
A detailed description of the INCAD algorithm and the motivation behind it has been presented in this paper. The model’s definition of an anomaly and its adaptable interpretation sets the model apart from the rest of the clustering based anomaly detection algorithms. While past anomaly detection methods lack the ability to simultaneously perform clustering and anomaly detection or to the INCAD model not only defines a new standard for such integrated methods but also breaks into the domain of streaming anomaly detection. The model’s ability to identify anomalies and cluster data using a completely data-driven strategy permits it to capture the evolution of multiple behaviors and patterns within the data.
Additionally, the INCAD model can be smoothly transformed into a streaming setting. The model is seen to be robust to the initial proportion of the data subset that was evaluated using the non-streaming INCAD model. Moreover, this sets up the model to be extended to distribution families beyond multivariate normal. Though one of the key shortcomings of the model is its computational complexity in Gibbs sampling in the DPMM clusters, the use of faster methods such as variational inference might prove to be useful.
Notes
- 1.
Non-anomalous behavior is described as “normal” behavior. Should not be confused with Gaussian/Normal distribution.
- 2.
Clustering and defining “normal/traditional” behavior in presence of anomalies develop in skewed and inconsistent results.
- 3.
Our modified model targets this aspect of concentration parameter to generate the desired simultaneous clustering and anomaly detection.
- 4.
It can be seen that when the data point \(x_n\) has extreme or rare features differentiating it from all existing clusters, the corresponding density \(f_y(x_n)\) decreases. This makes it a left tail point in the distribution \(G_y\). The farther away it is in the tail, the lower the probability of its \(\delta \)-nbd being in the tail and hence a higher \(f(\alpha |x_n,\mathbf x ,\mathbf z )\).
References
Al-Behadili, H., Grumpe, A., Migdadi, L., Wöhler, C.: Semi-supervised learning using incremental support vector machine and extreme value theory in gesture data. In: Computer Modelling and Simulation (UKSim), pp. 184–189. IEEE (2016)
Amer, M., Goldstein, M.: Nearest-neighbor and clustering based anomaly detection algorithms for rapidminer. In: Proceedings of the 3rd RCOMM 2012, pp. 1–12 (2012)
Antoniak, C.E.: Mixtures of Dirichlet processes with applications to Bayesian nonparametric problems. Ann. Stat. 2(6), 1152–1174 (1974)
Bay, S.D., Schwabacher, M.: Mining distance-based outliers in near linear time with randomization and a simple pruning rule. In: Proceedings of the 9th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp. 29–38. ACM (2003)
Blei, D.M., Frazier, P.I.: Distance dependent Chinese restaurant processes. In: ICML, pp. 87–94 (2010)
Blei, D.M., Jordan, M.I.: Variational methods for the Dirichlet process. In: Proceedings of the Twenty-first International Conference on Machine Learning, p. 12 (2004)
Chan, P.K., Mahoney, M.V., Arshad, M.H.: A machine learning approach to anomaly detection. Technical report (2003)
Chandola, V., Banerjee, A., Kumar, V.: Anomaly detection: a survey. ACM Comput. Surv. (CSUR) 41(3), 15 (2009)
Clifton, D.A., Clifton, L., Hugueny, S., Tarassenko, L.: Extending the generalised pareto distribution for novelty detection in high-dimensional spaces. J. Sig. Process. Syst. 74(3), 323–339 (2014)
Eskin, E., Arnold, A., Prerau, M., Portnoy, L., Stolfo, S.: A geometric framework for unsupervised anomaly detection. In: Barbará, D., Jajodia, S. (eds.) Applications of Data Mining in Computer Security. ADIS, vol. 6, pp. 77–101. Springer, Heidelberg (2002). https://doi.org/10.1007/978-1-4615-0953-0_4
French, J., Kokoszka, P., Stoev, S., Hall, L.: Quantifying the risk of heat waves using extreme value theory and spatio-temporal functional data. Comput. Stat. Data Anal. 131, 176–193 (2019)
Fu, Z., Hu, W., Tan, T.: Similarity based vehicle trajectory clustering and anomaly detection. In: ICIP, vol. 2, p. II–602. IEEE (2005)
Gama, J., Žliobaitė, I., Bifet, A., Pechenizkiy, M., Bouchachia, A.: A survey on concept drift adaptation. ACM Comput. Surv. (CSUR) 46(4), 44 (2014)
Garcia-Teodoro, P., Diaz-Verdejo, J., Maciá-Fernández, G., Vázquez, E.: Anomaly-based network intrusion detection: techniques, systems and challenges. Comput. Secur. 28(1–2), 18–28 (2009)
Goldstein, M., Uchida, S.: A comparative evaluation of unsupervised anomaly detection algorithms for multivariate data. PloS One 11(4), e0152173 (2016)
Görnitz, N., Kloft, M., Rieck, K., Brefeld, U.: Toward supervised anomaly detection. J. Artif. Intell. Res. 46, 235–262 (2013)
Guggilam, S., Arshad Zaidi, S.M., Chandola, V., Patra, A.: Bayesian anomaly detection using extreme value theory. arXiv preprint arXiv:1905.12150 (2019)
He, Z., Xiaofei, X., Deng, S.: Discovering cluster-based local outliers. Pattern Recogn. Lett. 24(9–10), 1641–1650 (2003)
Hjort, N., Holmes, C., Mueller, P., Walker, S.: Bayesian Nonparametrics: Principles and Practice. Cambridge University Press, Cambridge (2010)
Jiang, J., Castner, J., Hewner, S., Chandola, V.: Improving quality of care using data science driven methods. In: UNYTE Scientific Session - Hitting the Accelerator: Health Research Innovation Through Data Science (2015)
Jiang, N., Gruenwald, L.: Research issues in data stream association rule mining. ACM Sigmod Rec. 35(1), 14–19 (2006)
Kruegel, C., Vigna, G.: Anomaly detection of web-based attacks. In: Proceedings of the 10th ACM Conference on Computer and Communications Security, pp. 251–261 (2003)
Lavin, A., Ahmad, S.: Evaluating real-time anomaly detection algorithms-the numenta anomaly benchmark. In: 2015 IEEE 14th International Conference on Machine Learning and Applications (ICMLA), pp. 38–44. IEEE (2015)
Neal, R.M.: Markov chain sampling methods for Dirichlet process mixture models. J. Comput. Graph. Stat. 9(2), 249–265 (2000)
Rasmussen, C.E.: The infinite Gaussian mixture model. In: Advances in Neural Information Processing Systems, vol. 12, pp. 554–560. MIT Press (2000)
Shotwell, M.S., Slate, E.H.: Bayesian outlier detection with Dirichlet process mixtures. Bayesian Anal. 6(4), 665–690 (2011)
Siffer, A., Fouque, P.-A., Termier, A., Largouet, C.: Anomaly detection in streams with extreme value theory. In: Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp. 1067–1075 (2017). ISBN 978-1-4503-4887-4
Teh, Y.W., Jordan, M.I., Beal, M.J., Blei, D.M.: Hierarchical Dirichlet processes. J. Am. Stat. Assoc. 101(476), 1566–1581 (2006)
Varadarajan, J., Subramanian, R., Ahuja, N., Moulin, P., Odobez, J.M.: Active online anomaly detection using Dirichlet process mixture model and Gaussian process classification. In: 2017 IEEE WACV, pp. 615–623 (2017)
Acknowledgements
The authors would like to acknowledge University at Buffalo Center for Computational Research (http://www.buffalo.edu/ccr.html) for its computing resources that were made available for conducting the research reported in this paper. Financial support of the National Science Foundation Grant numbers NSF/OAC 1339765 and NSF/DMS 1621853 is acknowledged.
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Guggilam, S., Zaidi, S.M.A., Chandola, V., Patra, A.K. (2019). Integrated Clustering and Anomaly Detection (INCAD) for Streaming Data. In: Rodrigues, J., et al. Computational Science – ICCS 2019. ICCS 2019. Lecture Notes in Computer Science(), vol 11539. Springer, Cham. https://doi.org/10.1007/978-3-030-22747-0_4
Download citation
DOI: https://doi.org/10.1007/978-3-030-22747-0_4
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-22746-3
Online ISBN: 978-3-030-22747-0
eBook Packages: Computer ScienceComputer Science (R0)



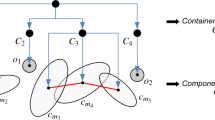



 and
and
 respectively. Note the evolution of the classification of top right cluster from anomalous to normal with incoming data
respectively. Note the evolution of the classification of top right cluster from anomalous to normal with incoming data


