Recovery of the Interface Velocity for the Incompressible Flow in Enhanced Velocity Mixed Finite Element Method

Abstract

The velocity, coupling term in the flow and transport problems, is important in the accurate numerical simulation or in the posteriori error analysis for adaptive mesh refinement. We consider Enhanced Velocity Mixed Finite Element Method (EVMFEM) for the incompressible Darcy flow. In this paper, our aim is to study the improvement of velocity at interface to achieve the better approximation of velocity between subdomains. We propose the reconstruction of velocity at interface by using the post-processed pressure. Numerical results at the interface show improvement on convergence rate.

1 Introduction

The numerical reservoir simulations have been utilized in many subsurface applications such as groundwater remediation, reservoir well evaluation, and contaminate transport problems. For such applications, it is common to deal with the flow and transport problem. The main component or coupling term of the flow and transport systems is the velocity and its accuracy the mostly achieved by employing classical mixed finite element system. Due to the heterogeneity of porous media multiphysics problems could be categorized systematically in which one physical phenomena influences within a subdomain and another physical phenomena dominates within another subdomain. Such solutions are coupled through continuity of normal flux at interface, shared region between differently discretized subdomains. To deal with these problems there are the well-known methods such as Multiscale Mortar and Enhanced Velocity schemes that are established in various applications. Recently, a novel adaptive method was studied in subsurface applications [2,3,4, 14] using Enhanced Velocity scheme. The main idea is here to utilize the EVMFEM as domain decomposition method to couple different discretized subdomains with more accurate upscaled subsurface parameters.

In the simulation of flow with adaptivity, the results obtained in [9] suggest that pressure values could be interpolated using neighboring elements values to approximate auxiliary pressure values within provided elements. Selection of interpolants is based on convex combinations of vertical and horizontal oriented pressure values.

In related reference [6], it was studied that the interface error of solution between subdomains for different numerical methods including Mortar Multiscale MixedFEM which provided better approximation for second-order elliptic problems. One of reasons is the iterative procedure in the mortar scheme that is a key in coupling two subdomains physics. According to author in [6] mortar scheme is general method in coupling for practical multiphysics problems. On the other hand, the efficient Enhanced Velocity scheme has not been investigated from the point of view of the improvement solution including velocity at interface in the previous studies.

The challenge here is to construct the velocity approximation of EVMFEM and specifically at interface to have a better velocity between subdomains that leads accurate approximation in the flow and transport problems. In [17], a priori error analysis states that the global error is

$$\begin{aligned} ||\mathbf {u}-\mathbf {u}_h||_{\varOmega } \le C \left( ||p||_{1, \infty , \varOmega ^*} + ||\mathbf {u}||_{1, \varOmega } h^{1/2}\right) h^{1/2} \end{aligned}$$

(1)

and away from the interface $\varGamma$ the velocity error convergence rate is better, since

$$\begin{aligned} ||\mathbf {u}-\mathbf {u}_h||_{\varOmega ^{'}} \le C_{\varepsilon } \left( ||p||_{1, \infty , \varOmega ^*} + ||\mathbf {u}||_{1, \varOmega } \right) h^{r-\varepsilon } \end{aligned}$$

(2)

where $\varepsilon > 0$, $r=1$ if $d=2$ and $r=5/6$ if $d=3$, and $\varOmega ^{'}_i$ is compactly contained in $\varOmega _i$, $\varOmega ^{'} = \bigcup _{i=1}^{N_b} \varOmega ^{'}_i$. This implies that the discrete velocity should be approximated more precise near interface region $\varOmega ^*$. On the question of pressure approximation, the convergence rate of pressure approximation is , if $d=2$, and , if $d=3$ [15, 17]. If one compares the error of velocity (1) and pressure approximation these results indicate that the velocity convergence rate is not strong as pressure in $\varOmega$. Similar a priori error result was shown in [4] for transient problems. Nevertheless, there are still problems including the velocity approximation at the interface to be addressed.

In this paper, we introduce the way to improve velocity accuracy at interface in the Enhanced Velocity MFEM for incompressible flow using the post-processed pressure from [5]. This improvement is important in flow coupled with transport problems and it also can be a good candidate for a recovery-based error estimate evaluation. In a recent work [2], a posteriori error analysis was shown for the incompressible flow problems without recovery of velocity.

The remaining part of the paper proceeds as follows. Section 2 of this paper will describe model formulation with different view of EVMFEM. In Sect. 3, the proposed numerical method will be discussed. Section 4 shows numerical results. Section 5 summarizes the results of this work and draws conclusions.

2 Model Formulation

We start by giving the model formulation for the incompressible single-phase flow. For the convenience of reader we repeat the relevant material of domain decomposition method, discrete formulation with Enhanced Velocity from [17]. We next describe the proposed different view of Enhanced Velocity Discrete Scheme with projection operator.

2.1 Governing Equations of the Incompressible Flow

We consider the incompressible single-phase flow model for pressure p and the Darcy velocity $\mathbf u$:

$$\begin{aligned} \mathbf u&=-\mathbf {K} \nabla p \qquad \text {in} \quad \varOmega , \end{aligned}$$

(3)

$$\begin{aligned} \nabla \cdot \mathbf u&=f \qquad \qquad \text {in} \quad \varOmega , \end{aligned}$$

(4)

$$\begin{aligned} p&=g \qquad \qquad \text {on} \quad \partial \varOmega , \end{aligned}$$

(5)

where $\varOmega \in \mathbb {R}^d(d=2$ or 3) is multiblock domain, $f \in L^2(\varOmega )$ and $\mathbf {K}$ is a symmetric, uniformly positive definite tensor representing the permeability divided by the viscosity with $L^{\infty }(\varOmega )$ components, for some $0<k_{min}<k_{max} < \infty$ $k_{min} \xi ^T \xi \le \xi ^T \mathbf {K}(x) \xi \le k_{max} \xi ^T \xi \;, \forall x \in \varOmega \;, \forall \xi \in \mathbb {R}^d$, under the Dirichlet boundary condition.

A weak variational form of the fluid flow problem (3)–(5) is to find a pair $\mathbf u \in \mathbf {V}$, $p \in W$

$$\begin{aligned} \left( \mathbf {K}^{-1}{} \mathbf u , \mathbf {v} \right) -\left( p, \nabla \cdot \mathbf {v} \right)&= - \langle g, \mathbf {v} \cdot {\varvec{\nu }} \rangle _{\partial \varOmega } \qquad&\forall \mathbf {v} \in \mathbf V , \end{aligned}$$

(6)

$$\begin{aligned} \left( \nabla \cdot \mathbf u , w \right)&=\left( f,w\right) \qquad \qquad&\forall w \in W, \end{aligned}$$

(7)

where ${\varvec{\nu }}$ is the outward unit normal to $\partial \varOmega$, $\mathbf V$ is $H(\mathrm{div}; \varOmega ) =\{\mathbf {v} \in \left( L^2(\varOmega )\right) ^d: \nabla \cdot \mathbf {v} \in L^2(\varOmega )\}$ and equipped with the norm $||\mathbf {v} ||_V=\left( ||\mathbf {v} ||^2+||\nabla \cdot \mathbf {v} ||^2\right) ^{\frac{1}{2}}$ and the pressure the space is $W =L^2(\varOmega )$ and the corresponding norm $||w||_W=||w||.$.

Discrete Formulation. Let $\varOmega$ be decomposed into non-overlapping small subdomains, see Fig. 1. We consider

$$\begin{aligned} \varOmega = \left( \bigcup _{i=1}^{N_b} \bar{\varOmega }_i \right) ^{o}, \; \varGamma _{i,j}=\partial \varOmega _i \bigcap \partial \varOmega _j, \; \varGamma = \left( \bigcup ^{N_b}_{i,j=1} \bar{\varGamma }_{i,j} \right) ^{o}, \; \varGamma _i = \varOmega _i \bigcap \varGamma =\partial \varOmega _j \setminus \partial \varOmega . \end{aligned}$$

This implies that the domain is divided into $N_b$ subdomains, the interface between $i^{th}$ and $j^{th}$ subdomains($i \ne j$), the interior subdomain interface for $i^{th}$ subdomain and union of all such interfaces, respectively. Let be a conforming, quasi-uniform and rectangular partition of $\varOmega _i$, $1 \le i \le N_b$, with maximal element diameter $h_i$. We then set and denote h the maximal element diameter in ; note that can be nonmatching as neighboring meshes and $\mathcal {T}_{h,j}$ need not match on $\varGamma _{i,j}$. We assume that all mesh families are shape-regular.

Fig. 1.

Illustration of a domain $\varOmega$ with subdomains $\varOmega _i$ and non-matching mesh discretization .

In Enhanced Velocity scheme setting, the velocity basis functions are based on the traditional Raviart-Thomas spaces of lowest order on rectangles for $d=2$ and bricks for $d=3$. The $RT_0$ spaces are defined for any element by the following spaces:

$$\begin{aligned}&\mathbf {V}_h(T)=\{\mathbf {v}=(v_1,v_2) \; \text {or} \; \mathbf {v}=(v_1,v_2,v_3): v_l=\alpha _l+\beta _l x_l: \alpha _l, \beta _l \in \mathbb {R};l=1,..d \}, \\&W_h(T) =\{w=\text {constant}\}. \end{aligned}$$

The pressure finite element approximation space on $\varOmega$ is taken to be as In addition, a vector function in $\mathbf {V}_h$ can be determined uniquely by its normal components $\mathbf {v} \cdot \nu$ at midpoints of edges (in 2D) or face (in 3D) of T. The degrees of freedom of $\mathbf {v} \in \mathbf {V}_h(T)$ were created by these normal components. The degree of freedom for a pressure function $p \in W_h(T)$ is at center of T and piecewise constant inside of T. Let us formulate $RT_0$ space on each subdomain $\varOmega _i$ for partition

and then

$$\begin{aligned} \mathbf {V}_{h}= \bigoplus _{i=1}^n \mathbf {V}_{h,i}. \end{aligned}$$

Although the normal components of vectors in $\mathbf {V}_h$ are continuous between elements within each subdomains, the reader may see $\mathbf {V}_h$ is not a subspace of $H(\mathrm{div}; \varOmega )$, because the normal components of the velocity vector may not match on subdomain interface $\varGamma$. Let us define as the intersection of the traces of and , and let . We require that and $\mathcal {T}_{h,j}$ need to align with the coordinate axes. Fluxes are constructed to match on each element . We consider any element that shares at least one edge with the interface $\varGamma$, i.e., $T\, \cap \,\varGamma _{i,j} \ne \emptyset$, where $1 \le i,j \le N_b$ and $i \ne j$. Then newly defined interface grid introduces a partition of the edge of T. This partition may be extended into the element T as shown in Fig. 2.

Fig. 2.

Degrees of freedom for the Enhanced Velocity space.

Such partitioning helps to construct fine-scale velocities that is in $H(\,\mathbf{div }, \varOmega )$. So we represent a basis function $\mathbf {v}_{T_k}$ in the $\mathbf {V}_h(T_k)$ space ($RT_0$) for given $T_k$ with the following way:

$$\begin{aligned} \mathbf {v}_{T_k} \cdot \nu = {\left\{ \begin{array}{ll} 1, \qquad &{}\mathrm{on} \; e_k \\ 0, \qquad &{}\mathrm{other} \, \mathrm{edges} \end{array}\right. } \end{aligned}$$

i.e. a normal component $\mathbf {v}_{T_k} \cdot \nu$ equal to one on $e_k$ and zero on all other edges(faces) of $T_k$. Let $\mathbf {V}^{\varGamma }_h$ be span of all such basis functions defined on all sub-elements induced the interface discretization . Thus, the enhanced velocity space $\mathbf {V}^*_h$ is taken to be as

$$\begin{aligned} \mathbf {V}^*_{h}= \bigoplus _{i=1}^n \mathbf {V}^0_{h,i} \bigoplus \mathbf {V}^{\varGamma }_{h} \cap H(\mathrm{div}; \varOmega ), \end{aligned}$$

where $\mathbf {V}^0_{h,i} = \{ \mathbf {v} \in \mathbf {V}_{h,i} : \mathbf {v} \cdot \nu =0 \text { on } \varGamma _{i}\}$ is the subspace of $\mathbf {V}_{h,i}$. The finer grid velocity allows to velocity approximation on the interface and then form the $H(\mathrm{div}, \varOmega )$ conforming velocity space. Some difficulties arise, however, in analysis of method and implementation of robust linear solver for such modification of $RT_0$ velocity space at all elements, which are adjacent to the interface $\varGamma$. We now formulate the discrete variational form of Eqs. (3)–(5) as: Find $\mathbf {u}_h \in \mathbf {V}^*_{h}$ and $p_h \in W_h$ such that

$$\begin{aligned} \left( K^{-1}{} \mathbf u _h, \mathbf {v} \right)&=\left( p_h, \nabla \cdot \mathbf {v} \right) - \langle g, \mathbf {v} \cdot {\varvec{\nu }} \rangle _{\partial \varOmega } \qquad&\forall \mathbf {v} \in \mathbf V ^*_h, \end{aligned}$$

(8)

$$\begin{aligned} \left( \nabla \cdot \mathbf u _h, w \right)&=\left( f,w\right) \qquad \qquad&\forall w \in W_h. \end{aligned}$$

(9)

2.2 A Different View of the EVMFEM in the Discrete Variational Formulation

We consider the discrete variational form that is given in (8)–(9). Find $\mathbf {u}_h \in \mathbf {V}^*_{h}$ and $p_h \in W_h$ such that

$$\begin{aligned} \left( K^{-1}{} \mathbf u _h, \mathbf {v} \right) _{M, T}&=\left( p_h, \nabla \cdot \mathbf {v} \right) - \langle g, \mathbf {v} \cdot {\varvec{\nu }} \rangle _{\partial \varOmega } \qquad&\forall \mathbf {v} \in \mathbf V ^*_h, \end{aligned}$$

(10)

$$\begin{aligned} \left( \nabla \cdot \mathbf u _h, w \right)&=\left( f,w\right) \qquad \qquad&\forall w \in W_h. \end{aligned}$$

(11)

We exploit the approximation inner product and for $\mathbf {v}, \mathbf {q} \in \mathbb {R}^d$

$$\begin{aligned} \left( \mathbf {v}, \mathbf {q} \right) _{M,T} = {\left\{ \begin{array}{ll} \left( v_{x}, q_y \right) _{T_x, M_y} + \left( v_{y}, q_y \right) _{M_x,T_y} \quad &{}\text {if } \text {d }=2, \\ \left( v_{x}, q_y \right) _{T_x, M_y, M_z} + \left( v_{y}, q_y \right) _{M_x, T_y, M_z}+\left( v_{z}, q_z \right) _{M_x,M_y,T_z} \quad &{}\text {if } \text {d}=3. \end{array}\right. } \end{aligned}$$

where $T_{(\cdot )}$ and $M_{(\cdot )}$ denote the trapezoidal and midpoint quadrature rules in each coordinate direction respectively, see [13]. In particularly, we take $\mathbf {v}=\mathbf {K}^{-1}\mathbf {u}_h$ and $\mathbf {q}=\mathbf {v}$. It is easily proven that the finite variational form (10)–(11) is equivalent to finding $\mathbf {u}_h \in \mathbf {V}^*_h$, $p_h \in W_h$, $1 \le i \le N_b$, such that

$$\begin{aligned} \left( \mathbf {K}^{-1}\mathbf {u}_h, \mathbf {v} \right) _{\varOmega _i, M, T} - \left( p_h, \nabla \cdot \mathbf {v} \right) _{\varOmega _i}&=- \langle g, \mathbf {v} \cdot {\varvec{\nu }} \rangle _{\partial \varOmega _i \cap \varGamma _D} \quad&\forall \mathbf {v} \in \mathbf {V}^0_{h,i}, \end{aligned}$$

(12)

$$\begin{aligned} \left( \nabla \cdot \mathbf {u}_h, w \right) _{\varOmega _i}&=\left( f,w\right) _{\varOmega _i} \quad \qquad&\forall w \in W_{h,i}, \end{aligned}$$

(13)

$$\begin{aligned} \sum _{i=1}^{N_b} \{\left( \mathbf {K}^{-1}\mathbf {u}_h, \mathbf {v}^{EV}\right) _{\varOmega _i, M, T}-\left( p_h, \nabla \cdot \mathbf {v}^{EV}\right) _{\varOmega _i}\}&= 0 \quad&\forall \mathbf {v}^{EV} \in \mathbf V ^{\varGamma }. \end{aligned}$$

(14)

We note that the discrete variational formulation was similarly proposed in [10] with conjugate gradient method. We want to share the idea for small number of discretization elements that can be applied for a large number of elements. Thus, we consider two subdomains, i.e., $\varOmega =\bar{\varOmega }_1 \cup \bar{\varOmega }_2$ and $\varGamma$ is the interface. Then

$$\begin{aligned} \mathbf {V}^*_{h}=\left( \mathbf {V}^0_{h,1} \oplus \mathbf {V}^0_{h,2} \oplus \mathbf {V}^{\varGamma }_{h} \right) . \end{aligned}$$

Consider equations

$$\begin{aligned} \left( \mathbf {K}^{-1}{} \mathbf u _h, \mathbf {v} \right) _{M, T}&=\left( p_h, \nabla \cdot \mathbf {v} \right) \qquad&\forall \mathbf {v} \in \mathbf {V}^{\varGamma }_{h}. \end{aligned}$$

(15)

Fig. 3.

The spatial domain and illustration of Enhanced Velocity values on the interface.

These allow us to express $\mathbf {u}^{\varGamma }_h$ in terms of the one-element layers along $\varGamma$, it is shown in Fig. 3:

$$\begin{aligned} \mathbf {u}^{\varGamma }_h=A_1p_L+A_2p_R. \end{aligned}$$

(16)

Now we consider each subdomain separately with ghost layers. We define $L_2$-projection of Enhanced Velocity space at interface $\varGamma _{i,j}$ to each subdomain space $\partial \varOmega _i \cap \varGamma _{i,j}$ such that .

We denote

In subdomain $\varOmega _i$, we define $p^e_i$ in the following way

$$\begin{aligned} \left( \mathbf {K}^{-1}\widetilde{\mathbf {u}}_h, \mathbf {v} \right) _{M, T, \varOmega _i}&=\left( p_h, \nabla \cdot \mathbf {v} \right) _{\varOmega _i}- \langle p^{e}_{i}, \mathbf {v} \cdot {\varvec{\nu }} \rangle _{\varGamma } \quad&\forall \mathbf {v} \in \mathbf {V}^{\varGamma }_{h, i} \text { s.t.} \mathbf {v}\cdot {\varvec{\nu }} =0 \text { on } \partial \varOmega ^*_i, \end{aligned}$$

(17)

where $\varOmega ^*$ is union of all elements T that shares edge (2D) or face (3D) with $\varGamma _i$ and $p^e_i$ ghost layers pressure values, and . Such ghost layers are depicted in the Fig. 4. Then, for $i=L$, we have

$$\begin{aligned} \mathbf u ^{\varGamma }_{h,L}=A^L_1 p_L +A^L_2 p^e_L. \end{aligned}$$

(18)

Fig. 4.

Example of left ($\varOmega _L$) and right ($\varOmega _R$) domains with ghost layers.

We compare Eq. (18) and the pressure Eq. (16) which is projected to $\varOmega _i$:

(19)

Since , we have the following

(20)

$A^L_2$ is non-singular and diagonal matrix, since $\mathbf {K}$ is SPD.

(21)

Similarly, we can obtain

(22)

In non-linear problems including slightly compressible flow or multiphase flow in heterogeneous porous media, this approach could be applied analogously by taking into account ghost layers values arising from $e_i$ in each Newton iteration. So during Block Jacobi iteration variables $p^{e,k-1}_{L}$, $p^{e, k-1}_{R}$ is computed by utilizing given $p^{k-1}_{L}$, $p^{k-1}_{R}$ and then solve decoupled subdomain problems with Dirichlet boundary conditions $p^{e, k-1}_{i}$, $i=L,R$ to find $u^{k},p^{k}$.

3 Methods

We use the postprocessing procedure associated to pressure and velocity. We first apply locally postprocessing algorithm for given pressure $p_h$ and velocity $\mathbf {u}_h$ which was previously proposed in [5] and then Oswald interpolation operator [1, 11, 12, 16] to have better pressure values. At the interface, we use two-point flux computation method in order to have better approximation of pressure. As a result, the Enhanced Velocity scheme solution of velocity can be improved by using a post-processed pressure. The key idea is illustrated in Fig. 5 for resulting approximation of EV scheme that is shown in Fig. 3.

The velocity at the edge or face is computed by using pressure values between subdomains $\varOmega _i$ and $\varOmega _j$. To be specific, $p_h \in \varOmega ^*$ is required in the original velocity for constructing in Enhanced Velocity MFEM. However, the post-processed pressure leads to the improved velocity and the visual representation is in Fig. 5. In case of multiscale setting, it is important to be able to approximate better pressure values nearby the interface. The recovery of velocity computation requires three steps

• 1. Compute locally $\tilde{p}_h$ from given $\left( p_h, \mathbf {u}_h\right)$,

• 2. Obtain $s_h$ by using Oswald operator,

• 3. Compute the velocity at the interface using the two-point flux scheme for $s_h$.

We describe construction of $\tilde{p}_h$ and then $s_h$ below.

Fig. 5.

The illustration of the velocity improvement at the interface using postprocessing.

Construction of $\tilde{{\varvec{p}}}_{{\varvec{h}}}$. In the Enhance Velocity setting, we may identify $\widehat{\mathbf {V}}_h$ be spaces omitting interface constraints $\mathbf {V}^{\varGamma }$, so $\widehat{\mathbf {V}}_{h,i} :=\bigoplus _{i=1}^n \mathbf {V}_{h,i}(T)$ and then $\widehat{\mathbf {V}}_h :=\bigoplus _{i=1}^n \widehat{\mathbf {V}}_{h,i}$. Let $\mathbf {u}_h$, $p_h$ be the solution of Eqs. (8)–(9). Initially, Lagrange multipliers can be computed in each element. In other words, we define $\lambda _{h, T} \in \varLambda _h$, which is piecewise constant polynomials at edge or face,

$$\begin{aligned} \langle \lambda _{h, T}, \mathbf {v}_h \cdot \mathbf {n}_T \rangle _e := \left( \mathbf {K}^{-1}\mathbf {u}_h,\mathrm v_h\right) _{T}-\left( p_h, \nabla \cdot \mathbf {v}_h \right) _{T} \qquad \forall \mathbf {v}_h \in \widehat{\mathbf {V}}_h\left( T \right) , \end{aligned}$$

(23)

where the element and its side e. We employ the $L^2$ projected velocity from the interface, which has a finer enhanced velocity approximation, to the edge or face of subdomain element and the formulation is provided in Subsect. 2.2. We denote polynomial space $\widetilde{W}_h$ in the following manner

(24)

where $\mathbb {Q}_m$ is standard polynomial space that is defined in [5, 8, 12]. We next set the post-processed $\tilde{p}_h$ which is proposed in [5] and the construction is performed with the following properties, for each

$$\begin{aligned} (\tilde{p}_h, w_h)_T&=(p_h, w_h)_T \qquad \forall w_h \in \widetilde{W}_h(T) \end{aligned}$$

(25)

$$\begin{aligned} \langle \tilde{p}_h, \mu _h\rangle _e&=\langle \lambda _h, \mu _h \rangle _e \qquad \forall \mu _h \in \varLambda _h(e), \forall e \in \partial T. \end{aligned}$$

(26)

Construction of ${\varvec{s}}_{\varvec{h}}$. We propose to construct $s_h$ in each subdomain $\varOmega _i$ that has the conforming mesh in order to be a computational efficient. Construction of $s_h$ involves the averaging operator . For definition of $\mathbb {Q}_m$ we refer reader to [8]. The operator is called Oswald operator and appeared in [1, 11, 12, 16] and the analysis can be found in [7, 11]. It is interesting to note that the mapping of the gradient of pressure through Oswald operator also considered in [18]. For given , we regard the values of as being defined at a Lagrange node $V \in \varOmega$ by averaging $\varphi _h$ values associated this node,

(27)

where $\vert A \vert$ is cardinality of sets A and is all collection of for fixed V. One can see that at those nodes that are inside of given . We set the value of is zero at boundary nodes. Now in our setting we define recovered pressure $s_h$ for the locally post-processed $\tilde{p}_h$ as follows:

3.1 Implementation Steps

For simplicity, we provide key steps of numerical implementation of post-processed pressure in two dimensional case. However, it can be extended for general cases. Based on piecewise pressure and velocity from the lowest order Raviart-Thomas spaces over rectangles our aim to reconstruct smoother pressure $s_h$. For given element , the main steps are

• 1. Evaluate $\lambda _{h, T}$ at edge $e_j$, $j=1,..4$ based on $(\mathbf {u}_h, p_h)$,

• 2. Compute $\tilde{p}_h$ from known $\lambda _{h, T}$, and $p_h$ by using (23),

• 3. Based on $\tilde{p}_h$ compute $s_h$ Eq. (27) at Lagrange nodes in $\varOmega _i$.

Step 1 is standard computation of Lagrange multiplier for each element. In step 2, we are relying on higher order polynomial, in our case, it is Span$\{1, x, y, x^2, y^2\}$. It is sufficient to store coefficients of polynomials. In step 3, we use Span$\{1, x, y, x^2, y^2, xy, x^2y, xy^2, x^2y^2\}$ and 9 Lagrange nodes of rectangle elements that are four rectangle nodes, four midpoints at edge and center of rectangle. This case each node requires to find neighboring elements values to compute coefficients of $s_h$.

Remark 1

It would be interesting to see the possibility of extension of the proposed method to high order polynomial approximation.

4 Numerical Examples

In this section, numerical results are presented to demonstrate challenging problems of velocity approximation at the interface of non-matching multiblock grids. We have conducted tests for several examples and we concentrate our attention on the interface error for heterogeneous permeability coefficients. We set same domain $\varOmega = \left( 0, 1\right) \times \left( 0, 1\right)$ for all tests and for some the ratio is $H/h =4$. Initial subdomains grids are chosen in way that has a checkerboard pattern for subdomains. Example of such discretization is shown in Fig. 6. The discrete $L^2$ velocity error $e_{\mathbf {u}_h, \varGamma }$ is based on the values of the normal component at the midpoint of the edges and is normalized by the analytical solution.

Fig. 6.

Example of non-matching grids for subdomains.

Numerical test 1

We consider the a diagonal oscillating tensor coefficient as follows.

$$\begin{aligned} \mathbf {K} = \begin{bmatrix} 15-10 \sin (3\pi x)\sin (3 \pi y)&0 \\ 0&15-10 \sin (3\pi x)\sin (3 \pi y) \end{bmatrix} \end{aligned}$$

We impose the source term f and Dirichlet boundary condition according to the analytical solution

$$\begin{aligned} p(x,y) = \sin (2\pi x) \sin (2\pi y). \end{aligned}$$

We set the ratio $H/h=4$ for the result that is shown in Table 1. We reported the velocity error and the improved velocity error.

From Table 1, we see a significant increase on the convergence rate for recovered velocity $O(h^{1.5})$ while the convergence rate of provided velocity stays . We observe that the numerical method is an effective way to improve velocity at the interface between subdomains.

Table 1. Convergence test 2: velocity and recovered velocity error using the post-processed pressure at interface.

Numerical test 2

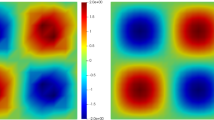
We consider the heterogeneous porous media and impose the no-flow boundary conditions for the flow problem, which is formulated in Eqs. (3)–(5). The permeability distribution profile in the log scale is shown in Fig. 7.

Fig. 7.

The fine permeability distribution in log scale.

In our simple scenario, a rate specified injection well and a pressure specified production well are located at the bottom left and top right corners, respectively. The fine scale subdomain dimension is $40 \times 40$ grid-blocks and the coarse scale subdomain dimension is 20 $\times$ 20 grid-blocks. The injection rate was assumed to be 1 m$^3$/s. The initial reservoir pressure is taken to be 1000 Pa. As reference solution we consider fine scale solution of the flow problem with $80 \times 80$ grid-blocks. In the coarse scale subdomains, the permeability distribution was evaluated or upscaled using numerical homogenization. We set the ratio $H/h=2$, see Fig. 6.

The overall error at interface is $e_{\mathbf {u}_h, \varGamma }=0.254656$ and the post-processed error is $e_{\mathbf {\tilde{u}}_h, \varGamma }=0.143014$. We note that the error of post-processed velocity at interface is less than the error of the original velocity, which is computed by the EV scheme.

5 Conclusion

The present study of velocity in Enhanced Velocity Mixed Finite Element Method was designed to investigate the effect of the post-processed pressure on velocity in the interface of subdomains. In this paper, the focus of attention is on the incompressible Darcy flow in the non-matching multiblock grid setting. Multiple numerical results demonstrate that the interface velocity approximation can be improved with using the post-processed pressure. These findings can contribute in several ways to our approximation of velocity and provide a good construction of velocity for a posteriori error analysis such as the recovery-based estimate.