Keywords

1 Introduction

Portfolio selections is an active topic on finance, and maybe, the most common problem for practitioners. On 1952, Markowitz introduced the modern portfolio theory [4] which proposed a mathematical framework, called mean-variance analysis, for assembling a portfolio of assets by solving one of the two optimization problems: To minimize the portfolio variance at a given level of expected or minimum required return. Or to maximize the portfolio expected return at a given level of expected or maximum required variance. The expected return is defined as:

$$\begin{aligned} {\text {E}}(R_{p}) = \sum _{i}w_{i} {\text {E}}(R_{i}) \end{aligned}$$
(1)

Where \(R_{p}\) is the return on the portfolio, \(R_{i}\) is the return on asset i and \(w_{i}\) is the proportion of asset i in the portfolio. Meanwhile, the variance is defined as:

$$\begin{aligned} \sigma _{p}^{2} = \sum _{i} \sum _{j} w_{i}w_{j}\sigma _{ij} \end{aligned}$$
(2)

Where \(\sigma _{p}^{2}\) is the portfolio variance and \(\sigma _{ij}\) is the covariance of assets i and j. Figure 1 shows 500 combinations of portfolios of four assets, whose x-axis is the portfolio standard deviation and the y-axis is the portfolio return. The optimal portfolios are given by the Pareto frontier: The upper edge of the hyperbola.

Fig. 1.
figure 1

Optimized markowitz portfolios

Full size image

However, Markowitz’ framework has issues related to instability, concentration, and under-performance given that the invertibility of the covariance matrix is required and not easy to satisfy. Therefore, [6] introduced an approach for building a diversified portfolio based on graph theory and machine-learning techniques like hierarchical clustering techniques. He presented evidence his approach produces less risky portfolios out of sample compared to traditional risk parity methods.

On [3], seven clustering techniques were tested for assembling portfolios using one-minute return data of 175 financial assets of the Russell 1000®index. The techniques were K-Means, Mini Batch K-Means, Spectral clustering, Birch and three hierarchical clustering methods (Average Linkage, Complete Linkage, and Ward’s Method). Results showed that the hierarchical clustering methods had a better trade-off between risk and return.

In this work, we will extend our analysis over the hierarchical clustering techniques, expand the testing dataset to approximately 2000 assets of the U.S. Stocks Market, and finally, propose an asset allocation tool based on inverse-variance weighting and a hierarchical clustering algorithm as an asset selection method.

This paper continues as follows: Sect. 2 presents a brief summary of hierarchical clustering methods, Sect. 3 explains the proposed method, Sect. 4 describes the experiment with real data and shows its results, and finally, Sect. 5 gives final remarks, conclusions, and further work opportunities.

2 Hierarchical Clustering Methods

Hierarchical Clustering Methods model data like a hierarchy of clusters [9]. There are two strategies for building the hierarchy: Agglomerative strategy (bottom-up approach) is that all observations start in its own cluster, and then, pairs of clusters are merged recursively. Whereas, divisive strategy (top-down approach) is that all observations start in a single cluster, and then, they are split into new clusters recursively. Divisive clustering is uncommon given that it requires an exhaustive search \(\mathcal {O} (2^{n})\) and not scales for large datasets [2].

On both strategies, merges and splits are determined in greedy manner by minimizing the distance (similarity) d(u, v) between clusters u and v, which are determined by the linkage criterion. It is a function of the pairwise distances of observations in the clusters. The most common linkage criterion are:

  • Single Linkage (Nearest Point Algorithm):

    $$\begin{aligned} d(u, v) = \min (\text {dist} (u_i, v_j)) \end{aligned}$$
    (3)

    Where \(u_i\) is the i-th observation in the cluster u, \(v_j\) is the j-th observation in the cluster v, and dist(a, b) is the euclidean, Manhattan, Mahalanobis or Maximum distance between observations a and b.

  • Complete Linkage (Farthest Point Algorithm or Voor Hees Algorithm):

    $$\begin{aligned} d(u, v) = \max (\text {dist} (u_i, v_j)) \end{aligned}$$
    (4)

  • Average Linkage (UPGMA algorithm):

    $$\begin{aligned} d(u, v) = \sum _{ij} \frac{\text {dist} (u_i, v_j)}{|u||v|} \end{aligned}$$
    (5)

    Where |u| and |v| are the cardinals of clusters u and v, respectively.

  • Weighted Linkage (WPGMA algorithm):

    $$\begin{aligned} d(u, v) = \frac{\text {dist} (s, v) + \text {dist} (t, v)}{2} \end{aligned}$$
    (6)

    Where u is formed by the merge between s and t.

  • Centroid Linkage (UPGMC algorithm):

    $$\begin{aligned} d(u, v) = || c_u - c_v ||_2 \end{aligned}$$
    (7)

    Where \(c_u\) and \(c_v\) are the centroids of clusters u and v, respectively.

  • Median Linkage (WPGMC algorithm):

    $$\begin{aligned} d(u, v) = || c_u - c_v ||_2 \end{aligned}$$
    (8)
    $$\begin{aligned} c_u = \frac{c_s + c_t}{2} \end{aligned}$$
    (9)

    Where u is formed by the merge between s and t, and \(c_s\), \(c_t\) and \(c_u\) are the centroids of clusters s, t and u, respectively.

  • Ward Linkage (Ward variance minimization algorithm):

    $$\begin{aligned} d(u,v) = \sqrt{\frac{|v|+|s|}{T}d(v,s)^2 + \frac{|v|+|t|}{T}d(v,t)^2 - \frac{|v|}{T} d(s,t)^2} \end{aligned}$$
    (10)

    Where u is formed by the merge between s and t, and \(T = |v| + |s| + |t|\).

3 Proposed Method for Portfolio Selection

The US Stock Market lists approximately 8000 stocks which worth above 30 trillion USD [8]. However, many stocks are unsuitable for algorithmic trading or portfolio managing given its liquidity restrictions or high-risk behavior. One of the most important requirements of a portfolio is to have low-risk exposure, therefore, the universe of stocks is filtered using the following rules:

  • The stock must be a common (for example, not preferred) stock, nor a depository receipt, nor a limited partnership, nor traded over the counter (OTC).

  • If a company has more than one share class, the most liquid share class is chosen and the others are discarded.

  • The stock must be liquid; it must have a 200-day median daily dollar volume that exceeds $2.5 Million USD.

  • The stock must not be an active M&A target (Mergers and Acquisitions).

  • The stock must have a market capitalization above $350 Million USD over a 20-day simple moving average.

  • ETFs are excluded.

The reduced universe size ranges from 1900 to 2100 stocks. Once the universe is filtered, the distance matrix is built using the correlation matrix of the one-minute returns over the last 10 trading days. The distance matrix is defined as follows [6]:

$$\begin{aligned} D_{ij} = \sqrt{\frac{1}{2} (1 - \rho _{ij})} \end{aligned}$$
(11)

Where \(\rho _{ij}\) is the Pearson correlation coefficient between the stocks i and j which ranges from −1 to 1. If this coefficient is close to 0, 1 or −1, it means uncorrelated, correlated, anti-correlated behavior, respectively. Given the fact that \(\rho _{ij}\) is bounded, \(D_{ij}\) ranges from 0 to 1. It is 0, \(\sqrt{\frac{1}{2}}\) or 1 when the pair stocks are perfectly correlated, uncorrelated, and anti-correlated, respectively.

After, the distance matrix’s clusters are formed using a hierarchical clustering method. The approach is to group stocks that are most similar within clusters. Figure 2 shows the comparison of seven hierarchical clustering methods: Single, Complete, Average, Weighted, Centroid, Median and Ward Linkages.

Fig. 2.
figure 2

Comparison of several hierarchical clustering methods

Full size image

The Cophenetic Correlation Coefficient (CCC) evaluates how well the dendrogram preserved the pairwise distances between the original modelled data points [10]. It is given by [1]:

$$\begin{aligned} CCC = \frac{\sum _{i<j} (x(i,j) - \bar{x})(t(i,j) - \bar{t})}{\sqrt{[\sum _{i<j}(x(i,j)-\bar{x})^2] [\sum _{i<j}(t(i,j)-\bar{t})^2]}}. \end{aligned}$$
(12)

Where x(i, j) is the Euclidean distance between the i-th and j-th observations. t(i, j) is the dendrogrammatic distance, which is the height of the node at which these two points are first joined together, between the model points \(T_i\) and \(T_j\). \(\bar{x}\) and \(\bar{t}\) is the average of all x(i, j) and t(i, j), respectively. Furthermore, the magnitude of CCC should be very close to 1 for a high-quality solution. Figure 2 also shows the CCC for each algorithm: The method Average has the highest CCC, meanwhile the method Single has the lowest CCC.

For each cluster, the optimal portfolio with the highest Sharpe-ratio is calculated using Markowitz theory and the critical line algorithm. Although, another more powerful method to generate the optimal portfolio within each cluster can be chosen like a multi-objective optimization, searching to optimize with liquidity and volume constraints or including aversion risk preferences or transaction costs.

Then, the Inverse-variance weighting technique is applied; the portfolio’s weights are rescaled by multiplying them by the inverse proportion to its portfolio variance. This technique is applied in order to have a portfolio with a leverage of 1 and minimize the variance of the weighted average.

$$\begin{aligned} \hat{w_k} = \frac{1/\sigma _k^2}{\sum _k 1/\sigma _k^2} w_k \end{aligned}$$
(13)

Where \(\sigma _k^2\) is the variance of the k-th portfolio and \(w_k\) is the weight vector of the k-th portfolio’s stocks.

4 Experiment and Results

A portfolio strategy was simulated with real data reaching a sample of 2,000 listed U.S. stocks. The strategy uses the previous portfolio selection method and rebalances weekly every Wednesday. The back-test took 25 months from January 6th, 2016 to January 31th, 2018 and initial capital of 10 million USD. The cumulative returns were 5.89%, namely, an annual return of 2.9%.

Fig. 3.
figure 3

Cumulative returns

Full size image
Fig. 4.
figure 4

Exposure

Full size image

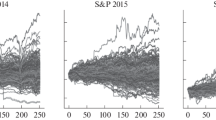
Figure 3 shows the total percentage return of the portfolio from the start to the end of the back-test. Also, it compares the evolution against the Standard & Poor’s 500 Index (S&P 500) which is the most representative index of the American stock market. It is based on the market capitalizations of 500 large companies listed on the New York Stock Exchange (NYSE) or Nasdaq Stock Market (NASDAQ). The maximal draw-down was −3.4%. Figure 4 shows strategy exposure over the back-test period. The strategy traded with an average leverage of 1 and used short and long positions.

Figure 5 shows the six-month rolling standard deviation of the portfolio’s returns. The portfolio had annual volatility of 3.2% which is lower to the benchmark volatility and is a desired quality for low-risk portfolios. Meanwhile, Fig. 6 presents the six-month rolling Sharpe ratio which measure of risk-adjusted performance, which divides the portfolio’s excess return over the risk-free rate by the portfolio’s standard deviation. The portfolio had an average Sharpe ratio of 0.89 and a Calmar ratio of 0.83, an Omega ratio of 1.16, and a Sortino ratio of 1.29.

Fig. 5.
figure 5

Rolling volatility

Full size image
Fig. 6.
figure 6

Rolling sharpe

Full size image

Another desired quality is that portfolios must be diversified over different economic sectors. Traditionally, the portfolio selection satisfies this need manually splitting the market into sectors using subjective experts’ criteria. But the clustering techniques allows removing this human parametrization because those techniques are able to learn and identify the economy sectors from data for themselves without human intervention. Figure 7 shows the exposure to various economic sectors. The rolling 63-day mean of sector exposures for all standard economy sectors is below of 7%. This behavior is stable over time.

Fig. 7.
figure 7

Rolling 63-day mean of sector exposures

Full size image
Fig. 8.
figure 8

Rolling 63-day mean of Style exposures

Full size image

Moreover, portfolios must be diversified over different styles of exposures in order to ensure that all positions on any kind of stock have homogeneous behaviors with respect to the entire portfolio. The relevant Quantopian’s styles are [7]:

  • Momentum: The difference in return between assets on an upswing and a down-swing over 11 months.

  • Size: The difference in returns between large capitalization and small capitalization assets.

  • Value: The difference in returns between expensive and inexpensive assets (as measured by Price/Book ratio).

  • Short Term Reversal: The difference in returns between assets with strong losses to reverse, and strong gains to reverse, over a short time period.

  • Volatility: The difference in return between high-volatility and low-volatility assets.

Figure 8 shows the portfolio style exposures. All style exposures are between −40% and 40% which is excellent for a low-risk portfolio. Figure 9 presents the rate at which assets are being bought and sold within the portfolio. The portfolio’s turnover ranges from 22% to 30% with an average of 26.8%. A low turnover reduces transaction costs. Moreover, Fig. 10 shows the percentage of the portfolio invested in its most-concentrated asset. A portfolio must not have a heavy concentration because it makes high-correlated with that asset.

Fig. 9.
figure 9

Rolling 63-day mean turnover

Full size image
Fig. 10.
figure 10

Position concentration

Full size image

Finally, a portfolio must be as less as possible correlated with the market. Figure 11 shows the beta statistic. The average portfolio Beta was 0.26.

Fig. 11.
figure 11

Six-month rolling beta

Full size image

5 Conclusions

We have tested seven hierarchical clustering techniques using actual data (sorted from best to worst performance according to CCC): Average, Centroid, Weighted, Ward, Complete, Median and Single Linkages.

Hierarchical clustering techniques allow to build diversified portfolios and achieve profits with reduced risk exposure. In conjunction with inverse-variance weighting, the technique allows a portfolio selection with the ability to consistently generate profits and portfolios with systematically stable and low volatility. The combination of these techniques produces portfolios with low sector exposure and low style exposure (Momentum, Sizes, Values, Short Term Reversal and Volatility).

Moreover, the Markowitz algorithm has issues related to instability, concentration, and under-performance given that the invertibility of the covariance matrix is required and not easy to satisfy. However, hierarchical clustering techniques do not have those issues. They are able to handle a lot of quantity of data with stable behavior.

Finally, another research opportunity would be to explore other machine learning techniques like hierarchical fuzzy clustering, to go beyond the work of [5]. Also is important to explore other methods for choosing the weight inside clusters that be more powerful than Markowitz algorithm, and other optimization objectives like Omega ratio.