High Performance Partial Coherent X-Ray Ptychography

Abstract

During the last century, X-ray science has enabled breakthrough discoveries in fields as diverse as medicine, material science or electronics, and recently, ptychography has risen as a reference imaging technique in the field. It provides resolutions of a billionth of a meter, macroscopic field of view, or the capability to retrieve chemical or magnetic contrast, among other features. The goal of ptychography is to reconstruct a 2D visualization of a sample from a collection of diffraction patterns generated from the interaction of a light source with the sample. Reconstruction involves solving a nonlinear optimization problem employing a large amount of measured data—typically two orders of magnitude bigger than the reconstructed sample—so high performance solutions are normally required. A common problem in ptychography is that the majority of the flux from the light sources is often discarded to define the coherence of an illumination. Gradient Decomposition of the Probe (GDP) is a novel method devised to address this issue. It provides the capability to significantly improve the quality of the image when partial coherence effects take place, at the expense of a three-fold increase of the memory requirements and computation. This downside, along with the fine-grained degree of parallelism of the operations involved in GDP, makes it an ideal target for GPU acceleration. In this paper we propose the first high performance implementation of GDP for partial coherence X-ray ptychography. The proposed solution exploits an efficient data layout and multi-gpu parallelism to achieve massive acceleration and efficient scaling. The experimental results demonstrate the enhanced reconstruction quality and performance of our solution, able process up to 4 million input samples per second on a single high-end workstation, and compare its performance with a reference HPC ptychography pipeline.

1 Introduction

Ptychography [1] permits imaging macroscopic specimens at nanometer wavelength resolutions while retrieving chemical, magnetic or atomic information about the sample. It has proven to be a remarkably robust technique for the characterization of nano materials, and it is currently used in scientific fields as diverse as condensed matter physics [2], cell biology [3], materials science [4] and electronics [5], among others. Ptychography is based on recording the distribution of the diffraction patterns produced by the interaction of an X-ray beam (illumination) with a sample. The diffracted signal contains information about features much smaller than the size of the beam, making it possible to achieve higher resolutions than with standard scanning transmission techniques. Only the intensities of the diffracted illumination are measured, and one has to retrieve the corresponding phases to be able to reconstruct an image of the sample. To solve this problem, diffraction patterns are obtained from overlapping regions of the sample, producing a redundancy that can be used to recover the original phases of the signal.

Fig. 1.

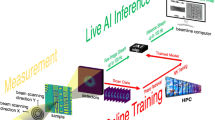
Overview of a ptychography experiment and reconstruction. An illumination source (X-ray beam) consecutively scans regions of the sample to produce a stack of phase-less intensities. The stack and the geometry of the measurements are fed to an iterative solver that retrieves the phases and reconstructs an image of the original sample.

An overview of ptychography is depicted in Fig. 1. First, a sample is repetitively scanned with an X-ray beam, producing diffraction patterns that are recorded on a 2D detector. Each measurement is stored as a frame, and its exact location in the sample is also registered. Secondly, the stack of frames and the measurements’ geometries are fed to a non-linear iterative solver that recovers the phases of the measurements. The solver optimizes based on two main constraints: (1) the match between overlapping regions of the frames, and (2) the match with a given model for the data. After the solver reaches an exit condition, the output is the overlap of the stack of frames (now with phases) in their corresponding geometries. This overlap corresponds to the 2D reconstructed image of the sample.

Normally, the ptychography reconstruction problem can only be solved if the illumination employed is coherent. The (spatial) coherence of an illumination defines how correlated are different points of its wavefront. To achieve higher coherence, X-ray microscopes employ apertures to filter the illumination, producing an homogeneous wavefront where different points are virtually identical in phase and amplitude. This solution wastes the majority of the X-ray flux, which is left behind the aperture. Overall, research institutions employ considerable resources to produce brighter X-ray sources, while over 90% of the photons are discarded to produce a coherent illumination.

A recent study from the CAMERA team at the Lawrence Berkeley National Laboratory (LBNL) proposed a novel algorithm that allows a ptychographic reconstruction with an incoherent source of illumination. The new algorithm, named Gradient Decomposition of the Probe (GDP) [6], has been proven to achieve successful reconstructions with significantly incoherent illuminations. The GDP algorithm also allows for a faster experimental data acquisition time: having more flux means you need less exposure time which can accelerate the whole measuring process up to an order of magnitude.

The benefits of GDP come at the expense of a remarkable increase in arithmetic operations and memory requirements with respect to a problem that is already computationally expensive. In ptychography, the stack of frames is normally two orders of magnitude bigger than the image reconstructed, and it is employed in practically all the operations of the solver. The GDP algorithm employs additional variables that require a three-fold increase of the memory footprint and computation with respect to baseline ptychography. On top of that, GDP employs an additional sub-solver that iteratively refines the illumination at every iteration. On the bright side, the operations employed in both baseline and GDP ptychography present high fine-grained parallelism and few dependencies. This parallelism is usually exploited in ptychographic reconstructions, frequently employing many-core accelerators, such as GPUs [7,8,9].

In this paper we propose the first high performance implementation of a partial coherent ptychography solution using GDP. We design an implementation that exploits the GDP parallelism and data requirements, making use of multiple GPU devices to achieve state-of-the-art reconstruction times. We compare the performance of the proposed implementation with that of baseline SHARP [7], a reference HPC ptychography solution, heavily optimized and also multi-GPU accelerated. The experimental results demonstrate how our implementation achieves only 2.5 times slower reconstruction times, on average, compared with standard coherent ptychography, while handling with 3 times more data and performing 4 to 5 times more arithmetic operations. The proposed solution has the key benefit of being able to process non-coherent illumination measurements, potentially leading to more flux utilization, increased robustness to non-stable sample exposures, and the capability to use less measurements when employing partially coherent illumination sources. Experimental results also assess the increased quality of the proposed method and implementation when handling partially coherent data, as compared with that of baseline coherent ptychography.

The paper is structured as follows. Section 2 overviews the main concepts regarding ptychography reconstruction, and introduces the GDP model. Section 3 presents the proposed algorithm and implementation with a detailed description of the challenges behind its design and the techniques employed, and Sect. 4 assesses its performance through experimental results. The last section summarizes this work.

2 Overview of Ptychography and GDP

A coherent ptychography problem can be defined as follows. A X-ray illumination (or probe) $\omega$ scans through a sample u, while a 2D detector collects a sequence J of phaseless intensities f. The goal is to retrieve a reconstruction of the sample u from the sequence of intensity measurements f. In a discrete setting, $u\in \mathbb C^n$ is a 2D image with $\sqrt{n}\times \sqrt{n}$ pixels, $\omega \in \mathbb C^{\bar{m}}$ is a localized 2D probe with $\sqrt{\bar{m}}\times \sqrt{\bar{m}}$ pixels, and $f_j=|\mathcal F(\omega \circ \mathcal S_j u)|^2$ is a stack of phaseless measurements, with $f_j\in \mathbb R_+^{\bar{m}}~\forall 0\le j\le J-1$. The operation $|\cdot |$ represents an element-wise absolute value of a vector, whereas $\circ$ denotes an element-wise multiplication, and $\mathcal F$ represents a normalized 2-dimensional discrete Fourier transform. Each $\mathcal S_j\in \mathbb R^{\bar{m}\times n}$ corresponds to a binary matrix that selects a region j of size $\bar{m}$ from the sample u.

Besides recovering the sample u, in a ptychographic experiment the illumination is rarely perfectly known, and thus both sample and illumination need to be retrieved jointly. This is commonly referred to as blind ptychographic phase retrieval [10]. The joint problem can be formulated as:

$$\begin{aligned} {\text {To find}\ \ \omega \in \mathbb C^{\bar{m}}\text {~and~} u\in \mathbb C^n,~~} s.t.~~|\mathcal A(\omega ,u)|^2= f, \end{aligned}$$

(1)

where bilinear operators $\mathcal A:\mathbb C^{\bar{m}}\times \mathbb C^{n}\rightarrow \mathbb C^{m}$ and $\mathcal A_j:\mathbb C^{\bar{m}}\times \mathbb C^{n}\rightarrow \mathbb C^{\bar{m}}~\forall 0\le j\le J-1$, are denoted as:

$$ \begin{aligned} \mathcal A(\omega ,u):=&(\mathcal A_0^T (\omega ,u), \mathcal A_1^T(\omega ,u),\cdots , \mathcal A_{J-1}^T(\omega ,u))^T,\\ \mathcal A_j(\omega ,u):=&\mathcal F(\omega \circ \mathcal S_j u), \end{aligned} $$

and $f:=(f^T_0, f^T_1, \cdots , f^T_{J-1})^T\in \mathbb R^m_+.$

There are multiple algorithms designed to solve the ptychography problem. The most popular ones are the extended Ptychographic Iterative Engine (ePIE) [11], Difference Map [10, 12], Maximum Likelihood (ML) method [13], Proximal Splitting algorithm [14], Relaxed Averaged Alternating Reflections (RAAR) [15] based algorithms [7], and generalized Alternating Direction Method of Multipliers (ADMM) [16, 17] for blind ptychography [18, 19].

When using a partial coherent illumination, modeling the ptychohraphy problem is more challenging. GDP proposes a model based on describing the illumination as the superposition of a single coherent illumination convolved with a separable translational kernel. This way, the partial coherence effect can be handled using this single illumination, its gradient, and the variance of the convolution kernel. Following this idea, GDP is based on the following model:

$$\begin{aligned} \sum \nolimits _{\xi } \left| \mathcal F_{x\rightarrow q}\left( \omega (x-\xi )\mathcal S_j u(x) \right) \right| ^2\kappa (\xi )= f_{pc,j}(q), \end{aligned}$$

(2)

where $f_{pc}$ represents a sequence of partially coherent intensity measurements, $\kappa (\xi )$ is a 2D kernel with variance (second order moments) $\sigma _{1}^2$, $\sigma _{1}^2$ and $\sigma _{12}$ ($\sigma _{1}^2\sigma _{2}^2 - \sigma _{12}^2 \ge 0$). Then, the Taylor expansion of $\omega$ can be derived and simplified as:

$$\begin{aligned} f_{pc} \simeq |\mathcal A(\tilde{\omega },u)|^2 + \sigma _{1}^2 |\mathcal A(\nabla _{1}\tilde{\omega },u)|^2 + \sigma _{2}^2 |\mathcal A(\nabla _{2}\tilde{\omega },u)|^2, \end{aligned}$$

(3)

with:

$$ \begin{aligned} \tilde{\omega }:= \omega + \dfrac{1}{2}(\sigma _{1}^2\nabla _{11}\omega + \sigma _{1}^2\nabla _{22}\omega + 2\sigma _{12}\nabla _{12}\omega ), \end{aligned} $$

and $\nabla _{1}$, $\nabla _{2}$, $\nabla _{11}$, $\nabla _{22}$, $\nabla _{12}$ corresponding to the forward first and second order finite difference operators (gradients) with respect to x, y, xx, yy and xy directions. Considering the sequence of measurements j, we can define the nonlinear operator ${\mathcal G}_{j} : \mathbb C^{\bar{m}}\times \mathbb C^{n} \times \mathbb R^{2} \rightarrow {\mathbb R}^{\bar{m}}_{+}$ as:

$$ \begin{aligned} {\mathcal G}_{j}(\tilde{\omega }, u, \sigma ) := |{\mathcal A}_{j}(\tilde{\omega },u)|^2 + \sigma _{1}^2 |{\mathcal A}_{j}(\nabla _{1}\tilde{\omega },u)|^2 + \sigma _{2}^2 |{\mathcal A}_{j}(\nabla _{2}\tilde{\omega },u)|^2, \end{aligned} $$

with $\sigma :=(\sigma _1, \sigma _2)$, and finally, we can establish the GDP nonlinear optimization model as:

$$\begin{aligned} \min \limits _{\tilde{\omega }, u, \sigma } \dfrac{1}{2} \sum || \sqrt{f_{pc,j}} - {\mathcal G}_{j}(\tilde{\omega }, u, \sigma )||^2, \end{aligned}$$

(4)

where $||\cdot ||$ represents the $L^2$ norm in Euclidean space.

3 High Performance GDP Solution

The GPD model is proposed in [6] together with an algorithm employing the ADMM framework to efficiently solve the derived subproblems (GDP-ADMM). In this work we design an implementation of GDP-ADMM and also propose a novel one employing the RAAR algorithm (GDP-RAAR). In the following section we focus on GDP-RAAR to describe the implementation, although the main insights and operations are common to both. The implementations and algorithms of this work are developed inside the SHARP framework, and some of the technologies and operations are common to the baseline coherent solutions. In this section, we focus on the main key operations unique to the GDP method; please refer to [7, 9] for a detailed description of other aspects of the end-to-end solution not described in here.

The challenge deriving from the GDP model is threefold. First, the algorithm requires to maintain in memory additional high dimensional variables. Second, the main ptychography operations need to be reformulated to handle the new problem. Third, to solve the illumination refinement, an additional inner solver needs to be considered at every ptychography iteration. The standard memory footprint of the ptychography problem involves the following structures. There are two main inputs: (1) a stack of 2D frames ($frames_m[x,y,z]$) containing the floating point values from the original measured intensities, and (2) a vector containing the coordinates of each one of the frames in the sample 2D image (int2 coord[z]). Then, at least three additional structures are required in the iteration process: sample[i, j], illum[x, y], and $frames_s[x,y,z]$, containing a 2D image of the object, the refined illumination and the stack of solution frames (with phases), respectively. Each one of these contains phase and amplitude information, and thus they are stored as complex values (float2).

The main idea behind the GPD model is to fit the stack of frames with constraints implying the original illumination and also its gradient on the x and y directions. Because of this, we need to consider three different variables for the stack of solution frames: ${frames_s}_{1}$, ${frames_s}_{2}$, and ${frames_s}_{3}$, each one float2 with size [x, y, z]. This increase in memory requirements is very relevant performance-wise. A real case example: to generate an image with size $1024 \times 1024$, a stack of measured frames of size $1500 \times 256 \times 256$ is collected, which represents a ratio of 1:94 output/input. When using GDP, every pixel in the output (float2) is iteratively produced from $94 \times 1$ float $frames_m \times 3$ float2 $frames_s$ elements, which constitutes a ratio of 2:658 in floating point values. On top of it, practically all the operations involved in a ptychography reconstruction are memory bounded, so proper memory managing and locality becomes a key factor to achieve performance.

3.1 The Implementation

Algorithm 1 describes the high level outline of the proposed implementation using the new GDP-RAAR algorithm¹. Note that all the operations are performed in GPU, using either custom CUDA kernels or Thrust operands. Most of the operations are implemented in a fused fashion in order to minimize GPU global memory transfers.

In this work we propose an scheme where all three ${frames_s}_{1,2,3}$ variables are stored as a single interleaved memory structure to maximize locality and performance. In Algortihm 1, ${frames_s}$ stores the three ${frames_s}_{1,2,3}$ variables, with a total size $[x \times y \times z \times n\_interleaved\;]$ and $n\_interleaved = 3$ being the stride. The motivation behind this design is related to the topology of the operations performed (how inputs contribute to the outputs). Baseline ptychography involves four kind of core operations: (1) Split, (2) Overlap, (3) 2D Fast Fourier Transforms (FFTs), and (4) and point-wise additions, multiplications, divisions, etc. The standard Overlap operation takes as inputs frames[x, y, z] and coord[z], and adds each frame into a 2D image², on its respective coordinate, as follows:

$$\begin{aligned} sample[\;:\;,\;:\;] = 0 \qquad \qquad \qquad \qquad \qquad \qquad \;\;\;\;\;\;\;\;\; \\ \quad for(\;i = 0;\;i < z;\;i++)\{ \qquad \qquad \qquad \qquad \;\;\;\;\;\;\;\;\;\;\;&\\ \qquad \qquad sample[\;coord[\;i\;]\;] \; += frames[\;:,\;:,\;i\;] \; \; \}, \; \end{aligned}$$

with the index”:” referring to the full slice in a dimension. The Split operation does the opposite: for each coordinate, a frame is extracted from an input 2D image, constructing an output 3D stack of frames. In GDP, the Overlap and Split operations are performed considering the three stack of frames variables. Each ${frames_s}_{1,2,3}$ is added into a single image for the Overlap, and a single image is split into three stack of frames. The interleaved strategy mentioned above permits to maximize data locality in these operations.

Algorithm 2 presents the interleaved Overlap CUDA kernel ($\varvec{Overlap_{int}}$) implemented for GDP. The thread to data mapping is as follows: each CUDA thread block processes a single frame from ${frames_s}$, iterating over the frame with a stride of samples equal to the thread block size ($block\_dim$) (line 12). For each pixel in the original frame size [x, y], each thread accumulates in a local register the contribution from all three ${frames_s}_{1,2,3}$ variables, iterating over the interleaved stride (line 7). Then, the accumulated value can be written into the output image employing a single atomic addition operation (line 11). The atomic operation is employed as an efficient way to handle the collision caused by having coordinates from different frames overlapping into the sample.

The interleaved Split operation ($\varvec{Split_{int}}$) is handled similarly as in the Overlap case. The main difference is that no atomic operation is required in it. When splitting the sample into frames, each frame is normally multiplied by the illumination. In GDP, each ${frames_s}_{1,2,3}$ variable needs to be multiplied by the illumination, its horizontal gradient and its vertical gradient, respectively. To reduce computation, the gradients of the illumination are computed once per iteration and stored as an interleaved variable with size $[x \times y \times n\_interleaved\;]$. This strategy permits performing efficient straightforward point-wise operations between the interleaved frames and the interleaved illumination variables. In Algorithm 1, illum stores the interleaved illumination structures; it is initialized in $\varvec{InitializeIllum}$ (line 2) employing the information from the measured frames ($frames_m$) to generate an initial guess. Then, the same function computes and stores the x and y gradients of the produced illumination.

The interleaved strategy is also beneficial when computing the L2 norm of the ${frames_s}_{1,2,3}$ variables. In $\varvec{UpdateFrames}$ and in the background noise modeling (not shown in Algortihm 1 for simplicity) the sum of the square root of the L2 norm needs to be computed, benefiting again from the enhanced locality of the interleaved structures. In the case of the 2D FTT operations, the interleaved layout actually reduces memory locality. To handle this issue with minimum performance impact we employ the in-build strided FFT feature implemented in cuFFT. This allows to transparently process our data through FFTs and back, without having to handle any reorganization of it or additional computation.

The GDP model requires to solve an additional subproblem for the illumination refinement step (Algorithm 1 line 8). The standard refinement is performed by fixing the current estimate of the sample and minimizing the difference with the $frames_{s}$, solving a problem in the form $\Vert \varvec{Split}(sample) \times illum-frames_s\Vert$, which is a linear problem with diagonal matrix that can be solved in a single step. In GDP, the illumination refinement step couples the GDP expansion of the illumination $(I,\nabla _1, \nabla _2) illum_{1}$, with the $\varvec{Split_{int}}(sample)$, and the interleaved $frames_s$ in the form:

$$ \begin{aligned} \Vert \varvec{Split_{int}}(sample) \times (I, \nabla _1, \nabla _2) illum_{1}-frames_s\Vert , \end{aligned} $$

with I and $illum_{1}$ referring to the identity matrix and the original illumination variable, respectively. This poses a linear problem with a sparse band-diagonal matrix, which we solve using the gradient descent algorithm with a fixed step size, referred in Algorithm 1 as $\varvec{GDescent}$. Instead of using the conjugate gradient described in the original GDP paper, we choose the gradient descent algorithm because it avoids the reduction operations used to compute the step size and conjugate directions scaling factors, thus offering an increased performance. The algorithm is implemented using custom CUDA kernels that allow pre-computing in place multiple factors, a custom manipulation of the interleaved structures, and permits fusing the iterating process with pre- and post-process operations, like the x, y gradient computation of the new illumination as a last step of the refinement.

The GDP-RAAR implementation proposed in this paper is also accelerated using multi-GPU over MPI/NCCL. The partition employed is similar to the one used in [7, 9]. The main idea is to divide both $frames_m$ and $frames_s$ variables across different GPUs so that each independent device process only a subset of frames. Then, communication is required every time the sample and the illumination are updated. The communication operation is essentially an AllReduce directive (Reduce and Broadcast) that performs a summation of the partial results of each independent GPU. The communication directives are performed in-place, using NCCL if it is installed on the system, or over standard MPI otherwise. Given the significant increase of the problem size of GDP, the proposed implementation greatly benefits from multi GPU execution when executed on high-end workstations. An additional feature is that the communication frequency can be adapted to occur every N iterations, employing previous iteration data for the non-local areas of the image. For the proposed GDP implementation, this features enhances performance only with small problem sizes per GPU (<30 millions measured samples).

4 Experimental Results

The results presented below have been executed in a dual socket workstation with two Intel Xeon E5-2683 v4, with a clock frequency of 2.10 GHz and 16 cores each. The machine is equipped with 4 dual-slot Tesla K80 GPUs, for a total of 8 GK210B devices, each device with 2496 CUDA cores. The implementations reported here have been compiled using gcc 5.4.0 and nvcc 8.0. The profiling results have been obtained with both Nvidia visual and inline profilers, nvvp and nvprof, respectively. All execution times and performance results consider the full pipeline execution time, including loading the data from memory, GPU runtime initialization, memory allocation and transfers, and writing back the reconstructed image and illumination. The experiments below all employ the GDP-RAAR algorithm described in the previous section but the reconstruction results and performance are also comparable when using GDP-ADMM. All experiments are measured using 100 solver iterations, which is enough to achieve convergence using standard tolerance thresholds for the datasets presented in here. The performance analysis and results below can also be extrapolated when running more iterations.

Fig. 2.

First column: baseline reconstruction using a standard coherent illumination using RAAR. Second column: reconstruction using a partial coherent illumination using RAAR. Third column: reconstruction using a partial coherent illumination using the proposed GDP-RAAR algorithm and implementation. Top row (a, b, c) corresponds to the amplitude images retrieved, whereas the bottom row (d, e, f) depicts the phase images from the same reconstructions.

The first experiment, reported in Fig. 2, evalutes the reconstruction quality of the proposed GDP-RAAR algorithm when retrieving a partial coherent illumination and sample, as compared with the baseline RAAR method from SHARP. In order to perform this test, a sample was measured with a standard coherent illumination first (Fig. 2 first column) and then it was measured again using a partial coherent illumination (Fig. 2 second and third columns). The first column represents our reference reconstruction and the second and third columns report an actual partial coherence experiment, reconstructed using RAAR and GDP-RAAR, respectively. Top and bottom rows correspond to the amplitude and phase contrast, respectively, from the same reconstruction. This experiment was conducted at the Advanced Light Source (ALS) in 2018, at the COSMIC beamline, and the sample corresponds to a conglomerate of nanometer-sized gold particles of uniform shape and size. Both coherent and partial coherent experiments have virtually the same configuration, with both datasets containing 1600 frames of size $256 \times 256$ each. We can clearly see in Fig. 2 second column how the RAAR algorithm introduces severe ghosting artifacts, specially around the contour of the sample. Some areas of this reconstruction become significantly blurry, specially on the top-right features of the amplitude image and top-center and top-left areas of the phase image. The results reported in the third column of Fig. 2 show how the main artifacts introduced by RAAR are removed by the proposed GDP-RAAR method. When using GDP, the ghosting artifacts are almost completely gone, and the heavily blurred areas present the same quality as the coherent reference reconstruction (see the top areas mentioned previously in both amplitude and phase).

Fig. 3.

Execution times of the proposed GDP-RAAR implementation, compared to those of baseline RAAR, when running on 1 to 8 GK210B GPUs. The dataset and configuration are the same presented in the experiment reported in Fig. 2.

Fig. 4.

Performance and scalability of the proposed GDP-RAAR implementation compared to that of baseline RAAR, both executed on 2, 4 and 8 GK210B GPUs. The size of the datasets employed range from $100 \times 256 \times 256$ to $2500 \times 256 \times 256$ measured frames.

The following test evaluates the execution time of the reconstruction results presented in the previous experiment. Results are reported in Fig. 3, and show the time in seconds of RAAR and GDP-RAAR, when being executed on a single GPU and on different multi-GPU settings. First, we can see the significant increase in execution time required by GDP-RAAR, presenting execution times ranging from 5.5 to 1.5 times slower than RAAR. This is consistent with the increase in arithmetic operations required in GDP-RAAR: almost all arithmetic involve 3 times more data, whereas the additional illumination solver performs 20 inner iterations per outer iteration, each iterations requiring multiple point-wise multiplications, divisions, and gradients with high dimensional data. The proposed implementation scales with the number of GPUs, achieving speedups of 1.94, 3.09 and 4.39 when using 2, 4, and 8 GPUs, respectively. The reported scaling is remarkably good, specially considering the fact that communication across GPUs is performed three times per outer iteration, in order to share the sample and illumination structures. This communication can significantly slow down execution, as seen in the time results reported by RAAR. The amount of computation and problem size that baseline RAAR handles is much less than GDP-RAAR, and that is why the speedup gain with the increase of GPUs is lower, as independent devices are not close to reach resource saturation. The communication overhead on its turn becomes higher with the number of independent executions, effectively reducing the performance of RAAR when running on 4, 6 and 8 GPUs.

The final experiment, reported in Fig. 4, analyzes the scalability of the proposed method with respect to the problem size. In this case we employ a dataset from an experiment performed in the ALS on 2015 that measured a cluster of iron catalyst particles. We have selected different size slices of said experiment to asses the performance of the proposed implementation with different input sizes. The performance metric is given in samples/second (the higher the better). The horizontal axis presents the different size datasets for their number of measured intensity samples (in millions). As a reference, we report the performance of baseline RAAR, together with the proposed method, and each algorithm is executed on 2, 4 and 8 GPUs. The experiment reveals how the proposed implementation achieves an almost perfect linear scaling when running on 2 GPUs. When running on 4 and 8 GPUs, the scaling achieved is better than linear due to the devices not being saturated at first by the smaller individual problem sizes. This effect is very noticeable with the RAAR results, where an (almost) saturation point is only reached with 2 GPUs and the biggest problem sizes. We can also see how the speedup achieved by the GDP-RAAR multi gpu execution effectively scales with the problem size: the biggest dataset (240 million samples) achieves an speedup of 1.92 and 3.13 when running on 4 and 8 GPUs, respectively, with respect to a dual-GPU execution.

5 Conclusions

This paper presents the first GPU-accelerated implementation of GDP for high performance partial coherent ptychography. We tackle the significant increase of computational costs of GDP to produce a solution with a minimum performance loss, while maintaining all the features offered by the method. We design our implementation using an efficient interleaved data layout strategy that enhances the memory locality and overall performance of the core operations of the solver. Multi-GPU parallelism is exploited, achieving linear scaling and capability to process up to 4 million measured samples per second, on a single high-end workstation. We also demonstrate how our implementation achieves a drastic increase of reconstruction quality when dealing with partially coherent light sources, with respect to standard ptychography. The proposed solution has the increased benefit of being able to employ more flux, potentially reducing the acquisition time up to an order of magnitude, while being more robust to non-stable sample exposures. It also offers the capability to use less measurements when employing partially coherent sources. The proposed implementation is currently installed and being used at the ptychography COSMIC beamline at the Advanced Light Source at LBNL, and the binaries and source code are also open to other DOE light sources.