Interfacial Phenomena

Abstract

This chapter introduces the interfacial concepts of surface tension, wetting phenomena, and contact angle, which are followed by a discussion on motion induced by capillarity. The interfacial balances and boun2dary conditions for mass, momentum, energy, and species for multicomponent and multiphase systems are presented. This chapter also delineates heat and mass transfer through the thin film region during evaporation and condensation, including the effect of interfacial resistance and disjoining pressure. The dynamics of interfaces, including stability and wave effects, are also presented in this chapter. Finally, a review is given on the numerical simulation of interfaces.

Problems

• 4.1. Liquid droplets that condense to form fog in the atmosphere can be as small as 2 µm in diameter when they first form. Determine the pressure in a droplet of this size at 20 °C (101.3 kPa). Note that for water in contact with air, the surface tension $\sigma$ is 0.0728 N/m. Describe any assumption you need to make in order to get the final answer.

• 4.2. A 0.2-mm-thick water film sits on a surface held at a temperature of 60 °C. The liquid film is exposed to air at a bulk temperature of T_G = 20 °C, and the convective heat transfer coefficient between the liquid film and the air is h_δ = 15 W/m² K. Suppose the wave number is $\hat{\alpha } = 2$. What is the critical Marangoni number, $Ma_{\text{c}}$ ? Is the liquid film stable?

• 4.3. A 0.2-mm-diameter tube is vertically placed in a pool of water at 20 °C. Find the capillary rise in tubes of the following materials: (a) aluminum, (b) brass, (c) copper, and (d) steel.

• 4.4. Consider the smooth flat plates shown in the sketch. The angle between plates is 2γ (γ < 90°). The contact angle of the liquid with the surface is θ (θ < 90°). For the cases showing in Fig. P4.4, sketch the shape of the liquid–vapor interface between the plates relative the surface of the liquid in the reservoir. Assume that the radius of the curvature along the interface is constant.

  

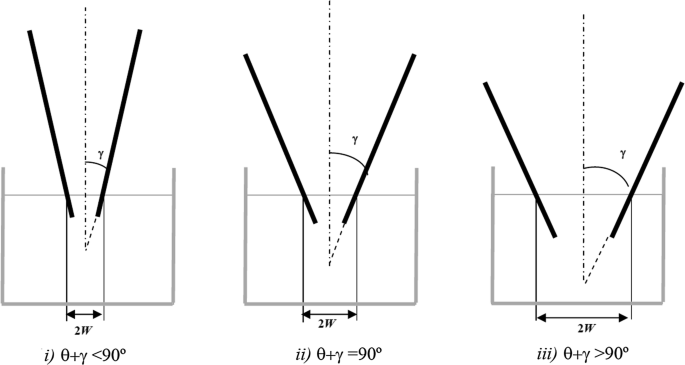
  Fig. P4.4

• 4.5. Consider water slug in the copper tube with 1-mm inner diameter (see Fig. P4.5). The receding and advancing contact angles of copper at 20 °C are given as 30° and 60°, respectively ($\theta_{\text{r}}$ = 30°, $\theta_{\text{a}}$ = 60°). Calculate the maximum stable length of the slug (i.e., before liquid slug starts to move) between the plates. $\rho_{\text{l}}$ = 1000 kg/m³; $\rho_{\text{g}}$ = 1 kg/m³, $\sigma_{\text{lv}}$ = 0.0725 N/m.

  

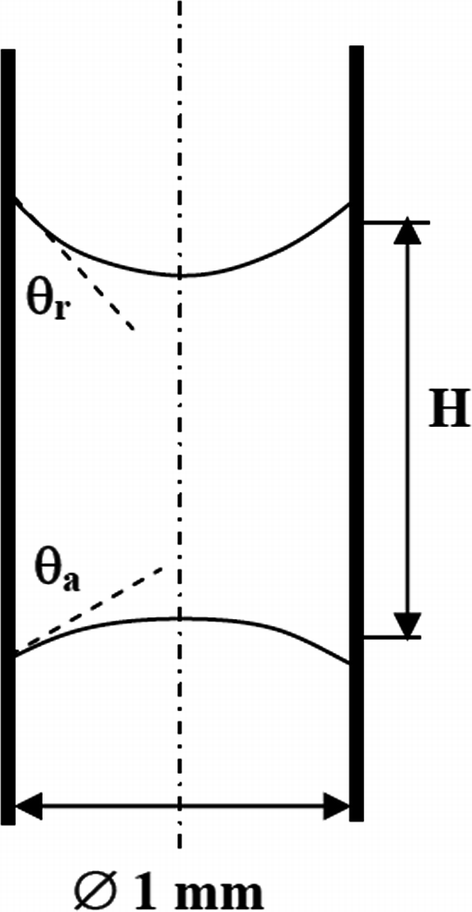
  Fig. P4.5

• 4.6. Two nearly vertical but nonparallel plates touch a pool of water with their parallel bottom edges. The angle between the plates is $2\gamma$ so that these plates would intersect somewhere under the pool surface. The distance between the plates at the pool surface level, 2 W, is small. The apparent contact angle is denoted by $\theta$. The liquid–vapor meniscus between the plates is elevated from the pool surface level due to capillary pressure. Assume that the meniscus curvature does not change along the liquid–vapor interface. Derive an algebraic equation for the height of the capillary rise H for this situation (for $\theta \ne 0$ and $\gamma \ne 0$). Using the derived equation, estimate H for the following data: $W = 0.5\;{\text{mm}}, \theta = 0, \gamma = 0, \rho_{\text{l}} = 1000\;{\text{kg/m}}^{3} ,\sigma = 0.06\;{\text{N/m}}.$

• 4.7. A small amount of liquid metal resides between two high melting point powder particles separated by a distance of $\ell \, (\ell > 2r_{0} )$ (see Fig. P4.7). If the effect of gravity on the liquid metal is negligible, estimate the force required to hold the two particles together.

  

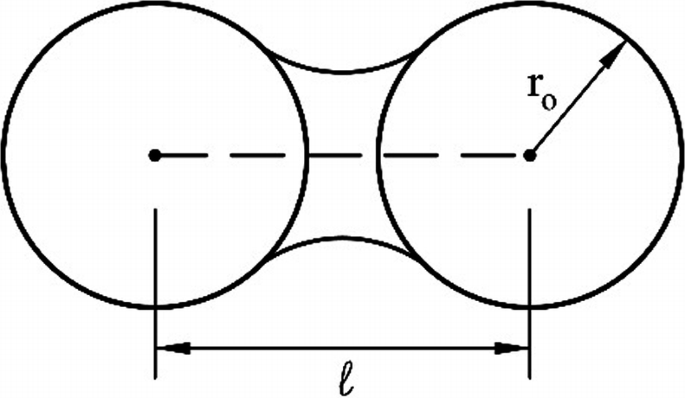
  Fig. P4.7

• 4.8. Write the continuity, momentum, energy, and species equations and the necessary boundary conditions for a very long capillary tube that is open at both ends, as shown in Fig. P4.8. The evaporation is driven by the concentration gradient of vapor in the air. The evaporation cools the interface while the wall heats the fluid, causing a temperature gradient along the interface. The assumptions are the same as Example 4.4.

  

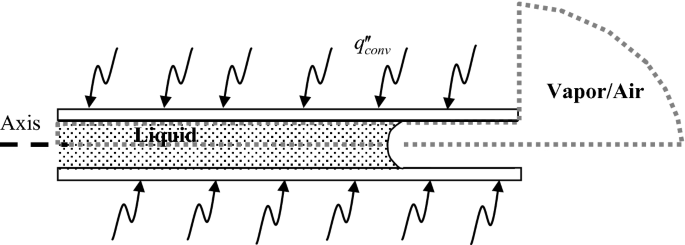
  Fig. P4.8

• 4.9. The generalized mass balance on a liquid–vapor interface is given in Eq. (4.62). Rewrite it in a three-dimensional Cartesian coordinate system.

• 4.10. The jump conditions at an interface can also be obtained by applying the various conservation laws to a control volume that includes the interface. Apply the conservation of mass principle to the control volume shown in Fig. P4.10, and show that when the thickness of the control volume Δx goes to zero, the conservation of mass is $\rho_{1} (u_{1} - u_{\text{I}} ) = \rho_{2} (u_{2} - u_{\text{I}} )$.

  

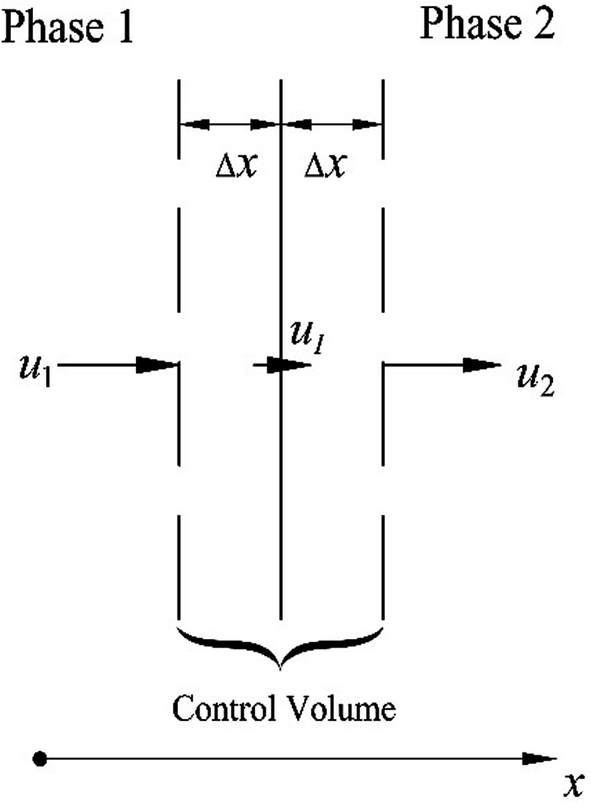
  Fig. P4.10

• 4.11. For the control volume shown in Fig. P4.10, show that the momentum balance at the interface is $p_{1} - p_{2} = \rho_{2} (u_{2} - u_{\text{I}} )u_{2} - \rho_{1} (u_{1} - u_{\text{I}} )u_{1}$ when the thickness of the control volume Δx goes to zero.

• 4.12. In a counter-current condenser shown in Fig. P4.12, the liquid flows downward with a mass flow rate of $\dot{m}_{\ell } ,$ while the vapor flows upward with a mass flow rate of $\dot{m}_{\text{v} }$. The heat flux at the external wall is $q^{\prime\prime}_{\text{w}}$. Derive the jump conditions using mass and energy balances at the liquid–vapor interface.

  

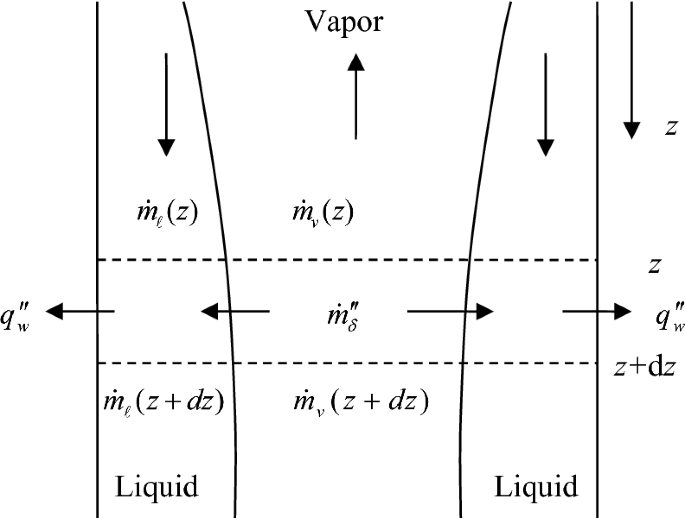
  Fig. P4.12

• 4.13. Redo the Problem 4.12 for the case of co-current condensation, i.e., both liquid and vapor flow downward.

• 4.14. Redo Problem 4.12 for the case of counter-current evaporation and discuss the effect of the heat transfer direction on the energy balance at the interface.

• 4.15. Consider an ultrathin evaporating liquid film on a hot solid surface of temperature T_w in the presence of a saturated vapor of temperature T_v. The film thickness $\delta$ is small and the disjoining pressure p_d is significant. The film is flat. Does the disjoining pressure increase or decrease the evaporation rate in comparison with the hypothetical case where $p_{\text{d}} = 0$ (for the same film thickness and temperatures)? Assuming that $T_{\text{w}} - T_{\text{v} }$ is extremely small, explain the effect of $p_{\text{d}}$ on the evaporation rate by referring to the extended Kelvin equation and interfacial resistance.

• 4.16. A liquid film of ammonia with thickness $\delta = 0.375 \times 10^{ - 8} \;{\text{m}}$ is evaporating from a smooth solid surface into bulk vapor. The solid surface temperature is T_w = 250.12 K. The bulk vapor temperature is T_v = 250 K. The constants in the correlation for disjoining pressure $p_{\text{d}} = - A^{\prime}\delta^{ - B}$ are $A^{\prime} = 10^{ - 21}$ and B = 3. The accommodation coefficient is equal to unity. In this particular case, the perfect gas law can be used instead of the saturation tables, for convenience. Estimate the heat flux at the liquid interface.

• 4.17. A slug of water 4.5 mm in length sits in a vertical copper tube with an inner radius of 2 mm at room temperature. The temperature of the whole system is slowly increasing. At what temperature will the water slug start to move?

• 4.18. Nusselt-type condensation takes place on a flat vertical plate made from aluminum. The thickness of the plate is 5 mm and there are 1-mm ID microchannels inside it containing cooling liquid. You must increase the rate of condensation, which is restricted primarily by the conduction through the condensate film. What would you do?

• 4.19. The effective heat transfer during evaporation of liquid is more extensive from a solid surface with small grooves than from a plain surface. How would you explain this?

• 4.20. A vertical capillary tube is connected to bulk liquid at the bottom end and to a heat source at the upper end. The liquid evaporates from the liquid–vapor meniscus, so a quasi-steady state exists. What is the heat load that would initiate dry-out of the upper end and lead to unbounded increase of its temperature? Write corresponding general formulas or equations.

• 4.21. The temperature at the meniscus of Problem 4.20 equals the saturation temperature, and the bulk liquid is at a lower temperature T_b. Repeat Problem 4.20 accounting for the conduction heat loss from the meniscus to the bulk liquid.

• 4.22. A capillary tube of inner radius r is vertically dipped into a liquid. The depth from the free surface to the lower end of the tube is a. When the liquid rises in the capillary tube due to capillary force, it can be viewed as a variable mass system with capillary force, gravity, and viscous force acting upon it. What is the governing equation for the liquid slug in the capillary tube? The shape of the meniscus in the tube can be assumed to be the same at all times.

• 4.23. A Newtonian liquid is in an open cylindrical container with a radius of R and height of H (see Fig. P4.23). A stationary continuous axisymmetric laser beam with an intensity of $I = I_{0} \exp ( - r^{2} /r_{0}^{2} )$ irradiates the top of the liquid surface. The side of the cylindrical container is maintained at a constant temperature, $T_{0}$, and the bottom of the container is adiabatic. Supposing the surface tension is a linear function of temperature $\sigma = C_{0} - C_{1} T$, write the governing equations and the corresponding boundary conditions of the problem. The effect of gravity is negligible, and the liquid flow induced by the laser beam can be assumed to be axisymmetric.

  

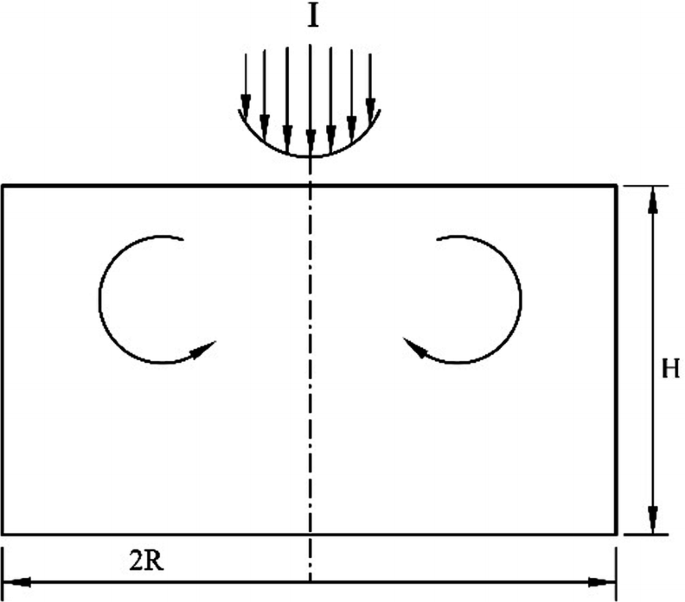
  Fig. P4.23

• 4.24. Introduce appropriate non-dimensional variables and non-dimensionalize the governing equations and boundary conditions in Problem 4.25. Identify the dominant dimensionless variables in the problem.

• 4.25. Saturated vapor enters a miniature channel with a radius of R and a length of L (see Fig. P4.25). Condensation takes place on the wall of the channel, since the wall temperature T_w is below the saturation temperature of the working fluid T_sat. The condensate fluid flows in the positive x-direction due to the effects of shear force and surface tension. The problem is condensation on the inner surface of the miniature channel with cocurrent vapor flow. The average vapor velocity is not constant along the x-direction because condensation occurring on the wall reduces the amount of vapor flow in the core of the tube. Capillary blocking occurs when capillary force causes the liquid to block the tube cross-section at some distance, $L_{\delta }$, from the condenser entrance. Supposing the effect of gravity on the two-phase flow in the miniature tube is negligible, write the governing equations and boundary conditions for the liquid and vapor flows.

  

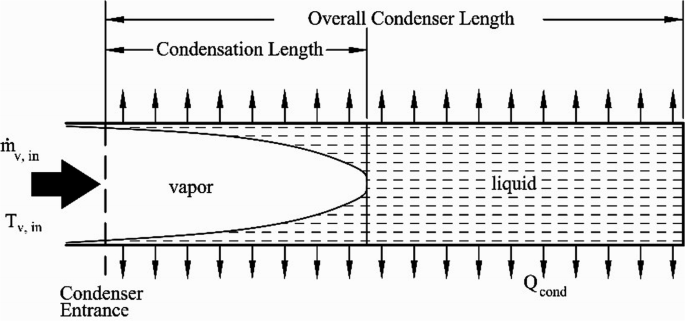
  Fig. P4.25

• 4.26. Heat is applied to the outer surface of a microchannel with inner and outer radii of $r_{\text{i}}$ and $r_{\text{o}}$, respectively, as shown in Fig. P4.26. Specify the governing equations that describe evaporation in the microchannel. The effects of disjoining pressure and interfacial thermal resistance must be taken into account.

  

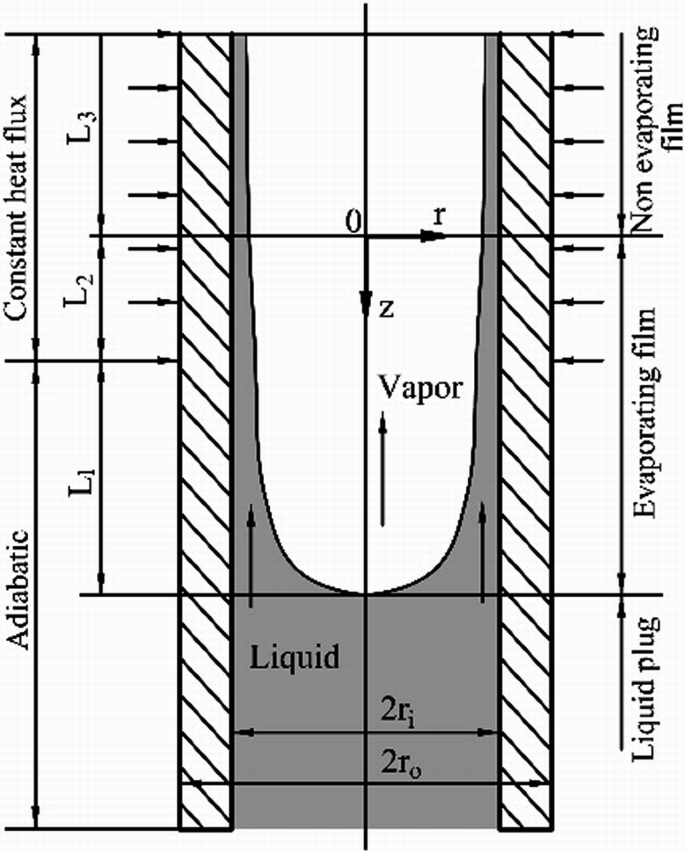
  Fig. P4.26

• 4.27. The physical model of the condenser section of the pulsating heat pipe (PHP) with an open end is shown in Fig. P4.27. It is assumed that the liquid film in the condenser section is divided into two regions: a thin film region and a meniscus region. These two regions are separated by a transition point where the film thickness is $\delta = \delta_{\text{tr}}$. The curvature of the liquid film in the meniscus region is assumed to be constant. Assuming the effect of disjoining pressure is negligible, specify the governing equation for the liquid film thickness in $0 < x < L_{2}$.

  

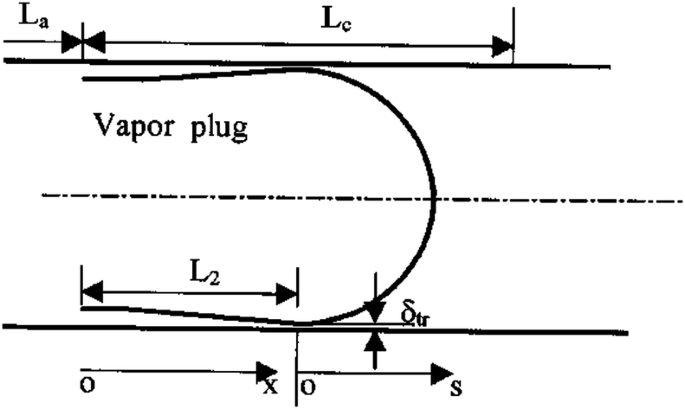
  Fig. P4.27

• 4.28. The fluid mechanics of capillary tubes and microchannels is of great interest for modeling transport phenomena in microdevices. Develop the physical formulation, including continuity and momentum equations with appropriate boundary and initial conditions, for a typical miniature channel with a free surface as depicted in Fig. P4.28 for both submerged and blocked end configuration. Neglect mass transfer and Marangoni effects.

  

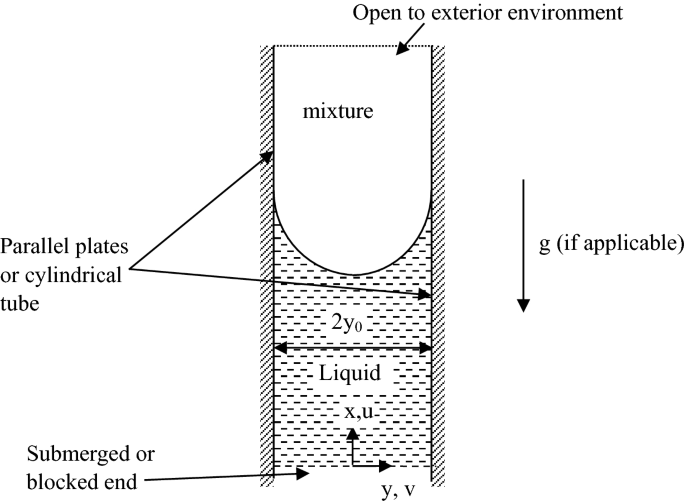
  Fig. P4.28

• 4.29. Describe the physical/mathematical formulation to model the problem related to instability growth of a free-flowing cylindrical column of fluid as shown in Fig. P4.29.

  

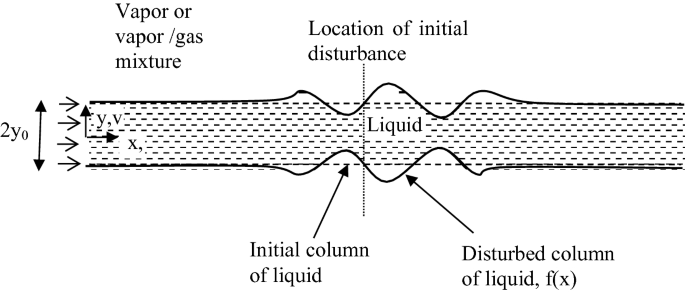
  Fig. P4.29

• 4.30. Obtain an analytical solution for the shape of the meniscus in a capillary tube in 1 g environment for mechanical equilibrium, as shown in Fig. P4.30 for both parallel plates and circular tubes. Assume the effect of the gaseous region is negligible with vapor pressure constant. You should get a second-order ordinary differential equation for $f(y)$ which can be solved by the Runge-Kutta method. Obtain numerical results for the working fluid as acetone with $y_{0} = 0.001\;{\text{m}}$ and contact angle $\theta = 0.0$. Obtain a closed analytical solution for the situation with no gravity.

  

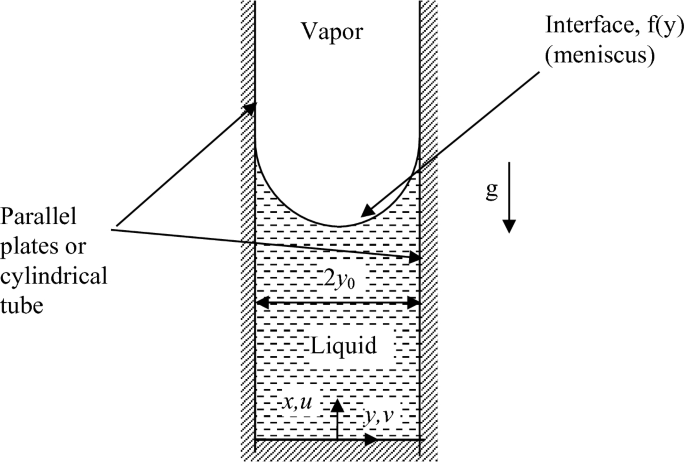
  Fig. P4.30

• 4.31. Obtain an analytical solution for the rise of a meniscus in a capillary tube with both ends open, as shown in Fig. P4.31, for both parallel plates and a circular tube. If $\overline{u}$ is the bulk motion or the average velocity, obtain your solution in terms of $\overline{u} = {\text{d}}H/{\text{d}}t$ where H is the mean height of the meniscus.

  

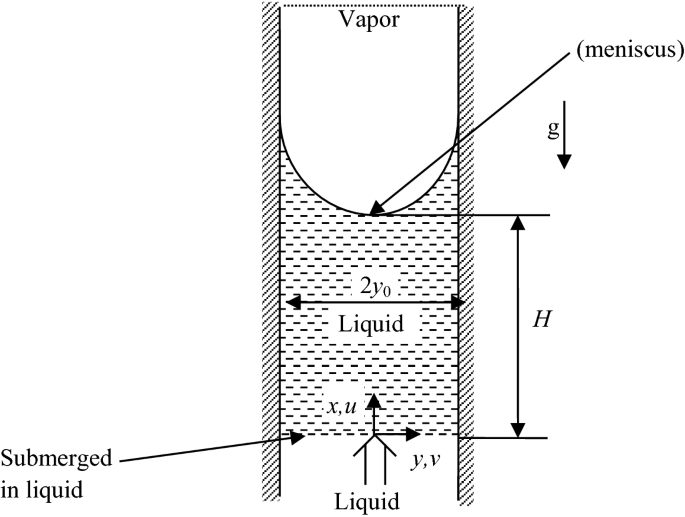
  Fig. P4.31

• 4.32. Consider the steady, laminar flow of a liquid film down an inclined flat plate (see Fig. P4.32). Assume the flow is fully developed. However, the presence of a small temperature gradient in the axial direction dT/dz produces a constant surface tension gradient dσ/dz = C. Assume the surface tension effect is only at the interface, which produces a nonzero shear stress and no other effect on physical properties of the system. Solve the momentum equation to determine the shear stress variation and velocity distribution as a function of distance perpendicular to the plate.

  

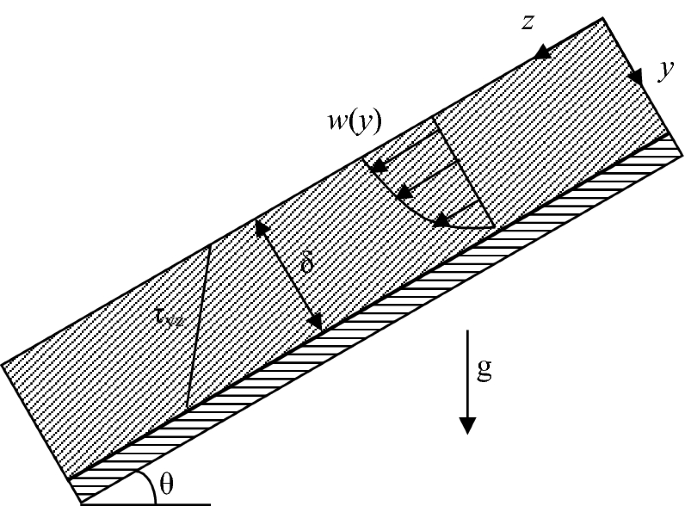
  Fig. P4.32

• 4.33. Consider the absorption of gas A (O₂) to a laminar, steady, fully developed, isothermal falling film of liquid B (water) (see Fig. P4.33). Since O₂ is slightly soluble in water, one can assume the properties of water are not affected. Since the diffusion of O₂ is taking place slowly and thermal diffusion is in the immediate vicinity of liquid, O₂ does not penetrate very far into the liquid. Obtain the total mole flow rate of gas A to liquid B.

  

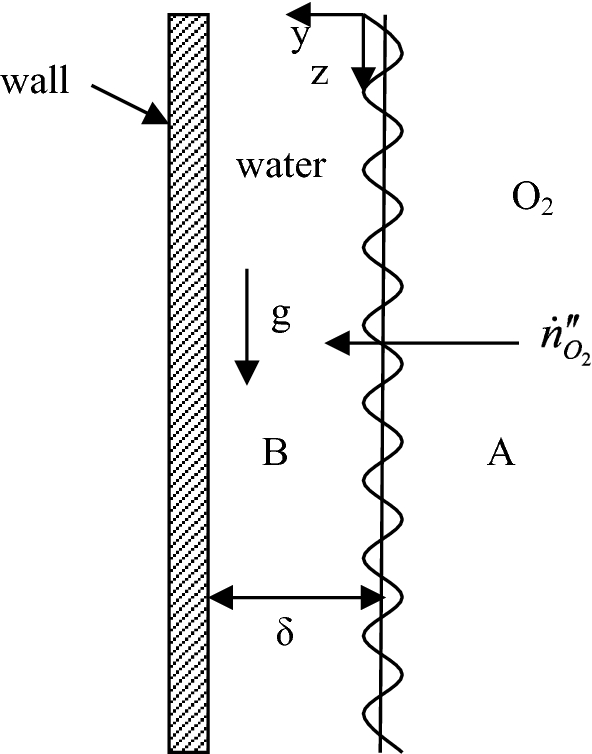
  Fig. P4.33

• 4.34. Consider the solid dissolution of a component A for a solid wall to a steady, laminar, isothermal falling liquid film B (see Fig. P4.34). Assume that species A is slightly soluble in B. Obtain the physical formulation of the simplified model.

  

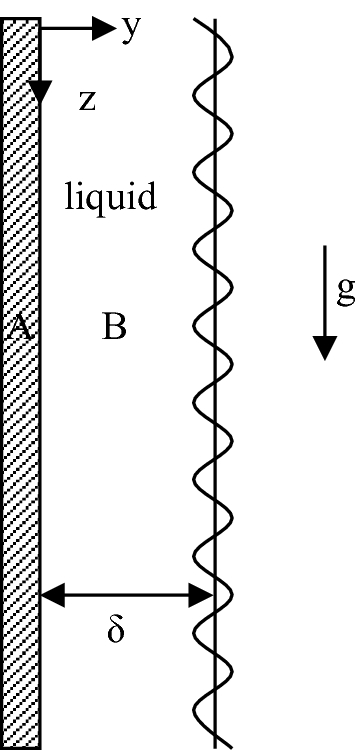
  Fig. P4.34

• 4.35. Saturated vapor at 100 °C flows inside a horizontal tube cooled at the external surface. A pool of the liquid water exists at the bottom of the tube and flows with a velocity of 0.5 m/s. Determine the critical velocity of the vapor when waves appear on the liquid–vapor interface.

• 4.36. In a stratified, horizontal, two-phase flow system, the saturated water vapor flows above the saturated liquid water. The pressure of the two-phase system is at 5 bar. What is the most dangerous wavelength, $\lambda_{\text{D}}$?