Abstract
Knowledge graphs are based on graph models enriched with (sets of) attribute-value pairs, called annotations, attached to vertices and edges. Many application scenarios of knowledge graphs crucially rely on the frequent use of annotations related to time. Building upon attributed logics, we design description logics enriched with temporal annotations whose values are interpreted over discrete time. Investigating the complexity of reasoning in this new formalism, it turns out that reasoning in our temporally attributed description logic \(\mathcal {ALCH} ^{\mathbb {T}}_@\) is highly undecidable; thus we establish restrictions where it becomes decidable, and even tractable.
This is a preview of subscription content, log in via an institution.
Buying options
Tax calculation will be finalised at checkout
Purchases are for personal use only
Learn about institutional subscriptionsNotes
- 1.
As of March 2019, the only more common annotations are reference (provenance) and determination method (context); see https://tools.wmflabs.org/sqid/#/browse?type=properties&sortpropertyqualifiers=fa-sort-desc.
- 2.
FAU is the official abbreviation for the Friedrich-Alexander University in Erlangen/Nuremberg.
- 3.
This is a simplification from previous works [24] where set variables were allowed to occur in the specifier prefix only under some circumstances. It is not hard to see that our simplification does not relinquish relevant expressivity if we permit some normalisation.
- 4.
As usual for the natural numbers, a finite interval \([k,\ell ]\) is \(\{n\in \mathbb {N}\mid k\le n \le \ell \}\) and an infinite interval \([k,\infty )\) is \(\{n \in \mathbb {N}\mid k\le n\}\).
- 5.
‘for some
 ’ is useful for attributes which universally quantify time points (e.g., \(\mathsf{until} \)).
’ is useful for attributes which universally quantify time points (e.g., \(\mathsf{until} \)). - 6.
Readers who long for greater precision may consult the literature [27].
References
Alur, R., Henzinger, T.A.: Real-time logics: complexity and expressiveness. Inf. Comput. 104(1), 35–77 (1993)
Artale, A., Franconi, E., Peñaloza, R., Sportelli, F.: A decidable very expressive description logic for databases. In: d’Amato, C., et al. (eds.) ISWC 2017. LNCS, vol. 10587, pp. 37–52. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-68288-4_3
Artale, A., Kontchakov, R., Lutz, C., Wolter, F., Zakharyaschev, M.: Temporalising tractable description logics. In 14th International Symposium on Temporal Representation and Reasoning (TIME 2007), 28–30 June 2007, Alicante, Spain, pp. 11–22 (2007)
Artale, A., Kontchakov, R., Wolter, F., Zakharyaschev, M.: Temporal description logic for ontology-based data access. In: Proceedings of the 23rd International Joint Conference on Artificial Intelligence, IJCAI 2013, pp. 711–717 (2013)
Baader, F., Borgwardt, S., Koopmann, P., Ozaki, A., Thost, V.: Metric temporal description logics with interval-rigid names. In: Dixon, C., Finger, M. (eds.) FroCoS 2017. LNCS (LNAI), vol. 10483, pp. 60–76. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-66167-4_4
Baader, F., Brandt, S., Lutz, C.: Pushing the \(\cal{EL}\) envelope. In: Kaelbling, L.P., Saffiotti, A. (eds.) Proceedings of the 19th International Joint Conference on Artificial Intelligence (IJCAI 2005), pp. 364–369. Professional Book Center (2005)
Baader, F., Calvanese, D., McGuinness, D., Nardi, D., Patel-Schneider, P. (eds.): The Description Logic Handbook Theory, Implementation, and Applications, 2nd edn. Cambridge University Press (2007)
Baader, F., Ghilardi, S., Lutz, C.: LTL over description logic axioms. ACM Trans. Comput. Log. 13(3) (2012)
Baader, F., Lutz, C., Turhan, A.-Y.: Small is again beautiful in description logics. KI 24(1), 25–33 (2010)
Berardi, D., Calvanese, D., De Giacomo, G.: Reasoning on UML class diagrams. Artif. Intell. 168(1–2), 70–118 (2005)
Borgwardt, S., Thost, V.: Temporal query answering in the description logic EL. In: Proceedings of the Twenty-Fourth International Joint Conference on Artificial Intelligence, IJCAI 2015, Buenos Aires, Argentina, 25–31 July 2015, pp. 2819–2825 (2015)
Bourgaux, C., Ozaki, A.: Querying attributed DL-Lite ontologies using provenance semirings. In: Proceedings of the 33rd AAAI Conference on Artificial Intelligence (2019)
Brandt, S., Kalayci, E., Kontchakov, R., Ryzhikov, V., Xiao, G., Zakharyaschev, M.: Ontology-based data access with a horn fragment of metric temporal logic. In: Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, 4–9 February 2017, San Francisco, California, USA, pp. 1070–1076 (2017)
Brandt, S., Kalayci, E., Ryzhikov, V., Xiao, G., Zakharyaschev, M.: Querying log data with metric temporal logic. J. Artif. Intell. Res. 62, 829–877 (2018)
Carapelle, C., Turhan, A.-Y.: Description logics reasoning w.r.t. general TBoxes is decidable for concrete domains with the EHD-property. In: ECAI 2016–22nd European Conference on Artificial Intelligence, pp. 1440–1448 (2016)
Chandra, A.K., Kozen, D.C., Stockmeyer, L.J.: Alternation. J. ACM 28(1), 114–133 (1981)
Chomicki, J.: Temporal query languages: a survey. In: Gabbay, D.M., Ohlbach, H.J. (eds.) ICTL 1994. LNCS, vol. 827, pp. 506–534. Springer, Heidelberg (1994). https://doi.org/10.1007/BFb0014006
Fisher, M.D., Gabbay, D.M., Vila, L. (eds.): Handbook of Temporal Reasoning in Artificial Intelligence. Elsevier (2005)
Gutiérrez-Basulto, V., Jung, J.C., Ozaki, A.: On metric temporal description logics. In Proceedings of the 22nd European Conference on Artificial Intelligence (ECAI 2016), pp. 837–845. IOS Press (2016)
Harel, D.: Effective transformations on infinite trees, with applications to high undecidability, dominoes, and fairness. J. ACM 33(1), 224–248 (1986)
Hoffart, J., Suchanek, F.M., Berberich, K., Weikum, G.: YAGO2: a spatially and temporally enhanced knowledge base from wikipedia. J. Artif. Intell. 194, 28–61 (2013)
Krötzsch, M.: Ontologies for knowledge graphs? In: Artale, A., Glimm, B., Kontchakov, R. (eds.) Proceedings of the 30th International Workshop on Description Logics (DL 2017). CEUR Workshop Proceedings, vol. 1879, CEUR-WS.org (2017)
Krötzsch, M., Marx, M., Ozaki, A., Thost, V.: Attributed description logics: ontologies for knowledge graphs. In: The Semantic Web - ISWC - 16th International Semantic Web Conference, pp. 418–435 (2017)
Krötzsch, M., Marx, M., Ozaki, A., Thost, V.: Attributed description logics: reasoning on knowledge graphs. In: Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence, IJCAI, pp. 5309–5313 (2018)
Krötzsch, M., Rudolph, S., Hitzler, P.: Complexities of horn description logics. ACM Trans. Comput. Log. 14(1), 2:1–2:36 (2013)
Leo, J., Sattler, U., Parsia, B.: Temporalising EL concepts with time intervals. In: Proceedings of the 27th International Workshop on Description Logics (DL 2014). CEUR Workshop Proceedings, vol. 1193, pp. 620–632. CEUR-WS.org (2014)
Lutz, C.: The complexity of description logics with concrete domains. Ph.D. thesis, RWTH Aachen University, Germany (2002)
Lutz, C.: Combining interval-based temporal reasoning with general TBoxes. Artif. Intell. 152(2), 235–274 (2004)
Lutz, C., Haarslev, V., Möller, R.: A concept language with role-forming predicate restrictions. Technical report, University of Hamburg (1997)
Lutz, C., Möller, R.: Defined topological relations in description logics. In: Brachman, R.J., et al. (eds.) Proceedings of the 1997 International Workshop on Description Logics (DL 1997). URA-CNRS, vol. 410 (1997)
Lutz, C., Wolter, F., Zakharyaschev, M.: Temporal description logics: a survey. In: 15th International Symposium on Temporal Representation and Reasoning, TIME, pp. 3–14 (2008)
Marx, M., Krötzsch, M., Thost, V.: Logic on MARS: ontologies for generalised property graphs. In: Sierra, C. (ed.) Proceedings of the 26th International Joint Conferences on Artificial Intelligence (IJCAI 2017). IJCAI, pp. 1188–1194 (2017)
openCypher community. Cypher Query Language Reference, Version 9. http://www.opencypher.org/resources (2019)
Rodriguez, M.A., Neubauer, P.: Constructions from dots and lines. Bull. Am. Soc. Inf. Sci. Technol. 36(6), 35–41 (2010)
Rogers Jr., H.: Theory of Recursive Functions and Effective Computability, Paperback edn. MIT Press (1987)
Rudolph, S., Krötzsch, M., Hitzler, P.: Cheap boolean role constructors for description logics. In: Hölldobler, S., Lutz, C., Wansing, H. (eds.) JELIA 2008. LNCS (LNAI), vol. 5293, pp. 362–374. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-87803-2_30
Sportelli, F., Franconi, E.: Formalisation of ORM derivation rules and their mapping into OWL. In: Debruyne, C., et al. (eds.) On the Move to Meaningful Internet Systems: OTM 2016 Conferences, OTM 2016. Lecture Notes in Computer Science, vol. 10033, pp. 827–843. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-48472-3_52
Vrandečić, D., Krötzsch, M.: Wikidata: a free collaborative knowledgebase. Commun. ACM 57(10), 78–85 (2014)
Wolter, F., Zakharyaschev, M.: Temporalizing description logics. Front. Combin. Syst. 2, 379–402 (1999)
Acknowledgements
This work is partly supported by the German Research Foundation (DFG) in CRC 248 (Perspicuous Systems), CRC 912 (HAEC), and Emmy Noether grant KR 4381/1-1; and by the European Research Council (ERC) Consolidator Grant 771779 (DeciGUT).
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Appendices
A Proofs for Section 4
Theorem 2
Satisfiability of \(\mathcal {ALCH} ^{\mathbb {T}}_@\) ontologies with the temporal attributes \(\mathsf{time},\mathsf{after} \) and \(\mathsf{before} \) but \(\mathsf{after} \) only in assertions is \(\Sigma ^0_1\)-complete. The problem is \(\Sigma ^0_1\)-hard even with at most one set variable per inclusion.
Proof
We first show hardness. We reduce the word problem for deterministic Turing machines (DTM) to satisfiability of \(\mathcal {ALCH} ^{\mathbb {T}}_@\) ontologies with the temporal attribute \(\mathsf{after} \) occurring only in assertions. A DTM is a tuple  , where:
, where:
-
Q is a finite set of states,
-
\(\Sigma \) is a finite alphabet containing the blank symbol
 ,
, -
\(\{q_{0},q_\mathsf{f}\} \subseteq Q\) are the initial and the final states, resp., and
-
 is the transition function.
is the transition function.
A configuration of \(\mathcal {M}\) is a word \(wqw'\) with \(w,w' \in \Sigma ^*\) and q in Q. The meaning is that the (one-sided infinite) tape contains the word \(ww'\) with only blanks behind it, the machine is in state q and the head is on the left-most symbol of \(w'\). The notion of a successive configuration is defined in the usual way, in terms of the transition relation \(\Theta \). A computation of \(\mathcal {M}\) on a word w is a sequence of successive configurations \(\alpha _0, \alpha _1, \ldots \), where \(\alpha _0=q_0 w\) is the initial configuration for the input w. Let \(\mathcal {M}\) be a DTM and \(w = \sigma _1 \sigma _2 \cdots \sigma _n\) an input word. Assume w.l.o.g. that \(\mathcal {M}\) never attempts to move to the left when its head is in the left-most tape position and that \(q_0\) occurs only in the domain of \(\Theta \) (but not in the range).
We construct an \(\mathcal {ALCH} ^{\mathbb {T}}_@\) ontology \(\mathcal {O} _{\mathcal {M},w} \) with \(\mathsf{after} \) occurring only in assertions that is satisfiable iff \(\mathcal {M}\) accepts w. Models of \(\mathcal {O} _{\mathcal {M},w} \) have a similar structure as in the proof of Theorem 1. We create a vertical chain with:
and ensure that horizontally the set of time points is the same:


Every element representing a tape cell is marked with A in at most one time point (in fact, it will be exactly one):

The main difference is that horizontally we do not have infinitely many sibling nodes. That is, over the naturals, adding the inclusion  would make \(\mathcal {O} _{\mathcal {M},w} \) unsatisfiable and here we cannot use \(\mathsf{after}\) in inclusions. Instead, for each \(q\ne q_\mathsf{f} \) in Q, we add to \(\mathcal {O} _{\mathcal {M},w} \) the inclusions:
would make \(\mathcal {O} _{\mathcal {M},w} \) unsatisfiable and here we cannot use \(\mathsf{after}\) in inclusions. Instead, for each \(q\ne q_\mathsf{f} \) in Q, we add to \(\mathcal {O} _{\mathcal {M},w} \) the inclusions:


where \(S_q\) is a concept name representing a state. Intuitively, each vertically aligned set of elements (w.r.t. time) represents a configuration and a sequence of configurations going backwards in time represents a computation of \(\mathcal {M}\) with input w. The goal is to ensure that \(\mathcal {O} _{\mathcal {M},w} \) is satisfiable iff we reach the final state, that is, w is accepted by \(\mathcal {M}\).
We now add to \(\mathcal {O} _{\mathcal {M},w} \) assertions to trigger the inclusions in Eqs. 24, 25, 26 and 27:

We also use in our encoding concepts \(C_{\sigma } \) for each symbol \(\sigma \in \Sigma \). To encode the input word \(w = \sigma _1 \sigma _2 \cdots \sigma _n\), we add:

for \(1\le i < n\). It is straightforward to add inclusions encoding that (i) the rest of the tape in the initial configuration is filled with the blank symbol, (ii) each node representing a tape cell in a configuration is associated with only one \(C_\sigma \) with \(\sigma \in \Sigma \) and (iii) at most one \(S_q\) with \(q \in Q\) (exactly the node representing the head position). Also, for each element, the time point associated with A is the same for the concepts of the form \(C_\sigma \) and \(S_q\) (if true in the node).
To access the ‘next’ configuration, we use an auxiliary concept F that keeps time points in the future. Recall that since a computation here goes backwards in time, these time points are associated with previous configurations:

We now ensure that tape contents are transferred to the ‘next’ configuration, except for the tape cell at the head position:

for each \(\sigma \in \Sigma \), where \(S_{\overline{q}}\) is a shorthand for \(\lnot \bigsqcup _{q\in Q}S_q\). Finally we encode the transition function. We explain for \(\Theta (q,\sigma )=(q',\tau ,D)\) with \(D = r\) (the case with \(D=l\) can be handled analogously). We encode that the ‘next’ state is \(q'\):

and change to \(\tau \) the tape cell at the (previous) head position:

Equation 28 also increments the head position.
This finishes our reduction.
For the upper bound, we point out that if an \(\mathcal {ALCH} ^{\mathbb {T}}_@\) ontology \(\mathcal {O}\) with \(\mathsf{after}\) only in assertions is satisfiable then there is a satisfiable ontology \(\mathcal {O} '\) that is the result of replacing each occurrence of \(\mathsf{after}:k\) in \(\mathcal {O}\) by some \(\mathsf{time}:l\) with \(k<l\in \mathbb {N}\). By Theorem 5, one can decide satisfiability of \(\mathcal {O} '\) (that is, satisfiability of ontologies with only the temporal attributes \(\mathsf{time} \) and \(\mathsf{before} \)). As the replacements of \(\mathsf{after}:k\) by \(\mathsf{time}:l\) in assertions can be enumerated, it follows that satisfiability of \(\mathcal {ALCH} ^{\mathbb {T}}_@\) ontologies is in \(\Sigma ^0_1\). \(\square \)
Proofs for Section 5
Theorem 3
Satisfiability of ground \(\mathcal {ALCH} ^{\mathbb {T}}_@\) ontologies is ExpTime-complete.
Proof
The construction of an ontology \(\mathcal {O} ^\dagger \) was already given in the main text. It remains to show that \(\mathcal {O} \) is satisfiable iff \(\mathcal {O} ^\dagger \) is satisfiable. Given a model  of \(\mathcal {O} \), we directly obtain an \(\mathcal {ALCH} {b}\) interpretation \(\mathcal {J}\) over
of \(\mathcal {O} \), we directly obtain an \(\mathcal {ALCH} {b}\) interpretation \(\mathcal {J}\) over  by undoing the renaming and applying
by undoing the renaming and applying  , i.e., by mapping \(A_{S} \in \mathsf {N_{C}} \) to
, i.e., by mapping \(A_{S} \in \mathsf {N_{C}} \) to  , \(r_{S} \in \mathsf {N_{R}} \) to
, \(r_{S} \in \mathsf {N_{R}} \) to  , and
, and  to
to  . By the semantics of \(\mathcal {ALCH} ^{\mathbb {T}}_@\), \(\mathcal {J}\models \mathcal {O} ^\dagger \). Conversely, given an \(\mathcal {ALCH} {b}\) model \(\mathcal {J}\) of \(\mathcal {O} ^{\dagger }\), we construct an interpretation
. By the semantics of \(\mathcal {ALCH} ^{\mathbb {T}}_@\), \(\mathcal {J}\models \mathcal {O} ^\dagger \). Conversely, given an \(\mathcal {ALCH} {b}\) model \(\mathcal {J}\) of \(\mathcal {O} ^{\dagger }\), we construct an interpretation  of \(\mathcal {ALCH} ^{\mathbb {T}}_@\) with \(\Delta ^{\mathcal {I}}_T=[\max (0,k_\mathsf{min}-2),k_\mathsf{max}+2]\) and
of \(\mathcal {ALCH} ^{\mathbb {T}}_@\) with \(\Delta ^{\mathcal {I}}_T=[\max (0,k_\mathsf{min}-2),k_\mathsf{max}+2]\) and  , where \(\mathbb {T}\) is the set of temporal attributes and \(\star \) is a fresh individual name. We define
, where \(\mathbb {T}\) is the set of temporal attributes and \(\star \) is a fresh individual name. We define  for all \(a \in \mathsf {N_{I}} \cup \mathsf {N_{T}} \cup \mathsf {N^2_{T}} \).
for all \(a \in \mathsf {N_{I}} \cup \mathsf {N_{T}} \cup \mathsf {N^2_{T}} \).
For a ground closed specifier S with \(a_{1}{:}\,b_{1}, \cdots , a_{n}{:}\,b_{n}\) as non-temporal attributes, we define:

Similarly, for a ground open specifier S with \(a_{1}{:}\,b_{1}, \cdots , a_{n}{:}\,b_{n}\) as non-temporal attribute-value pairs, we define:

To simplify the presentation, we write \(a{:}\,b \in S\) if \(a{:}\,b\) occurs in S. Furthermore, let  be the set of all tuples
be the set of all tuples  such that one of the following holds:
such that one of the following holds:
-
\(\delta \in A_{S}^{\mathcal {J}}, \mathsf{during} {:}\,v \in S\) and \( i\in v\);
-
\(\delta \in A_{S}^{\mathcal {J}}, \mathsf{after} {:}\,k_\mathsf{max} \in S\) and \( i=k_\mathsf{max} + 1\);
-
\(\delta \in A_{S}^{\mathcal {J}}, \mathsf{since} {:}\,k_\mathsf{max} \in S\) and \( k_\mathsf{max} + 1\le i\le k_\mathsf{max} + 2\);
-
\(\delta \in A_{S}^{\mathcal {J}}, \mathsf{before} {:}\,k_\mathsf{min} \in S, i=k_\mathsf{min} - 1\) and \( k_\mathsf{min} >0\);
-
\(\delta \in A_{S}^{\mathcal {J}}, \mathsf{until} {:}\,k_\mathsf{min} \in S, \max (k_\mathsf{min} - 2,0)\le i\le k_\mathsf{min} - 1\) and \( k_\mathsf{min}>0\).
We define \(r^{\mathcal {I} _i}\) analogously. Given the definitions of \(A^{\mathcal {I} _i}\) and \(r^{\mathcal {I} _i}\), for all \(i \in \mathbb {N}\), \(A \in \mathsf {N_{C}} \) and \(r \in \mathsf {N_{R}} \), we define \(\cdot ^\mathcal {I} \) as in Definition 8.
Claim
For all \(A_S,r_S\) occurring in \(\mathcal {O} ^\dagger \): (1)  and (2)
and (2)  .
.
Proof of the Claim
If no temporal attribute occurs in S then by definition of \(\mathcal {I}\) (in particular, \(F_S\)), we clearly have that \(\delta \in A^\mathcal {J} _S\) iff  . Also, by semantics of \(\mathcal {ALCH} ^{\mathbb {T}}_@\), for a ground specifier S with a non-empty set \(S_\mathbb {T} \) of temporal attributes the following holds for any \(\mathcal {I}\) and concept
. Also, by semantics of \(\mathcal {ALCH} ^{\mathbb {T}}_@\), for a ground specifier S with a non-empty set \(S_\mathbb {T} \) of temporal attributes the following holds for any \(\mathcal {I}\) and concept  :
:

So we can consider  with S containing only one temporal attribute. We argue for \(\mathsf{during}\) and \(\mathsf{between}\) (one can give a similar argument for the other temporal attributes):
with S containing only one temporal attribute. We argue for \(\mathsf{during}\) and \(\mathsf{between}\) (one can give a similar argument for the other temporal attributes):
-
if the temporal attribute-value pair \(\mathsf{during} {:}\,v\) is in S then, by definition of \(\mathcal {I}\) (and \(F_S\)), \(\delta \in A^\mathcal {J} _S\) iff
 ;
; -
if the temporal attribute-value pair \(\mathsf{between} {:}\,v\) is in S then, by Eq. 23, \(\delta \in A^\mathcal {J} _S\) iff \(\delta \in \bigcup _{k\in v\cap \mathbb {N}_\mathcal {O} }A^\mathcal {J} _{S(\mathsf{during} {:}\,[k,k])}\). By definition of \(\mathcal {I}\), \(\delta \in A^\mathcal {J} _{S(\mathsf{during} {:}\,[k,k])}\) iff
 , for \(k\in v\cap \mathbb {N}_\mathcal {O} \). Then,
, for \(k\in v\cap \mathbb {N}_\mathcal {O} \). Then, 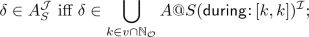
so
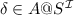 .
.
In the definition of \(\mathbb {N}_\mathcal {O} \), we add \(k_i+1\) for each \(k_i\) occurring in \(\mathcal {O} \), to ensure that axioms such as  with \(l-k\ge 2\) remain satisfiable. Also, in the definition of \(\mathcal {I}\) we use the interval \(\Delta ^\mathcal {I} _T = [\max (0,k_\mathsf{min} -2),k_\mathsf{max} +2]\), and so, we give a margin of two ‘additional’ points in each side of the interval \([k_\mathsf{min},k_\mathsf{max}]\) used in the translation. This is to ensure that axioms such as
with \(l-k\ge 2\) remain satisfiable. Also, in the definition of \(\mathcal {I}\) we use the interval \(\Delta ^\mathcal {I} _T = [\max (0,k_\mathsf{min} -2),k_\mathsf{max} +2]\), and so, we give a margin of two ‘additional’ points in each side of the interval \([k_\mathsf{min},k_\mathsf{max}]\) used in the translation. This is to ensure that axioms such as  with \(k_\mathsf{min}\ge 2\) remain satisfiable. Point (2) can be proven with an easy adaptation of Point (1).
with \(k_\mathsf{min}\ge 2\) remain satisfiable. Point (2) can be proven with an easy adaptation of Point (1).
The Claim directly implies that  . Note that \(\star \) ensures that axioms such as
. Note that \(\star \) ensures that axioms such as  remain satisfiable. \(\square \)
remain satisfiable. \(\square \)
Theorem 4
Satisfiability in \(\mathcal {ALCH} ^{\mathbb {T}}_@\) is 2ExpTime-complete for ontologies without expressions of the form X.a; \(a{:}\,x\) with x in \(\mathsf{Var}(\mathsf {N_{T}}) \); and \(a{:}\,[t,t']\) with one of \(t,t'\) in \(\mathsf{Var}(\mathsf {N_{T}}) \), where a is a temporal attribute.
Proof
The 2ExpTime lower bound follows from the fact that satisfiability of \(\mathcal {ALCH} _@\) (so without temporal attributes) is already 2ExpTime-hard [23]. Our proof strategy for the upper bound consists on defining an ontology with grounded versions of inclusion axioms. Let \(\mathcal {O} \) be an \(\mathcal {ALCH} ^{\mathbb {T}}_@\) ontology and let  be the union of the sets of individual names, time points, and intervals, occurring in \(\mathcal {O} \), respectively. Let
be the union of the sets of individual names, time points, and intervals, occurring in \(\mathcal {O} \), respectively. Let  be an interpretation of \(\mathcal {ALCH} ^{\mathbb {T}}_@\) over the domain
be an interpretation of \(\mathcal {ALCH} ^{\mathbb {T}}_@\) over the domain  , where \(x\) is a fresh individual name, satisfying
, where \(x\) is a fresh individual name, satisfying  for all \(a \in \mathsf{N}\). Let
for all \(a \in \mathsf{N}\). Let  be a variable assignment, where
be a variable assignment, where  . Consider a concept inclusion \(\alpha \) of the form \({X_1}\,{\varvec{:}}\,{S_1}, \ldots , {X_n}\,{\varvec{:}}\,{S_n}\ (C\sqsubseteq D)\). We say that \(\mathcal {Z}\) is compatible with \(\alpha \) if
. Consider a concept inclusion \(\alpha \) of the form \({X_1}\,{\varvec{:}}\,{S_1}, \ldots , {X_n}\,{\varvec{:}}\,{S_n}\ (C\sqsubseteq D)\). We say that \(\mathcal {Z}\) is compatible with \(\alpha \) if  for all \(1 \le i \le n\). In this case, the \(\mathcal {Z}\)-instance \(\alpha _{\mathcal {Z}}\) of \(\alpha \) is the concept inclusion \(C' \sqsubseteq D'\) obtained by
for all \(1 \le i \le n\). In this case, the \(\mathcal {Z}\)-instance \(\alpha _{\mathcal {Z}}\) of \(\alpha \) is the concept inclusion \(C' \sqsubseteq D'\) obtained by
-
replacing each \(X_{i}\) by
 ;
; -
replacing every \(a {:}\,X_{i}.b\) occurring in some specifier (with a, b non-temporal attributes) by all \(a {:}\,c\) such that
 ; and
; and -
replacing each object variable x by \(\mathcal {Z}(x)\).
Then, the grounding \(\mathcal {O} _g \) of \(\mathcal {O} \) contains all \(\mathcal {Z}\)-instances \(\alpha _{\mathcal {Z}}\) for all concept inclusions \(\alpha \) in \(\mathcal {O} \) and all compatible variable assignments \(\mathcal {Z}\); and analogous axioms for role inclusions.
There may be (at most) exponentially many different instances for each terminological axiom in \(\mathcal {O} \), thus \(\mathcal {O} _g \) is of exponential size. We show that \(\mathcal {O} \) is satisfiable iff \(\mathcal {O} _g \) is satisfiable. By construction, we have \(\mathcal {O} \models \mathcal {O} _g \), i.e., any model of \(\mathcal {O} \) is also a model of \(\mathcal {O} _g \). Conversely, let  be a model of \(\mathcal {O} _g \). W.l.o.g., assume that there is \(x\in \Delta ^\mathcal {I} \) such that
be a model of \(\mathcal {O} _g \). W.l.o.g., assume that there is \(x\in \Delta ^\mathcal {I} \) such that  for all \(a \in \mathsf {N_I^{\mathcal {O} }} \setminus \{x\}\). For an annotation set
for all \(a \in \mathsf {N_I^{\mathcal {O} }} \setminus \{x\}\). For an annotation set  , we define \(\mathop {{\text {rep}}}_{x}\!{\left( {F}\right) }\) to be the annotation set obtained from F by replacing any individual
, we define \(\mathop {{\text {rep}}}_{x}\!{\left( {F}\right) }\) to be the annotation set obtained from F by replacing any individual  in F by \(x\).
in F by \(x\).
Let \(\sim \) be the equivalence relation induced by \(\mathop {{\text {rep}}}_{x}\!{\left( {F}\right) } = \mathop {{\text {rep}}}_{x}\!{\left( {G}\right) }\) and define an interpretation \(\mathcal {J}\) of \(\mathcal {ALCH} ^{\mathbb {T}}_@\) over the domain  , where
, where  for all \(A \in \mathsf {N_{C}} \),
for all \(A \in \mathsf {N_{C}} \),  for all \(r \in \mathsf {N_{R}} \), and
for all \(r \in \mathsf {N_{R}} \), and  for all \(a \in \mathsf {N_{I}} \cup \mathsf {N_{T}} \cup \mathsf {N^2_{T}} \). It remains to show that \(\mathcal {J}\) is indeed a model of \(\mathcal {O} \). Suppose for a contradiction that there is a concept inclusion \(\alpha \) in \(\mathcal {O} \) that is not satisfied by \(\mathcal {J}\) (the case for role inclusions is analogous). Then we have some compatible variable assignment \(\mathcal {Z}\) that leaves \(\alpha \) unsatisfied. Let \({\mathcal {Z}}_{x}\) be the variable assignment \(X \mapsto \mathop {{\text {rep}}}_{x}\!{\left( {\mathcal {Z}(X)}\right) }\) for all \(X\in \mathsf {N_{V}} \). Clearly, as expressions of the form \(a {:}\,X_{i}.b\), \(a{:}\,x\), and \(a{:}\,[t,t']\) with at least one of \(t,t'\) an object variable, are not allowed for a, b being temporal attributes, \(\mathcal {Z}_{x}\) is also compatible with \(\alpha \). But now we have
for all \(a \in \mathsf {N_{I}} \cup \mathsf {N_{T}} \cup \mathsf {N^2_{T}} \). It remains to show that \(\mathcal {J}\) is indeed a model of \(\mathcal {O} \). Suppose for a contradiction that there is a concept inclusion \(\alpha \) in \(\mathcal {O} \) that is not satisfied by \(\mathcal {J}\) (the case for role inclusions is analogous). Then we have some compatible variable assignment \(\mathcal {Z}\) that leaves \(\alpha \) unsatisfied. Let \({\mathcal {Z}}_{x}\) be the variable assignment \(X \mapsto \mathop {{\text {rep}}}_{x}\!{\left( {\mathcal {Z}(X)}\right) }\) for all \(X\in \mathsf {N_{V}} \). Clearly, as expressions of the form \(a {:}\,X_{i}.b\), \(a{:}\,x\), and \(a{:}\,[t,t']\) with at least one of \(t,t'\) an object variable, are not allowed for a, b being temporal attributes, \(\mathcal {Z}_{x}\) is also compatible with \(\alpha \). But now we have  for all \(\mathcal {ALCH} ^{\mathbb {T}}_@\) concepts C, yielding the contradiction
for all \(\mathcal {ALCH} ^{\mathbb {T}}_@\) concepts C, yielding the contradiction  . Thus, \(\mathcal {O} \) is satisfiable iff \(\mathcal {O} _g \) is satisfiable. The result then follows from Theorem 3. \(\square \)
. Thus, \(\mathcal {O} \) is satisfiable iff \(\mathcal {O} _g \) is satisfiable. The result then follows from Theorem 3. \(\square \)
Theorem 5
Satisfiability of \(\mathcal {ALCH} ^{\mathbb {T}}_@\) ontologies with only the temporal attributes \(\mathsf{during},\mathsf{time},\mathsf{before} \) and \(\mathsf{until} \) is in 3ExpTime.
Proof
The difference w.r.t. the proof of Theorem 4 is that here expressions of the form \(a {:}\,X_{i}.b\), \(a{:}\,x\), and \(a{:}\,[t,t']\) with at least one of \(t,t'\) an object variable, may occur in front of the temporal attributes \(\mathsf{during},\mathsf{before},\mathsf{time} \) and \(\mathsf{until} \) and the other temporal attributes are not allowed (not even in assertions). Let v be the internal [0, k], where k is the largest number occurring in \(\mathcal {O} \) (or 0 if no number occurs). To define our ground translation, we consider variable assignments  , where
, where  and \(\Delta ^\mathcal {I} \) is the set of all individual names in \(\mathcal {O} \) plus a fresh individual name \(x\), all time points in v and all intervals contained in v. This gives us a ground ontology \(\mathcal {O} _g \) with size double-exponential in the size of \(\mathcal {O} \). Clearly, \(\mathcal {O} \) is satisfiable iff \(\mathcal {O} _g \) is satisfiable. \(\square \)
and \(\Delta ^\mathcal {I} \) is the set of all individual names in \(\mathcal {O} \) plus a fresh individual name \(x\), all time points in v and all intervals contained in v. This gives us a ground ontology \(\mathcal {O} _g \) with size double-exponential in the size of \(\mathcal {O} \). Clearly, \(\mathcal {O} \) is satisfiable iff \(\mathcal {O} _g \) is satisfiable. \(\square \)
Theorem 6
Satisfiability of \(\mathcal {ALCH} ^{\mathbb {T}}_@\) ontologies with only \(\mathsf{time} \) and \(\mathsf{before} \) is 3ExpTime-hard.
Proof
We reduce the word problem for double-exponentially space-bounded alternating Turing machines (ATMs) to the entailment problem for \(\mathcal {ALCH} ^{\mathbb {T}}_@\) ontologies. We consider w.l.o.g. ATMs with only finite computations on any input. As usual, an ATM is a tuple  , where:
, where:
-
\(Q = Q_{\exists } \uplus Q_{\forall }\) is a finite set of states, partitioned into existential states \(Q_{\exists }\) and universal states \(Q_{\forall }\),
-
\(\Sigma \) is a finite alphabet containing the blank symbol
 ,
, -
\(q_{0} \in Q\) is the initial state, and
-
 is the transition relation.
is the transition relation.
We use the same notions of configuration, computation and initial configuration given in the proof of Theorem 2. We recall the acceptance condition of an ATM. A configuration \(\alpha =wqw'\) is accepting iff
-
\(\alpha \) is a universal configuration and all its successor configurations are accepting, or
-
\(\alpha \) is an existential configuration and at least one of its successor configurations is accepting.
Note that, by the definition above, universal configurations without any successors are accepting. We assume w.l.o.g. that all configurations wqw of a computation of \(\mathcal {M}\) satisfy \(|ww'|\le 2^{2^n}\). \(\mathcal {M}\) accepts a word in  (in space double-exponential in the size of the input) iff the initial configuration is accepting.
(in space double-exponential in the size of the input) iff the initial configuration is accepting.
There exists a double-exponentially space bounded ATM  whose word problem is 3ExpTime-hard [16]. Let \(\mathcal {M}\) be such a double-exponentially space bounded ATM and \(w = \sigma _{1}\sigma _{2}\cdots \sigma _{n}\) an input word. W.l.o.g., we assume that \(\mathcal {M}\) never attempts to move to the left (right) when the head is on the left-most (right-most) tape cell.
whose word problem is 3ExpTime-hard [16]. Let \(\mathcal {M}\) be such a double-exponentially space bounded ATM and \(w = \sigma _{1}\sigma _{2}\cdots \sigma _{n}\) an input word. W.l.o.g., we assume that \(\mathcal {M}\) never attempts to move to the left (right) when the head is on the left-most (right-most) tape cell.
We construct an \(\mathcal {ALCH} ^{\mathbb {T}}_@\) ontology \(\mathcal {O} _{\mathcal {M},w} \) that entails A(a) iff \(\mathcal {M}\) accepts w. We represent configurations using individuals in \(\mathcal {O} _{\mathcal {M},w} \), which are connected to the corresponding successor configurations by roles encoding the transition. W.l.o.g., we assume that these individuals form a tree, which we call the configuration tree. Furthermore, each node of this tree, i.e., each configuration, is connected to \(2^{2^{n}}\) individuals representing the tape cells. The main ingredients of our construction are:
-
an individual a denoting the root of the configuration tree;
-
an attribute \(\mathsf {bit} \), with values in
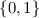 , used to encode double-exponentially many tape positions;
, used to encode double-exponentially many tape positions; -
an attribute \(\mathsf {flip}\) which has value 1 at a (unique) time point where \(\mathsf {bit} \) has value 0 and \(\mathsf {bit} \) has value 1 in all subsequent time points;
-
a concept A marking accepting configurations;
-
a concept H marking the head position;
-
a concept T marking tape cells;
-
a concept I marking the initial configuration;
-
concepts \(S_{q}\) for each state \(q \in Q\);
-
concepts \(C_{\sigma } \) for each symbol \(\sigma \in \Sigma \);
-
roles \(r_{\theta }\) for all transitions \(\theta \in \Theta \);
-
a role \(\mathsf {tape} \) connecting configurations to tape cells; and
-
attributes \(a_0,\ldots ,a_n\) to encode the binary representation of time values.
To encode the binary representation of time values we first state that for \(\mathsf{time} {:}\,2^n-1\) we have all \(a_i\) set to 1:

We now use the following intuition: if the \(a_i\) attributes represent a pattern \(s\cdot 1000\), where s is a binary sequence and \(\cdot \) means concatenation, then \(s\cdot 0111\) should occur before that pattern in the time line. To ensure this, we add concept inclusions of the form, for all \(0\le i\le n\):

where S is  and \(P^X_{a_{i}}\) abbreviates
and \(P^X_{a_{i}}\) abbreviates
By further adding a concept inclusion encoding that \(a_i\) can only be one of 1, 0 at the same time point we have that, in any model, the \(a_i\) attributes encode the binary representation of the corresponding time value, for time points in \([0,2^n-1]\). This means that, for time points in \([0,2^n-1]\), we can simulate the temporal attribute \(\mathsf{after} \) by using variables and specifiers of the form  and
and  , for all \(0\le i\le n\).
, for all \(0\le i\le n\).
Remark 1
To simplify the presentation, in the following, we use the temporal attributes \(\mathsf{after} \) and \(\mathsf{during} \) (the latter is used to encode the initial configuration). Given the construction above it is straightforward to replace the inclusions using \(\mathsf{after} \) and \(\mathsf{during} \) with inclusions using the attributes \(a_i\).
We encode the meaning of the attribute \(\mathsf {flip}\) (i.e., it has value 1 at the time point from which bits should be flipped to increment a tape position) with the following concept inclusions:



Intuitively, in Eq. 29 we say that if there is a time point where we have \(\mathsf {bit} \) with value 0 then there is a time point where we should flip some bit to increment the tape position, i.e., where \(\mathsf {flip} \) is 1. In Eq. 30 we state that there is no \(\mathsf {bit} \) with value 0 after a time point marked with \(\mathsf {flip} \) set to 1. Finally, in Eq. 31, we state that \(\mathsf {bit} \) has value 0 where \(\mathsf {flip} \) has value 1. Thus, Eqs. 30 and 31 ensure that there is at most one time point where \(\mathsf {flip} \) has value 1.
Let \(\mathbf {\Omega }\) be a sequence with the following variables \(X^j_i\), with \(1\le i\le n\) and \(1\le j\le 5\), and their respective specifiers:
-
 , we look at our auxiliary attribute that indicates from which time point we should flip our bits to obtain the next tape position (this will be a time point with bit value 0);
, we look at our auxiliary attribute that indicates from which time point we should flip our bits to obtain the next tape position (this will be a time point with bit value 0); -
we also define
 and
and  , to filter time points with \(\mathsf {bit} \) values 0 and 1, respectively, before the time point with \(\mathsf {flip}: 1\), related to \(X^1_i\);
, to filter time points with \(\mathsf {bit} \) values 0 and 1, respectively, before the time point with \(\mathsf {flip}: 1\), related to \(X^1_i\); -
we use
 and
and  to filter time points \(\mathsf {bit} \) values 0 and 1, respectively.
to filter time points \(\mathsf {bit} \) values 0 and 1, respectively.
Basically, the first three variables are related to specifiers that filter the information needed to increment the tape position encoded with the \(\mathsf {bit} \) attribute. The last two variables \(X^j_i\) are related to specifiers that filter the information needed to copy the tape position. We now define specifiers \(S^j_i, S_i\), for \(1\le i\le n\) and \(1\le j\le 5\). Intuitively, the next four specifiers are used to increment the tape position, using the information given by the \(X^j_i\) variables. The last two specifiers copy the tape position, again using the information given by the \(X^j_i\) variables:
-
the negation of a concept expression associated with
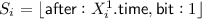 ensures that we have \(\mathsf {bit}:0\) in all time points after the time point marked with \(\mathsf {flip}:1\) in the previous position;
ensures that we have \(\mathsf {bit}:0\) in all time points after the time point marked with \(\mathsf {flip}:1\) in the previous position; -
we use
 to flip to 1 the bit marked with \(\mathsf {flip}:1\) in the previous position;
to flip to 1 the bit marked with \(\mathsf {flip}:1\) in the previous position; -
in addition, we define
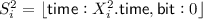 and
and 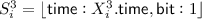 to transfer to the next tape position bit values which should not be flipped (i.e., those that are before the time point with \(\mathsf {flip}: 1\));
to transfer to the next tape position bit values which should not be flipped (i.e., those that are before the time point with \(\mathsf {flip}: 1\)); -
finally, we define
 and
and 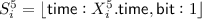 , to receive a copy of the \(\mathsf {bit} \) values.
, to receive a copy of the \(\mathsf {bit} \) values.
To simplify the presentation, we define the abbreviations \(P_i,P^+_i,P^=_i\) for the following concepts, respectively, to be used in concept inclusions with \(\mathbf {\Omega }\):
-
\(\bigsqcap _{1\le j\le 5} T @ X^j_i \), we filter the bits encoding a tape position and the information of which bits should be flipped in order to increment it;
-
\(\bigsqcap _{1\le j\le 3} T @ S^j_i \sqcap \lnot T @ S_i \), we increment the tape position,
-
\(\bigsqcap _{4\le j\le 5} T @ S^j_i\), we copy the tape position.
We may also write \(P,P^+,P^=\) if \(i=1\).
Encoding the Initial Configuration. We add assertions to \(\mathcal {O} _{\mathcal {M},w} \) that encode the initial configuration of \(\mathcal {M}\). We mark the root of the configuration tree with the initial state by adding \(S_{q_{0}}(a)\) and initialise the tape cells with the input word by adding I(a) and the concept inclusions:

The intuition is as follows. In the first inclusion, we place the head, represented by the concept H, in the first position of the tape and fill the tape cell with the first symbol of the input word, represented by the concept \(C_{\sigma _1} \). We then add the remaining symbols of the input word in their corresponding tape positions. In the last inclusion we add a blank symbol after the input word. We now add the following concept inclusion fill the remaining tape cells with blank in the initial configuration marked with the concept I:

Synchronising Configurations. For each transition \(\theta \in \Theta \), we make sure that tape contents are transferred to successor configurations, except for the tape cell at the head position:
We now encode our transitions \(\theta = (q, \sigma , q', \tau , D ) \in \Theta \) with concept inclusions of the form (we explain for \(D=r\), the case \(D=l\) is analogous):
Essentially, if the head is at position P then, to move it to the right, we increment the head position using \(P^{+}\) in the successor configuration. We use the specifiers in \(\mathbf {\Omega }\) to modify the tape cell with \(C_{\sigma } \) in the head position to \(C_{\tau } \) in the successor configuration.
Acceptance Condition. Finally, we add concept inclusions that propagate acceptance from the leaf nodes of the configuration tree backwards to the root of the tree. For existential configurations, we add \(S_{q} \sqcap \exists r_{\theta }.A \sqsubseteq A\) for each \(q \in Q_{\exists }\), whereas to handle universal configurations, we add, for each \(q \in Q_{\forall }\), the concept inclusion

where the conjunction may be empty if there are no suitable \(\theta \in \Theta \).
With an inductive argument along the recursive definition of acceptance, we show that \(\mathcal {O} _{\mathcal {M},w} \models A(a)\) iff \(\mathcal {M}\) accepts w.
Given a natural number \(i< 2^{2^{n}}\), we write \(i_{\mathbf {b}}[j]\) for the value of the j-th bit of the binary representation of i using \(2^n\) bits, where \(i_{\mathbf {b}}[0]\) is the value the most significant bit. In the following, we write \(B_i\) as a shorthand for the concept:

Following the terminology provided in [25], given an interpretation \(\mathcal {I}\) of \(\mathcal {ALCH} ^{\mathbb {T}}_@\), we say that an element \(\delta \in \Delta ^\mathcal {I} _I\) represents a configuration \(\tau _1 \ldots \tau _{i-1}q \tau _{i}\ldots \tau _m\) if  , for some \(F \in \Phi ^{\mathcal {I}}\), \(\delta \in (\exists \mathsf {tape}.(B_i\sqcap H))^\mathcal {I} \) and \(\delta \in (\exists \mathsf {tape}.(B_j\sqcap C_{\tau _j}))^\mathcal {I} \), for all \(0\le j < 2^{2^n}\). We are now ready to show Claims 1 and 2.
, for some \(F \in \Phi ^{\mathcal {I}}\), \(\delta \in (\exists \mathsf {tape}.(B_i\sqcap H))^\mathcal {I} \) and \(\delta \in (\exists \mathsf {tape}.(B_j\sqcap C_{\tau _j}))^\mathcal {I} \), for all \(0\le j < 2^{2^n}\). We are now ready to show Claims 1 and 2.
Claim 1
If \(\delta \in \Delta ^\mathcal {I} _I\) represents a configuration \(\alpha \) and some transition \(\theta \in \Theta \) is applicable to \(\alpha \) then \(\delta \) has an \(r_\theta \)-successor that represents the result of applying \(\theta \) to \(\alpha \).
Proof of the Claim 1
Let \(\delta \in \Delta ^\mathcal {I} _I\) be an element representing a configuration \(\alpha \) and assume \(\theta \in \Theta \) is applicable to \(\alpha \). To synchronise configurations, we added to \(\mathcal {O} _{\mathcal {M},w}\) concept inclusions that (1) ensure that tape contents other than the content at the head position are copied to all \(r_\theta \)-successors of \(\delta \); and (2) create an \(r_\theta \)-successor that represents the correct state, position of the head and corresponding symbols at the previous and current position of the head. Then our concept inclusions ensure that \(\delta \) has an \(r_\theta \)-successor that represents the result of applying \(\theta \) to \(\alpha \).
Claim 2
w is accepted by \(\mathcal {M}\) iff \(\mathcal {O} _{\mathcal {M},w} \models A(a)\).
Proof of the Claim 2
Consider an arbitrary interpretation \(\mathcal {I}\) of \(\mathcal {ALCH} ^{\mathbb {T}}_@\) that satisfies \(\mathcal {O} _{\mathcal {M},w}\). First we show that if any element \(\delta \in \Delta ^\mathcal {I} _I\) represents an accepting configuration then  , for some \(F \in \Phi ^{\mathcal {I}}\). We make a case distinction.
, for some \(F \in \Phi ^{\mathcal {I}}\). We make a case distinction.
-
If \(\alpha \) is a universal configuration, then all successor configurations of \(\alpha \) must be accepting. By Claim 1, for any \(\theta \)-successor configuration \(\alpha '\) of \(\alpha \) there is a corresponding \(r_\theta \)-successor \(\delta '\) of \(\delta \). By induction hypothesis for \(\alpha '\), \((\delta ',F')\) is in \(A^\mathcal {I} \), for some \(F' \in \Phi ^{\mathcal {I}}\). Since this holds for all \(\theta \)-successor configurations of \(\alpha \), our concept inclusion encoding acceptance of universal configurations implies that
 , for some \(F \in \Phi ^{\mathcal {I}}\), as required. This argument covers the base case where \(\alpha \) has no successors.
, for some \(F \in \Phi ^{\mathcal {I}}\), as required. This argument covers the base case where \(\alpha \) has no successors. -
If \(\alpha \) is an existential configuration, then there is some accepting \(\theta \)-successor configuration \(\alpha '\) of \(\alpha \). By Claim 1, there is an \(r_\theta \)-successor \(\delta '\) of \(\delta \) that represents \(\alpha '\) and, by induction hypothesis,
 , for some \(F' \in \Phi ^{\mathcal {I}}\). Then, our concept inclusion encoding acceptance of existential configurations applies and so, we conclude that
, for some \(F' \in \Phi ^{\mathcal {I}}\). Then, our concept inclusion encoding acceptance of existential configurations applies and so, we conclude that  , for some \(F \in \Phi ^{\mathcal {I}}\).
, for some \(F \in \Phi ^{\mathcal {I}}\).
Since elements in \(I^\mathcal {I} \) represent the initial configuration of \(\mathcal {M}\), this shows that \(I^\mathcal {I} \subseteq A^\mathcal {I} \) when the initial configuration is accepting. As I(a) is an assertion in \(\mathcal {O} _{\mathcal {M},w}\), we have that \((a^\mathcal {I},G)\in A^\mathcal {I} \), for some \(G \in \Phi ^{\mathcal {I}}\).
We now show that if the initial configuration is not accepting, then there is some interpretation \(\mathcal {I}\) of \(\mathcal {ALCH} ^{\mathbb {T}}_@\) such that \(I^\mathcal {I} \not \subseteq A^\mathcal {I} \), in particular, \((a^\mathcal {I},G)\not \in A^\mathcal {I} \), for all \(G \in \Phi ^{\mathcal {I}}\). To show this we construct a canonical interpretation \(\mathcal {J} \) of \(\mathcal {O} _{\mathcal {M},w}\) as follows. Let  be the set of all possible \(\mathcal {M}\) configurations with size bounded by \(2^{2^n}\). Also, we define a set
be the set of all possible \(\mathcal {M}\) configurations with size bounded by \(2^{2^n}\). Also, we define a set  , containing individuals that represent tape cells, related to each possible configuration of a computation of \(\mathcal {M}\). The domain \(\Delta ^\mathcal {J} \) is a disjoint union of \(\Delta ^\mathcal {J} _I\cup \Delta ^\mathcal {J} _T\cup \Delta ^\mathcal {J} _{2T}\), where:
, containing individuals that represent tape cells, related to each possible configuration of a computation of \(\mathcal {M}\). The domain \(\Delta ^\mathcal {J} \) is a disjoint union of \(\Delta ^\mathcal {J} _I\cup \Delta ^\mathcal {J} _T\cup \Delta ^\mathcal {J} _{2T}\), where:
-
\(\Delta ^\mathcal {J} _I = \mathsf{Con}_\mathcal {M} \cup \mathsf{Tp}_\mathcal {M} \cup \mathbb {T}\), where \(\mathbb {T}\subseteq \mathsf {N_{I}} \) is either \(\mathsf{time} \) or \(\mathsf{before} \);
-
\(\Delta ^\mathcal {J} _T = \{0^\mathcal {J},\ldots , (2^n-1)^\mathcal {J} \}\); and \(\Delta ^\mathcal {J} _{2T} = \Delta ^\mathcal {J} _T \times \Delta ^\mathcal {J} _T\).
The extension of the concepts \(C_\sigma \), H and \(B_j\) in the interpretation is defined as expected so that every element \(\alpha \cdot c^i_\sigma \in \mathsf{Tp}_\mathcal {M} \) is in \(C_\sigma \) and \(B_i\) and no other \(C_{\tau }\) or \(B_j\), with \(\tau \ne \sigma \) or \(i\ne j\). Also, \(\alpha \cdot c^i_\sigma \) is in H iff \(\alpha \) is of the form \(wqw'\) and \(|w| = i-1\). We connect \(\alpha \) to \(\alpha \cdot c^i_\sigma \) using the role \(\mathsf {tape} \) iff \(\alpha \) has \(\sigma \) at position i. Moreover, \(\alpha \) is in \(S_q\) iff \(\alpha \) is of the form \(wqw'\). We then have that every configuration \(\alpha \in \mathsf{Con}_\mathcal {M} \) represents itself and no other configuration. \(I^\mathcal {J} \) is the singleton set containing the initial configuration \(a^\mathcal {J} \). Given two configurations \(\alpha \) and \(\alpha '\) and a transition \(\theta \in \Theta \), we connect \(\alpha \) to \(\alpha '\) using the role \(r_\theta \) iff there is a transition \(\theta \) from \(\alpha \) to \(\alpha '\). Finally, \(A^\mathcal {J} \) is defined to be the set of tuples  , for some \(F \in \Phi ^{\mathcal {J}}\), where \(\alpha \) is an accepting configuration.
, for some \(F \in \Phi ^{\mathcal {J}}\), where \(\alpha \) is an accepting configuration.
Now, if the initial configuration \(a^{\mathcal {J}}\) is not accepting then, by construction, \((a,G) \not \in A^\mathcal {J} \), for all \(G \in \Phi ^{\mathcal {J}}\). By checking the concept inclusions in \(\mathcal {O} _{\mathcal {M},w}\), we can see that \(\mathcal {J}\) satisfies \(\mathcal {O} _{\mathcal {M},w}\). Then, \(\mathcal {J}\) is a counterexample for \(\mathcal {O} _{\mathcal {M},w} \models A(a)\), and so \(\mathcal {O} _{\mathcal {M},w} \not \models A(a)\). \(\square \)
Theorem 7
In \(\mathcal {ALCH} ^{\mathbb {T}}_@\), any combination of temporal attributes containing \(\{\mathsf{time},\mathsf{after} \}\) is undecidable. Moreover, the combination \(\{\mathsf{time},\mathsf{before} \}\) is 3ExpTime-complete, and the combination \(\{\mathsf{time},\mathsf{during}, \mathsf{since}, \mathsf{until} \}\) and every subset of it are 2ExpTime-complete.
Proof
The proof of Theorem 1 uses only the temporal attributes \(\mathsf{time} \) and \(\mathsf{after} \). Thus, any combination containing these attributes is \(\Sigma ^1_1\)-hard. By Theorems 5 and 6 the combination \(\{\mathsf{time},\mathsf{before} \}\) is 3ExpTime-complete. It remains to show that the combination \(\{\mathsf{time},\mathsf{during}, \mathsf{since}, \mathsf{until} \}\) is in 2ExpTime (since 2ExpTime-hardness is already known for \(\mathcal {ALCH} _@\) [23]).
Our proof strategy consists in showing that, given an \(\mathcal {ALCH} ^{\mathbb {T}}_@\) interpretation and an \(\mathcal {ALCH} ^{\mathbb {T}}_@\) ontology that contains only the temporal attributes in \(\{\mathsf{time},\mathsf{during}, \mathsf{since}, \mathsf{until} \}\), one can always transform this interpretation so that only time points explicitly mentioned in the ontology are relevant to determine if the interpretation is a model of the ontology. Then one can check satisfiability by grounding the ontology using only those time points explicitly mentioned. We start by providing some notation.
Given an \(\mathcal {ALCH} ^{\mathbb {T}}_@\) ontology \(\mathcal {O} \), we define a set \(\mathbb {N}_\mathcal {O} \) as in Theorem 3, except that we do not need \(k_i+1\) here. To this end, let \(k_0<\ldots <k_n\) be the ascending sequence of all numbers mentioned in time points or in time intervals (as endpoints) in \(\mathcal {O} \). We define \(\mathbb {N}_\mathcal {O} \) as \(\{k_i\mid 0\le i\le n\}\), and let  and \(k_\mathsf{max}=\max (\mathbb {N}_\mathcal {O} )\), where we assume \(k_\mathsf{min}=k_\mathsf{max}=0\) if \(\mathbb {N}_\mathcal {O} =\emptyset \).
and \(k_\mathsf{max}=\max (\mathbb {N}_\mathcal {O} )\), where we assume \(k_\mathsf{min}=k_\mathsf{max}=0\) if \(\mathbb {N}_\mathcal {O} =\emptyset \).
Let \(\mathcal {I} = (\Delta ^\mathcal {I},\cdot ^\mathcal {I})\) be an \(\mathcal {ALCH} ^{\mathbb {T}}_@\) interpretation. By Definition 8, \(\mathcal {I}\) is a global interpretation of a sequence  of \(\mathcal {ALCH_{@}}\) interpretations with domain
of \(\mathcal {ALCH_{@}}\) interpretations with domain  . We now define a sequence \((\mathcal {J}_i)_{i\in \Delta ^\mathcal {J}_T}\) of \(\mathcal {ALCH_{@}}\) interpretations as follows. Let
. We now define a sequence \((\mathcal {J}_i)_{i\in \Delta ^\mathcal {J}_T}\) of \(\mathcal {ALCH_{@}}\) interpretations as follows. Let  and let \(\Delta ^\mathcal {J}_T = \{k^\mathcal {J}_\mathsf{min},\ldots , k^\mathcal {J}_\mathsf{max}\}\). For all \(A\in \mathsf {N_{C}} \), all \(F\in \Phi ^{\mathcal {I}}\) with \(F\setminus F_I\ne \emptyset \) and \(k\in [k_\mathsf{min}, k_\mathsf{max}]\):
and let \(\Delta ^\mathcal {J}_T = \{k^\mathcal {J}_\mathsf{min},\ldots , k^\mathcal {J}_\mathsf{max}\}\). For all \(A\in \mathsf {N_{C}} \), all \(F\in \Phi ^{\mathcal {I}}\) with \(F\setminus F_I\ne \emptyset \) and \(k\in [k_\mathsf{min}, k_\mathsf{max}]\):
and either:
-
(1)
\(k\in \mathbb {N}_\mathcal {O} \); or
-
(2)
there is \(k_i<k\) such that \(k_i\in \mathbb {N}_\mathcal {O} \) and \((\delta ,F_I)\in A^{\mathcal {I} _j}\) for all \(k_i\le j\le k_\mathsf{max}\); or
-
(3)
there is \(k_i> k\) such that \(k_i\in \mathbb {N}_\mathcal {O} \) and \((\delta ,F_I)\in A^{\mathcal {I} _j}\) for all \(k_\mathsf{min}\le j\le k_i\).
We analogously apply the definition above for all role names \(r\in \mathsf {N_{R}} \). We define \(\mathcal {I} _\mathcal {O} \) as a global interpretation of the sequence \((\mathcal {J}_i)_{i\in \Delta ^\mathcal {J}_T}\) and set \((\delta ,F)\in A^{\mathcal {I} _\mathcal {O}}\text { iff }(\delta ,F)\in A^{\mathcal {I}}\) for all \(A\in \mathsf {N_{C}} \) with \(F=F_I\), and similarly for all role names \(r\in \mathsf {N_{R}} \). Let \(\mathcal {O} _\mathsf{g}\) be the result of grounding \(\mathcal {O}\) in the same way as in the proof of Theorem 4 using time points in \(\mathbb {N}_\mathcal {O} \) (here \(\mathcal {O}\) may have expressions of the form X.a, \(a{:}\,x\), or \(a{:}\,[t,t']\), with \(a\in \{\mathsf{time},\mathsf{during}, \mathsf{since}, \mathsf{until} \}\), and \(t,t'\in \mathsf {N_{T}} \cup \mathsf{Var}(\mathsf {N_{T}}) \)).
Claim
For all  occurring in \(\mathcal {O} _\mathsf{g}\):
occurring in \(\mathcal {O} _\mathsf{g}\):  and
and  .
.
Proof of the Claim
This claim follows by definition of \((\mathcal {J}_i)_{i\in \Delta ^\mathcal {J}_T}\) and the fact that only the temporal attributes \(\{\mathsf{time},\mathsf{during}, \mathsf{since}, \mathsf{until} \}\) are allowed. Correctness for the temporal attributes \(\mathsf{time} \) and \(\mathsf{during} \) follows from item (1), whereas correctness for the temporal attributes \(\mathsf{since} \) and \(\mathsf{until} \) follows from items (2) and (3), respectively.
By definition of \(\mathcal {O} _\mathsf{g}\), we know that \(\mathcal {O} \models \mathcal {O} _\mathsf{g}\). So if \(\mathcal {O}\) is satisfiable then \(\mathcal {O} _\mathsf{g}\) is satisfiable. Conversely, by the Claim, one can show with an inductive argument that  for all \(\mathcal {ALCH} ^{\mathbb {T}}_@\) concepts C occurring in \(\mathcal {O} _\mathsf{g}\). So, if an \(\mathcal {ALCH} ^{\mathbb {T}}_@\) interpretation \(\mathcal {I}\) satisfies \(\mathcal {O} _\mathsf{g}\) then \(\mathcal {I} _\mathcal {O} \) satisfies \(\mathcal {O}\). Since \(\mathcal {O} _g \) is at most exponentially larger than \(\mathcal {O} \), it follows that satisfiability in this fragment is in 2ExpTime. \(\square \)
for all \(\mathcal {ALCH} ^{\mathbb {T}}_@\) concepts C occurring in \(\mathcal {O} _\mathsf{g}\). So, if an \(\mathcal {ALCH} ^{\mathbb {T}}_@\) interpretation \(\mathcal {I}\) satisfies \(\mathcal {O} _\mathsf{g}\) then \(\mathcal {I} _\mathcal {O} \) satisfies \(\mathcal {O}\). Since \(\mathcal {O} _g \) is at most exponentially larger than \(\mathcal {O} \), it follows that satisfiability in this fragment is in 2ExpTime. \(\square \)
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Ozaki, A., Krötzsch, M., Rudolph, S. (2019). Temporally Attributed Description Logics. In: Lutz, C., Sattler, U., Tinelli, C., Turhan, AY., Wolter, F. (eds) Description Logic, Theory Combination, and All That. Lecture Notes in Computer Science(), vol 11560. Springer, Cham. https://doi.org/10.1007/978-3-030-22102-7_21
Download citation
DOI: https://doi.org/10.1007/978-3-030-22102-7_21
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-22101-0
Online ISBN: 978-3-030-22102-7
eBook Packages: Computer ScienceComputer Science (R0)


 ’ is useful for attributes which universally quantify time points (e.g.,
’ is useful for attributes which universally quantify time points (e.g.,  ,
, is the transition function.
is the transition function. ;
; , for
, for 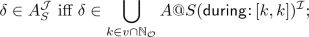
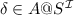 .
. ;
; ; and
; and ,
, is the transition relation.
is the transition relation.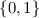 , used to encode double-exponentially many tape positions;
, used to encode double-exponentially many tape positions;
 , we look at our auxiliary attribute that indicates from which time point we should flip our bits to obtain the next tape position (this will be a time point with bit value 0);
, we look at our auxiliary attribute that indicates from which time point we should flip our bits to obtain the next tape position (this will be a time point with bit value 0); and
and  , to filter time points with
, to filter time points with  and
and  to filter time points
to filter time points 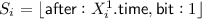 ensures that we have
ensures that we have  to flip to 1 the bit marked with
to flip to 1 the bit marked with 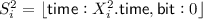 and
and 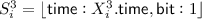 to transfer to the next tape position bit values which should not be flipped (i.e., those that are before the time point with
to transfer to the next tape position bit values which should not be flipped (i.e., those that are before the time point with  and
and 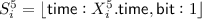 , to receive a copy of the
, to receive a copy of the  , for some
, for some  , for some
, for some  , for some
, for some