States of Strain and Stress-Strain Relations

Abstract

The six components ε_x, ε_y, ε_z, γ_xy, γ_xz, and γ_yz of the state of strain at a point in terms of a given cartesian coordinate system were defined in Chapter 2. The definition of plane strain and the derivation of relations for the strain components ε_x′, ε_y′ and γ_x′y′ as functions of θ are presented which are entirely analogous to the corresponding results for plane stress. A description is given of the strain gauges commonly used for measuring normal strains. A set of three strain gauges measuring normal strains in three different directions near a given point are known as a strain-gauge rosette. The results can be used to determine the state of plane strain, including the shear strain, at the point. Determination of the maximum and minimum normal strains and the maximum magnitude of the shear strain is discussed. The application of Mohr’s circle to states of plane strain, altogether equivalent to the process for states of stress, is described. The stress-strain relations of a linear elastic material and the concept of isotropy are introduced. A relationship for the shear modulus in terms of the modulus of elasticity and Poisson’s ratio is derived. The bulk modulus of a material is defined and given as an expression in terms of the modulus of elasticity and Poisson’s ratio.

Appendices

Chapter Summary

8.1.1 Components of Strain

In terms of a given coordinate system, the state of strain at a point p of a material is defined by the components of strain:

$$ \left[\begin{array}{ccc}{\varepsilon}_x& {\gamma}_{xy}& {\gamma}_{xz}\\ {}{\gamma}_{yx}& {\varepsilon}_y& {\gamma}_{yz}\\ {}{\gamma}_{zx}& {\gamma}_{zy}& {\varepsilon}_z\end{array}\right]. $$

(8.1)

The components ε_x, ε_y, and ε_z are the normal strains in the x, y, and z directions. The component γ_xy = γ_yx is the shear strain referred to the positive directions of the x and y axes, and the components γ_yz = γ_zy and γ_xz = γ_zx are defined similarly.

Consider a volume dV₀ of material in a reference state. Its volume in the deformed state is

$$ dV=\left(1+{\varepsilon}_x+{\varepsilon}_y+{\varepsilon}_z\right)\;{dV}_0. $$

(8.2)

The dilatation is the change in volume of the material per unit volume:

$$ e=\frac{dV-{dV}_0}{dV_0}={\varepsilon}_x+{\varepsilon}_y+{\varepsilon}_z. $$

(8.3)

8.1.2 Transformations of Plane Strain

The strain at a point p is said to be a state of plane strain if it is of the form

$$ \left[\begin{array}{ccc}{\varepsilon}_x& {\gamma}_{xy}& 0\\ {}{\gamma}_{yx}& {\varepsilon}_y& 0\\ {}0& 0& 0\end{array}\right]. $$

(8.4)

In terms of a coordinate system x^′y^′z^′ oriented as shown in Fig. (a), the components of strain are

$$ {\varepsilon}_{x^{\prime }}=\frac{\varepsilon_x+{\varepsilon}_y}{2}+\frac{\varepsilon_x-{\varepsilon}_y}{2}\cos\;2\theta +\frac{\gamma_{xy}}{2}\sin\;2\theta, $$

(8.7)

$$ {\varepsilon}_{y^{\prime }}=\frac{\varepsilon_x+{\varepsilon}_y}{2}-\frac{\varepsilon_x-{\varepsilon}_y}{2}\cos\;2\theta -\frac{\gamma_{xy}}{2}\sin\;2\theta, $$

(8.8)

$$ \frac{\gamma_{x^{\prime }{y}^{\prime }}}{2}=-\frac{\varepsilon_x-{\varepsilon}_y}{2}\sin\;2\theta +\frac{\gamma_{xy}}{2}\cos\;2\theta . $$

(8.9)

For an isotropic linear elastic material, Eqs. (8.7), (8.8), and (8.9) also apply to the components of strain resulting from a state of plane stress.

8.1.3 Strain Gauge Rosette

Suppose that a material is subject to an unknown state of plane strain relative to the x-y coordinate system in Fig. (a). A strain gauge rosette measures the normal strain ${\varepsilon}_{x^{\prime }}$ in three different directions: θ_a, θ_b, and θ_c. Let the measured strains be ε_a, ε_b, and ε_c. Using Eq. (8.6) to express these strains in terms of the strain components ε_x, ε_y, and γ_xy gives

$$ {\displaystyle \begin{array}{c}{\varepsilon}_a={\varepsilon}_x\;{\cos}^2{\theta}_a+{\varepsilon}_y\;{\sin}^2{\theta}_a+{\gamma}_{xy}\;\sin\;{\theta}_a\;\cos\;{\theta}_a,\\ {}{\varepsilon}_b={\varepsilon}_x\;{\cos}^2{\theta}_b+{\varepsilon}_y\;{\sin}^2{\theta}_b+{\gamma}_{xy}\;\sin\;{\theta}_b\;\cos\;{\theta}_b,\\ {}{\varepsilon}_c={\varepsilon}_x\;{\cos}^2{\theta}_c+{\varepsilon}_y\;{\sin}^2{\theta}_c+{\gamma}_{xy}\;\sin\;{\theta}_c\;\cos\;{\theta}_c.\end{array}} $$

(8.10)

This system of equations can be solved for the strain components ε_x, ε_y, and γ_xy.

8.1.4 Maximum and Minimum Strains in Plane Strain

A value of θ for which the normal strain is a maximum or minimum is determined from the equation

$$ \tan\;2{\theta}_{\mathrm{p}}=\frac{\gamma_{xy}}{\varepsilon_x-{\varepsilon}_y}. $$

(8.11)

The values of the principal strains can be obtained by substituting θ_p into Eqs. (8.7) and (8.8). Their values can also be determined from the equation

$$ {\varepsilon}_1,{\varepsilon}_2=\frac{\varepsilon_x+{\varepsilon}_y}{2}\pm \sqrt{{\left(\frac{\varepsilon_x-{\varepsilon}_y}{2}\right)}^2+{\left(\frac{\gamma_{xy}}{2}\right)}^2}, $$

(8.14)

although this equation does not indicate their directions. An infinitesimal square element oriented as shown in Fig. (b) is subjected to the principal strains in the x^′ and y^′ directions and undergoes no shear strain.

A value of θ for which the in-plane shear strain is a maximum or minimum is determined from the equation

$$ \tan\;2{\theta}_{\mathrm{s}}=-\frac{\varepsilon_x-{\varepsilon}_y}{\gamma_{xy}}. $$

(8.15)

The corresponding shear strain can be obtained by substituting θ_s into Eq. (8.9). The magnitude of the maximum in-plane shear strain can be determined from the equation

$$ {\gamma}_{\mathrm{max}}=\sqrt{{\left({\varepsilon}_x-{\varepsilon}_y\right)}^2+{\gamma}_{xy}^2}. $$

(8.18)

The absolute maximum shear strain is

$$ {\gamma}_{\mathrm{abs}}=\operatorname{Max}\left(\left|{\varepsilon}_1\right|,\left|{\varepsilon}_2\right|,\left|{\varepsilon}_1-{\varepsilon}_2\right|\right). $$

(8.22)

8.1.5 Mohr’s Circle for Plane Strain

Given a state of plane strain ε_x, ε_y, and γ_xy, establish a set of horizontal and vertical axes with normal strain measured to the right along the horizontal axis and shear strain measured downward along the vertical axis. Plot two points, point P with coordinates (ε_x, γ_xy/2) and point Q with coordinates (ε_x, −γ_xy/2). Draw a straight line connecting points P and Q. Using the intersection of the straight line with the horizontal axis as the center, draw a circle that passes through the two points (Fig. (c)). Draw a straight line through the center of the circle at an angle 2θ measured counterclockwise from point P. Point P^′ at which this line intersects the circle has coordinates $\left({\varepsilon}_{x^{\prime }},{\gamma}_{x^{\prime }{y}^{\prime }}/2\right),$ and point Q^′ has coordinates $\left({\varepsilon}_{y^{\prime }},-{\gamma}_{x^{\prime }{y}^{\prime }}/2\right)$ (Fig. (d)).

8.1.6 Stress-Strain Relations

A material for which the state of stress at a point is a single-valued function of the current state of strain at that point is said to be elastic. If the function is invariant under changes of orientation of the coordinate system relative to the material, the material is isotropic. If the components of strain are linear functions of the components of stress, the material is linear elastic. The stress-strain relations for an isotropic linear elastic material are

$$ {\varepsilon}_x=\frac{1}{E}{\sigma}_x-\frac{v}{E}\left({\sigma}_y+{\sigma}_z\right), $$

(8.43)

$$ {\varepsilon}_y=\frac{1}{E}{\sigma}_y-\frac{v}{E}\left({\sigma}_x+{\sigma}_z\right), $$

(8.44)

$$ {\varepsilon}_z=\frac{1}{E}{\sigma}_z-\frac{v}{E}\left({\sigma}_x+{\sigma}_y\right), $$

(8.45)

$$ {\gamma}_{xy}=\frac{1}{G}{\tau}_{xy}, $$

(8.46)

$$ {\gamma}_{yz}=\frac{1}{G}{\tau}_{yz}, $$

(8.47)

$$ {\gamma}_{xz}=\frac{1}{G}{\tau}_{xz}. $$

(8.48)

The shear modulus is related to the modulus of elasticity and Poisson’s ratio by

$$ G=\frac{E}{2\left(1+v\right)}. $$

(8.50)

The stress-strain relations can also be expressed as

$$ {\sigma}_x=\left(\lambda +2\mu \right){\varepsilon}_x+\lambda \left({\varepsilon}_y+{\varepsilon}_z\right), $$

(8.51)

$$ {\sigma}_y=\left(\lambda +2\mu \right){\varepsilon}_y+\lambda \left({\varepsilon}_x+{\varepsilon}_z\right), $$

(8.52)

$$ {\sigma}_z=\left(\lambda +2\mu \right){\varepsilon}_z+\lambda \left({\varepsilon}_x+{\varepsilon}_y\right), $$

(8.53)

$$ {\tau}_{xy}={\mu \gamma}_{xy}, $$

(8.54)

$$ {\tau}_{yz}={\mu \gamma}_{yz}, $$

(8.55)

$$ {\tau}_{xz}={\mu \gamma}_{xz}, $$

(8.56)

where λ and μ are the Lamé constants. The constant μ = G, and the constant λ is given in terms of the modulus of elasticity and Poisson’s ratio by

$$ \lambda =\frac{vE}{\left(1+v\right)\left(1-2v\right)}. $$

(8.57)

Let an isotropic linear elastic material be subjected to a pressure P so that σ_x = −P, σ_y = −P, and σ_z = −P. The bulk modulus K of the material is the ratio of −P to the dilatation

$$ K=\frac{-P}{e}. $$

(8.58)

In terms of the modulus of elasticity and Poisson’s ratio, the bulk modulus is

$$ K=\frac{E}{3\left(1-2v\right)}. $$

(8.59)

Review Problems

• 8.68 The components of plane strain at point p are ε_x = 0, ε_y = 0, and γ_xy = 0.004. If θ = 45^º, what are the strains ${\varepsilon}_{x^{\prime }},{\varepsilon}_{y^{\prime }}$, and ${\gamma}_{x^{\prime }{y}^{\prime }}$ at point p?

  

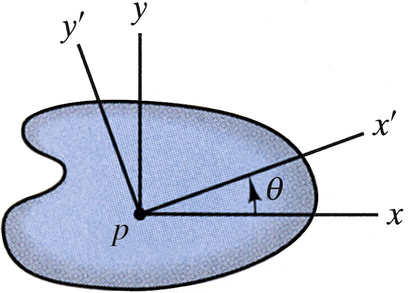
  Problems 8.68–8.69

• 8.69 The components of plane strain at point p are ε_x = −0.0024, ε_y = 0.0012, and γ_xy = −0.0012. If θ = 25^º, what are the strains ${\varepsilon}_{x^{\prime }},{\varepsilon}_{y^{\prime }}$, and ${\gamma}_{x^{\prime }{y}^{\prime }}$ at point p?

• 8.70 A point p of the bearing’s housing is subjected to a state of plane stress, and the strain components ε_x' = 0.0024, ε_y' = 0.0044, and γ_x' y' = −0.0030. If θ = 20^º, what are the strains ε_x, ε_y, and γ_xy at p?

  

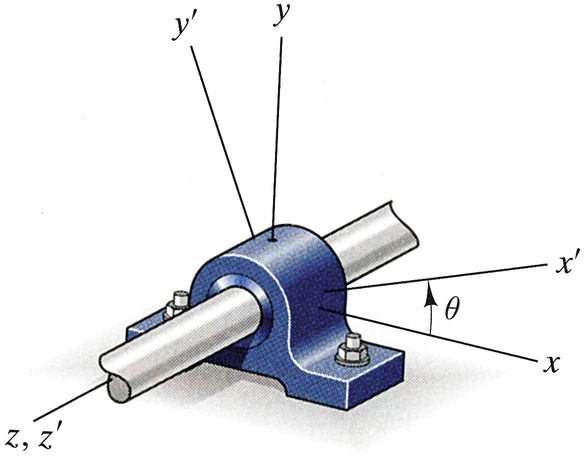
  Problems 8.70–8.71

• 8.71∗ A point p of the bearing’s housing is subjected to the state of plane strain ε_x = 0.0032, ε_y = −0.0026, and γ_xy = 0.0044. If ${\varepsilon}_{x^{\prime }}=0.0037$ and ${\varepsilon}_{y^{\prime }}=-0.0031,$determine the angle θ and the strain ${\gamma}_{x^{\prime }{y}^{\prime }}$ at p.

• 8.72 The strains measured by a strain gauge rosette oriented as shown are ε_a = −0.00116, ε_b = −0.00065, and ε_c = 0.00130. Determine the strains ε_x, ε_y, and γ_xy.

  

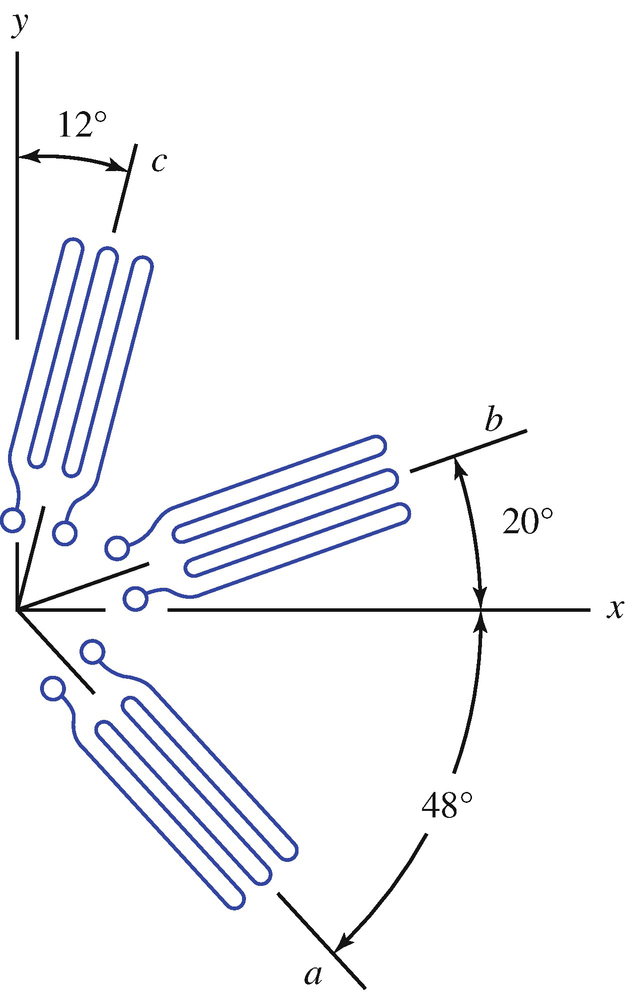
  Problem 8.72

• 8.73 The state of plane strain at a point is ε_x = 0.003, ε_y = 0.001, and γ_xy = –0.006. Determine the magnitude of the maximum in-plane shear strain.

• 8.74 For the state of plane strain ε_x = 0.0025, ε_y = 0, and γ_xy = −0.005, what is the absolute maximum shear strain?

• 8.75 For the state of plane strain ε_x = −0.008, ε_y = −0.006, and γ_xy = −0.012, what is the absolute maximum shear strain?

• 8.76 A drill bit is made of steel with modulus of elasticity E = 200 GPa and Poisson’s ratioν = 0.28. At a point p, the bit is subjected to a state of plane stress, and the components of strainε_x = −0.0024, ε_y = 0.0044, and γ_xy = −0.0030. What is the state of stress at p?

• 8.77 A drill bit is made of steel with modulus of elasticity E = 200 GPa and Poisson’s ratioν = 0.28. At a point p, the bit is subjected to a state of plane stress, and the components of strainε_x = 0.0038, ε_y = 0.0066, and γ_xy = −0.0048. What is the component of strain ε_z at p?

• 8.78∗ Beginning with Eq. (8.59), show that the bulk modulus is given in terms of the Lamé constants by

  $$ K=\lambda +\frac{2}{3}\mu . $$