States of Stress

Abstract

The six components σ_x, σ_y, σ_z, τ_xy, τ_xz and τ_yz of the state of stress at a point in terms of a given cartesian coordinate system were defined in Chap. 2. In a state of plane stress, the only nonzero components are σ_x, σ_y and τ_xy. Let the x ‐ y plane lie in the plane of the page, with the z axis directed out of the page. Let a second cartesian coordinate system x′y′z′ be superimposed on the xyz system, then its orientation by rotating it about the z′ axis through a counterclockwise angle θ. By passing an oblique plane through a cubic element with its faces perpendicular to the xyz system and applying the equilibrium equations, expressions are obtained for the stress components σ_x′, σ_y′ and τ_x′y′ in terms of θ. Because of their importance in design, the maximum and minimum values of the normal stresses and the maximum value of the magnitude of the shear stress on any plane through the point are discussed. A graphical procedure known as Mohr’s circle, which helps in visualizing and interpreting the equations for determining the components σ_x′, σ_y′ and τ_x′y′ in terms of θ, is described. Attention is then given to the problem of determining the maximum and minimum normal stresses and the magnitude of the maximum shear stress for a general state of stress. The normal stresses are given by a cubic equation whose coefficients are functions of the components of stress. Its three solutions are called the principal stresses. The maximum magnitude of the shear stress is given by an expression in terms of the principal stresses. A special case called triaxial stress, in which the only nonzero stress components are σ_x, σ_y and σ_z, is discussed. Two applications giving rise to interesting states of stress, bars subjected to combined loads and pressure vessels, are then covered. The chapter closes with a discussion of the tetrahedron argument, which allows determination of the normal and shear stresses acting on any plane through a point in terms of the state of stress at the point.

Appendices

Chapter Summary

7.1.1 Components of Stress

In terms of a given coordinate system, the state of stress at a point p of a material is specified by the components of stress:

$$ \left[\begin{array}{ccc}{\sigma}_x& {\tau}_{xy}& {\tau}_{xz}\\ {}{\tau}_{yx}& {\sigma}_y& {\tau}_{yz}\\ {}{\tau}_{zx}& {\tau}_{zy}& {\sigma}_z\end{array}\right]. $$

(7.1)

The directions of these stresses, and the orientations of the planes on which they act, are shown in Fig. (a). The shear stresses τ_xy = τ_yx, τ_yz = τ_zy and τ_xz = τ_zx.

7.1.2 Transformations of Plane Stress

The stress at a point is said to be a state of plane stress if it is of the form

$$ \left[\begin{array}{ccc}{\sigma}_x& {\tau}_{xy}& 0\\ {}{\tau}_{yx}& {\sigma}_y& 0\\ {}0& 0& 0\end{array}\right]. $$

(7.3)

In terms of a coordinate system x^′ y^′ z^′ oriented as shown in Fig. (b), the components of stress are

$$ {\sigma}_{x^{\prime }}=\frac{\sigma_x+{\sigma}_y}{2}+\frac{\sigma_x-{\sigma}_y}{2}\cos 2\theta +{\tau}_{xy}\sin 2\theta, $$

(7.6)

$$ {\tau}_{x^{\prime }{y}^{\prime }}=-\frac{\sigma_x-{\sigma}_y}{2}\sin 2\theta +{\tau}_{xy}\cos 2\theta, $$

(7.7)

$$ {\sigma}_{y^{\prime }}=\frac{\sigma_x+{\sigma}_y}{2}-\frac{\sigma_x-{\sigma}_y}{2}\cos 2\theta -{\tau}_{xy}\sin 2\theta . $$

(7.8)

7.1.3 Maximum and Minimum Stresses in Plane Stress

The orientation of the element on which the principal stresses act (Fig. (c)) is determined from the equation

$$ \tan 2{\theta}_{\mathrm{p}}=\frac{2{\tau}_{xy}}{\sigma_x-{\sigma}_y}. $$

(7.12)

The values of the principal stresses can be obtained by substituting θ_p into Eqs. (7.6) and (7.8). Their values can also be determined from the equation

$$ {\sigma}_1,{\sigma}_2=\frac{\sigma_x+{\sigma}_y}{2}\pm \sqrt{{\left(\frac{\sigma_x-{\sigma}_y}{2}\right)}^2+{\tau}_{xy}^2}, $$

(7.15)

although this equation does not indicate the planes on which they act.

The orientation of the element on which the maximum in-plane shear stresses act (Fig. (d)) can be determined from the equation

$$ \tan 2{\theta}_{\mathrm{s}}=-\frac{\sigma_x-{\sigma}_y}{2{\tau}_{xy}}, $$

(7.16)

or by using the relation θ_s = θ_p + 45^°. The normal stresses σ_s acting on this element are shown in Fig. (d). The value of the maximum in-plane shear stress can be obtained by substituting θ_s into Eq. (7.7). Its value can also be determined from the equation

$$ {\tau}_{\mathrm{max}}=\sqrt{{\left(\frac{\sigma_x-{\sigma}_y}{2}\right)}^2+{\tau}_{xy}^2}, $$

(7.19)

although this equation does not indicate the direction of the stress on the element.

The absolute maximumshear stress (the maximum shear stress on any plane through p) resulting from a state of plane stress is

$$ {\tau}_{\mathrm{abs}}=\operatorname{Max}\left(\left|\frac{\sigma_1}{2}\right|,\left|\frac{\sigma_2}{2}\right|,\left|\frac{\sigma_1-{\sigma}_2}{2}\right|\right). $$

(7.24)

7.1.4 Mohr’s Circle for Plane Stress

Given a state of plane stress σ_x, τ_xy, and σ_y, establish a set of horizontal and vertical axes with normal stress measured to the right along the horizontal axis and shear stress measured downward along the vertical axis. Plot two points, point P with coordinates (σ_x, τ_xy) and point Q with coordinates (σ_y, −τ_xy). Draw a straight line connecting points P and Q. Using the intersection of the straight line with the horizontal axis as the center, draw a circle that passes through the two points (Fig. (e)). Draw a straight line through the center of the circle at an angle 2θ measured counterclockwise from point P. Point P^′ at which this line intersects the circle has coordinates $\left({\sigma}_{x^{\prime }},{\tau}_{x^{\prime }{y}^{\prime }}\right),$ and point Q^′ has coordinates $\left({\sigma}_{y^{\prime }},-{\tau}_{x^{\prime }{y}^{\prime }}\right),$ as shown in Fig. (f).

7.1.5 Principal Stresses in Three Dimensions

For a general state of stress, the principal stresses are the roots of the cubic equation

$$ {\sigma}^3-{I}_1{\sigma}^2+{I}_2\sigma -{I}_3=0, $$

(7.25)

where the stress invariants are

$$ {\displaystyle \begin{array}{c}{I}_1={\sigma}_x+{\sigma}_y+{\sigma}_z,\\ {}{I}_2={\sigma}_x{\sigma}_y+{\sigma}_y{\sigma}_z+{\sigma}_z{\sigma}_x-{\tau}_{xy}^2-{\tau}_{yz}^2-{\tau}_{zx}^2,\\ {}{I}_3={\sigma}_x{\sigma}_y{\sigma}_z-{\sigma}_x{\tau}_{yz}^2-{\sigma}_y{\tau}_{xz}^2-{\sigma}_z{\tau}_{xy}^2+2{\tau}_{xy}{\tau}_{yz}{\tau}_{zx}.\end{array}} $$

(7.26)

The absolute maximum shear stress resulting from a general state of stress is

$$ {\tau}_{\mathrm{abs}}=\operatorname{Max}\left(\left|\frac{\sigma_1-{\sigma}_2}{2}\right|,\left|\frac{\sigma_1-{\sigma}_3}{2}\right|,\left|\frac{\sigma_2-{\sigma}_3}{2}\right|\right). $$

(7.27)

The state of stress at a point is said to be triaxial if it is of the form

$$ \left[\begin{array}{ccc}{\sigma}_x& 0 & 0 \\ {}0 & {\sigma}_y& 0 \\ {}0 & 0 & {\sigma}_z\end{array}\right]. $$

(7.28)

In triaxial stress, x, y, and z are principal axes, and σ_x, σ_y, and σ_z are the principal stresses. The absolute maximum shear stress in triaxial stress is

$$ {\tau}_{\mathrm{abs}}=\operatorname{Max}\left(\left|\frac{\sigma_x-{\sigma}_y}{2}\right|,\left|\frac{\sigma_x-{\sigma}_z}{2}\right|,\left|\frac{\sigma_y-{\sigma}_z}{2}\right|\right). $$

(7.29)

7.1.6 Tetrahedron Argument

Given the state of stress at a point p, the components of the tractiont at p acting on a plane through p whose orientation is defined by a perpendicular unit vector n (Fig. (g)) are

$$ {\displaystyle \begin{array}{c}{t}_x={\sigma}_x{n}_x+{\tau}_{xy}{n}_y+{\tau}_{xz}{n}_z,\\ {}{t}_y={\tau}_{yx}{n}_x+{\sigma}_y{n}_y+{\tau}_{yz}{n}_z,\\ {}{t}_z={\tau}_{zx}{n}_x+{\tau}_{zy}{n}_y+{\sigma}_z{n}_z.\end{array}} $$

(7.43)

The normal stress at p is

$$ \sigma =\mathbf{t}\cdot \mathbf{n}={t}_x{n}_x+{t}_y{n}_y+{t}_z{n}_z, $$

(7.45)

and the magnitude of the shear stress is

$$ \mid \tau \mid =\mid \mathbf{t}-\sigma\;\mathbf{n}\mid . $$

(7.46)

Review Problems

• 7.106∗ The components of plane stress at a point p of a drill bit are σ_x = 40 ksi, σ_y = −30 ksi, and τ_xy = 30 ksi, and the components referred to the x^′ y^′ z^′ coordinate system are ${\sigma}_{x^{\prime }}=12.5\ \mathrm{ksi},{\sigma}_{y^{\prime }}=-2.5\ \mathrm{ksi}$, and ${\tau}_{x^{\prime }{y}^{\prime }}=45.5\ \mathrm{ksi}.$ What is the angle θ?

  

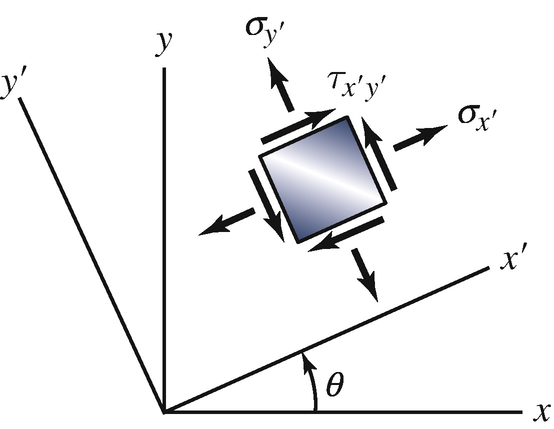
  Problems 7.106–7.107

• 7.107 The components of plane stress at a point p of the drill bit referred to the x^′ y^′ z^′ coordinate system are ${\sigma}_{x^{\prime }}=-8\ \mathrm{MPa},{\sigma}_{y^{\prime }}=6\ \mathrm{MPa}$, and ${\tau}_{x^{\prime }{y}^{\prime }}=-16\ \mathrm{MPa}.$ If θ = 20^°, what are the stresses σ_x, σ_y, and τ_xy at point p?

• 7.108 Determine the stresses σ and τ (a) by writing equilibrium equations for the element shown and (b) by using Eqs. (7.6) and (7.7).

  

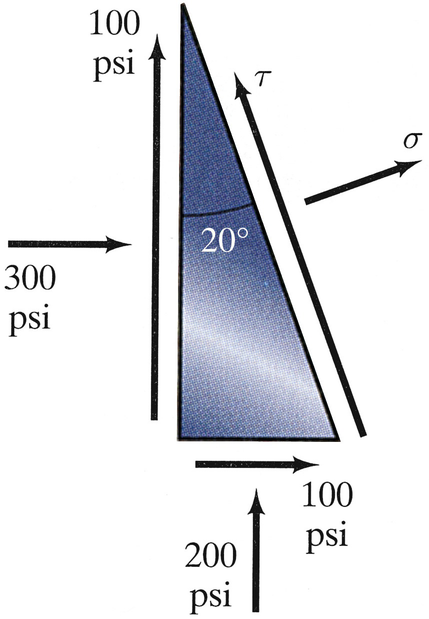
  Problems 7.108–7.109

• 7.109 Solve Problem 7.108 if the 300-psi stress on the element is in tension instead of compression.

• 7.110 For the state of plane stress σ_x = 8 ksi, σ_y = 6 ksi, and τ_xy = −6 ksi, what is the absolute maximum shear stress?

• 7.111 For the state of plane stress σ_x = 240 MPa, σ_y = −120 MPa, and τ_xy = 240 MPa, what is the absolute maximum shear stress?

• 7.112 The components of plane stress acting on an element of a bar subjected to axial loads are shown. The stress σ_x = 4000 psi. Consider a plane through the bar whose normal is 20^∘ relative to the x axis. Use Mohr’s circle to determine the normal stress and the magnitude of the shear stress on the plane.

  

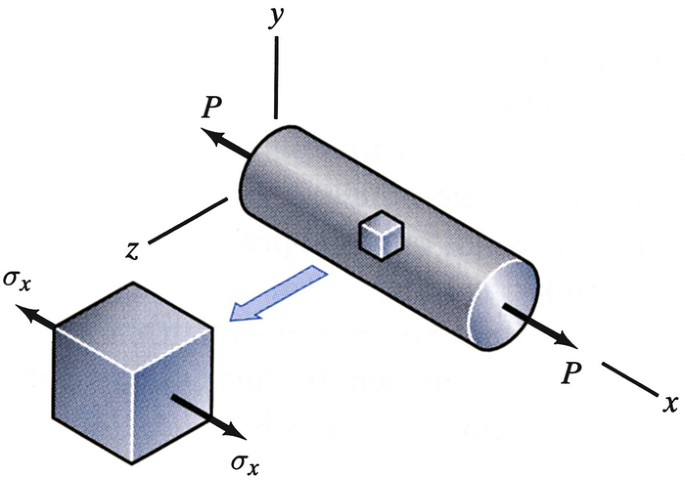
  Problem 7.112

• 7.113 The components of plane stress acting on an element of a bar subjected to torsion are shown. The stress τ_xy = 4000 psi. Use Mohr’s circle to determine the principal stresses to which the material is subjected.

  

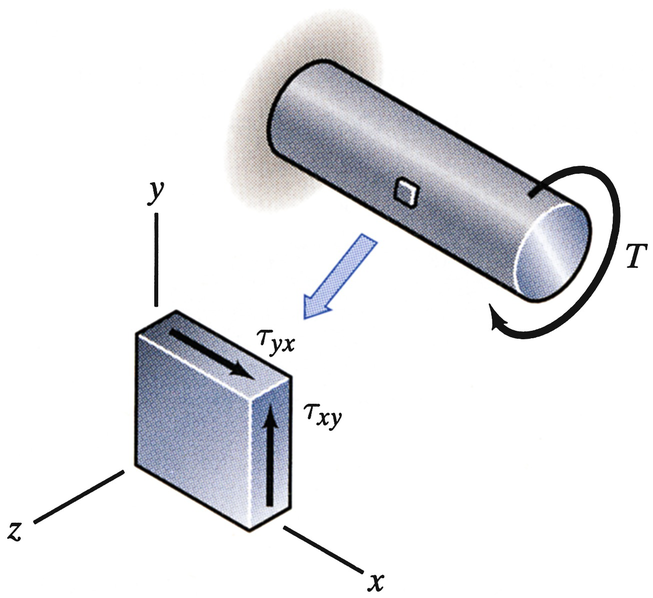
  Problem 7.113

• 7.114 A machine element is subjected to the state of triaxial stress σ_x = 300 MPa, σ_y = −200 MPa, σ_z = −100 MPa. What is the absolute maximum shear stress?

• 7.115∗ At a point p, a material is subjected to the state of stress (in MPa):

  $$ \left[\begin{array}{ccc}{\sigma}_x& {\tau}_{xy}& {\tau}_{xz}\\ {}{\tau}_{yx}& {\sigma}_y& {\tau}_{yz}\\ {}{\tau}_{zx}& {\tau}_{zy}& {\sigma}_z\end{array}\right]=\left[\begin{array}{rrr}4&2&1\\ {}2& -2&1\\ {}1&1& -3\end{array}\right] . $$

  Determine the principal stresses and the absolute maximum shear stress.

• 7.116 The cylindrical bar has radius R = 20 mm. It is subjected to a torque about its axis T = 60 N‐m and a couple M_y = 85 N‐m about the y axis in the direction shown. In terms of the coordinate system shown, determine the state of stress at point p, which is located at x = 60 mm, y = 0, z = 20 mm.

  

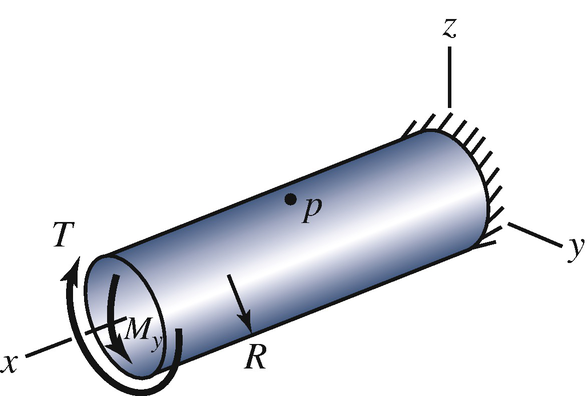
  Problems 7.116–7.117

• 7.117 The cylindrical bar has radius R = 20 mm. It is subjected to a torque about its axis T = 60 N‐m and a couple M_y = 85 N‐m about the y axis in the direction shown. Determine the principal stresses and the maximum in-plane shear stress at point p, which is located at x = 60 mm, y = 0, z = 20 mm.

• 7.118 The beam is subjected to an axial load P = 1200 lb that does not act at the centroid of the cross section. The dimensions of the cross section are b = 4 in and h = 2 in. In terms of the coordinate system shown, determine the state of stress at point p, which has coordinates $y=\frac{1}{2}h$ and $z=\frac{1}{4}b$.

  

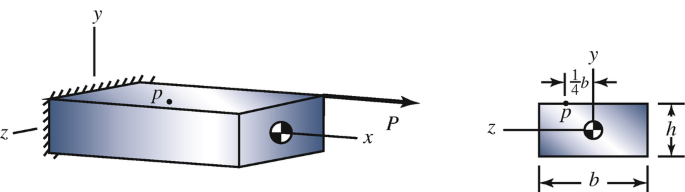
  Problem 7.118

• 7.119 The spherical pressure vessel has a 1-m radius and a 0.002-m wall thickness. It contains a gas with pressure p_i = 1.8E5 Pa, and the outer wall is subjected to atmospheric pressure p_o = 1E5 Pa. Determine the maximum normal stress and the absolute maximum shear stress at the vessel’s inner surface.

  

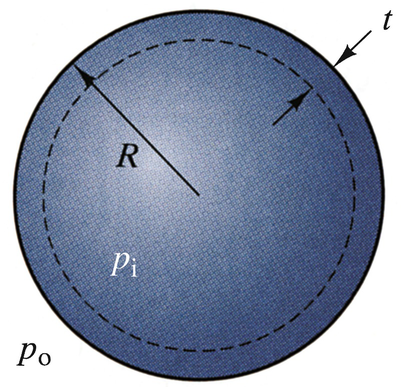
  Problems 7.119–7.120

• 7.120 The spherical pressure vessel has a 1-m radius and a 0.002-m wall thickness. The allowable value of the absolute maximum shear stress is τ_allow = 14 MPa. If the outer wall is subjected to atmospheric pressure p_o = 1E5 Pa, what is the maximum allowable internal pressure?