Abstract
Unfolding-based Dynamic Partial Order Reduction (UDPOR) is a recent technique mixing Dynamic Partial Order Reduction (DPOR) with concepts of concurrency such as unfoldings to efficiently mitigate state space explosion in model-checking of concurrent programs. It is optimal in the sense that each Mazurkiewicz trace, i.e. a class of interleavings equivalent by commuting independent actions, is explored exactly once. This paper shows that UDPOR can be extended to verify asynchronous distributed applications, where processes both communicate by messages and synchronize on shared resources. To do so, a general model of asynchronous distributed programs is formalized in TLA+. This allows to define an independence relation, a main ingredient of the unfolding semantics. Then, the adaptation of UDPOR, involving the construction of an unfolding, is made efficient by a precise analysis of dependencies. A prototype implementation gives promising experimental results.
This work has been supported by INRIA collaborative project IPL HAC-SPECIS (http://hacspecis.gforge.inria.fr/).
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Developing distributed applications that run on parallel computers and communicate by message passing is hard due to their size, heterogeneity, asynchronicity and dynamicity. Besides performance, their correction is crucial but very challenging due to the complex interactions of parallel components.
Model-checking (see e.g. [4]) is a set of techniques allowing to verify automatically and effectively some properties on models of such systems. The principle is usually to explore all possible behaviors (states and transitions) of the system model. However, state spaces increase exponentially with the number of concurrent processes. Unfoldings and Partial order reduction (POR) are two candidate alternative techniques born in the 90’s to mitigate this state space explosion and scale to large applications.
Unfoldings (see e.g. [6]) is a concept of concurrency theory providing a representation of the behaviors of a model in the form of an event structure aggregating causal dependencies or concurrency between events (occurrence of actions), and conflicts that indicate choices in the evolution of the program. This representation may be exponentially more compact than an interleaving semantics, while still allowing to verify some properties, such as safety.
POR comprises a set of exploration techniques (see e.g. [8]), sharing the idea that, to detect deadlocks (and, by extension, for checking safety properties) it is sufficient to cover each Mazurkiewicz trace, i.e. a class of interleavings equivalent by commutation of consecutive independent actions. This state space reduction is obtained by choosing at each state, based on the independence of actions, only a subset of actions to explore (ample, stubborn or persistent sets, depending on the method), or to avoid (sleep set). Dynamic partial order reduction (DPOR) [7] was later introduced to combat state space explosion for stateless model-checking of software. In this context, while POR relies on a statically defined and imprecise independence relation, DPOR may be much more efficient by dynamically collecting it at run-time. Nevertheless, redundant explorations, named sleep-set blocked (SSB) [1], may still exist that would lead to an already visited interleaving, and detected by using sleep sets.
In the last few years, two research directions were investigated to improve DPOR. The first one tries to refine the independence relation: the more precise, the less Mazurkiewicz traces exist, thus the more efficient could be DPOR. For example [2] proposes to consider conditional independence relations where commutations are specified by constraints, while in [3] independence is built lazily, conditionally to future actions called observers. The other direction proposes alternatives to persistent sets, in order to minimize the number of explored interleavings. Optimality is obtained when exactly one interleaving per Mazurkiewicz trace is built. In [1] authors propose source sets that outperform DPOR, but optimality requires expensive computations of wake-up trees to avoid SSB explorations. In [16] the authors propose unfolding-based DPOR (UDPOR), an optimal DPOR method combining the strengths of PORs and unfoldings with the notion of alternatives. The approach is generalized [13] with a notion of k-partial alternative allowing to balance between optimal DPOR and sometimes more efficient sub-optimal DPOR.
Some approaches already try to use DPOR techniques for the verification of asynchronous distributed applications, such as MPI programs (Message Passing Interface). In the absence of model, determining global states of the system and checking equality [15] are already challenging. In [14], an approach is taken that is tight to MPI. A significant subset of MPI primitives is considered, formally specified in order to define the dependency relation, and then to use the DPOR technique of [7]. In [18], the efficiency is improved by focusing on particular deadlocks, but at the price of incompleteness.
We propose first steps to adapt UDPOR for asynchronous distributed applications. In [17] authors proposed an abstract model of distributed applications with a small set of primitives, sufficient to express most communication actions. We revise and extend this model with synchronization primitives and formally specify it in TLA+ [11]. A clear advantage of this model is its abstraction: it remains concise, but its generality allows e.g. the encoding of MPI primitives. Already defining a correct independence relation from this formal model is difficult, due to the variety and complex semantics of actions. In addition, making UDPOR and in particular the computation of unfoldings and extensions efficient cannot directly rely on solutions of [13], which are tuned for concurrent programs with only mutexes, thus clever algorithms need to be designed. For now we prototyped our solutions in a simplified context, but we target the SimGrid tool which allows to run HPC code (in particular MPI) in a simulation environment [5]. The paper is organized as follows. Section 2 recalls notions of interleaving and concurrency semantics, and how a transition system is unfolded into an event structure with respect to an independence relation. In Sect. 3 the programming model is presented together with a sketch of the independence relation. Section 4 presents the UDPOR algorithm, its adaptation to our programming model, and how to make it efficient. Finally we present a prototype implementation and its experimental evaluation.
2 Interleaving and Unfolding Semantics
The behaviors of a distributed program can be described in an interleaving semantics by a labelled transition system, or in a true concurrency semantics by an event structure. An LTS equipped with an independence relation can be unfolded into an event structure [16]. This is a main step for UDPOR.
Definition 1
(Labelled transition system). A labelled transition system (LTS) is a tuple \(\mathcal{T} = \langle S, s_0, \varSigma , \rightarrow \rangle \) where S is the set of states, \(s_0\in S\) the initial state, \(\varSigma \) is the alphabet of actions, and \(\rightarrow \subseteq S \times \varSigma \times S\) is the transition relation.
We note \(s\xrightarrow a s'\) when \((s,a,s') \in \rightarrow \) and extend the notation to execution sequences: \(s\xrightarrow {a_1\cdot a_2 \cdots a_n} s'\) if \(\exists s_0=s, s_1, \ldots s_n=s'\) with \(s_{i-1} \xrightarrow a_i s_i\) for \(i \in [1,n]\). For a state s in S, we denote by \(enabled(s)=\{a\in \varSigma :\exists s'\in S, s\xrightarrow a s'\}\) the set of actions enabled at s.
Independence is a key notion in both POR techniques and unfoldings, linked to the possibility to commute actions:
Definition 2
(Commutation and independence). Two actions \(a_1\), \(a_2\) of an LTS \(\mathcal{T}=\langle S, s_0, \varSigma , \rightarrow \rangle \) commute in a state s if they satisfy the two conditions:
-
executing one action does not enable nor disable the other one:
$$\begin{aligned} a_1 \in enabled(s) \wedge s\xrightarrow {a_{1}} s' \implies (a_2 \in enabled(s) \Leftrightarrow a_2 \in enabled(s')) \end{aligned}$$(1) -
their execution order does not change the overall result:
$$\begin{aligned} a_1, a_2 \in enabled(s) \implies ( s\xrightarrow {a_1\cdot a_2} s' \wedge s\xrightarrow {a_2\cdot a_1} s'' \implies s' = s'') \end{aligned}$$(2)
A relation \(I \subseteq \varSigma \times \varSigma \) is a valid independence relation if it under-approximates commutation, i.e. \(\forall a_1, a_2, I(a_1,a_2)\) implies that \(a_1\) and \(a_2\) commute in all states. Conversely \(a_1\) and \(a_2\) are dependent and we note \(D(a_1, a_2)\) when \(\lnot (I(a_1,a_2))\).
A Mazurkiewicz trace is an equivalence class of executions (or interleavings) of an LTS \(\mathcal T\) obtained by commuting adjacent independent actions. By the second item of Definition 2, all these interleavings reach a unique state. The principle of all DPOR approaches is precisely to reduce the state space exploration while covering at least one execution per Mazurkiewicz trace. If a deadlock exists, a Mazurkiewicz trace leads to it and will be discovered. More generally, safety properties are preserved.
The UDPOR technique that we consider also uses concurrency notions. A classical model of true concurrency is prime event structures:
Definition 3
(Prime event structure). Given an alphabet of actions \(\varSigma \), a \(\varSigma \)-prime event structure (\(\varSigma \)-PES) is a tuple \(\mathcal{E} = \langle E,<,\#,\lambda \rangle \) where E is a set of events, < is a partial order relation on E, called the causality relation, \(\lambda : E \rightarrow \varSigma \) is a function labelling each event e with an action \(\lambda (e)\), \(\#\) is an irreflexive and symmetric relation called the conflict relation such that, the set of causal predecessors or history of any event e, \(\lceil e \rceil = \{ e' \in E: e'<e\}\) is finite, and conflicts are inherited by causality: \(\forall e, e', e'' \in E, e \# e' \wedge e' < e'' \implies e \# e''\).
Intuitively, \(e <e'\) means that e must happen before \(e'\), and \(e \# e'\) that those two events cannot belong to the same execution. Two distinct events that are neither causally ordered nor in conflict are said concurrent. The set \([e]:=\lceil e \rceil \cup \{e\}\) is called the local configuration of e. An event e can be characterized by a pair \(< \lambda (e), H>\) where \(\lambda (e)\) is its action, and \(H=\lceil e \rceil \) its history.
We note conf(E) the set of configurations of \(\mathcal{E}\), where a configuration is a set of events \(C \subseteq E\) that is both causally closed (\(e \in C \implies \lceil e \rceil \subseteq C\)) and conflict free (\(e, e' \in C \implies \lnot (e \# e')\)). A configuration C is characterized by its causally maximal events \(maxEvents(C)=\{e \in C: \not \exists e' \in C, e<e'\}\), since it is exactly the union of local configurations of these events: \(C=\bigcup _{e\, \in \, maxEvents(C)} [e]\); conversely a conflict free set K of incomparable events for < defines a configuration config(K) and \(C=config(maxEvents(C))\).
A configuration C, together with the causal and independence relations defines a Mazurkiewicz trace: all interleavings are obtained by causally ordering all events in the configuration C but commuting concurrent ones. The state of a configuration C denoted by state(C) is the state in \(\mathcal{T}\) reached by any of these executions, and it is unique as discussed above. We write \(enab(C)=enabled(state(C))\subseteq \varSigma \) for the set of actions enabled at state(C), while actions(C) denotes the set of actions labelling events in C, i.e. \(actions(C) = \{ \lambda (e) : e \in C \}\).
The set of extensions of C is \(ex(C)=\{e \in E \setminus C : \lceil e \rceil \subseteq C\}\), i.e. the set of events not in C but whose causal predecessors are all in C. When appending an extension to C, only resulting conflict-free sets of events are indeed configurations. These extensions constitute the set of enabled events \(en(C) =\{e \in ex(C) : \not \exists e' \in C, e \# e'\}\) while the other ones are conflicting extensions \(cex(C) := ex(C) \setminus en(C)\).
Parametric Unfolding Semantics. Given an LTS \(\mathcal{T}\) and an independence relation I, one can build a prime event structure \(\mathcal{E}\) such that each linearization of a maximal (for inclusion) configuration represents an execution in \(\mathcal{T}\), and conversely, to each Mazurkiewicz trace in \(\mathcal{T}\) corresponds a configuration in \(\mathcal{E}\) [13].
Definition 4
(Unfolding). The unfolding of an LTS \(\mathcal{T}\) under an independence relation I is the \(\varSigma \)-PES \(\mathcal{E} = \langle E,<,\#,\lambda ,\rangle \) incrementally constructed from the initial \(\varSigma \)-PES \(\langle \emptyset , \emptyset , \emptyset , \emptyset \rangle \) by the following rules until no new event can be created:
-
for any configuration \(C \in conf(E)\), any action \(a \in enabled(state(C))\), if for any \(e' \in maxEvents(C)\), \(\lnot I(a,\lambda (e'))\), add a new event \(e=\langle a,C\rangle \) to E;
-
for any such new event \(e=\langle a,C \rangle \), update <, \(\#\) and \(\lambda \) as follows: \(\lambda (e):=a\) and for every \(e' \in E\setminus \{e\}\), consider three cases:
-
(i)
if \(e' \in C\) then \(e'<e\),
-
(ii)
if \(e' \notin C\) and \(\lnot I(a,\lambda (e'))\), then \(e \# e'\),
-
(iii)
otherwise, i.e. if \(e' \notin C\) and \(I(a,\lambda (e'))\), then e and \(e'\) are concurrent.
-
(i)
3 Programming Model and Independence Relation
In this section we introduce the abstract model of asynchronous distributed systems that we consider. While abstract, this model is sufficient to represent concrete MPI programs, as it encompasses all building blocks of the SMPI implementation of the standard [5]. We formalized this model in the specification language TLA+ [11], to later infer an independence relation (Fig. 1).
3.1 Abstract Model
In our model an asynchronous distributed system P consists in a set of n actors
 that perform local actions, communicate asynchronously with each others, and share some resources. We assume that the program is terminating, which implies that all actions are terminating. All local actions are abstracted into a unique one
that perform local actions, communicate asynchronously with each others, and share some resources. We assume that the program is terminating, which implies that all actions are terminating. All local actions are abstracted into a unique one
 . Communication actions are of four types:
. Communication actions are of four types:
 ,
,
 ,
,
 , and
, and
 . Actions on shared resources called synchronizations are of four types:
. Actions on shared resources called synchronizations are of four types:
 ,
,
 ,
,
 and
and
 .
.
At the semantics level, P is a tuple
 where
where
 and
and
 respectively describe the abstract objects, and the effects on these of the communication and synchronizations actions. The
respectively describe the abstract objects, and the effects on these of the communication and synchronizations actions. The
 subsystem provides facilities for the
subsystem provides facilities for the
 to asynchronously communicate with each others, while the subsystem
to asynchronously communicate with each others, while the subsystem
 allows the synchronization of actors on access to shared resources.
allows the synchronization of actors on access to shared resources.
Network Subsystem. The state of the
 subsystem is defined as a pair
subsystem is defined as a pair
 , where
, where
 is a set of mailboxes storing unpaired communications, while
is a set of mailboxes storing unpaired communications, while
 stores only paired ones. Each communication c has a status in
stores only paired ones. Each communication c has a status in
 , ids of source and destination actors, data addresses for those. A
, ids of source and destination actors, data addresses for those. A
 is a rendez-vous point where
is a rendez-vous point where
 and
and
 communications meet. It is modelled as an unbounded FIFO queue that is either empty, or stores
communications meet. It is modelled as an unbounded FIFO queue that is either empty, or stores
 s with all same
s with all same
 or
or
 status, waiting for a matching opposite communication. When matching occurs, this paired
status, waiting for a matching opposite communication. When matching occurs, this paired
 gets a
gets a
 status and is appended to the set
status and is appended to the set
 . We now detail the effect in actor \(A_i\) of the communication actions on
. We now detail the effect in actor \(A_i\) of the communication actions on
 and
and
 :
:
-
 drops an asynchronous
drops an asynchronous
 communication c to the mailbox m. If pending
communication c to the mailbox m. If pending
 communications exist in the mailbox, c is paired with the oldest one \(c'\) to form a communication with
communications exist in the mailbox, c is paired with the oldest one \(c'\) to form a communication with
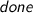 status in
status in
 , the
, the
 communication is removed from m and the data is copied from the source to the destination. Otherwise, a pending communication with
communication is removed from m and the data is copied from the source to the destination. Otherwise, a pending communication with
 status is appended to m.
status is appended to m. -
 drops an asynchronous
drops an asynchronous
 communication to mailbox m; the way a
communication to mailbox m; the way a
 communication is processed is similar to
communication is processed is similar to
 . If pending
. If pending
 communications exist, c is paired with the oldest one \(c'\) to form a communication with
communications exist, c is paired with the oldest one \(c'\) to form a communication with
 status in
status in
 , the
, the
 communication is removed from m, and the data of the
communication is removed from m, and the data of the
 is copied to d. Otherwise, a pending
is copied to d. Otherwise, a pending
 with
with
 status is appended to m.
status is appended to m. -
 tests a set of communications Com of \(A_i\). It returns a boolean, true if and only if some communication in Com with
tests a set of communications Com of \(A_i\). It returns a boolean, true if and only if some communication in Com with
 status exists.
status exists. -
 waits for a set of communications Com of \(A_i\). The action is blocking until at least one communication in Com has a
waits for a set of communications Com of \(A_i\). The action is blocking until at least one communication in Com has a
 status.
status.
Synchronization Subsystem. The
 subsystem consists in a pair
subsystem consists in a pair
 where
where
 is a set of asynchronous mutexes used to synchronize the actors, and
is a set of asynchronous mutexes used to synchronize the actors, and
 is a vector indexed by actors ids of sets of requested mutexes. Each mutex \(m_j\) is represented by a FIFO queue of actors ids i who declared their interest on a mutex \(m_j\) by executing the action
is a vector indexed by actors ids of sets of requested mutexes. Each mutex \(m_j\) is represented by a FIFO queue of actors ids i who declared their interest on a mutex \(m_j\) by executing the action
 . A mutex \(m_j\) is free if its queue is empty, busy otherwise. The owner is the actor whose id is the first in the queue. In actor \(A_i\), the effect of the synchronization actions on
. A mutex \(m_j\) is free if its queue is empty, busy otherwise. The owner is the actor whose id is the first in the queue. In actor \(A_i\), the effect of the synchronization actions on
 and
and
 is as follows:
is as follows:
-
 requests a mutex \(m_j\) with the effect of appending the actor id i to \(m_j\)’s queue and adding j to
requests a mutex \(m_j\) with the effect of appending the actor id i to \(m_j\)’s queue and adding j to
 . \(A_i\) is waiting until owning \(m_j\) but, unlike classical mutexes, waiting is not necessarily blocking.
. \(A_i\) is waiting until owning \(m_j\) but, unlike classical mutexes, waiting is not necessarily blocking. -
 removes its interest to a mutex \(m_j\) by deleting the actor id i from the \(m_j\)’s queue and removing j from
removes its interest to a mutex \(m_j\) by deleting the actor id i from the \(m_j\)’s queue and removing j from
 .
. -
 returns true if actor \(A_i\) owns some previously requested mutex \(m_j\) in M (i is first in FIFO \(m_j \in M\) s.t. j in
returns true if actor \(A_i\) owns some previously requested mutex \(m_j\) in M (i is first in FIFO \(m_j \in M\) s.t. j in
 ).
). -
 blocks until \(A_i\) owns some mutex \(m_j\) in M. Note that
blocks until \(A_i\) owns some mutex \(m_j\) in M. Note that
 (resp.
(resp.
 ) are similar to
) are similar to
 (resp.
(resp.
 ) and could be merged. We keep them separate here for simplicity of explanations.
) and could be merged. We keep them separate here for simplicity of explanations.
Beside those actions, a program can have local computations named
 actions. Such actions do not intervene with shared objects (
actions. Such actions do not intervene with shared objects (
 ,
,
 and
and
 ), and they can be responsible for I/O tasks.
), and they can be responsible for I/O tasks.
We specified our model of asynchronous distributed systems in the formal language TLA+ [11]. Our TLA+ modelFootnote 1 focuses on how actions transform the global state of the system. An instance P of a program is described by a set of actors and their actions (representing their source code). Following the semantics of TLA+, and since programs are terminating, the interleaving semantics of a program P can be described by an acyclic LTS representing all its behaviors. Formally, the LTS of P is a tuple \(\mathcal{T_P} = \langle S, s_0, \varSigma , \rightarrow \rangle \) where \(\varSigma \) represent the actions of P; a state \(s = <l,g>\) in S consists of the local state l of all actors (i.e. local variables,
 ) and g the state of all shared objects including
) and g the state of all shared objects including
 ,
,
 and
and
 ; in the initial state \(s_0\) all actors are in their initial local state, sets and FIFO queues are empty; a transition \(s\xrightarrow {\text {a}}s'\) is defined if, according to the TLA+ model, the action encoded by a is enabled at s and executing a transforms the state from s to \(s'\).
; in the initial state \(s_0\) all actors are in their initial local state, sets and FIFO queues are empty; a transition \(s\xrightarrow {\text {a}}s'\) is defined if, according to the TLA+ model, the action encoded by a is enabled at s and executing a transforms the state from s to \(s'\).
Notice that when verifying a real program, we only observe its actions and assume that they respect the proposed TLA+ model and the independence relation discussed below. These assumptions are necessary to suppose that the LTS correctly models the actual program behaviors.
3.2 Additional Property of the Model
The model presented in the previous section may appear unusual, because the lock action on mutexes is split into an
 and a
and a
 while most works in the literature consider atomic locks. Our model does not induce any loss of generality, since synchronous locks can trivially be simulated with asynchronous locks. One reason to introduce this specificity is that this entails the following lemma, that is the key to the efficiency of UDPOR in our model.
while most works in the literature consider atomic locks. Our model does not induce any loss of generality, since synchronous locks can trivially be simulated with asynchronous locks. One reason to introduce this specificity is that this entails the following lemma, that is the key to the efficiency of UDPOR in our model.
Lemma 1
(Persistence). Let u be a prefix of an execution v of a program in our model. If an action a is enabled after u, it is either executed in v or still enabled after v.
Intuitively, persistence says that once enabled, actions are never disabled by any subsequent action, thus remain enabled until executed. Persistence does not hold for classical synchronous locks, as some enabled lock(m) action of an actor may become disabled by the lock(m) of another actor. This persistence property has been early introduced by Karp and Miller [9], and later studied for Petri Nets [12]. It should not be confused with the notion of persistent set used in DPORFootnote 2. Persistent sets are linked to independence, while persistence is not.
Proof
When a is a
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 , or
, or
 action, a cannot be disabled by any new action. Indeed, these actions are never blocking (e.g.
action, a cannot be disabled by any new action. Indeed, these actions are never blocking (e.g.
 comes down to the addition of an element in a FIFO, which is always enabled) and only depend on the execution of the action right before them by the same actor.
comes down to the addition of an element in a FIFO, which is always enabled) and only depend on the execution of the action right before them by the same actor.
 and
and
 may seem more complex. If a is a
may seem more complex. If a is a
 , being enabled after u means that one communication it refers to was paired. Similarly, if a is a
, being enabled after u means that one communication it refers to was paired. Similarly, if a is a
 , being enabled after u means that the corresponding actor is first in the FIFO of a mutex it refers to. In both cases these facts cannot be modified by any subsequent action, so a remains enabled until executed.
, being enabled after u means that the corresponding actor is first in the FIFO of a mutex it refers to. In both cases these facts cannot be modified by any subsequent action, so a remains enabled until executed.
3.3 Independence Theorems
In order to use DPOR algorithms for our model of distributed programs, and in particular UDPOR that is based on the unfolding semantics, we need to define a valid independence relation for this model. Intuitively, two actions in distinct actors are independent when they do not compete on shared objects, namely
 ,
,
 , or
, or
 . This relation is formally expressed in TLA+ as so-called “independence theorems”. We use the term “theorem” since the validity of the independence relation with respect to commutation should be proved. We proved them manually and implemented them as rules in the model-checker. These independence theorems are as followsFootnote 3:
. This relation is formally expressed in TLA+ as so-called “independence theorems”. We use the term “theorem” since the validity of the independence relation with respect to commutation should be proved. We proved them manually and implemented them as rules in the model-checker. These independence theorems are as followsFootnote 3:
-
1.
A
 is independent with any other action of another actor.
is independent with any other action of another actor. -
2.
Any synchronization action is independent of any communication action of a distinct actor.
-
3.
Any pair of communication actions in distinct actors concerning distinct mailboxes are independent.
-
4.
An
 is independent of an
is independent of an
 of another actor.
of another actor. -
5.
Any pair of actions in
 in distinct actors is independent.
in distinct actors is independent. -
6.
Any action in
 is independent with any action of another actor in
is independent with any action of another actor in
 as soon as they do not both concern the first paired communication in the set ComFootnote 4.
as soon as they do not both concern the first paired communication in the set ComFootnote 4. -
7.
Any pair of synchronization actions of distinct actors concerning distinct mutexes are independent.
-
8.
An
 is independent with a
is independent with a
 of another actor.
of another actor. -
9.
Any pair of actions in
 of distinct actors is independent.
of distinct actors is independent. -
10.
A
 is independent of a
is independent of a
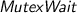 or
or
 of another actor, except if the same mutex is involved and one of the two actors owns it.
of another actor, except if the same mutex is involved and one of the two actors owns it. -
11.
An
 is independent of any
is independent of any
 and
and
 of another actor.
of another actor.
4 Adapting UDPOR
This section first recalls the UDPOR algorithm of [16] and then explains how it may be adapted to our context, in particular how the computation of extensions, a key operation, can be made efficient in our programming model.
4.1 The UDPOR Algorithm
Algorithm 1 presents the UDPOR exploration algorithm of [16]. Like other DPOR algorithms, it explores only a part of the LTS of a given terminating distributed program P according to an independence relation I, while ensuring that the explored part is sufficient to detect all deadlocks. The particularity of UDPOR is to use the concurrency semantics explicitly, namely unfoldings, which makes it both complete and optimal: it explores exactly one interleaving per Mazurkiewicz trace, never reaching any sleep-set blocked execution.

The algorithm works as follows. Executions are represented by configurations, thus equivalent to their Mazurkiewicz traces. The set U, initially empty, contains all events met so far in the exploration. The procedure Explore has three parameters: a configuration C encoding the current execution; a set D (for disabled) of events to avoid (playing a role similar to a sleep set in [8]), thus preventing revisits of configurations; a set A (for add) of events conflicting with D and used to guide the search to events in conflicting configurations in cex(C) to explore alternative executions.
First, all extensions of C are computed and added to U (line 4). The search backtracks (line 6) in two cases: when C is maximal (\(en(C)=\emptyset \)), i.e. a deadlock (or the program end) is reached, or when all events enabled in C should be avoided (\(en(C) \subseteq D\)), which corresponds to a redundant call, thus a sleep-set blocked execution. Otherwise, an enabled event e is chosen (line 7–10), in A if this guiding information is non empty (line 10), and a “left” recursive exploration \(Explore(C\cup \{e\}, D, A\setminus \{e\})\) is called (line 11) from this extended configuration \(C \cup \{e\}\), it continues trying to avoid D, but e is removed from A in the guiding information. When this call is completed, all configurations containing C and e have been explored, thus it remains to explore those that contain C but not e. In this aim alternatives are computed (line 12) with the function call \(Alt(C,D\cup \{e\})\). Alternatives play a role similar to “backtracking sets” in the original DPOR algorithm, i.e. sets of actions that must be explored from the current state. Formally, an alternative to \(D'=D\cup \{e\}\) after C in U is a subset J of U that, does not intersect \(D'\), forms a configuration \(C \cup J\) after C, and such that all events in \(D'\) conflict with some event in J. If an Alternatives J exists, a right “recursive” exploration is called \(Explore(C, D\cup \{e\},J\setminus C)\): C is still the configuration to extend, but e is now also to be avoided, thus added to D, while events in \(J\setminus C\) are used as guides. Upon completion (line 14), U is intersected with \(Q_{C,D}\) which includes all events in C and D as well as every event in U conflicting with some events in \(C \cup D\).
In order to avoid sleep-set blocked executions (SSB) and obtain the optimality of DPOR, the function \(Alt(C, D \cup \{e\})\) has to solve an NP-complete problem [13]: find a subset J of U that can be used for backtracking, conflicts with all \(D\cup \{e\}\) thus necessarily leading to a configuration \(C\cup J\) that is not already visited. In this case \(en(C)\subseteq D\) can then be replaced by \(en(C)=\emptyset \) in line 5. Note that with a different encoding, Optimal DPOR must solve the same problem [1] as explained in [13]. In [13], a variant of the algorithm is proposed for the function Alt that computes k-partial alternatives rather than alternatives, i.e. sets of events J conflicting with only k events in D, not necessarily all of them. Depending on k, (e.g. \(k=\infty \) (or \(k=|D|+1\)) for alternatives, \(k=1\) for source sets of [1]) this variant allows to tune between an optimal or a quasi-optimal algorithm that may be more efficient.
4.2 Computing Extensions Efficiently
Computing the extensions ex(C) of a configuration C may be costly in general. It is for example an NP-complete problem for Petri Nets since all sub-configurations must be enumerated. Fortunately this algorithm can be specially tuned for sub-classes. In particular for the programming model of [13, 16] it is tuned in an algorithm working in time \(O(n^2log(n))\), using the fact that events have a maximum of two causal predecessors, thus limiting the subsets to consider.
This section tunes the algorithm to our more complex model, using the fact that the amount of causal predecessors of events is also bounded. Next section shows how to incrementally compute ex(C) to avoid recomputations. Figure 2 illustrates some aspects of an extension.
This section mandates some additional notations. Given a configuration C and an extension with action a, let pre(a) denote the action right before a in the same actor, while preEvt(a, C) denotes the event in C associated with pre(a) (formally \(e = preEvt(a,C) \iff e \in C, \lambda (e) = pre(a)\)). Given a set F of events \(F\subseteq E\), Depend(a, F) means that a depends on all actions labeling events in F.
The definition of ex(C) (set of extensions of a configuration C) \(\{ e \in E\setminus C : \lceil e \rceil \subseteq C\}\) can be rewritten using the definitions of Sect. 2 as follows: \(\{ e=\langle a,H \rangle \in E \setminus C: a = \lambda (e) \wedge H = \lceil e \rceil \wedge H\in 2^C \cap conf(E) \wedge a \in enab(H)\}\).
Fortunately, it is not necessary to enumerate all subsets H of C, that are in exponential numbers, to compute this set. According to the unfolding construction in Definition 4, an event \(e = \langle a, H\rangle \) only exists in ex(C) if the action a is dependant with the actions of all maximal events of H. This gives: \(ex(C) = \{ e=\langle a,H \rangle \in E \setminus C: a = \lambda (e) \wedge H = \lceil e \rceil \wedge H \in 2^C \cap conf(E) \wedge a \in enab(H) \wedge Depend(a, maxEvents(H)) \}\). Now ex(C) can be simplified and decomposed by enumerating \(\varSigma \), yielding to: \(ex(C) = \bigcup _{a\, \in \, \varSigma } \{\langle a,H \rangle : H \in S_{a,C}\}\setminus C\) where \(S_{a,C} = \{ H \in conf(E): H \subseteq C \wedge a \in enab(H) \wedge Depend(a, maxEvents(H)) \}\).
The above formulation of ex(C) iterates on all actions in \(\varSigma \). However, interpreting the persistence property (Lemma 1) for configurations entails that for two configurations H and C with \(H\subseteq C\), an action a in enab(H) is either in actions(C) or enab(C).
Therefore, ex(C) can be rewritten by restricting a to \(actions(C) \cup enab(C):\)
Now, instead of enumerating possible configurations \(H\in S_{a,C}\), we can enumerate their maximal sets \(K=maxEvents(H)\). Hence,
with \(S^{max}_{a,C} = \{ K \in 2^C : \text{ K } \text{ is } \text{ maximal } \wedge a\in enab(config(K)) \wedge Depend(a, K)) \}\) and K is maximal if \((\not \exists e, e' \in K : e < e' \vee e \# e')\).
One can then specialize the computation of ex(C) according to the type of action a. Due to space limitations, we only detail the computation for
 actions, the other ones being similar.
actions, the other ones being similar.
Computing Extensions for
 Actions. Let C be a configuration, and a an action of type
Actions. Let C be a configuration, and a an action of type
 of an actor \(A_i\). We want to compute the set \(S^{max}_{a,C}\) of sets K of maximal events from which a depends.
of an actor \(A_i\). We want to compute the set \(S^{max}_{a,C}\) of sets K of maximal events from which a depends.
According to independence theorems (see Sect. 3.3), a only depends on the following actions: pre(a), all
 actions of distinct actors \(A_j\) which concern the same mailbox m, and all
actions of distinct actors \(A_j\) which concern the same mailbox m, and all
 (resp.
(resp.
 ) actions that wait (resp. test) a
) actions that wait (resp. test) a
 which concerns the same communication c. Considering this, we now examine the composition of maximal events sets K in \(S^{max}_{a,C}\).
which concerns the same communication c. Considering this, we now examine the composition of maximal events sets K in \(S^{max}_{a,C}\).
First, two events labelled by
 actions cannot co-exist in K, formally \(\not \exists e, e' \in K : \lambda (e), \lambda (e')\) in
actions cannot co-exist in K, formally \(\not \exists e, e' \in K : \lambda (e), \lambda (e')\) in
 : indeed, if two such events exist in a configuration, they are dependent but cannot conflict, thus are causality related and cannot be both maximal.
: indeed, if two such events exist in a configuration, they are dependent but cannot conflict, thus are causality related and cannot be both maximal.
Second, if a
 action concerns communication c, there are two cases: (i) either c is not the first
action concerns communication c, there are two cases: (i) either c is not the first
 communication in Com, then
communication in Com, then
 and the action a are independent. (ii) or c is the first
and the action a are independent. (ii) or c is the first
 communication in Com and
communication in Com and
 is enabled only after a. Thus the only possibility for a maximal event to be labelled by a
is enabled only after a. Thus the only possibility for a maximal event to be labelled by a
 is when pre(a) is a
is when pre(a) is a
 of the same actor. We can then write: \(\not \exists e \in K: \lambda (e)\) in
of the same actor. We can then write: \(\not \exists e \in K: \lambda (e)\) in
 \(\wedge \lambda (e) \ne pre(a)\).
\(\wedge \lambda (e) \ne pre(a)\).
Third, all
 events for the mailbox m are causally related in configuration C, and c can only be paired with one of them, say \(c'\). Thus a can only depend on actions
events for the mailbox m are causally related in configuration C, and c can only be paired with one of them, say \(c'\). Thus a can only depend on actions
 such that \(c' \in Com'\) and c and \(c'\) form the first
such that \(c' \in Com'\) and c and \(c'\) form the first
 communication in \(Com'\), and all those
communication in \(Com'\), and all those
 events are ordered. Thus, there is at most one event e labelled by
events are ordered. Thus, there is at most one event e labelled by
 in K such that \(\lambda (e) \ne pre(a)\).
in K such that \(\lambda (e) \ne pre(a)\).
To conclude, K contains at most three events: preEvt(a, C), some event labelled with an action
 on the same mailbox, and some
on the same mailbox, and some
 for some matching
for some matching
 communication. There is thus only a cubic number of such sets, which is the worse case among considered action types. Algorithm 2 generates all events in ex(C) labelled by an
communication. There is thus only a cubic number of such sets, which is the worse case among considered action types. Algorithm 2 generates all events in ex(C) labelled by an
 action a.
action a.

Example 1
We illustrate the Algorithm 2 by the example of Fig. 3. Suppose we want to compute the extensions of C = {\(e_1, e_2, e_3, e_4, e_5\)} associated with a, the action
 of \(Actor_2\). First
of \(Actor_2\). First
 because \(preEvt(a,C) = e_2\) (line 1). We then iterate on all
because \(preEvt(a,C) = e_2\) (line 1). We then iterate on all
 events in C, combining them with \(e_2\) to create maximal event sets K (lines 2–8). We only have one
events in C, combining them with \(e_2\) to create maximal event sets K (lines 2–8). We only have one
 event \(e_3\). Since \(\lnot (e_2 < e_3) \) and \(\lnot (e_3 < e_2)\), we form a first set \(K = \{ e_2, e_3\}\), and add
event \(e_3\). Since \(\lnot (e_2 < e_3) \) and \(\lnot (e_3 < e_2)\), we form a first set \(K = \{ e_2, e_3\}\), and add
 to ex(C). Next all
to ex(C). Next all
 events that concern the mailbox m should be considered. Events \(e_2\) and \(e_5\) can be combined to form a new maximal event set \(K = \{e_2, e_5\}\), but since a and \(\lambda (e_5)\) are not related to the same communication, \(D(a, \lambda (e_5))\) is not satisfied and no event is created. Finally combinations of \(e_2\) with an
events that concern the mailbox m should be considered. Events \(e_2\) and \(e_5\) can be combined to form a new maximal event set \(K = \{e_2, e_5\}\), but since a and \(\lambda (e_5)\) are not related to the same communication, \(D(a, \lambda (e_5))\) is not satisfied and no event is created. Finally combinations of \(e_2\) with an
 event and a
event and a
 event are examined (lines 9–17). We then get \(K = \{e_2, e_5, e_3\}\), and \(e_{8}\) is added to ex(C) since \(D(a,\lambda (e_5))\) holds in the configuration \(config(\{ e_2, e_5, e_3\})\).
event are examined (lines 9–17). We then get \(K = \{e_2, e_5, e_3\}\), and \(e_{8}\) is added to ex(C) since \(D(a,\lambda (e_5))\) holds in the configuration \(config(\{ e_2, e_5, e_3\})\).
4.3 Computing Extensions Incrementally
In the UDPOR exploration algorithm, after extending a configuration \(C'\) by adding a new event e, one must compute the extensions of \(C=C'\cup \{e\}\), thus resulting in redundant computations of events. The next theorem improves this by providing an incremental computation of extensions.
Theorem 1
Suppose \(C = C' \cup \{e\}\) where e is the last event added to C by the Algorithm 1. We can compute ex(C) incrementally as follows:
where \(S_{a,C} = \{ H \in 2^C \cap conf(E): a \in enab(H) \wedge Depend(a, maxEvents(H)) \}\).
Proof
With the definition of \(S_{a,C}\) as above, recall that
Applying the same Eq. (6) to \(C'\) we get:
Now, exploring e from \(C'\) leads to C, which entails that \(\lambda (e)\) belongs to \(enab(C')\) and \(actions(C')\cup \lambda (e)=actions(C)\), thus the range of a in \(ex(C')\) which is \(actions(C')\cup enab(C')\) can be rewritten \(actions(C)\cup (enab(C') \setminus \lambda (e))\).
First, separating action(C) from the rest in both ex(C) and \(ex(C')\) we prove:
(\(\supseteq \)) This inclusion is obvious since \(C \supseteq C'\), and thus \(S_{a,C} \supseteq S_{a,C'}\).
(\(\subseteq \)) Suppose there exists some event \(e_n = <a, H>\) belonging to the left but not the right set. If \(a = \lambda (e_n)=\lambda (e)\), then \(H \in S_{a,C} \cap S_{a,C'}\), so \(e_n\) is in both sets, resulting in a contradiction. If \(a =\lambda (e_n)\ne \lambda (e)\), there are two cases: (i) either \(e \notin H\) then \(H \in S_{a,C'}\) and \(e_n\) belongs to the right set, a contradiction. (ii) or \(e \in H\), then \(\lambda (e_n) \in actions(C)\setminus \{\lambda (e)\}= actions(C')\), thus there is another event \(e' \in C'\) such that \(\lambda (e') = \lambda (e_n)\), then \(e'\) cannot belong to H (one action a cannot appear twice in \(\lceil e_n \rceil \)). Besides, e is the last event explored in C, thus a depends on \(\lambda (e)\) by Definition 4. Then, \(e'\) conflicts with e, contradicting their membership to the same configuration C. This proves (7).
Second, since \(C' \subseteq C\), according to persistence of the programming model (Lemma 1), (\(enab(C') \setminus \{\lambda (e) \}) \subseteq enab(C)\). We thus have:
Now, using Eqs. (7) and (8), ex(C) can be rewritten as follows:
But since no event in \( \bigcup _{a\, \in \, enab(C) } \{\langle a,H \rangle : H \in S_{a,C}\}\) is in \(( C' \cup \{ e \})\), Eq. (9) can be rewritten as Eq. (5) in Theorem 1.
4.4 Experiments
We implemented the quasi-optimal version of UDPOR with k-partial alternatives [13] in a prototype adapted to the distributed programming model of Sect. 3, i.e. with its independence relation. The computation of k-partial alternatives is essentially inspired by [13]. Recall the algorithm reaches optimality when \(k=|D|+1\), while \(k=1\) corresponds to Source DPOR [1]. The prototype is still limited, not connected to the SimGrid environment, thus can only be experimented on simple examples.
We first compare optimal UDPOR with an exhaustive stateless search on several benchmarks (see Table 1). The first five benchmarks come from Umpire_TestsFootnote 5, while DTG and RMQ-receiving belong to [10] and [17], respectively. The last benchmark is an implementation of a simple Master-Worker pattern. We expressed them in our programming model and explored their state space with our prototype. The experiments were performed on an HP computer, Intel Core i7-6600U 2.60 GHz processors, 16 GB of RAM, and Ubuntu version 18.04.1. Table 1 presents the number of explored traces and running time for both an exhaustive search and optimal UDPOR. In all benchmarks UDPOR outperforms the exhaustive search. For example, for RMQ-receiving with 4 processes, the exhaustive search explores more than 20000 traces in around 8 s, while UDPOR explores only 6 traces in 0.2 s. Besides, UDPOR is optimal, exploring only one trace per Mazurkiewicz trace. For example in RMQ-receiving with 5 processes, with only 4
 actions that concern the same mailbox, UDPOR explores exactly 24 (=4!) non-equivalent traces. Similarly, the DTG benchmark has only two dependent
actions that concern the same mailbox, UDPOR explores exactly 24 (=4!) non-equivalent traces. Similarly, the DTG benchmark has only two dependent
 actions, thus two non-equivalent traces. Furthermore, deadlocks are also detected in the prototype.
actions, thus two non-equivalent traces. Furthermore, deadlocks are also detected in the prototype.
We also tried to vary the value of k. When k is decreased, one gains in efficiency in computing alternatives, but looses optimality by producing more traces. It is then interesting to analyse, whether this can be globally more efficient than optimal UDPOR. Similar to [13], we observed that in some cases, fixing smaller values of k may improve the efficiency. For example with RMQ-receiving, \(k=7\) is optimal, but reducing to \(k=4\) still produces 24 traces (thus is optimal) a bit more quickly (2.3 s), while for \(k=3\) the number of traces and time diverge. We have to analyse this more precisely on more examples in the future.
Note that with our simple prototype, we do not yet make experiments with concrete programs (e.g. MPI programs), for which running time may somehow diverge. We expect to make it in the next months and then experiment the algorithms in more depth. However, we believe that the results are already significant and that UDPOR is effective for asynchronous distributed programs.
5 Conclusion and Future Work
The paper adapts the unfolding-based dynamic partial order reduction (UDPOR) approach [16] to the verification of asynchronous distributed programs. The programming model we consider is generic enough to properly model a large class of asynchronous distributed systems, including e.g. MPI applications, while exhibiting some interesting properties. From a formal specification of this model in TLA+, an independence relation is built, that is used by UDPOR to partly build the unfolding semantics of programs. We show that, thanks to the properties of our model, some usually expensive operations of UDPOR can be made efficient. A prototype of UDPOR has been implemented and experimented on some benchmarks, gaining promising first results.
In the future we aim at extending our model of asynchronous distributed systems, while both preserving good properties, getting a more precise independence relation, and implementing UDPOR in the SimGrid model-checker and verify real MPI applications. Once done, we should experiment UDPOR more deeply, and compare it with state of the art tools on more significant benchmarks, get a more precise analysis about the efficiency of UDPOR compared to simpler DPOR approaches, analyse the impact of quasi-optimality on efficiency.
Notes
- 1.
- 2.
A set of transitions T is called persistent in a state s if all transitions not in T and, either enabled in T or enabled in a state reachable by transitions not in T, are independent with all transitions in T. As a consequence, exploring only transitions in persistent sets is sufficient to detect all deadlocks.
- 3.
Some independence theorems could be enlarged but we give these ones for simplicity.
- 4.
Intuitively,
 needs only one done communication (the first paired
needs only one done communication (the first paired
 ) in Com to become enabled. Similarly, the effect of
) in Com to become enabled. Similarly, the effect of
 only depends on this first done communication.
only depends on this first done communication. - 5.
References
Abdulla, P.A., Aronis, S., Jonsson, B., Sagonas, K.F.: Optimal dynamic partial order reduction. In: 41st Annual ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL 2014, San Diego, CA, USA, pp. 373–384, January 2014. https://doi.org/10.1145/2535838.2535845
Albert, E., Gómez-Zamalloa, M., Isabel, M., Rubio, A.: Constrained dynamic partial order reduction. In: 30th International Conference on Computer Aided Verification, CAV 2018, Oxford, UK, pp. 392–410, July 2018. https://doi.org/10.1007/978-3-319-96142-2_24
Aronis, S., Jonsson, B., Lång, M., Sagonas, K.: Optimal dynamic partial order reduction with observers. In: Beyer, D., Huisman, M. (eds.) TACAS 2018. LNCS, vol. 10806, pp. 229–248. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-89963-3_14
Baier, C., Katoen, J.: Principles of Model Checking. MIT Press, Cambridge (2008)
Degomme, A., Legrand, A., Markomanolis, G.S., Quinson, M., Stillwell, M., Suter, F.: Simulating MPI applications: the SMPI approach. IEEE Trans. Parallel Distrib. Syst. 28(8), 2387–2400 (2017). https://doi.org/10.1109/TPDS.2017.2669305
Esparza, J., Heljanko, K.: Unfoldings - A Partial-Order Approach to Model Checking. Monographs in Theoretical Computer Science. An EATCS Series. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-77426-6
Flanagan, C., Godefroid, P.: Dynamic partial-order reduction for model checking software. In: 32nd ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL 2005, Long Beach, California, USA, pp. 110–121, January 2005. https://doi.org/10.1145/1040305.1040315
Godefroid, P. (ed.): Partial-Order Methods for the Verification of Concurrent Systems. LNCS, vol. 1032. Springer, Heidelberg (1996). https://doi.org/10.1007/3-540-60761-7
Karp, R.M., Miller, R.E.: Parallel program schemata. J. Comput. Syst. Sci. 3(2), 147–195 (1969). https://doi.org/10.1016/S0022-0000(69)80011-5
Khanna, D., Sharma, S., Rodríguez, C., Purandare, R.: Dynamic symbolic verification of MPI programs. In: 22nd International Symposium on Formal Methods, FM 2018, Oxford, UK, pp. 466–484, July 2018. https://doi.org/10.1007/978-3-319-95582-7_28
Lamport, L.: Specifying Systems. The TLA+ Language and Tools for Hardware and Software Engineers. Addison-Wesley, Boston (2002)
Landweber, L.H., Robertson, E.L.: Properties of conflict-free and persistent Petri Nets. J. ACM 25(3), 352–364 (1978). https://doi.org/10.1145/322077.322079
Nguyen, H.T.T., Rodríguez, C., Sousa, M., Coti, C., Petrucci, L.: Quasi-optimal partial order reduction. In: 30th International Conference on Computer Aided Verification, CAV 2018, Oxford, UK, pp. 354–371, July 2018. https://doi.org/10.1007/978-3-319-96142-2_22
Palmer, R., Gopalakrishnan, G., Kirby, R.M.: Semantics driven dynamic partial-order reduction of MPI-based parallel programs. In: Proceedings of the 2007 ACM Workshop on Parallel and Distributed Systems: Testing and Debugging, PADTAD 2007, pp. 43–53. ACM (2007)
Pham, A., Jéron, T., Quinson, M.: Verifying MPI applications with SimGridMC. In: Proceedings of the 1st International Workshop on Software Correctness for HPC Applications, CORRECTNESS@SC 2017, Denver, CO, USA, pp. 28–33, November 2017. https://doi.org/10.1145/3145344.3145345
Rodríguez, C., Sousa, M., Sharma, S., Kroening, D.: Unfolding-based partial order reduction. In: 26th International Conference on Concurrency Theory, CONCUR 2015, Madrid, Spain, pp. 456–469, September 2015. https://doi.org/10.4230/LIPIcs.CONCUR.2015.456
Rosa, C.D., Merz, S., Quinson, M.: A simple model of communication APIs - application to dynamic partial order reduction. In: 10th International Workshop on Automated Verification of Critical Systems, AVOCS 2010, Düsseldorf, Germany, September 2010. http://journal.ub.tu-berlin.de/eceasst/article/view/562
Sharma, S., Gopalakrishnan, G., Bronevetsky, G.: A sound reduction of persistent-sets for deadlock detection in MPI applications. In: Gheyi, R., Naumann, D. (eds.) SBMF 2012. LNCS, vol. 7498, pp. 194–209. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-33296-8_15
Acknowledgement
We wish to thank the reviewers for their constructive comments to improve the paper.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 IFIP International Federation for Information Processing
About this paper
Cite this paper
Pham, T.A., Jéron, T., Quinson, M. (2019). Unfolding-Based Dynamic Partial Order Reduction of Asynchronous Distributed Programs. In: Pérez, J., Yoshida, N. (eds) Formal Techniques for Distributed Objects, Components, and Systems. FORTE 2019. Lecture Notes in Computer Science(), vol 11535. Springer, Cham. https://doi.org/10.1007/978-3-030-21759-4_13
Download citation
DOI: https://doi.org/10.1007/978-3-030-21759-4_13
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-21758-7
Online ISBN: 978-3-030-21759-4
eBook Packages: Computer ScienceComputer Science (R0)






 ,
,
 and
and

 drops an asynchronous
drops an asynchronous
 communication c to the mailbox m. If pending
communication c to the mailbox m. If pending
 communications exist in the mailbox, c is paired with the oldest one
communications exist in the mailbox, c is paired with the oldest one 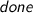 status in
status in
 , the
, the
 communication is removed from m and the data is copied from the source to the destination. Otherwise, a pending communication with
communication is removed from m and the data is copied from the source to the destination. Otherwise, a pending communication with
 status is appended to m.
status is appended to m. drops an asynchronous
drops an asynchronous
 communication to mailbox m; the way a
communication to mailbox m; the way a
 communication is processed is similar to
communication is processed is similar to
 . If pending
. If pending
 communications exist, c is paired with the oldest one
communications exist, c is paired with the oldest one  status in
status in
 , the
, the
 communication is removed from m, and the data of the
communication is removed from m, and the data of the
 is copied to d. Otherwise, a pending
is copied to d. Otherwise, a pending
 with
with
 status is appended to m.
status is appended to m. tests a set of communications Com of
tests a set of communications Com of  status exists.
status exists. waits for a set of communications Com of
waits for a set of communications Com of  status.
status. requests a mutex
requests a mutex  .
.  removes its interest to a mutex
removes its interest to a mutex  .
. returns true if actor
returns true if actor  ).
). blocks until
blocks until  (resp.
(resp.
 ) are similar to
) are similar to
 (resp.
(resp.
 ) and could be merged. We keep them separate here for simplicity of explanations.
) and could be merged. We keep them separate here for simplicity of explanations. is independent with any other action of another actor.
is independent with any other action of another actor. is independent of an
is independent of an
 of another actor.
of another actor. in distinct actors is independent.
in distinct actors is independent. is independent with any action of another actor in
is independent with any action of another actor in
 as soon as they do not both concern the first paired communication in the set Com
as soon as they do not both concern the first paired communication in the set Com is independent with a
is independent with a
 of another actor.
of another actor. of distinct actors is independent.
of distinct actors is independent. is independent of a
is independent of a
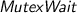 or
or
 of another actor, except if the same mutex is involved and one of the two actors owns it.
of another actor, except if the same mutex is involved and one of the two actors owns it. is independent of any
is independent of any
 and
and
 of another actor.
of another actor.

 needs only one done communication (the first paired
needs only one done communication (the first paired
 ) in Com to become enabled. Similarly, the effect of
) in Com to become enabled. Similarly, the effect of
 only depends on this first done communication.
only depends on this first done communication.