Abstract
Uninorms play a prominent role both in the theory and applications of Aggregations, Fuzzy Theory, and of Mathematical Fuzzy Logic. In this paper the class of group-like uninorms is introduced. First, two variants of a construction method – called partial-lexicographic product – will be recalled; it constructs a large subclass of group-like FL\(_e\)-algebras. Then two specific ways of applying the partial-lexicographic product construction to construct uninorms will be presented. The first one constructs starting from \(\mathbb R\) and modifying it in some way by \(\mathbb Z\)’s, what we call basic group-like uninorms, whereas with the second one may extend group-like uninorms by using \(\mathbb Z\) and a basic uninorm to obtain further group-like uninorms. All group-like uninorms obtained this way have finitely many idempotents. On the other hand, we assert that the only way to construct group-like uninorms which have finitely many idempotents is to apply this extension (by a basic group-like uninorm) consecutively, starting from a basic group-like uninorm. In this way a complete characterization for group-like uninorms which possess finitely many idempotents is given. The obtained uninorm class can be candidate for the aggregation operation of several applications. The paper is illustrated with several 3D plots.
This work was supported by the GINOP 2.3.2-15-2016-00022 grant.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
Other terminologies for FL\(_e\)-algebras are: pointed commutative residuated lattices or pointed commutative residuated lattice-ordered monoids.
- 2.
That is, there exists a binary operation
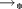 such that
such that 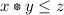 if and only if
if and only if 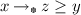 ; this equivalence is called residuation condition or adjointness condition, (
; this equivalence is called residuation condition or adjointness condition, ( ) is called an adjoint pair. Equivalently, for any x, z, the set
) is called an adjoint pair. Equivalently, for any x, z, the set 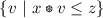 has its greatest element, and
has its greatest element, and  is defined as this element:
is defined as this element: 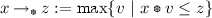 .
. - 3.
Note that intuitively it would make up for a coordinatewise definition, too, in the second line of (1) to define it as
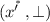 . But \(\bot \) is not amongst the set of possible second coordinates. However, since \(X_{gr}\) is discretely embedded into X, if
. But \(\bot \) is not amongst the set of possible second coordinates. However, since \(X_{gr}\) is discretely embedded into X, if 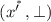 would be an element of the algebra then it would be equal to
would be an element of the algebra then it would be equal to 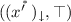 .
. - 4.
The rank of an involutive FL\(_e\)-algebra is positive if \(t>f\), negative if \(t<f\), and 0 if \(t=f\).
- 5.
The negative cone consists of the elements which are smaller or equal to t.
References
Akella, P.: Structure of n-uninorms. Fuzzy Sets Syst. 158(15), 1631–1651 (2007)
De Baets, B.: Idempotent uninorms. Eur. J. Oper. Res. 118(3), 631–642 (1999)
Fodor, J.C.: On rational uninorms. In: Proceedings of the First Slovakian-Hungarian Joint Symposium on Applied Machine Intelligence, Herlany, Slovakia, pp. 139–147 (2003)
De Baets, B., Fodor, J.C.: On the structure of uninorms and their residual implicators. In: Gottwald, S., Klement, E.P. (eds.) 18th Linz Seminar on Fuzzy Set Theory: Enriched Lattice Structures for Many-Valued and Fuzzy Logics, Johannes Kepler Universitt, Linz, Austria, 25 February–1 March 1997, pp. 81–87 (1997)
Drygas, P.: On the structure of continuous uninorms. Kibernetika 43(2), 183–196 (2007)
Drygas, P.: On the structure of uninorms on L\(^\ast \). In: Magdalena, L., Ojeda-Aciego, M., Verdegay, J.L. (eds.) Proceedings of IPMU2008, Torremolinos, Malaga, pp. 1795–1800 (2004)
Fodor, J.C., Yager, R., Rybalov, A.: Structure of uninorms. Int. J. Uncertainty Fuzziness Knowl. Based Syst. 5, 411–427 (1997)
Galatos, N., Jipsen, P., Kowalski, T., Ono, H.: Residuated Lattices: An Algebraic Glimpse at Substructural Logics. Studies in Logic and the Foundations of Mathematics, vol. 151. Elsevier, Amsterdam (2007)
Galatos, N., Raftery, J.G.: A category equivalence for odd Sugihara monoids and its applications. J. Pure Appl. Algebra 216, 2177–2192 (2012)
Hájek, P.: Metamathematics of Fuzzy Logic. Kluwer Academic Publishers, Dordrecht (1998)
Jenei, S.: On the structure of rotation-invariant semigroups. Arch. Math. Logic 42, 489–514 (2003)
Jenei, S.: The Hahn embedding theorem for a class of residuated semigroups (submitted)
Klement, E.P., Mesiar, R., Pap, E.: Triangular Norms. Kluwer Academic Publishers, Dordrecht (2000)
Mesiarová-Zemánková, A.: Characterization of uninorms with continuous underlying t-norm and t-conorm by their set of discontinuity points. IEEE Trans. Fuzzy Syst. 28(2), 705–714 (2018)
Mesiarová-Zemánková, A.: Characterizing set-valued functions of uninorms with continuous underlying t-norm and t-conorm. Fuzzy Sets Syst. 334, 83–93 (2018)
Metcalfe, G., Montagna, F.: Substructural fuzzy logics. J. Symb. Logic 72(3), 834–864 (2007)
Mostert, P.S., Shields, A.L.: On the structure of semigroups on a compact manifold with boundary. Ann. Math. 65, 117–143 (1957)
Petrik, M., Mesiar, R.: On the structure of special classes of uninorms. Fuzzy Sets Syst. 240, 22–38 (2014)
Su, Y., Zong, W., Drygas, P.: Properties of uninorms with the underlying operation given as ordinal sums. Fuzzy Sets Syst. https://doi.org/10.1016/j.fss.2018.04.011
Yager, R.R., Rybalov, A.: Uninorm aggregation operators. Fuzzy Sets Syst. 80, 111–120 (1996)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Jenei, S. (2019). A New Class of Uninorm Aggregation Operations for Fuzzy Theory. In: Rutkowski, L., Scherer, R., Korytkowski, M., Pedrycz, W., Tadeusiewicz, R., Zurada, J. (eds) Artificial Intelligence and Soft Computing. ICAISC 2019. Lecture Notes in Computer Science(), vol 11508. Springer, Cham. https://doi.org/10.1007/978-3-030-20912-4_28
Download citation
DOI: https://doi.org/10.1007/978-3-030-20912-4_28
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-20911-7
Online ISBN: 978-3-030-20912-4
eBook Packages: Computer ScienceComputer Science (R0)


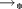 such that
such that 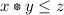 if and only if
if and only if 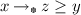 ; this equivalence is called residuation condition or adjointness condition, (
; this equivalence is called residuation condition or adjointness condition, ( ) is called an adjoint pair. Equivalently, for any x, z, the set
) is called an adjoint pair. Equivalently, for any x, z, the set 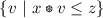 has its greatest element, and
has its greatest element, and  is defined as this element:
is defined as this element: 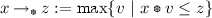 .
.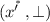 . But
. But 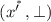 would be an element of the algebra then it would be equal to
would be an element of the algebra then it would be equal to 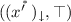 .
.