Compliance with Social Norms as an Evolutionary Stable Equilibrium

Abstract

This paper analyzes the compliance with social norms optimally established by a benevolent central planner. Since compliance is costly, agents have an incentive to free-ride on others, in a public good game. We distinguish two types of agents: standard pro-self agents (Sanchos) whose payoffs are defined by a prisoner’s dilemma game dominated by the non-compliance strategy, and pro-social Quixotes, who still have an incentive to free-ride, although prefer compliance over mutual defection (as in a snowdrift game). Compliance is analyzed in a two-population evolutionary game considering an imitative revision protocol. Individuals from one population play against and imitate agents within their own but also the other population. Inter-population interaction and imitation allow us to investigate under which circumstances some Sanchos might imitate compliant Quixotes, so escaping the non-compliance equilibrium characteristic of an isolated population of Sanchos. Correspondingly, we analyze the conditions under which the interaction with the population of selfish Sanchos increases or decreases the compliance rate among altruistic Quixotes.

Appendix: Proof of Propositions

Proof of Proposition 1

The system dynamics reads:

(26)

(27)

From this system, the evolution of the compliance rates among Sanchos, p, and Quixotes, q, is analyzed separately for each of the five regions in the α − y plane, resumed in Fig. 2. We can distinguish two situations depending on whether α < 1∕2 (Δ _wg < Δ _cp), or α > 1∕2 (Δ _wg > Δ _cp). The possible equilibria in each region and their stability are also studied.

• U: y > Δ. The dynamics reads:

  $$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle &\displaystyle \dot{p}=-p\left\{(1-y)(y-\varDelta)\sigma+[(1-p)s+(1-q)(1-s)\alpha]\varepsilon]\right\}\le0, \end{array} \end{aligned} $$

  (28)
  $$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle &\displaystyle \dot{q}=-q\left\{(1-y)(y-\varDelta)\sigma+(1-p)s(1-\alpha)\varepsilon]\right\}\le0. \end{array} \end{aligned} $$

  (29)

  $\dot {p}<0$, except if p = 0 or p = q = 1, when $\dot {p}=0$. Similarly, $\dot {q}<0$, except for q = 0 or p = q = 1, when $\dot {q}=0$. The point (0, 0)∉U, while (1, 1) ∈U. Thus (1, 1) is the only equilibrium in this region and it is unstable.

• M: $\;\max \left \{\varDelta _{wg},\varDelta _{cp}\right \}<y\le \varDelta$. The dynamics in this region reads:

  $$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle &\displaystyle \dot{p}=-p\left\{(1-p)s[(y-\varDelta)\sigma+\varepsilon]+(1-q)(1-s)(y-\varDelta_{cp})\sigma\right\}\le0,\\ &\displaystyle &\displaystyle \dot{q}=q\left\{(1-y)(\varDelta-y)\sigma-(1-p)s(1-\alpha)\varepsilon\right\}. \end{array} \end{aligned} $$

  As in region U, $\dot {p}<0$, except if p = 0 or p = q = 1, when $\dot {p}=0$, but (1, 1)∉M. Furthermore:

  $$\displaystyle \begin{aligned} \dot{q}\gtrless 0\Leftrightarrow (1-y)(\varDelta-y)\sigma\gtrless (1-\alpha)(1-p)s\varepsilon. \end{aligned}$$

  From this dynamics, the only possible equilibrium in this region must satisfy p = 0. In this situation $\dot {q}=0$ under equation:

  $$\displaystyle \begin{aligned}{}[1-q(1-s)][\varDelta-q(1-s)]=(1-\alpha)s\frac{\varepsilon}{\sigma}. \end{aligned} $$

  (30)

  Or equivalently, for p = 0, $\dot {q}/q$ is given by the second order polynomial in q:

  $$\displaystyle \begin{aligned} q^2(1-s)^2-q(1-s)(1+\varDelta)+\varDelta-(1-\alpha)s\frac{\varepsilon}{\sigma}, \end{aligned}$$

  which has one stable and one unstable root. The stable root is given by (16).

• L: Δ _wg < y ≤ Δ _cp ≤ Δ (α < 1∕2). The dynamics in this region reads:

  

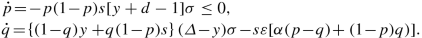
  Still in this region $\dot {p}<0$, except if p = 0 or p = 1, when $\dot {p}=0$. For Quixotes:

  

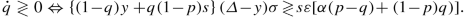
  The equilibrium in this region also requires p = 0. Plugging this into the dynamics of $\dot {q}$ and equating to zero leads again to Eq. (30).

  The equilibrium $(0,q^*_{\mbox{{ {Q}}}})$ may lie within this region M or region L. It will be located in region M if $\max \left \{\varDelta _{wg},\varDelta _{cp}\right \}<q^*_{\mbox{{ {Q}}}}(1-s)\le \varDelta$, and it will lie in region L if $\varDelta _{wg}<q^*_{\mbox{{ {Q}}}}(1-s)\le \varDelta _{cp}\le \varDelta$.

• R: Δ _cp < y ≤ Δ _wg ≤ Δ (α > 1∕2)

  $$\displaystyle \begin{aligned} \begin{array}{rcl} \dot{p}&\displaystyle {=}&\displaystyle \left\{p(1{-}y){+}(1{-}s)q(1{-}p)\right\}(\varDelta-y)\sigma-\varepsilon\left\{(1-p)y+(1-s)\alpha(p-q)\right\},\\ \dot{q}&\displaystyle =&\displaystyle (1-q)q(1-s)(\varDelta-y)\sigma \ge0. \end{array} \end{aligned} $$

  In this region $\dot {q}\ge 0$, and $\dot {q}=0$ if q = 0 (which does not belong to R) or q = 1. For Sanchos, $\dot {p}\gtrless 0$ if and only if:

  $$\displaystyle \begin{aligned} \left[y+(1-s)p\frac{1-q}{1-p}\right](\varDelta-y)\sigma\gtrless\varepsilon\left[y+(1-s)\alpha\frac{p-q}{1-p}\right], \end{aligned}$$

  In the limiting case of a very small ratio of compliant Sanchos, $\dot {p}$ can be approximated by:

  $$\displaystyle \begin{aligned} \dot{p}|{}_{p=0}=(1-s)q\sigma\left[\varDelta_{wg}-y\right], \end{aligned}$$

  which in this region is positive, increasing in α and decreasing in s.

  The equilibrium in this region requires q = 1, and hence y = ps + 1 − s. Plugging this into the dynamics $\dot {p}$, it follows that p must be either equal to 1 (but p = q = 1 does not belong to R) or satisfy equation:

  $$\displaystyle \begin{aligned}{}[ps+(1-s)](\varDelta-ps-(1-s))\sigma=\varepsilon[ps+(1-s)(1-\alpha)]. \end{aligned} $$

  (31)

  Equivalently, when q = 1, the expression $\dot {p}/((1-p)\sigma )$ is given by the second order polynomial in p:

  $$\displaystyle \begin{aligned} -p^2s^2-ps\left[2(1-s)+d-1\right]+(1-s)\left[\varDelta_{wg}-(1-s)\right], \end{aligned}$$

  which has one stable and one unstable root. The stable root is given by (19).

• B: $y\le \min \left \{\varDelta _{wg},\varDelta _{cp}\right \}\le \varDelta$. The dynamics reads:

  $$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle &\displaystyle \dot{p}=(1-p)\left\{(\varDelta-y)y\sigma-\varepsilon[y-q(1-s)\alpha)]\right\},\\ &\displaystyle &\displaystyle \dot{q}=(1-q)\left\{ps\sigma(\varDelta_{cp}-y)+q(1-s)(\varDelta-y)\sigma\right\}\ge0. \end{array} \end{aligned} $$

  Since y < Δ _cp then $\dot {q}\ge 0$ except if q = 1 or p = q = 0, when $\dot {q}=0$. For Sanchos:

  $$\displaystyle \begin{aligned} \dot{p}\gtrless 0\Leftrightarrow (\varDelta-y)y\sigma\gtrless\varepsilon[y-q(1-s)\alpha]. \end{aligned}$$

  This system has three equilibria. Two unstable equilibria (p ^∗, q ^∗) = (0, 0), (p ^∗, q ^∗) = (1, 1) (which does not belong to this region), and a stable equilibrium with q = 1 and p given by Eq. (31).

  The equilibrium $\left (p^*_{\mbox{{ {S}}}\mbox{{ {Q}}}},1\right )$ may belong to region R or region B. It will lie in region R if $\varDelta _{cp}<p^*_{\mbox{{ {S}}}\mbox{{ {Q}}}}s+(1-s)\le \varDelta _{wg}\le \varDelta$, and it will lie in region B if $p^*_{\mbox{{ {S}}}\mbox{{ {Q}}}}s+(1-s)\le \min \{\varDelta _{cp},\varDelta _{wg}\}\le \varDelta$.

It is easy to see that $q^*_{\mbox{{ {Q}}}}>0$ for all s ∈ (0, 1). Moreover, under condition $s<1-\varDelta _{wg}\equiv \hat {s}$, it can be seen that $q^*_{\mbox{{ {Q}}}}<1$.

It is also immediate to see that condition s < 1 − Δ _wg implies $p^*_{\mbox{{ {S}}}\mbox{{ {Q}}}}>0$. Likewise, $p^*_{\mbox{{ {S}}}\mbox{{ {Q}}}}<1$ under condition − αεs < c − d − αε. But this inequality is always true under condition (2).

The proof of the asymptotic stability can be found in Cabo and García (2018).

Proof of Proposition 2

Conditions (21) and (22) are straightforward from the definition of $q_{\mbox{{ {Q}}}}^*$ in (16).

Under scenario Q, condition $y^*_{\mbox{{ {Q}}}}>\varDelta _{wg}$ is equivalent to $q^*_{\mbox{{ {Q}}}}(1-s)>\varDelta _{wg}$, or:

$$\displaystyle \begin{aligned} \frac{1+\varDelta-\sqrt{(1-\varDelta)^2+4(1-\alpha)s\varepsilon/\sigma}}{2}>\varDelta-(1-\alpha)\frac{\varepsilon}{\sigma}, \end{aligned}$$

or equivalently:

$$\displaystyle \begin{aligned} 1-\varDelta+2(1-\alpha)\frac{\varepsilon}{\sigma}>\sqrt{(1-\varDelta)^2+4(1-\alpha)s\varepsilon/\sigma}. \end{aligned}$$

The LHS is positive, hence, if we square both sides, after some algebra, we end up with condition:

$$\displaystyle \begin{aligned} s<1-\varDelta_{wg}, \end{aligned}$$

which is equivalent to condition (14) that characterizes scenario Q.

Likewise, under scenario SQ, condition $y^*_{\mbox{{ {S}}}\mbox{{ {Q}}}}<\varDelta _{wg}$ is equivalent to $p^*_{\mbox{{ {S}}}\mbox{{ {Q}}}}s+(1-s)<\varDelta _{wg}$. Following a similar analysis, we end up with condition s > 1 − Δ _wg, which is equivalent to condition (17) that characterizes scenario SQ.

Proof of Proposition 3

In the scenario with $p^*_{\mbox{{ {Q}}}}=0$ and $q^*_{\mbox{{ {Q}}}}>0$,

$$\displaystyle \begin{aligned} \frac{\partial q^*_{\mbox{{{Q}}}}}{\partial \alpha}=\frac{s \varepsilon}{(1-s)\sigma\sqrt{(1-\varDelta)^2+4(1-\alpha)s\varepsilon/\sigma}}>0, \end{aligned}$$

and

$$\displaystyle \begin{aligned} \frac{\partial q^*_{\mbox{{{Q}}}}}{\partial \varepsilon}=\frac{\sqrt{(1-\varDelta)^2+4(1-\alpha)s\varepsilon/\sigma}+1-\varDelta-2(1-\alpha)s}{2\sigma(1-s)\sqrt{(1-\varDelta)^2+4(1-\alpha)s\varepsilon/\sigma}}. \end{aligned}$$

This latter derivative is positive if and only if:

$$\displaystyle \begin{aligned} \sqrt{(1-\varDelta)^2+4(1-\alpha)s\varepsilon/\sigma}>2(1-\alpha)s-(1-\varDelta). \end{aligned}$$

If the RHS of this inequality was negative, $\partial q^*_{\mbox{{ {Q}}}}/\partial \varepsilon >0$. Conversely, if the RHS was positive, raising both sides to the square, and rearranging terms,

$$\displaystyle \begin{aligned} s\alpha>s-\left[1-\varDelta+\frac{\varepsilon}{\sigma}\right]. \end{aligned}$$

But according to (15), an equilibrium with no compliance among Sanchos requires s < 1 − Δ + (1 − α)ε∕σ < 1 − Δ + ε∕σ. Therefore, the RHS in inequation above is negative and hence, it always holds, which proves $\partial q^*_{\mbox{{ {Q}}}}/\partial \varepsilon >0$.

In the scenario with $q^*_{\mbox{{ {S}}}\mbox{{ {Q}}}}=1$ and $p^*_{\mbox{{ {S}}}\mbox{{ {Q}}}}>0,$

The marginal effect of α and ε in the global compliance rates immediately follows, provided that $y^*_{\mbox{{ {Q}}}}=q^*_{\mbox{{ {Q}}}}(1-s)$ and $y^*_{\mbox{{ {S}}}\mbox{{ {Q}}}}=p^*_{\mbox{{ {S}}}\mbox{{ {Q}}}}s+(1-s)$.

Proof of Proposition 5

Considering $q_{\mbox{{ {Q}}}}^*$ in (16) as a function of s, one can prove that $(q_{\mbox{{ {Q}}}}^*)'(s)\gtreqless 0$ if and only if:

$$\displaystyle \begin{aligned} (1-\alpha)^2(1-s)^2\left(\frac{\varepsilon}{\sigma}\right)^2-\varDelta_{wg}\left(1-\varDelta^2+4(1-\alpha)\frac{\varepsilon}{\sigma}\right)\lesseqgtr0. \end{aligned} $$

(32)

It is ease to see that αε < d − 1 implies that the expression in (32) is positive, and therefore, $(q_{\mbox{{ {Q}}}}^*)'(s)<0$, regardless of the value of s.

For the more general case of αε > d − 1, the expression in (32) vanishes for two values of s, one greater than one and the other given by $\underline {s}_{q}$ in (24). From Proposition 1 we know that $q_{\mbox{{ {Q}}}}^*<1$ for all $s\in (0,\hat {s})$ and $q_{\mbox{{ {Q}}}}^*(\hat {s})=1$.

• If $\underline {s}_{q}\in (0,\hat {s})$, then, being $q_{\mbox{{ {Q}}}}^*(s)$ a continuous function, it must hold true that $(q_{\mbox{{ {Q}}}}^*)'(s)<0$ for $s\in (0, \underline {s}_{q})$ and $(q_{\mbox{{ {Q}}}}^*)'(s)>0$ for $s\in ( \underline {s}_{q},\hat {s})$. Therefore, if $\underline {s}_{q}\in (0,\hat {s})$, $q_{\mbox{{ {Q}}}}^*(s)$ would start at $q_{\mbox{{ {Q}}}}^*(0)=\varDelta$, decrease to reach its minimum at $q_{\mbox{{ {Q}}}}^*( \underline {s}_{q})$, and increase from that point till $q_{\mbox{{ {Q}}}}^*(\hat {s})=1$.

• It is nonetheless possible that $\underline {s}_{q}<0$ and in that case, $q_{\mbox{{ {Q}}}}^*(s)$ would monotonously increase from $q_{\mbox{{ {Q}}}}^*(0)=\varDelta$, for all $s\in (0,\hat {s}$), again to $q(\hat {s})=1$.

We can compute, with the help of Mathematica, the unique value of α at which $\underline {s}_{q}=0$, given by $\tilde {\alpha }=1-\varDelta (1-\varDelta )\sigma /\varepsilon$. Moreover, after some algebra, it can be proven that $\partial \underline {s}_{q}/\partial \alpha <0$ if and only if:

$$\displaystyle \begin{aligned} (1+\varDelta)^2(1-\alpha)^2\left(\frac{\varepsilon}{\sigma}\right)^2+4(1-\varDelta)^2\varDelta_{wg}\varDelta>0. \end{aligned}$$

And this is true whenever αε > d − 1 and hence Δ _wg > 0. In consequence, if $\alpha >\tilde \alpha$, $\underline {s}_{q}<0$ and $q_{\mbox{{ {Q}}}}^*(s)$ increases for all $s\in (0,\hat {s}$), while for $\alpha <\tilde \alpha$, $\underline {s}_{q}>0$ and $q_{\mbox{{ {Q}}}}^*(s)$ shows a u-shape within $(0,\hat {s}$).

Proof of Corollary 3

The derivatives $\partial \bar {s}_{p}/\partial \alpha$ and $\partial \bar {s}_{p}/\partial \varepsilon$ are both negative under the same condition:

$$\displaystyle \begin{aligned}{}[2(c-d)-\alpha\varepsilon](c-d+\sigma)>4(c-d)\sigma\sqrt{(1-\varDelta_{wg})}. \end{aligned}$$

After some tedious algebra, this condition can be transformed to:

$$\displaystyle \begin{aligned} (1-\varDelta_{wg})[(c-d-\sigma)^2+2(c-d)]+4\alpha\varepsilon(c-d)>0, \end{aligned}$$

which clearly holds.

Proving that $\partial \hat {s}/\partial wg<0$ is straightforward.

Finally, as stated in Proposition 3, $\partial p_{\mbox{{ {S}}}\mbox{{ {Q}}}}^*/\partial \alpha >0$ and $\partial p_{\mbox{{ {S}}}\mbox{{ {Q}}}}^*/\partial \varepsilon >$. Therefore, also the maximum is reached at a higher value.