Abstract
These are the handouts of an undergraduate minicourse at the Università di Bari (see Fig. 1), in the context of the 2017 INdAM Intensive Period “Contemporary Research in elliptic PDEs and related topics”. Without any intention to serve as a throughout epitome to the subject, we hope that these notes can be of some help for a very initial introduction to a fascinating field of classical and modern research.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
〈〈The longest appendix measured 26cm (10.24in) when it was removed from 72-year-old Safranco August (Croatia) during an autopsy at the Ljudevit Jurak University Department of Pathology, Zagreb, Croatia, on 26 August 2006.〉〉
(Source: http://www.guinnessworldrecords.com/world-records/largest-appendix-removed)
Notes
- 1.
The notion (or, better to say, several possible notions) of fractional derivatives attracted the attention of many distinguished mathematicians, such as Leibniz, Bernoulli, Euler, Fourier, Abel, Liouville, Riemann, Hadamard and Riesz, among the others. A very interesting historical outline is given in pages xxvii–xxxvi of [104].
- 2.
We think that it is quite remarkable that the operator obtained by the inverse Fourier Transform of \( \,|\xi |{ }^{2} \,\widehat u\), the classical Laplacian, reduces to a local operator. This is not true for the inverse Fourier Transform of \( \,|\xi |{ }^{2s} \,\widehat u\). In this spirit, it is interesting to remark that the fact that the classical Laplacian is a local operator is not immediate from its definition in Fourier space, since computing Fourier Transforms is always a nonlocal operation.
- 3.
Some care has to be used with extension methods, since the solution of (2.6) is not unique (if U solves (2.6), then so does U(x, y) + cy for any \(c\in \mathbb {R}\)). The “right” solution of (2.6) that one has to take into account is the one with “decay at infinity”, or belonging to an “energy space”, or obtained by convolution with a Poisson-type kernel. See e.g. [24] for details.
Also, the extension method in (2.6) and (2.7) can be related to an engineering application of the fractional Laplacian motivated by the displacement of elastic membranes on thin (i.e. codimension one) obstacles, see [28]. The intuition for such application can be grasped from Figs. 7, 10, and 12. These pictures can be also useful to develop some intuition about extension methods for fractional operators and boundary reaction-diffusion equations.
- 4.
See Appendix A in [103] for a very nice explanation of the dimensional analysis and for a throughout discussion of its role in detecting fundamental solutions.
- 5.
Some colleagues pointed out to us that the use of R and r in some steps of formula (5.5) of [54] are inadequate. We take this opportunity to amend such a flaw, presenting a short proof of (5.5) of [54]. Given ε > 0, we notice that

where the constants are also allowed to depend on Ω and u. Furthermore, if we define Ωε to be the set of all the points in Ω with distance less than ε from ∂ Ω, the regularity of ∂ Ω implies that the measure of Ωε is bounded by const ε, and therefore
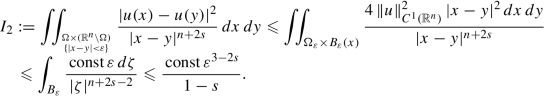
These observations imply that

Taking ε as small as we wish, we obtain formula (5.5) in [54].
- 6.
From the geometric point of view, one can also take radial coordinates, compute the derivatives of K along the unit sphere and use scaling.
- 7.
The difficulty in proving (G.1) is that the function u 1∕2 is not differentiable at ± 1 and the derivative taken inside the integral might produce a singularity (in fact, formula (G.1) exactly says that such derivative can be performed with no harm inside the integral). The reader who is already familiar with the basics of functional analysis can prove (G.1) by using the theory of absolutely continuous functions, see e.g. Theorem 8.21 in [98]. We provide here a direct proof, available to everybody.
- 8.
As a historical remark, we recall that e −|ξ| is sometimes called the “Abel Kernel” and its Fourier Transform the “Poisson Kernel”, which in dimension 1 reduces to the “Cauchy-Lorentz, or Breit-Wigner, Distribution” (that has also classical geometric interpretations as the “Witch of Agnesi”, and so many names attached to a single function clearly demonstrate its importance in numerous applications).
- 9.
Let us mention another conceptual simplification of nonlocal problems: in this setting, the integral representation often allows the formulation of problems with minimal requirements on the functions involved (such as measurability and possibly minor pointwise or integral bounds). Conversely, in the classical setting, even to just formulate a problem, one often needs assumptions and tools from functional analysis, comprising e.g. Sobolev differentiability, distributions or functions of bounded variations.
- 10.
In complex variables, one can also interpret the function U in terms of the principal argument function
$$\displaystyle \begin{aligned}{\mathrm{Arg}}(r e^{i\varphi})=\varphi\in(-\pi,\pi],\end{aligned}$$with branch cut along the nonpositive real axis. Notice indeed that, if z = x + iy and y > 0,
$$\displaystyle \begin{aligned}{\mathrm{Arg}}(z+i)=\frac\pi2-\arctan\frac{x}{y+1}=\frac\pi2\left(1-U(x,y) \right).\end{aligned}$$This observation would also lead to (L.1).
- 11.
- 12.
A slightly different approach as that in (3.7) is to consider the energy functional in (3.9) and prove, e.g. by Taylor expansion, that it converges to the energy functional
$$\displaystyle \begin{aligned}\,{\mathrm{const}}\, \int_{\mathbb{R}^n}a_{ij}(x) \,\partial_i u(x)\,\partial_j u(x)\,dx.\end{aligned}$$On the other hand, a different proof of (3.7), that was nicely pointed out to us by Jonas Hirsch (who has also acted as a skilled cartoonist for Fig. 13) after a lecture, can be performed by taking into account the weak form of the operator in (3.5), i.e. integrating such expression against a test function \(\varphi \in C^\infty _0(\mathbb {R}^n)\), thus finding
$$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle &\displaystyle (1-s)\,\iint_{\mathbb{R}^n\times\mathbb{R}^n} \frac{ \big(u(x)-u(x-y)\big)\,\varphi(x)}{ |M(x-y,y)\, y|{}^{n+2s}}\,dx\,dy \\ &\displaystyle =&\displaystyle (1-s)\,\iint_{\mathbb{R}^n\times\mathbb{R}^n} \frac{ \big(u(x)-u(z)\big)\,\varphi(x)}{ |M(z,x-z)\,(x-z)|{}^{n+2s}}\,dx\,dz \\ \noalign{} &\displaystyle =&\displaystyle (1-s)\,\iint_{\mathbb{R}^n\times\mathbb{R}^n} \frac{ \big(u(z)-u(x)\big)\,\varphi(z)}{ |M(x,z-x)\,(x-z)|{}^{n+2s}}\,dx\,dz \\ &\displaystyle =&\displaystyle -(1-s)\,\iint_{\mathbb{R}^n\times\mathbb{R}^n} \frac{ \big(u(x)-u(z)\big)\,\varphi(z)}{ |M(z,x-z)\,(x-z)|{}^{n+2s}}\,dx\,dz ,\end{array} \end{aligned} $$where the structural condition (3.6) has been used in the last line. This means that the weak formulation of the operator in (3.5) can be written as
$$\displaystyle \begin{aligned}\frac{1-s}{2}\,\iint_{\mathbb{R}^n\times\mathbb{R}^n} \frac{ \big(u(x)-u(z)\big)\,\big(\varphi(x)-\varphi(z)\big)}{ |M(z,x-z)\,(x-z)|{}^{n+2s}}\,dx\,dz.\end{aligned}$$So one can expand this expression and take the limit as
 , to obtain $$\displaystyle \begin{aligned}\,{\mathrm{const}}\, \int_{\mathbb{R}^n}a_{ij}(x) \,\partial_i u(x)\,\partial_j\varphi(x)\,dx,\end{aligned}$$
, to obtain $$\displaystyle \begin{aligned}\,{\mathrm{const}}\, \int_{\mathbb{R}^n}a_{ij}(x) \,\partial_i u(x)\,\partial_j\varphi(x)\,dx,\end{aligned}$$which is indeed the weak formulation of the classical divergence form operator.
References
N. Abatangelo, Large s-harmonic functions and boundary blow-up solutions for the fractional Laplacian. Discrete Contin. Dyn. Syst. 35(12), 5555–5607 (2015). https://doi.org/10.3934/dcds.2015.35.5555. MR3393247
N. Abatangelo, L. Dupaigne, Nonhomogeneous boundary conditions for the spectral fractional Laplacian. Ann. Inst. H. Poincaré Anal. Non Linéaire 34(2), 439–467 (2017). https://doi.org/10.1016/j.anihpc.2016.02.001. MR3610940
N. Abatangelo, S. Jarohs, A. Saldaña, Positive powers of the Laplacian: from hypersingular integrals to boundary value problems. Commun. Pure Appl. Anal. 17(3), 899–922 (2018). https://doi.org/10.3934/cpaa.2018045. MR3809107
N. Abatangelo, S. Jarohs, A. Saldaña, Green function and Martin kernel for higher-order fractional Laplacians in balls. Nonlinear Anal. 175, 173–190 (2018). https://doi.org/10.1016/j.na.2018.05.019. MR3830727
N. Abatangelo, S. Jarohs, A. Saldaña, On the loss of maximum principles for higher-order fractional Laplacians. Proc. Am. Math. Soc. 146(11), 4823–4835 (2018). https://doi.org/10.1090/proc/14165. MR3856149
E. Affili, S. Dipierro, E. Valdinoci, Decay estimates in time for classical and anomalous diffusion. arXiv e-prints (2018), available at 1812.09451
M. Allen, L. Caffarelli, A. Vasseur, A parabolic problem with a fractional time derivative. Arch. Ration. Mech. Anal. 221(2), 603–630 (2016). https://doi.org/10.1007/s00205-016-0969-z. MR3488533
F. Andreu-Vaillo, J.M. Mazón, J.D. Rossi, J.J. Toledo-Melero, Nonlocal Diffusion Problems, Mathematical Surveys and Monographs, vol. 165 (American Mathematical Society, Providence, 2010); Real Sociedad Matemática Española, Madrid, 2010. MR2722295
D. Applebaum, Lévy Processes and Stochastic Calculus. Cambridge Studies in Advanced Mathematics, 2nd edn., vol. 116 (Cambridge University Press, Cambridge, 2009). MR2512800
V.E. Arkhincheev, É.M. Baskin, Anomalous diffusion and drift in a comb model of percolation clusters. J. Exp. Theor. Phys. 73, 161–165 (1991)
A.V. Balakrishnan, Fractional powers of closed operators and the semigroups generated by them. Pac. J. Math. 10, 419–437 (1960). MR0115096
R. Bañuelos, K. Bogdan, Lévy processes and Fourier multipliers. J. Funct. Anal. 250(1), 197–213 (2007). https://doi.org/10.1016/j.jfa.2007.05.013. MR2345912
B. Barrios, I. Peral, F. Soria, E. Valdinoci, A Widder’s type theorem for the heat equation with nonlocal diffusion. Arch. Ration. Mech. Anal. 213(2), 629–650 (2014). https://doi.org/10.1007/s00205-014-0733-1. MR3211862
R.F. Bass, D.A. Levin, Harnack inequalities for jump processes. Potential Anal. 17(4), 375–388 (2002). https://doi.org/10.1023/A:1016378210944. MR1918242
A. Bendikov, Asymptotic formulas for symmetric stable semigroups. Expo. Math. 12(4), 381–384 (1994). MR1297844
J. Bertoin, Lévy Processes. Cambridge Tracts in Mathematics, vol. 121 (Cambridge University Press, Cambridge, 1996). MR1406564
R.M. Blumenthal, R.K. Getoor, Some theorems on stable processes. Trans. Am. Math. Soc. 95, 263–273 (1960). https://doi.org/10.2307/1993291. MR0119247
K. Bogdan, T. Byczkowski, Potential theory for the α-stable Schrödinger operator on bounded Lipschitz domains. Stud. Math. 133(1), 53–92 (1999). MR1671973
K. Bogdan, T. Żak, On Kelvin transformation. J. Theor. Probab. 19(1), 89–120 (2006). MR2256481
M. Bonforte, A. Figalli, J.L. Vázquez, Sharp global estimates for local and nonlocal porous medium-type equations in bounded domains. Anal. PDE 11(4), 945–982 (2018). https://doi.org/10.2140/apde.2018.11.945. MR3749373
L. Brasco, S. Mosconi, M. Squassina, Optimal decay of extremals for the fractional Sobolev inequality. Calc. Var. Partial Differ. Equ. 55(2), 23, 32 (2016). https://doi.org/10.1007/s00526-016-0958-y. MR3461371
C. Bucur, Some observations on the Green function for the ball in the fractional Laplace framework. Commun. Pure Appl. Anal. 15(2), 657–699 (2016). https://doi.org/10.3934/cpaa.2016.15.657. MR3461641
C. Bucur, Local density of Caputo-stationary functions in the space of smooth functions. ESAIM Control Optim. Calc. Var. 23(4), 1361–1380 (2017). https://doi.org/10.1051/cocv/2016056. MR3716924
C. Bucur, E. Valdinoci, Nonlocal Diffusion and Applications. Lecture Notes of the Unione Matematica Italiana, vol. 20 (Springer, Cham, 2016); Unione Matematica Italiana, Bologna. MR3469920
C. Bucur, L. Lombardini, E. Valdinoci, Complete stickiness of nonlocal minimal surfaces for small values of the fractional parameter. Ann. Inst. H. Poincaré Anal. Non Linéaire 36(3), 655–703 (2019)
X. Cabré, M. Cozzi, A gradient estimate for nonlocal minimal graphs. Duke Math. J. 168(5), 775–848 (2019)
X. Cabré, Y. Sire, Nonlinear equations for fractional Laplacians II: existence, uniqueness, and qualitative properties of solutions. Trans. Am. Math. Soc. 367(2), 911–941 (2015). https://doi.org/10.1090/S0002-9947-2014-05906-0. MR3280032
L.A. Caffarelli, Further regularity for the Signorini problem. Commun. Partial Differ. Equ. 4(9), 1067–1075 (1979). https://doi.org/10.1080/03605307908820119. MR542512
L. Caffarelli, F. Charro, On a fractional Monge-Ampère operator. Ann. PDE 1(1), 4, 47 (2015). MR3479063
L. Caffarelli, L. Silvestre, An extension problem related to the fractional Laplacian. Commun. Partial Differ. Equ. 32(7–9), 1245–1260 (2007). https://doi.org/10.1080/03605300600987306. MR2354493
L. Caffarelli, L. Silvestre, Regularity theory for fully nonlinear integro-differential equations. Commun. Pure Appl. Math. 62(5), 597–638 (2009). MR2494809
L. Caffarelli, L. Silvestre, Hölder regularity for generalized master equations with rough kernels, in Advances in Analysis: The Legacy of Elias M. Stein. Princeton Mathematical Series, vol. 50 (Princeton University Press, Princeton, 2014), pp. 63–83. MR3329847
L.A. Caffarelli, J.L. Vázquez, Asymptotic behaviour of a porous medium equation with fractional diffusion. Discrete Contin. Dyn. Syst. 29(4), 1393–1404 (2011). MR2773189
L. Caffarelli, F. Soria, J.L. Vázquez, Regularity of solutions of the fractional porous medium flow. J. Eur. Math. Soc. (JEMS) 15(5), 1701–1746 (2013). https://doi.org/10.4171/JEMS/401. MR3082241
M. Caputo, Linear models of dissipation whose Q is almost frequency independent. II. Fract. Calc. Appl. Anal. 11(1), 4–14 (2008). Reprinted from Geophys. J. R. Astr. Soc. 13(1967), no. 5, 529–539. MR2379269
A. Carbotti, S. Dipierro, E. Valdinoci, Local Density of Solutions to Fractional Equations. Graduate Studies in Mathematics (De Gruyter, Berlin, 2019)
A. Carbotti, S. Dipierro, E. Valdinoci, Local density of Caputo-stationary functions of any order. Complex Var. Elliptic Equ. (to appear). https://doi.org/10.1080/17476933.2018.1544631
R. Carmona, W.C. Masters, B. Simon, Relativistic Schrödinger operators: asymptotic behavior of the eigenfunctions. J. Funct. Anal. 91(1), 117–142 (1990). https://doi.org/10.1016/0022-1236(90)90049-Q. MR1054115
A. Cesaroni, M. Novaga, Symmetric self-shrinkers for the fractional mean curvature flow. ArXiv e-prints (2018), available at 1812.01847
A. Cesaroni, S. Dipierro, M. Novaga, E. Valdinoci, Fattening and nonfattening phenomena for planar nonlocal curvature flows. Math. Ann. (to appear). https://doi.org/10.1007/s00208-018-1793-6
E. Cinti, C. Sinestrari, E. Valdinoci, Neckpinch singularities in fractional mean curvature flows. Proc. Am. Math. Soc. 146(6), 2637–2646 (2018). https://doi.org/10.1090/proc/14002. MR3778164
E. Cinti, J. Serra, E. Valdinoci, Quantitative flatness results and BV-estimates for stable nonlocal minimal surfaces. J. Differ. Geom. (to appear)
J. Coville, Harnack type inequality for positive solution of some integral equation. Ann. Mat. Pura Appl. 191(3), 503–528 (2012). https://doi.org/10.1007/s10231-011-0193-2. MR2958346
J.C. Cox, The valuation of options for alternative stochastic processes. J. Finan. Econ. 3(1–2), 145–166 (1976). https://doi.org/10.1016/0304-405X(76)90023-4
M. Cozzi, E. Valdinoci, On the growth of nonlocal catenoids. Atti Accad. Naz. Lincei Rend. Lincei Mat. Appl. (to appear)
J. Dávila, M. del Pino, J. Wei, Nonlocal s-minimal surfaces and Lawson cones. J. Differ. Geom. 109(1), 111–175 (2018). https://doi.org/10.4310/jdg/1525399218. MR3798717
C.-S. Deng, R.L. Schilling, Exact Asymptotic Formulas for the Heat Kernels of Space and Time-Fractional Equations, ArXiv e-prints (2018), available at 1803.11435
A. de Pablo, F. Quirós, A. Rodríguez, J.L. Vázquez, A fractional porous medium equation. Adv. Math. 226(2), 1378–1409 (2011). https://doi.org/10.1016/j.aim.2010.07.017. MR2737788
E. Di Nezza, G. Palatucci, E. Valdinoci, Hitchhiker’s guide to the fractional Sobolev spaces. Bull. Sci. Math. 136(5), 521–573 (2012). https://doi.org/10.1016/j.bulsci.2011.12.004. MR2944369
S. Dipierro, H.-C. Grunau, Boggio’s formula for fractional polyharmonic Dirichlet problems. Ann. Mat. Pura Appl. 196(4), 1327–1344 (2017). https://doi.org/10.1007/s10231-016-0618-z. MR3673669
S. Dipierro, E. Valdinoci, A simple mathematical model inspired by the Purkinje cells: from delayed travelling waves to fractional diffusion. Bull. Math. Biol. 80(7), 1849–1870 (2018). https://doi.org/10.1007/s11538-018-0437-z. MR3814763
S. Dipierro, G. Palatucci, E. Valdinoci, Dislocation dynamics in crystals: a macroscopic theory in a fractional Laplace setting. Commun. Math. Phys. 333(2), 1061–1105 (2015). https://doi.org/10.1007/s00220-014-2118-6. MR3296170
S. Dipierro, O. Savin, E. Valdinoci, Graph properties for nonlocal minimal surfaces. Calc. Var. Partial Differ. Equ. 55(4), 86, 25 (2016). https://doi.org/10.1007/s00526-016-1020-9. MR3516886
S. Dipierro, X. Ros-Oton, E. Valdinoci, Nonlocal problems with Neumann boundary conditions. Rev. Mat. Iberoam. 33(2), 377–416 (2017). https://doi.org/10.4171/RMI/942. MR3651008
S. Dipierro, O. Savin, E. Valdinoci, All functions are locally s-harmonic up to a small error. J. Eur. Math. Soc. (JEMS) 19(4), 957–966 (2017). https://doi.org/10.4171/JEMS/684. MR3626547
S. Dipierro, O. Savin, E. Valdinoci, Boundary behavior of nonlocal minimal surfaces. J. Funct. Anal. 272(5), 1791–1851 (2017). https://doi.org/10.1016/j.jfa.2016.11.016. MR3596708
S. Dipierro, N. Soave, E. Valdinoci, On stable solutions of boundary reaction-diffusion equations and applications to nonlocal problems with Neumann data. Indiana Univ. Math. J. 67(1), 429–469 (2018). https://doi.org/10.1512/iumj.2018.67.6282. MR3776028
S. Dipierro, O. Savin, E. Valdinoci, Local approximation of arbitrary functions by solutions of nonlocal equations. J. Geom. Anal. 29(2), 1428–1455 (2019)
S. Dipierro, O. Savin, E. Valdinoci, Definition of fractional Laplacian for functions with polynomial growth. Rev. Mat. Iberoam (to appear)
S. Dipierro, J. Serra, E. Valdinoci, Improvement of flatness for nonlocal phase transitions. Amer. J. Math. (to appear)
B. Dyda, Fractional calculus for power functions and eigenvalues of the fractional Laplacian. Fract. Calc. Appl. Anal. 15(4), 536–555 (2012). https://doi.org/10.2478/s13540-012-0038-8. MR2974318
L.C. Evans, Partial Differential Equations. Graduate Studies in Mathematics, vol. 19 (American Mathematical Society, Providence, 1998). MR1625845
M.M. Fall, T. Weth, Nonexistence results for a class of fractional elliptic boundary value problems. J. Funct. Anal. 263(8), 2205–2227 (2012). https://doi.org/10.1016/j.jfa.2012.06.018. MR2964681
M.M. Fall, T. Weth, Liouville theorems for a general class of nonlocal operators. Potential Anal. 45(1), 187–200 (2016). https://doi.org/10.1007/s11118-016-9546-1. MR3511811
A. Farina, E. Valdinoci, The state of the art for a conjecture of De Giorgi and related problems, in Recent Progress on Reaction-Diffusion Systems and Viscosity Solutions (World Scientific Publishing, Hackensack, 2009), pp. 74–96. https://doi.org/10.1142/9789812834744_0004. MR2528756
P. Felmer, A. Quaas, Boundary blow up solutions for fractional elliptic equations. Asymptot. Anal. 78(3), 123–144 (2012). MR2985500
A. Figalli, J. Serra, On stable solutions for boundary reactions: a De Giorgi-type result in dimension 4 + 1, preprint at arXiv:1705.02781 (2017, submitted)
R.L. Frank, E. Lenzmann, L. Silvestre, Uniqueness of radial solutions for the fractional Laplacian. Commun. Pure Appl. Math. 69(9), 1671–1726 (2016). https://doi.org/10.1002/cpa.21591. MR3530361
R.K. Getoor, First passage times for symmetric stable processes in space. Trans. Am. Math. Soc. 101, 75–90 (1961). https://doi.org/10.2307/1993412. MR0137148
T. Ghosh, M. Salo, G. Uhlmann, The Calderón problem for the fractional Schrödinger equation. ArXiv e-prints (2016), available at 1609.09248
D. Gilbarg, N.S. Trudinger, Elliptic Partial Differential Equations of Second Order. Classics in Mathematics (Springer, Berlin, 2001). Reprint of the 1998 edition. MR1814364
E. Giusti, Direct Methods in the Calculus of Variations (World Scientific Publishing, River Edge, 2003). MR1962933
Q. Han, F. Lin, Elliptic Partial Differential Equations. Courant Lecture Notes in Mathematics, 2nd edn., vol. 1 (Courant Institute of Mathematical Sciences/American Mathematical Society, New York/Providence, 2011). MR2777537
N. Jacob, Pseudo-Differential Operators and Markov Processes. Mathematical Research, vol. 94 (Akademie Verlag, Berlin, 1996). MR1409607
M. Kaßmann, Harnack-Ungleichungen Für nichtlokale Differentialoperatoren und Dirichlet-Formen (in German). Bonner Mathematische Schriften [Bonn Mathematical Publications], vol. 336 (Universität Bonn, Mathematisches Institut, Bonn, 2001). Dissertation, Rheinische Friedrich-Wilhelms-Universität Bonn, Bonn, 2000. MR1941020
M. Kaßmann, A new formulation of Harnack’s inequality for nonlocal operators. C. R. Math. Acad. Sci. Paris 349(11–12), 637–640 (2011). https://doi.org/10.1016/j.crma.2011.04.014 (English, with English and French summaries). MR2817382
M. Kaßmann, Jump processes and nonlocal operators, in Recent Developments in Nonlocal Theory (De Gruyter, Berlin, 2018), pp. 274–302. MR3824215
V. Kolokoltsov, Symmetric stable laws and stable-like jump-diffusions. Proc. Lond. Math. Soc. 80(3), 725–768 (2000). https://doi.org/10.1112/S0024611500012314. MR1744782
N.V. Krylov, On the paper “All functions are locally s-harmonic up to a small error” by Dipierro, Savin, and Valdinoci. ArXiv e-prints (2018), available at 1810.07648
T. Kuusi, G. Mingione, Y. Sire, Nonlocal equations with measure data. Commun. Math. Phys. 337(3), 1317–1368 (2015). https://doi.org/10.1007/s00220-015-2356-2. MR3339179
M. Kwaśnicki, Ten equivalent definitions of the fractional Laplace operator. Fract. Calc. Appl. Anal. 20(1), 7–51 (2017). https://doi.org/10.1515/fca-2017-0002. MR3613319
N.S. Landkof, Foundations of Modern Potential Theory (Springer, New York, 1972). Translated from the Russian by A. P. Doohovskoy; Die Grundlehren der mathematischen Wissenschaften, Band 180. MR0350027
H.C. Lara, G. Dávila, Regularity for solutions of non local parabolic equations. Calc. Var. Partial Differ. Equ. 49(1–2), 139–172 (2014). https://doi.org/10.1007/s00526-012-0576-2. MR3148110
F. Mainardi, Fractional Calculus and Waves in Linear Viscoelasticity (Imperial College Press, London, 2010). An introduction to mathematical models. MR2676137
F. Mainardi, Y. Luchko, G. Pagnini, The fundamental solution of the space-time fractional diffusion equation. Fract. Calc. Appl. Anal. 4(2), 153–192 (2001). MR1829592
F. Mainardi, P. Paradisi, R. Gorenflo, Probability distributions generated by fractional diffusion equations. preprint at arXiv:0704.0320v1 (2007, submitted)
B. Mandelbrot, The variation of certain speculative prices. J. Bus. 36, 394 (1963)
J.M. Mazón, J.D. Rossi, J. Toledo, The heat content for nonlocal diffusion with non-singular kernels. Adv. Nonlinear Stud. 17(2), 255–268 (2017). https://doi.org/10.1515/ans-2017-0005. MR3641640
R. Metzler, J. Klafter, The restaurant at the end of the random walk: recent developments in the description of anomalous transport by fractional dynamics. J. Phys. A 37(31), R161–R208 (2004). https://doi.org/10.1088/0305-4470/37/31/R01. MR2090004
E. Montefusco, B. Pellacci, G. Verzini, Fractional diffusion with Neumann boundary conditions: the logistic equation. Discrete Contin. Dyn. Syst. Ser. B 18(8), 2175–2202 (2013). https://doi.org/10.3934/dcdsb.2013.18.2175. MR3082317
R. Musina, A.I. Nazarov, On fractional Laplacians. Commun. Partial Differ. Equ. 39(9), 1780–1790 (2014). https://doi.org/10.1080/03605302.2013.864304. MR3246044
G. Palatucci, O. Savin, E. Valdinoci, Local and global minimizers for a variational energy involving a fractional norm. Ann. Mat. Pura Appl. 192(4), 673–718 (2013). https://doi.org/10.1007/s10231-011-0243-9. MR3081641
V. Pareto, Cours D’économie Politique, vol. I/II (F. Rouge, Lausanne, 1896)
I. Podlubny, Fractional Differential Equations. Mathematics in Science and Engineering, vol. 198 (Academic Press, San Diego, CA, 1999). An introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications. MR1658022
G. Pólya, On the zeros of an integral function represented by Fourier’s integral. Messenger 52, 185–188 (1923)
M. Riesz, L’intégrale de Riemann-Liouville et le problème de Cauchy (French). Acta Math. 81, 1–223 (1949). MR0030102
X. Ros-Oton, J. Serra, The Dirichlet problem for the fractional Laplacian: regularity up to the boundary. J. Math. Pures Appl. 101(3), 275–302 (2014). https://doi.org/10.1016/j.matpur.2013.06.003 (English, with English and French summaries). MR3168912
W. Rudin, Real and Complex Analysis (McGraw-Hill, New York, 1966). MR0210528
A. Rüland, M. Salo, The fractional Calderón problem: low regularity and stability. ArXiv e-prints (2017), available at 1708.06294
A. Rüland, M. Salo, Quantitative approximation properties for the fractional heat equation. ArXiv e-prints (2017), available at 1708.06300
L.A. Sakhnovich, Levy Processes, Integral Equations, Statistical Physics: Connections and Interactions. Operator Theory: Advances and Applications, vol. 225 (Birkhäuser/Springer, Basel, 2012). MR2963050
L. Saloff-Coste, The heat kernel and its estimates, in Probabilistic Approach to Geometry. Advanced Studies in Pure Mathematics, vol. 57 (Mathematical Society of Japan, Tokyo, 2010), pp. 405–436. MR2648271
S. Salsa, Equazioni a Derivate Parziali. Metodi, Modelli e Applicazioni (Italian), 2nd edn. (Springer, Milano, 2010)
S.G. Samko, A.A. Kilbas, O.I. Marichev, Fractional Integrals and Derivatives (Gordon and Breach Science Publishers, Yverdon, 1993). Theory and applications; Edited and with a foreword by S. M. Nikol′skiı̆; Translated from the 1987 Russian original; Revised by the authors. MR1347689
T. Sandev, A. Schulz, H. Kantz, A. Iomin, Heterogeneous diffusion in comb and fractal grid structures. Chaos Solitons Fractals 114, 551–555 (2018). https://doi.org/10.1016/j.chaos.2017.04.041. MR3856678
R. Servadei, E. Valdinoci, Mountain pass solutions for non-local elliptic operators. J. Math. Anal. Appl. 389(2), 887–898 (2012). https://doi.org/10.1016/j.jmaa.2011.12.032. MR2879266
R. Servadei, E. Valdinoci, On the spectrum of two different fractional operators. Proc. R. Soc. Edinburgh Sect. A 144(4), 831–855 (2014). https://doi.org/10.1017/S0308210512001783. MR3233760
E.M. Stein, Singular Integrals and Differentiability Properties of Functions. Princeton Mathematical Series, vol. 30 (Princeton University Press, Princeton, 1970). MR0290095
P.R. Stinga, J.L. Torrea, Extension problem and Harnack’s inequality for some fractional operators. Commun. Partial Differ. Equ. 35(11), 2092–2122 (2010). https://doi.org/10.1080/03605301003735680. MR2754080
J.F. Toland, The Peierls-Nabarro and Benjamin-Ono equations. J. Funct. Anal. 145(1), 136–150 (1997). https://doi.org/10.1006/jfan.1996.3016. MR1442163
E. Valdinoci, From the long jump random walk to the fractional Laplacian. Bol. Soc. Esp. Mat. Apl. SeMA 49, 33–44 (2009). MR2584076
E. Valdinoci, All functions are (locally) s-harmonic (up to a small error)—and applications, in Partial Differential Equations and Geometric Measure Theory. Lecture Notes in Mathematics, vol. 2211 (Springer, Cham, 2018), pp. 197–214. MR3790948
J.L. Vázquez, Recent progress in the theory of nonlinear diffusion with fractional Laplacian operators. Discrete Contin. Dyn. Syst. Ser. S 7(4), 857–885 (2014). https://doi.org/10.3934/dcdss.2014.7.857. MR3177769
J.L. Vázquez, The Dirichlet problem for the fractional p-Laplacian evolution equation. J. Differ. Equ. 260(7), 6038–6056 (2016). https://doi.org/10.1016/j.jde.2015.12.033. MR3456825
J.L. Vázquez, The mathematical theories of diffusion: nonlinear and fractional diffusion, in Nonlocal and Nonlinear Diffusions and Interactions: New Methods and Directions. Lecture Notes in Mathematics, vol. 2186 (Springer, Cham, 2017), pp. 205–278. MR3588125
Acknowledgements
It is a great pleasure to thank the Università degli Studi di Bari for its very warm hospitality and the Istituto Nazionale di Alta Matematica for the strong financial and administrative support which made this minicourse possible. And of course special thanks go to all the participants, for their patience in attending the course, their competence, empathy and contagious enthusiasm. This work was supported by INdAM and ARC Discovery Project N.E.W. Nonlocal Equations at Work.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
Appendix A: Confirmation of (2.7)
We write Δx to denote the Laplacian in the coordinates \(x\in \mathbb {R}^n\). In this way, the total Laplacian in the variables \((x,y)\in \mathbb {R}^n\times (0,+\infty )\) can be written as
Given a (smooth and bounded, in the light of footnote 3 on page 5) \(u:\mathbb {R}^n\to \mathbb {R}\), we take U := E u be (smooth and bounded) as in (2.6).
We also consider the operator
and we take V (x, y) := −∂ y U(x, y). Notice that ΔV = −∂ y ΔU = 0 in \(\mathbb {R}^n\times (0,+\infty )\) and V (x, 0) = Lu(x) for any \(x\in \mathbb {R}^n\). In this sense, V is the harmonic extension of Lu and so we can write V = E Lu and so, in the notation of (A.2), and recalling (2.6) and (A.1), we have
This gives that L 2 = − Δ, which is consistent with L = (− Δ)1∕2, thanks to (2.5).
Appendix B: Proof of (2.10)
Let \(u\in {\mathcal {S}}\). By (2.9), we can write
Fixed \(x\in \mathbb {R}^n\) (with |x| to be taken large), recalling the notation in (2.3), we consider the map y↦δ u(x, y) and we observe that
Hence, if \(|Y|\leqslant |x|/2\) we have that \(|x\pm Y|\geqslant |x|-|Y|\geqslant |x|/2\), and thus
thanks to (B.1).
Therefore, a second order Taylor expansion of δ u in the variable y gives that, if \(|y|\leqslant |x|/2\),
Consequently,
Moreover, by (B.1),
This and (B.2), recalling (2.3), establish (2.10).
Appendix C: Proof of (2.14)
Let \(M:=\frac 1{2n}\,\left (1+\sup _{B_1}|f|\right )\) and v(x) := M(1 −|x|2) − u(x). Notice that v = 0 along ∂B 1 and
in B 1. Consequently, v⩾0 in B 1, which gives that \(u(x)\leqslant M(1-|x|{ }^2)\).
Arguing similarly, by looking at \(\tilde v(x):= M(1-|x|{ }^2)+u(x)\), one sees that \(-u(x) \leqslant M(1-|x|{ }^2)\). Accordingly, we have that
This proves (2.14).
Appendix D: Proof of (2.17)
The idea of the proof is described in Fig. 7. The trace of the function in Fig. 7 is exactly the function u 1∕2 in (2.16). The function plotted in Fig. 7 is the harmonic extension of u 1∕2 in the halfplane (like an elastic membrane pinned at the halfcircumference along the trace). Our objective is to show that the normal derivative of such extended function along the trace is constant, and so we can make use of the extension method in (2.6) and (2.7) to obtain (2.17).
In further detail, we use complex coordinates, identifying \((x,y)\in \mathbb {R}\times (0,+\infty )\) with \(z:=x+iy\in \mathbb {C}\) with ℑ(z) > 0. Also, as customary, we define the principal square root in the cut complex plane
by defining, for any \(z=re^{{i\varphi }}\in \mathbb {C}_\star \),
see Fig. 8 (for typographical convenience, we distinguish between the complex and the real square root, by using the symbols √(⋅) and \(\sqrt {\cdot }\) respectively).
The principal square root function is defined using the nonpositive real axis as a “branch cut” and
Moreover,
To check these facts, we take \(z\in \mathbb {C}_\star \): since \(\mathbb {C}_\star \) is open, we have that \(z+w\in \mathbb {C}_\star \) for any \(w\in \mathbb {C}\setminus \{0\}\) with small module. Consequently, by (D.2), we obtain that
Dividing by w and taking the limit, we thus find that
Since \(\mathbb {C}_\star \subseteq \mathbb {C}\setminus \{0\}\), we have that z≠0, and thus √(z)≠0. As a result, we can divide (D.5) by 2√(z) and conclude that
which establishes, at the same time, both (D.3) and (D.4), as desired.
We also remark that
To check this, if z = x + iy with y > 0, we observe that
Hence, if 1 − z 2 lies on the real axis, we have that xy = 0, and so x = 0. Then, the real part of 1 − z 2 in this case is equal to 1 + y 2 which is strictly positive. This proves (D.6).
Thanks to (D.6), for any \(z\in \mathbb {C}\) with ℑ(z) > 0 we can define the function √(1 − z 2). From (D.7), we can write
Notice that

As a consequence,

This says that, if x 2 > 1 then

while if x 2 < 1 then

On this account, we deduce that

and therefore, recalling (D.1),

This implies that

Now we define
The function U 1∕2 is the harmonic extension of u 1∕2 in the halfplane, as plotted in Fig. 7. Indeed, from (D.10),

Furthermore, from (D.3), we have that U 1∕2 is the real part of a holomorphic function in the halfplane and so it is harmonic.
These considerations give that U 1∕2 solves the harmonic extension problem in (2.6), hence, in the light of (2.7),

Now, recalling (D.4), we see that, for any x ∈ (−1, 1) and small y > 0,
We stress that the latter denominator does not vanish when x ∈ (−1, 1) and y > 0 is small. So, using that \(\Re (ZW)=\Re Z\Re W-\Im Z\Im W\) for any Z, \(W\in \mathbb {C}\), we obtain that
From (D.9), for any x ∈ (−1, 1) we have that

This and the fact that ∂ y √(1 − z 2) is bounded (in view of (D.12)) give that, for any x ∈ (−1, 1),

This, (D.9) and (D.13) imply that, for any x ∈ (−1, 1),

and therefore

Plugging this information into (D.11), we conclude the proof of (2.17), as desired.
Appendix E: Deducing (2.19) from (2.15) Using a Space Inversion
From (2.15), up to a translation, we know that
We let w s be the space inversion of v s induced by the Kelvin transform in the fractional setting, namely
By (E.1), see Corollary 2.3 in [63], it follows that w s(x) is s-harmonic in (0, 1). Consequently, the function
is also s-harmonic in (0, 1). We thereby conclude that the function
is also s-harmonic in (0, 1). See Fig. 9 for a picture of w s and \(W^\star _s\) when s = 1∕2. Let now
and notice that U s is the primitive of \(s W^\star _s\). Since the latter function is s-harmonic in (0, 1), after an integration we thereby deduce that (− Δ)s U s = const in (0, 1). This and the fact that
imply (2.19).
Appendix F: Proof of (2.21)
Fixed \(y\in \mathbb {R}^n\setminus \{0\}\) we let \({\mathcal {R}}^y\) be a rotation which sends \(\frac {y}{|y|}\) into the vector e 1 = (1, 0, …, 0), that is
for any i ∈{1, …, n}. We also denote by
the so-called Kelvin Transform. We recall that for any i, j ∈{1, …, n},
and so, by (F.1),
This says that \( {\mathcal {R}}^y\;(DK(y))\;({\mathcal {R}}^y)^{-1}\) is a diagonalFootnote 6 matrix, with first entry equal to \(-\frac {1}{|y|{ }^2}\) and the others equal to \(\frac {1}{|y|{ }^2}\).
As a result,
The Kelvin Transform is also useful to write the Green function of the ball B 1, see e.g. formula (41) on p. 40 and Theorem 13 on p. 35 of [62]. Namely, we take n⩾3 for simplicity, and we write
and, for a suitable choice of the constant, for any x ∈ B 1 we can write the solution of (2.20) in the form
see e.g. page 35 in [62].
On this account, we have that, for any x ∈ B 1,
Notice that here we have used the transformations ζ := x − y and η := K(y), exploiting also (F.2). The claim in (2.21) is thus established.
Appendix G: Proof of (2.24) and Probabilistic Insights
We give a proof of (2.24) by taking a derivative of (2.17). To this aim, we claimFootnote 7 that
To this end, we fix x ∈ (−1, 1) and \(h\in \mathbb {R}\). We define
In the sequel, we will take |h| as small as we wish in order to compute incremental quotients, hence we can assume that
We also define
Since I x(h) ⊆ (x−1−2|h|, x−1+2|h|)∪(x+1−2|h|, x+1+2|h|)∪(1−x−2|h|, 1−x+2|h|)∪(−1−x−2|h|, −1−x+2|h|), we have that
Furthermore,
To check this, let y ∈ I x(h). Then, by (G.3), there exist σ 1,x,y, σ 2,x,y ∈{−1, 1} such that
and therefore
where the last inequality is a consequence of (G.2), and this establishes (G.5).
Now, we introduce the following notation for the incremental quotient
and we observe that, since u 1∕2 is globally Hölder continuous with exponent 1∕2, it holds that
for any x, \(y\in \mathbb {R}\). Consequently, recalling (G.4) and (G.5), we conclude that
Now we take derivatives of u 1∕2. For this, we observe that, for any ξ ∈ (−1, 1),
Since the values outside (−1, 1) are trivial, this implies that
Now, by (G.3), we know that if \(y\in \mathbb {R}\setminus I_x(h)\) we have that \(x+y+t\in \mathbb {R}\setminus \{-1,1\}\) for all \(t\in \mathbb {R}\) with |t| < |h| and therefore we can exploit (G.7) and find that
Similar arguments show that, for any \(y\in \mathbb {R}\setminus I_x(h)\),
Consequently, for any \(y\in \mathbb {R}\setminus I_x(h)\),
Now we set
and we claim that
for a suitable C x > 0, possibly depending on x. For this, we first observe that if |y|⩾3 then |x ± y|⩾1 and also |x ± y + h|⩾1. This implies that if |y|⩾3, then u 1∕2(x ± y) = u 1∕2(x ± y + h) = 0 and therefore
This and the fact that u 1∕2 is smooth in the vicinity of the fixed x ∈ (−1, 1) imply that (G.9) holds true when |y|⩾3. Therefore, from now on, to prove (G.9) we can suppose that
We will also distinguish two regimes, the one in which \(|y|\leqslant \frac {\ell _x}4\) and the one in which \(|y|>\frac {\ell _x}4\).
If \(|y|\leqslant \frac {\ell _x}4\) and \(|t|\leqslant h\), we have that
due to (G.2), and similarly \(|(x-y+t)-1|\geqslant \frac {\ell _x}2\). This implies that
for some C x > 0 that depends on ℓ x. Consequently, we find that if \(|y|\leqslant \frac {\ell _x}4\) then
Conversely, if \(y\in \mathbb {R}\setminus I_x(h)\), with \(|y|>\frac {\ell _x}4\), then we make use of (G.7) and (G.10) to see that
Also, if \(y\in \mathbb {R}\setminus I_x(h)\) we deduce from (G.3) that \(|1\pm (x+y)|\geqslant 2 |h|\) and therefore, if \(|\tau |\leqslant |h|\), then
Therefore
Hence, we insert this information into (G.12) and we conclude that
Similarly, one sees that
In view of (G.13) and (G.14), we get that, for any \(y\in \mathbb {R}\setminus I_x(h)\) with \(|y|>\frac {\ell _x}4\),
Combining this with (G.11), we obtain (G.9), up to renaming constants.
Now, we point out that the right hand side of (G.9) belongs to \(L^1(\mathbb {R})\). Accordingly, using (G.9) and the Dominated Convergence Theorem, and recalling also (G.7), it follows that
where the last identity is a consequence of (G.8).
From this and (G.6), the claim in (G.1) follows, as desired.
Now, we rewrite (G.1) as
We claim that
This follows plainly for x = 0, since u −1∕2 is even. Hence, from here on, to prove (G.16) we assume without loss of generality that x ∈ (0, 1). Moreover, by changing variable y↦ − y, we see that
and therefore
Now, we apply the change of variable
We observe that when z ranges in (−1, 1), then ξ ranges therein as well. Moreover,
thus, by (G.17),
We now apply another change of variable
which gives
where
Now we notice that
Inserting this identity into (G.18), we obtain (G.16), as desired.
Then, from (G.15) and (G.16) we get that
that is
From this and (2.17) we infer that x (− Δ)1∕2 u −1∕2 = 0 and so (− Δ)1∕2 u −1∕2 = 0 in (−1, 1).
These consideration establish (2.24), as desired. Now, we give a brief probabilistic insight on it. In probability—and in stochastic calculus—a measurable function \(f:\mathbb {R}^n\to \mathbb {R}\) is said to be harmonic in an open set \(D\subset \mathbb {R}^n\) if, for any D 1 ⊂ D and any x ∈ D 1,
Notice that, since W t has (a.s.) continuous trajectories, then (a.s.) \(W_{\tau _{D_1}}\in \partial D_1\). This notion of harmonicity coincides with the analytic one.
If one considers a Lévy-type process X t in place of the Brownian motion, the definition of harmonicity (with respect to this other process) can be given in the very same way. When X t is an isotropic (2s)-stable process, the definition amounts to having zero fractional Laplacian (− Δ)s at every point of D and replace (G.19) by
In this identity, we can consider a sequence \(\{D_j:D_j\subset D,j\in \mathbb {N}\}\), with  , and equality
, and equality
When f = 0 in \(\mathbb {R}^n\setminus D\), the right-hand side of (G.20) can be not 0 (since \(X_{\tau _{D_j}}\) may also end up in D ∖ D j), and this leaves the possibility of finding f which satisfies (G.20) without vanish identically (an example of this phenomenon is exactly given by the function u −1∕2 in (2.24)).
It is interesting to observe that if f vanishes outside D and does not vanish identically, then, the only possibility to satisfy (G.20) is that f diverges along ∂D. Indeed, if \(|f|\leqslant \kappa \), since \(f(X_{\tau _{D_j}})\neq 0\) only when x ∈ D ∖ D
j and  as j →∞, we would have that
as j →∞, we would have that
and (G.20) would imply that f must vanish identically.
Of course, the function u −1∕2 in (2.23) embodies exactly this singular boundary behavior.
Appendix H: Another Proof of (2.24)
Here we give a different proof of (2.24) by using complex analysis and extension methods. We use the principal complex square root introduced in (D.2) and, for any \(x\in \mathbb {R}\) and y > 0 we define
where z := x + iy.
The function U −1∕2 is plotted in Fig. 10. We recall that the function U −1∕2 is well-defined, thanks to (D.6). Also, the denominator never vanishes when y > 0 and so U −1∕2 is harmonic in the halfplane, being the real part of a holomorphic function in such domain.
Furthermore, in light of (D.9), we have that

and therefore

This gives that U −1∕2 is the harmonic extension of u −1∕2 to the halfplane. Therefore, by (2.6), (2.7), and (D.14), for any x ∈ (−1, 1) we have that

that is (2.24).
Appendix I: Proof of (2.29) (Based on Fourier Methods)
When n = 1, we use (2.28) to find thatFootnote 8
This proves (2.28) when n = 1.
Let us now deal with the case n⩾2. By changing variable Y := 1∕y, we see that
Therefore, summing up the left hand side to both sides of this identity and using the transformation \(\eta :=y-\frac 1y\),
As a result,
where the substitution t := |ξ| y 2 has been used.
Accordingly, by (2.28), the Gaussian Fourier transform and the change of variable τ := t(1 + |x|2),
This establishes (2.29).
Appendix J: Another Proof of (2.29) (Based on Extension Methods)
The idea is to consider the fundamental solution in the extended space and take a derivative (the time variable acting as a translation and, to favor the intuition, one may keep in mind that the Poisson kernel is the normal derivative of the Green function). Interestingly, this proof is, in a sense, “conceptually simpler”, and “less technical” than that in Appendix I, thus demonstrating that, at least in some cases, when appropriately used, fractional methods may lead to cultural advantagesFootnote 9 with respect to more classical approaches.
For this proof, we consider variables \(X:=(x,y)\in \mathbb {R}^n\times (0,+\infty )\subset \mathbb {R}^{n+1}\) and fix t > 0. We let Γ be the fundamental solution in \(\mathbb {R}^{n+1}\), namely
By construction Δ Γ is the Delta Function at the origin and so, for any t > 0, we have that \(\tilde \Gamma (X;t)=\tilde \Gamma (x,y;t):=\Gamma (x,y+t)\) is harmonic for \((x,y)\in \mathbb {R}^n\times (0,+\infty )\). Accordingly, the function \(U(x,y;t):=\partial _y\tilde \Gamma (x,y;t)\) is also harmonic for \((x,y)\in \mathbb {R}^n\times (0,+\infty )\). We remark that
This function is plotted in Fig. 11 (for the model case in the plane). We observe that

As a consequence, by (2.6) and (2.7) (and noticing that the role played by the variables y and t in the function U is the same),

This shows that u solves the fractional heat equation, with u approaching a Delta function when  . Hence
. Hence
that is (2.29).
Appendix K: Proof of (2.36)
First, we construct a useful barrier. Given A > 1, we define
We claim that if A is sufficiently large, then
To prove this, fix t⩾3 (the case \(t\leqslant -3\) being similar). Then, if |ξ − t| < 1, we have that
As a consequence, if |τ − t| < 1,
This implies that
On the other hand,
In addition, if |τ|⩽1 then \(|\tau -t|\geqslant t-\tau \geqslant 3-1>1\), hence
Accordingly,
We also observe that if |τ|⩽1 then \(|t-\tau |\leqslant t+1\leqslant 2t\) and therefore
So, we plug this information into (K.4), assuming A > 1 and we obtain that
Thus, gathering together the estimates in (K.2), (K.3) and (K.5), we conclude that
as long as A is sufficiently large. This proves (K.1).
Now, to prove (2.36), we define \(v:=\dot u>0\). From (2.40), we know that
Given ε > 0, we define
We claim that
Indeed, for large ε, it holds that w ε < 0 < v and so (K.7) is satisfied. In addition, for any ε > 0,
Suppose now that ε ⋆ > 0 produces a touching point between \(w_{\varepsilon _\star }\) and v, namely \(w_{\varepsilon _\star }\leqslant v\) and \(w_{\varepsilon _\star }(t_\star )=v(t_\star )\) for some \(t_\star \in \mathbb {R}\). Notice that, if |τ|⩽3,
and therefore |t ⋆| > 3. Accordingly, if we set \(v_\star :=v-w_{\varepsilon _\star }\), using (K.1) and (K.6), we see that
Since the latter integrand is nonnegative, we conclude that v ⋆ must vanish identically, and thus \(w_{\varepsilon _\star }\) must coincide with v. But this is in contradiction with (K.8) and so the proof of (K.7) is complete.
Then, by sending  in (K.7) we find that \(v\geqslant \frac \iota {A}\,w\), and therefore, for t⩾1 we have that \(\dot u(t)= v(t)\geqslant \kappa t^{-1-2s}\), for all t > 1, for some κ > 0.
in (K.7) we find that \(v\geqslant \frac \iota {A}\,w\), and therefore, for t⩾1 we have that \(\dot u(t)= v(t)\geqslant \kappa t^{-1-2s}\), for all t > 1, for some κ > 0.
Consequently, for any t > 1,
and a similar estimates holds for 1 + u(t) when t < −1.
These considerations establish (2.36), as desired.
Appendix L: Proof of (2.38)
Here we prove that (2.38) is a solution of (2.37). The idea of the proof, as showed in Fig. 12, is to consider the harmonic extension of the function \(\mathbb {R}\ni x\mapsto \frac 2\pi \,\arctan x\) in the halfplane \(\mathbb {R}\times (0,+\infty )\) and use the method described in (2.6) and (2.7).
We let
The function U is depictedFootnote 10 in Fig. 12. Of course, it coincides with u when y = 0 and, for any \(x\in \mathbb {R}\) and y > 0,
Hence, the setting in (2.6) is satisfied and so, in light of (2.7). we have

Also, by the trigonometric Double-angle Formula, for any \(\theta \in \left (-\frac \pi 2,\frac \pi 2\right )\),
Hence, taking \(\theta :=\arctan x\),
This and (L.2) show that (2.38) is a solution of (2.37).
Appendix M: Another Proof of (2.38) (Based on (2.29))
This proof of (2.38) is based on the fractional heat kernel in (2.29). This approach has the advantage of being quite general (see e.g. Theorem 3.1 in [27]) and also to relate the two “miraculous” explicit formulas (2.29) and (2.38), which are available only in the special case s = 1∕2.
For this, we let P = P(x, t) the fundamental solution of the heat flow in (2.25) with n = 1 and s = 1∕2. Notice that, by (2.29), we know that
with
Also, by scaling,
For any \(x\in \mathbb {R}\) and any t > 0, we define
In light of (M.2), we see that
which is bounded in \(\mathbb {R}\times [0,+\infty )\), and infinitesimal as t → +∞ for any fixed \(x\in \mathbb {R}\).
Notice also that
by (2.5). As a consequence,
where the last identity follows from (M.2).
Besides, from (M.2) we have that
and so
In view of this, we have that
Accordingly, from (M.4) and (M.5), using the extension method in (2.6) and (2.7) (with the variable y called t here), we conclude that, if
then
We remark that, by (M.1) and (M.3),
This, (M.1) and (M.6) give that
that is (2.38), as desired.
Appendix N: Proof of (2.46)
Due to translation invariance, we can reduce ourselves to proving (2.46) at the origin. We consider a measurable \(u:\mathbb {R}^n\to \mathbb {R}\) such that
Assume first that
for some r > 0. As a matter of fact, under these assumptions on u, the right-hand side of (2.46) vanishes at 0 regardless the size of r. Indeed,

This proves (2.46) under the additional assumption in (N.1), that we are now going to remove. To this end, for r ∈ (0, 1), denote by χ r the characteristic function of B r, i.e. χ r(x) = 1 if x ∈ B r and χ r(x) = 0 otherwise. Consider now u ∈ C 2, α(B r), for some α ∈ (0, 1), with
for simplicity (note that one can always modify u by considering \(\tilde u(x)=u(x)-u(0)-\nabla u(0)\cdot x\) and without affecting the operators in (2.46)). Then, the right hand side of (2.46) becomes in this case

The second addend is trivial for any r ∈ (0, 1), in view of the above remark, since u(1 − χ r) is constantly equal to 0 in B r. For the first one, we have
Now, we recall (N.2) and we notice that
which in turn implies that
On the other hand, a Taylor expansion and (N.2) yield

in view of (1.1), for some \(\eta :B_r\to \mathbb {R}\) such that \(|\eta (x)|\leqslant c|x|{ }^\alpha \). From this, (N.3) and (N.4) we deduce that

which finally justifies (2.46).
It is interesting to remark that the main contribution to prove (2.46) comes in this case from the “intermediate ring” in (N.5).
Appendix O: Proof of (2.48)
Take for instance Ω to be the unit ball and \(\bar u=1-|x|{ }^2\). Suppose that \(\|\bar u-v_\varepsilon \|{ }_{C^2(\Omega )}\leqslant \varepsilon \). Then, for small ε, if \(x\in \mathbb {R}^n\setminus B_{1/2}\) it holds that
while
This implies that there exists \(x_\varepsilon \in \overline {B_{1/2}}\) such that
As a result,
This says that (− Δ)s v ε cannot vanish at x ε and so (2.48) is proved.
Appendix P: Proof of (2.52)
Let us first notice that the identity
holds for any λ > 0 and s ∈ (0, 1), because
We also observe that when \(u\in C^\infty _0(\Omega )\), the coefficients \(\hat u_j\) decay fast as j →∞: indeed
Therefore, applying equality (P.1) to the μ j’s in (2.51) we obtainFootnote 11
where \(\{ e^{t \Delta _{N,\Omega } }\}_{t>0}\) stands for the heat semigroup associated to ΔN,Ω. i.e. \(e^{t{\Delta _{N,\Omega }}}u\) solves
To check (P.2), it is sufficient to notice that
and that
Under suitable regularity assumptions on Ω, write now the heat semigroup in terms of the heat kernel \(p_{N}^\Omega \) as
where the following two-sided estimate on \(p_{{N}}^\Omega \) holds (see, for example, [102, Theorem 3.1])
Recall also that \(p_{N}^\Omega (t,x,y)=p_{N}^\Omega (t,y,x)\) for any t > 0 and x, y ∈ Ω, and that
which follows from noticing that, for any \(u\in C^\infty _0(\Omega )\),
and therefore
By (P.5), for any x ∈ Ω and t > 0,
and, exchanging the order of integration in (P.2) (see below for a justification of this passage), one gets
where, in view of (P.4), we have
These considerations establish (2.52). Note however that in the above computations there is a limit exiting the integral in the t variable, namely:

To properly justify this we are going to build an integrable majorant in t and independent of ε of the integrand
To this end, first of all we observe that, by the boundedness of u and (P.5),
which is integrable at infinity. So, to obtain an integrable bound for (P.7), we can now focus on small values of t, say t ∈ (0, 1). For this, we denote by p the heat kernel in \(\mathbb {R}^N\) and we write
We first manipulate A. We reformulate u as
so that
In the last expression, the first integral on the right-hand side is 0 by odd symmetry, while for the second one
As for the last integral in (P.8), we have that
Equations (P.9) and (P.10) imply that
which is integrable for t ∈ (0, 1).
We turn now to the estimation of B which we rewrite as
where χ U stands for the characteristic function of a set \(U\subset \mathbb {R}^n\). By definition, B solves the heat equation in Ω with zero initial condition. Moreover, since u is supported in a compact subset K of Ω, B is satisfying the (lateral) boundary condition
for some c 1, c 2 > 0, in view of (P.4) and that, for x ∈ ∂ Ω and y ∈ K, \(|x-y|\geqslant \text{dist}(K,\partial \Omega )>0\). Then, by the parabolic maximum principle (see, for example, Section 7.1.4 in [62]),
which again is integrable for t ∈ (0, 1). These observations provide an integrable bound for the integrand in (P.8), thus completing the justification of the claim in (P.6), as desired.
Appendix Q: Proof of (2.53)
If u is periodic, we can write it in Fourier series as
and the Fourier basis is also a basis of eigenfunctions. We have that
and this shows (2.53).
Appendix R: Proof of (2.54)
We fix \(\bar k\in \mathbb {N}\). We consider the \(\bar k\)th eigenvalue \(\lambda _{\bar k}>0\) and the corresponding normalized eigenfunction \(\phi _{\bar k}=:\bar u\). We argue by contradiction and suppose that for any ε > 0 we can find v ε such that \( \|\bar u-v_\varepsilon \|{ }_{C^2(B_1)}\leqslant \varepsilon \), with \((-\Delta )^s_{D,\Omega } v_\varepsilon =0\) in B 1.
Using the notation in (2.49), we have that \(\bar u_k=\delta _{k\bar k}\) and therefore
Furthermore
Comparing this with (R.1), we obtain that \(\lambda _{\bar k}^{2s}\leqslant \,{\mathrm {const}}\,\varepsilon \), which is a contradiction for small ε. Hence, the proof of (2.54) is complete.
Appendix S: Proof of (2.60)
Let
Then, by (2.59) and writing 𝜗 := ω (t − τ), we see that
where Γ denotes here the Euler’s Gamma Function. This and (2.56) give (2.60), up to neglecting normalizing constants, as desired.
It is also worth pointing out that, as  , formula (2.60) recovers the classical derivative, since, by (2.59),
, formula (2.60) recovers the classical derivative, since, by (2.59),
which is (2.60) when s = 1.
Appendix T: Proof of (2.61)
First, we compute the Laplace Transform of the constant function. Namely, by (2.59), for any \(b\in \mathbb {R}\),
We also set
and we use (2.59) and the substitution 𝜗 := ω (t − τ) to calculate that
where Γ denotes here the Euler’s Gamma Function.
Exploiting this and (T.1), and making use also of (2.60), we can write the expression \(\partial ^s_{C,t} u=f\) in terms of the Laplace Transform as
with b := u(0). Hence, dividing by ω s and inverting the Laplace Transform, we obtain that
which is (2.61).
Appendix U: Proof of (2.62)
We take G to be the fundamental solution of the operator “identity minus Laplacian”, namely
being δ 0 the Dirac’s Delta. The study of this fundamental solution can be done by Fourier Transform in the sense of distributions, and this leads to an explicit representation in dimension 1 recalling (I.1); we give here a general argument, valid in any dimension, based on the heat kernel
Notice that ∂ t g = Δg and g(⋅, 0) = δ 0(⋅). Let also
Notice that
hence G, as defined in (U.2) solves (U.1).
Notice also that G is positive and bounded, due to (U.2). We also claim that
for some c, C > 0. To this end, let us fix \(x\in \mathbb {R}^n\setminus B_1\) and distinguish two regimes. If t ∈ [0, |x|], we have that \(\frac {|x|{ }^{2}}{t}\geqslant |x|\) and thus
Consequently, using the substitution \(\rho :=\frac {|x|{ }^{2}}{8t}\),
for some C > 0 possibly varying from line to line. Furthermore
for some C > 0. This and (U.4) give that
up to renaming C, which implies (U.3) in view of (U.2).
Now we compute the Laplace Transform of t s: namely, by (2.59),
We compare this result with the Laplace Transform of the mean squared displacement related to the diffusion operator in (2.62). For this, we take u to be as in (2.62) and, in the light of (2.42), we consider the function
In addition, by taking the Laplace Transform (in the variable t, for a fixed \(x\in \mathbb {R}^n\)) of the equation in (2.62), making use of (2.60) we find that
Now, we let
From (U.7), we have that
and so, comparing with (U.1), we have that W(x, ω) = G(x).
Accordingly, by (U.8),
We insert this information into (U.6) and we conclude that
We remark that the latter integral is finite, thanks to (U.3), hence we can write that
for some C > 0.
Therefore, we can compare this result with (U.5) and use the inverse Laplace Transform to obtain that the mean squared displacement in this case is proportional to t s, as desired.
Appendix V: Memory Effects of Caputo Type
It is interesting to observe that the Caputo derivative models a simple memory effect that the classical derivative cannot comprise. For instance, integrating a classical derivative of a function u with u(0) = 0, one obtains the original function “independently on the past”, namely if we set
we just obtain in this case that M u(t) = u(t) − u(0) = u(t). On the other hand, an expression as in (V.1) which takes into account the Caputo derivative does “remember the past” and takes into account the preceding events in such a way that recent events “weight” more than far away ones. To see this phenomenon, we can modify (V.1) by defining, for every s ∈ (0, 1),
To detect the memory effect, for the sake of concreteness, we take a large time \(t:=N\in \mathbb {N}\) and we suppose that the function u is constant on unit intervals, that is u = u k in [k − 1, k), for each k ∈{1, …, N}, with \(u_k\in \mathbb {R}\), and u(0) = u 1 = 0. We see that \(M_u^s\) in this case does not produce just the final outcome u N, but a weighted average of the form
To check this, we notice that, for all τ ∈ (0, N),
and hence we exploit (2.56) and (V.2) to see that
with
This completes the proof of the memory effect claimed in (V.3).
Appendix W: Proof of (3.7)
Since M is bounded and positive and u is bounded, it holds that
Moreover, for y ∈ B 1,
To simplify the notation, we now fix \(x\in \mathbb {R}^n\) and we define \({\mathcal {M}}(y):= M(x-y,y)\). Then, for y ∈ B 1, we have that
and so
Consequently, since \({\mathcal {M}}(0)=M(x,0)\) is non-degenerate, we can write
and
Hence (for smooth and bounded functions u, and y ∈ B 1) we obtain that
Thus, since the map \(y\mapsto \frac {\nabla u(x)\cdot y}{|{\mathcal {M}}(0)\,y|{ }^{n+2s} }\) is odd, recalling (W.2) we conclude that

Now we observe that, for any α⩾0,
Indeed, using polar coordinates and the fact that φ(ρω) = ρ 2+α φ(ω), for any ρ⩾0 and ω ∈ S n−1, thanks to the homogeneity, we see that
which implies (W.5).
Using (W.5) (with α := 0 and α := 2), we obtain that

and

Thanks to this, (W.1) and (W.4), we find that

with
We observe that
To check this, we first compute that
Now, we write a Taylor expansion of M(x, y) in the variable y of the form
for some \(A_{\ell m}:\mathbb {R}^n\to \mathbb {R}\) and \(B_{\ell m}:\mathbb {R}^n\to \mathbb {R}^n\). We notice that
Also,
Furthermore, we use the structural assumption (3.6), and we see that
Comparing the linear terms, this gives that
This and (W.10) imply that
Comparing this with (W.9), we see that
So, we insert this information into (W.8) and we conclude that
This establishes (W.7), as desired.
Then, plugging (W.7) into (W.6), we obtain the equation in divergence formFootnote 12 which was claimed in (3.7).
Appendix X: Proof of (3.12)
First we observe that
Furthermore, for y ∈ B 1,
Consequently,
and so, from the non-degeneracy of M(⋅, ⋅),
Using this and the expansion in (W.2), we see that, for y ∈ B 1,
Thus, since, in the light of (3.11), we know that the map \(y\mapsto \frac { \nabla u(x)\cdot y }{|M(x,y)\,y|{ }^{n+2s}}\) is odd, we can write that
where the last identity follows by using (W.5) (with α := 0). From this and (X.1) we obtain that

which gives (3.12).
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Abatangelo, N., Valdinoci, E. (2019). Getting Acquainted with the Fractional Laplacian. In: Dipierro, S. (eds) Contemporary Research in Elliptic PDEs and Related Topics. Springer INdAM Series, vol 33. Springer, Cham. https://doi.org/10.1007/978-3-030-18921-1_1
Download citation
DOI: https://doi.org/10.1007/978-3-030-18921-1_1
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-18920-4
Online ISBN: 978-3-030-18921-1
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)



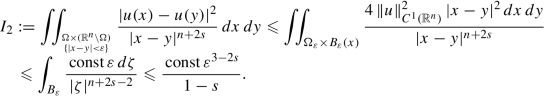

 , to obtain
, to obtain 




