Abstract
The aim of this work is to construct exact solutions of Einstein–Maxwell(-dilaton) equations possessing a discrete translational symmetry. We present two approaches to the problem. The first one is to solve Einstein–Maxwell equations in 4D, the second one relies on dimensional reduction from 5D. We examine the geometry of the solutions, their horizons and singularities and compare them.
Grants GAUK 80918, GACR 14-37086G.
This is a preview of subscription content, log in via an institution.
Buying options
Tax calculation will be finalised at checkout
Purchases are for personal use only
Learn about institutional subscriptionsNotes
- 1.
The term extremal refers to the fact that the charges of the black holes are equal to their masses, rendering their horizons degenerate.
- 2.
The number of space-like dimensions is denoted as n.
- 3.
Latin indices range over 1, …, n and label only spatial components, Greek indices are 0, …, n.
- 4.
The Laplacian for the spatial metric h is defined as \(\Delta _h f \equiv h^{ij} \nabla _{i} \nabla _{j} f = \frac {1}{\sqrt {\mathfrak {h}}} \left (\sqrt {\mathfrak {h}} h^{ij} f_{i}\right )_{,j}\).
- 5.
Let \(f_k(x): I \rightarrow \mathbb {C}\) be functions and assume that there exist a k such that \(\left |{f_k(x) - f(x)}\right | \leq a_k\) for ∀x ∈ I and a k → 0 when k →∞. Then \(f_k(x) \rightrightarrows f(x)\) in I.
- 6.
Leibniz theorem: Let \(f_k(x): I \rightarrow \mathbb {C}\) such that \(f_k \rightrightarrows 0\) in I and let f k(x) be monotonous for ∀x ∈ I. Then \(\sum (-1)^k f_k(x)\) converges uniformly in I.
- 7.
Weierstrass M-test: Let \(f_k(x): I \rightarrow \mathbb {C}\) be functions and assume that there exist a k such that \(\left |{f_k(x)}\right | \leq a_k\) and \(\left |{\sum a_k}\right | < \infty \). Then \(\sum f_k(x)\) converges absolutely uniformly in I.
- 8.
The Hurwitz–Lerch transcendent is defined as \(\Phi (z,s,a)=\sum _{k=0}^{\infty } z^k(a+k)^{-s}\).
- 9.
The Hurwitz zeta function, \(\zeta _s(a)=\sum _{k=0}^{\infty } (a+k)^{-s}\), has singularities at a = −n for non-negative integers n.
- 10.
Here \(\bar {\zeta }(s)=\sum _{k=1}^{\infty } k^{-s}\) is the Riemann zeta function.
- 11.
Moore–Osgood: Let f, f n be defined in a punctured neighbourhood of x 0. Let \(f_n \rightrightarrows f\) in I and \(c_n = \lim _{x \rightarrow x_0} f_n(x)\) be finite. Then \(\lim _{x \rightarrow x_0} \lim _{n \rightarrow \infty } f_n(x) = \lim _{n \rightarrow \infty } \lim _{x \rightarrow x_0} f_n(x)\).
- 12.
Equations of motion for electrogeodesics are derived from the Lagrangian \(\mathcal {L} = \frac {1}{2}g_{\mu \nu }\dot {x}^{\mu }\dot {x}^{\nu }+qA_{\mu }\dot {x}^{\mu }\), the dot denotes derivative with respect to affine parameter τ.
- 13.
Formally \(\nabla \varphi _{\neg 0} = (\nabla f) \sum f^{-1} \varphi _n - f \sum \varphi _n f^{-2} \nabla f + f \sum f^{-1} \nabla \varphi _n\). Under suitable assumptions the first two terms cancel each other.
- 14.
Harmonic number \(H(z) = \gamma _e + \frac {\mathrm {d}{(\ln \Gamma (z+1))}}{\mathrm {d}{z}}\), where γ e is the Euler gamma constant and Γ is the Euler gamma function.
- 15.
Capital Latin indices range over 0, …, D + 1, Greek indices are 0, …, D.
- 16.
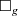 denotes the d’Alembertian of a Lorentzian metric g, which is defined as
denotes the d’Alembertian of a Lorentzian metric g, which is defined as 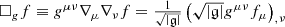 .
.
References
S.D. Majumdar, A class of exact solutions of Einstein’s field equations. Phys. Rev. 72, 390–398 (1947)
A. Papaetrou, A static solution of the equations of the gravitational field for an arbitrary charge distribution. Proc. R. Irish Acad. (Sect. A) A51, 191–204 (1947)
J.B. Hartle, S.W. Hawking, Solutions of the Einstein-Maxwell equations with many black holes. Commun. Math. Phys. 26(2), 87–101 (1972)
J. Ryzner, M. Žofka, Electrogeodesics in the di-hole Majumdar-Papapetrou spacetime. Class. Quant. Gravit. 32(20), 205010 (2015)
J. Ryzner, M. Žofka, Extremally charged line. Class. Quant. Gravit. 33(24), 245005 (2016)
J.P.S. Lemos, V.T. Zanchin, Class of exact solutions of Einstein’s field equations in higher dimensional spacetimes, d ≥ 4: Majumdar-Papapetrou solutions. Phys. Rev. D 71, 124021 (2005)
D.L. Welch, On the smoothness of the horizons of multi-black-hole solutions. Phys. Rev. D 52, 985–991 (1995)
V.P. Frolov, A. Zelnikov, Scalar and electromagnetic fields of static sources in higher dimensional Majumdar-Papapetrou spacetimes. Phys. Rev. D 85, 064032 (2012)
J.P.S. Lemos, V.T. Zanchin, Rotating charged black strings and three-dimensional black holes. Phys. Rev. D 54, 3840–3853 (1996)
R. Deszcz, M. Głogowska, J. Jełowicki, G. Zafindratafa, Curvature properties of some class of warped product manifolds. Int. J. Geom. Methods Mod. Phys. 13(1), 1550135 (2016)
Acknowledgements
J.R. was supported by grant No. 80918 of Charles University Grant Agency. M.Ž. Acknowledges support by GACR 17-13525S.
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Ryzner, J., Žofka, M. (2019). Crystal Spacetimes with Discrete Translational Symmetry. In: Cacciatori, S., Güneysu, B., Pigola, S. (eds) Einstein Equations: Physical and Mathematical Aspects of General Relativity. DOMOSCHOOL 2018. Tutorials, Schools, and Workshops in the Mathematical Sciences . Birkhäuser, Cham. https://doi.org/10.1007/978-3-030-18061-4_10
Download citation
DOI: https://doi.org/10.1007/978-3-030-18061-4_10
Published:
Publisher Name: Birkhäuser, Cham
Print ISBN: 978-3-030-18060-7
Online ISBN: 978-3-030-18061-4
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


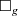 denotes the d’Alembertian of a Lorentzian metric g, which is defined as
denotes the d’Alembertian of a Lorentzian metric g, which is defined as 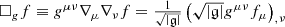 .
.