Abstract
We propose new constructions of leakage-resilient public-key encryption (PKE) and identity-based encryption (IBE) schemes in the bounded retrieval model (BRM). In the BRM, adversaries are allowed to obtain at most \(\ell \)-bit leakage from a secret key and we can increase \(\ell \) only by increasing the size of secret keys without losing efficiency in any other performance measure. We call \(\ell /|\mathsf {sk}|\) leakage-ratio where \(|\mathsf {sk}|\) denotes a bit-length of a secret key. Several PKE/IBE schemes in the BRM are known. However, none of these constructions achieve a constant leakage-ratio under a standard assumption in the standard model. Our PKE/IBE schemes are the first schemes in the BRM that achieve leakage-ratio \(1-\epsilon \) for any constant \(\epsilon >0\) under standard assumptions in the standard model.
As previous works, we use identity-based hash proof systems (IB-HPS) to construct IBE schemes in the BRM. It is known that a parameter for IB-HPS called the universality-ratio is translated into the leakage-ratio of the resulting IBE scheme in the BRM. We construct an IB-HPS with universality-ratio \(1-\epsilon \) for any constant \(\epsilon >0\) based on any inner-product predicate encryption (IPE) scheme with compact secret keys. Such IPE schemes exist under the d-linear, subgroup decision, learning with errors, or computational bilinear Diffie-Hellman assumptions. As a result, we obtain IBE schemes in the BRM with leakage-ratio \(1-\epsilon \) under any of these assumptions. Our PKE schemes are immediately obtained from our IBE schemes.
This is a preview of subscription content, log in via an institution.
Buying options
Tax calculation will be finalised at checkout
Purchases are for personal use only
Learn about institutional subscriptionsNotes
- 1.
They can be proven secure in the standard model if one assumes non-standard interactive versions of these assumptions.
- 2.
- 3.
Here, it is crucial that an adversary obtains at most one secret key for each identity in the security model of IB-HPS.
- 4.
Here we assumed that \(\mathsf {KeyGen}_{\mathsf {IBE}}\) is deterministic so that \(\mathsf {sk}'_{\mathsf {id}}\) is determined by \(\mathsf {id}\). This can be assumed without loss of generality since we can derandomize \(\mathsf {KeyGen}_{\mathsf {IBE}}\) by using a pseudorandom function.
- 5.
In their paper, they use “n” instead of “m” for representing a “key-size” parameter. We use m for avoiding confusion with the dimension for IPE.
- 6.
Since we consider a leakage resilient IBE, we give the leakage parameter \(1^{\ell }\) as input, which means a maximum amount of leakage bits the scheme tolerates.
- 7.
In [ADN+09], they only consider the adaptive security. We also define the selective security similarly.
- 8.
Though Alwen et al. [ADN+09] only gave a proof for the case of the adaptive security, the proof can be straightforwardly extended to the selective case.
References
Alwen, J., Dodis, Y., Naor, M., Segev, G., Walfish, S., Wichs, D.: Public-key encryption in the bounded-retrieval model. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 113–134. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13190-5_6. IACR Cryptology ePrint Archive, 2009:512, 2009. Version 20091028:202321
Alwen, J., Dodis, Y., Wichs, D.: Leakage-resilient public-key cryptography in the bounded-retrieval model. In: Halevi, S. (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 36–54. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03356-8_3
Agrawal, S., Freeman, D.M., Vaikuntanathan, V.: Functional encryption for inner product predicates from learning with errors. In: Lee, D.H., Wang, X. (eds.) ASIACRYPT 2011. LNCS, vol. 7073, pp. 21–40. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-25385-0_2
Akavia, A., Goldwasser, S., Vaikuntanathan, V.: Simultaneous hardcore bits and cryptography against memory attacks. In: Reingold, O. (ed.) TCC 2009. LNCS, vol. 5444, pp. 474–495. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-00457-5_28
Boneh, D., Boyen, X.: Efficient selective-ID secure identity based encryption without random oracles. In: Cachin, C., Camenisch, J. (eds.) EUROCRYPT 2004. LNCS, vol. 3027, pp. 223–238. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24676-3_14
Brakerski, Z., Goldwasser, S.: Circular and leakage resilient public-key encryption under subgroup indistinguishability - (or: Quadratic residuosity strikes back). In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 1–20. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14623-7_1
Brakerski, Z., Kalai, Y.T., Katz, J., Vaikuntanathan, V.: Overcoming the hole in the bucket: public-key cryptography resilient to continual memory leakage. In: 51st FOCS, pp. 501–510. IEEE Computer Society Press, October 2010
Brakerski, Z., Lombardi, A., Segev, G., Vaikuntanathan, V.: Anonymous IBE, leakage resilience and circular security from new assumptions. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018, Part I. LNCS, vol. 10820, pp. 535–564. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78381-9_20
Boyle, E., Segev, G., Wichs, D.: Fully leakage-resilient signatures. J. Cryptol. 26(3), 513–558 (2013)
Chow, S.S.M., Dodis, Y., Rouselakis, Y., Waters, B.: Practical leakage-resilient identity-based encryption from simple assumptions. In: Al-Shaer, E., Keromytis, A.D., Shmatikov, V. (eds.) ACM CCS 2010, pp. 152–161. ACM Press, October 2010
Chen, J., Gay, R., Wee, H.: Improved dual system ABE in prime-order groups via predicate encodings. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015, Part II. LNCS, vol. 9057, pp. 595–624. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46803-6_20
Cramer, R., Shoup, V.: Universal hash proofs and a paradigm for adaptive chosen ciphertext secure public-key encryption. In: Knudsen, L.R. (ed.) EUROCRYPT 2002. LNCS, vol. 2332, pp. 45–64. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-46035-7_4
Chen, Y., Zhang, Z., Lin, D., Cao, Z.: Generalized (identity-based) hash proof system and its applications. Secur. Commun. Netw. 9(12), 1698–1716 (2016)
Dodis, Y., Goldwasser, S., Tauman Kalai, Y., Peikert, C., Vaikuntanathan, V.: Public-key encryption schemes with auxiliary inputs. In: Micciancio, D. (ed.) TCC 2010. LNCS, vol. 5978, pp. 361–381. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-11799-2_22
Dodis, Y., Haralambiev, K., López-Alt, A., Wichs, D.: Cryptography against continuous memory attacks. In: 51st FOCS, pp. 511–520. IEEE Computer Society Press, October 2010
Dodis, Y., Haralambiev, K., López-Alt, A., Wichs, D.: Efficient public-key cryptography in the presence of key leakage. In: Abe, M. (ed.) ASIACRYPT 2010. LNCS, vol. 6477, pp. 613–631. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-17373-8_35
Dodis, Y., Kalai, Y.T., Lovett, S.: On cryptography with auxiliary input. In: Mitzenmacher, M. (ed.) 41st ACM STOC, pp. 621–630. ACM Press, May/June 2009
Di Crescenzo, G., Lipton, R., Walfish, S.: Perfectly secure password protocols in the bounded retrieval model. In: Halevi, S., Rabin, T. (eds.) TCC 2006. LNCS, vol. 3876, pp. 225–244. Springer, Heidelberg (2006). https://doi.org/10.1007/11681878_12
Dziembowski, S.: Intrusion-resilience via the bounded-storage model. In: Halevi, S., Rabin, T. (eds.) TCC 2006. LNCS, vol. 3876, pp. 207–224. Springer, Heidelberg (2006). https://doi.org/10.1007/11681878_11
Garg, S., Jain, A., Sahai, A.: Leakage-resilient zero knowledge. In: Rogaway, P. (ed.) CRYPTO 2011. LNCS, vol. 6841, pp. 297–315. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22792-9_17
Goldreich, O., Levin, L.A.: A hard-core predicate for all one-way functions. In: 21st ACM STOC, pp. 25–32. ACM Press, May 1989
Hazay, C., López-Alt, A., Wee, H., Wichs, D.: Leakage-resilient cryptography from minimal assumptions. J. Cryptol. 29(3), 514–551 (2016)
Kurosawa, K., Phong, L.T.: Anonymous and leakage resilient IBE and IPE. Des. Codes Crypt. 85(2), 273–298 (2017)
Katz, J., Sahai, A., Waters, B.: Predicate encryption supporting disjunctions, polynomial equations, and inner products. In: Smart, N. (ed.) EUROCRYPT 2008. LNCS, vol. 4965, pp. 146–162. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78967-3_9
Katz, J., Vaikuntanathan, V.: Signature schemes with bounded leakage resilience. In: Matsui, M. (ed.) ASIACRYPT 2009. LNCS, vol. 5912, pp. 703–720. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-10366-7_41
Lewko, A., Rouselakis, Y., Waters, B.: Achieving leakage resilience through dual system encryption. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 70–88. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19571-6_6
Naor, M., Segev, G.: Public-key cryptosystems resilient to key leakage. SIAM J. Comput. 41(4), 772–814 (2012)
Qin, B., Liu, S.: Leakage-resilient chosen-ciphertext secure public-key encryption from hash proof system and one-time lossy filter. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013, Part II. LNCS, vol. 8270, pp. 381–400. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-42045-0_20
Qin, B., Liu, S.: Leakage-flexible CCA-secure public-key encryption: simple construction and free of pairing. In: Krawczyk, H. (ed.) PKC 2014. LNCS, vol. 8383, pp. 19–36. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54631-0_2
Wee, H.: Dual system encryption via predicate encodings. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 616–637. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54242-8_26
Yu, Z., Au, M.H., Xu, Q., Yang, R., Han, J.: Leakage-resilient functional encryption via pair encodings. In: Liu, J.K.K., Steinfeld, R. (eds.) ACISP 2016, Part I. LNCS, vol. 9722, pp. 443–460. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-40253-6_27
Yuen, T.H., Chow, S.S.M., Zhang, Y., Yiu, S.M.: Identity-based encryption resilient to continual auxiliary leakage. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 117–134. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_9
Zhang, J., Chen, J., Gong, J., Ge, A., Ma, C.: Leakage-resilient attribute based encryption in prime-order groups via predicate encodings. Des. Codes Crypt. 86(6), 1339–1366 (2018)
Acknowledgments
We thank Daniel Wichs for helpful comments on the presentation.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
A Key-Compact IPE from CBDH or DBDH
A Key-Compact IPE from CBDH or DBDH
Here, we give constructions of a fully key-compact selectively secure IPE scheme based on the CBDH or DBDH assumptions. The constructions are simple extensions of the Boneh-Boyen IBE [BB04] and can be seen as selectively secure variants of the adaptively secure short secret key IPE scheme by Chen, Gay, and Wee [CGW15].
1.1 A.1 Definitions
First, we define pairing groups and CBDH and DBDH assumptions for it. Let \(\mathbb {G}_1\), \(\mathbb {G}_2\) and \(\mathbb {G}_T\) be groups of prime order q associated with a pairing \(e:\mathbb {G}_1\times \mathbb {G}_2\rightarrow \mathbb {G}_T\). We require e to satisfy the following two properties.
- Bilinearity:
-
For all \(g_1 \in \mathbb {G}_1\), \(g_2 \in \mathbb {G}_2\) and \(a,b\in \mathbb {Z}_q\), it holds that \(e (g_1^{a},g_2^{b})= e (g_1,g_2)^{ab}\).
- Non-degeneracy:
-
If \(g_1\) and \(g_2\) generate \(\mathbb {G}_1\) and \(\mathbb {G}_2\) respectively, then \(e (g_1,g_2)\ne ~1\).
Definition 8
(Computational Bilinear Diffie-Hellman Assumption). We say that the computational bilinear Diffie-Hellman (CBDH) assumption holds if for any PPT adversary \(\mathcal {A}\), we have

where \(g_1\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathbb {G}_1\), \(g_2\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathbb {G}_2\) and \(\alpha ,\beta ,\gamma \overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathbb {Z}_q\).
Definition 9
(Decisional Bilinear Diffie-Hellman Assumption). We say that the decisional bilinear Diffie-Hellman (DBDH) assumption holds if for any PPT adversary \(\mathcal {A}\), we have
where \(g_1\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathbb {G}_1\), \(g_2\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathbb {G}_2\), \(\alpha ,\beta ,\gamma \overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathbb {Z}_q\),  , and \(T_1\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathbb {G}_T\).
, and \(T_1\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathbb {G}_T\).
By the Goldreich-Levin theorem [GL89], the following lemma holds.
Lemma 3
(Hardcore security of CBDH). If the CBDH assumption holds, then there exists a family \(\mathcal {G}\mathcal {L}\) of functions \(\mathsf {hc}:\mathbb {G}_T\rightarrow \{0,1\}\) such that
where \(g_1\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathbb {G}_1\), \(g_2\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathbb {G}_2\), \(\alpha ,\beta ,\gamma \overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathbb {Z}_q\), \(\mathsf {hc}\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathcal {G}\mathcal {L}\),  , and \(T_1 \overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\{0,1\}\).
, and \(T_1 \overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\{0,1\}\).
1.2 A.2 Construction
We first describe our IPE scheme based on the CBDH assumption.
- \(\mathsf {Setup}(1^\lambda ,1^{n})\)::
-
It generates parameters of a pairing group
 , chooses \(\mathsf {hc}\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathcal {G}\mathcal {L}\), \(\alpha ,\beta \overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathbb {Z}_q\) and \(r_i\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathbb {Z}_q\) for \(i\in [n]\), sets
, chooses \(\mathsf {hc}\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathcal {G}\mathcal {L}\), \(\alpha ,\beta \overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathbb {Z}_q\) and \(r_i\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathbb {Z}_q\) for \(i\in [n]\), sets  ,
,  and
and  for \(i\in [n]\), and outputs
for \(i\in [n]\), and outputs  and
and  ). All other algorithms implicitly include \(\mathsf {pp}\) as an input. The message space is \(\{0,1\}\) and the vector space \(\mathbb {Z}_q^n\).
). All other algorithms implicitly include \(\mathsf {pp}\) as an input. The message space is \(\{0,1\}\) and the vector space \(\mathbb {Z}_q^n\). - \(\mathsf {KeyGen}(\mathsf {msk},\varvec{y}=(y_1,...,y_n))\)::
-
It chooses \(s\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathbb {Z}_q\), sets
 ,
, 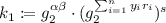 , and outputs
, and outputs  .
. - \(\mathsf {Enc}(\varvec{x}=(x_1,...,x_n), \mathsf {m}\in \mathbb {G}_T)\)::
-
It chooses \(\gamma \overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathbb {Z}_q\), computes
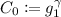 ,
,  for \(i\in [n]\), and
for \(i\in [n]\), and  , and outputs
, and outputs 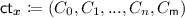 .
. - \(\mathsf {Dec}(\mathsf {sk}_{\varvec{y}}, \varvec{y}=(k_0,k_1), \mathsf {ct}_x=(C_0,C_1,...,C_n,C_\mathsf {m}))\)::
-
It outputs
 .
.
Correctness. Let \(\varvec{x}\in \mathbb {Z}_q^n\) and \(\varvec{y}\in \mathbb {Z}_q^n\) be vectors such that \(\varvec{x} ^{T}\cdot \varvec{y}=0\) and \(\mathsf {m}\in \{0,1\}\) be any message. Suppose that \(\mathsf {ct}_{\varvec{x}}=(C_0,C_1,...,C_n,C_\mathsf {m})\) and \(\mathsf {sk}_{\varvec{y}}=(k_1,k_2)\) are generated as \((\mathsf {msk},\mathsf {pp})\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathsf {Setup}(1^{\lambda },1^n)\), \(\mathsf {ct}_{\varvec{x}}\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathsf {Enc}(\varvec{x}, \mathsf {m})\), and \(\mathsf {sk}_{\varvec{y}}\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathsf {KeyGen}(\mathsf {msk},\varvec{y}=(y_1,...,y_n))\). Then we have
Thus, the decryption correctly works since \(w^\gamma = e(g_1,g_2)^{\alpha \beta \gamma }\).
Key-Compactness. A secret key \(\mathsf {sk}_{\varvec{y}}\) for a vector \(\varvec{y}\) consists of two group elements of \(\mathbb {G}_2\), and its size is independent from the demension n. Therefore the scheme is fully key-compact.
Security
Theorem 4
If the CBDH assumption holds, then the above scheme is selectively secure.
Proof
Suppose that there exists a PPT adversary \(\mathcal {A}=((\mathcal {A}_{1\text {-}1},\mathcal {A}_{1\text {-}2}),\mathcal {A}_2)\) that breaks the selective security of the above IPE scheme. We construct a PPT algorithm \(\mathcal {B}\) that breaks the hardcore security of CBDH as follows.
- \(\mathcal {B}(g_1,g_1^\alpha ,g_1^\beta ,g_1^\gamma ,g_2, g_2^\alpha ,g_2^\beta ,g_2^\gamma ,\mathsf {hc},T)\)::
-
The goal of \(\mathcal {B}\) is to distinguish if \(T=\mathsf {hc}(e(g_1,g_2)^{\alpha \beta \gamma })\) or \(T\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\{0,1\}\). It first runs \((\varvec{x}^*,\mathsf {st}_{\mathcal {A},\mathsf {pre}})\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathcal {A}_{1\text {-}1}(1^{\lambda },1^{n})\). Then it picks \(r'_i\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathbb {Z}_q\) for \(i\in [n]\), sets \(v\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }g_1^{\alpha }\),
 ,
,  (this implicitly sets
(this implicitly sets  ), and
), and 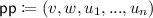 , and runs \((\mathsf {m}_0,\mathsf {m}_1,\mathsf {st})\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathcal {A}_{1\text {-}2}^{\mathsf {KeyGen}(\mathsf {msk},\cdot )}(\mathsf {pp},\mathsf {st}_{\mathcal {A},\mathsf {pre}})\) where the way to simulate the oracle \(\mathsf {KeyGen}(\mathsf {msk},\cdot )\) is described below. Then \(\mathcal {B}\) picks \(\mathsf {coin}\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\{0,1\}\), sets
, and runs \((\mathsf {m}_0,\mathsf {m}_1,\mathsf {st})\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathcal {A}_{1\text {-}2}^{\mathsf {KeyGen}(\mathsf {msk},\cdot )}(\mathsf {pp},\mathsf {st}_{\mathcal {A},\mathsf {pre}})\) where the way to simulate the oracle \(\mathsf {KeyGen}(\mathsf {msk},\cdot )\) is described below. Then \(\mathcal {B}\) picks \(\mathsf {coin}\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\{0,1\}\), sets  ,
, 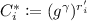 for \(i\in [n]\),
for \(i\in [n]\),  , and
, and  , and runs \(\widehat{\mathsf {coin}}\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathcal {A}_2^{\mathsf {KeyGen}(\mathsf {msk},\cdot )}(\mathsf {ct}^*,\mathsf {st})\) where the way to simulate the oracle \(\mathsf {KeyGen}(\mathsf {msk},\cdot )\) is described below. Finally, \(\mathcal {B}\) outputs \((\widehat{\mathsf {coin}}{\mathop {=}\limits ^{?}}\mathsf {coin})\).
, and runs \(\widehat{\mathsf {coin}}\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathcal {A}_2^{\mathsf {KeyGen}(\mathsf {msk},\cdot )}(\mathsf {ct}^*,\mathsf {st})\) where the way to simulate the oracle \(\mathsf {KeyGen}(\mathsf {msk},\cdot )\) is described below. Finally, \(\mathcal {B}\) outputs \((\widehat{\mathsf {coin}}{\mathop {=}\limits ^{?}}\mathsf {coin})\). - \(\mathsf {KeyGen}(\mathsf {msk},\cdot )\)::
-
Here, we describe the way to simulate \(\mathsf {KeyGen}(\mathsf {msk},\cdot )\) by \(\mathcal {B}\). Given a key query \(\varvec{y} = (y_1,...,y_n)\), it first computes
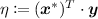 . If \(\eta =0\), then it aborts. Otherwise it picks \(s'\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathbb {Z}_q \), sets
. If \(\eta =0\), then it aborts. Otherwise it picks \(s'\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathbb {Z}_q \), sets  and
and  , and returns
, and returns  . We omit sub/super-script of \(\sum _{i=1}^n\) below for ease of notation. Now, we set
. We omit sub/super-script of \(\sum _{i=1}^n\) below for ease of notation. Now, we set  , then we can rewrite $$\begin{aligned} k_1&= g^{s'\sum _{}^{}y_i (r_i + \alpha x_i^*) - s' \alpha \eta + \beta /\eta \sum _{}^{}y_i(r_i + \alpha x_i^*) }\\&= g^{(s' + \beta /\eta )\sum _{}^{}y_i r_i + s'\alpha (\sum _{}^{}y_i x_i^* -\eta ) + \alpha \beta /\eta \sum _{}^{}y_i x_i^*}\\&= g^{s\sum _{}^{}y_i r_i + \alpha \beta }\ \ \ (\because (\varvec{x}^*)^T\cdot \varvec{y} = \sum _{}^{}y_i x_i^* = \eta ) \end{aligned}$$
, then we can rewrite $$\begin{aligned} k_1&= g^{s'\sum _{}^{}y_i (r_i + \alpha x_i^*) - s' \alpha \eta + \beta /\eta \sum _{}^{}y_i(r_i + \alpha x_i^*) }\\&= g^{(s' + \beta /\eta )\sum _{}^{}y_i r_i + s'\alpha (\sum _{}^{}y_i x_i^* -\eta ) + \alpha \beta /\eta \sum _{}^{}y_i x_i^*}\\&= g^{s\sum _{}^{}y_i r_i + \alpha \beta }\ \ \ (\because (\varvec{x}^*)^T\cdot \varvec{y} = \sum _{}^{}y_i x_i^* = \eta ) \end{aligned}$$This perfectly simulate secret keys.
For the target ciphertext, \(C_0^*=g^{\gamma }\), and for \(i=1,...,n\), we have
$$\begin{aligned} C_i^*&= (g^{r'_i})^\gamma \\&= (g_1^{\alpha x_i^*} \cdot g_1^{r'_i - \alpha x_i^*})^\gamma \\&= (v^{x_i^*} u_i)^\gamma \end{aligned}$$If \(T=\mathsf {hc}(e(g_1,g_2)^{\alpha \beta \gamma })\), then \(C^*_{\mathsf {m}}\) is also simulated correctly. On the other hand, if \(T\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\{0,1\}\), no information of \(\mathsf {coin}\) is given to \(\mathcal {A}\), and thus the probability that \(\mathcal {B}\) outputs 1 is 1/2. Therefore we have
$$\begin{aligned} \Pr [1\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathcal {B}|T=\mathsf {hc}(e(g_1,g_2)^{\alpha \beta \gamma })]-\Pr [1\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\mathcal {B}|T\overset{\scriptscriptstyle \mathsf {R}}{\leftarrow }\{0,1\}]=\frac{\mathsf {Adv}_{\mathsf {IPE},\mathcal {A}}^{\mathsf {CPA}}(\lambda )}{2}. \end{aligned}$$i Thus, \(\mathcal {B}\) can break the hardcore security of CBDH if \(\mathcal {A}\) breaks the selective security of the IPE scheme. This immediately implies that if the CBDH assumption holds, then the scheme is selectively secure by Lemma 3.
\(\blacksquare \)
If we use the DBDH assumption, we can set the message space of the scheme to \(\mathbb {G}_T\).
Rights and permissions
Copyright information
© 2019 International Association for Cryptologic Research
About this paper
Cite this paper
Nishimaki, R., Yamakawa, T. (2019). Leakage-Resilient Identity-Based Encryption in Bounded Retrieval Model with Nearly Optimal Leakage-Ratio. In: Lin, D., Sako, K. (eds) Public-Key Cryptography – PKC 2019. PKC 2019. Lecture Notes in Computer Science(), vol 11442. Springer, Cham. https://doi.org/10.1007/978-3-030-17253-4_16
Download citation
DOI: https://doi.org/10.1007/978-3-030-17253-4_16
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-17252-7
Online ISBN: 978-3-030-17253-4
eBook Packages: Computer ScienceComputer Science (R0)


 , chooses
, chooses  ,
,  and
and  for
for  and
and  ). All other algorithms implicitly include
). All other algorithms implicitly include  ,
, 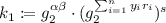 , and outputs
, and outputs  .
.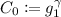 ,
,  for
for  , and outputs
, and outputs 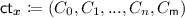 .
. .
. ,
,  (this implicitly sets
(this implicitly sets  ), and
), and 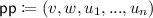 , and runs
, and runs  ,
, 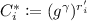 for
for  , and
, and  , and runs
, and runs 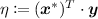 . If
. If  and
and  , and returns
, and returns  . We omit sub/super-script of
. We omit sub/super-script of  , then we can rewrite
, then we can rewrite 