Abstract
We establish proof-theoretic, constructive and coalgebraic foundations for proof search in coinductive Horn clause theories. Operational semantics of coinductive Horn clause resolution is cast in terms of coinductive uniform proofs; its constructive content is exposed via soundness relative to an intuitionistic first-order logic with recursion controlled by the later modality; and soundness of both proof systems is proven relative to a novel coalgebraic description of complete Herbrand models.
This work is supported by the European Research Council (ERC) under the EU’s Horizon 2020 programme (CoVeCe, grant agreement No. 678157) and by the EPSRC research grants EP/N014758/1, EP/K031864/1-2.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Horn clause logic is a Turing complete and constructive fragment of first-order logic, that plays a central role in verification [22], automated theorem proving [52, 53, 57] and type inference. Examples of the latter can be traced from the Hindley-Milner type inference algorithm [55, 73], to more recent uses of Horn clauses in Haskell type classes [26, 51] and in refinement types [28, 43]. Its popularity can be attributed to well-understood fixed point semantics and an efficient semi-decidable resolution procedure for automated proof search.
According to the standard fixed point semantics [34, 52], given a set P of Horn clauses, the least Herbrand model for P is the set of all (finite) ground atomic formulae inductively entailed by P. For example, the two clauses below define the set of natural numbers in the least Herbrand model.
Formally, the least Herbrand model for the above two clauses is the set of ground atomic formulae obtained by taking a (forward) closure of the above two clauses. The model for \(\mathbf {nat}\) is given by  .
.
We can also view Horn clauses coinductively. The greatest complete Herbrand model for a set P of Horn clauses is the largest set of finite and infinite ground atomic formulae coinductively entailed by P. For example, the greatest complete Herbrand model for the above two clauses is the set

obtained by taking a backward closure of the above two inference rules on the set of all finite and infinite ground atomic formulae. The greatest Herbrand model is the largest set of finite ground atomic formulae coinductively entailed by P. In our example, it would be given by  already. Finally, one can also consider the least complete Hebrand model, which interprets entailment inductively but over potentially infinite terms. In the case of \(\mathbf {nat}\), this interpretation does not differ from
already. Finally, one can also consider the least complete Hebrand model, which interprets entailment inductively but over potentially infinite terms. In the case of \(\mathbf {nat}\), this interpretation does not differ from  . However, finite paths in coinductive structures like transition systems, for example, require such semantics.
. However, finite paths in coinductive structures like transition systems, for example, require such semantics.
The need for coinductive semantics of Horn clauses arises in several scenarios: the Horn clause theory may explicitly define a coinductive data structure or a coinductive relation. However, it may also happen that a Horn clause theory, which is not explicitly intended as coinductive, nevertheless gives rise to infinite inference by resolution and has an interesting coinductive model. This commonly happens in type inference. We will illustrate all these cases by means of examples.
Horn Clause Theories as Coinductive Data Type Declarations. The following clause defines, together with \(\kappa _{\mathbf {nat}0}\) and \(\kappa _{\mathbf {nat}s}\), the type of streams over natural numbers.
This Horn clause does not have a meaningful inductive, i.e. least fixed point, model. The greatest Herbrand model of the clauses is given by

In trying to prove, for example, the goal \((\mathbf {stream}\, x)\), a goal-directed proof search may try to find a substitution for x that will make \((\mathbf {stream}\, x)\) valid relative to the coinductive model of this set of clauses. This search by resolution may proceed by means of an infinite reduction \(\underline{\mathbf {stream}\, x} {\mathop {\rightsquigarrow }\limits ^{\kappa _{\mathbf {stream}}:[\mathrm {scons}\ y\ x'/x]}} \mathbf {nat}\, y \wedge \mathbf {stream}\, x' {\mathop {\rightsquigarrow }\limits ^{\kappa _{\mathbf {nat}0}:[0/y]}} \underline{\mathbf {stream}\, x'} {\mathop { \rightsquigarrow }\limits ^{\kappa _{\mathbf {stream}}:[\mathrm {scons}\ y'\ x''/x']}} \cdots \), thereby generating a stream Z of zeros via composition of the computed substitutions: \(Z = (\mathrm {scons}\, 0 \, x')[\mathrm {scons}\, 0 \, x''/x'] \cdots \). Above, we annotated each resolution step with the label of the clause it resolves against and the computed substitution. A method to compute an answer for this infinite sequence of reductions was given by Gupta et al. [41] and Simon et al. [69]: the underlined loop gives rise to the circular unifier \(x = \mathrm {scons}\, 0\, x\) that corresponds to the infinite term Z. It is proven that, if a loop and a corresponding circular unifier are detected, they provide an answer that is sound relative to the greatest complete Herbrand model of the clauses. This approach is known under the name of CoLP.
Horn Clause Theories in Type Inference. Below clauses give the typing rules of the simply typed \(\lambda \)-calculus, and may be used for type inference or type checking:
It is well known that the Y-combinator is not typable in the simply-typed \(\lambda \)-calculus and, in particular, self-application \(\lambda x. \, x \, x\) is not typable either. However, by switching off the occurs-check in Prolog or by allowing circular unifiers in CoLP [41, 69], we can resolve the goal “\(\mathbf {typed}\, [] \, (\lambda \, x \, (\mathrm {app}\, x\, x)) \, a\)” and would compute the circular substitution: \(a = b \rightarrow c, b = b \rightarrow c\) suggesting that an infinite, or circular, type may be able to type this \(\lambda \)-term. A similar trick would provide a typing for the Y-combinator. Thus, a coinductive interpretation of the above Horn clauses yields a theory of infinite types, while an inductive interpretation corresponds to the standard type system of the simply typed \(\lambda \)-calculus.
Horn Clause Theories in Type Class Inference. Haskell type class inference does not require circular unifiers but may require a cyclic resolution inference [37, 51]. Consider, for example, the following mutually defined data structures in Haskell.

This type declaration gives rise to the following equality class instance declarations, where we leave the, here irrelevant, body out.

The above two type class instance declarations have the shape of Horn clauses. Since the two declarations mutually refer to each other, an instance inference for, e.g.,
 will give rise to an infinite resolution that alternates between the subgoals
will give rise to an infinite resolution that alternates between the subgoals
 and
and
 . The solution is to terminate the computation as soon as the cycle is detected [51], and this method has been shown sound relative to the greatest Herbrand models in [36]. We will demonstrate this later in the proof systems proposed in this paper.
. The solution is to terminate the computation as soon as the cycle is detected [51], and this method has been shown sound relative to the greatest Herbrand models in [36]. We will demonstrate this later in the proof systems proposed in this paper.
The diversity of these coinductive examples in the existing literature shows that there is a practical demand for coinductive methods in Horn clause logic, but it also shows that no unifying proof-theoretic approach exists to allow for a generic use of these methods. This causes several problems.
 for the clause \(\gamma _1\) and
for the clause \(\gamma _1\) and  for the others.
for the others.Problem 1. The existing proof-theoretic coinductive interpretations of cycle and loop detection are unclear, incomplete and not uniform. To see this, consider Table 1, which exemplifies three kinds of circular phenomena in Horn clauses: The clause \(\gamma _1\) is the easiest case. Its coinductive models are given by the finite set \(\{ p \, a\}\). On the other extreme is the clause \(\gamma _3\) that, just like \(\kappa _{\mathbf {stream}}\), admits only an infinite formula in its coinductive model. The intermediate case is \(\gamma _2\), which could be interpreted by an infinite set of finite formulae in its greatest Herbrand model, or may admit an infinite formula in its greatest complete Herbrand model. Examples like \(\gamma _1\) appear in Haskell type class resolution [51], and examples like \(\gamma _2\) in its experimental extensions [37]. Cycle detection would only cover computations for \(\gamma _1\), whereas \(\gamma _2\), \(\gamma _3\) require some form of loop detectionFootnote 1. However, CoLP’s loop detection gives confusing results here. It correctly fails to infer \(p\, a\) from \(\gamma _3\) (no unifier for subgoals \(p \, a\) and \(p \, (f \, a)\) exists), but incorrectly fails to infer \(p \, a\) from \(\gamma _2\) (also failing to unify \(p \, a\) and \(p \, (f \, a)\)). The latter failure is misleading bearing in mind that \(p\, a\) is in fact in the coinductive model of \(\gamma _2\). Vice versa, if we interpret the CoLP answer \(x = f \, x\) as a declaration of an infinite term \((f \, f \, \ldots )\) in the model, then CoLP’s answer for \(\gamma _3\) and \(p \, x\) is exactly correct, however the same answer is badly incomplete for the query involving \(p \, x\) and \(\gamma _2\), because \(\gamma _2\) in fact admits other, finite, formulae in its models. And in some applications, e.g. in Haskell type class inference, a finite formula would be the only acceptable answer for any query to \(\gamma _2\).
This set of examples shows that loop detection is too coarse a tool to give an operational semantics to a diversity of coinductive models.
Problem 2. Constructive interpretation of coinductive proofs in Horn clause logic is unclear. Horn clause logic is known to be a constructive fragment of FOL. Some applications of Horn clauses rely on this property in a crucial way. For example, inference in Haskell type class resolution is constructive: when a certain formula F is inferred, the Haskell compiler in fact constructs a proof term that inhabits F seen as type. In our earlier example
 of the Haskell type classes, Haskell in fact captures the cycle by a fixpoint term t and proves that t inhabits the type
of the Haskell type classes, Haskell in fact captures the cycle by a fixpoint term t and proves that t inhabits the type
 . Although we know from [36] that these computations are sound relative to greatest Herbrand models of Horn clauses, the results of [36] do not extend to Horn clauses like \(\gamma _3\) or \(\kappa _{\mathbf {stream}}\), or generally to Horn clauses modelled by the greatest complete Herbrand models. This shows that there is not just a need for coinductive proofs in Horn clause logic, but constructive coinductive proofs.
. Although we know from [36] that these computations are sound relative to greatest Herbrand models of Horn clauses, the results of [36] do not extend to Horn clauses like \(\gamma _3\) or \(\kappa _{\mathbf {stream}}\), or generally to Horn clauses modelled by the greatest complete Herbrand models. This shows that there is not just a need for coinductive proofs in Horn clause logic, but constructive coinductive proofs.
Problem 3. Incompleteness of circular unification for irregular coinductive data structures. Table 1 already showed some issues with incompleteness of circular unification. A more famous consequence of it is the failure of circular unification to capture irregular terms. This is illustrated by the following Horn clause, which defines the infinite stream of successive natural numbers.
The reductions for \(\mathbf {from}\, 0 \, y\) consist only of irregular (non-unifiable) formulae:

The composition of the computed substitutions would suggest an infinite term as answer: \(\mathbf {from}\, 0 \, (\mathrm {scons}\ 0\ (\mathrm {scons}\ (s \, 0)\ \ldots ))\). However, circular unification no longer helps to compute this answer, and CoLP fails. Thus, there is a need for more general operational semantics that allows irregular coinductive structures.
A New Theory of Coinductive Proof Search in Horn Clause Logic
In this paper, we aim to give a principled and general theory that resolves the three problems above. This theory establishes a constructive foundation for coinductive resolution and allows us to give proof-theoretic characterisations of the approaches that have been proposed throughout the literature.
To solve Problem 1, we follow the footsteps of the uniform proofs by Miller et al. [53, 54], who gave a general proof-theoretic account of resolution in first-order Horn clause logic (fohc) and three extensions: first-order hereditary Harrop clauses (fohh), higher-order Horn clauses (hohc), and higher-order hereditary Harrop clauses (hohh). In Sect. 3, we extend uniform proofs with a general coinduction proof principle. The resulting framework is called coinductive uniform proofs (CUP). We show how the coinductive extensions of the four logics of Miller et al., which we name co-fohc, co-fohh, co-hohc and co-hohh, give a precise proof-theoretic characterisation to the different kinds of coinduction described in the literature. For example, coinductive proofs involving the clauses \(\gamma _1\) and \(\gamma _2\) belong to co-fohc and co-fohh, respectively. However, proofs involving clauses like \(\gamma _3\) or \(\kappa _{\mathbf {stream}}\) require in addition fixed point terms to express infinite data. These extentions are denoted by  ,
,  ,
,  and
and  .
.
Section 3 shows that this yields the cube in Fig. 1, where the arrows show the increase in logical strength. The invariant search for regular infinite objects done in CoLP is fully described by the logic  , including proofs for clauses like \(\gamma _3\) and \(\kappa _{\mathbf {stream}}\). An important consequence is that CUP is complete for \(\gamma _1\), \(\gamma _2\), and \(\gamma _3\), e.g. \(p \, a\) is provable from \(\gamma _2\) in CUP, but not in CoLP.
, including proofs for clauses like \(\gamma _3\) and \(\kappa _{\mathbf {stream}}\). An important consequence is that CUP is complete for \(\gamma _1\), \(\gamma _2\), and \(\gamma _3\), e.g. \(p \, a\) is provable from \(\gamma _2\) in CUP, but not in CoLP.
In tackling Problem 3, we will find that the irregular proofs, such as those for \(\kappa _{\mathbf {from}}\), can be given in  . The stream of successive numbers can be defined as a higher-order fixed point term
. The stream of successive numbers can be defined as a higher-order fixed point term  , and the proposition \(\forall x. \, \mathbf {from}\, x \, (s_\mathrm {fr}\, x)\) is provable in
, and the proposition \(\forall x. \, \mathbf {from}\, x \, (s_\mathrm {fr}\, x)\) is provable in  . This requires the use of higher-order syntax, fixed point terms and the goals of universal shape, which become available in the syntax of Hereditary Harrop logic.
. This requires the use of higher-order syntax, fixed point terms and the goals of universal shape, which become available in the syntax of Hereditary Harrop logic.
In order to solve Problem 2 and to expose the constructive nature of the resulting proof systems, we present in Sect. 4 a coinductive extension of first-order intuitionistic logic and its sequent calculus. This extension ( ) is based on the so-called later modality (or Löb modality) known from provability logic [16, 71], type theory [8, 58] and domain theory [20]. However, our way of using the later modality to control recursion in first-order proofs is new and builds on [13, 14]. In the same section we also show that CUP is sound relative to
) is based on the so-called later modality (or Löb modality) known from provability logic [16, 71], type theory [8, 58] and domain theory [20]. However, our way of using the later modality to control recursion in first-order proofs is new and builds on [13, 14]. In the same section we also show that CUP is sound relative to  , which gives us a handle on the constructive content of CUP. This yields, among other consequences, a constructive interpretation of CoLP proofs.
, which gives us a handle on the constructive content of CUP. This yields, among other consequences, a constructive interpretation of CoLP proofs.
Section 5 is dedicated to showing soundness of both coinductive proof systems relative to complete Herbrand models [52]. The construction of these models is carried out by using coalgebras and category theory. This frees us from having to use topological methods and will simplify future extensions of the theory to, e.g., encompass typed logic programming. It also makes it possible to give original and constructive proofs of soundness for both CUP and  in Sect. 5. We finish the paper with discussion of related and future work.
in Sect. 5. We finish the paper with discussion of related and future work.
Originality of the Contribution
The results of this paper give a comprehensive characterisation of coinductive Horn clause theories from the point of view of proof search (by expressing coinductive proof search and resolution as coinductive uniform proofs), constructive proof theory (via a translation into an intuitionistic sequent calculus), and coalgebraic semantics (via coinductive Herbrand models and constructive soundness results). Several of the presented results have never appeared before: the coinductive extension of uniform proofs; characterisation of coinductive properties of Horn clause theories in higher-order logic with and without fixed point operators; coalgebraic and fibrational view on complete Herbrand models; and soundness of an intuitionistic logic with later modality relative to complete Herbrand models.
2 Preliminaries: Terms and Formulae
In this section, we set up notation and terminology for the rest of the paper. Most of it is standard, and blends together the notation used in [53] and [11].
Definition 1
We define the sets \(\mathbb {T}\) of types and \(\mathbb {P}\) of proposition types by the following grammars, where \(\iota \) and \(o\) are the base type and base proposition type.
We adapt the usual convention that \(\rightarrow \) binds to the right.
Definition 2
A term signature \(\varSigma \) is a set of pairs \(c : \tau \), where \(\tau \in \mathbb {T}\), and a predicate signature is a set \(\varPi \) of pairs \(p : \rho \) with \(\rho \in \mathbb {P}\). The elements in \(\varSigma \) and \(\varPi \) are called term symbols and predicate symbols, respectively. Given term and predicate signatures \(\varSigma \) and \(\varPi \), we refer to the pair \((\varSigma , \varPi )\) as signature. Let \(\mathrm {Var}\) be a countable set of variables, the elements of which we denote by \(x, y, \cdots \) We call a finite list \(\varGamma \) of pairs \(x : \tau \) of variables and types a context. The set \(\varLambda _{\varSigma }\) of (well-typed) terms over \(\varSigma \) is the collection of all M with  for some context \(\varGamma \) and type \(\tau \in \mathbb {T}\), where
for some context \(\varGamma \) and type \(\tau \in \mathbb {T}\), where  is defined inductively in Fig. 2. A term is called closed if
is defined inductively in Fig. 2. A term is called closed if  , otherwise it is called open. Finally, we let \(\varLambda ^{-}_{\varSigma }\) denote the set of all terms M that do not involve
, otherwise it is called open. Finally, we let \(\varLambda ^{-}_{\varSigma }\) denote the set of all terms M that do not involve  .
.
Definition 3
Let \((\varSigma , \varPi )\) be a signature. We say that \(\varphi \) is a (first-order) formula in context \(\varGamma \), if \(\varGamma \Vdash \varphi \) is inductively derivable from the rules in Fig. 3.
Definition 4
The reduction relation \(\longrightarrow \) on terms in \(\varLambda _{\varSigma }\) is given as the compatible closure (reduction under applications and binders) of \(\beta \)- and  -reduction:
-reduction:

We denote the reflexive, transitive closure of \(\longrightarrow \) by  . Two terms M and N are called convertible, if \(M \equiv N\), where \(\equiv \) is the equivalence closure of \(\longrightarrow \). Conversion of terms extends to formulae in the obvious way: if \(M_k \equiv M'_k\) for \(k = 1, \cdots , n\), then \(p \> M_1 \cdots M_n \equiv p \> M'_1 \cdots \> M'_n\).
. Two terms M and N are called convertible, if \(M \equiv N\), where \(\equiv \) is the equivalence closure of \(\longrightarrow \). Conversion of terms extends to formulae in the obvious way: if \(M_k \equiv M'_k\) for \(k = 1, \cdots , n\), then \(p \> M_1 \cdots M_n \equiv p \> M'_1 \cdots \> M'_n\).
We will use in the following that the above calculus features subject reduction and confluence, cf. [61]: if  and \(M \equiv N\), then
and \(M \equiv N\), then  ; and \(M \equiv N\) iff there is a term P, such that
; and \(M \equiv N\) iff there is a term P, such that  and
and  .
.
The order of a type \(\tau \in \mathbb {T}\) is given as usual by  and
and  . If
. If  , then the arity of \(\tau \) is given by
, then the arity of \(\tau \) is given by  and
and  . A signature \(\varSigma \) is called first-order, if for all \(f : \tau \in \varSigma \) we have
. A signature \(\varSigma \) is called first-order, if for all \(f : \tau \in \varSigma \) we have  . We let the arity of f then be
. We let the arity of f then be  and denote it by
and denote it by  .
.
Definition 5
The set of guarded base terms over a first-order signature \(\varSigma \) is given by the following type-driven rules.

General guarded terms are terms M, such that all  -subterms are guarded base terms, which means that they are generated by the following grammar.
-subterms are guarded base terms, which means that they are generated by the following grammar.
Finally, M is a first-order term over \(\varSigma \) with  if
if  and the types of all variables occurring in \(\varGamma \) are of order 0. We denote the set of guarded first-order terms M with
and the types of all variables occurring in \(\varGamma \) are of order 0. We denote the set of guarded first-order terms M with  by \(\varLambda ^{G,1}_{\varSigma }(\varGamma )\) and the set of guarded terms in \(\varGamma \) by \(\varLambda ^{G}_{\varSigma }(\varGamma )\). If \(\varGamma \) is empty, we just write \(\varLambda ^{G,1}_{\varSigma }\) and \(\varLambda ^{G}_{\varSigma }\), respectively.
by \(\varLambda ^{G,1}_{\varSigma }(\varGamma )\) and the set of guarded terms in \(\varGamma \) by \(\varLambda ^{G}_{\varSigma }(\varGamma )\). If \(\varGamma \) is empty, we just write \(\varLambda ^{G,1}_{\varSigma }\) and \(\varLambda ^{G}_{\varSigma }\), respectively.
Note that an important aspect of guarded terms is that no free variable occurs under a  -operator. Guarded base terms should be seen as specific fixed point terms that we will be able to unfold into potentially infinite trees. Guarded terms close guarded base terms under operations of the simply typed \(\lambda \)-calculus.
-operator. Guarded base terms should be seen as specific fixed point terms that we will be able to unfold into potentially infinite trees. Guarded terms close guarded base terms under operations of the simply typed \(\lambda \)-calculus.
Example 6
Let us provide a few examples that illustrate (first-order) guarded terms. We use the first-order signature  .
.
-
1.
Let
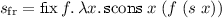 be the function that computes the streams of numerals starting at the given argument. It is easy to show that
be the function that computes the streams of numerals starting at the given argument. It is easy to show that  and so \(s_\mathrm {fr}\; 0 \in \varLambda ^{G,1}_{\varSigma }\).
and so \(s_\mathrm {fr}\; 0 \in \varLambda ^{G,1}_{\varSigma }\). -
2.
For the same signature \(\varSigma \) we also have
 . Thus \(x \in \varLambda ^{G,1}_{\varSigma }(x : \iota )\) and \(s \; x \in \varLambda ^{G,1}_{\varSigma }(x : \iota )\).
. Thus \(x \in \varLambda ^{G,1}_{\varSigma }(x : \iota )\) and \(s \; x \in \varLambda ^{G,1}_{\varSigma }(x : \iota )\). -
3.
We have
 , but \((x \; 0) \not \in \varLambda ^{G,1}_{\varSigma }(x : \iota \rightarrow \iota )\).
, but \((x \; 0) \not \in \varLambda ^{G,1}_{\varSigma }(x : \iota \rightarrow \iota )\).
The purpose of guarded terms is that these are productive, that is, we can reduce them to a term that either has a function symbol at the root or is just a variable. In other words, guarded terms have head normal forms: We say that a term M is in head normal form, if  for some \(f \in \varSigma \) or if \(M = x\) for some variable x. The following lemma is a technical result that is needed to show in Lemma 8 that all guarded terms have a head normal form.
for some \(f \in \varSigma \) or if \(M = x\) for some variable x. The following lemma is a technical result that is needed to show in Lemma 8 that all guarded terms have a head normal form.
Lemma 7
Let M and N be guarded base terms with  and
and  . Then
. Then  is a guarded base term with
is a guarded base term with  .
.
Lemma 8
If M is a first-order guarded term with \(M \in \varLambda ^{G,1}_{\varSigma }(\varGamma )\), then M reduces to a unique head normal form. This means that either (i) there is a unique \(f \in \varSigma \) and terms  with
with  and
and  , and for all L if
, and for all L if  , then
, then  ; or (ii)
; or (ii)  for some \(x : \iota \in \varGamma \).
for some \(x : \iota \in \varGamma \).
We end this section by introducing the notion of an atom and refinements thereof. This will enable us to define the different logics and thereby to analyse the strength of coinduction hypotheses, which we promised in the introduction.
Definition 9
A formula \(\varphi \) of the shape \(\top \) or \(p \; M_1 \cdots \; M_n\) is an atom and a
-
first-order atom, if p and all the terms \(M_i\) are first-order;
-
guarded atom, if all terms \(M_i\) are guarded; and
-
simple atom, if all terms \(M_i\) are non-recursive, that is, are in \(\varLambda ^{-}_{\varSigma }\).
First-order, guarded and simple atoms are denoted by \(\mathrm {At}_1\),  and
and  . We denote conjunctions of these predicates by
. We denote conjunctions of these predicates by  and
and  .
.
Note that the restriction for \(\mathrm {At}^g_{\omega }\) only applies to fixed point terms. Hence, any formula that contains terms without  is already in
is already in  and
and  . Since these notions are rather subtle, we give a few examples
. Since these notions are rather subtle, we give a few examples
Example 10
We list three examples of first-order atoms.
-
1.
For \(x : \iota \) we have \(\mathbf {stream}\; x \in \mathrm {At}_1\), but there are also “garbage” formulae like “
 ” in \(\mathrm {At}_1\). Examples of atoms that are not first-order are \(p \; M\), where \(p : (\iota \rightarrow \iota ) \rightarrow o\) or
” in \(\mathrm {At}_1\). Examples of atoms that are not first-order are \(p \; M\), where \(p : (\iota \rightarrow \iota ) \rightarrow o\) or  .
. -
2.
Our running example “\(\mathbf {from}\; 0 \; (s_\mathrm {fr}\; 0)\)” is a first-order guarded atom in \(\mathrm {At}_1^g\).
-
3.
The formulae in \(\mathrm {At}_1^s\) may not contain recursion and higher-order features. However, the atoms of Horn clauses in a logic program fit in here.
3 Coinductive Uniform Proofs
This section introduces the eight logics of the coinductive uniform proof framework announced and motivated in the introduction. The major difference of uniform proofs with, say, a sequent calculus is the “uniformity” property, which means that the choice of the application of each proof rule is deterministic and all proofs are in normal form (cut free). This subsumes the operational semantics of resolution, in which the proof search is always goal directed. Hence, the main challenge, that we set out to solve in this section, is to extend the uniform proof framework with coinduction, while preserving this valuable operational property.
We begin by introducing the different goal formulae and definite clauses that determine the logics that were presented in the cube for coinductive uniform proofs in the introduction. These clauses and formulae correspond directly to those of the original work on uniform proofs [53] with the only difference being that we need to distinguish atoms with and without fixed point terms. The general idea is that goal formulae (G-formulae) occur on the right of a sequent, thus are the goal to be proved. Definite clauses (D-formulae), on the other hand, are selected from the context as assumptions. This will become clear once we introduce the proof system for coinductive uniform proofs.
Definition 11
Let \(D_i\) be generated by the following grammar with  .
.

The sets of definite clauses (D-formulae) and goals (G-formulae) of the four logics  , \(\textit{co-fohh}\), \(\textit{co-hohc}\), \(\textit{co-hohh}\) are the well-formed formulae of the corresponding shapes defined in Table 2. For the variations
, \(\textit{co-fohh}\), \(\textit{co-hohc}\), \(\textit{co-hohh}\) are the well-formed formulae of the corresponding shapes defined in Table 2. For the variations  etc. of these logics with fixed point terms, we replace upper index “s” with “g” everywhere in Table 2. A D-formula of the shape
etc. of these logics with fixed point terms, we replace upper index “s” with “g” everywhere in Table 2. A D-formula of the shape  is called H-formula or Horn clause if \(A_k \in \mathrm {At}_1^s\), and \(H^g\)-formula if \(A_k \in \mathrm {At}_1^g\). Finally, a logic program (or program) P is a set of H-formulae. Note that any set of D-formulae in fohc can be transformed into an intuitionistically equivalent set of H-formulae [53].
is called H-formula or Horn clause if \(A_k \in \mathrm {At}_1^s\), and \(H^g\)-formula if \(A_k \in \mathrm {At}_1^g\). Finally, a logic program (or program) P is a set of H-formulae. Note that any set of D-formulae in fohc can be transformed into an intuitionistically equivalent set of H-formulae [53].
We are now ready to introduce the coinductive uniform proofs. Such proofs are composed of two parts: an outer coinduction that has to be at the root of a proof tree, and the usual the usual uniform proofs by Miller et al. [54]. The latter are restated in Fig. 4. Of special notice is the rule \(\textsc {decide}\) that mimics the operational behaviour of resolution in logic programming, by choosing a clause D from the given program to resolve against. The coinduction is started by the rule co-fix in Fig. 5. Our proof system mimics the typical recursion with a guard condition found in coinductive programs and proofs [5, 8, 19, 31, 40]. This guardedness condition is formalised by applying the guarding modality \({\langle \_\rangle }\) on the formula being proven by coinduction and the proof rules that allow us to distribute the guard over certain logical connectives, see Fig. 5. The guarding modality may be discharged only if the guarded goal was resolved against a clause in the initial program or any hypothesis, except for the coinduction hypotheses. This is reflected in the rule  , where we may only pick a clause from P, and is in contrast to the rule \(\textsc {decide}\), in which we can pick any hypothesis. The proof may only terminate with the \(\textsc {initial}\) step if the goal is no longer guarded.
, where we may only pick a clause from P, and is in contrast to the rule \(\textsc {decide}\), in which we can pick any hypothesis. The proof may only terminate with the \(\textsc {initial}\) step if the goal is no longer guarded.
Note that the  rule introduces a goal as a new hypothesis. Hence, we have to require that this goal is also a definite clause. Since coinduction hypotheses play such an important role, they deserve a separate definition.
rule introduces a goal as a new hypothesis. Hence, we have to require that this goal is also a definite clause. Since coinduction hypotheses play such an important role, they deserve a separate definition.
Definition 12
Given a language L from Table 2, a formula \(\varphi \) is a  of L if \(\varphi \) simultaneously is a D- and a G-formula of L.
of L if \(\varphi \) simultaneously is a D- and a G-formula of L.
Note that the  of co-fohc and co-fohh can be transformed into equivalent H- or \(H^g\)-formulae, since any
of co-fohc and co-fohh can be transformed into equivalent H- or \(H^g\)-formulae, since any  is a D-formula.
is a D-formula.
Let us now formally introduce the coinductive uniform proof system.
Definition 13
Let P and \(\varDelta \) be finite sets of, respectively, definite clauses and  , over the signature \(\varSigma \), and suppose that G is a goal and \(\varphi \) is a
, over the signature \(\varSigma \), and suppose that G is a goal and \(\varphi \) is a  . A sequent is either a uniform provability sequent of the form
. A sequent is either a uniform provability sequent of the form  or
or  as defined in Fig. 4, or it is a coinductive uniform provability sequent of the form
as defined in Fig. 4, or it is a coinductive uniform provability sequent of the form  as defined in Fig. 5. Let L be a language from Table 2. We say that \(\varphi \) is coinductively provable in L, if P is a set of D-formulae in L, \(\varphi \) is a
as defined in Fig. 5. Let L be a language from Table 2. We say that \(\varphi \) is coinductively provable in L, if P is a set of D-formulae in L, \(\varphi \) is a  in L and
in L and  holds.
holds.
The logics we have introduced impose different syntactic restrictions on D- and G-formulae, and will therefore admit coinduction goals of different strength. This ability to explicitly use stronger coinduction hypotheses within a goal-directed search was missing in CoLP, for example. And it allows us to account for different coinductive properties of Horn clauses as described in the introduction. We finish this section by illustrating this strengthening.
The first example is one for the logic co-fohc, in which we illustrate the framework on the problem of type class resolution.
Example 14
Let us restate the Haskell type class inference problem discussed in the introduction in terms of Horn clauses:

To prove \(\mathbf {eq}\ (\mathrm {odd}\ \mathrm {i})\) for this set of Horn clauses, it is sufficient to use this formula directly as coinduction hypothesis, as shown in Fig. 6. Note that this formula is indeed a  of co-fohc, hence we find ourselves in the simplest scenario of coinductive proof search. In Table 1, \(\gamma _1\) is a representative for this kind of coinductive proofs with simplest atomic goals.
of co-fohc, hence we find ourselves in the simplest scenario of coinductive proof search. In Table 1, \(\gamma _1\) is a representative for this kind of coinductive proofs with simplest atomic goals.
It was pointed out in [37] that Haskell’s type class inference can also give rise to irregular corecursion. Such cases may require the more general coinduction hypothesis (e.g. universal and/or implicative) of co-fohh or co-hohh. The below set of Horn clauses is a simplified representation of a problem given in [37]:

Trying to prove \(\mathbf {eq}\; (s \; \mathrm {i})\) by using \(\mathbf {eq}\; (s \; \mathrm {i})\) directly as a coinduction hypothesis is deemed to fail, as the coinductive proof search is irregular and this coinduction hypothesis would not be applicable in any guarded context. But it is possible to prove \(\mathbf {eq}\; (s \; \mathrm {i})\) as a corollary of another theorem: \(\forall x. \,(\mathbf {eq}\; x) \rightarrow \mathbf {eq}\; (s \; x)\). Using this formula as coinduction hypothesis leads to a successful proof, which we omit here. From this more general goal, we can derive the original goal by instantiating the quantifier with \(\mathrm {i}\) and eliminating the implication with \(\kappa _{\mathrm {i}}\). This second derivation is sound with respect to the models, as we show in Theorem 34.
We encounter \(\gamma _2\) from Table 1 in a similar situation: To prove \(p \, a\), we first have to prove \(\forall x. \,p \ x\) in co-fohh, and then obtain \(p \ a\) as a corollary by appealing to Theorem 34. The next example shows that we can cover all cases in Table 1 by providing a proof in  that involves irregular recursive terms.
that involves irregular recursive terms.
Example 15
Recall the clause \(\forall x \; y. \, \mathbf {from}\; (s\; x) \; y \rightarrow \mathbf {from}\; x \; (\mathrm {scons}\; x \; y)\) that we named \(\kappa _{\mathbf {from}}\) in the introduction. Proving \(\exists y. \, \mathbf {from}\; 0 \; y\) is again not possible directly. Instead, we can use the term  from Example 6 and prove \(\forall x. \, \mathbf {from}\; x \; (s_\mathrm {fr}\; x)\) coinductively, as shown in Fig. 7. This formula gives a coinduction hypothesis of sufficient generality. Note that the correct coinduction hypothesis now requires the fixed point definition of an infinite stream of successive numbers and universal quantification in the goal. Hence the need for the richer language of
from Example 6 and prove \(\forall x. \, \mathbf {from}\; x \; (s_\mathrm {fr}\; x)\) coinductively, as shown in Fig. 7. This formula gives a coinduction hypothesis of sufficient generality. Note that the correct coinduction hypothesis now requires the fixed point definition of an infinite stream of successive numbers and universal quantification in the goal. Hence the need for the richer language of  . From this more general goal we can derive our initial goal \(\exists \ y. \mathbf {from}\; 0 \; y\) by instantiating y with \(s_\mathrm {fr}\; 0\).
. From this more general goal we can derive our initial goal \(\exists \ y. \mathbf {from}\; 0 \; y\) by instantiating y with \(s_\mathrm {fr}\; 0\).
There are examples of coinductive proofs that require a fixed point definition of an infinite stream, but do not require the syntax of higher-order terms or hereditary Harrop formulae. Such proofs can be performed in the  logic. A good example is a proof that the stream of zeros satisfies the Horn clause theory defining the predicate \(\mathbf {stream}\) in the introduction. The goal \((\mathbf {stream}\ s_{0})\), with
logic. A good example is a proof that the stream of zeros satisfies the Horn clause theory defining the predicate \(\mathbf {stream}\) in the introduction. The goal \((\mathbf {stream}\ s_{0})\), with  can be proven directly by coinduction. Similarly, one can type self-application with the infinite type
can be proven directly by coinduction. Similarly, one can type self-application with the infinite type  for some given type b. The proof for
for some given type b. The proof for  is then in
is then in  . Finally, the clause \(\gamma _3\) is also in this group. More generally, circular unifiers obtained from CoLP’s [41] loop detection yield immediately guarded fixed point terms, and thus CoLP corresponds to coinductive proofs in the logic
. Finally, the clause \(\gamma _3\) is also in this group. More generally, circular unifiers obtained from CoLP’s [41] loop detection yield immediately guarded fixed point terms, and thus CoLP corresponds to coinductive proofs in the logic  . A general discussion of Horn clause theories that describe infinite objects was given in [48], where the above logic programs were identified as being productive.
. A general discussion of Horn clause theories that describe infinite objects was given in [48], where the above logic programs were identified as being productive.
4 Coinductive Uniform Proofs and Intuitionistic Logic
In the last section, we introduced the framework of coinductive uniform proofs, which gives an operational account to proofs for coinductively interpreted logic programs. Having this framework at hand, we need to position it in the existing ecosystem of logical systems. The goal of this section is to prove that coinductive uniform proofs are in fact constructive. We show this by first introducing an extension of intuitionistic first-order logic that allows us to deal with recursive proofs for coinductive predicates. Afterwards, we show that coinductive uniform proofs are sound relative to this logic by means of a proof tree translation. The model-theoretic soundness proofs for both logics will be provided in Sect. 5.
We begin by introducing an extension of intuitionistic first-order logic with the so-called later modality, written  . This modality is the essential ingredient that allows us to equip proofs with a controlled form of recursion. The later modality stems originally from provability logic, which characterises transitive, well-founded Kripke frames [30, 72], and thus allows one to carry out induction without an explicit induction scheme [16]. Later, the later modality was picked up by the type-theoretic community to control recursion in coinductive programming [8, 9, 21, 56, 58], mostly with the intent to replace syntactic guardedness checks for coinductive definitions by type-based checks of well-definedness.
. This modality is the essential ingredient that allows us to equip proofs with a controlled form of recursion. The later modality stems originally from provability logic, which characterises transitive, well-founded Kripke frames [30, 72], and thus allows one to carry out induction without an explicit induction scheme [16]. Later, the later modality was picked up by the type-theoretic community to control recursion in coinductive programming [8, 9, 21, 56, 58], mostly with the intent to replace syntactic guardedness checks for coinductive definitions by type-based checks of well-definedness.
Formally, the logic  is given by the following definition.
is given by the following definition.
Definition 16
The formulae of  are given by Definition 3 and the rule:
are given by Definition 3 and the rule:

Conversion extends to these formulae in the obvious way. Let \(\varphi \) be a formula and \(\varDelta \) a sequence of formulae in  . We say \(\varphi \) is provable in context \(\varGamma \) under the assumptions \(\varDelta \) in
. We say \(\varphi \) is provable in context \(\varGamma \) under the assumptions \(\varDelta \) in  , if
, if  holds. The provability relation \(\vdash \) is thereby given inductively by the rules in Figs. 8 and 9.
holds. The provability relation \(\vdash \) is thereby given inductively by the rules in Figs. 8 and 9.
The rules in Fig. 8 are the usual rules for intuitionistic first-order logic and should come at no surprise. More interesting are the rules in Fig. 9, where the rule  introduces recursion into the proof system. Furthermore, the rule
introduces recursion into the proof system. Furthermore, the rule  allows us to to distribute the later modality over implication, and consequently over conjunction and universal quantification. This is essential in the translation in Theorem 18 below. Finally, the rule
allows us to to distribute the later modality over implication, and consequently over conjunction and universal quantification. This is essential in the translation in Theorem 18 below. Finally, the rule  gives us the possibility to proceed without any recursion, if necessary.
gives us the possibility to proceed without any recursion, if necessary.
Note that so far it is not possible to use the assumption  introduced in the
introduced in the  -rule. The idea is that the formulae of a logic program provide us the obligations that we have to prove, possibly by recursion, in order to prove a coinductive predicate. This is cast in the following definition.
-rule. The idea is that the formulae of a logic program provide us the obligations that we have to prove, possibly by recursion, in order to prove a coinductive predicate. This is cast in the following definition.
Definition 17
Given an \(H^g\)-formula \(\varphi \) of the shape  , we define its guarding
, we define its guarding  to be
to be  . For a logic program P, we define its guarding
. For a logic program P, we define its guarding  by guarding each formula in P.
by guarding each formula in P.
The translation given in Definition 17 of a logic program into formulae that admit recursion corresponds unfolding a coinductive predicate, cf. [14]. We show now how to transform a coinductive uniform proof tree into a proof tree in  , such that the recursion and guarding mechanisms in both logics match up.
, such that the recursion and guarding mechanisms in both logics match up.
Theorem 18
If P is a logic program over a first-order signature \(\varSigma \) and the sequent  is provable in
is provable in  , then
, then  is provable in
is provable in  .
.
To prove this theorem, one uses that each coinductive uniform proof tree starts with an initial tree that has an application of the  -rule at the root and that eliminates the guard by using the rules in Fig. 5. At the leaves of this tree, one finds proof trees that proceed only by means of the rules in Fig. 4. The initial tree is then translated into a proof tree in
-rule at the root and that eliminates the guard by using the rules in Fig. 5. At the leaves of this tree, one finds proof trees that proceed only by means of the rules in Fig. 4. The initial tree is then translated into a proof tree in  that starts with an application of the
that starts with an application of the  -rule, which corresponds to the
-rule, which corresponds to the  -rule, and that simultaneously transforms the coinduction hypothesis and applies introduction rules for conjunctions etc. This ensures that we can match the coinduction hypothesis with the guarded formulae of the program P.
-rule, and that simultaneously transforms the coinduction hypothesis and applies introduction rules for conjunctions etc. This ensures that we can match the coinduction hypothesis with the guarded formulae of the program P.
The results of this section show that it is irrelevant whether the guarding modality is used on the right (CUP-style) or on the left ( -style), as the former can be translated into the latter. However, CUP uses the guarding on the right to preserve proof uniformity, whereas
-style), as the former can be translated into the latter. However, CUP uses the guarding on the right to preserve proof uniformity, whereas  extends a general sequent calculus. Thus, to obtain the reverse translation, we would have to have an admissible cut rule in CUP. The main ingredient to such a cut rule is the ability to prove several coinductive statements simultaneously. This is possible in CUP by proving the conjunction of these statements. Unfortunately, we cannot eliminate such a conjunction into one of its components, since this would require non-deterministic guessing in the proof construction, which in turn breaks uniformity. Thus, we leave a solution of this problem for future work.
extends a general sequent calculus. Thus, to obtain the reverse translation, we would have to have an admissible cut rule in CUP. The main ingredient to such a cut rule is the ability to prove several coinductive statements simultaneously. This is possible in CUP by proving the conjunction of these statements. Unfortunately, we cannot eliminate such a conjunction into one of its components, since this would require non-deterministic guessing in the proof construction, which in turn breaks uniformity. Thus, we leave a solution of this problem for future work.
5 Herbrand Models and Soundness
In Sect. 4 we showed that coinductive uniform proofs are sound relative to the intuitionistic logic  . This gives us a handle on the constructive nature of coinductive uniform proofs. Since
. This gives us a handle on the constructive nature of coinductive uniform proofs. Since  is a non-standard logic, we still need to provide semantics for that logic. We do this by interpreting in Sect. 5.4 the formulae of
is a non-standard logic, we still need to provide semantics for that logic. We do this by interpreting in Sect. 5.4 the formulae of  over the well-known (complete) Herbrand models and prove the soundness of the accompanying proof system with respect to these models. Although we obtain soundness of coinductive uniform proofs over Herbrand models from this, this proof is indirect and does not give a lot of information about the models captured by the different calculi co-fohc etc. For this reason, we will give in Sect. 5.3 a direct soundness proof for coinductive uniform proofs. We also obtain coinduction invariants from this proof for each of the calculi, which allows us to describe their proof strength.
over the well-known (complete) Herbrand models and prove the soundness of the accompanying proof system with respect to these models. Although we obtain soundness of coinductive uniform proofs over Herbrand models from this, this proof is indirect and does not give a lot of information about the models captured by the different calculi co-fohc etc. For this reason, we will give in Sect. 5.3 a direct soundness proof for coinductive uniform proofs. We also obtain coinduction invariants from this proof for each of the calculi, which allows us to describe their proof strength.
5.1 Coinductive Herbrand Models and Semantics of Terms
Before we come to the soundness proofs, we introduce in this section (complete) Herbrand models by using the terminology of final coalgebras. We then utilise this description to give operational and denotational semantics to guarded terms. These semantics show that guarded terms allow the description and computation of potentially infinite trees.
The coalgebraic approach has been proven very successful both in logic and programming [1, 75, 76]. We will only require very little category theoretical vocabulary and assume that the reader is familiar with the category \(\mathbf {Set}\) of sets and functions, and functors, see for example [12, 25, 50]. The terminology of algebras and coalgebras [4, 47, 64, 65] is given by the following definition.
Definition 19
A coalgebra for a functor \(F :\mathbf {Set}\rightarrow \mathbf {Set}\) is a map \(c :X \rightarrow FX\). Given coalgebras \(d : Y \rightarrow FY\) and \(c :X \rightarrow FX\), we say that a map \(h : Y \rightarrow X\) is a homomorphism \(d \rightarrow c\) if \(Fh \mathbin {\circ }d = c \mathbin {\circ }h\). We call a coalgebra \(c :X \rightarrow FX\) final, if for every coalgebra d there is a unique homomorphism \(h :d \rightarrow c\). We will refer to h as the coinductive extension of d.
The idea of (complete) Herbrand models is that a set of Horn clauses determines for each predicate symbol a set of potentially infinite terms. Such terms are (potentially infinite) trees, whose nodes are labelled by function symbols and whose branching is given by the arity of these function symbols. To be able to deal with open terms, we will allow such trees to have leaves labelled by variables. Such trees are a final coalgebra for a functor determined by the signature.
Definition 20
Let \(\varSigma \) be first-order signature. The extension of a first-order signature \(\varSigma \) is a (polynomial) functor [38]  given by
given by

where  is defined in Sect. 2 and \(X^n\) is the n-fold product of X. We define for a set V a functor
is defined in Sect. 2 and \(X^n\) is the n-fold product of X. We define for a set V a functor  by
by  , where \(+\) is the coproduct (disjoint union) in \(\mathbf {Set}\).
, where \(+\) is the coproduct (disjoint union) in \(\mathbf {Set}\).
To make sense of the following definition, we note that we can view \(\varPi \) as a signature and we thus obtain its extension  . Moreover, we note that the final coalgebra of
. Moreover, we note that the final coalgebra of  exists because
exists because  is a polynomial functor.
is a polynomial functor.
Definition 21
Let  be a first-order signature. The coterms over \(\varSigma \) are the final coalgebra
be a first-order signature. The coterms over \(\varSigma \) are the final coalgebra  . For brevity, we denote the coterms with no variables, i.e. \(\varSigma ^{\infty }(\emptyset )\), by
. For brevity, we denote the coterms with no variables, i.e. \(\varSigma ^{\infty }(\emptyset )\), by  , and call it the (complete) Herbrand universe and its elements ground coterms. Finally, we let the (complete) Herbrand base \(\mathcal {B}^{\infty }\) be the set
, and call it the (complete) Herbrand universe and its elements ground coterms. Finally, we let the (complete) Herbrand base \(\mathcal {B}^{\infty }\) be the set  .
.
The construction \(\varSigma ^{\infty }(V)\) gives rise to a functor \(\varSigma ^{\infty } :\mathbf {Set}\rightarrow \mathbf {Set}\), called the free completely iterative monad [5]. If there is no ambiguity, we will drop the injections \(\kappa _i\) when describing elements of \(\varSigma ^{\infty }(V)\). Note that \(\varSigma ^{\infty }(V)\) is final with property that for every \(s \in \varSigma ^{\infty }(V)\) either there are \(f \in \varSigma \) and  with
with  , or there is \(x \in V\) with
, or there is \(x \in V\) with  . Finality allows us to specify unique maps into \(\varSigma ^{\infty }(V)\) by giving a coalgebra
. Finality allows us to specify unique maps into \(\varSigma ^{\infty }(V)\) by giving a coalgebra  . In particular, one can define for each \(\theta :V \rightarrow \varSigma ^{\infty }\) the substitution \(t[\theta ]\) of variables in the coterm t by \(\theta \) as the coinductive extension of the following coalgebra.
. In particular, one can define for each \(\theta :V \rightarrow \varSigma ^{\infty }\) the substitution \(t[\theta ]\) of variables in the coterm t by \(\theta \) as the coinductive extension of the following coalgebra.

Now that we have set up the basic terminology of coalgebras, we can give semantics to guarded terms from Definition 5. The idea is that guarded terms guarantee that we can always compute with them so far that we find a function symbol in head position, see Lemma 8. This function symbol determines then the label and branching of a node in the tree generated by a guarded term. If the computation reaches a constant or a variable, then we stop creating the tree at the present branch. This idea is captured by the following lemma.
Lemma 22
There is a map \([\![-]\!]_1 :\varLambda ^{G,1}_{\varSigma }(\varGamma ) \rightarrow \varSigma ^{\infty }(\varGamma )\) that is unique with
-
1.
if \(M \equiv N\), then \([\![M]\!]_1 = [\![N]\!]_1\), and
-
2.
for all M, if
 then
then  , and if
, and if  then
then  .
.
Proof
(sketch). By Lemma 8, we can define a coalgebra on the quotient of guarded terms by convertibility  with
with  and \(c[M] = x\) if
and \(c[M] = x\) if  . This yields a homomorphism \(h :{\varLambda ^{G,1}_{\varSigma }(\varGamma )}/\!{\scriptstyle \equiv } \rightarrow \varSigma ^{\infty }(\varGamma )\) and we can define \([\![-]\!]_1 = h \mathbin {\circ }[-]\). The rest follows from uniqueness of h.
. This yields a homomorphism \(h :{\varLambda ^{G,1}_{\varSigma }(\varGamma )}/\!{\scriptstyle \equiv } \rightarrow \varSigma ^{\infty }(\varGamma )\) and we can define \([\![-]\!]_1 = h \mathbin {\circ }[-]\). The rest follows from uniqueness of h.
5.2 Interpretation of Basic Intuitionistic First-Order Formulae
In this section, we give an interpretation of the formulae in Definition 3, in which we restrict ourselves to guarded terms. This interpretation will be relative to models in the complete Herbrand universe. Since we later extend these models to Kripke models to be able to handle the later modality, we formulate these models already now in the language of fibrations [17, 46].
Definition 23
Let \(p :\mathbf {E}\rightarrow \mathbf {B}\) be a functor. Given an object \(I \in \mathbf {B}\), the fibre \(\mathbf {E}_I\) above I is the category of objects \(A \in \mathbf {E}\) with \(p(A) = I\) and morphisms \(f :A \rightarrow B\) with \(p(f) = \mathrm {id}_I\). The functor p is a (split) fibration if for every morphism \(u :I \rightarrow J\) in \(\mathbf {B}\) there is functor \(u^{*} :\mathbf {E}_J \rightarrow \mathbf {E}_I\), such that \(\mathrm {id}_I^{*} = \mathrm {Id}_{\mathbf {E}_I}\) and \((v \mathbin {\circ }u)^{*} = u^{*} \mathbin {\circ }v^{*}\). We call \(u^{*}\) the reindexing along u.
To give an interpretation of formulae, consider the following category \(\mathbf {Pred}\).
The functor \(\mathbb {P}:\mathbf {Pred}\rightarrow \mathbf {Set}\) with \(\mathbb {P}(X, P) = X\) and \(\mathbb {P}(f) = f\) is a split fibration, see [46], where the reindexing functor for \(f :X \rightarrow Y\) is given by taking preimages: \(f^{*}(Q) = f^{-1}(Q)\). Note that each fibre \(\mathbf {Pred}_X\) is isomorphic to the complete lattice of predicates over X ordered by set inclusion. Thus, we refer to this fibration as the predicate fibration.
Let us now expose the logical structure of the predicate fibration. This will allow us to conveniently interpret first-order formulae over this fibration, but it comes at the cost of having to introduce a good amount of category theoretical language. However, doing so will pay off in Sect. 5.4, where we will construct another fibration out of the predicate fibration. We can then use category theoretical results to show that this new fibration admits the same logical structure and allows the interpretation of the later modality.
The first notion we need is that of fibred products, coproducts and exponents, which will allow us to interpret conjunction, disjunction and implication.
Definition 24
A fibration \(p :\mathbf {E}\rightarrow \mathbf {B}\) has fibred finite products \((\mathbf {1}, \times )\), if each fibre \(\mathbf {E}_I\) has finite products \((\mathbf {1}_I, \times _I)\) and these are preserved by reindexing: for all \(f :I \rightarrow J\), we have \(f^{*}(\mathbf {1}_J) = \mathbf {1}_I\) and \(f^{*}(A \times _J B) = f^{*}(A) \times _I f^{*}(B)\). Fibred finite coproducts and exponents are defined analogously.
The fibration \(\mathbb {P}\) is a so-called first-order fibration, which allows us to interpret first-order logic, see [46, Def. 4.2.1].
Definition 25
A fibration \(p :\mathbf {E}\rightarrow \mathbf {B}\) is a first-order fibration ifFootnote 2
-
\(\mathbf {B}\) has finite products and the fibres of p are preorders;
-
p has fibred finite products \((\top , \wedge )\) and coproducts \((\bot , \vee )\) that distribute;
-
p has fibred exponents \(\rightarrow \); and
-
p has existential and universal quantifiers \(\exists _{I,J} \dashv \pi _{I,J}^{*} \dashv \forall _{I,J}\) for all projections \(\pi _{I,J} :I \times J \rightarrow I\).
A first-order \(\lambda \)-fibration is a first-order fibration with Cartesian closed base \(\mathbf {B}\).
The fibration \(\mathbb {P}:\mathbf {Pred}\rightarrow \mathbf {Set}\) is a first-order \(\lambda \)-fibration, as all its fibres are posets and \(\mathbf {Set}\) is Cartesian closed; \(\mathbb {P}\) has fibred finite products \((\top , \cap )\), given by \(\top _X = X\) and intersection; fibred distributive coproducts \((\emptyset , \cup )\); fibred exponents \(\mathrel {\Rightarrow }\), given by  ; and universal and existential quantifiers given for \(P \in \mathbf {Pred}_{X \times Y}\) by
; and universal and existential quantifiers given for \(P \in \mathbf {Pred}_{X \times Y}\) by

The purpose of first-order fibrations is to capture the essentials of first-order logic, while the \(\lambda \)-part takes care of higher-order features of the term language. In the following, we interpret types, contexts, guarded terms and formulae in the fibration \(\mathbb {P}:\mathbf {Pred}\rightarrow \mathbf {Set}\): We define for types \(\tau \) and context \(\varGamma \) sets  and
and  ; for guarded terms M with
; for guarded terms M with  we define a map
we define a map  in \(\mathbf {Set}\); and for a formula \(\varGamma \Vdash \varphi \) we give a predicate
in \(\mathbf {Set}\); and for a formula \(\varGamma \Vdash \varphi \) we give a predicate  .
.
The semantics of types and contexts are given inductively in the Cartesian closed category \(\mathbf {Set}\), where the base type \(\iota \) is interpreted as coterms, as follows.

We note that a coterm \(t \in \varSigma ^{\infty }(V)\) can be seen as a map \((\varSigma ^{\infty })^V \rightarrow \varSigma ^{\infty }\) by applying a substitution in \((\varSigma ^{\infty })^V\) to t: \(\sigma \mapsto t[\sigma ]\). In particular, the semantics of a guarded first-order term \(M \in \varLambda ^{G,1}_{\varSigma }(\varGamma )\) is equivalently a map  . We can now extend this map inductively to
. We can now extend this map inductively to  for all guarded terms \(M \in \varLambda ^{G}_{\varSigma }(\varGamma )\) with
for all guarded terms \(M \in \varLambda ^{G}_{\varSigma }(\varGamma )\) with  by
by

Lemma 26
The mapping  is a well-defined function from guarded terms to functions, such that
is a well-defined function from guarded terms to functions, such that  implies
implies  .
.
Since \(\mathbb {P}:\mathbf {Pred}\rightarrow \mathbf {Set}\) is a first-order fibration, we can interpret inductively all logical connectives of the formulae from Definition 3 in this fibration. The only case that is missing is the base case of predicate symbols. Their interpretation will be given over a Herbrand model that is constructed as the largest fixed point of an operator over all predicate interpretations in the Herbrand base. Both the operator and the fixed point are the subjects of the following definition.
Definition 27
We let the set of interpretations \(\mathcal {I}\) be the powerset \(\mathcal {P}({\mathcal {B}^{\infty }})\) of the complete Herbrand base. For \(I \in \mathcal {I}\) and \(p \in \varPi \), we denote by \(I{p}\) the interpretation of p in I (the fibre of I above p)

Given a set P of \(H^g\)-formulae, we define a monotone map  by
by

where \([\![-]\!]_1 [\theta ]\) is the extension of semantics and substitution from coterms to the Herbrand base by functoriality of  . The (complete) Herbrand model
. The (complete) Herbrand model  of P is the largest fixed point of
of P is the largest fixed point of  , which exists because \(\mathcal {I}\) is a complete lattice.
, which exists because \(\mathcal {I}\) is a complete lattice.
Given a formula \(\varphi \) with \(\varGamma \Vdash \varphi \) that contains only guarded terms, we define the semantics of \(\varphi \) in \(\mathbf {Pred}\) from an interpretation \(I \in \mathcal {I}\) inductively as follows.

Lemma 28
The mapping  is a well-defined function from formulae to predicates, such that \(\varGamma \Vdash \varphi \) implies
is a well-defined function from formulae to predicates, such that \(\varGamma \Vdash \varphi \) implies  or, equivalently,
or, equivalently,  .
.
This concludes the semantics of types, terms and formulae. We now turn to show that coinductive uniform proofs are sound for this interpretation.
5.3 Soundness of Coinductive Uniform Proofs for Herbrand Models
In this section, we give a direct proof of soundness for the coinductive uniform proof system from Sect. 3. Later, we will obtain another soundness result by combining the proof translation from Theorem 18 with the soundness of  (Theorems 39 and 42). The purpose of giving a direct soundness proof for uniform proofs is that it allows the extraction of a coinduction invariant, see Lemma 32.
(Theorems 39 and 42). The purpose of giving a direct soundness proof for uniform proofs is that it allows the extraction of a coinduction invariant, see Lemma 32.
The main idea is as follows. Given a formula \(\varphi \) and a uniform proof \(\pi \) for  , we construct an interpretation \(I \in \mathcal {I}\) that validates \(\varphi \), i.e.
, we construct an interpretation \(I \in \mathcal {I}\) that validates \(\varphi \), i.e.  , and that is contained in the complete Herbrand model
, and that is contained in the complete Herbrand model  . Combining these two facts, we obtain that
. Combining these two facts, we obtain that  , and thus the soundness of uniform proofs.
, and thus the soundness of uniform proofs.
To show that the constructed interpretation I is contained in  , we use the usual coinduction proof principle, as it is given in the following definition.
, we use the usual coinduction proof principle, as it is given in the following definition.
Definition 29
An invariant for \(K \in \mathcal {I}\) is a set \(I \in \mathcal {I}\), such that \(K \subseteq I\) and I is a  -invariant, that is,
-invariant, that is,  . If K has an invariant, then
. If K has an invariant, then  .
.
Thus, our goal is now to construct an interpretation together with an invariant. This invariant will essentially collect and iterate all the substitutions that appear in a proof. For this we need the ability to compose substitutions of coterms, which we derive from the monad [5] \((\varSigma ^{\infty }, \eta , \mu )\) with \(\mu :\varSigma ^{\infty }\varSigma ^{\infty } \Rightarrow \varSigma ^{\infty }\).
Definition 30
A (Kleisli-)substitution \(\theta \) from V to W, written  , is map \(V \rightarrow \varSigma ^{\infty }(W)\). Composition of
, is map \(V \rightarrow \varSigma ^{\infty }(W)\). Composition of  and
and  is given by
is given by
The notions in the following definition will allow us to easily organise and iterate the substitutions that occur in a uniform proof.
Definition 31
Let S be a set with  for some \(n \in \mathbb {N}\). We call the set \(S^{*}\) of lists over S the set of substitution identifiers. Suppose that we have substitutions
for some \(n \in \mathbb {N}\). We call the set \(S^{*}\) of lists over S the set of substitution identifiers. Suppose that we have substitutions  and
and  for each \(k \in S\). Then we can define a map
for each \(k \in S\). Then we can define a map  , which turns each substitution identifier into a substitution, by iteration from the right:
, which turns each substitution identifier into a substitution, by iteration from the right:
After introducing these notations, we can give the outline of the soundness proof for uniform proofs relative to the complete Herbrand model. Given an \(H^g\)-formula  , we note that a uniform proof \(\pi \) for
, we note that a uniform proof \(\pi \) for  starts with
starts with

where the eigenvariables in  are all distinct. Let \(\varSigma ^c\) be the signature
are all distinct. Let \(\varSigma ^c\) be the signature  and C the set of variables in
and C the set of variables in  . Suppose the following is a valid subtree of \(\pi \).
. Suppose the following is a valid subtree of \(\pi \).

This proof tree gives rise to a substitution  by
by  , which we call an agent of \(\pi \). We let \(D \subseteq \mathrm {At}_1^g\) be the set of atoms that are proven in \(\pi \):
, which we call an agent of \(\pi \). We let \(D \subseteq \mathrm {At}_1^g\) be the set of atoms that are proven in \(\pi \):

From the agents and atoms in \(\pi \) we extract an invariant for the goal formula.
Lemma 32
Suppose that \(\varphi \) is an \(H^g\)-formula of the form  and that there is a proof \(\pi \) for
and that there is a proof \(\pi \) for  . Let D be the proven atoms in \(\pi \) and \(\theta _0, \cdots , \theta _s\) be the agents of \(\pi \). Define
. Let D be the proven atoms in \(\pi \) and \(\theta _0, \cdots , \theta _s\) be the agents of \(\pi \). Define  and suppose further that \(I_1\) is an invariant for
and suppose further that \(I_1\) is an invariant for  . If we put
. If we put
then \(I_1 \cup I_2\) is an invariant for  .
.
Once we have Lemma 32 the following soundness theorem is easily proven.
Theorem 33
If \(\varphi \) is an \(H^g\)-formula and  , then
, then  .
.
Finally, we show that extending logic programs with coinductively proven lemmas is sound. This follows easily by coinduction.
Theorem 34
Let \(\varphi \) be an \(H^g\)-formula of the shape  , such that, for all substitutions \(\theta \) if
, such that, for all substitutions \(\theta \) if  , then
, then  . Then
. Then  implies
implies  , that is,
, that is,  is a conservative extension of P with respect to the Herbrand model.
is a conservative extension of P with respect to the Herbrand model.
As a corollary we obtain that, if there is a proof for  , then a proof for
, then a proof for  is sound with respect to
is sound with respect to  . Indeed, by Theorem 34 we have that
. Indeed, by Theorem 34 we have that  and by Theorem 33 that
and by Theorem 33 that  is sound with respect to
is sound with respect to  . Thus, the proof of
. Thus, the proof of  is also sound with respect to
is also sound with respect to  . We use this property implicitly in our running examples, and refer the reader to [15, 49] for proofs, further examples and discussion.
. We use this property implicitly in our running examples, and refer the reader to [15, 49] for proofs, further examples and discussion.
5.4 Soundness of  over Herbrand Models
over Herbrand Models
In this section, we demonstrate how the logic  can be interpreted over Herbrand models. Recall that we obtained a fixed point model from the monotone map
can be interpreted over Herbrand models. Recall that we obtained a fixed point model from the monotone map  on interpretations. In what follows, it is crucial that we construct the greatest fixed point of
on interpretations. In what follows, it is crucial that we construct the greatest fixed point of  by iteration, c.f. [6, 32, 77]: Let
by iteration, c.f. [6, 32, 77]: Let  be the class of all ordinals equipped with their (well-founded) order. We denote by
be the class of all ordinals equipped with their (well-founded) order. We denote by  the class of ordinals with their reversed order and define a monotone function
the class of ordinals with their reversed order and define a monotone function  , where we write the argument ordinal in the subscript, by
, where we write the argument ordinal in the subscript, by

Note that this definition is well-defined because < is well-founded and because  is monotone, see [14]. Since \(\mathcal {I}\) is a complete lattice, there is an ordinal \(\alpha \) such that
is monotone, see [14]. Since \(\mathcal {I}\) is a complete lattice, there is an ordinal \(\alpha \) such that  , at which point
, at which point  is the largest fixed point
is the largest fixed point  of
of  . In what follows, we will utilise this construction to give semantics to
. In what follows, we will utilise this construction to give semantics to  .
.
The fibration \(\mathbb {P}:\mathbf {Pred}\rightarrow \mathbf {Set}\) gives rise to another fibration as follows. We let \(\overline{\mathbf {Pred}}\) be the category of functors (monotone maps) with fixed predicate domain:

The fibration \(\overline{\mathbb {P}} :\mathbf {Pred}\rightarrow \mathbf {Set}\) is defined by evaluation at any ordinal (here 0), i.e. by \(\overline{\mathbb {P}}(u) = \mathbb {P}(u(0))\) and \(\overline{\mathbb {P}}(f) = (\mathbb {P}f)_0\), and reindexing along \(f :X \rightarrow Y\) by applying the reindexing of \(\mathbb {P}\) point-wise, i.e. by \(f^{\#}(u)_\alpha = f^{*}(u_\alpha )\).
Note that there is a (full) embedding \(K :\mathbf {Pred}\rightarrow \overline{\mathbf {Pred}}\) that is given by \(K(X, P) = (X, \overline{P})\) with \(\overline{P}_\alpha = P\). One can show [14] that \(\overline{\mathbb {P}}\) is again a first-order fibration and that it models the later modality, as in the following theorem.
Theorem 35
The fibration \(\overline{\mathbb {P}}\) is a first-order fibration. If necessary, we denote the first-order connectives by \(\dot{\top }\), \(\mathrel {\dot{\wedge }}\) etc. to distinguish them from those in \(\mathbf {Pred}\). Otherwise, we drop the dots. Finite (co)products and quantifiers are given point-wise, while for \(X \in \mathbf {Set}\) and \(u,v \in \overline{\mathbf {Pred}}_X\) exponents are given by
There is a fibred functor  with
with  given on objects by
given on objects by

and a natural transformation  from the identity functor to
from the identity functor to  . The functor
. The functor  preserves reindexing, products, exponents and universal quantification:
preserves reindexing, products, exponents and universal quantification:  ,
,  ,
,  ,
,  . Finally, for all \(X \in \mathbf {Set}\) and \(u \in \overline{\mathbf {Pred}}_X\), there is
. Finally, for all \(X \in \mathbf {Set}\) and \(u \in \overline{\mathbf {Pred}}_X\), there is  in \(\overline{\mathbf {Pred}}_X\).
in \(\overline{\mathbf {Pred}}_X\).
Using the above theorem, we can extend the interpretation of formulae to  as follows. Let
as follows. Let  be a descending sequence of interpretations. As before, we define the restriction of u to a predicate symbol \(p \in \varPi \) by
be a descending sequence of interpretations. As before, we define the restriction of u to a predicate symbol \(p \in \varPi \) by  . The semantics of formulae in
. The semantics of formulae in  as objects in \(\overline{\mathbf {Pred}}\) is given by the following iterative definition.
as objects in \(\overline{\mathbf {Pred}}\) is given by the following iterative definition.

The following lemma is the analogue of Lemma 28 for the interpretation of formulae without the later modality.
Lemma 36
The mapping  is a well-defined map from formulae in
is a well-defined map from formulae in  to sequences of predicates, such that \(\varGamma \Vdash \varphi \) implies
to sequences of predicates, such that \(\varGamma \Vdash \varphi \) implies  .
.
Lemma 37
All rules of  are sound with respect to the interpretation
are sound with respect to the interpretation  of formulae in \(\overline{\mathbf {Pred}}\), that is, if
of formulae in \(\overline{\mathbf {Pred}}\), that is, if  , then
, then  . In particular,
. In particular,  implies
implies  .
.
The following lemma shows that the guarding of a set of formulae is valid in the chain model that they generate.
Lemma 38
If \(\varphi \) is an H-formula in P, then  .
.
Combining this with soundness from Lemma 37, we obtain that provability in  relative to a logic program P is sound for the model of P.
relative to a logic program P is sound for the model of P.
Theorem 39
For all logic programs P, if  then
then  .
.
The final result of this section is to show that the descending chain model, which we used to interpret formulae of  , is sound and complete for the fixed point model, which we used to interpret the formulae of coinductive uniform proofs. This will be proved in Theorem 42 below. The easiest way to prove this result is by establishing a functor \(\overline{\mathbf {Pred}} \rightarrow \mathbf {Pred}\) that maps the chain
, is sound and complete for the fixed point model, which we used to interpret the formulae of coinductive uniform proofs. This will be proved in Theorem 42 below. The easiest way to prove this result is by establishing a functor \(\overline{\mathbf {Pred}} \rightarrow \mathbf {Pred}\) that maps the chain  to the model
to the model  , and that preserves and reflects truth of first-order formulae (Proposition 41). We will phrase the preservation of truth of first-order formulae by a functor by appealing to the following notion of fibrations maps, cf. [46, Def. 4.3.1].
, and that preserves and reflects truth of first-order formulae (Proposition 41). We will phrase the preservation of truth of first-order formulae by a functor by appealing to the following notion of fibrations maps, cf. [46, Def. 4.3.1].
Definition 40
Let \(p :\mathbf {E}\rightarrow \mathbf {B}\) and \(q :\mathbf {D} \rightarrow \mathbf {A}\) be fibrations. A fibration map \(p \rightarrow q\) is a pair \((F :\mathbf {E}\rightarrow \mathbf {D}, G :\mathbf {B}\rightarrow \mathbf {A})\) of functors, s.t. \(q \mathbin {\circ }F = G \mathbin {\circ }p\) and F preserves Cartesian morphisms: if \(f :X \rightarrow Y\) in \(\mathbf {E}\) is Cartesian over p(f), then F(f) is Cartesian over G(p(f)). (F, G) is a map of first-order (\(\lambda \) -)fibrations, if p and q are first-order (\(\lambda \)-)fibrations, and F and G preserve this structure.
Let us now construct a first-order \(\lambda \)-fibration map \(\overline{\mathbf {Pred}} \rightarrow \mathbf {Pred}\). We note that since every fibre of the predicate fibration is a complete lattice, for every chain \(u \in \overline{\mathbf {Pred}}_X\) there exists an ordinal \(\alpha \) at which u stabilises. This means that there is a limit \(\lim u\) of u in \(\mathbf {Pred}_X\), which is the largest subset of X, such that \(\forall \alpha . \, \lim u \subseteq u_\alpha \). This allows us to define a map  by
by

In the following proposition, we show that L gives us the ability to express first-order properties of limits equivalently through their approximating chains. This, in turn, provides soundness and completeness for the interpretation of the logic  over descending chains with respect to the largest Herbrand model.
over descending chains with respect to the largest Herbrand model.
Proposition 41
\(L :\overline{\mathbf {Pred}} \rightarrow \mathbf {Pred}\), as defined above, is a map of first-order fibrations. Furthermore, L is right-adjoint to the embedding \(K :\mathbf {Pred}\rightarrow \overline{\mathbf {Pred}}\). Finally, for each \(p \in \varPi \) and \(u \in \overline{\mathbf {Pred}}_{\mathcal {B}^{\infty }}\), we have  .
.
We get from Proposition 41 soundness and completeness of  for Herbrand models. More precisely, if \(\varphi \) is a formula of plain first-order logic (
for Herbrand models. More precisely, if \(\varphi \) is a formula of plain first-order logic ( -free), then its interpretation in the coinductive Herbrand model is true if and only if its interpretation over the chain approximation of the Herbrand model is true.
-free), then its interpretation in the coinductive Herbrand model is true if and only if its interpretation over the chain approximation of the Herbrand model is true.
Theorem 42
If \(\varphi \) is  -free (Definition 3) then
-free (Definition 3) then  if and only if
if and only if  .
.
Proof
(sketch). First, one shows for all  -free formulae \(\varphi \) that
-free formulae \(\varphi \) that  by induction on \(\varphi \) and using Proposition 41. Using this identity and \(K \dashv L\), the result is then obtained from the following adjoint correspondence.
by induction on \(\varphi \) and using Proposition 41. Using this identity and \(K \dashv L\), the result is then obtained from the following adjoint correspondence.

6 Conclusion, Related Work and the Future
In this paper, we provided a comprehensive theory of resolution in coinductive Horn-clause theories and coinductive logic programs. This theory comprises of a uniform proof system that features a form of guarded recursion and that provides operational semantics for proofs of coinductive predicates. Further, we showed how to translate proofs in this system into proofs for an extension of intuitionistic FOL with guarded recursion, and we provided sound semantics for both proof systems in terms of coinductive Herbrand models. The Herbrand models and semantics were thereby presented in a modern style that utilises coalgebras and fibrations to provide a conceptual view on the semantics.
Related Work. It may be surprising that automated proof search for coinductive predicates in first-order logic does not have a coherent and comprehensive theory, even after three decades [3, 60], despite all the attention that it received as programming [2, 29, 42, 44] and proof [33, 35, 39, 40, 45, 59, 64,65,66,67] method. The work that comes close to algorithmic proof search is the system CIRC [63], but it cannot handle general coinductive predicates and corecursive programming. Inductive and coinductive data types are also being added to SMT solvers [24, 62]. However, both CIRC and SMT solving are inherently based on classical logic and are therefore not suited to situations where proof objects are relevant, like programming, type class inference or (dependent) type theory. Moreover, the proposed solutions, just like those in [41, 69] can only deal with regular data, while our approach also works for irregular data, as we saw in the \(\mathbf {from}\)-example.
This paper subsumes Haskell type class inference [37, 51] and exposes that the inference presented in those papers corresponds to coinductive proofs in \(\textit{co-fohc}\) and \(\textit{co-hohh}\). Given that the proof systems proposed in this paper are constructive and that uniform proofs provide proofs (type inhabitants) in normal form, we could give a propositions-as-types interpretation to all eight coinductive uniform proof systems. This was done for \(\textit{co-fohc}\) and \(\textit{co-hohh}\) in [37], but we leave the remaining cube from the introduction for future work.
Future Work. There are several directions that we wish to pursue in the future. First, we know that CUP is incomplete for the presented models, as it is intuitionistic and it lacks an admissible cut rule. The first can be solved by moving to Kripke/Beth-models, as done by Clouston and Goré [30] for the propositional part of  . However, the admissible cut rule is more delicate. To obtain such a rule one has to be able to prove several propositions simultaneously by coinduction, as discussed at the end of Sect. 4. In general, completeness of recursive proof systems depends largely on the theory they are applied to, see [70] and [18]. However, techniques from cyclic proof systems [27, 68] may help. We also aim to extend our ideas to other situations like higher-order Horn clauses [28, 43] and interactive proof assistants [7, 10, 23, 31], typed logic programming, and logic programming that mix inductive and coinductive predicates.
. However, the admissible cut rule is more delicate. To obtain such a rule one has to be able to prove several propositions simultaneously by coinduction, as discussed at the end of Sect. 4. In general, completeness of recursive proof systems depends largely on the theory they are applied to, see [70] and [18]. However, techniques from cyclic proof systems [27, 68] may help. We also aim to extend our ideas to other situations like higher-order Horn clauses [28, 43] and interactive proof assistants [7, 10, 23, 31], typed logic programming, and logic programming that mix inductive and coinductive predicates.
Notes
- 1.
We follow the standard terminology of [74] and say that two formulae F and G form a cycle if \(F = G\), and a loop if \(F[\theta ] = G[\theta ]\) for some (possibly circular) unifier \(\theta \).
- 2.
Technically, the quantifiers should also fulfil the Beck-Chevalley and Frobenius conditions, and the fibration should admit equality. Since these are fulfilled in all our models and we do not need equality, we will not discuss them here.
References
Abbott, M., Altenkirch, T., Ghani, N.: Containers: constructing strictly positive types. TCS 342(1), 3–27 (2005). https://doi.org/10.1016/j.tcs.2005.06.002
Abel, A., Pientka, B., Thibodeau, D., Setzer, A.: Copatterns: programming infinite structures by observations. In: POPL 2013, pp. 27–38 (2013). https://doi.org/10.1145/2429069.2429075
Aczel, P.: Non-well-founded sets. Center for the Study of Language and Information, Stanford University (1988)
Aczel, P.: Algebras and coalgebras. In: Backhouse, R., Crole, R., Gibbons, J. (eds.) Algebraic and Coalgebraic Methods in the Mathematics of Program Construction. LNCS, vol. 2297, pp. 79–88. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-47797-7_3
Aczel, P., Adámek, J., Milius, S., Velebil, J.: Infinite trees and completely iterative theories: a coalgebraic view. TCS 300(1–3), 1–45 (2003). https://doi.org/10.1016/S0304-3975(02)00728-4
Adámek, J.: On final coalgebras of continuous functors. Theor. Comput. Sci. 294(1/2), 3–29 (2003). https://doi.org/10.1016/S0304-3975(01)00240-7
P.L. group on Agda: Agda Documentation. Technical report, Chalmers and Gothenburg University (2015). http://wiki.portal.chalmers.se/agda/, version 2.4.2.5
Appel, A.W., Melliès, P.A., Richards, C.D., Vouillon, J.: A very modal model of a modern, major, general type system. In: POPL, pp. 109–122. ACM (2007). https://doi.org/10.1145/1190216.1190235
Atkey, R., McBride, C.: Productive coprogramming with guarded recursion. In: ICFP, pp. 197–208. ACM (2013). https://doi.org/10.1145/2500365.2500597
Baelde, D., et al.: Abella: a system for reasoning about relational specifications. J. Formaliz. Reason. 7(2), 1–89 (2014). https://doi.org/10.6092/issn.1972-5787/4650
Barendregt, H., Dekkers, W., Statman, R.: Lambda Calculus with Types. Cambridge University Press, Cambridge (2013)
Barr, M., Wells, C.: Category Theory for Computing Science. Prentice Hall International Series in Computer Science, 2nd edn. Prentice Hall, Upper Saddle River (1995). http://www.tac.mta.ca/tac/reprints/articles/22/tr22abs.html
Basold, H.: Mixed inductive-coinductive reasoning: types, programs and logic. Ph.D. thesis, Radboud University Nijmegen (2018). http://hdl.handle.net/2066/190323
Basold, H.: Breaking the Loop: Recursive Proofs for Coinductive Predicates in Fibrations. ArXiv e-prints, February 2018. https://arxiv.org/abs/1802.07143
Basold, H., Komendantskaya, E., Li, Y.: Coinduction in uniform: foundations for corecursive proof search with horn clauses. Extended version of this paper. CoRR abs/1811.07644 (2018). http://arxiv.org/abs/1811.07644
Beklemishev, L.D.: Parameter free induction and provably total computable functions. TCS 224(1–2), 13–33 (1999). https://doi.org/10.1016/S0304-3975(98)00305-3
Bénabou, J.: Fibered categories and the foundations of naive category theory. J. Symb. Logic 50(1), 10–37 (1985). https://doi.org/10.2307/2273784
Berardi, S., Tatsuta, M.: Classical system of Martin-Löf’s inductive definitions is not equivalent to cyclic proof system. In: Esparza, J., Murawski, A.S. (eds.) FoSSaCS 2017. LNCS, vol. 10203, pp. 301–317. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-54458-7_18
Birkedal, L., Møgelberg, R.E.: Intensional type theory with guarded recursive types qua fixed points on universes. In: LICS, pp. 213–222. IEEE Computer Society (2013). https://doi.org/10.1109/LICS.2013.27
Birkedal, L., Møgelberg, R.E., Schwinghammer, J., Støvring, K.: First steps in synthetic guarded domain theory: step-indexing in the topos of trees. In: Proceedings of LICS 2011, pp. 55–64. IEEE Computer Society (2011). https://doi.org/10.1109/LICS.2011.16
Bizjak, A., Grathwohl, H.B., Clouston, R., Møgelberg, R.E., Birkedal, L.: Guarded dependent type theory with coinductive types. In: Jacobs, B., Löding, C. (eds.) FoSSaCS 2016. LNCS, vol. 9634, pp. 20–35. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49630-5_2. https://arxiv.org/abs/1601.01586
Bjørner, N., Gurfinkel, A., McMillan, K., Rybalchenko, A.: Horn clause solvers for program verification. In: Beklemishev, L.D., Blass, A., Dershowitz, N., Finkbeiner, B., Schulte, W. (eds.) Fields of Logic and Computation II. LNCS, vol. 9300, pp. 24–51. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-23534-9_2
Blanchette, J.C., Meier, F., Popescu, A., Traytel, D.: Foundational nonuniform (co)datatypes for Higher-Order Logic. In: LICS 2017, pp. 1–12. IEEE Computer Society (2017). https://doi.org/10.1109/LICS.2017.8005071
Blanchette, J.C., Peltier, N., Robillard, S.: Superposition with datatypes and codatatypes. In: Galmiche, D., Schulz, S., Sebastiani, R. (eds.) IJCAR 2018. LNCS (LNAI), vol. 10900, pp. 370–387. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-94205-6_25
Borceux, F.: Handbook of Categorical Algebra. Basic Category Theory, vol. 1. Cambridge University Press, Cambridge (2008)
Bottu, G., Karachalias, G., Schrijvers, T., Oliveira, B.C.D.S., Wadler, P.: Quantified class constraints. In: Haskell Symposium, pp. 148–161. ACM (2017). https://doi.org/10.1145/3122955.3122967
Brotherston, J., Simpson, A.: Sequent calculi for induction and infinite descent. J. Log. Comput. 21(6), 1177–1216 (2011). https://doi.org/10.1093/logcom/exq052
Burn, T.C., Ong, C.L., Ramsay, S.J.: Higher-order constrained horn clauses for verification. PACMPL 2(POPL), 11:1–11:28 (2018). https://doi.org/10.1145/3158099
Capretta, V.: General Recursion via Coinductive Types. Log. Methods Comput. Sci. 1(2), July 2005. https://doi.org/10.2168/LMCS-1(2:1)2005
Clouston, R., Goré, R.: Sequent calculus in the topos of trees. In: Pitts, A. (ed.) FoSSaCS 2015. LNCS, vol. 9034, pp. 133–147. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46678-0_9
Coquand, T.: Infinite objects in type theory. In: Barendregt, H., Nipkow, T. (eds.) TYPES 1993. LNCS, vol. 806, pp. 62–78. Springer, Heidelberg (1994). https://doi.org/10.1007/3-540-58085-9_72
Cousot, P., Cousot, R.: Constructive versions of Tarski’s fixed point theorems. Pac. J. Math. 82(1), 43–57 (1979). http://projecteuclid.org/euclid.pjm/1102785059
Dax, C., Hofmann, M., Lange, M.: A proof system for the linear time \({\mu }\)-calculus. In: Arun-Kumar, S., Garg, N. (eds.) FSTTCS 2006. LNCS, vol. 4337, pp. 273–284. Springer, Heidelberg (2006). https://doi.org/10.1007/11944836_26
van Emden, M., Kowalski, R.: The semantics of predicate logic as a programming language. J. Assoc. Comput. Mach. 23, 733–742 (1976). https://doi.org/10.1145/321978.321991
Endrullis, J., Hansen, H.H., Hendriks, D., Polonsky, A., Silva, A.: A coinductive framework for infinitary rewriting and equational reasoning. In: RTA 2015, pp. 143–159 (2015). https://doi.org/10.4230/LIPIcs.RTA.2015.143
Farka, F., Komendantskaya, E., Hammond, K.: Coinductive soundness of corecursive type class resolution. In: Hermenegildo, M.V., Lopez-Garcia, P. (eds.) LOPSTR 2016. LNCS, vol. 10184, pp. 311–327. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63139-4_18
Fu, P., Komendantskaya, E., Schrijvers, T., Pond, A.: Proof relevant corecursive resolution. In: Kiselyov, O., King, A. (eds.) FLOPS 2016. LNCS, vol. 9613, pp. 126–143. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-29604-3_9
Gambino, N., Kock, J.: Polynomial functors and polynomial monads. Math. Proc. Cambridge Phil. Soc. 154(1), 153–192 (2013). https://doi.org/10.1017/S0305004112000394
Giesl, J., et al.: Analyzing program termination and complexity automatically with AProVE. J. Autom. Reason. 58(1), 3–31 (2017). https://doi.org/10.1007/s10817-016-9388-y
Giménez, E.: Structural recursive definitions in type theory. In: Larsen, K.G., Skyum, S., Winskel, G. (eds.) ICALP 1998. LNCS, vol. 1443, pp. 397–408. Springer, Heidelberg (1998). https://doi.org/10.1007/BFb0055070
Gupta, G., Bansal, A., Min, R., Simon, L., Mallya, A.: Coinductive logic programming and its applications. In: Dahl, V., Niemelä, I. (eds.) ICLP 2007. LNCS, vol. 4670, pp. 27–44. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-74610-2_4
Hagino, T.: A typed lambda calculus with categorical type constructors. In: Pitt, D.H., Poigné, A., Rydeheard, D.E. (eds.) Category Theory and Computer Science. LNCS, vol. 283, pp. 140–157. Springer, Heidelberg (1987). https://doi.org/10.1007/3-540-18508-9_24
Hashimoto, K., Unno, H.: Refinement type inference via horn constraint optimization. In: Blazy, S., Jensen, T. (eds.) SAS 2015. LNCS, vol. 9291, pp. 199–216. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48288-9_12
Howard, B.T.: Inductive, coinductive, and pointed types. In: Harper, R., Wexelblat, R.L. (eds.) Proceedings of ICFP 1996, pp. 102–109. ACM (1996). https://doi.org/10.1145/232627.232640
Hur, C.K., Neis, G., Dreyer, D., Vafeiadis, V.: The power of parameterization in coinductive proof. In: Proceedings of POPL 2013, pp. 193–206. ACM (2013). https://doi.org/10.1145/2429069.2429093
Jacobs, B.: Categorical Logic and Type Theory. Studies in Logic and the Foundations of Mathematics, vol. 141. North Holland, Amsterdam (1999)
Jacobs, B.: Introduction to Coalgebra: Towards Mathematics of States and Observation. Cambridge Tracts in Theoretical Computer Science, vol. 59. Cambridge University Press, Cambridge (2016). https://doi.org/10.1017/CBO9781316823187. http://www.cs.ru.nl/B.Jacobs/CLG/JacobsCoalgebraIntro.pdf
Komendantskaya, E., Li, Y.: Productive corecursion in logic programming. J. TPLP (ICLP 2017 post-proc.) 17(5–6), 906–923 (2017). https://doi.org/10.1017/S147106841700028X
Komendantskaya, E., Li, Y.: Towards coinductive theory exploration in horn clause logic: Position paper. In: Kahsai, T., Vidal, G. (eds.) Proceedings 5th Workshop on Horn Clauses for Verification and Synthesis, HCVS 2018, Oxford, UK, 13th July 2018, vol. 278, pp. 27–33 (2018). https://doi.org/10.4204/EPTCS.278.5
Lambek, J., Scott, P.J.: Introduction to Higher-Order Categorical Logic. Cambridge University Press, Cambridge (1988)
Lämmel, R., Peyton Jones, S.L.: Scrap your boilerplate with class: extensible generic functions. In: ICFP 2005, pp. 204–215. ACM (2005). https://doi.org/10.1145/1086365.1086391
Lloyd, J.W.: Foundations of Logic Programming, 2nd edn. Springer, Heidelberg (1987). https://doi.org/10.1007/978-3-642-83189-8
Miller, D., Nadathur, G.: Programming with Higher-order logic. Cambridge University Press, Cambridge (2012)
Miller, D., Nadathur, G., Pfenning, F., Scedrov, A.: Uniform proofs as a foundation for logic programming. Ann. Pure Appl. Logic 51(1–2), 125–157 (1991). https://doi.org/10.1016/0168-0072(91)90068-W
Milner, R.: A theory of type polymorphism in programming. J. Comput. Syst. Sci. 17(3), 348–375 (1978). https://doi.org/10.1016/0022-0000(78)90014-4
Møgelberg, R.E.: A type theory for productive coprogramming via guarded recursion. In: CSL-LICS, pp. 71:1–71:10. ACM (2014). https://doi.org/10.1145/2603088.2603132
Nadathur, G., Mitchell, D.J.: System description: Teyjus—a compiler and abstract machine based implementation of \(\lambda \)Prolog. CADE-16. LNCS (LNAI), vol. 1632, pp. 287–291. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-48660-7_25
Nakano, H.: A modality for recursion. In: LICS, pp. 255–266. IEEE Computer Society (2000). https://doi.org/10.1109/LICS.2000.855774
Niwinski, D., Walukiewicz, I.: Games for the \(\mu \)-Calculus. TCS 163(1&2), 99–116 (1996). https://doi.org/10.1016/0304-3975(95)00136-0
Park, D.: Concurrency and automata on infinite sequences. In: Deussen, P. (ed.) GI-TCS 1981. LNCS, vol. 104, pp. 167–183. Springer, Heidelberg (1981). https://doi.org/10.1007/BFb0017309
Plotkin, G.D.: LCF considered as a programming language. Theor. Comput. Sci. 5(3), 223–255 (1977). https://doi.org/10.1016/0304-3975(77)90044-5
Reynolds, A., Kuncak, V.: Induction for SMT solvers. In: D’Souza, D., Lal, A., Larsen, K.G. (eds.) VMCAI 2015. LNCS, vol. 8931, pp. 80–98. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46081-8_5
Roşu, G., Lucanu, D.: Circular coinduction: a proof theoretical foundation. In: Kurz, A., Lenisa, M., Tarlecki, A. (eds.) CALCO 2009. LNCS, vol. 5728, pp. 127–144. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03741-2_10
Rutten, J.: Universal coalgebra: a theory of systems. TCS 249(1), 3–80 (2000). https://doi.org/10.1016/S0304-3975(00)00056-6
Sangiorgi, D.: Introduction to Bisimulation and Coinduction. Cambridge University Press, New York (2011)
Santocanale, L.: A calculus of circular proofs and its categorical semantics. In: Nielsen, M., Engberg, U. (eds.) FoSSaCS 2002. LNCS, vol. 2303, pp. 357–371. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45931-6_25
Santocanale, L.: \(\mu \)-bicomplete categories and parity games. RAIRO - ITA 36(2), 195–227 (2002). https://doi.org/10.1051/ita:2002010
Shamkanov, D.S.: Circular proofs for the Gödel-Löb provability logic. Math. Notes 96(3), 575–585 (2014). https://doi.org/10.1134/S0001434614090326
Simon, L., Bansal, A., Mallya, A., Gupta, G.: Co-logic programming: extending logic programming with coinduction. In: Arge, L., Cachin, C., Jurdziński, T., Tarlecki, A. (eds.) ICALP 2007. LNCS, vol. 4596, pp. 472–483. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-73420-8_42
Simpson, A.: Cyclic arithmetic is equivalent to Peano arithmetic. In: Esparza, J., Murawski, A.S. (eds.) FoSSaCS 2017. LNCS, vol. 10203, pp. 283–300. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-54458-7_17
Smoryński, C.: Self-Reference and Modal Logic. Universitext. Springer, New York (1985). https://doi.org/10.1007/978-1-4613-8601-8
Solovay, R.M.: Provability interpretations of modal logic. Israel J. Math. 25(3), 287–304 (1976). https://doi.org/10.1007/BF02757006
Sulzmann, M., Stuckey, P.J.: HM(X) type inference is CLP(X) solving. J. Funct. Program. 18(2), 251–283 (2008). https://doi.org/10.1017/S0956796807006569
Terese: Term Rewriting Systems. Cambridge University Press, Cambridge (2003)
Turner, D.A.: Elementary strong functional programming. In: Hartel, P.H., Plasmeijer, R. (eds.) FPLE 1995. LNCS, vol. 1022, pp. 1–13. Springer, Heidelberg (1995). https://doi.org/10.1007/3-540-60675-0_35
van den Berg, B., de Marchi, F.: Non-well-founded trees in categories. Ann. Pure Appl. Logic 146(1), 40–59 (2007). https://doi.org/10.1016/j.apal.2006.12.001
Worrell, J.: On the final sequence of a finitary set functor. Theor. Comput. Sci. 338(1–3), 184–199 (2005). https://doi.org/10.1016/j.tcs.2004.12.009
Acknowledgements
We would like to thank Damien Pous and the anonymous reviewers for their valuable feedback.
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2019 The Author(s)
About this paper
Cite this paper
Basold, H., Komendantskaya, E., Li, Y. (2019). Coinduction in Uniform: Foundations for Corecursive Proof Search with Horn Clauses. In: Caires, L. (eds) Programming Languages and Systems. ESOP 2019. Lecture Notes in Computer Science(), vol 11423. Springer, Cham. https://doi.org/10.1007/978-3-030-17184-1_28
Download citation
DOI: https://doi.org/10.1007/978-3-030-17184-1_28
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-17183-4
Online ISBN: 978-3-030-17184-1
eBook Packages: Computer ScienceComputer Science (R0)








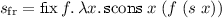 be the function that computes the streams of numerals starting at the given argument. It is easy to show that
be the function that computes the streams of numerals starting at the given argument. It is easy to show that  and so
and so  . Thus
. Thus  , but
, but  ” in
” in  .
.



 proof for
proof for 

 then
then  , and if
, and if  then
then  .
. over Herbrand Models
over Herbrand Models