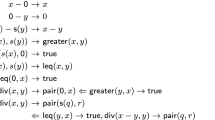A Static Higher-Order Dependency Pair Framework

Abstract

We revisit the static dependency pair method for proving termination of higher-order term rewriting and extend it in a number of ways: (1) We introduce a new rewrite formalism designed for general applicability in termination proving of higher-order rewriting, Algebraic Functional Systems with Meta-variables. (2) We provide a syntactically checkable soundness criterion to make the method applicable to a large class of rewrite systems. (3) We propose a modular dependency pair framework for this higher-order setting. (4) We introduce a fine-grained notion of formative and computable chains to render the framework more powerful. (5) We formulate several existing and new termination proving techniques in the form of processors within our framework.

The framework has been implemented in the (fully automatic) higher-order termination tool WANDA.

1 Introduction

Term rewriting [3, 48] is an important area of logic, with applications in many different areas of computer science [4, 11, 18, 23, 25, 36, 41]. Higher-order term rewriting – which extends the traditional first-order term rewriting with higher-order types and binders as in the $\lambda$-calculus – offers a formal foundation of functional programming and a tool for equational reasoning in higher-order logic. A key question in the analysis of both first- and higher-order term rewriting is termination; both for its own sake, and as part of confluence and equivalence analysis.

In first-order term rewriting, a hugely effective method for proving termination (both manually and automatically) is the dependency pair (DP) approach [2]. This approach has been extended to the DP framework [20, 22], a highly modular methodology which new techniques for proving termination and non-termination can easily be plugged into in the form of processors.

In higher-order rewriting, two DP approaches with distinct costs and benefits are used: dynamic [31, 45] and static [6, 32,33,34, 44, 46] DPs. Dynamic DPs are more broadly applicable, yet static DPs often enable more powerful analysis techniques. Still, neither approach has the modularity and extendability of the DP framework, nor can they be used to prove non-termination. Also, these approaches consider different styles of higher-order rewriting, which means that for all results certain language features are not available.

In this paper, we address these issues for the static DP approach by extending it to a full higher-order dependency pair framework for both termination and non-termination analysis. For broad applicability, we introduce a new rewriting formalism, AFSMs, to capture several flavours of higher-order rewriting, including AFSs [26] (used in the annual Termination Competition [50]) and pattern HRSs [37, 39] (used in the annual Confluence Competition [10]). To show the versatility and power of this methodology, we define various processors in the framework – both adaptations of existing processors from the literature and entirely new ones.

Detailed Contributions. We reformulate the results of [6, 32, 34, 44, 46] into a DP framework for AFSMs. In doing so, we instantiate the applicability restriction of [32] by a very liberal syntactic condition, and add two new flags to track properties of DP problems: one completely new, one from an earlier work by the authors for the first-order DP framework [16]. We give eight processors for reasoning in our framework: four translations of techniques from static DP approaches, three techniques from first-order or dynamic DPs, and one completely new.

This is a foundational paper, focused on defining a general theoretical framework for higher-order termination analysis using dependency pairs rather than questions of implementation. We have, however, implemented most of these results in the fully automatic termination analysis tool WANDA [28].

Related Work. There is a vast body of work in the first-order setting regarding the DP approach [2] and framework [20, 22, 24]. We have drawn from the ideas in these works for the core structure of the higher-order framework, but have added some new features of our own and adapted results to the higher-order setting.

There is no true higher-order DP framework yet: both static and dynamic approaches actually lie halfway between the original “DP approach” of first-order rewriting and a full DP framework as in [20, 22]. Most of these works [30,31,32, 34, 46] prove “non-loopingness” or “chain-freeness” of a set $\mathcal {P}$ of DPs through a number of theorems. Yet, there is no concept of DP problems, and the set $\mathcal {R}$ of rules cannot be altered. They also fix assumptions on dependency chains – such as minimality [34] or being “tagged” [31] – which frustrate extendability and are more naturally dealt with in a DP framework using flags.

The static DP approach for higher-order term rewriting is discussed in, e.g., [34, 44, 46]. The approach is limited to plain function passing (PFP) systems. The definition of PFP has been made more liberal in later papers, but always concerns the position of higher-order variables in the left-hand sides of rules. These works include non-pattern HRSs [34, 46], which we do not consider, but do not employ formative rules or meta-variable conditions, or consider non-termination, which we do. Importantly, they do not consider strictly positive inductive types, which could be used to significantly broaden the PFP restriction. Such types are considered in an early paper which defines a variation of static higher-order dependency pairs [6] based on a computability closure [7, 8]. However, this work carries different restrictions (e.g., DPs must be type-preserving and not introduce fresh variables) and considers only one analysis technique (reduction pairs).

Definitions of DP approaches for functional programming also exist [32, 33], which consider applicative systems with ML-style polymorphism. These works also employ a much broader, semantic definition than PFP, which is actually more general than the syntactic restriction we propose here. However, like the static approaches for term rewriting, they do not truly exploit the computability [47] properties inherent in this restriction: it is only used for the initial generation of dependency pairs. In the present work, we will take advantage of our exact computability notion by introducing a $\mathtt {computable}$ flag that can be used by the computable subterm criterion processor (Theorem 63) to handle benchmark systems that would otherwise be beyond the reach of static DPs. Also in these works, formative rules, meta-variable conditions and non-termination are not considered.

Regarding dynamic DP approaches, a precursor of the present work is [31], which provides a halfway framework (methodology to prove “chain-freeness”) for dynamic DPs, introduces a notion of formative rules, and briefly translates a basic form of static DPs to the same setting. Our formative reductions consider the shape of reductions rather than the rules they use, and they can be used as a flag in the framework to gain additional power in other processors. The adaptation of static DPs in [31] was very limited, and did not for instance consider strictly positive inductive types or rules of functional type.

For a more elaborate discussion of both static and dynamic DP approaches in the literature, we refer to [31] and the second author’s PhD thesis [29].

Organisation of the Paper. Section 2 introduces higher-order rewriting using AFSMs and recapitulates computability. In Sect. 3 we impose restrictions on the input AFSMs for which our framework is soundly applicable. In Sect. 4 we define static DPs for AFSMs, and derive the key results on them. Section 5 formulates the DP framework and a number of DP processors for existing and new termination proving techniques. Section 6 concludes. Detailed proofs for all results in this paper and an experimental evaluation are available in a technical report [17]. In addition, many of the results have been informally published in the second author’s PhD thesis [29].

2 Preliminaries

In this section, we first define our notation by introducing the AFSM formalism. Although not one of the standards of higher-order rewriting, AFSMs combine features from various forms of higher-order rewriting and can be seen as a form of IDTSs [5] which includes application. We will finish with a definition of computability, a technique often used for higher-order termination methods.

2.1 Higher-Order Term Rewriting Using AFSMs

Unlike first-order term rewriting, there is no single, unified approach to higher-order term rewriting, but rather a number of similar but not fully compatible systems aiming to combine term rewriting and typed $\lambda$-calculi. For generality, we will use Algebraic Functional Systems with Meta-variables: a formalism which admits translations from the main formats of higher-order term rewriting.

Definition 1

(Simple types). We fix a set $\mathcal {S}$ of sorts. All sorts are simple types, and if $\sigma ,\tau$ are simple types, then so is $\sigma \rightarrow \tau$.

We let $\rightarrow$ be right-associative. Note that all types have a unique representation in the form $\sigma _1 \rightarrow \dots \rightarrow \sigma _m\rightarrow \iota$ with $\iota \in \mathcal {S}$.

Definition 2

(Terms and meta-terms). We fix disjoint sets $\mathcal {F}$ of function symbols, $\mathcal {V}$ of variables and $\mathcal {M}$ of meta-variables, each symbol equipped with a type. Each meta-variable is additionally equipped with a natural number. We assume that both $\mathcal {V}$ and $\mathcal {M}$ contain infinitely many symbols of all types. The set $\mathcal {T}(\mathcal {F},\mathcal {V})$ of terms over $\mathcal {F},\mathcal {V}$ consists of expressions s where $s : \sigma$ can be derived for some type $\sigma$ by the following clauses:

Meta-terms are expressions whose type can be derived by those clauses and:

The $\lambda$ binds variables as in the $\lambda$-calculus; unbound variables are called free, and $FV (s)$ is the set of free variables in s. Meta-variables cannot be bound; we write $FMV (s)$ for the set of meta-variables occurring in s. A meta-term s is called closed if $FV (s) = \emptyset$ (even if $FMV (s) \ne \emptyset$). Meta-terms are considered modulo $\alpha$-conversion. Application (@) is left-associative; abstractions ($\mathsf {\Lambda }$) extend as far to the right as possible. A meta-term s has type $\sigma$ if $s : \sigma$; it has base type if $\sigma \in \mathcal {S}$. We define $\mathsf {head}(s) = \mathsf {head}(s_1)$ if $s = s_1\ s_2$, and $\mathsf {head}(s) = s$ otherwise.

A (meta-)term s has a sub-(meta-)term t, notation $s \unrhd t$, if either $s = t$ or $s \rhd t$, where $s \rhd t$ if (a) $s = \lambda x{.}s'$ and $s' \unrhd t$, (b) $s = s_1\ s_2$ and $s_2 \unrhd t$ or (c) $s = s_1\ s_2$ and $s_1 \unrhd t$. A (meta-)term s has a fully applied sub-(meta-)term t, notation $s \mathbin {\underline{\blacktriangleright }}t$, if either $s = t$ or $s \blacktriangleright t$, where $s \blacktriangleright t$ if (a) $s = \lambda x{.}s'$ and $s' \mathbin {\underline{\blacktriangleright }}t$, (b) $s = s_1\ s_2$ and $s_2 \mathbin {\underline{\blacktriangleright }}t$ or (c) $s = s_1\ s_2$ and $s_1 \blacktriangleright t$ (so if $s = x\ s_1\ s_2$, then x and $x\ s_1$ are not fully applied subterms, but s and both $s_1$ and $s_2$ are).

For $Z : (\sigma ,k) \in \mathcal {M}$, we call $k$ the arity of Z, notation $arity (Z)$.

Clearly, all fully applied subterms are subterms, but not all subterms are fully applied. Every term s has a form $t\ s_1 \cdots s_n$ with $n \ge 0$ and $t = \mathsf {head}(s)$ a variable, function symbol, or abstraction; in meta-terms t may also be a meta-variable application $F\langle s_1, \dots ,s_k\rangle$. Terms are the objects that we will rewrite; meta-terms are used to define rewrite rules. Note that all our terms (and meta-terms) are, by definition, well-typed. For rewriting, we will employ patterns:

Definition 3

(Patterns). A meta-term is a pattern if it has one of the forms $Z\langle x_1, \dots ,x_k\rangle$ with all $x_i$ distinct variables; $\lambda x{.}\ell$ with $x \in \mathcal {V}$ and $\ell$ a pattern; or $a\ \ell _1 \cdots \ell _n$ with $a \in \mathcal {F}\cup \mathcal {V}$ and all $\ell _i$ patterns ($n \ge 0$).

In rewrite rules, we will use meta-variables for matching and variables only with binders. In terms, variables can occur both free and bound, and meta-variables cannot occur. Meta-variables originate in very early forms of higher-order rewriting (e.g., [1, 27]), but have also been used in later formalisms (e.g., [8]). They strike a balance between matching modulo $\beta$ and syntactic matching. By using meta-variables, we obtain the same expressive power as with Miller patterns [37], but do so without including a reversed $\beta$-reduction as part of matching.

Notational Conventions: We will use x, y, z for variables, X, Y, Z for meta-variables, $b$ for symbols that could be variables or meta-variables, $\mathtt {f},\mathtt {g},\mathtt {h}$ or more suggestive notation for function symbols, and s, t, u, v, q, w for (meta-)terms. Types are denoted $\sigma ,\tau$, and $\iota ,\kappa$ are sorts. We will regularly overload notation and write $x \in \mathcal {V}$, $\mathtt {f}\in \mathcal {F}$ or $Z \in \mathcal {M}$ without stating a type (or minimal arity). For meta-terms $Z\langle \rangle$ we will usually omit the brackets, writing just Z.

Definition 4

(Substitution). A meta-substitution is a type-preserving function $\gamma$ from variables and meta-variables to meta-terms. Let the domain of $\gamma$ be given by: $\mathtt {dom}(\gamma ) = \{ (x : \sigma ) \in \mathcal {V}\mid \gamma (x) \ne x \} \cup \{ (Z : (\sigma ,k)) \in \mathcal {M}\mid \gamma (Z) \ne \lambda y_1 \dots y_{k}{.}Z\langle y_1,\dots ,y_{k}\rangle \}$; this domain is allowed to be infinite. We let $[b_1:=s_1,\dots ,b_n:=s_n]$ denote the meta-substitution $\gamma$ with $\gamma (b_i) = s_i$ and $\gamma (z) = z$ for $(z : \sigma ) \in \mathcal {V}\setminus \{b_1, \dots ,b_n\}$, and $\gamma (Z) = \lambda y_1\dots y_{k}{.} Z\langle y_1,\dots , y_{k}\rangle$ for $(Z : (\sigma ,k)) \in \mathcal {M}\setminus \{b_1,\dots ,b_n\}$. We assume there are infinitely many variables x of all types such that (a) $x \notin \mathtt {dom}(\gamma )$ and (b) for all $b\in \mathtt {dom}(\gamma )$: $x \notin FV (\gamma (b))$.

A substitution is a meta-substitution mapping everything in its domain to terms. The result $s\gamma$ of applying a meta-substitution $\gamma$ to a term s is obtained by:

For meta-terms, the result $s\gamma$ is obtained by the clauses above and:

Note that for fixed $k$, any term has exactly one of the two forms above ($\lambda x_1 \dots x_n{.}s$ with $n < k$ and s not an abstraction, or $\lambda x_1 \dots x_k{.}s$).

Essentially, applying a meta-substitution that has meta-variables in its domain combines a substitution with (possibly several) $\beta$-steps. For example, we have that: $\mathtt {deriv}\ (\lambda x{.}\mathtt {sin}\ (F\langle x\rangle ))[F :=\lambda y{.}\mathtt {plus}\ y\ x]$ equals $\mathtt {deriv}\ (\lambda z{.}\mathtt {sin}\ (\mathtt {plus}\ z\ x))$. We also have: $X\langle \mathtt {0},\mathtt {nil}\rangle [X:=\lambda x{.}\mathtt {map}\ (\lambda y{.}x)]$ equals $\mathtt {map}\ (\lambda y{.}\mathtt {0})\ \mathtt {nil}$.

Definition 5

(Rules and rewriting). Let $\mathcal {F},\mathcal {V},\mathcal {M}$ be fixed sets of function symbols, variables and meta-variables respectively. A rule is a pair $\ell \Rightarrow r$ of closed meta-terms of the same type such that $\ell$ is a pattern of the form $\mathtt {f}\ \ell _1 \cdots \ell _n$ with $\mathtt {f}\in \mathcal {F}$ and $FMV (r) \subseteq FMV (\ell )$. A set of rules $\mathcal {R}$ defines a rewrite relation $\Rightarrow _{\mathcal {R}}$ as the smallest monotonic relation on terms which includes:

We say $s \Rightarrow _{\beta } t$ if $s \Rightarrow _{\mathcal {R}} t$ is derived using a (Beta) step. A term s is terminating under $\Rightarrow _{\mathcal {R}}$ if there is no infinite reduction $s = s_0 \Rightarrow _{\mathcal {R}} s_1 \Rightarrow _{\mathcal {R}} \dots$, is in normal form if there is no t such that $s \Rightarrow _{\mathcal {R}} t$, and is $\beta$-normal if there is no t with $s \Rightarrow _{\beta } t$. Note that we are allowed to reduce at any position of a term, even below a $\lambda$. The relation $\Rightarrow _{\mathcal {R}}$ is terminating if all terms over $\mathcal {F},\mathcal {V}$ are terminating. The set $\mathcal {D}\subseteq \mathcal {F}$ of defined symbols consists of those $(\mathtt {f}: \sigma ) \in \mathcal {F}$ such that a rule $\mathtt {f}\ \ell _1 \cdots \ell _n \Rightarrow r$ exists; all other symbols are called constructors.

Note that $\mathcal {R}$ is allowed to be infinite, which is useful for instance to model polymorphic systems. Also, right-hand sides of rules do not have to be in $\beta$-normal form. While this is rarely used in practical examples, non-$\beta$-normal rules may arise through transformations, and we lose nothing by allowing them.

Example 6

Let $\mathcal {F}\supseteq \{ \mathtt {0}: \mathtt {nat},\ \mathtt {s}: \mathtt {nat}\rightarrow \mathtt {nat},\ \mathtt {nil}: \mathtt {list}, \mathtt {cons}: \mathtt {nat}\rightarrow \mathtt {list}\rightarrow \mathtt {list},\ \mathtt {map}: (\mathtt {nat}\rightarrow \mathtt {nat}) \rightarrow \mathtt {list}\rightarrow \mathtt {list}\}$ and consider the following rules $\mathcal {R}$:

$$ \begin{array}{rcl} \mathtt {map}\ (\lambda x{.}Z\langle x\rangle )\ \mathtt {nil}&{} \Rightarrow &{} \mathtt {nil}\\ \mathtt {map}\ (\lambda x{.}Z\langle x\rangle )\ (\mathtt {cons}\ H\ T) &{} \Rightarrow &{} \mathtt {cons}\ Z\langle H\rangle \ (\mathtt {map}\ (\lambda x{.}Z\langle x\rangle )\ T) \\ \end{array} $$

Then $\mathtt {map}\ (\lambda y{.}\mathtt {0})\ (\mathtt {cons}\ (\mathtt {s}\ \mathtt {0})\ \mathtt {nil}) \Rightarrow _{\mathcal {R}} \mathtt {cons}\ \mathtt {0}\ (\mathtt {map}\ (\lambda y{.}\mathtt {0})\ \mathtt {nil}) \Rightarrow _{\mathcal {R}} \mathtt {cons}\ \mathtt {0}\ \mathtt {nil}$. Note that the bound variable y does not need to occur in the body of $\lambda y{.}\mathtt {0}$ to match $\lambda x{.}Z\langle x\rangle$. However, a term like $\mathtt {map}\ \mathtt {s}\ (\mathtt {cons}\ \mathtt {0}\ \mathtt {nil})$ cannot be reduced, because $\mathtt {s}$ does not instantiate $\lambda x{.}Z\langle x\rangle$. We could alternatively consider the rules:

$$ \begin{array}{rcl} \mathtt {map}\ Z\ \mathtt {nil}&{} \Rightarrow &{} \mathtt {nil}\\ \mathtt {map}\ Z\ (\mathtt {cons}\ H\ T) &{} \Rightarrow &{} \mathtt {cons}\ (Z\ H)\ (\mathtt {map}\ Z\ T) \\ \end{array} $$

Where the system before had $(Z : (\mathtt {nat}\rightarrow \mathtt {nat}, 1)) \in \mathcal {M}$, here we assume $(Z : (\mathtt {nat}\rightarrow \mathtt {nat}, 0)) \in \mathcal {M}$. Thus, rather than meta-variable application $Z\langle H\rangle$ we use explicit application $Z\ H$. Then $\mathtt {map}\ \mathtt {s}\ (\mathtt {cons}\ \mathtt {0}\ \mathtt {nil}) \Rightarrow _{\mathcal {R}} \mathtt {cons}\ (\mathtt {s}\ \mathtt {0})\ (\mathtt {map}\ \mathtt {s}\ \mathtt {nil})$. However, we will often need explicit $\beta$-reductions; e.g., $\mathtt {map}\ (\lambda y{.}\mathtt {0})\ (\mathtt {cons}\ (\mathtt {s}\ \mathtt {0})\ \mathtt {nil}) \Rightarrow _{\mathcal {R}} \mathtt {cons}\ ((\lambda y{.}\mathtt {0})\ (\mathtt {s}\ \mathtt {0}))\ (\mathtt {map}\ (\lambda y{.}\mathtt {0})\ \mathtt {nil}) \Rightarrow _{\beta } \mathtt {cons}\ \mathtt {0}\ (\mathtt {map}\ (\lambda y{.}\mathtt {0})\ \mathtt {nil})$.

Definition 7

(AFSM). An AFSM is a tuple $(\mathcal {F},\mathcal {V},\mathcal {M},\mathcal {R})$ of a signature and a set of rules built from meta-terms over $\mathcal {F},\mathcal {V},\mathcal {M}$; as types of relevant variables and meta-variables can always be derived from context, we will typically just refer to the AFSM $(\mathcal {F},\mathcal {R})$. An AFSM implicitly defines the abstract reduction system $(\mathcal {T}(\mathcal {F},\mathcal {V}), \Rightarrow _{\mathcal {R}})$: a set of terms and a rewrite relation on this set. An AFSM is terminating if $\Rightarrow _{\mathcal {R}}$ is terminating (on all terms in $\mathcal {T}(\mathcal {F},\mathcal {V})$).

Discussion: The two most common formalisms in termination analysis of higher-order rewriting are algebraic functional systems [26] (AFSs) and higher-order rewriting systems [37, 39] (HRSs). AFSs are very similar to our AFSMs, but use variables for matching rather than meta-variables; this is trivially translated to the AFSM format, giving rules where all meta-variables have arity 0, like the “alternative” rules in Example 6. HRSs use matching modulo $\beta /\eta$, but the common restriction of pattern HRSs can be directly translated into AFSMs, provided terms are $\beta$-normalised after every reduction step. Even without this $\beta$-normalisation step, termination of the obtained AFSM implies termination of the original HRS; for second-order systems, termination is equivalent. AFSMs can also naturally encode CRSs [27] and several applicative systems (cf. [29, Chapter 3]).

Example 8

(Ordinal recursion). A running example is the AFSM $(\mathcal {F},\mathcal {R})$ with $\mathcal {F}\supseteq \{ \mathtt {0}: \mathtt {ord},\ \mathtt {s}: \mathtt {ord} \rightarrow \mathtt {ord}, \mathtt {lim} : (\mathtt {nat} \rightarrow \mathtt {ord}) \rightarrow \mathtt {ord},\ \mathtt {rec} : \mathtt {ord} \rightarrow \mathtt {nat} \rightarrow (\mathtt {ord} \rightarrow \mathtt {nat} \rightarrow \mathtt {nat}) \rightarrow ((\mathtt {nat} \rightarrow \mathtt {ord}) \rightarrow (\mathtt {nat} \rightarrow \mathtt {nat}) \rightarrow \mathtt {nat}) \rightarrow \mathtt {nat} \}$ and $\mathcal {R}$ given below. As all meta-variables have arity 0, this can be seen as an AFS.

$$ \begin{array}{rcl} \mathtt {rec}\ \mathtt {0}\ K\ F\ G &{} \Rightarrow &{} K \\ \mathtt {rec}\ (\mathtt {s}\ X)\ K\ F\ G &{} \Rightarrow &{} F\ X\ (\mathtt {rec}\ X\ K\ F\ G) \\ \mathtt {rec}\ (\mathtt {lim}\ H)\ K\ F\ G &{} \Rightarrow &{} G\ H\ (\lambda m{.} \mathtt {rec}\ (H\ m)\ K\ F\ G) \\ \end{array} $$

Observant readers may notice that by the given constructors, the type $\mathtt {nat}$ in Example 8 is not inhabited. However, as the given symbols are only a subset of $\mathcal {F}$, additional symbols (such as constructors for the $\mathtt {nat}$ type) may be included. The presence of additional function symbols does not affect termination of AFSMs:

Theorem 9

(Invariance of termination under signature extensions). For an AFSM $(\mathcal {F},\mathcal {R})$ with $\mathcal {F}$ at most countably infinite, let $\mathtt {funs}(\mathcal {R}) \subseteq \mathcal {F}$ be the set of function symbols occurring in some rule of $\mathcal {R}$. Then $(\mathcal {T}(\mathcal {F},\mathcal {V}), \Rightarrow _{\mathcal {R}})$ is terminating if and only if $(\mathcal {T}(\mathtt {funs}(\mathcal {R}),\mathcal {V}), \Rightarrow _{\mathcal {R}})$ is terminating.

Proof

Trivial by replacing all function symbols in $\mathcal {F}\setminus \mathtt {funs}(\mathcal {R})$ by corresponding variables of the same type.    $\square$

Therefore, we will typically only state the types of symbols occurring in the rules, but may safely assume that infinitely many symbols of all types are present (which for instance allows us to select unused constructors in some proofs).

2.2 Computability

A common technique in higher-order termination is Tait and Girard’s computability notion [47]. There are several ways to define computability predicates; here we follow, e.g., [5, 7,8,9] in considering accessible meta-terms using strictly positive inductive types. The definition presented below is adapted from these works, both to account for the altered formalism and to introduce (and obtain termination of) a relation $\Rrightarrow _{C}$ that we will use in the “computable subterm criterion processor” of Theorem 63 (a termination criterion that allows us to handle systems that would otherwise be beyond the reach of static DPs). This allows for a minimal presentation that avoids the use of ordinals that would otherwise be needed to obtain $\Rrightarrow _{C}$ (see, e.g., [7, 9]).

To define computability, we use the notion of an RC-set:

Definition 10

A set of reducibility candidates, or RC-set, for a rewrite relation $\Rightarrow _{\mathcal {R}}$ of an AFSM is a set I of base-type terms s such that: every term in I is terminating under $\Rightarrow _{\mathcal {R}}$; I is closed under $\Rightarrow _{\mathcal {R}}$ (so if $s \in I$ and $s \Rightarrow _{\mathcal {R}} t$ then $t \in I$); if $s = x\ s_1 \cdots s_n$ with $x \in \mathcal {V}$ or $s = (\lambda x{.}u)\ s_0 \cdots s_n$ with $n \ge 0$, and for all t with $s \Rightarrow _{\mathcal {R}} t$ we have $t \in I$, then $s \in I$ (for any $u,s_0,\dots ,s_n \in \mathcal {T}(\mathcal {F},\mathcal {V})$).

We define I-computability for an RC-set I by induction on types. For $s \in \mathcal {T}(\mathcal {F},\mathcal {V})$, we say that s is I-computable if either s is of base type and $s \in I$; or $s : \sigma \rightarrow \tau$ and for all $t : \sigma$ that are I-computable, $s\ t$ is I-computable.

The traditional notion of computability is obtained by taking for I the set of all terminating base-type terms. Then, a term s is computable if and only if (a) s has base type and is terminating; or (b) $s : \sigma \rightarrow \tau$ and for all computable $t : \sigma$ the term $s\ t$ is computable. This choice is simple but, for reasoning, not ideal: we do not have a property like: “if $\mathtt {f}\ s_1 \cdots s_n$ is computable then so is each $s_i$”. Such a property would be valuable to have for generalising termination proofs from first-order to higher-order rewriting, as it allows us to use computability where the first-order proof uses termination. While it is not possible to define a computability notion with this property alongside case (b) (as such a notion would not be well-founded), we can come close to this property by choosing a different set for I. To define this set, we will use the notion of accessible arguments, which is used for the same purpose also in the General Schema [8], the Computability Path Ordering [9], and the Computability Closure [7].

Definition 11

(Accessible arguments). We fix a quasi-ordering $\succeq ^{\mathcal {S}}$ on $\mathcal {S}$ with well-founded strict part $\succ ^{\mathcal {S}}\ :=\ \succeq ^{\mathcal {S}}\setminus \preceq ^{\mathcal {S}}$.¹ For a type $\sigma \equiv \sigma _1 \!\rightarrow \! \dots \!\rightarrow \! \sigma _m\!\rightarrow \! \kappa$ (with $\kappa \in \mathcal {S}$) and sort $\iota$, let $\iota \succeq ^{\mathcal {S}}_+\sigma$ if $\iota \succeq ^{\mathcal {S}}\kappa$ and $\iota \succ ^{\mathcal {S}}_-\sigma _i$ for all i, and let $\iota \succ ^{\mathcal {S}}_-\sigma$ if $\iota \succ ^{\mathcal {S}}\kappa$ and $\iota \succeq ^{\mathcal {S}}_+\sigma _i$ for all i.²

For $\mathtt {f}: \sigma _1 \rightarrow \dots \rightarrow \sigma _m\rightarrow \iota \in \mathcal {F}$, let $Acc (\mathtt {f}) = \{ i \mid 1 \le i \le m\wedge \iota \succeq ^{\mathcal {S}}_+\sigma _i \}$. For $x : \sigma _1 \rightarrow \dots \rightarrow \sigma _m\rightarrow \iota \in \mathcal {V}$, let $Acc (x) = \{ i \mid 1 \le i \le m\wedge \sigma _i$ has the form $\tau _1 \rightarrow \dots \rightarrow \tau _n \rightarrow \kappa$ with $\iota \succeq ^{\mathcal {S}}\kappa \}$. We write $s \unrhd _{\mathtt {acc}}t$ if either $s = t$, or $s = \lambda x{.}s'$ and $s' \unrhd _{\mathtt {acc}}t$, or $s = a\ s_1 \cdots s_n$ with $a \in \mathcal {F}\cup \mathcal {V}$ and $s_i \unrhd _{\mathtt {acc}}t$ for some $i\in Acc (a)$ with $a \notin FV (s_i)$.

With this definition, we will be able to define a set C such that, roughly, s is C-computable if and only if (a) $s : \sigma \rightarrow \tau$ and $s\ t$ is C-computable for all C-computable t, or (b) s has base type, is terminating, and if $s = \mathtt {f}\ s_1 \cdots s_m$ then $s_i$ is C-computable for all accessible i (see Theorem 13 below). The reason that $Acc (x)$ for $x \in \mathcal {V}$ is different is proof-technical: computability of $\lambda x{.}x\ s_1 \cdots s_m$ implies the computability of more arguments $s_i$ than computability of $\mathtt {f}\ s_1 \cdots s_m$ does, since x can be instantiated by anything.

Example 12

Consider a quasi-ordering $\succeq ^{\mathcal {S}}$ such that $\mathtt {ord} \succ ^{\mathcal {S}}\mathtt {nat}$. In Example 8, we then have $\mathtt {ord} \, \succeq ^{\mathcal {S}}_+\, \mathtt {nat} \rightarrow \mathtt {ord}$. Thus, $1 \in Acc (\mathtt {lim})$, which gives $\mathtt {lim}\ H \unrhd _{\mathtt {acc}}H$.

Theorem 13

Let $(\mathcal {F},\mathcal {R})$ be an AFSM. Let $\mathtt {f}\ s_1 \cdots s_m \Rrightarrow _{I} s_i\ t_1 \cdots t_n$ if both sides have base type, $i \in Acc (\mathtt {f})$, and all $t_j$ are I-computable. There is an RC-set C such that $C = \{ s \in \mathcal {T}(\mathcal {F},\mathcal {V}) \mid s$ has base type $\wedge \ s$ is terminating under $\Rightarrow _{\mathcal {R}} \cup \Rrightarrow _{C} \wedge {}$ if $s \Rightarrow _{\mathcal {R}}^* \mathtt {f}\ s_1 \cdots s_m$ then $s_i$ is C-computable for all $i \in Acc (\mathtt {f}) \}$.

Proof

(sketch). Note that we cannot define C as this set, as the set relies on the notion of C-computability. However, we can define C as the fixpoint of a monotone function operating on RC-sets. This follows the proof in, e.g., [8, 9].    $\square$

The complete proof is available in [17, Appendix A].

3 Restrictions

The termination methodology in this paper is restricted to AFSMs that satisfy certain limitations: they must be properly applied (a restriction on the number of terms each function symbol is applied to) and accessible function passing (a restriction on the positions of variables of a functional type in the left-hand sides of rules). Both are syntactic restrictions that are easily checked by a computer (mostly; the latter requires a search for a sort ordering, but this is typically easy).

3.1 Properly Applied AFSMs

In properly applied AFSMs, function symbols are assigned a certain, minimal number of arguments that they must always be applied to.

Definition 14

An AFSM $(\mathcal {F},\mathcal {R})$ is properly applied if for every $\mathtt {f}\in \mathcal {D}$ there exists an integer $k$ such that for all rules $\ell \Rightarrow r \in \mathcal {R}$: (1) if $\ell = \mathtt {f}\ \ell _1 \cdots \ell _n$ then $n = k$; and (2) if $r \mathbin {\underline{\blacktriangleright }}\mathtt {f}\ r_1 \cdots r_n$ then $n \ge k$. We denote $minar (\mathtt {f}) = k$.

That is, every occurrence of a function symbol in the right-hand side of a rule has at least as many arguments as the occurrences in the left-hand sides of rules. This means that partially applied functions are often not allowed: an AFSM with rules such as $\mathtt {double}\ X \Rightarrow \mathtt {plus}\ X\ X$ and $\mathtt {doublelist}\ L \Rightarrow \mathtt {map}\ \mathtt {double}\ L$ is not properly applied, because $\mathtt {double}$ is applied to one argument in the left-hand side of some rule, and to zero in the right-hand side of another.

This restriction is not as severe as it may initially seem since partial applications can be replaced by $\lambda$-abstractions; e.g., the rules above can be made properly applied by replacing the second rule by: $\mathtt {doublelist}\ L \Rightarrow \mathtt {map}\ (\lambda x{.}\mathtt {double}\ x)\ L$. By using $\eta$-expansion, we can transform any AFSM to satisfy this restriction:

Definition 15

($\mathcal {R}^\uparrow$). Given a set of rules $\mathcal {R}$, let their $\eta$-expansion be given by $\mathcal {R}^\uparrow = \{ (\ell \ Z_1 \cdots Z_m)\!\!\uparrow ^\eta \ \Rightarrow (r\ Z_1 \cdots Z_m)\!\!\uparrow ^\eta \mid \ell \Rightarrow r \in \mathcal {R}$ with $r : \sigma _1 \rightarrow \dots \rightarrow \sigma _m\rightarrow \iota$, $\iota \in \mathcal {S}$, and $Z_1,\dots , Z_m$ fresh meta-variables$\}$, where

• $s\!\!\uparrow ^\eta = \lambda x_1 \dots x_m{.}\overline{s}\ (x_1\!\!\uparrow ^\eta ) \cdots (x_m\!\!\uparrow ^\eta )$ if s is an application or element of $\mathcal {V}\cup \mathcal {F}$, and $s\!\!\uparrow ^\eta = \overline{s}$ otherwise;

• $\overline{\mathtt {f}} = \mathtt {f}$ for $\mathtt {f}\in \mathcal {F}$ and $\overline{x} = x$ for $x \in \mathcal {V}$, while $\overline{Z\langle s_1,\dots ,s_k\rangle } = Z\langle \overline{s_1},\dots ,\overline{s_k}\rangle$ and $\overline{(\lambda x{.}s)} = \lambda x{.}(s\!\!\uparrow ^\eta )$ and $\overline{s_1\ s_2} = \overline{s_1}\ (s_2\!\!\uparrow ^\eta )$.

Note that $\ell \!\!\uparrow ^\eta$ is a pattern if $\ell$ is. By [29, Thm. 2.16], a relation $\Rightarrow _{\mathcal {R}}$ is terminating if $\Rightarrow _{\mathcal {R}^\uparrow }$ is terminating, which allows us to transpose any methods to prove termination of properly applied AFSMs to all AFSMs.

However, there is a caveat: this transformation can introduce non-termination in some special cases, e.g., the terminating rule $\mathtt {f}\ X \Rightarrow \mathtt {g}\ \mathtt {f}$ with $\mathtt {f} : \mathtt {o} \rightarrow \mathtt {o}$ and $\mathtt {g} : (\mathtt {o} \rightarrow \mathtt {o}) \rightarrow \mathtt {o}$, whose $\eta$-expansion $\mathtt {f}\ X \Rightarrow \mathtt {g}\ (\lambda x{.}(\mathtt {f}\ x))$ is non-terminating. Thus, for a properly applied AFSM the methods in this paper apply directly. For an AFSM that is not properly applied, we can use the methods to prove termination (but not non-termination) by first $\eta$-expanding the rules. Of course, if this analysis leads to a counterexample for termination, we may still be able to verify whether this counterexample applies in the original, untransformed AFSM.

Example 16

Both AFSMs in Example 6 and the AFSM in Example 8 are properly applied.

Example 17

Consider an AFSM $(\mathcal {F},\mathcal {R})$ with $\mathcal {F}\supseteq \{ \mathtt {sin}, \mathtt {cos} : \mathtt {real}\rightarrow \mathtt {real}, \mathtt {times} : \mathtt {real}\rightarrow \mathtt {real}\rightarrow \mathtt {real},\ \mathtt {deriv}: (\mathtt {real}\rightarrow \mathtt {real}) \rightarrow \mathtt {real}\rightarrow \mathtt {real}\}$ and $\mathcal {R}= \{ \mathtt {deriv}\ (\lambda x{.}\mathtt {sin}\ F\langle x\rangle ) \Rightarrow \lambda y{.}\mathtt {times}\ (\mathtt {deriv}\ (\lambda x{.}F\langle x\rangle )\ y)\ (\mathtt {cos}\ F\langle y\rangle ) \}$. Although the one rule has a functional output type ($\mathtt {real}\rightarrow \mathtt {real}$), this AFSM is properly applied, with $\mathtt {deriv}$ having always at least 1 argument. Therefore, we do not need to use $\mathcal {R}^\uparrow$. However, if $\mathcal {R}$ were to additionally include some rules that did not satisfy the restriction (such as the $\mathtt {double}$ and $\mathtt {doublelist}$ rules above), then $\eta$-expanding all rules, including this one, would be necessary. We have: $\mathcal {R}^\uparrow = \{ \mathtt {deriv}\ (\lambda x{.}\mathtt {sin}\ F\langle x\rangle )\ Y \Rightarrow (\lambda y{.}\mathtt {times}\ (\mathtt {deriv}\ (\lambda x{.}F\langle x\rangle )\ y)\ (\mathtt {cos}\ F\langle y\rangle ))\ Y \}$. Note that the right-hand side of the $\eta$-expanded $\mathtt {deriv}$ rule is not $\beta$-normal.

3.2 Accessible Function Passing AFSMs

In accessible function passing AFSMs, variables of functional type may not occur at arbitrary places in the left-hand sides of rules: their positions are restricted using the sort ordering $\succeq ^{\mathcal {S}}$ and accessibility relation $\unrhd _{\mathtt {acc}}$ from Definition 11.

Definition 18

(Accessible function passing). An AFSM $(\mathcal {F},\mathcal {R})$ is accessible function passing (AFP) if there exists a sort ordering $\succeq ^{\mathcal {S}}$ following Definition 11 such that: for all $\mathtt {f}\ \ell _1 \cdots \ell _n \Rightarrow r \in \mathcal {R}$ and all $Z \in FMV (r)$: there are variables $x_1,\dots ,x_k$ and some i such that $\ell _i \unrhd _{\mathtt {acc}}Z\langle x_1,\dots ,x_k\rangle$.

The key idea of this definition is that computability of each $\ell _i$ implies computability of all meta-variables in r. This excludes cases like Example 20 below. Many common examples satisfy this restriction, including those we saw before:

Example 19

Both systems from Example 6 are AFP: choosing the sort ordering $\succeq ^{\mathcal {S}}$ that equates $\mathtt {nat}$ and $\mathtt {list}$, we indeed have $\mathtt {cons}\ H\ T \unrhd _{\mathtt {acc}}H$ and $\mathtt {cons}\ H\ T \unrhd _{\mathtt {acc}}T$ (as $Acc (\mathtt {cons}) = \{1,2\}$) and both $\lambda x{.}Z\langle x\rangle \unrhd _{\mathtt {acc}}Z\langle x\rangle$ and $Z \unrhd _{\mathtt {acc}}Z$. The AFSM from Example 8 is AFP because we can choose $\mathtt {ord} \succ ^{\mathcal {S}}\mathtt {nat}$ and have $\mathtt {lim}\ H \unrhd _{\mathtt {acc}}H$ following Example 12 (and also $\mathtt {s}\ X \unrhd _{\mathtt {acc}}X$ and $K \unrhd _{\mathtt {acc}}K,\ F \unrhd _{\mathtt {acc}}F,\ G \unrhd _{\mathtt {acc}}G$). The AFSM from Example 17 is AFP, because $\lambda x{.}\mathtt {sin}\ F\langle x\rangle \unrhd _{\mathtt {acc}}F\langle x\rangle$ for any $\succeq ^{\mathcal {S}}$: $\lambda x{.}\mathtt {sin}\ F\langle x\rangle \unrhd _{\mathtt {acc}}F\langle x\rangle$ because $\mathtt {sin}\ F\langle x\rangle \unrhd _{\mathtt {acc}}F\langle x\rangle$ because $1 \in Acc (\mathtt {sin})$.

In fact, all first-order AFSMs (where all fully applied sub-meta-terms of the left-hand side of a rule have base type) are AFP via the sort ordering $\succeq ^{\mathcal {S}}$ that equates all sorts. Also (with the same sort ordering), an AFSM $(\mathcal {F},\mathcal {R})$ is AFP if, for all rules $\mathtt {f}\ \ell _1 \cdots \ell _k \Rightarrow r \in \mathcal {R}$ and all $1 \le i \le k$, we can write: $\ell _i = \lambda x_1 \dots x_{n_i}{.}\ell '$ where $n_i \ge 0$ and all fully applied sub-meta-terms of $\ell '$ have base type.

This covers many practical systems, although for Example 8 we need a non-trivial sort ordering. Also, there are AFSMs that cannot be handled with any $\succeq ^{\mathcal {S}}$.

Example 20

(Encoding the untyped $\lambda$-calculus). Consider an AFSM with $\mathcal {F}\supseteq \{ \mathtt {ap} : \mathtt {o} \rightarrow \mathtt {o} \rightarrow \mathtt {o},\ \mathtt {lm} : (\mathtt {o} \rightarrow \mathtt {o}) \rightarrow \mathtt {o} \}$ and $\mathcal {R}= \{ \mathtt {ap}\ (\mathtt {lm}\ F) \Rightarrow F \}$ (note that the only rule has type $\mathtt {o} \rightarrow \mathtt {o}$). This AFSM is not accessible function passing, because $\mathtt {lm}\ F \unrhd _{\mathtt {acc}}F$ cannot hold for any $\succeq ^{\mathcal {S}}$ (as this would require $\mathtt {o} \succ ^{\mathcal {S}}\mathtt {o}$).

Note that this example is also not terminating. With $t = \mathtt {lm}\ (\lambda x{.}\mathtt {ap}\ x\ x)$, we get this self-loop as evidence: $\mathtt {ap}\ t\ t\ \Rightarrow _{\mathcal {R}} (\lambda x{.}\mathtt {ap}\ x\ x)\ t \Rightarrow _{\beta } \mathtt {ap}\ t\ t$.

Intuitively: in an accessible function passing AFSM, meta-variables of a higher type may occur only in “safe” places in the left-hand sides of rules. Rules like the ones in Example 20, where a higher-order meta-variable is lifted out of a base-type term, are not admitted (unless the base type is greater than the higher type).

In the remainder of this paper, we will refer to a properly applied, accessible function passing AFSM as a PA-AFP AFSM.

Discussion: This definition is strictly more liberal than the notions of “plain function passing” in both [34] and [46] as adapted to AFSMs. The notion in [46] largely corresponds to AFP if $\succeq ^{\mathcal {S}}$ equates all sorts, and the HRS formalism guarantees that rules are properly applied (in fact, all fully applied sub-meta-terms of both left- and right-hand sides of rules have base type). The notion in [34] is more restrictive. The current restriction of PA-AFP AFSMs lets us handle examples like ordinal recursion (Example 8) which are not covered by [34, 46]. However, note that [34, 46] consider a different formalism, which does take rules whose left-hand side is not a pattern into account (which we do not consider). Our restriction also quite resembles the “admissible” rules in [6] which are defined using a pattern computability closure [5], but that work carries additional restrictions.

In later work [32, 33], Kusakari extends the static DP approach to forms of polymorphic functional programming, with a very liberal restriction: the definition is parametrised with an arbitrary RC-set and corresponding accessibility (“safety”) notion. Our AFP restriction is actually an instance of this condition (although a more liberal one than the example RC-set used in [32, 33]). We have chosen a specific instance because it allows us to use dedicated techniques for the RC-set; for example, our computable subterm criterion processor (Theorem 63).

4 Static Higher-Order Dependency Pairs

To obtain sufficient criteria for both termination and non-termination of AFSMs, we will now transpose the definition of static dependency pairs [6, 33, 34, 46] to AFSMs. In addition, we will add the new features of meta-variable conditions, formative reductions, and computable chains. Complete versions of all proof sketches in this section are available in [17, Appendix B].

Although we retain the first-order terminology of dependency pairs, the setting with meta-variables makes it more suitable to define DPs as triples.

Definition 21

((Static) Dependency Pair). A dependency pair (DP) is a triple $\ell \Rrightarrow p\ (A)$, where $\ell$ is a closed pattern $\mathtt {f}\ \ell _1 \cdots \ell _k$, p is a closed meta-term $\mathtt {g}\ p_1 \cdots p_n$, and A is a set of meta-variable conditions: pairs Z : i indicating that Z regards its $i^{\text {th}}$ argument. A DP is conservative if $FMV (p) \subseteq FMV (\ell )$.

A substitution $\gamma$ respects a set of meta-variable conditions A if for all Z : i in A we have $\gamma (Z) = \lambda x_1 \dots x_j{.}t$ with either $i > j$, or $i \le j$ and $x_i \in FV (t)$. DPs will be used only with substitutions that respect their meta-variable conditions.

For $\ell \Rrightarrow p\ (\emptyset )$ (so a DP whose set of meta-variable conditions is empty), we often omit the third component and just write $\ell \Rrightarrow p$.

Like the first-order setting, the static DP approach employs marked function symbols to obtain meta-terms whose instances cannot be reduced at the root.

Definition 22

(Marked symbols). Let $(\mathcal {F},\mathcal {R})$ be an AFSM. Define $\mathcal {F}^\sharp := \mathcal {F}\uplus \{ \mathtt {f}^\sharp : \sigma \mid \mathtt {f}: \sigma \in \mathcal {D}\}$. For a meta-term $s = \mathtt {f}\ s_1 \cdots s_k$ with $\mathtt {f}\in \mathcal {D}$ and $k= minar (\mathtt {f})$, we let $s^\sharp = \mathtt {f}^\sharp \ s_1 \cdots s_k$; for s of other forms $s^\sharp$ is not defined.

Moreover, we will consider candidates. In the first-order setting, candidate terms are subterms of the right-hand sides of rules whose root symbol is a defined symbol. Intuitively, these subterms correspond to function calls. In the current setting, we have to consider also meta-variables as well as rules whose right-hand side is not $\beta$-normal (which might arise for instance due to $\eta$-expansion).

Definition 23

($\beta$-reduced-sub-meta-term, $\unrhd _{\beta }$, $\unrhd _{A}$). A meta-term s has a fully applied $\beta$-reduced-sub-meta-term t (shortly, BRSMT), notation $s \unrhd _{\beta } t$, if there exists a set of meta-variable conditions A with $s \unrhd _{A} t$. Here $s \unrhd _{A} t$ holds if:

• $s = t$, or

• $s = \lambda x{.}u$ and $u \unrhd _{A} t$, or

• $s = (\lambda x{.}u)\ s_0 \cdots s_n$ and some $s_i \unrhd _{A} t$, or $u[x:=s_0]\ s_1 \cdots s_n \unrhd _{A} t$, or

• $s = a\ s_1 \cdots s_n$ with $a \in \mathcal {F}\cup \mathcal {V}$ and some $s_i \unrhd _{A} t$, or

• $s = Z\langle t_1,\dots ,t_k\rangle \ s_1 \cdots s_n$ and some $s_i \unrhd _{A} t$, or

• $s = Z\langle t_1,\dots ,t_k\rangle \ s_1 \cdots s_n$ and $t_i \unrhd _{A} t$ for some $i \in \{1,\dots ,k\}$ with $(Z : i) \in A$.

Essentially, $s \,\unrhd _{A}\, t$ means that t can be reached from s by taking $\beta$-reductions at the root and “subterm”-steps, where Z : i is in A whenever we pass into argument i of a meta-variable Z. BRSMTs are used to generate candidates:

Definition 24

(Candidates). For a meta-term s, the set $\mathsf {cand}(s)$ of candidates of s consists of those pairs $t\ (A)$ such that (a) t has the form $\mathtt {f}\ s_1 \cdots s_k$ with $\mathtt {f} \in \mathcal {D}$ and $k= minar (\mathtt {f})$, and (b) there are $s_{k+1},\dots ,s_n$ (with $n \ge k$) such that $s \unrhd _{A} t\ s_{k+1} \cdots s_n$, and (c) A is minimal: there is no subset $A' \subsetneq A$ with $s \unrhd _{A'} t$.

Example 25

In AFSMs where all meta-variables have arity 0 and the right-hand sides of rules are $\beta$-normal, the set $\mathsf {cand}(s)$ for a meta-term s consists exactly of the pairs $t\ (\emptyset )$ where t has the form $\mathtt {f}\ s_1 \cdots s_{ minar (\mathtt {f})}$ and t occurs as part of s. In Example 8, we thus have $\mathsf {cand}(G\ H\ (\lambda m{.}\mathtt {rec}\ (H\ m)\ K\ F\ G)) =\{\,\mathtt {rec}\ (H\ m)\ K\ F\ G\ (\emptyset )\,\}$.

If some of the meta-variables do take arguments, then the meta-variable conditions matter: candidates of s are pairs $t\ (A)$ where A contains exactly those pairs Z : i for which we pass through the $i^{\text {th}}$ argument of Z to reach t in s.

Example 26

Consider an AFSM with the signature from Example 8 but a rule using meta-variables with larger arities:

$$ \begin{array}{c} \mathtt {rec}\ (\mathtt {lim}\ (\lambda n{.}H\langle n\rangle ))\ K\ (\lambda x{.}\lambda n{.}F\langle x,n\rangle )\ (\lambda f{.}\lambda g{.}G\langle f,g\rangle )\ \Rightarrow \\ G\langle \lambda n{.}H\langle n\rangle ,\ \lambda m{.}\mathtt {rec}\ H\langle m\rangle \ K\ (\lambda x{.}\lambda n{.}F\langle x,n\rangle )\ (\lambda f{.}\lambda g{.}G\langle f,g\rangle )\rangle \end{array} $$

The right-hand side has one candidate:

$$ \mathtt {rec}\ H\langle m\rangle \ K\ (\lambda x{.}\lambda n{.}F\langle x,n\rangle )\ (\lambda f{.}\lambda g{.}G\langle f,g\rangle )\ (\{G : 2 \}) $$

The original static approaches define DPs as pairs $\ell ^\sharp \Rrightarrow p^\sharp$ where $\ell \Rightarrow r$ is a rule and p a subterm of r of the form $\mathtt {f}\ r_1 \cdots r_m$ – as their rules are built using terms, not meta-terms. This can set variables bound in r free in p. In the current setting, we use candidates with their meta-variable conditions and implicit $\beta$-steps rather than subterms, and we replace such variables by meta-variables.

Definition 27

($SDP$). Let s be a meta-term and $(\mathcal {F},\mathcal {R})$ be an AFSM. Let $metafy (s)$ denote s with all free variables replaced by corresponding meta-variables. Now $SDP (\mathcal {R}) = \{ \ell ^\sharp \Rrightarrow metafy (p^\sharp )\ (A) \mid \ell \Rightarrow r \in \mathcal {R}\wedge p\ (A) \in \mathsf {cand}(r) \}$.

Although static DPs always have a pleasant form $\mathtt {f}^\sharp \ \ell _1 \cdots \ell _k \Rrightarrow \mathtt {g}^\sharp \ p_1 \cdots p_n\ (A)$ (as opposed to the dynamic DPs of, e.g., [31], whose right-hand sides can have a meta-variable at the head, which complicates various techniques in the framework), they have two important complications not present in first-order DPs: the right-hand side p of a DP $\ell \Rrightarrow p\ (A)$ may contain meta-variables that do not occur in the left-hand side $\ell$ – traditional analysis techniques are not really equipped for this – and the left- and right-hand sides may have different types. In Sect. 5 we will explore some methods to deal with these features.

Example 28

For the non-$\eta$-expanded rules of Example 17, the set $SDP (\mathcal {R})$ has one element: $\mathtt {deriv}^\sharp \ (\lambda x{.}\mathtt {sin}\ F\langle x\rangle ) \Rrightarrow \mathtt {deriv}^\sharp \ (\lambda x{.}F\langle x\rangle )$. (As $\mathtt {times}$ and $\mathtt {cos}$ are not defined symbols, they do not generate dependency pairs.) The set $SDP (\mathcal {R}^\uparrow )$ for the $\eta$-expanded rules is $\{ \mathtt {deriv}^\sharp \ (\lambda x{.}\mathtt {sin}\ F\langle x\rangle )\ Y \Rrightarrow \mathtt {deriv}^\sharp \ (\lambda x{.}F\langle x\rangle )\ Y \}$. To obtain the relevant candidate, we used the $\beta$-reduction step of BRSMTs.

Example 29

The AFSM from Example 8 is AFP following Example 19; here $SDP (\mathcal {R})$ is:

$$ \begin{array}{rcll} \mathtt {rec}^\sharp \ (\mathtt {s}\ X)\ K\ F\ G &{} \Rrightarrow &{} \mathtt {rec}^\sharp \ X\ K\ F\ G\ (\emptyset ) \\ \mathtt {rec}^\sharp \ (\mathtt {lim}\ H)\ K\ F\ G &{} \Rrightarrow &{} \mathtt {rec}^\sharp \ (H\ M)\ K\ F\ G\ (\emptyset ) \\ \end{array} $$

Note that the right-hand side of the second DP contains a meta-variable that is not on the left. As we will see in Example 64, that is not problematic here.

Termination analysis using dependency pairs importantly considers the notion of a dependency chain. This notion is fairly similar to the first-order setting:

Definition 30

(Dependency chain). Let $\mathcal {P}$ be a set of DPs and $\mathcal {R}$ a set of rules. A (finite or infinite) $(\mathcal {P},\mathcal {R})$-dependency chain (or just $(\mathcal {P},\mathcal {R})$-chain) is a sequence $[(\ell _0 \Rrightarrow p_0\ (A_0),s_0,t_0), (\ell _1 \Rrightarrow p_1\ (A_1),s_1,t_1),\ldots ]$ where each $\ell _i \Rrightarrow p_i\ (A_i) \in \mathcal {P}$ and all $s_i,t_i$ are terms, such that for all i:

• 1. there exists a substitution $\gamma$ on domain $FMV (\ell _i) \cup FMV (p_i)$ such that $s_i = \ell _i\gamma ,\ t_i = p_i\gamma$ and for all $Z \in \mathtt {dom}(\gamma )$: $\gamma (Z)$ respects $A_i$;

• 2. we can write $t_i = \mathtt {f}\ u_1 \cdots u_n$ and $s_{i+1} = \mathtt {f}\ w_1 \cdots w_n$ and each $u_j \Rightarrow _{\mathcal {R}}^* w_j$.

Example 31

In the (first) AFSM from Example 6, we have $SDP (\mathcal {R}) = \{ \mathtt {map}^{\sharp }\ (\lambda x{.}Z\langle x\rangle ) (\mathtt {cons}\ H\ T) \Rrightarrow \mathtt {map}^{\sharp }\ (\lambda x{.}Z\langle x\rangle )\ T \}$. An example of a finite dependency chain is $[(\rho ,s_1,t_1),(\rho ,s_2,t_2)]$ where $\rho$ is the one DP, $s_1 = \mathtt {map}^\sharp \ (\lambda x{.}\mathtt {s}\ x)\ (\mathtt {cons}\ \mathtt {0}\ (\mathtt {cons}\ (\mathtt {s}\ \mathtt {0})\ (\mathtt {map}\ (\lambda x{.}x)\ \mathtt {nil})))$ and $t_1 = \mathtt {map}^\sharp \ (\lambda x{.}\mathtt {s}\ x)\ (\mathtt {cons}\ (\mathtt {s}\ \mathtt {0})\ (\mathtt {map}\ (\lambda x{.}x)\ \mathtt {nil}))$ and $s_2 = \mathtt {map}^\sharp \ (\lambda x{.}\mathtt {s}\ x)\ (\mathtt {cons}\ (\mathtt {s}\ \mathtt {0})\ \mathtt {nil})$ and $t_2 = \mathtt {map}^\sharp \ (\lambda x{.}\mathtt {s}\ x)\ \mathtt {nil}$.

Note that here $t_1$ reduces to $s_2$ in a single step ($\mathtt {map}\ (\lambda x{.}x)\ \mathtt {nil}\Rightarrow _{\mathcal {R}} \mathtt {nil}$).

We have the following key result:

Theorem 32

Let $(\mathcal {F},\mathcal {R})$ be a PA-AFP AFSM. If $(\mathcal {F},\mathcal {R})$ is non-terminating, then there is an infinite $( SDP (\mathcal {R}),\mathcal {R})$-dependency chain.

Proof

(sketch). The proof is an adaptation of the one in [34], altered for the more permissive definition of accessible function passing over plain function passing as well as the meta-variable conditions; it also follows from Theorem 37 below.

   $\square$

By this result we can use dependency pairs to prove termination of a given properly applied and AFP AFSM: if we can prove that there is no infinite $( SDP (\mathcal {R}),\mathcal {R})$-chain, then termination follows immediately. Note, however, that the reverse result does not hold: it is possible to have an infinite $( SDP (\mathcal {R}),\mathcal {R})$-dependency chain even for a terminating PA-AFP AFSM.

Example 33

Let $\mathcal {F}\supseteq \{ \mathtt {0},\mathtt {1}: \mathtt {nat}$, $\mathtt {f} : \mathtt {nat}\rightarrow \mathtt {nat}$, $\mathtt {g} : (\mathtt {nat}\rightarrow \mathtt {nat}) \rightarrow \mathtt {nat}\}$ and $\mathcal {R}= \{ \mathtt {f}\ \mathtt {0}\Rightarrow \mathtt {g}\ (\lambda x{.}\mathtt {f}\ x), \mathtt {g}\ (\lambda x{.} F\langle x\rangle ) \Rightarrow F\langle \mathtt {1}\rangle \}$. This AFSM is PA-AFP, with $SDP (\mathcal {R}) = \{ \mathtt {f}^\sharp \ \mathtt {0}\Rrightarrow \mathtt {g}^\sharp \ (\lambda x{.}\mathtt {f}\ x),\ \mathtt {f}^\sharp \ \mathtt {0}\Rrightarrow \mathtt {f}^\sharp \ X\}$; the second rule does not cause the addition of any dependency pairs. Although $\Rightarrow _{\mathcal {R}}$ is terminating, there is an infinite $( SDP (\mathcal {R}),\mathcal {R})$-chain $[(\mathtt {f}^\sharp \ \mathtt {0}\Rrightarrow \mathtt {f}^\sharp \ X, \mathtt {f}^\sharp \ \mathtt {0}, \mathtt {f}^\sharp \ \mathtt {0}), (\mathtt {f}^\sharp \ \mathtt {0}\Rrightarrow \mathtt {f}^\sharp \ X, \mathtt {f}^\sharp \ \mathtt {0}, \mathtt {f}^\sharp \ \mathtt {0}),\ldots ]$.

The problem in Example 33 is the non-conservative DP $\mathtt {f}^\sharp \ \mathtt {0}\Rrightarrow \mathtt {f}^\sharp \ X$, with X on the right but not on the left. Such DPs arise from abstractions in the right-hand sides of rules. Unfortunately, abstractions are introduced by the restricted $\eta$-expansion (Definition 15) that we may need to make an AFSM properly applied. Even so, often all DPs are conservative, like Examples 6 and 17. There, we do have the inverse result:

Theorem 34

For any AFSM $(\mathcal {F},\mathcal {R})$: if there is an infinite $( SDP (\mathcal {R}),\mathcal {R})$-chain $[(\rho _0, s_0, t_0),(\rho _1, s_1, t_1),\ldots ]$ with all $\rho _i$ conservative, then $\Rightarrow _{\mathcal {R}}$ is non-terminating.

Proof

(sketch). If $FMV (p_i) \subseteq FMV (\ell _i)$, then we can see that $s_i \Rightarrow _{\mathcal {R}} \cdot \Rightarrow _{\beta }^* t_i'$ for some term $t_i'$ of which $t_i$ is a subterm. Since also each $t_i \Rightarrow _{\mathcal {R}}^* s_{ i+1}$, the infinite chain induces an infinite reduction $s_0 \Rightarrow _{\mathcal {R}}^+ t_0' \Rightarrow _{\mathcal {R}}^* s_1' \Rightarrow _{\mathcal {R}}^+ t_1'' \Rightarrow _{\mathcal {R}}^* \dots$.    $\square$

The core of the dependency pair framework is to systematically simplify a set of pairs $(\mathcal {P},\mathcal {R})$ to prove either absence or presence of an infinite $(\mathcal {P},\mathcal {R})$-chain, thus showing termination or non-termination as appropriate. By Theorems 32 and 34 we can do so, although with some conditions on the non-termination result. We can do better by tracking certain properties of dependency chains.

Definition 35

(Minimal and Computable chains). Let $(\mathcal {F},{\mathcal {U}})$ be an AFSM and $C_{{\mathcal {U}}}$ an RC-set satisfying the properties of Theorem 13 for $(\mathcal {F},{\mathcal {U}})$. Let $\mathcal {F}$ contain, for every type $\sigma$, at least countably many symbols $\mathtt {f}: \sigma$ not used in ${\mathcal {U}}$.

A $(\mathcal {P},\mathcal {R})$-chain $[(\rho _0,s_0,t_0),(\rho _1,s_1,t_1),\ldots ]$ is ${\mathcal {U}}$-computable if: $\Rightarrow _{{\mathcal {U}}} \mathop {\supseteq } \Rightarrow _{\mathcal {R}}$, and for all $i \in \mathbb {N}$ there exists a substitution $\gamma _i$ such that $\rho _i = \ell _i \Rrightarrow p_i\ (A_i)$ with $s_i = \ell _i \gamma _i$ and $t_i = p_i\gamma _i$, and $(\lambda x_1 \dots x_n{.}v)\gamma _i$ is $C_{{\mathcal {U}}}$-computable for all v and B such that $p_i \unrhd _{B} v$, $\gamma _i$ respects B, and $FV (v) = \{x_1,\dots ,x_n\}$.

A chain is minimal if the strict subterms of all $t_i$ are terminating under $\Rightarrow _{\mathcal {R}}$.

In the first-order DP framework, minimal chains give access to several powerful techniques to prove absence of infinite chains, such as the subterm criterion [24] and usable rules [22, 24]. Computable chains go a step further, by building on the computability inherent in the proof of Theorem 32 and the notion of accessible function passing AFSMs. In computable chains, we can require that (some of) the subterms of all $t_i$ are computable rather than merely terminating. This property will be essential in the computable subterm criterion processor (Theorem 63).

Another property of dependency chains is the use of formative rules, which has proven very useful for dynamic DPs [31]. Here we go further and consider formative reductions, which were introduced for the first-order DP framework in [16]. This property will be essential in the formative rules processor (Theorem 58).

Definition 36

(Formative chain, formative reduction). A $(\mathcal {P},\mathcal {R})$-chain $[(\ell _0 \Rrightarrow p_0\ (A_0),s_0,t_0), (\ell _1 \Rrightarrow p_1\ (A_1),s_1,t_1),\ldots ]$ is formative if for all i, the reduction $t_i \Rightarrow _{\mathcal {R}}^* s_{i+1}$ is $\ell _{i+1}$-formative. Here, for a pattern $\ell$, substitution $\gamma$ and term s, a reduction $s \Rightarrow _{\mathcal {R}}^* \ell \gamma$ is $\ell$-formative if one of the following holds:

• $\ell$ is not a fully extended linear pattern; that is: some meta-variable occurs more than once in $\ell$ or $\ell$ has a sub-meta-term $\lambda x{.}C[Z\langle \mathbf {s}\rangle ]$ with $x \notin \{ \mathbf {s}\}$

• $\ell$ is a meta-variable application $Z\langle x_1,\dots ,x_k\rangle$ and $s = \ell \gamma$

• $s = a\ s_1 \cdots s_n$ and $\ell = a\ \ell _1 \cdots \ell _n$ with $a \in \mathcal {F}^\sharp \cup \mathcal {V}$ and each $s_i \Rightarrow _{\mathcal {R}}^* \ell _i \gamma$ by an $\ell _i$-formative reduction

• $s = \lambda x{.}s'$ and $\ell = \lambda x{.}\ell '$ and $s' \Rightarrow _{\mathcal {R}}^* \ell '\gamma$ by an $\ell '$-formative reduction

• $s = (\lambda x{.}u)\ v\ w_1 \cdots w_n$ and $u[x:=v]\ w_1 \cdots w_n \Rightarrow _{\mathcal {R}}^* \ell \gamma$ by an $\ell$-formative reduction

• $\ell$ is not a meta-variable application, and there are $\ell ' \Rightarrow r' \in \mathcal {R}$, meta-variables $Z_1 \dots Z_n$ ($n \ge 0$) and $\delta$ such that $s \Rightarrow _{\mathcal {R}}^* (\ell '\ Z_1 \cdots Z_n)\delta$ by an $(\ell '\ Z_1 \cdots Z_n)$-formative reduction, and $(r'\ Z_1 \cdots Z_n)\delta \Rightarrow _{\mathcal {R}}^* \ell \gamma$ by an $\ell$-formative reduction.

The idea of a formative reduction is to avoid redundant steps: if $s \Rightarrow _{\mathcal {R}}^* \ell \gamma$ by an $\ell$-formative reduction, then this reduction takes only the steps needed to obtain an instance of $\ell$. Suppose that we have rules $\mathtt {plus}\ \mathtt {0}\ Y \Rightarrow Y,\ \mathtt {plus}\ (\mathtt {s}\ X)\ Y \Rightarrow \mathtt {s}\ (\mathtt {plus}\ X\ Y)$. Let $\ell := \mathtt {g}\ \mathtt {0}\ X$ and $t := \mathtt {plus}\ \mathtt {0}\ \mathtt {0}$. Then the reduction $\mathtt {g}\ t\ t \Rightarrow _{\mathcal {R}} \mathtt {g}\ \mathtt {0}\ t$ is $\ell$-formative: we must reduce the first argument to get an instance of $\ell$. The reduction $\mathtt {g}\ t\ t \Rightarrow _{\mathcal {R}} \mathtt {g}\ t\ \mathtt {0}\Rightarrow _{\mathcal {R}} \mathtt {g}\ \mathtt {0}\ \mathtt {0}$ is not $\ell$-formative, because the reduction in the second argument does not contribute to the non-meta-variable positions of $\ell$. This matters when we consider $\ell$ as the left-hand side of a rule, say $\mathtt {g}\ \mathtt {0}\ X \Rightarrow \mathtt {0}$: if we reduce $\mathtt {g}\ t\ t \Rightarrow _{\mathcal {R}} \mathtt {g}\ t\ \mathtt {0}\Rightarrow _{\mathcal {R}} \mathtt {g}\ \mathtt {0}\ \mathtt {0}\Rightarrow _{\mathcal {R}} \mathtt {0}$, then the first step was redundant: removing this step gives a shorter reduction to the same result: $\mathtt {g}\ t\ t \Rightarrow _{\mathcal {R}} \mathtt {g}\ \mathtt {0}\ t \Rightarrow _{\mathcal {R}} \mathtt {0}$. In an infinite reduction, redundant steps may also be postponed indefinitely.

We can now strengthen the result of Theorem 32 with two new properties.

Theorem 37

Let $(\mathcal {F},\mathcal {R})$ be a properly applied, accessible function passing AFSM. If $(\mathcal {F},\mathcal {R})$ is non-terminating, then there is an infinite $\mathcal {R}$-computable formative $( SDP (\mathcal {R}),\mathcal {R})$-dependency chain.

Proof

(sketch). We select a minimal non-computable (MNC) term $s := \mathtt {f}\ s_1 \cdots s_k$ (where all $s_i$ are $C_\mathcal {R}$-computable) and an infinite reduction starting in s. Then we stepwise build an infinite dependency chain, as follows. Since s is non-computable but each $s_i$ terminates (as computability implies termination), there exist a rule $\mathtt {f}\ \ell _1 \cdots \ell _k \Rightarrow r$ and substitution $\gamma$ such that each $s_i \Rightarrow _{\mathcal {R}}^* \ell _i\gamma$ and $r\gamma$ is non-computable. We can then identify a candidate $t\ (A)$ of r such that $\gamma$ respects A and $t\gamma$ is a MNC subterm of $r\gamma$; we continue the process with $t\gamma$ (or a term at its head). For the formative property, we note that if $s \Rightarrow _{\mathcal {R}}^* \ell \gamma$ and u is terminating, then $u \Rightarrow _{\mathcal {R}}^* \ell \delta$ by an $\ell$-formative reduction for substitution $\delta$ such that each $\delta (Z) \Rightarrow _{\mathcal {R}}^* \gamma (Z)$. This follows by postponing those reduction steps not needed to obtain an instance of $\ell$. The resulting infinite chain is $\mathcal {R}$-computable because we can show, by induction on the definition of $\unrhd _{\mathtt {acc}}$, that if $\ell \Rightarrow r$ is an AFP rule and $\ell \gamma$ is a MNC term, then $\gamma (Z)$ is $C_{\mathcal {R}}$-computable for all $Z \in FMV (r)$.    $\square$

As it is easily seen that all $C_{{\mathcal {U}}}$-computable terms are $\Rightarrow _{{\mathcal {U}}}$-terminating and therefore $\Rightarrow _{\mathcal {R}}$-terminating, every ${\mathcal {U}}$-computable $(\mathcal {P},\mathcal {R})$-dependency chain is also minimal. The notions of $\mathcal {R}$-computable and formative chains still do not suffice to obtain a true inverse result, however (i.e., to prove that termination implies the absence of an infinite $\mathcal {R}$-computable chain over $SDP (\mathcal {R})$): the infinite chain in Example 33 is $\mathcal {R}$-computable.

To see why the two restrictions that the AFSM must be properly applied and accessible function passing are necessary, consider the following examples.

Example 38

Consider $\mathcal {F}\supseteq \{ \mathtt {fix}: ((\mathtt {o} \rightarrow \mathtt {o}) \rightarrow \mathtt {o} \rightarrow \mathtt {o}) \rightarrow \mathtt {o} \rightarrow \mathtt {o} \}$ and $\mathcal {R}= \{ \mathtt {fix}\ F\ X \Rightarrow F\ (\mathtt {fix}\ F)\ X \}$. This AFSM is not properly applied; it is also not terminating, as can be seen by instantiating F with $\lambda y{.}y$. However, it does not have any static DPs, since $\mathtt {fix}\ F$ is not a candidate. Even if we altered the definition of static DPs to admit a dependency pair $\mathtt {fix}^\sharp \ F\ X \Rrightarrow \mathtt {fix}^\sharp \ F$, this pair could not be used to build an infinite dependency chain.

Note that the problem does not arise if we study the $\eta$-expanded rules $\mathcal {R}^\uparrow = \{ \mathtt {fix}\ F\ X \Rightarrow F\ (\lambda z{.}\mathtt {fix}\ F\ z)\ X \}$, as the dependency pair $\mathtt {fix}^\sharp \ F\ X \Rrightarrow \mathtt {fix}^\sharp \ F\ Z$ does admit an infinite chain. Unfortunately, as the one dependency pair does not satisfy the conditions of Theorem 34, we cannot use this to prove non-termination.

Example 39

The AFSM from Example 20 is not accessible function passing, since $Acc (\mathtt {lm}) = \emptyset$. This is good because the set $SDP (\mathcal {R})$ is empty, which would lead us to falsely conclude termination without the restriction.

Discussion: Theorem 37 transposes the work of [34, 46] to AFSMs and extends it by using a more liberal restriction, by limiting interest to formative, $\mathcal {R}$-computable chains, and by including meta-variable conditions. Both of these new properties of chains will support new termination techniques within the DP framework.

The relationship with the works for functional programming [32, 33] is less clear: they define a different form of chains suited well to polymorphic systems, but which requires more intricate reasoning for non-polymorphic systems, as DPs can be used for reductions at the head of a term. It is not clear whether there are non-polymorphic systems that can be handled with one and not the other. The notions of formative and $\mathcal {R}$-computable chains are not considered there; meta-variable conditions are not relevant to their $\lambda$-free formalism.

5 The Static Higher-Order DP Framework

In first-order term rewriting, the DP framework [20] is an extendable framework to prove termination and non-termination. As observed in the introduction, DP analyses in higher-order rewriting typically go beyond the initial DP approach [2], but fall short of the full framework. Here, we define the latter for static DPs. Complete versions of all proof sketches in this section are in [17, Appendix C].

We have now reduced the problem of termination to non-existence of certain chains. In the DP framework, we formalise this in the notion of a DP problem:

Definition 40

(DP problem). A DP problem is a tuple $(\mathcal {P},\mathcal {R},m,f)$ with $\mathcal {P}$ a set of DPs, $\mathcal {R}$ a set of rules, $m \in \{ \mathtt {minimal}, \mathtt {arbitrary}\} \cup \{ \mathtt {computable}_{\mathcal {U}}\mid \text {any set of rules}\ {\mathcal {U}}\}$, and $f \in \{ \mathtt {formative}, \mathtt {all}\}$.³

A DP problem $(\mathcal {P},\mathcal {R},m,f)$ is finite if there exists no infinite $(\mathcal {P},\mathcal {R})$-chain that is ${\mathcal {U}}$-computable if $m = \mathtt {computable}_{\mathcal {U}}$, is minimal if $m = \mathtt {minimal}$, and is formative if $f = \mathtt {formative}$. It is infinite if $\mathcal {R}$ is non-terminating, or if there exists an infinite $(\mathcal {P},\mathcal {R})$-chain where all DPs used in the chain are conservative.

To capture the levels of permissiveness in the m flag, we use a transitive-reflexive relation $\succeq$ generated by $\mathtt {computable}_{{\mathcal {U}}} \succeq \mathtt {minimal}\succeq \mathtt {arbitrary}$.

Thus, the combination of Theorems 34 and 37 can be rephrased as: an AFSM $(\mathcal {F},\mathcal {R})$ is terminating if $( SDP (\mathcal {R}),\mathcal {R},\mathtt {computable}_\mathcal {R},\mathtt {formative})$ is finite, and is non-terminating if $( SDP (\mathcal {R}),\mathcal {R},m,f)$ is infinite for some $m \in \{\mathtt {computable}_{\mathcal {U}},\mathtt {minimal},\mathtt {arbitrary}\}$ and $f \in \{\mathtt {formative},\mathtt {all}\}$.⁴

The core idea of the DP framework is to iteratively simplify a set of DP problems via processors until nothing remains to be proved:

Definition 41

(Processor). A dependency pair processor (or just processor) is a function that takes a DP problem and returns either NO or a set of DP problems. A processor $Proc$ is sound if a DP problem $M$ is finite whenever $Proc (M) \ne \texttt {NO}$ and all elements of $Proc (M)$ are finite. A processor $Proc$ is complete if a DP problem $M$ is infinite whenever $Proc (M) = \texttt {NO}$ or contains an infinite element.

To prove finiteness of a DP problem $M$ with the DP framework, we proceed analogously to the first-order DP framework [22]: we repeatedly apply sound DP processors starting from $M$ until none remain. That is, we execute the following rough procedure: (1) let $A := \{ M\}$; (2) while $A \ne \emptyset$: select a problem $Q\in A$ and a sound processor $Proc$ with $Proc (Q) \ne \texttt {NO}$, and let $A := (A \setminus \{ Q\}) \cup Proc (Q)$. If this procedure terminates, then $M$ is a finite DP problem.

To prove termination of an AFSM $(\mathcal {F},\mathcal {R})$, we would use as initial DP problem $( SDP (\mathcal {R}),\mathcal {R},\mathtt {computable}_{\mathcal {R}},\mathtt {formative})$, provided that $\mathcal {R}$ is properly applied and accessible function passing (where $\eta$-expansion following Definition 15 may be applied first). If the procedure terminates – so finiteness of $M$ is proved by the definition of soundness – then Theorem 37 provides termination of $\Rightarrow _{\mathcal {R}}$.

Similarly, we can use the DP framework to prove infiniteness: (1) let $A := \{ M\}$; (2) while $A \ne \texttt {NO}$: select a problem $Q\in A$ and a complete processor $Proc$, and let $A := \texttt {NO}$ if $Proc (Q) = \texttt {NO}$, or $A := (A \setminus \{ Q\}) \cup Proc (Q)$ otherwise. For non-termination of $(\mathcal {F},\mathcal {R})$, the initial DP problem should be $( SDP (\mathcal {R}),\mathcal {R},m,f)$, where m, f can be any flag (see Theorem 34). Note that the algorithms coincide while processors are used that are both sound and complete. In a tool, automation (or the user) must resolve the non-determinism and select suitable processors.

Below, we will present a number of processors within the framework. We will typically present processors by writing “for a DP problem $M$ satisfying X, Y, Z, $Proc (M) = \dots$”. In these cases, we let $Proc (M) = \{ M\}$ for any problem $M$ not satisfying the given properties. Many more processors are possible, but we have chosen to present a selection which touches on all aspects of the DP framework:

• processors which map a DP problem to $\texttt {NO}$ (Theorem 65), a singleton set (most processors) and a non-singleton set (Theorem 42);

• changing the set $\mathcal {R}$ (Theorems 54, 58) and various flags (Theorem 54);

• using specific values of the f (Theorem 58) and m flags (Theorems 54, 61, 63);

• using term orderings (Theorems 49, 52), a key part of many termination proofs.

5.1 The Dependency Graph

We can leverage reachability information to decompose DP problems. In first-order rewriting, a graph structure is used to track which DPs can possibly follow one another in a chain [2]. Here, we define this dependency graph as follows.

Definition 42

(Dependency graph). A DP problem $(\mathcal {P},\mathcal {R},m,f)$ induces a graph structure $DG$, called its dependency graph, whose nodes are the elements of $\mathcal {P}$. There is a (directed) edge from $\rho _1$ to $\rho _2$ in $DG$ iff there exist $s_1,t_1,s_2,t_2$ such that $[(\rho _1,s_1,t_1),(\rho _2,s_2,t_2)]$ is a $(\mathcal {P},\mathcal {R})$-chain with the properties for m, f.

Example 43

Consider an AFSM with $\mathcal {F}\supseteq \{ \mathtt {f} : (\mathtt {nat}\rightarrow \mathtt {nat}) \rightarrow \mathtt {nat}\rightarrow \mathtt {nat}\}$ and $\mathcal {R}= \{ \mathtt {f}\ (\lambda x{.}F\langle x\rangle )\ (\mathtt {s}\ Y) \Rightarrow F\langle \mathtt {f}\ (\lambda x{.}\mathtt {0})\ (\mathtt {f}\ (\lambda x{.}F\langle x\rangle )\ Y)\rangle \}$. Let $\mathcal {P}:= SDP (\mathcal {R}) =$

$$ \left\{ \begin{array}{rrcll} (1) &{} \mathtt {f}^\sharp \ (\lambda x{.}F\langle x\rangle )\ (\mathtt {s}\ Y) &{} \Rrightarrow &{} \mathtt {f}^\sharp \ (\lambda x{.}\mathtt {0})\ (\mathtt {f}\ (\lambda x{.}F\langle x\rangle )\ Y) &{} (\{ F : 1 \}) \\ (2) &{} \mathtt {f}^\sharp \ (\lambda x{.}F\langle x\rangle )\ (\mathtt {s}\ Y) &{} \Rrightarrow &{} \mathtt {f}^\sharp \ (\lambda x{.}F\langle x\rangle )\ Y &{} (\{ F : 1 \}) \\ \end{array} \right\} $$

The dependency graph of $(\mathcal {P},\mathcal {R},\mathtt {minimal},\mathtt {formative})$ is:

There is no edge from (1) to itself or (2) because there is no substitution $\gamma$ such that $(\lambda x{.}\mathtt {0})\gamma$ can be reduced to a term $(\lambda x{.}F\langle x\rangle )\delta$ where $\delta (F)$ regards its first argument (as $\Rightarrow _{\mathcal {R}}^*$ cannot introduce new variables).

In general, the dependency graph for a given DP problem is undecidable, which is why we consider approximations.

Definition 44

(Dependency graph approximation [31]). A finite graph $G_\theta$ approximates $DG$ if $\theta$ is a function that maps the nodes of $DG$ to the nodes of $G_\theta$ such that, whenever $DG$ has an edge from $\rho _1$ to $\rho _2$, $G_\theta$ has an edge from $\theta (\rho _1)$ to $\theta (\rho _2)$. ($G_\theta$ may have edges that have no corresponding edge in $DG$.)

Note that this definition allows for an infinite graph to be approximated by a finite one; infinite graphs may occur if $\mathcal {R}$ is infinite (e.g., the union of all simply-typed instances of polymorphic rules).

If $\mathcal {P}$ is finite, we can take a graph approximation $G_{\mathtt {id}}$ with the same nodes as $DG$. A simple approximation may have an edge from $\ell _1 \Rrightarrow p_1\ (A_1)$ to $\ell _2 \Rrightarrow p_2\ (A_2)$ whenever both $p_1$ and $\ell _2$ have the form $\mathtt {f}^\sharp \ s_1 \cdots s_k$ for the same $\mathtt {f}$ and $k$. However, one can also take the meta-variable conditions into account, as we did in Example 43.

Theorem 45

(Dependency graph processor). The processor $Proc _{G_\theta }$ that maps a DP problem $M= (\mathcal {P},\mathcal {R},m,f)$ to $\{ (\{ \rho \in \mathcal {P}\mid \theta (\rho ) \in C_i \},\mathcal {R},m,f) \mid 1 \le i \le n \}$ if $G_\theta$ is an approximation of the dependency graph of $M$ and $C_1,\dots ,C_n$ are the (nodes of the) non-trivial strongly connected components (SCCs) of $G_\theta$, is both sound and complete.

Proof

(sketch). In an infinite $(\mathcal {P},\mathcal {R})$-chain $[(\rho _0,s_0,t_0),(\rho _1,s_1,t_1),\ldots ]$, there is always a path from $\rho _i$ to $\rho _{i+1}$ in DG. Since $G_\theta$ is finite, every infinite path in DG eventually remains in a cycle in $G_\theta$. This cycle is part of an SCC.    $\square$

Example 46

Let $\mathcal {R}$ be the set of rules from Example 43 and G be the graph given there. Then $Proc _{G}( SDP (\mathcal {R}),\mathcal {R}, \mathtt {computable}_\mathcal {R},\mathtt {formative}) = \{ (\{ \mathtt {f}^\sharp \ (\lambda x{.}F\langle x\rangle )\ (\mathtt {s}\ Y) \Rrightarrow \mathtt {f}^\sharp \ (\lambda x{.}F\langle x\rangle )\ Y\ (\{ F : 1 \}) \}, \mathcal {R}, \mathtt {computable}_\mathcal {R},\mathtt {formative}) \}$.

Example 47

Let $\mathcal {R}$ consist of the rules for $\mathtt {map}$ from Example 6 along with $\mathtt {f}\ L \Rightarrow \mathtt {map}\ (\lambda x{.} \mathtt {g}\ x)\ L$ and $\mathtt {g}\ X \Rightarrow X$. Then $SDP (\mathcal {R}) = \{ (1)\ \mathtt {map}^\sharp \ (\lambda x{.}Z\langle x\rangle )\ (\mathtt {cons}\ H\ T)$ $\Rrightarrow \mathtt {map}^\sharp \ (\lambda x{.}Z\langle x\rangle )\ T,\ (2)\ \mathtt {f}^\sharp \ L \Rrightarrow \mathtt {map}^\sharp \ (\lambda x{.}\mathtt {g}\ x)\ L,\ (3)\ \mathtt {f}^\sharp \ L \Rrightarrow \mathtt {g}^\sharp \ X \}$. DP (3) is not conservative, but it is not on any cycle in the graph approximation $G_{\mathtt {id}}$ obtained by considering head symbols as described above:

As (1) is the only DP on a cycle, $Proc _{ SDP _{G_{\mathtt {id}}}}( SDP (\mathcal {R}),\mathcal {R}, \mathtt {computable}_\mathcal {R},\mathtt {formative}) = \{\ (\{(1)\},\mathcal {R},\mathtt {computable}_\mathcal {R},\mathtt {formative})\ \}$.

Discussion: The dependency graph is a powerful tool for simplifying DP problems, used since early versions of the DP approach [2]. Our notion of a dependency graph approximation, taken from [31], strictly generalises the original notion in [2], which uses a graph on the same node set as DG with possibly further edges. One can get this notion here by using a graph $G_{\mathtt {id}}$. The advantage of our definition is that it ensures soundness of the dependency graph processor also for infinite sets of DPs. This overcomes a restriction in the literature [34, Corollary 5.13] to dependency graphs without non-cyclic infinite paths.

5.2 Processors Based on Reduction Triples

At the heart of most DP-based approaches to termination proving lie well-founded orderings to delete DPs (or rules). For this, we use reduction triples [24, 31].

Definition 48

(Reduction triple). A reduction triple $(\succsim ,\succcurlyeq ,\succ )$ consists of two quasi-orderings $\succsim$ and $\succcurlyeq$ and a well-founded strict ordering $\succ$ on meta-terms such that $\succsim$ is monotonic, all of $\succsim ,\succcurlyeq ,\succ$ are meta-stable (that is, $\ell \succsim r$ implies $\ell \gamma \succsim r\gamma$ if $\ell$ is a closed pattern and $\gamma$ a substitution on domain $FMV (\ell ) \cup FMV (r)$, and the same for $\succcurlyeq$ and $\succ$), $\Rightarrow _{\beta } \mathop {\subseteq } \succsim$, and both $\succsim \circ \succ \mathop {\subseteq } \succ$ and $\succcurlyeq \circ \succ \mathop {\subseteq } \succ$.

In the first-order DP framework, the reduction pair processor [20] seeks to orient all rules with $\succsim$ and all DPs with either $\succsim$ or $\succ$; if this succeeds, those pairs oriented with $\succ$ may be removed. Using reduction triples rather than pairs, we obtain the following extension to the higher-order setting:

Theorem 49

(Basic reduction triple processor). Let $M = (\mathcal {P}_1 \uplus \mathcal {P}_2,\mathcal {R},m,f)$ be a DP problem. If $(\succsim ,\succcurlyeq ,\succ )$ is a reduction triple such that

• 1. for all $\ell \Rightarrow r \in \mathcal {R}$, we have $\ell \succsim r$;

• 2. for all $\ell \Rrightarrow p\ (A) \in \mathcal {P}_1$, we have $\ell \succ p$;

• 3. for all $\ell \Rrightarrow p\ (A) \in \mathcal {P}_2$, we have $\ell \succcurlyeq p$;

then the processor that maps M to $\{(\mathcal {P}_2,\mathcal {R},m,f)\}$ is both sound and complete.

Proof

(sketch). For an infinite $(\mathcal {P}_1 \uplus \mathcal {P}_2, \mathcal {R})$-chain $[(\rho _0,s_0,t_0),(\rho _1,s_1,t_1),\ldots ]$ the requirements provide that, for all i: (a) $s_i \succ t_i$ if $\rho _i \in \mathcal {P}_1$; (b) $s_i \succcurlyeq t_i$ if $\rho _i \in \mathcal {P}_2$; and (c) $t_i \succsim s_{i+1}$. Since $\succ$ is well-founded, only finitely many DPs can be in $\mathcal {P}_1$, so a tail of the chain is actually an infinite $(\mathcal {P}_2,\mathcal {R},m,f)$-chain.    $\square$

Example 50

Let $(\mathcal {F},\mathcal {R})$ be the (non-$\eta$-expanded) rules from Example 17, and $SDP (\mathcal {R})$ the DPs from Example 28. From Theorem 49, we get the following ordering requirements:

$$ \begin{array}{rcl} \mathtt {deriv}\ (\lambda x{.}\mathtt {sin}\ F\langle x\rangle ) &{} \succsim &{} \lambda y{.}\mathtt {times}\ (\mathtt {deriv}\ (\lambda x{.}F\langle x\rangle )\ y)\ (\mathtt {cos}\ F\langle y\rangle ) \\ \mathtt {deriv}^\sharp \ (\lambda x{.}\mathtt {sin}\ F\langle x\rangle ) &{} \succ &{} \mathtt {deriv}^\sharp \ (\lambda x{.}F\langle x\rangle ) \\ \end{array} $$

We can handle both requirements by using a polynomial interpretation $\mathcal {J}$ to $\mathbb {N}$ [15, 43], by choosing $\mathcal {J}_{\mathtt {sin}}(n) = n + 1$, $\mathcal {J}_{\mathtt {cos}}(n) = 0$, $\mathcal {J}_{\mathtt {times}}(n_1,n_2) = n_1$, $\mathcal {J}_{\mathtt {deriv}}(f) = \mathcal {J}_{\mathtt {deriv}^\sharp }(f) = \lambda n.f(n)$. Then the requirements are evaluated to: $\lambda n.f(n) + 1 \ge \lambda n.f(n)$ and $\lambda n.f(n) + 1 > \lambda n.f(n)$, which holds on $\mathbb {N}$.

Theorem 49 is not ideal since, by definition, the left- and right-hand side of a DP may have different types. Such DPs are hard to handle with traditional techniques such as HORPO [26] or polynomial interpretations [15, 43], as these methods compare only (meta-)terms of the same type (modulo renaming of sorts).

Example 51

Consider the toy AFSM with $\mathcal {R}= \{ \mathtt {f}\ (\mathtt {s}\ X)\ Y \Rightarrow \mathtt {g}\ X\ Y,\ \mathtt {g}\ X \Rightarrow \lambda z{.}\mathtt {f}\ X\ z \}$ and $SDP (\mathcal {R}) = \{ \mathtt {f}^\sharp \ (\mathtt {s}\ X)\ Y \Rrightarrow \mathtt {g}^\sharp \ X,\ \mathtt {g}^\sharp \ X \Rrightarrow \mathtt {f}^\sharp \ X\ Z \}$. If $\mathtt {f}$ and $\mathtt {g}$ both have a type $\mathtt {nat}\rightarrow \mathtt {nat}\rightarrow \mathtt {nat}$, then in the first DP, the left-hand side has type $\mathtt {nat}$ while the right-hand side has type $\mathtt {nat}\rightarrow \mathtt {nat}$. In the second DP, the left-hand side has type $\mathtt {nat}\rightarrow \mathtt {nat}$ and the right-hand side has type $\mathtt {nat}$.

To be able to handle examples like the one above, we adapt [31, Thm. 5.21] by altering the ordering requirements to have base type.

Theorem 52

(Reduction triple processor). Let $\mathsf {Bot}$ be a set $\{ \bot _\sigma : \sigma \mid$ $\sigma \text { a type}\} \subseteq \mathcal {F}^\sharp$ of unused constructors, $M= (\mathcal {P}_1 \uplus \mathcal {P}_2,\mathcal {R},m,f)$ a DP problem and $(\succsim ,\succcurlyeq ,\succ )$ a reduction triple such that: (a) for all $\ell \Rightarrow r \in \mathcal {R}$, we have $\ell \succsim r$; and (b) for all $\ell \Rrightarrow p\ (A) \in \mathcal {P}_1 \uplus \mathcal {P}_2$ with $\ell : \sigma _1 \rightarrow \dots \rightarrow \sigma _m\rightarrow \iota$ and $p : \tau _1 \rightarrow \dots \rightarrow \tau _n \rightarrow \kappa$ we have, for fresh meta-variables $Z_1 : \sigma _1,\dots ,Z_m: \sigma _m$:

• $\ell \ Z_1 \cdots Z_m \succ p\ \bot _{\tau _1} \cdots \bot _{\tau _n}$ if $\ell \Rrightarrow p\ (A) \in \mathcal {P}_1$

• $\ell \ Z_1 \cdots Z_m \succcurlyeq p\ \bot _{\tau _1} \cdots \bot _{\tau _n}$ if $\ell \Rrightarrow p\ (A) \in \mathcal {P}_2$

Then the processor that maps M to $\{(\mathcal {P}_2,\mathcal {R},m,f)\}$ is both sound and complete.

Proof

(sketch). If $(\succsim ,\succcurlyeq ,\succ )$ is such a triple, then for $R \in \{\succcurlyeq ,\succ \}$ define $R'$ as follows: for $s : \sigma _1 \rightarrow \dots \rightarrow \sigma _m\rightarrow \iota$ and $t : \tau _1 \rightarrow \dots \rightarrow \tau _n \rightarrow \kappa$, let $s\ R'\ t$ if for all $u_1 : \sigma _1,\dots , u_m: \sigma _m$ there exist $w_1 : \tau _1,\dots ,w_n : \tau _n$ such that $s\ u_1 \cdots u_m\ R\ t\ w_1 \cdots w_n$. Now apply Theorem 49 with the triple $(\succsim ,\succcurlyeq ',\succ ')$.    $\square$

Here, the elements of $\mathsf {Bot}$ take the role of minimal terms for the ordering. We use them to flatten the type of the right-hand sides of ordering requirements, which makes it easier to use traditional methods to generate a reduction triple.

While $\succ$ and $\succcurlyeq$ may still have to orient meta-terms of distinct types, these are always base types, which we could collapse to a single sort. The only relation required to be monotonic, $\succsim$, regards pairs of meta-terms of the same type. This makes it feasible to apply orderings like HORPO or polynomial interpretations.

Both the basic and non-basic reduction triple processor are difficult to use for non-conservative DPs, which generate ordering requirements whose right-hand side contains a meta-variable not occurring on the left. This is typically difficult for traditional techniques, although possible to overcome, by choosing triples that do not regard such meta-variables (e.g., via an argument filtering [35, 46]):

Example 53

We apply Theorem 52 on the DP problem $( SDP (\mathcal {R}), \mathcal {R},$$\mathtt {computable}_\mathcal {R}, \mathtt {formative})$ of Example 51. This gives for instance the following ordering requirements:

$$ \begin{array}{rclcrcl} \mathtt {f}\ (\mathtt {s}\ X)\ Y &{} \succsim &{} \mathtt {g}\ X\ Y &{} \quad &{} \mathtt {f}^\sharp \ (\mathtt {s}\ X)\ Y &{} \succ &{} \mathtt {g}^\sharp \ X\ \bot _\mathtt {nat}\\ \mathtt {g}\ X &{} \succsim &{} \lambda z{.}\mathtt {f}\ X\ z &{} \quad &{} \mathtt {g}^\sharp \ X\ Y &{} \succcurlyeq &{} \mathtt {f}^\sharp \ X\ Z \\ \end{array} $$

The right-hand side of the last DP uses a meta-variable Z that does not occur on the left. As neither $\succ$ nor $\succcurlyeq$ are required to be monotonic (only $\succsim$ is), function symbols do not have to regard all their arguments. Thus, we can use a polynomial interpretation $\mathcal {J}$ to $\mathbb {N}$ with $\mathcal {J}_{\bot _\mathtt {nat}} = 0$, $\mathcal {J}_{\mathtt {s}}(n) = n + 1$ and $\mathcal {J}_{\mathtt {h}}(n_1,n_2) = n_1$ for $\mathtt {h} \in \{ \mathtt {f},\mathtt {f}^\sharp ,\mathtt {g},\mathtt {g}^\sharp \}$. The ordering requirements then translate to $X + 1 \ge X$ and $\lambda y.X \ge \lambda z.X$ for the rules, and $X + 1 > X$ and $X \ge X$ for the DPs. All these inequalities on $\mathbb {N}$ are clearly satisfied, so we can remove the first DP. The remaining problem is quickly dispersed with the dependency graph processor.

5.3 Rule Removal Without Search for Orderings

While processors often simplify only $\mathcal {P}$, they can also simplify $\mathcal {R}$. One of the most powerful techniques in first-order DP approaches that can do this are usable rules. The idea is that for a given set $\mathcal {P}$ of DPs, we only need to consider a subset $UR (\mathcal {P},\mathcal {R})$ of $\mathcal {R}$. Combined with the dependency graph processor, this makes it possible to split a large term rewriting system into a number of small problems.

In the higher-order setting, simple versions of usable rules have also been defined [31, 46]. We can easily extend these definitions to AFSMs:

Theorem 54

Given a DP problem $M= (\mathcal {P},\mathcal {R},m,f)$ with $m \succeq \mathtt {minimal}$ and $\mathcal {R}$ finite, let $UR (\mathcal {P},\mathcal {R})$ be the smallest subset of $\mathcal {R}$ such that:

• if a symbol $\mathtt {f}$ occurs in the right-hand side of an element of $\mathcal {P}$ or $UR (\mathcal {P},\mathcal {R})$, and there is a rule $\mathtt {f}\ \ell _1 \cdots \ell _k \Rightarrow r$, then this rule is also in $UR (\mathcal {P}, \mathcal {R})$;

• if there exists $\ell \Rightarrow r \in \mathcal {R}$ or $\ell \Rrightarrow r\ (A) \in \mathcal {P}$ such that $r \unrhd F\langle s_1,\dots , s_k\rangle \ t_1 \cdots t_n$ with $s_1,\dots ,s_k$ not all distinct variables or with $n > 0$, then $UR (\mathcal {P},\mathcal {R}) = \mathcal {R}$.

Then the processor that maps $M$ to $\{(\mathcal {P}, UR (\mathcal {P},\mathcal {R}),\mathtt {arbitrary},\mathtt {all})\}$ is sound.

For the proof we refer to the very similar proofs in [31, 46].

Example 55

For the set $SDP (\mathcal {R})$ of the ordinal recursion example (Examples 8 and 29), all rules are usable due to the occurrence of $H\ M$ in the second DP. For the set $SDP (\mathcal {R})$ of the map example (Examples 6 and 31), there are no usable rules, since the one DP contains no defined function symbols or applied meta-variables.

This higher-order processor is much less powerful than its first-order version: if any DP or usable rule has a sub-meta-term of the form $F\ s$ or $F\langle s_1,\dots ,s_k\rangle$ with $s_1,\dots ,s_k$ not all distinct variables, then all rules are usable. Since applying a higher-order meta-variable to some argument is extremely common in higher-order rewriting, the technique is usually not applicable. Also, this processor imposes a heavy price on the flags: minimality (at least) is required, but is lost; the formative flag is also lost. Thus, usable rules are often combined with reduction triples to temporarily disregard rules, rather than as a way to permanently remove rules.

To address these weaknesses, we consider a processor that uses similar ideas to usable rules, but operates from the left-hand sides of rules and DPs rather than the right. This adapts the technique from [31] that relies on the new formative flag. As in the first-order case [16], we use a semantic characterisation of formative rules. In practice, we then work with over-approximations of this characterisation, analogous to the use of dependency graph approximations in Theorem 45.

Definition 56

A function $FR$ that maps a pattern $\ell$ and a set of rules $\mathcal {R}$ to a set $FR (\ell ,\mathcal {R}) \subseteq \mathcal {R}$ is a formative rules approximation if for all s and $\gamma$: if $s \Rightarrow _{\mathcal {R}}^* \ell \gamma$ by an $\ell$-formative reduction, then this reduction can be done using only rules in $FR (\ell ,\mathcal {R})$.

We let $FR (\mathcal {P},\mathcal {R}) = \bigcup \{ FR (\ell _i, \mathcal {R}) \mid \mathtt {f}\ \ell _1 \cdots \ell _n \Rrightarrow p\, (A)\, \in \, \mathcal {P}\wedge 1 \le i \le n \}$.

Thus, a formative rules approximation is a subset of $\mathcal {R}$ that is sufficient for a formative reduction: if $s \Rightarrow _{\mathcal {R}}^*\ell \gamma$, then $s \Rightarrow _{ FR (\ell ,\mathcal {R})}^* \ell \gamma$. It is allowed for there to exist other formative reductions that do use additional rules.

Example 57

We define a simple formative rules approximation: (1) $FR (Z,\mathcal {R}) = \emptyset$ if Z is a meta-variable; (2) $FR (\mathtt {f}\ \ell _1 \cdots \ell _m,\mathcal {R}) = FR (\ell _1,\mathcal {R}) \cup \dots \cup FR (\ell _m,\mathcal {R})$ if $\mathtt {f} : \sigma _1 \rightarrow \dots \rightarrow \sigma _m\rightarrow \iota$ and no rules have type $\iota$; (3) $FR (s,\mathcal {R}) = \mathcal {R}$ otherwise. This is a formative rules approximation: if $s \Rightarrow _{\mathcal {R}}^* Z\gamma$ by a Z-formative reduction, then $s = Z\gamma$, and if $s \Rightarrow _{ \mathcal {R}}^* \mathtt {f}\ \ell _1 \cdots \ell _m$ and no rules have the same output type as s, then $s = \mathtt {f}\ s_1 \cdots s_m$ and each $s_i \Rightarrow _{\mathcal {R}}^* \ell _i\gamma$ (by an $\ell _i$-formative reduction).

The following result follows directly from the definition of formative rules.

Theorem 58

(Formative rules processor). For a formative rules approximation $FR$, the processor $Proc _{ FR }$ that maps a DP problem $(\mathcal {P},\mathcal {R},m,\mathtt {formative})$ to $\{ (\mathcal {P}, FR (\mathcal {P}, \mathcal {R}),m,\mathtt {formative}) \}$ is both sound and complete.

Proof

(sketch). A processor that only removes rules (or DPs) is always complete. For soundness, if the chain is formative then each step $t_i \Rightarrow _{\mathcal {R}}^* s_{i+1}$ can be replaced by $t_i \Rightarrow _{ FR (\mathcal {P}, \mathcal {R})}^* s_{i+1}$. Thus, the chain can be seen as a $(\mathcal {P}, FR (\mathcal {P}, \mathcal {R}))$-chain.    $\square$

Example 59

For our ordinal recursion example (Examples 8 and 29), none of the rules are included when we use the approximation of Example 57 since all rules have output type $\mathtt {ord}$. Thus, $Proc _ FR$ maps $( SDP (\mathcal {R}),\mathcal {R},$$\mathtt {computable}_\mathcal {R}, \mathtt {formative})$ to $( SDP (\mathcal {R}),\emptyset ,\mathtt {computable}_\mathcal {R},\mathtt {formative})$. Note: this example can also be completed without formative rules (see Example 64). Here we illustrate that, even with a simple formative rules approximation, we can often delete all rules of a given type.

Formative rules are introduced in [31], and the definitions can be adapted to a more powerful formative rules approximation than the one sketched in Example 59. Several examples and deeper intuition for the first-order setting are given in [16].

5.4 Subterm Criterion Processors

Reduction triple processors are powerful, but they exert a computational price: we must orient all rules in $\mathcal {R}$. The subterm criterion processor allows us to remove DPs without considering $\mathcal {R}$ at all. It is based on a projection function [24], whose higher-order counterpart [31, 34, 46] is the following:

Definition 60

For $\mathcal {P}$ a set of DPs, let $\mathtt {heads}(\mathcal {P})$ be the set of all symbols $\mathtt {f}$ that occur as the head of a left- or right-hand side of a DP in $\mathcal {P}$. A projection function for $\mathcal {P}$ is a function $\nu : \mathtt {heads}(\mathcal {P}) \rightarrow \mathbb {N}$ such that for all DPs $\ell \Rrightarrow p\ (A) \in \mathcal {P}$, the function $\overline{\nu }$ with $\overline{\nu }(\mathtt {f}\ s_1 \cdots s_n) = s_{\nu (\mathtt {f})}$ is well-defined both for $\ell$ and for p.

Theorem 61

(Subterm criterion processor). The processor $Proc _{\mathtt {subcrit}}$ that maps a DP problem $(\mathcal {P}_1 \uplus \mathcal {P}_2,\mathcal {R},m,f)$ with $m \succeq \mathtt {minimal}$ to $\{(\mathcal {P}_2,\mathcal {R},m,f)\}$ if a projection function $\nu$ exists such that $\overline{\nu }(\ell ) \rhd \overline{\nu }(p)$ for all $\ell \Rrightarrow p\ (A) \in \mathcal {P}_1$ and $\overline{\nu }(\ell ) = \overline{\nu }(p)$ for all $\ell \Rrightarrow p\ (A) \in \mathcal {P}_2$, is sound and complete.

Proof

(sketch). If the conditions are satisfied, every infinite $(\mathcal {P}, \mathcal {R})$-chain induces an infinite $\unrhd \mathop {\cdot } \Rightarrow _{\mathcal {R}}^*$ sequence that starts in a strict subterm of $t_1$, contradicting minimality unless all but finitely many steps are equality. Since every occurrence of a pair in $\mathcal {P}_1$ results in a strict $\rhd$ step, a tail of the chain lies in $\mathcal {P}_2$.    $\square$

Example 62

Using $\nu (\mathtt {map}^\sharp ) = 2$, $Proc _{\mathtt {subcrit}}$ maps the DP problem $(\{(1)\},$$\mathcal {R}, \mathtt {computable}_\mathcal {R},\mathtt {formative})$ from Example 47 to $\big \{(\emptyset ,\mathcal {R},\mathtt {computable}_\mathcal {R},$$\mathtt {formative})\big \}$.

The subterm criterion can be strengthened, following [34, 46], to also handle DPs like the one in Example 28. Here, we focus on a new idea. For computable chains, we can build on the idea of the subterm criterion to get something more.

Theorem 63

(Computable subterm criterion processor). The processor $Proc _{\mathtt {statcrit}}$ that maps a DP problem $(P_1 \uplus \mathcal {P}_2,\mathcal {R},\mathtt {computable}_{\mathcal {U}},f)$ to $\{(\mathcal {P}_2,\mathcal {R}, \mathtt {computable}_{\mathcal {U}}, f)\}$ if a projection function $\nu$ exists such that $\overline{\nu }(\ell ) \sqsupset \overline{\nu }(p)$ for all $\ell \Rrightarrow p\ (A) \in \mathcal {P}_1$ and $\overline{\nu }(\ell ) = \overline{\nu }(p)$ for all $\ell \Rrightarrow p\ (A) \in \mathcal {P}_2$, is sound and complete. Here, $\sqsupset$ is the relation on base-type terms with $s \sqsupset t$ if $s \ne t$ and (a) $s \unrhd _{\mathtt {acc}}t$ or (b) a meta-variable Z exists with $s \unrhd _{\mathtt {acc}}Z\langle x_1,\dots ,x_k\rangle$ and $t = Z\langle t_1,\dots ,t_k\rangle \ s_1 \cdots s_n$.

Proof

(sketch). By the conditions, every infinite $(\mathcal {P}, \mathcal {R})$-chain induces an infinite $(\Rrightarrow _{C_{\mathcal {U}}} \cup \Rightarrow _{\beta })^* \cdot \Rightarrow _{\mathcal {R}}^*$ sequence (where $C_{\mathcal {U}}$ is defined following Theorem 13). This contradicts computability unless there are only finitely many inequality steps. As pairs in $\mathcal {P}_1$ give rise to a strict decrease, they may occur only finitely often.

   $\square$

Example 64

Following Examples 8 and 29, consider the projection function $\nu$ with $\nu (\mathtt {rec}^\sharp ) = 1$. As $\mathtt {s}\ X \unrhd _{\mathtt {acc}}X$ and $\mathtt {lim}\ H \unrhd _{\mathtt {acc}}H$, both $\mathtt {s}\ X \sqsupset X$ and $\mathtt {lim}\ H \sqsupset H\ M$ hold. Thus $Proc _{\mathtt {statc}}(\mathcal {P},\mathcal {R},\mathtt {computable}_\mathcal {R},\mathtt {formative}) = \{ (\emptyset ,\mathcal {R},\mathtt {computable}_\mathcal {R}, \mathtt {formative}) \}$. By the dependency graph processor, the AFSM is terminating.

The computable subterm criterion processor fundamentally relies on the new $\mathtt {computable}_{\mathcal {U}}$ flag, so it has no counterpart in the literature so far.

5.5 Non-termination

While (most of) the processors presented so far are complete, none of them can actually return NO. We have not yet implemented such a processor; however, we can already provide a general specification of a non-termination processor.

Theorem 65

(Non-termination processor). Let $M = (\mathcal {P},\mathcal {R},m,f)$ be a DP problem. The processor that maps M to NO if it determines that a sufficient criterion for non-termination of $\Rightarrow _{\mathcal {R}}$ or for existence of an infinite conservative $(\mathcal {P},\mathcal {R})$-chain according to the flags m and f holds is sound and complete.

Proof

Obvious.    $\square$

This is a very general processor, which does not tell us how to determine such a sufficient criterion. However, it allows us to conclude non-termination as part of the framework by identifying a suitable infinite chain.

Example 66

If we can find a finite $(\mathcal {P},\mathcal {R})$-chain $[(\rho _0,s_0,t_0),\dots , (\rho _n,s_n,t_n)]$ with $t_n = s_0\gamma$ for some substitution $\gamma$ which uses only conservative DPs, is formative if $f = \mathtt {formative}$ and is ${\mathcal {U}}$-computable if $m = \mathtt {computable}_{\mathcal {U}}$, such a chain is clearly a sufficient criterion: there is an infinite chain $[(\rho _0,s_0,t_0),\dots , (\rho _0,s_0\gamma ,t_0\gamma ), \dots , (\rho _0,s_0\gamma \gamma ,t_0\gamma \gamma ),\ldots ]$. If $m = \mathtt {minimal}$ and we find such a chain that is however not minimal, then note that $\Rightarrow _{\mathcal {R}}$ is non-terminating, which also suffices.

For example, for a DP problem $(\mathcal {P},\mathcal {R},\mathtt {minimal},\mathtt {all})$ with $\mathcal {P}= \{ \mathtt {f}^\sharp \ F\ X \Rrightarrow \mathtt {g}^\sharp \ (F\ X),\ \mathtt {g}^\sharp \ X \Rrightarrow \mathtt {f}^\sharp \ \mathtt {h}\ X \}$, there is a finite dependency chain: $[(\mathtt {f}^\sharp \ F\ X \Rrightarrow \mathtt {g}^\sharp \ (F\ X),\ \mathtt {f}^\sharp \ \mathtt {h}\ x,\ \mathtt {g}^\sharp \ (\mathtt {h}\ x)),\ \; (\mathtt {g}^\sharp \ X \Rrightarrow \mathtt {f}^\sharp \ \mathtt {h}\ X,\ \mathtt {g}^\sharp \ (\mathtt {h}\ x),\ \mathtt {f}^\sharp \ \mathtt {h}\ (\mathtt {h}\ x))]$. As $\mathtt {f}^\sharp \ \mathtt {h}\ (\mathtt {h}\ x)$ is an instance of $\mathtt {f}^\sharp \ \mathtt {h}\ x$, the processor maps this DP problem to $\texttt {NO}$.

To instantiate Theorem 65, we can borrow non-termination criteria from first-order rewriting [13, 21, 42], with minor adaptions to the typed setting. Of course, it is worthwhile to also investigate dedicated higher-order non-termination criteria.

6 Conclusions and Future Work

We have built on the static dependency pair approach [6, 33, 34, 46] and formulated it in the language of the DP framework from first-order rewriting [20, 22]. Our formulation is based on AFSMs, a dedicated formalism designed to make termination proofs transferrable to various higher-order rewriting formalisms.

This framework has two important additions over existing higher-order DP approaches in the literature. First, we consider not only arbitrary and minimally non-terminating dependency chains, but also minimally non-computable chains; this is tracked by the $\mathtt {computable}_{\mathcal {U}}$ flag. Using the flag, a dedicated processor allows us to efficiently handle rules like Example 8. This flag has no counterpart in the first-order setting. Second, we have generalised the idea of formative rules in [31] to a notion of formative chains, tracked by a $\mathtt {formative}$ flag. This makes it possible to define a corresponding processor that permanently removes rules.

Implementation and Experiments. To provide a strong formal groundwork, we have presented several processors in a general way, using semantic definitions of, e.g., the dependency graph approximation and formative rules rather than syntactic definitions using functions like $TCap$ [21]. Even so, most parts of the DP framework for AFSMs have been implemented in the open-source termination prover WANDA [28], alongside a dynamic DP framework [31] and a mechanism to delegate some ordering constraints to a first-order tool [14]. For reduction triples, polynomial interpretations [15] and a version of HORPO [29, Ch. 5] are used. To solve the constraints arising in the search for these orderings, and also to determine sort orderings (for the accessibility relation) and projection functions (for the subterm criteria), WANDA employs an external SAT-solver. WANDA has won the higher-order category of the International Termination Competition [50] four times. In the International Confluence Competition [10], the tools ACPH  [40] and  [38] use WANDA as their “oracle” for termination proofs on HRSs.

We have tested WANDA on the Termination Problems Data Base [49], using AProVE [19] and MiniSat [12] as back-ends. When no additional features are enabled, WANDA proves termination of 124 (out of 198) benchmarks with static DPs, versus 92 with only a search for reduction orderings; a 34% increase. When all features except static DPs are enabled, WANDA succeeds on 153 benchmarks, versus 166 with also static DPs; an 8% increase, or alternatively, a 29% decrease in failure rate. The full evaluation is available in [17, Appendix D].

Future Work. While the static and the dynamic DP approaches each have their own strengths, there has thus far been little progress on a unified approach, which could take advantage of the syntactic benefits of both styles. We plan to combine the present work with the ideas of [31] into such a unified DP framework.

In addition, we plan to extend the higher-order DP framework to rewriting with strategies, such as implicit $\beta$-normalisation or strategies inspired by functional programming languages like OCaml and Haskell. Other natural directions are dedicated automation to detect non-termination, and reducing the number of term constraints solved by the reduction triple processor via a tighter integration with usable and formative rules with respect to argument filterings.