Abstract
We consider a class of interrupt-driven programs that model the kernel API libraries of some popular real-time embedded operating systems and the synchronization mechanisms they use. We define a natural notion of data races and a happens-before ordering for such programs. The key insight is the notion of disjoint blocks to define the synchronizes-with relation. This notion also suggests an efficient and effective lockset based analysis for race detection. It also enables us to define efficient “sync-CFG” based static analyses for such programs, which exploit data race freedom. We use this theory to carry out static analysis on the FreeRTOS kernel library to detect races and to infer simple relational invariants on key kernel variables and data-structures.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Embedded software is widespread and increasingly employed in safety-critical applications in medical, automobile, and aerospace domains. These programs are typically multi-threaded applications, running on uni-processor systems, that are compiled along with a kernel library that provides priority-based scheduling, and other task management and communication functionality. The applications themselves are similar to classical multi-threaded programs (using lock, semaphore, or queue based synchronization) although they are distinguished by their priority-based execution semantics. The kernel on the other hand typically makes use of non-standard low-level synchronization mechanisms (like disabling-enabling interrupts, suspending the scheduler, and flag-based synchronization) to ensure thread-safe access to its data-structures. In the literature such software (both applications and kernels) are referred to as interrupt-driven programs. Our interest in this paper is in the subclass of interrupt-driven programs corresponding to kernel libraries.
Efficient static analysis of concurrent programs is a challenging problem. One could carry out a precise analysis by considering the product of the control flow graphs (CFGs) of the threads, however this is prohibitively expensive due to the exponential number of program points in the product graph. A promising direction is to focus on the subclass of race-free programs. This is an important class of programs, as most developers aim to write race-free code, and one could try to exploit this property to give an efficient way of analyzing programs that fall in this class. In recent years there have been many techniques [7, 11, 12, 18, 21] that exploit the race-freedom property to perform sound and efficient static analysis. In particular [11, 21] create an appealing structure called a “sync-CFG” which is the union of the control flow graphs of the threads augmented with possible “synchronization” edges, and essentially perform sequential analysis on this graph to obtain sound facts about the concurrent program. However these techniques are all for classical lock-based concurrent programs. A natural question asks if we can analyze interrupt-driven programs in a similar way.
There are several challenges in doing this. Firstly one needs to define what constitutes a data race in a generalized setting that includes these programs. Secondly, how does one define the happens-before order, and in particular the synchronizes-with relation that many of the race-free analysis techniques rely on, given the ad-hoc synchronization mechanisms used in these programs.
A natural route that suggests itself is to translate a given interrupt-driven program into one that uses classical locks, and faithfully captures the interleaved executions of the original program. One could then use existing techniques for lock-based concurrency to analyze these programs. However, this route is fraught with many challenges. To begin with, it is not clear how one would handle flag-based synchronization which is one of the main synchronization mechanisms used in these programs. Even if one could handle this, such a translation may not preserve data races, in that the original program might have had a race but the translated program does not. Finally, some of the synchronizes-with edges in the translated program are clearly unnecessary, leading to imprecise data-flow facts in the analyses.
In this paper, we show that it is possible to take a more organic route and address these challenges in a principled way that could apply to other non-standard classes of concurrent systems as well. Firstly, we propose a general definition of a data race that is not based on a happens-before order, but on the operational semantics of the class of programs under consideration. The definition essentially says that two statements s and t can race, if two notional “blocks” around them can overlap in time during an execution. We believe that this definition accurately captures what it is that a programmer tries to avoid while dealing with shared variables whose values matter. Secondly we propose a way of defining the synchronizes-with relation, based on the notion of disjoint blocks. These are statically identifiable pairs of path segments in the CFGs of different threads that are guaranteed to never overlap (in time) during an execution of the program, much like blocks of code that lie between an acquire and release of the same lock. This relation now suggests a natural sync-CFG structure on which we can perform analyses like value-set (including interval, null-deference, and points-to analysis), and region-based relational invariant analysis, in a sound and efficient manner. We also use the notion of disjoint blocks to define an efficient and precise lock-set-based analysis for detecting races in interrupt-driven programs.
We implement some of these analyses on the FreeRTOS kernel library [3] which is one of the most widely used open-source real-time kernels for embedded systems, comprising about 3,500 lines of C code. Our race-detection analysis reports a total of 64 races in kernel methods, of which 18 turn out to be true positives. We also carry out a region-based relational analysis using an implementation based on CIL [22]/Apron [15], to prove several relational invariants on the kernel variables and abstracted data-structures.
2 Overview
We give an overview of our contributions via an illustrative example modelled on a portion of the FreeRTOS kernel library. Figure 1 shows an interrupt-driven program that contains a main thread that first initializes the kernel variables. The variables represent components of a message queue, like msgw (the number of messages waiting in the queue), len (max length of the queue), wtosend (the number of tasks waiting to send to the queue), wtorec (the number of tasks waiting to receive from the queue), and RxLock (a counter which also acts as a synchronization flag that mediates access to the waiting queues). The main thread then creates (or spawns) two threads: qsend which models the kernel API method for sending a message to the queue, and qrec_ISR which models a method for receiving a message, and which is meant to be called from an interrupt-service routine. The basic semantics of this program is that the ISR thread can interrupt qsend at any time (provided interrupts are not disabled), but always runs to completion itself. The threads use disableint/enableint to disable and enable interrupts, suspendsch/resumesch to suspend/resume the scheduler (thereby preventing preemption by another non-ISR thread), and finally flag-based synchronization (using the RxLock variable), as different means to ensure mutual exclusion.
Our first contribution is a general notion of data races which is applicable to such programs. We say that two conflicting statements s and t in two different threads are involved in a data race if assuming s and t were enclosed in a notional “block” of skip statements, there is an execution in which the two blocks “overlap” in time. The given program can be seen to be free of races. However if we were to remove the disableint statement of line 10, then the statements accessing msgw in lines 12 and 42 would be racy, since soon after the access of msgw in qsend at line 12, there could be preemption by qrec_ISR which goes on to execute line 42.
Next we illustrate the notion of “disjoint blocks” which is the key to defining synchronizes-with edges, which we need in our sync-CFG analysis as well as to define an appropriate happens-before relation. Disjoint blocks are also used in our race-detection algorithm. A pair of blocks of code (for example any of the like-shaded blocks of code in the figure) are disjoint if they can never overlap during an execution. For example, the block comprising lines 11–14 in qsend and the whole of qrec_ISR, form a pair of disjoint blocks.
Next we give an analysis for checking race-freedom, by adapting the standard lockset analysis [24] for classical concurrent programs. We associate a unique lock with each pair of disjoint blocks, and add notional acquires and releases of this lock at the beginning and end (respectively) of these blocks. We now do the standard lockset analysis on this version of the program, and declare two accesses to be non-racy if they hold sets of locks with a non-empty intersection.
Finally, we show how to do data-flow analysis for such programs in a sound and efficient way. The basic idea is to construct a “sync-CFG” for the program by unioning the control-flow graphs of the threads, and adding sync edges that capture the synchronizes-with edges (going from the end of a block to the beginning of its paired block), for example line 14 to line 41 and line 49 to line 11. The sync-edges are shown by dashed arrows in the figure. We now do a standard “value-set” analysis (for example interval analysis) on this graph, keeping track of a set of values each variable can take. The resulting facts about a variable are guaranteed to be sound at points where the variable is accessed (or even “owned” in the sense that a notional read of the variable at that point is non-racy). For example an interval analysis on this program would give us that \(0 < \mathtt {msgw}\) at line 14. Finally, we could do a region-based value-set analysis, by identifying regions of variables that are accessed as a unit – for example msgw and len could be in one region, while wtosend and wtorec could be in another. The figure shows some facts inferred by a polyhedral analysis based on these regions, for the given program.
3 Interrupt-Driven Programs
The programs we consider have a finite number of (static) threads, with a designated “main” thread in which execution begins. The threads access a set of shared global variables, some of which are used as “synchronization flags”, using a standard set of commands like assignment statements of the form x := e, conditional statements (if-then-else), loop statements (while), etc. In addition, the threads can use commands like disableint, enableint (to disable and enable interrupts, respectively), suspendsch, resumesch (to suspend and resume the scheduler, respectively), while the main thread can also create a thread (enable it for execution). Table 1 shows the set of basic statements \( cmd _{V,T}\) over a set of variables \(V\) and a set of threads \(T\).
We allow standard integer and Boolean expressions over a set of variables \(V\). For an integer expression e over \(V\), and an environment \(\phi \) for \(V\), we denote by  the integer value that e evaluates to in \(\phi \). Similarly for a Boolean expression b, we denote the Boolean value (\( true \) or \( false \)) that b evaluates to in \(\phi \) by
the integer value that e evaluates to in \(\phi \). Similarly for a Boolean expression b, we denote the Boolean value (\( true \) or \( false \)) that b evaluates to in \(\phi \) by  . For a set of environments \(\varPhi \) for a set of variables V, we define the set of integer values that e can evaluate to in an environment in \(\varPhi \), by
. For a set of environments \(\varPhi \) for a set of variables V, we define the set of integer values that e can evaluate to in an environment in \(\varPhi \), by  . Similarly, for a boolean expression b, we define the set of environments in \(\varPhi \) that satisfy b to be
. Similarly, for a boolean expression b, we define the set of environments in \(\varPhi \) that satisfy b to be  .
.
Each thread is of one of two types: “task” threads that are like standard threads, and “ISR” threads that represent threads that run as interrupt service routines. The main thread is a task thread, which is the only task thread enabled initially. The main thread can enable other threads (both task and ISR) for execution using the create command. Task threads can be preempted by other task threads (whenever interrupts are not disabled, and the scheduler is not suspended) or by ISR threads (whenever interrupts are not disabled). On the other hand ISR threads cannot be preempted and are assumed to run to completion.
Only task threads are allowed to use disableint, enableint, suspendsch and resumesch commands. Similarly, if flag-based synchronization is used, only task threads can modify the flag variable, while an ISR can only check whether the flag is set or not, and perform some actions accordingly.
Formally we represent an interrupt-driven program P as a tuple \((V,T)\) where \(V\) is a finite set of integer variables, and \(T\) is a finite set of named threads. Each thread \(t \in T\) has a type which is one of task or ISR, and an associated control-flow graph of the form \(G_t = (L_t, s _t, inst _t)\) where \(L_t\) is a finite set of locations of thread t, \( s _t \in L_t\) is the start location of thread t, \( inst _t \subseteq L_t \times cmd _{V,T} \times L_t\) is a finite set of instructions of thread t.
Some definitions related to threads will be useful going forward. We denote by \(L_P = \bigcup _{t \in T}L_t\) the disjoint union of the thread locations. Whenever P is clear from the context we will drop the subscript of P from \(L_P\) and its decorations. For a location \( l \in L\) we denote by \( tid ( l )\) the thread t which contains location \( l \). We denote the set of instructions of P by \( inst _P = \bigcup _{t\in T} inst _t\). For an instruction \(\iota \in inst _t\), we will also write \( tid (\iota )\) to mean the thread t. For an instruction \(\iota = \langle l ,c, l ' \rangle \), we call \( l \) the source location, and \( l '\) the target location of \(\iota \).
We denote the set of commands appearing in program P by \( cmd (P)\). We will consider an assignment \(\texttt {x := e}\) as a write-access to x, and as a read-access to every variable that appears in the expression e. Similarly, \(\mathtt {assume(}b\mathtt {)}\) is considered to be a read-access of every variable that occurs in expression b. We say two accesses are conflicting accesses if they are read/write accesses to the same variable, and at least one of them is a write. We assume that the control-flow graph of each thread comes from a well-structured program. Finally, we assume that the \( main \) thread begins by initializing the variables to constant values. Figure 2 shows an example program and the control-flow-graphs of its threads.
We define the operational semantics of an interrupt-driven program using a labeled transition system (LTS). Let \(P = (V, T)\) be a program. We define an LTS \(\mathcal {T}_P = (Q, \varSigma , s, \Rightarrow _{})\) corresponding to P, where:
-
Q is a set of states of the form \(( pc , \phi , enab , rt, it, id , ss )\), where \( pc \in T\rightarrow L\) is the program counter giving the current location of each thread, \(\phi \in V\rightarrow \mathbb {Z}\) is a valuation for the variables, \( enab \subseteq T\) is the set of enabled threads, \(rt\in T\) is the currently running thread; \(it\in T\) is the task thread which is interrupted when the scheduler is suspended; and \( id \) and \( ss \) are Boolean values telling us whether interrupts are disabled (\( id = true \)) or not (\( id = false \)) and whether the scheduler is suspended (\( ss = true \)) or not (\( ss = false \)).
-
The set of labels \(\varSigma \) is the set of instructions \( inst _P\) of P.
-
The initial state s is \((\lambda t. s _t, \lambda x.0, \{ main \}, main , main , false , false )\). Thus all threads are at their entry locations, the initial environment sets all variables to 0, only the main thread is enabled and running, the interrupted task is set to \( main \) (this is a dummy value as it is used only when the scheduler is suspended), interrupts are enabled, and the scheduler is not suspended.
-
For an instruction \(\iota = \langle l ,c, l ' \rangle \) in \( inst _P\), with \( tid (\iota ) = t\), we define
$$ ( pc , \phi , enab , rt, it, id , ss ) \Rightarrow _{\iota } ( pc ', \phi ', enab ', rt', it', id ', ss ') $$iff the following conditions are satisfied:
-
\(t \in enab \); \( pc (t) = l \); \( pc ' = pc [t\mapsto l ']\);
-
if \( id \) is true or \(rt\) is an ISR then \(t = rt\);
-
if \( ss \) is true, then either \(t = rt\) or t is an ISR thread;
-
Based on the command c, the following conditions must be satisfied:
-
\(*\) If c is the skip command then \(\phi ' = \phi \), \( enab ' = enab \), \( id ' = id \), and \( ss ' = ss \).
-
\(*\) If c is an assignment statement of the form \(x := e\) then
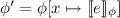 , \( enab ' = enab \), \( id ' = id \), and \( ss ' = ss \).
, \( enab ' = enab \), \( id ' = id \), and \( ss ' = ss \). -
\(*\) If c is a command of the form \(\mathtt {assume(}b\mathtt {)}\) then
 , \(\phi ' = \phi \), \( enab ' = enab \), \( id ' = id \), and \( ss ' = ss \).
, \(\phi ' = \phi \), \( enab ' = enab \), \( id ' = id \), and \( ss ' = ss \). -
\(*\) If c is a \(\texttt {create}(u)\) command then \(t = main \), \(\phi ' = \phi \), \( enab ' = enab \cup \{u\}\), \( id ' = id \), and \( ss ' = ss \).
-
\(*\) If c is the \(\texttt {disableint}\) command then \(\phi ' = \phi \), \( enab ' = enab \), \( id ' = true \), and \( ss ' = ss \).
-
\(*\) If c is the \(\texttt {enableint}\) command then \(\phi ' = \phi \), \( enab ' = enab \), \( id ' = false \), and \( ss ' = ss \).
-
\(*\) If c is the \(\texttt {suspendsch}\) command then \(\phi ' = \phi [ssflag\mapsto 1]\), \( enab ' = enab \), \( id ' = id \), and \( ss ' = true \).
-
\(*\) If c is the \(\texttt {resumesch}\) command then \(\phi ' = \phi [ssflag\mapsto 0]\), \( enab ' = enab \), \( id ' = id \), and \( ss ' = false \).
-
-
In addition, the transitions set the new running thread \(rt'\) and interrupted task \(it'\) as follows. If t is an ISR thread, \( ss \) is true, and \(\iota \) is the first statement of t then \(it' = rt\), \(rt' = t\). If t is an ISR thread, \( ss \) is true, and \(\iota \) is the last statement of t then \(it' = it\), \(rt' = it\). In all other cases, \(rt' = t\) and \(it' = it\).
-
An execution \(\sigma \) of P is a finite sequence of transitions in \(\mathcal {T}_P\) from the initial state s: \(\sigma = \tau _0,\tau _1,\ldots ,\tau _n\) (\(n \ge 0\)) from \(\Rightarrow _{}\), such that there exists a sequence of states \(q_0, q_1, \ldots , q_{n+1}\) from Q, with \(q_0 = s\) and \(\tau _i = (q_i,\iota _i,q_{i+1})\) for each \(0 \le i \le n\). Wherever convenient we will also represent an execution like \(\sigma \) above as a sequence of the form \( q_0 \Rightarrow _{\iota _0} q_1 \Rightarrow _{\iota _1} \cdots \Rightarrow _{\iota _n} q_{n+1}. \) We say that a state \(q \in Q\) is reachable in program P if there is an execution of P leading to state q.
4 Data Races and Happens-Before Ordering
In this section we propose a definition of a data race which has general applicability, and also define a natural happens-before order for interrupt-driven programs.
4.1 Data Races
Data races have typically been defined in the literature in terms of a happens-before order on program executions. In the classical setting of lock-based synchronization, the happens-before relation is a partial order on the instructions in an execution, that is reflexive-transitive closure of the union of the program-order relation between two instructions in the same thread, and the synchronizes-with relation which relates a release of a lock in a thread to the next acquire of the same lock in another thread. Two instructions in an execution are then defined to be involved in a data race if they are conflicting accesses to a shared variable and are not ordered by the happens-before relation.
We feel it is important to have a definition of a data race that is based on the operational semantics of the class of programs we are interested in, and not on a happens-before relation. Such a definition would more tangibly capture what it is that a programmer typically tries to avoid when dealing with shared variables whose consistency she is worried about. Moreover, when coming up with a definition of the happens-before order (the synchronizes-with relation in particular) for non-standard concurrent programs like interrupt-driven programs, it is useful to have a reference notion to relate to. For instance, one could show that a proposed happens-before order is strong enough to ensure the absence of races.
We propose to define a race between two conflicting statements in a program in terms of whether two imaginary blocks enclosing each of these statements can overlap in an execution. Let us consider a multi-threaded program P in a class of concurrent programs with a certain operational execution semantics. Consider a block of contiguous instructions in a thread t of a program P and another block in thread \(t'\) of P. We say that these two blocks are involved in a high-level race in an execution of P if they overlap with each other during the execution, in that one block begins in between the beginning and ending of the other. We say two conflicting statements s and t in P are involved in a data race (or are racy), if the following condition is true: Consider the program \(P'\) which is obtained from P by replacing the statement s by the block “skip; s; skip”, and similarly for statement t. Then there is an execution of \(P'\) in which the two blocks containing s and t are involved in a high-level race. The definition is illustrated in Fig. 3. We say a program P is race-free if no pair of instructions in it are racy.
The rationale for this definition is that the concerned statements s and t may be compiled down to a sequence of instructions (represented by the blocks with skip’s around s and t) depending on the underlying processor and compiler, and if these instructions interleave in an execution, it may lead to undesirable results.
To illustrate the definition, consider the program in Fig. 2a. The accesses to x in line 7 and line 11 can be seen to be racy, since there is an execution of the augmented program \(P'\) in which \( t1 \) performs the skip followed by the increment to x at line 7, followed by a context switch to thread \( t2 \) which goes on to execute lines 9 and 10 and then the read of x in line 11. On the other hand, the version of the program in which line 7 is enclosed in a disableint-enableint block, does not contain a race.
We note that for classical concurrent programs, it might suffice to define a race as consecutive occurrences of conflicting accesses in an execution, as done in [4, 17]. However, this definition is not general enough to apply to interrupt-driven programs. By this definition, the statements in lines 7 and 11 of the program in Fig. 2a are not racy, as there is no execution in which they happen consecutively. This is because the disableint-enableint block containing the access in line 11 is “atomic” in that the statements in the block must happen contiguously in any execution, and hence the instructions corresponding to line 7 and line 11 can never happen immediately one after another.
4.2 Disjoint Blocks and the Happens-Before Relation
Now that we have a proposed definition of races, we can proceed to give a principled way to define the happens-before relation for our class of interrupt-driven programs. The main question is how does one define the synchronizes-with relation. Our insight here is that the key to defining the synchronizes-with relation lies in identifying what we call disjoint blocks for the class of programs. Disjoint blocks are statically identifiable pairs of path segments in the CFGs of different threads, which are guaranteed by the execution semantics of the class of programs never to overlap in an execution of the program. Disjoint block structures – for example in the form of blocks enclosed between locks/unlocks of the same lock – are the primary mechanism used by developers to ensure race-freedom. The synchronizes-with relation in an execution can then be defined as relating, for every pair (A, B) of disjoint blocks in the program, the end of block A to the beginning of the succeeding occurrence of block B in the execution. The happens-before order for an execution can now be defined, as before, in terms of the program order and the synchronizes-with order, and is easily seen to be sufficient to ensure non-raciness.
Let us illustrate this hypothesis on classical lock-based programs. The disjoint block pairs for this class of programs are segments of code enclosed between acquires and releases of the same lock; or the portion of a thread’s code before it spawns a thread t, and the whole of thread t’s code; and similarly for joins. The synchronizes-with relation between instructions in an execution essentially goes from a release to the succeeding acquire of the same lock. If two accesses are related by the resulting happens-before order, they clearly cannot be involved in a race.
We now focus on defining a happens-before relation based on disjoint blocks for our class of interrupt-driven programs. We have identified eight pairs of disjoint block patterns for this class of programs, which are depicted in Fig. 4. We use the following types of blocks to define the pairs. A block of type D is a path segment in a task thread that begins with a disableint and ends with an enableint with no intervening enableint in between. A block of type S is a path segment in a task thread that begins with a suspendsch and ends with a resumesch with no intervening resumesch. An I block is an initial and terminating path segment in an ISR thread (i.e. begins with the first instruction and ends with a terminating instruction). Similarly, for a task thread t, \(T_t\) is an initial and terminating path in t, while \(M_t\) is an initial segment of the main thread that ends with a \(\texttt {create}(t)\) command. A block of type \(C_{ssflag}\) is a path segment in an ISR thread corresponding to the then block of a conditional that checks if \(ssflag = 0\). For a synchronization flag f, \(C_f\) is the path segment in an ISR thread corresponding to the then block of a conditional that checks if \(f = 0\). Finally \(F_f\) is a segment between statements that set f to 1 and back to 0, in a task thread. We also require that an \(F_f\) segment be within the scope of a suspendsch command.
We can now describe the pairs of disjoint blocks depicted in Fig. 4. Case (a) says that two D blocks in different task threads are disjoint. Clearly two such blocks can never overlap in an execution, since once one of the blocks begins execution no context-switch can occur until interrupts are enabled again. Case (b) says that D and I blocks are disjoint. Once again this is because once the D block begins execution no ISR can run until interrupts are enabled again, and once an ISR begins execution it runs to completion without any context-switches. Case (e) says that S blocks in different task threads are disjoint, because once the scheduler is suspended no context-switch to another task thread can occur. Case (f) says that \(M_t\) and \(T_t\) blocks are disjoint, since a thread cannot begin execution before it is created in main. Case (g) says that an S block is disjoint from a \(C_{\mathtt {ssflag}}\) block. This is because once the scheduler is suspended by the suspendsch command, and even if a context-switch to an ISR occurs, the then block of the if statement will not execute. Conversely, if the ISR is running there can be no context-switch to another thread. Finally, case (h) is similar to case (g). We note that the disjoint block pairs are not ordered (the relation is symmetric).
We can now define the synchronizes-with relation as follows. Let \(\sigma = q_0 \Rightarrow _{\iota _0} q_1 \Rightarrow _{\iota _1} \cdots \Rightarrow _{\iota _n} q_{n+1}\) be an execution of P. We say instruction \(\iota _i\) synchronizes-with an instruction \(\iota _j\) of P in \(\sigma \), if \(i < j\), \( tid (\iota _i) \ne tid (\iota _j)\), and there exists a pair of disjoint blocks A and B, with \(\iota _i\) ending block A and \(\iota _j\) beginning block B. As usual we say \(\iota _i\) is program-order related to \(\iota _j\) iff \(i < j\) and \( tid (\iota _i) = tid (\iota _j)\). We define the happens-before relation on \(\sigma \) as the reflexive-transitive closure of the union of the program-order and synchronizes-with relations for \(\sigma \).
We can now define a HB-race in an execution \(\sigma \) of P as follows: we say that two instructions \(\iota _i\) and \(\iota _j\) in \(\sigma \) are involved in a HB-race if they are conflicting instructions that are not ordered by the happens-before relation in \(\sigma \). We say that two instructions in P are HB-racy if there is an execution of P in which they are involved in a HB-race. Finally, we say a program P is HB-race-free if no two of its instructions are HB-racy.
Once again, it is fairly immediate to see that if two statements of a program are not involved in a HB-race, they cannot be involved in a race. Further, if two statements belong to disjoint blocks, then they are clearly happens-before ordered in every execution. Hence belonging to disjoint blocks is sufficient to ensure that the statements are happens-before ordered, which in turn ensures that the statements cannot be involved in a race.
5 Sync-CFG Analysis for Interrupt-Driven Programs
In this section we describe a way of lifting a sequential value-set analysis in a sound way for a HB-race free interrupt-driven program, in a similar way to how it is done for lock-based concurrent programs in [11]. A value-set analysis keeps track of the set of values each variable can take at each program point. The basic idea is to create a “sync-CFG” for a given interrupt-driven program P, which is essentially the union of the CFGs of each thread of P, along with “may-synchronize-with” edges between statements that may be synchronizes-with related in an execution of P, and then perform the value-set analysis on the resulting graph. Whenever the given program is HB-race free, the result of the analysis is guaranteed to be sound, in a sense made clear in Theorem 1.
5.1 Sync-CFG
We begin by defining the “sync-CFG” for an interrupt-driven program. It is on this structure that we will do the value-set analysis. Let \(P=(V,T)\) be an interrupt-driven program, and let G be the disjoint union (over threads \(t \in T\)) of the CFGs \(G_t\). We define a set of may-synchronize-with edges in G, denoted \( MSW (G)\), as follows. The edges correspond to the pairs of disjoint blocks depicted in Fig. 4, in that they connect the ending of one block to the beginning of the other block in the pair. Consider two instructions \(\iota = \langle l ,c,m \rangle \in inst _t\) and \(\kappa = \langle l ',c',m' \rangle \in inst _{t'}\), with \(t \ne t'\). We add the edge \((m, l ')\) in \( MSW (G)\), iff for some pair of disjoint blocks (A, B), \(\iota \) ends a block of type A in thread t and \(\kappa \) begins a block of type B in thread \(t'\). For example, corresponding to a (D, D) pair of disjoint blocks, we add the edge \((m, l ')\) when c is an enableint command, and \(c'\) is a disableint command.
The sync-CFG induced by P is the control flow graph given by G along with the additional edges in \( MSW \)(G). Figure 6 shows a program \(P_2\) and its induced sync-CFG.
5.2 Value Set Analysis
We first spell out the particular form of abstract interpretation we will be using. It is similar to the standard formulation of [9], except that it is a little more general to accommodate non-standard control-flow graphs like the sync-CFG.
An abstract interpretation of a program \(P = (V,T)\) is a structure of the form \(\mathcal {A}= (D, \le , d_{o}, F)\) where
-
D is the set of abstract states.
-
\((D, \le )\) forms a complete lattice. We denote the join (least upper bound) in this lattice by \(\sqcup _{\le }\), or simply \(\sqcup \) when the ordering is clear from the context.
-
\(d_0 \in D\) is the initial abstract state.
-
\(F : inst _P \rightarrow (D \rightarrow D)\) associates a transfer function \(F(\iota )\) (or simply \(F_\iota \)) with each instruction \(\iota \) of P. We require each transfer function \(F_{\iota }\) to be monotonic, in that whenever \(d \le d'\) we have \(F_{\iota }(d) \le F_\iota (d')\).
An abstract interpretation \(\mathcal {A}= (D, \le , d_0, F)\) of P induces a “global” transfer function \(\mathcal {F}_\mathcal {A}: D \rightarrow D\), given by \( \mathcal {F}_{\mathcal {A}}(d) = d_0 \sqcup \bigsqcup _{\iota \in inst _P} F_\iota (d). \) This transfer function can also be seen to be monotonic. By the Knaster-Tarski theorem [28], \(\mathcal {F}_\mathcal {A}\) has a least fixed point (\( LFP \)) in D, which we denote by \( LFP (\mathcal {F}_\mathcal {A})\), and refer to as the resulting value of the analysis.
A value set for a set of variables \(V\) is a map \( vs : V\rightarrow 2^{\mathbb {Z}}\), associating a set of integer values with each variable in \(V\). A value set \( vs \) induces a set of environments \(\varPhi _{ vs }\) in a natural way: \(\varPhi _{ vs } = \{ \phi \ | \ \mathrm {for \ all\ } x \in V,\ \phi (x) \in vs (x) \}\) (i.e. essentially the Cartesian product of the values sets). Conversely, a set of environments \(\varPhi \) for \(V\), induces a value set \( valset (\varPhi )\) given by \( valset (\varPhi )(x) = \{ v \in \mathbb {Z}\ | \ \exists \phi \in \varPhi ,\ \phi (x) = v \}\), which is the “projection” of the environments to each variable \(x \in V\). Finally, we define a point-wise ordering on value sets as follows: \( vs \preceq vs '\) iff \( vs (x) \subseteq vs '(x)\) for each variable x in \(V\). We denote the least element in this ordering by \( vs _{\bot } = \lambda x. \emptyset \).
We can now define the value-set analysis \(\mathcal {A}_{ vset }\) for an interrupt-driven program \(P=(V,T)\) as follows. Let \(\mathcal {A}_{ vset } = (D, \le , d_0, F)\) where
-
D is the set \(L_P \rightarrow (V \rightarrow 2^\mathbb {Z})\) (thus an element of D associates a value-set with each program location)
-
The ordering \(d \le d'\) holds iff \(d(l) \preceq d'(l)\) for each \(l \in L_P\)
-
The initial abstract value \(d_0\) is given by:

-
The transfer functions are given as follows. Given an abstract value d, and a location \(l \in L_P\), we define \( vs _l^d\) to be the join of the value-set at l, and the value-set at all may-synchronizes-with edges coming into l. Thus \( vs _l^d = d(l) \sqcup _{\preceq } \bigsqcup _{(n,l) \in MSW (G)} d(n)\). Below we will use \(\varPhi \) as an abbreviation of the set \(\varPhi _{ vs _l^d}\) of environments induced by \( vs _l^d\). Let \(\iota = \langle l ,c, l ' \rangle \) be an instruction in P.
-
If c is the command x := e then \(F_\iota (d) = d'\) where
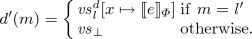
-
If c is the command \(\mathtt {assume(}b\mathtt {)}\), then \(F_\iota (d) = d'\) where

-
If c is any other command (skip, disableint, enableint, suspendsch, resumesch, or create) then \(F_\iota (d) = d'\) where

-
Figure 6 shows the results of a value-set analysis on the sync-CFG of program \(P_2\). The data-flow facts are shown just before a statement, at selected points in the program.
Soundness. The value-set analysis is sound in the following sense: if P is a HB-race free program, and we have a reachable state of P at a location l in a thread where a variable x is read; then the value of x in this state is contained in the value-set for x, obtained by the analysis at point l. More formally:
Theorem 1
Let \(P=(V,T)\) be an HB-race free interrupt-driven program, and let \(d^*\) be the result of the analysis \(\mathcal {A}_{ vset }\) on P. Let l be a location in a thread \(t \in T\) where a variable x is read (i.e. P contains an instruction of the form \(\langle l ,c, l ' \rangle \) where c is a read access of x). Let \(\phi \) be an environment at l reachable via some execution of P. Then \(\phi (x) \in d^*(l)(x)\).
The proof of this theorem is similar to the one for classical concurrent programs in [11] (see [10] for a more accurate proof). The soundness claim can be extended to locations where a variable is “owned” (which includes locations where it is read). We say a variable x is owned by a thread t at location l, if an inserted read of x at this point is non-HB-racy in the resulting program.
Region-Based Analysis. One problem with the value-set analysis is that it may not be able to prove relational invariants (like \(x \le y\)) for a program. One way to remedy this is to exploit the fact that concurrent programs often ensure race-free access to a region of variables, and to essentially do a region-based value-set analysis, as originally done in [21]. More precisely, let us say we have a partition of the set of variables \(V\) of a program P into a set of regions \(R_1, \ldots , R_n\). We classify each read (write) access to a variable x in a region R, as an read (write) access to region R. We say that two instructions in an execution of P are involved in a HB-region-race, if the two instructions are conflicting accesses to the same region R, and are not happens-before ordered in the execution. A program is HB-region-race free if none of its executions contain a HB-region-race.
We can now define a region-based version of the value-set analysis for a program P, which we call \(\mathcal {A}_{ rvset }\). The value-set for a region R is a set of valuations (or sub-environments) for the variables in R. The transfer functions are defined in an analogous way to the value-set analysis. The analogue of Theorem 1 for regions gives us that for a HB-region-race free program, at any location where a region R is accessed, the region-value-set computed by the analysis at that point will contain every sub-environment of R reachable at that point.
6 Translation to Classical Lock-Based Programs
In this section we address the question of why an execution-preserving translation to a classical lock-based program is not a fruitful route to take. In a nutshell, such a translation would not preserve races and would induce a sync-CFG with many unnecessary MSW edges, leading to much more imprecise facts than the analysis on the native sync-CFG described in the previous section. We also describe how our approach can be viewed as a lightweight translation of an interrupt-driven program to a classical lock-based one. The translation is “lightweight” in the sense that it does not attempt to preserve the execution semantics of the given interrupt-driven program, but instead preserves races and the sync-CFG structure of the original program.
6.1 Execution-Preserving Lock Translation
One could try to translate a given interrupt-driven program P into a classical lock-based program \(P^L\) in a way that preserves the interleaved execution semantics of P. By this we mean that every execution of P has a corresponding execution in \(P^L\) that follows essentially the same sequence of interleaved instructions from the different threads (modulo of course the synchronization statements which may differ); and vice-versa. For example, to capture the semantics of disableint-enableint, one could introduce an “execution” lock E which is acquired in place of disabling interrupts, and released in place of enabling interrupts. Every instruction in a task thread outside a disableint-enableint block must also acquire and release E immediately before and after the instruction. Note that the latter step is necessary if we want to capture the fact that once a thread disables interrupts it cannot be preempted by any thread. Figure 5a shows an interrupt-driven program \(P_1\) and its lock translation \(P^L_1\) in Fig. 5b. There are still issues with the translation related to re-entrancy of locks and it is not immediately clear how one would handle flag-based synchronization – but let us keep this aside for now.
The first problem with this translation is that it does not preserve race information. Consider the program \(P_1\) in Fig. 5a and its translation \(P_1^L\). The original program clearly has a race on x in statements 4 and 9. However the translation \(P_1^L\) does not have a race as the accesses are protected by the lock E. Hence checking for races in \(P^L\) does not substitute for checking in P. An alternative around this would be to first construct \(P'\) (recall that this is the version of P in which we introduce the skip-blocks around statements we want to check for races), then construct its lock translation \((P')^L\), and check this program for high-level races on the introduced skip-blocks. However this is expensive as it involves a 3x blow-up in going from P to \(P'\) and another 3x blow-up in going from \(P'\) to \((P')^L\). Further, checking for high-level races (for example using a lock-set analysis) is more expensive than just checking for races. In contrast, as we show next, our lock-set analysis on the native program P does not incur any of these expenses.
The second problem with a precise lock translation is that the sync-CFG of the translated program has many unnecessary MSW-edges, leading to imprecision in the ensuing analysis. Consider the program \(P_2\) in Fig. 6, and its lock translation \(P_2^L\) in Fig. 7. \(P_2\) is similar to \(P_1\) except that line 4 is now an increment of y instead of x, and the resulting program is race-free (in fact HB-race-free). Notice that the may-sync-with edges from line 13 to 4, and line 6 to 10 in the sync-CFG of \(P_2^L\) in Fig. 7 are unnecessary (they are not present in the native sync-CFG) and lead to imprecise facts in an interval analysis on this graph. Some of the final facts in an interval analysis on these graphs are shown alongside the programs in Figs. 6 and 7. In particular the analysis on \(P_2^L\) is unable to prove the assertion in line 10 of the original program.
6.2 A Lightweight Lock-Translation
Our disjoint block-based approach of Sect. 5 can be viewed as a lightweight lock translation which does not attempt to preserve execution semantics, but preserves disjoint blocks and hence also races and the sync-CFG structure of the original interrupt-driven program.
Let us first spell out the translation. Let us fix an interrupt-driven program \(P=(V,T)\). The idea is simply to introduce a lock corresponding to each pattern of disjoint block pairs listed in Fig. 4, and to insert at the entry and exit to these blocks an acquire and release (respectively) of the corresponding lock. For each of the cases (a) through (h) we introduce locks named A through H, with some exceptions. Firstly, for case (f) regarding the create of a thread t, we simply translate these as a \(\texttt {spawn}(t)\) command in a classical lock-based programming language, which has a standard acquire-release semantics. Secondly, for case (h), we need a copy of H for each thread t, which we call \(H_t\). This is because the concerned blocks (say between a set and unset of the flag f) are not disjoint across task threads, but only with the “then” block of an ISR thread statement that checks if \(f = 0\). The ISR thread now acquires the set of locks \(\{H_t \ | \ t \in T\}\) at the beginning of the “then” block of the if statement, and releases them at the end of that block. We call the resulting classical lock-based program \(P^W\). Figure 5c shows this translation for the program \(P_1\).
Figure 8 shows this translation along with the sync-CFG edges and some of the final facts in an interval analysis for the program \(P_2\).
It is not difficult to see that \(P^W\) allows all executions that are possible in P. However it also allows more: for example the execution of \(P_1^W\) (Fig. 5c) in which thread t1 preempts t2 at line 9 to execute the statement at line 4, is not allowed in \(P_1\). Thus it only weakly captures the execution semantics of P. However, every race in P is also a race in \(P^W\). To see this, suppose we have a race on statements s and t in P. This means there is a high-level race on the two skip blocks around s and t in the augmented program \(P'\). Since an execution exhibiting the high-level race on these blocks would also be present in \((P')^W\) which is identical to \((P^W)'\), it follows that the corresponding statements are racy in \(P^W\) as well.
Further, since our translation preserves disjoint blocks by construction, if s and t are in disjoint blocks in P, the corresponding statements will be in disjoint blocks in \(P^W\); and vice-versa. It follows that the sync-CFGs induced by P and \(P^W\) are essentially isomorphic (modulo the synchronization statements). As a result, any value-set-based analysis will produce identical results on the two graphs.
Finally, if statements s and t are HB-racy in P, they must also be HB-racy in \(P^W\). This is because disjoint blocks are preserved and the synchronizes-with relation is inherited from the disjoint blocks. Hence the execution witnessing the HB-race in P would also be present in \(P^W\), and would also witness a HB-race on the corresponding statements.
We summarize these observations below:
Proposition 1
Let P be an interrupt-driven program and \(P^W\) the classical lock program obtained using our lightweight lock translation. Then:
-
1.
If statements s and t are racy in P, the corresponding statements are racy in \(P^W\) as well.
-
2.
If statements s and t are HB-racy in P, the corresponding statements are HB-racy in \(P^W\) as well.
-
3.
The sync-CFGs induced by P and \(P^W\) are essentially isomorphic. As a result the final facts in a value-set-based analysis on these graphs will be identical.
\(\square \)
6.3 Lockset Analysis for Race Detection
For classical lock-based programs, the lockset analysis [24] essentially tracks whether two statements are in disjoint blocks. Here two blocks are disjoint if they hold the same lock for the duration of the block. When two statements are in disjoint blocks, they are necessarily happens-before ordered, and hence this gives us a way to declare pairs of statements to be non-HB-racy.
A lockset analysis computes the set of locks held at each program point as follows: at program entry it is assumed that no locks are held. When a call to acquire(l) is encountered, the analysis adds the lock l at the out point of the call. When a call to release(l) is encountered the lockset at the out point of the call is the lockset computed at the in point with the lock l removed. For any other statement, the lockset from the in point of the statement is copied to its out point. The join operation is the simple intersection of the input locksets. Once locksets are computed at each point, a pair of conflicting statements s and t in different threads are declared to may HB-race if the locksets held at these points have no lock in common.
Using our lock translation above, we can detect races as follows. Given an interrupt-driven program P, we first translate it to the lock-based program \(P^W\), and do a lockset analysis on \(P^W\). If any pair of conflicting statements s and t are found to be may-HB-racy in \(P^W\), we declare them to be may-HB-racy in P. By Proposition 1(2), it follows that this is a sound analysis for interrupt-driven programs.

7 Analyzing the FreeRTOS Kernel Library
We now perform an experimental evaluation of the proposed race detection algorithm and sync-CFG-based relational analysis for interrupt-driven programs. We use the FreeRTOS kernel library [3], on which our interrupt-driven program semantics are based, to perform our evaluation. FreeRTOS is a collection of functions mostly written in C, that an application developer compiles with and invokes in the application code. We view the FreeRTOS kernel library as an interrupt-driven program as follows: we build an interrupt-driven program out of the FreeRTOS kernel as shown in the figure alongside. The main thread is responsible for initializing the kernel data structures and then creating two threads: a task thread which branches out calling each task kernel API function, and loops on this; and an ISR thread which similarly branches and loops on the ISR kernel API functions. FreeRTOS provides versions of API functions that can be called from interrupt service routines. These functions have “FromISR” appended to their name. While it is sufficient to have one ISR thread, we assume (in the analysis) that there could be any number of task threads running. To achieve this we simply add sync-edges within each task kernel function, in addition to the usual sync-edges between task functions. We used FreeRTOS version 10.0.0 for our experiments. We conducted these experiments on an Intel Core i7 machine with 32 GB RAM running Ubuntu 16.04.
7.1 Race Detection
We consider 49 task and queue API functions that can be called from an application (termed top-level functions) for race detection. The functions operating on semaphores and mutexes were not considered.
We prepared the API functions for analysis, in two steps: (1) inlining and (2) lock insertion, as follows: The function vTaskStartScheduler and the queue initialization code in the function xQueueGenericCreate were treated as part of the main thread, which initializes kernel data structures. All the helper function calls made inside the top-level functions were inlined. After inlining, the functions are modified to acquire and release locks using the strategy explained in Sect. 6.2. We consider each pair of disjoint blocks as taking the same distinct lock. For example, the pair of disjoint blocks protected by disableint-enableint take lock A. That is disableint is replaced with acquire(A) and enableint is replaced with release(A). A total of 9 locks corresponding to disjoint blocks were employed in the modification of the FreeRTOS code. The two steps outlined above are automated. Inlining is achieved using the inline pass in the CIL framework [22]. Lock insertion is accomplished using a script.
The modified code, which has over 3.5K lines of code, is used for race detection. We tracked 24 variables and check whether the statements accessing them are racy. These variables include fields in the queue data-structure, task control block, and queue registry, as well as variables related to tasks. FreeRTOS maintains lists for the states of the tasks like “ready”, “suspended”, “waiting to send”, etc. The pointers to these lists are also analysed. Access to any portion of a list (like the delayed list) is treated as an access of a corresponding variable of the same name.
Races are detected in this modified FreeRTOS code in three steps - (1) compute locks held, (2) identify whether access of a variable is a read or write, and (3) report potential races. First a lockset analysis, as explained in Sect. 6.3, to compute locks held at each access to variables, is implemented as a pass in CIL. The modified FreeRTOS code is analyzed using this new pass and the lockset at each access to the 24 variables of interest is computed. Then, a writes pass to identify whether accesses to variables are “read” or “write”, also implemented in CIL, is run on the modified FreeRTOS code. Finally, a shell script to interpret both the results in the previous steps and report potential races is employed. The script identifies the conflicting access pairs (using the writes pass) and the locks held by the conflicting accesses (using lockset pass).
Our analysis reports 64 pairs of conflicting accesses as being potentially racy. On manual inspection we classified 18 of them are real races and the rest as false positives. Table 2 summarizes our findings. The second column in the table lists the variables of interest involved in the race, like various task list pointers, queue registry fields pcQueueName and xHandle, task variable uxCurrentNumberOfTasks, tick count xTickCount, etc. The third column lists the functions in which the conflicting accesses are made and the fourth gives the number of racing pairs. The fifth column assesses the potential races based on our manual inspection of the code. The analysis took 3.91 s.
The false positives were typically due to the fact that we had abstracted data-structures (like the delayed list which is a linked-list) by a synonymous variable. Thus even if the accesses were to different parts of the structure (like the container field of a list item and the next pointer of a different list item) our analysis flagged them as races.
We were in touch with the developers of FreeRTOS regarding the 18 pairs we classified as true positives. The 14 races on the queue registry were deemed to be non-issues as the queue delete function is usually invoked only once the application is about to terminate. The 2 races on uxCurrentNumberOfTasks are known (going by comments in the code) but are considered benign as the variable is of “base type”. The remaining couple of races on the delayed task lists appear to be real issues as they have been fixed (independent of our work) in v10.1.1.
7.2 Region-Based Relational Analysis
Our aim here is to do a region-based interval and polyhedral analysis of a region-race-free subset of the FreeRTOS kernel APIs, and to prove some simple assertions about the kernel variables in each region.
We first identified six regions for this purpose. One region corresponds to variables protected by disabling interrupts (like xTickCount, xNextTaskUnblockTime, etc.), while variables protected by suspend and resume scheduler commands (like uxPendedTicks, xPendingReadyList, etc.) are in another region. Fields of the queue structure like pcHead, pcTail, etc. are in a third region, while the waiting lists for a queue form another region. The queue registry fields like pcQueueName and xHandle are in region 5. The pointer variable pxCurrentTCB, pointing to the current Task Control Block (TCB), is put in the sixth region.
The FreeRTOS code was modified further to reflect access to regions. For this new variables \(R_1,\ldots , R_6\), are declared. Wherever there is a write (or read) access to a variable in region i an assignment statement that defines (or reads from) variable \(R_i\) is inserted just before the access. This is done using a script which takes the result of the writes pass to find where in the source code an appropriate assignment statement has to be inserted. We selected 15 APIs that did not contain any region races.
Next, we prepared the API functions for the analysis in two steps. They are described below:
Abstraction of FreeRTOS API Functions. We abstracted the FreeRTOS source code to prepare it for the relational analysis. In this abstraction, we basically model the various lists (ready list, delayed list) by their lengths and the value at the head of the list (if required). Using this abstraction, we are able to convert list operations to operations on integers.
Similarly, to model insertion into a list, we abstract it by incrementing the variable which represents the length of the list. We abstracted all the API functions in a similar fashion.
Creation of the Sync-CFG. The next step is to create a sync-CFG out of the abstracted program. For doing this, we used the abstracted version of the FreeRTOS code (along with acquire-release added as explained in Sect. 7.1).
Next, we used a script to insert non-deterministic gotos from the point of release of a lock to the acquire of the same lock. Since we are using gotos for creation of sync-CFG, we keep all the API functions in main itself and evaluate a non-deterministic “if” condition before entering the code for an API function.
Results. For the purpose of analysis we listed out some numerical relations between kernel variables in the same region, which we believed should hold. We identified a total of 15 invariants including 4 invariants which involve relations between kernel variables. We then inserted assertions for these invariants at the key points in our source code like the exit of a block protecting a region.
We have implemented an interval-based value-set analysis and a region-based octagon and polyhedral analysis for C programs using CIL [22] as the front-end and the Apron library (version 0.9.11) [16]. We represent the sync-with edges of the sync-CFG of a program using goto statements from the source (release) to the target (acquire) of the may-synchronizes-with (MSW) edges.
We ran our implementation on the abstracted version of the FreeRTOS kernel library, with the aim of checking how many of the invariants it was able to prove. The abstracted code along with addition of gotos is about 1500 lines of code. We did a preliminary interval analysis on this abstracted sync-CFG and were able to prove 11 out of these 15 invariants. With a widening threshold of 30, the interval analysis takes under 5 min to run. As expected, the interval analysis could not prove the relational invariants.
We then did a region-based polyhedral analysis using the six regions identified above. For the region-based analysis, we used convex polyhedra domain with a widening threshold of 30. It is able to prove all the assertions we believed to be true. The analysis takes about 30 min to complete with the convex polyhedra domain and about 20 min with the octagon domain.
The results obtained by our analysis are shown in Table 3.
8 Related Work
We classify related work based on the main topics touched upon in this paper.
Data Races. Adve and Hill [1] introduce the notion of a data race using a happens-before relation, and identify instructions that form release-acquire pairs, for low-level concurrent programs. Boehm and Adve [4] define races in terms of consecutive occurrences in a sequentially consistent execution, as well as using a happens-before order, in the context of the C++ semantics. They show their notions are equivalent as far as race-free programs go. As pointed out earlier, the definition of races as consecutive occurrences is inadequate in our setting. Schwarz et al. [26] define a notion of data race for priority-based interrupt-driven programs, where there is a single main task and multiple ISRs. A race occurs when the main thread is accessing a variable at a certain dynamic priority, and an ISR thread with higher priority also accesses the variable. Our definition can be seen to be stronger and more accurately captures racy situations. In particular, if the ISR thread with higher priority does not actually execute the conflicting access, due to say a condition not being enabled, then we would not call it a race. The term “high-level” race was coined by Artho et al. [2]. Our definition of a high-level race follows that of [20].
Analysis of Interrupt-Driven Programs. Regehr and Cooprider [23] describe a source-to-source translation of an interrupt-driven program to a standard multi-threaded program, and analyze the translated program for races. Their translation is inadequate for our setting in many ways: in particular, disable-enable of interrupts is translated by acquiring and releasing all ISR-specific locks; however this does not prevent interaction with another task while one task has disabled interrupts. In [8] they also describe an analysis framework for constant-propagation analysis on TinyOS applications. They use a similar idea of adding “control-flow” edges between disable-enable blocks and ISRs. However no soundness argument is given, and other kinds of blocks (suspend/resume, flag-based synchronization) are not handled. The works in [5, 6, 13] analyze timing properties, interrupt-latency, and stack sizes for interrupt-driven programs, using model-checking, algebraic, and algorithmic approaches. Schwarz et al. [25, 26] give analyses for race-detection and invariants based on linear-equalities for their aforementioned class of priority-based interrupt-driven programs. Our work differs in several ways: Their analysis is directed towards applications (we target libraries where task priorities do not matter), their analyses are specific (we provide a basis for carrying out a variety of value-set and relational analyses, targeting race-free programs), they consider priority and flag-based synchronization (but not disable-enable and suspend-resume based synchronization). Sung and others [27] consider interrupt-driven applications in the form of ISRs with different priorities, and perform interval-based static analysis for checking assertions. They do not handle libraries and do not leverage race-freedom. Finally, [20] uses a model-checking approach to find all high-level races in FreeRTOS with a completeness guarantee.
Analysis of Race-Free Programs. Chugh et al. [7] use race information to do thread-modular null-dereference analysis, by killing facts at a point whenever a notional read of a variable is found to be racy. De et al. [11] propose the sync-CFG and value-set analysis for race-free programs, while Mukherjee et al. [21] extend the framework to region and relational analyses. Gotsman et al. [12] and Miné et al. [18, 19] define relational shape/value analyses for concurrent programs that exploit race-freedom and lock invariants respectively. All these works are for classical lock-based synchronization while we target interrupt-driven programs.
9 Conclusion
In this paper our aim has been to give efficient static analyses for classes of non-standard concurrent programs like interrupt-driven kernels, that exploit the property of race-freedom. Towards this goal, we have proposed a definition of data races which we feel is applicable to general concurrent programs. We have also proposed a general principle for defining synchronizes-with edges, which is the key ingredient of a happens-before relation, based on the notion of disjoint blocks. We have implemented our theory to perform sound and effective static analysis for race-detection and invariant inference, on the popular real-time kernel FreeRTOS.
We feel this framework should be applicable to other kinds of concurrent systems, like other embedded kernels (for example TI-RTOS [14]) and application programs, and event-driven programs. There are additional challenges in these systems like priority-based preemption and priority inheritance conventions which need to be addressed. Apart from investigating these systems we would like to apply this theory to perform other static analyses like null-dereference, points-to, and shape analysis, for these non-standard classes of concurrent programs.
References
Adve, S.V., Hill, M.D.: A unified formalization of four shared-memory models. IEEE Trans. Parallel Distrib. Syst. 4(6), 613–624 (1993)
Artho, C., Havelund, K., Biere, A.: High-level data races. J. Softw. Test. Verif. Reliab. 13, 207–227 (2003)
Barry, R.: The FreeRTOS kernel, v10.0.0 (2017). https://freertos.org
Boehm, H., Adve, S.V.: Foundations of the C++ concurrency memory model. In: Proceedings of the ACM SIGPLAN 2008 Conference on Programming Language Design and Implementation, Tucson, USA, pp. 68–78. ACM (2008)
Brylow, D., Damgaard, N., Palsberg, J.: Static checking of interrupt-driven software. In: Proceedings of the 23rd International Conference on Software Engineering, ICSE 2001, Toronto, Ontario, Canada, 12–19 May 2001, pp. 47–56 (2001)
Chatterjee, K., Ma, D., Majumdar, R., Zhao, T., Henzinger, T.A., Palsberg, J.: Stack size analysis for interrupt-driven programs. In: Cousot, R. (ed.) SAS 2003. LNCS, vol. 2694, pp. 109–126. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-44898-5_7
Chugh, R., Voung, J.W., Jhala, R., Lerner, S.: Dataflow analysis for concurrent programs using data race detection. In: Proceedings of the ACM SIGPLAN 2008 Conference on Programming Language Design and Implementation, Tucson, AZ, USA, 7–13 June 2008, pp. 316–326 (2008)
Cooprider, N., Regehr, J.: Pluggable abstract domains for analyzing embedded software. In: Proceedings of the ACM SIGPLAN/SIGBED Conference on Languages, Compilers, and Tools for Embedded Systems (LCTES 2006), Ottawa, Canada, 14–16 June 2006, pp. 44–53 (2006)
Cousot, P., Cousot, R.: Abstract interpretation: a unified lattice model for static analysis of programs by construction or approximation of fixpoints. In: Proceedings of the ACM SIGACT-SIGPLAN Symposium on Principles of Programming Languages, pp. 238–252. ACM (1977)
De, A.: Access path based dataflow analysis for sequential and concurrent programs. Ph.D. thesis, Indian Institute of Science, Bangalore, December 2012
De, A., D’Souza, D., Nasre, R.: Dataflow analysis for data race-free programs. In: Proceedings of the 20th European Symposium on Programming ESOP 2011, Saarbrücken, Germany, 26 March – 3 April 2011, pp. 196–215 (2011)
Gotsman, A., Berdine, J., Cook, B., Sagiv, M.: Thread-modular shape analysis. In: Proceedings of the ACM SIGPLAN 2007 Conference on Programming Language Design and Implementation, San Diego, California, USA, 10–13 June 2007, pp. 266–277 (2007)
Huang, Y., Zhao, Y., Shi, J., Zhu, H., Qin, S.: Investigating time properties of interrupt-driven programs. In: Gheyi, R., Naumann, D. (eds.) SBMF 2012. LNCS, vol. 7498, pp. 131–146. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-33296-8_11
Texas Instruments: TI-RTOS: A Real-Time Operating System for Microcontrollers (2017). http://www.ti.com/tool/ti-rtos
Jeannet, B., Miné, A.: Apron: a library of numerical abstract domains for static analysis. In: Bouajjani, A., Maler, O. (eds.) CAV 2009. LNCS, vol. 5643, pp. 661–667. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-02658-4_52
Jeannet Bertrand, M.A.: Apron numerical abstract domain library (2009). http://apron.cri.ensmp.fr/library/
Kini, D., Mathur, U., Viswanathan, M.: Dynamic race prediction in linear time. In: Proceedings of the 38th ACM SIGPLAN Conference on Programming Language Design and Implementation, PLDI 2017, pp. 157–170. ACM, New York (2017)
Miné, A.: Relational thread-modular static value analysis by abstract interpretation. In: McMillan, K.L., Rival, X. (eds.) VMCAI 2014. LNCS, vol. 8318, pp. 39–58. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54013-4_3
Monat, R., Miné, A.: Precise thread-modular abstract interpretation of concurrent programs using relational interference abstractions. In: Bouajjani, A., Monniaux, D. (eds.) VMCAI 2017. LNCS, vol. 10145, pp. 386–404. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-52234-0_21
Mukherjee, S., Kumar, A., D’Souza, D.: Detecting all high-level dataraces in an RTOS kernel. In: Bouajjani, A., Monniaux, D. (eds.) VMCAI 2017. LNCS, vol. 10145, pp. 405–423. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-52234-0_22
Mukherjee, S., Padon, O., Shoham, S., D’Souza, D., Rinetzky, N.: Thread-local semantics and its efficient sequential abstractions for race-free programs. In: Ranzato, F. (ed.) SAS 2017. LNCS, vol. 10422, pp. 253–276. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-66706-5_13
Necula, G.: CIL – infrastructure for c program analysis and transformation (v. 1.3.7) (2002). http://people.eecs.berkeley.edu/~necula/cil/
Regehr, J., Cooprider, N.: Interrupt verification via thread verification. Electr. Notes Theor. Comput. Sci. 174(9), 139–150 (2007)
Savage, S., Burrows, M., Nelson, G., Sobalvarro, P., Anderson, T.E.: Eraser: a dynamic data race detector for multithreaded programs. ACM Trans. Comput. Syst. 15(4), 391–411 (1997)
Schwarz, M.D., Seidl, H., Vojdani, V., Apinis, K.: Precise analysis of value-dependent synchronization in priority scheduled programs. In: McMillan, K.L., Rival, X. (eds.) VMCAI 2014. LNCS, vol. 8318, pp. 21–38. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54013-4_2
Schwarz, M.D., Seidl, H., Vojdani, V., Lammich, P., Müller-Olm, M.: Static analysis of interrupt-driven programs synchronized via the priority ceiling protocol. In: Proceedings of the ACM SIGPLAN-SIGACT Principles of Programming Languages (POPL), pp. 93–104 (2011)
Sung, C., Kusano, M., Wang, C.: Modular verification of interrupt-driven software. In: Proceedings of the 32nd IEEE/ACM International Conference on Automated Software Engineering, ASE 2017, Urbana, IL, USA, 30 October – 3 November 2017, pp. 206–216 (2017)
Tarski, A., et al.: A lattice-theoretical fixpoint theorem and its applications. Pac. J. Math. 5, 285–309 (1955)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2019 The Author(s)
About this paper
Cite this paper
Chopra, N., Pai, R., D’Souza, D. (2019). Data Races and Static Analysis for Interrupt-Driven Kernels. In: Caires, L. (eds) Programming Languages and Systems. ESOP 2019. Lecture Notes in Computer Science(), vol 11423. Springer, Cham. https://doi.org/10.1007/978-3-030-17184-1_25
Download citation
DOI: https://doi.org/10.1007/978-3-030-17184-1_25
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-17183-4
Online ISBN: 978-3-030-17184-1
eBook Packages: Computer ScienceComputer Science (R0)







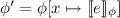 ,
,  ,
,