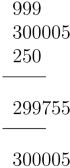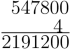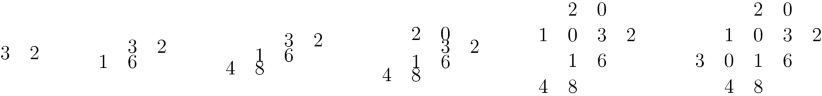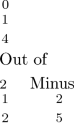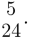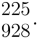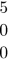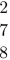Abstract
In the Name of God, Most Gracious Most merciful. Lord make it easy, not hard.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
Means “son of” and commonly used in Arabic names.
- 2.
Found in the right margin. Also, underneath in that right margin, there is a text which is independent from the name. The text is open to a few interpretations but what is clear is “Mortmain property ‘Waqf’ of the pole of the department of justice and center of governance. Written to the Sultan, son of Sultan, the Sultan Abu Said Othman Khan, son on the Sultan Mustafa Khan may his fortune and his hopes last. May God The Provider give him long life and honer and surround the name of Haj Amine the inspector of the two holy noble mosques.” The italic parts of the text are not definite as they are hard to read.
- 3.
- 4.
Here it is“Zij Ilkhani” which is from zij, the astronomical tables and “Ilkhani” the “subordinate Khan” which is most likely referring to Hulagu Khan, the Mongol ruler, who was the patron of the author of the astronomical tables in his time.
- 5.
Tashilat literally means ease or shortcuts and the title Zij al-Tashilat may just mean the book that is of shortcuts in computing the astronomical tables.
- 6.
Written by Claudius Ptolemy in the second century CE, Almagest was the main astronomy book in the Greek scientific tradition. It received much attention from the scholars in the medieval Islamic scholars. See [32] for more on the importance of Almagest in the medieval Islamic science.
- 7.
At the bottom of some pages, the first word of the next page is written.
- 8.
“Tabaq Al-Manatiq” is a mechanical planetary computer.
- 9.
The 1416 “Nuzhat Al-Hada’iq” book has been translated by E. S. Kennedy in 1960 as “The Planetary Equatorium.”
- 10.
Here, al-Kāshı̄ is referring to the jummal notation to represent sexagesimal numbers in which the letters of the Arabic alphabet are used as digits.
- 11.
The Arabic word al-jabr that appears in the title Kitab al-Jabr wa’l Muqabala of a book written by al-Khwarizmi around 820 is the source of the term algebra.
- 12.
Following the tradition in the study of algebra in Islam, al-Kāshı̄ is using “shai” which literally means “thing” to mean an unknown like x, and its square x 2 for māl, and its cube x 3 for the cube.
- 13.
Stroke out in the manuscript as a correction.
- 14.
These numbers are written in al-Kāshı̄’s book from right to left just like Arabic using the following numerals

. Note that these numbers are similar to what is nowadays called Persian or Farsi numerals except for number 6 which is similar to Indian numerals instead.
- 15.
Note that the terms million and billion did not exist and therefore, forty three billion is written as forty three thousand thousand thousand. The full number mentioned is forty three thousand thousand thousand, eight hundred and twenty three thousand thousand, four thousand, sixty five.
- 16.
We observe that the fraction here does not have a fraction line, although it has been used in early Arabic mathematics. The fraction bar is a regional variation found in mathematics texts west of Egypt since the late twelfth century.
- 17.
The zero before the nine is in reality before it in terms of position (9 is in the tens of thousands position and the 0 before it is in the thousands position) as well as in the reading of Arabic from right to left.
- 18.
The example below that al-Kāshı̄ produces clarifies the situation. For example, 5 is in the million position in the second number. There is no corresponding digit in the million position in the first number. So, al-Kāshı̄ will just write the 5 in the result line. The digit 2 in the hundred thousand position in the second number doesn’t have a corresponding digit in the same position in the first number, but according to al-Kāshı̄’s description of the addition algorithm, we need to add to 2 the 1 that is a carryover from the addition of 6 and 9.
- 19.
Subtraction is defined only if a smaller [positive] number is subtracted from a larger [positive] number. The notion of negative number did not exist at the time.
- 20.
The positions of numbers from right to left grow by a multiple of ten, and therefore it does make sense that al-Kāshı̄ defines the next position to the left as that of ten relative to its predecessor to the right.
- 21.
The process is that of borrowing from the next position (al-Kāshı̄ calls it that of ten relative to the previous position) if not zero otherwise, it is borrowing from the second next position, that al-Kāshı̄ calls hundreds relative to the position to borrow for.
- 22.
In the upper right margin there is the following: “Example of subtraction. To check, we add the remainder to the subtrahend to find the minuend. To understand better the example, if there is zero in the hundred place we take away from the thousands or what is there after to get the remainder. An inspiration from the scribe.”
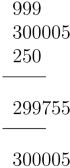
- 23.
Actually, al-Kāshı̄ puts the minuend below the subtrahend. We switched the order to make it easier to read for the modern reader.
- 24.
That is, if n = n 1 ⋅ n 2, then \(\frac {n}{n_1}=\frac {n_2}{1}\) or \(\frac {n}{n_2}=\frac {n_1}{1}\cdot \)
- 25.
Recall that in this context tens is a relative term for al-Kāshı̄ to say the next position.
- 26.
This example is written in vertical format on the top left of the page with the expression “easier than.” The note also contains the name of the scribe.
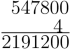
- 27.
Lattice or net.
- 28.
Throughout the book, al-Kāshı̄ provides multiple methods and techniques for tackling a given problem. This illustrates his teaching and pedagogical approach as discussed by Taani in [38].
- 29.
This is found on the right margin and indicated in the text with an insert symboľ.
- 30.
This multiplication is tedious, but it shows that al-Kāshı̄ has a great understanding of the position system when multiplying. Here are all steps. At the end, one needs to add vertically to find the result. Al-Kāshı̄ provides other multiplication algorithms that are easier to deal with.
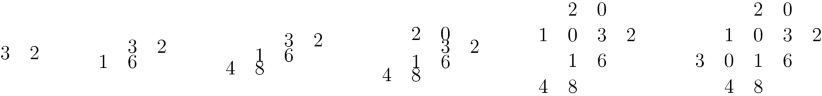

Also, in the right margin, there is a set up for the same multiplication that seems to be a bit different, in the sense that it is going upward instead of setting up the numbers downward.
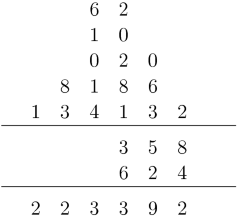
- 31.
A note on the left margin that seems to be written by the scribe showing a vertical format multiplication, similar to the modern multiplication. It says: “Easier than it and shorter.” Also, it is written “to its scribe” and possibly “Ibrahim, the forgiveness” or it could be his last name. The scan of the book does not show the complete far left side and a physical check of the paper book is necessary. A check on other manuscripts such as [3, 4] shows a similar multiplication with 456 on top and 2783.

- 32.
This is found on the right margin and indicated in the text with an insert symbol ̌.
- 33.
In the right margin it is written “ the work of Zanjid” or “the work of Zanjir.”
- 34.
Here, the term “deduce” could mean “invent,” “relate,” or “survey.”
- 35.
This is found above the text with an insert symboľ. There is also the phrase “smaller in terms of form” in the top margin which is found in [4] as well.
- 36.
- 37.
There seems to be a correction as 47.
- 38.
The result of the division is \(7507+\dfrac {83}{475}\cdot \)
- 39.
On the top right margin of the page it is written: “And what is left of the dividend is one, that is a fraction with its denominator being the divisor.”
- 40.
Al-Kāshı̄ is considering here the sequence a, a 2, a 3, …
- 41.
Al-Kāshı̄ calls a the first power in the sequence a, a 2, a 3, … but a is called a [square] root for a 2 and a cubic root for a 3. Al-Kāshı̄ is showing an understanding of the relationship between roots and powers like \(a=\sqrt {a^2}\) and \(a={\sqrt [3]{a^3}}\).
- 42.
Majdhur. a 2 is named rooted because it has its root in the sequence a, a 2, a 3, …
- 43.
Arabs refer to their livestock as m \(\bar a\) l. Even today, the livestock market is called Sook al-m \(\bar a\) l. Sook is market. In general m \(\bar a\) l is wealth. Al-Kāshı̄ is considering m \(\bar a\) l to be a 2. See [23] for more on the meaning of the term m \(\bar a\) l in Arabic mathematics.
- 44.
Refers to a 2, the first result of the operations described above. It is also called m \(\bar a\) l and square.
- 45.
It refers to a 3, the second result of the operations described above.
- 46.
The sequence considered here is literally a 2 a 2 = a 4, a 2 a 3 = a 5, a 3 a 3 = a 6, a 2 a 2 a 3 = a 7, a 2 a 3 a 3 = a 8, a 3 a 3 a 3 = a 9.
- 47.
Al-Kāshı̄ seems to be considering the ratios 1 : a = a : a 2 = a 2 : a 3 = …
- 48.
On the right margin it is written: “Know that the ratio of the reciprocal of something to the reciprocal of the square is the same as the ratio of the reciprocal of the square to the reciprocal of the cube and it is the same as the ratio of the reciprocal of the cube to the reciprocal of the square-square (power 4) and so forth all the other reciprocals indefinitely will be on the same ratio as I described.”
- 49.
Al-Kāshı̄ is defining the degree using addition instead of multiplication. For example, square-square leads to a degree of 2 + 2 = 4 and square-cube leads to a degree of 2 + 3 = 5.
- 50.
If the degree is 6, then 6 = 3 + 3 and the name of the power is cube-cube.
- 51.
Al-Kāshı̄ is writing a positive integer as the sum of 3’s and 2’s, starting with the 3’s first. For example, al-Kāshı̄ considers 6 = 3 + 3 instead of 6 = 2 + 2 + 2 so that the degree 6 gives the name cube-cube for the power. As for the numbers that are not divisible by 3, say 7, al-Kāshı̄ will take away 2 to get 5 and because 5 is not divisible by 3 then he takes away 2 to get 3 which is divisible by 3. So, 7 = 2 + 2 + 3 and according to al-Kāshı̄, the degree 7 will provide a power square-square-cube. Note that the fact that al-Kāshı̄ is using 3’s first and then 2’s is not in contradiction with him giving priority to the term square over the term cube. This is true because the first is a partition of the degree using 3’s and then 2’s and the second is the naming of the degree. For example, 5 = 3 + 2, but he will use the term square-cube to name the degree instead of cube-square.
- 52.
The Arabic word for perfect is munṭaq which literally means “audible,” or “spoken,” and the Arabic word for imperfect is aṣamm which literally means “deaf” or “inaudible.” As explained in [31], munṭaq is called so because we can pronounce its exact value whereas aṣamm cannot be expressed because no number gives its exact value. In general, any quantity whose value can only be given approximately in a given operation is called aṣamm with respect to that operation. In the context of root extraction, if a number (integer) is not a perfect power, then its root will be irrational hence it is not possible to express its exact value as a specific number.
- 53.
In obtaining the fractional part of the approximate square root, al-Kāshı̄ is in fact, using a linear approximation. When looking for the square root on an imperfect square N, al-Kāshı̄ is saying that r 2 < N < (r + 1)2, equivalently, \(r<\sqrt {N}<r+1\) where r is the largest number with the condition r 2 < N. Furthermore, he states that \(\displaystyle \sqrt {N}\approx r+\frac {N-r}{2r+1}\cdot \) One should consult [7, 11] for a full explanation and further developments of al-Kāshı̄’s root extraction algorithm.
- 54.
There is a typo in the text. This number should be 331781.
- 55.
Al-Kāshı̄ found that \(\displaystyle \sqrt {331781}= 576+\frac {5}{1153}\approx 576.004337\) Using a modern calculator, we found \(\sqrt {331781}\approx 576.004340.\) This is a remarkable approximation.
- 56.
This is found on the right margin and indicated in the text with an insert symboľ.
- 57.
The condition mentioned is relative to the alignments of digits as above.
- 58.
This is found on the left margin and indicated in the text with an insert symboľ.
- 59.
It is written “below” in the main text but in the margin on top of this word it is written “above.” In [3] it is written “below” only and in [4, 6] it is written “above” only. We believe it is above because in the next sentence al-Kāshı̄ speaks about how the numbers are fixed, not erased, below the line at the row of the number.
- 60.
- 61.
We want to extract the fifth root.
- 62.
44,240,899,506,197 forty four trillion, two hundred and forty billion, eight hundred and ninety nine million, five hundred and six thousand, one hundred and ninety seven.
- 63.
This is found on the left margin and indicated in the text with an insert symboľ.
- 64.
A detailed explanation on how the operation works with computations showing how to find all the numbers in the next table can be found in [11]. It is also worth noting that key numbers in al-Kāshı̄’s table are coefficients of polynomials in the Ruffini-Horner Method.
- 65.
\(\root 5 \of { 44240899506197} \approx 536+\frac {21}{414237740281}\approx 536.0000000000506.\) Using a modern calculator we found 442408995061975 ≈ 536.0000000000508. This is an approximation accurate to the twelve decimal digits.
- 66.
Misprint as 69 = 10077696. It is correct though in [3]
- 67.
Since there is a misprint in 69, 610 is not correct here, as 610 = 60466176. It is correct though in [3].
- 68.
Misprint as 78 = 5764901. It is correct though in [3]. Observe here that 79 and 710 are correct.
- 69.
Misprint as 99 = 387420489. It is correct though in [3].
- 70.
Since there is a misprint in 99, 910 is not correct here, as 910 = 3486784401. It is correct though in [3].
- 71.
Al-Kāshı̄ calls such numbers “uṣul” which literally means origins, roots, sources, or provenance. We opted for the word coefficients because they are the coefficients of the terms in the expansion of (a + 1)n bar 1’s, according to the text below.
- 72.
The coefficients here are those of the binomial expansion of (a + 1)n in general, bar 1. Al-Kāshı̄ is giving the example of the coefficients of (a + 1)5 = a 5 + 5a 4 + 10a 3 + 10a 2 + 5a + 1 bar 1. He basically considers the coefficients that he calls uṣul 5 for row of square-square (power 4), 10 for the row of cube (power 3), 10 for the row of square (power 2), and 5 for the row of root (power 1). Al-Kāshı̄ is not interested here by the 1’s that are coefficients of a 5 and the constant term 1. If we omit the 1’s in Pascal’s triangle, al-Kāshı̄ is considering all the other entries of Pascal’s triangle.
- 73.
Al-Kāshı̄ is using the two terms here of coefficients and entries which later allows him to use them interchangeably.
- 74.
Al-Kāshı̄ is giving here and below with examples a property of the coefficients of the binomial expansion which is a property of Pascal’s triangle entries.
- 75.
Continuing the observations from the previous notes, the coefficients of the binomial expansion of degree 3 are 1, 3, 3, 1. Since al-Kāshı̄ is not considering here the 1’s, he focuses on 3 and 3. Their sum is 6 which is the middle coefficient of the binomial expansion of degree 4. Those coefficients are 1, 4, 6, 4, 1. He does the same argument below regarding 4 + 6 = 6 + 4 = 10 and generalizes the argument to say, one can continue in this way indefinitely.
- 76.
Here, al-Kāshı̄ goes one step further in giving how to find the coefficients of the binomial expansion or Pascal’s triangle entries in the table starting with the power 2 till the power 9 by adding the entries before them, like we do in Pascal’s triangle. Moreover he clearly states that one can continue in this way indefinitely. If we read the entries of the table from bottom to top and right to left, then we clearly see Pascal’s triangle.
- 77.
Canceled sentences here and in the previous page are because of repetitions.
- 78.
We observe that the number al-Kāshı̄ is computing is needed in the approximation of nth roots, namely, the denominator (a + 1)n − a n of the fractional part of the approximation of the nth root of a number N with a being the largest integer such that a n ≤ N (see [7, 11] for further details). Here, al-Kāshı̄ is considering (4 + 1)5 − 45 = 55 − 45 = (5)44 + (10)43 + (10)42 + (5)41 + 1 = 2101. If we apply what has been said here to al-Kāshı̄’s earlier example of \(\displaystyle \root 5 \of {44240899506197} \approx 536+\frac {21}{414237740281}\), we see that the denominator 414237740281 = (536 + 1)5 − 5365 is obtained using the binomial expansions after many operations in the table of roots.
- 79.
Now, al-Kāshı̄ is generalizing the method of finding the difference of powers from (a + 1)n − a n to that of any numbers (a + b)n − a n using the example of \(7^5-4^5= (4+3)^5-4^5= 5\left (4^4\right )(3) + 10\left (4^3\right )\left (3^2\right )+ 10\left (4^2\right )\left (3^3\right )+ 5\left (4^1\right )\left (3^4\right ) + 3^5=15783\).
- 80.
This is the method called “casting out nines.”
- 81.
This method is not completely reliable as it does not detect all the errors but al-Kāshı̄ is aware of the fact that it is only a sufficient condition (see [37]).
- 82.
This is found on the top margin with an insert symboľ in the text.
- 83.
A fraction like two thirds is considered to be a ratio, or relation of 2 to 3. If we take 3 to be our unit or “one,” then the fraction represents how large 2 is with respect to 3. We will express a fraction such as \({2\over 3}\) either as “2 with respect to 3” or more familiar “2 out of 3.”
- 84.
Al-Kāshı̄ uses the word “kasr” to denote either a fraction or the numerator of a fraction. Because of the context in the sentences, there is no ambiguity to which term he refers.
- 85.
In this sentence and the two previous ones, al-Kāshı̄ is defining fractions as having infinite ways of being represented and that the best representation is the completely simplified fraction where completely simplified is to be understood in our modern mathematics terms as irreducible (numerator and denominator are relatively prime).
- 86.
A fraction over another.
- 87.
The operation of addition is not intended in “additive fractions.” These are just simple fractions gathered together.
- 88.
\(\displaystyle \frac {1}{2}\cdot \frac {1}{6}\) or \(\displaystyle \frac {1}{4}\cdot \frac {3}{5}\cdot \)
- 89.
\(\displaystyle \frac {1}{2}\cdot \frac {3}{5}\cdot \frac {4}{9}\cdot \frac {1}{10}\cdot \)
- 90.
Al-Kāshı̄ is giving an alternative way of doing the previous multiplications of fractions. Here he explains it in this way: \(\displaystyle \frac {3\left [\displaystyle \frac {4\left (\displaystyle \frac {(1/10)}{9}\right )}{5}\right ]}{2}\).
- 91.
These are divisions of the Islamic currency, the Dinar. So, we keep their names respectively as anglicized plurals of Daniq, Tasuj, and Shoir. The Daniq is the smallest subdivision of the Dinar in Gold or Silver like the Dinar itself, and then the Tasuj and Shoir are in copper.
- 92.
Most likely the Dinar is being the whole.
- 93.
1 Dinar = 6 Daniqs; 1 Daniq = 4 Tasujs; 1 Tasuj = 4 Shoirs.
- 94.
1 Shoir = \(\displaystyle \frac {1}{4}\) Tasuj = \(\displaystyle \frac {1}{16}\) Daniqs, 1 Tasuj = \(\displaystyle \frac {1}{4}\) Daniq. This means that there are fractions of shoirs.
- 95.
- 96.
- 97.
The line here refers to the fraction line as per our previous footnote.
- 98.
The entries here do not match the word description. The description is the correct one as it fits the context and is confirmed by the same description in [3] with the correct entries. Here are the entries:
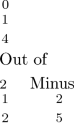
.
- 99.
Having common divisors or factors beside one. In other words, not co-prime or not relatively prime.
- 100.
The divisor being the greatest among all common divisors is implicit.
- 101.
Al-Kāshı̄ is defining the sequence of reciprocals of the divisors of a number and calling it or its members as harmonic.
- 102.
Taking al-Kāshı̄’s example of partner numbers, 10 and 4, \(\displaystyle \frac {1}{2}\) is a harmonic and is in both 10 an 4.
- 103.
Continuing the previous example, \(\displaystyle \frac {1}{2}\cdot 10=5\) is a part of the harmonic or divisor of 10. Indeed, 5 is a divisor of 10 and according to the previous footnote, \(\displaystyle \frac {1}{5}\) as well as \(\displaystyle \frac {1}{2}\) are harmonics of 10. Similarly, \(\displaystyle \frac {1}{2}\cdot 4=2\) is called part of the harmonic or divisor of 4.
- 104.
This is the well-known Euclidean Algorithm.
- 105.
- 106.
Converting a mixed fraction to improper fraction.
- 107.
Al-Kāshı̄ uses the word “bast” which is in modern Arabic mathematics the numerator of a fraction. We translated it here as extending because al-Kāshı̄ is using the word “bast” to extend the fraction to include the integer part. Moreover, in literary Arabic, the word “bast” means extend as well.
- 108.
Converting an improper fractions to mixed fraction.
- 109.
This is the least common multiple of the denominators of fractions and as stated by al-Kāshı̄ if all the fractions involved are multiplied by that number it will make the fractions integers.
- 110.
We multiply each numerator by the result of the division of the common denominator by the denominator of the fraction.
- 111.
We multiply one of them by the other one divided by the common factor.
- 112.
- 113.
The notion of negative number was not developed yet, hence they did not talk about “the sum of negative numbers.”
- 114.
- 115.
This is found on the right margin and indicated in the text with an insert symboľ.
- 116.
This is found on the right margin and indicated in the text with an insert symboľ.
- 117.
- 118.
A detailed work out of all of these operations is on left margin: “Margin for the author may God have mercy on him. In the operation of the previous work in the text body, the subtractive after the singling is
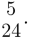
We took it over the denominator mentioned in the text; I mean 2784. The result is 580 that we added to its numerator which is 95. The result is 675 which we put in the numerator and the denominator underneath it

which is the minuend. Since the numerator and denominator have a third in common we multiply by it and get
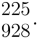
As in the text, we divide its denominator by four which is the denominator of the multiplier. We get 232. We multiply it by two and half which is the numerator of the multiplier. The result is 580 which is aligned with five and four fifths. We divide it by five and four fifths which is the denominator of the fractional part of the multiplicand. We get hundred. We multiply it by two and a quarter which is the fractional numerator. The result is 225 which is the desired numerator obtained in this work.
- 119.
Al-Kāshı̄ is using the fact that \(1+{a \over b}={a+b\over b}\).
- 120.
- 121.
We observe here that by writing
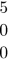
al-Kāshı̄ is considering 5 as whole number with no fraction added to it even though he is putting zero in the numerator and in the denominator. It is merely to say there is no fraction.
- 122.
- 123.
- 124.
It has been noted in [6] P. 129 that the integer part is not correct here. Indeed when we do the calculation we see that the desired answer is
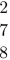
.
- 125.
We commented earlier on the writing of zeros in the numerator and denominator as being the absence of a fraction. Here we see a confirmation of that given al-Kāshı̄’s early definition of the product of fractions, and the fact that he is not multiplying the numerator and denominator with zeros with the other fraction. Moreover, he is not multiplying the integer part 10 with the integer part of the other fraction as it is zero.
- 126.
Al-Kāshı̄ is using the formulas \(\displaystyle \left ( \frac {a}{b} \right )^n= \frac {a^n}{b^n},\) and \(\displaystyle {\sqrt [n]{\frac {a}{b}}}= \frac {{\sqrt [n]{a}}}{{\sqrt [n]{b}}}\).
- 127.
Al-Kāshı̄ is using the formula \(\displaystyle {\sqrt [n]{\frac {a}{b}}}= \frac {{\sqrt [n]{a b^{n-1}}}}{b}\).
- 128.
- 129.
Al-Kāshı̄ is using the following formula \(\displaystyle \frac {\sqrt {ab^2}}{b}=\sqrt {a}\) to say that an approximation of the root \(\displaystyle \frac {\sqrt {ab^2}}{b}\) is more accurate than the direct approximation of \(\sqrt {a}\).
- 130.
Adding to the previous statement, al-Kāshı̄ is asserting that the bigger the number b is, the more accurate the approximation of \(\displaystyle \frac {\sqrt {ab^2}}{b}\) is of that of \(\sqrt {a}\).
- 131.
Al-Kāshı̄ is using the formula \(\displaystyle \frac {{\sqrt [n]{a10^{nm}}}{10^m}}={\sqrt [n]{a}}\) to say that an approximation of the root \(\displaystyle \frac {{\sqrt [n]{a10^{nm}}}}{10^m}\) is more accurate than the direct approximation of \({\sqrt [n]{a}}\) and the bigger m is the better the approximation is.
- 132.
Found in the left margin.
- 133.
We gave the definitions and relations of Dinar, Daniq, Tasuj, and Shoir in the first chapter of the second treatise. Here are the relations as explained in the manuscript. 1 Daniq= \(\displaystyle \frac {1}{6}\) Dinar, 1 Tasuj= \(\displaystyle \frac {1}{4}\) Daniq = \(\displaystyle \frac {1}{24}\) Dinar, 1 Shoir = \(\displaystyle \frac {1}{4}\) Tasuj= \(\displaystyle \frac {1}{16}\) Daniq = \(\displaystyle \frac {1}{96}\) Dinar.
- 134.
The “right” is actually “left” in our table, and vice versa. This is the case for most of the tables that follow.
- 135.
This sentence is to be understood as “The result is four Daniqs, and a Tasuj, and a Shoir, and a Daniq out of Shoir, two Tasujs out of Shoir, and two Shoirs out of Shoir.”
- 136.
These are the Arabic alphabet arranged in Abjad way which are read from right to left as “abjad hawwaz hutti kalaman sa’fas qarashat thakhadh dhazagh.”
- 137.
Here are the Arabic alphabet with their numerical values
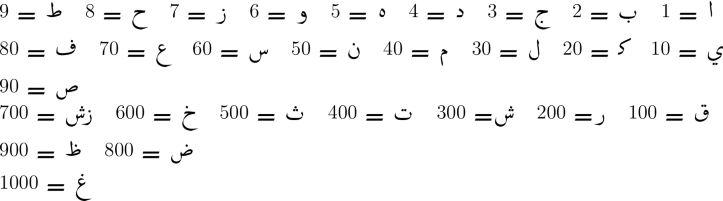
.
- 138.
It looks like

.
- 139.
We translated “burj” as sign in reference to the astrological signs which are twelve in the circle at 30∘ apart.
- 140.
Apparently, al-Kāshı̄ is alluding to some connections between astronomy and the sexagesimal system here whose details are not elaborated on.
- 141.
In the rest of the chapter, what al-Kāshı̄ writes right should be regarded as left, and vice versa. We translate these words as written in the text, but they should be interchanged to conform to the modern convention.
- 142.
An insert found in the margin, indicated by ̌.
- 143.
Recall that 30 degrees is a sign.
- 144.
The degrees here are degrees of rising, suggesting the idea of angular height. Indeed al-Kāshı̄ is taking the total degrees minus a whole circle; 466 − 360 = 106.
- 145.
We separate sexagesimal digits by colons, and we use a semicolon to separate the whole part from the fractional part.
- 146.
20;48:39 seconds = 20:48:38:59:59:59:60 sixths and when we subtract from it 20:48:39 sixths we obtain 20:48:38:59:45:34:10 sixths.
- 147.
In this manuscript, the word “Indians” is written here but it is “beginners” in other manuscripts which makes more sense.
- 148.
Multiplication table in base 60.
- 149.
Found on the right margin, indicated by the symbol ̌.
- 150.
Here al-Kāshı̄ uses the term “extended” to refer to the units digit (degrees) of the product and “raised” for the digit in the first elevates. Later, he generalizes this to refer to the digit in the lowest position as extended, and the digit in one position higher as raised.
- 151.
Al-Kāshı̄ is explaining the laws of exponents a n a m = a n+m, a n a −m = a n−m, and a −n a −m = a −n−m. He is applying them to powers of 60.
- 152.
According to al-Kāshı̄, minutes have a rank of one and fourths have rank of four. So, the multiplying minutes by fourths results in fifths. The elevated part of the result should be in the fourth position.
- 153.
Found on the left margin, indicated by the symboľ.
- 154.
- 155.
This is another indication that the previous letter ƹ is actually 0.
- 156.
Digit here is in terms of sexagesimal numbers.
- 157.
Found in the left margin, indicated by the symboľ.
- 158.
This was described for the decimal system at the end of the first treatise (Chapter 6 of Treatise 1). The same method can be applied to the sexagesimal system with 9 replaced by 59.
- 159.
To save space, we used obvious abbreviations such as Elv. for Elevate and the use of numerals instead of writing numbers in words.
- 160.
This chapter of Miftāḥ was translated to English with commentary in [13].
- 161.
Found on the right margin, indicated by the symboľ.
- 162.
Found on the right margin.
- 163.
There are two different notions of perfect in this context. a) An integer N is perfect nth power if \({\sqrt [n]{N}}\) is an integer. b) A place/position/digit in a number N is perfect with respect to power n if the position is divisible by n. For example, if N = 10, 7, 1, 35, 5; 28, 15, 9, 40 is considered to be a cube, then its perfect places are 7, 5, and 9 corresponding to powers − 3, 0, −3, all divisible by 3.
- 164.
- 165.
Found on the left margin with a ظ=900 which has no place in the computation or in the tables.
- 166.
It is written in [4] “according to what preceded in the first treatise.”
- 167.
Here, al-Kāshı̄ is referring to his remarkable approximation to π in his Al-Risala al-Muhitiyya, Treatise on Circumference in which his approximation to π was correct to 9 digits in sexagesimal that translates to 16-digit accuracy in the decimal system.
- 168.
Found in the left margin, indicated by the symbol ̌.
- 169.
- 170.
In this context, part means degrees.
- 171.
Multiply the fraction part but not the integer part.
- 172.
Found on the right margin, indicated by the symboľ.
- 173.
Note that the orientation of the table is reversed.
- 174.
Found in the top margin, indicated by the symboľ.
- 175.
We believe it is “left” which is confirmed by the crossing of “right” and adding of “left” in [3].
- 176.
Al-Kāshı̄ is ignoring the digits after 2588.
References
Al-Kāshı̄: Miftāḥ al-Ḥisab. Manuscript H. Hüsnü Paşa 1268, Istanbul, Turkey
Al-Kāshı̄: Miftāḥ al-Ḥisab. Manuscript M. Atıf 1719, Istanbul, Turkey
Al-Kāshı̄: Miftāḥ al-Ḥisab. Edition, and translation by Ahmad Sa’id al-Dimirdash and Muhammad amdi al-Hifni al-Shaykh. Dar al-Katib al-Arabi, Cairo (1969)
Al-Kāshı̄: Miftāḥ al-Ḥisab. Edition, notes and translation by Nabulsi Nader. University of Damascus Press, Damascus (1977)
Aydin, N., Hammoudi, L.: Root extraction by Al-Kāshı̄ and Stevin. Arch. Hist. Exact Sci. 69(3), 291–310 (2015)
Berggren, J.L.: Episodes in the Mathematics of Medieval Islam. Springer, Berlin (1986)
Dakhel, A.: The extraction of the n-th root in the sexagesimal notation. In: Hijab, W.A., Kennedy, E.S. (eds.) A study of chapter 5, treatise 3 of Miftāḥ al-Ḥisab. American University of Beirut, Beirut (1960)
Oaks, J.A., Alkhateeb, H.M.: Māl, enunciations, and the prehistory of Arabic algebra. Hist. Math. 32, 400–425 (2005)
Saidan, A.: The Arithmetic of al-Uqlı̄disı̄: The Story of Hindu-Arabic Arithmetic as Told inKitāb al-fuṣūl fı̄ al-Ḥisāb al-Hindı̄. Translated and Annotated by A.S. Saidan. Reidel Publishing, Dordrecht (1978)
Saliba, G.: Islamic Science and the Making of the European Renaissance. The MIT Press, Cambridge (2007)
Taani, O.H.: An analysis of the contents and pedagogy of al-Kāshı̄’s 1427 “Key to Arithmetic” (Miftāḥ Al-Ḥisab). Ph.D. dissertation, New Mexico State University, New Mexico State University, ProQuest Dissertations Publishing, 3534149 (2011)
Taani, O.: Multiple paths to mathematics practice in al-Kāshı̄s key to arithmetic. Sci. Educ. 23(1), 125–141 (2014)
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Aydin, N., Hammoudi, L. (2019). The Miftāḥ Translation. In: Al-Kāshī's Miftāḥ al-Ḥisab, Volume I: Arithmetic. Birkhäuser, Cham. https://doi.org/10.1007/978-3-030-14950-5_2
Download citation
DOI: https://doi.org/10.1007/978-3-030-14950-5_2
Published:
Publisher Name: Birkhäuser, Cham
Print ISBN: 978-3-030-14949-9
Online ISBN: 978-3-030-14950-5
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)