Keywords

6.1 Introduction

Historically, scholars understand there are “two fundamentally different purposes when teaching mathematical modelling” (Stillman et al. 2016, p. 283) in the classroom (Julie and Mudaly 2007; Niss et al. 2007). One is to use “modelling as a vehicle for facilitation and support of students’ learning of mathematics as a subject” (Niss et al. 2007, p. 5). The other is to learn mathematics “so as to develop competency in applying mathematics and building mathematical models” (Niss et al. 2007, p. 5). These authors stressed that these approaches are not a dichotomy, meaning neither tasks nor facilitators’ intentions in using the tasks must be classified as one or the other. Though the role of mathematical modelling in achieving curricular aims has both amplified in recent years (e.g. National Governors Association Center for Best Practices and Council of Chief State School Officers 2010; Niss and Hojgaard 2011; OECD 2017) and undergone attempts at standardization (e.g., Bliss et al. 2016), in many classrooms the emphasis remains on the teaching of modelling as a vehicle for teaching mathematical concepts and processes.

A wide variety of tasks are used to further curricular aims, ranging from word problems, to application problems, to original projects (Blum and Niss 1991). Using such tasks to plan and sequence learning trajectories for students means the tasks must have intended solutions , a predetermined strategy, heuristic, process, or outcome that aligns with mathematical learning objectives. In this chapter, I focus on tasks which were designed to further specific curricular aims and therefore have intended solutions from the task setter’s perspective.

However, one challenge in using modelling in classrooms is that the solution of a modelling task is not inherent to the task itself (Czocher 2015; Murata and Kattubadi 2012; Schwarzkopf 2007). For example, Manouchehri and Lewis (2017) reported on 1000 middle school students’ solutions to the word problem Which is the best job option, one that pays $7.50/hour or one that pays $300/week? The task is used to address the topic of linear equations. The intended solution is to formulate two linear equations, y = 7.5x and y = 300 and seek their intersection. Since x = 40 at the intersection, the two job offers are supposed to be equivalent. However, the intended solution only makes sense under two implicit assumptions: (i) only the number of hours worked per week matters (ii) 40 h per week is expected. The students in the study did not operate under these assumptions. They considered issues like the cost of transportation, health care benefits, and whether or not full-time employment was feasible. These considerations do not lead to the intended solution, but they are not “wrong.”

The difference between student reasoning and the intended solution can be accounted for in terms of socio-mathematical norms developed at school. Watson (2008) argued that school mathematics is its own discipline, and therefore is apart from professional mathematics. For example, some word and applications problems can be solved by referring to semantic cues, without any reference to mathematics or the story in the problem (Martin and Bassok 2005). For students and teachers this may mean that modelling devolves into a search for official formulas, recalling a similar problem from class, or attending only to keywords. Even in a laboratory setting, students working on problems couched in a real-world context can be influenced by the expectations of school mathematics to give “more legitimate” solutions based on known formulas (Schoenfeld 1982b). Similarly, Julie and Mudaly 2007) hypothesized that teachers express a preference for models that are relevant to their immediate circumstances. Thus, a typical response to students using their “real world” reasoning, like those in Manouchehri and Lewis’s (2017) study, might be to dismiss it as incorrect in order to refocus the student toward the intended solution. While this option may lead to short-term success, it can also have long-term consequences. Students who receive consistent negative feedback may learn to respond to problems in ways consistent with the expectations of “school mathematics” rather than with their own reasoning (see, for example, Engle 2006). Indeed, the literature is full of examples of students who generalize their own (non-mathematical) rules based on this kind of feedback or who do not check whether their own responses make sense (Erlwanger 1973; Greer 1997; Schoenfeld 1982a, 1991; Verschaffel et al. 2000).

These lines of inquiry have influenced research into the teaching and learning of modelling. Scholars have shifted their focus onto students’ current knowledge and understanding (Blum and Borromeo Ferri 2009; Doerr 2006; Schukajlow et al. 2015; Stender and Kaiser 2015; Wischgoll et al. 2015). While a socio-mathematical perspective articulates the tension between school mathematics and student thinking, it does not yet account for how students might make sense of modelling tasks that are used to further curricular aims. Some work still needs to be done on how to anticipate what students might suggest and how to productively interpret those suggestions. The purpose of this study was to explore the ways in which students’ ways of reasoning might diverge from the intended solutions of the task setter who aims to provide students with experiences addressing particular curricular objectives.

6.2 Empirical and Theoretical Background

There are many theoretical perspectives on the nature of mathematical modelling and what it entails. Kaiser (2017) provides a recent and comprehensive survey. One perspective is termed a cognitive approach because it foregrounds mathematical thinking and emphasizes analysis of students’ modelling processes. Since the main goals of the cognitive approach are to reconstruct individuals’ modelling routes or to identify difficulties encountered by students during their modelling activities (Kaiser 2017), it is an appropriate approach for studying how student reasoning diverges from intended solutions while working on tasks with intended curricular aims.

In the cognitive view, modelling is a process that transforms a non-mathematical question into a mathematical problem to solve. A model is then a conceptual correspondence between real-world entities and phenomena and a mathematical expression. The modelling process can be decomposed into a series of cognitive and mathematical activities (e.g. Blum and Leiß 2007; Maaß 2006) which replace a real-world system with a mathematical interpretation that can be analysed mathematically. Results are then interpreted in terms of real-world constraints and assumptions and the model is modified if necessary. Simplifying/structuring and mathematizing are central to setting up the mathematical problem to solve. They are most challenging to carry out (Galbraith and Stillman 2006; Stillman et al. 2010). Simplifying/structuring includes identifying conditions and assumptions from the real-world context, establishing variables, and acknowledging that some variables or constraints are unimportant. Mathematizing refers to introducing conventional representational systems (e.g., equations, graphs, tables, algorithms) to present mathematical “properties and parameters that correspond to the situational conditions and assumptions that have been specified” (Zbiek and Conner 2006, p. 99).

The cognitive approach highlights the role individuals’ prior knowledge and decision-making play in mathematical modelling. Stillman (2000) reported on a tripartite framework distinguishing three knowledge sources used by secondary students during mathematical modelling: academic, episodic , and encyclopaedic. Each knowledge source derives from the individuals’ prior experiences. Academic knowledge derives from the study of academic topics (e.g. linear equations, kinematics). Encyclopaedic knowledge is general knowledge about the world (e.g. that one ought to check for traffic before crossing a road). Episodic knowledge is truly personal and experiential (e.g. recalling a ride to the top of the Empire State Building on a recent trip to New York City). Most reasoning during mathematical modelling occurs as a blend (Fauconnier and Turner 2003) of real-world knowledge and mathematical knowledge (Czocher 2013). Yet, Stillman (2000) found that episodic knowledge has a stronger influence on mathematical modelling than the other two forms of knowledge, suggesting that students draw more from their personal experiences than from what they learn in other subject areas or general world knowledge. Therefore, how individuals engage in modelling depends as much on their prior non-mathematical experiences as an on their mathematical knowledge.

Yet knowledge on its own is not a good predictor of task performance. Research from a long line of inquiry into transfer of knowledge has demonstrated that possessing relevant knowledge of mathematics or of the modelling task context is not sufficient for addressing the task (Nunes et al. 1985; Verschaffel et al. 2000). Equally important are whether the individual brings her knowledge to bear on the task and the decisions she makes about how to use that knowledge. Specifically, because modelling involves generating idealizations of the real world situation (Borromeo Ferri 2006), any decision made by the modeller to simplify the problem filters, and is filtered by, the individual’s knowledge sources. As the study of Manouchehri and Lewis (2017) shows, differences between the intended solution and the students’ ideas are not limited to the peculiarities of school mathematics—they depend on students’ encyclopaedic and episodic knowledge. In their Job Problem, the intended solution assumes that the only meaningful variable is number of weekly hours worked. The students raised issues based on their encyclopaedic and episodic knowledge; they wished to consider health care benefits and ease of transportation. Considering these important variables necessarily changes the mathematics used. For example, if transportation is the most important factor (rather than hours worked) an individual should choose the job she can get to reliably rather than the job she cannot get to at all.

The interdependency of phases of modelling with individuals’ knowledge leads to idiosyncratic and non-linear individual modelling routes (Ärlebäck 2009; Borromeo Ferri 2006, 2007; Czocher 2016). The term idiosyncratic responses means that making sense of, or responding to, student work on modelling tasks, even in tasks purportedly as straightforward as those with intended solutions , is difficult. For example, Schoenfeld (1982b) asked undergraduate mathematics majors to estimate the number of cells in an adult human body. The intended solution was a “ballpark estimate,” based on the assumption that a human is shaped roughly like a cylinder and crude estimates of the cylinder dimensions. Instead, the participants sought increasingly finer estimates of the volume of the human body, without pausing to evaluate their own productivity. Since the marginal increases in precision for measurements of human volume would not have impacted the cell estimate substantially, Schoenfeld interpreted the students’ work as an example of metacognitive failure. A teacher’s response in this situation might also have been to classify the student’s work as incorrect because the student did not use the intended strategies. However, given the relative scale of human volume to cell size, the students’ activity can be understood as sensible. Likewise, a student who answers the Job Problem with the question “Is there a bus stop at both jobs?” might be considered to be evading the mathematical problem.

The foregoing discussion raises questions about how to interpret students’ thinking on modelling tasks productively. In particular, we can wonder: How does learners’ real-world knowledge guide their selection of relevant variables and assumptions? and Are there productive ways to frame students’ choices that can guide facilitators? To answer such questions, it is necessary to examine students’ modelling behaviour within the task environments that they may encounter in classrooms from a perspective that assumes the students’ responses are sensible.

To study how student work diverges from intended solutions , I selected Lobato’s (2006, 2012) actor-oriented theory of transfer as a theoretical lens. This is an appropriate choice because from a cognitive perspective, the modelling process is conceived as a blend of disparate knowledge bases, implying that some form of transfer of knowledge to a novel setting occurs. Viewing individuals’ knowledge as experiences then allows examination of how “rational operations emerge from experience” (Jornet et al. 2016, p. 290). That is, actor-oriented theory begins from the perspective that students’ activities are sensible.

As a premise, actor-oriented theory distinguishes between an actor’s perspective and an observer’s perspective. Thus, there is a natural mapping between the (actor, observer) pair to the (student work, intended solution) pair. In the language of actor-oriented theory , “taking an observer’s point of view entails predetermining the particular strategy, principle, or heuristic that learners need to demonstrate in order for their work on a novel task to count” (Lobato 2012, p. 245). In contrast, from an actor’s point of view, the researcher investigates how the student’s prior experiences shaped their activity in the novel situation, even if the result is non-normative or incorrect performance (Lobato 2012). In summary, “solutions which might be viewed as erroneous from a disciplinary perspective, are treated instead as the learner’s interpretation” of the task (Danish et al. 2017). In this way, the operational definition for intended solution becomes a “predetermined particular strategy, principle, or heuristic” and the focus of the present study is on how the participants interpret the task situation. Under actor-oriented theory , the authenticity of a task is determined by the extent to which the task context aligns with, and is amenable to, the participants’ lived experiences. Thus, modelling problems are those that permit students to bring their knowledge to bear in defining their own variables and introducing their own assumptions.

The actor-oriented theory of transfer can be applied to modelling because it acknowledges that knowing and representation are products of how the student interprets the task situation and that the selection of ideas need not be intentional (Jornet et al. 2016; Lobato 2012). Within modelling, structuring refers to imposing mathematical structure on a real-world situation. This is accomplished through introducing variables and parameters which measure attributes of entities in the real world (Thompson 2011). Real-world conditions and assumptions are also identified. The variables, parameters, conditions, and assumptions are then put in relation to one another, using mathematical objects, their properties and structures, and relations and operations to join them. As discussed above, each of these activities depends on the individual modeller’s current interpretations and prior experiences. The idea that structuring is an active process carried out by the modeller, rather than a passive process where an inherent structure is present in a situation and then discovered and extracted, is also emphasized in the actor-oriented theory perspective.

To study how individuals’ models may diverge from intended solutions , an analytic framework capable of capturing student decision making while tracing the intended solution was needed. The framework needed to allow me to document how the participants defined a mathematical problem from a nonmathematical one. The process is not straightforward and there are many cognitive obstacles within it (Galbraith and Stillman 2006). Since the process includes anticipating the mathematical structures and procedures that could be used and then implementing that anticipation, the framework needed to include identifying, prioritizing, and mathematizing appropriate variables, conditions, and assumptions (Czocher and Fagan 2016; Niss 2010; Stillman and Brown 2014). The analytic framework, summarized in Fig. 6.1, zooms in on the simplifying/structuring phase of modelling (see Blum and Leiß 2007). The framework is appropriate because each successive step is a site where the modeller’s choices may diverge from the intended solution. Therefore, the framework allows for divergence to be documented as described below in the methods section and allows for the research questions to be addressed.

Fig. 6.1
figure 1

Analytic framework to examine students’ decisions while structuring the problem situation to be mathematized

Full size image

6.3 Methods

I conducted a laboratory-based study of how student thinking diverged from intended solutions on tasks with intended curricular aims.

6.3.1 Data Collection

Data were generated via a set of one-on-one task-based interviews with twelve students enrolled in high schools (8) and universities (4) from different states in the United States. There were four participants from each of the following levels: high school algebra, post-algebra (high school geometry and calculus), and undergraduate differential equations. The purpose of including mathematically and geographically diverse students in the sample was to explicitly seek similarities in their ways of approaching the problems, not to treat them as comparison groups.

This study examines student work on the four tasks presented in Table 6.1. As shown, the tasks were drawn from prior research and research-based educational materials. Tasks were appropriate to each student’s mathematical level and each had a clear curricular objective, that is, mathematics content that would be brought out if the student carried out the task writer’s intended solution. However, the tasks were presented in a way that allowed the participants to generate their own variables and assumptions. In this way, each task would allow me to trace the cognitive pathways learners might take which would reveal the tensions between student thinking and the intended solution.

Table 6.1 Task and participant details in task-based interview
Full size table

At the start of each session, the participant was presented with a task and asked to read it aloud. I assured participants that they would not be graded as I was interested only in their thinking. Participants worked for as much time as needed to come to a conclusion (usually within 30 min). Follow up questions focused on understanding how important the students’ choices for variables and assumptions were to them. In this way, the interviews elicited the students’ mathematical thinking as they engaged in the modelling tasks, not on guiding the student to an intended solution.

6.3.2 Data Analysis

The participants generated 24 sessions, which were transcribed. Analysis focused on how students defined a mathematical problem to solve by decomposing student work according to the analytic framework (Fig. 6.1) and comparing their work to the intended solution for each task. Each student’s work on each task was analysed for whether they engaged in mathematical modelling, what variables and assumptions were identified (mentioned explicitly), whether they were prioritized (designated as being important to the model), and whether or not they were mathematized (represented mathematically). “Variables ” designated independent and dependent variables, parameters, or constants that referred to measurable attributes of a physical entity (see Thompson 2011). “Assumptions ” were defined as constraints of the real-world situation that participants identified explicitly or implicitly as impacting the values of, or relationships, among variables of interest.

To understand how student-generated models diverged from the solutions envisioned by task writers, I examined the extent to which student-generated variables and assumptions differed from those in the task writers’ intended solution. In the intended solutions , I classified a variable or assumption as identified under two conditions: (1) if it was mathematized or (2) if the intended mathematisation necessitated that a variable or assumption be ignored. An outline of the intended solutions , along with intended variables and assumptions, and curricular objectives (aligned with CCSSM 2010) follows:

Letter Carrier : Assume a straight road with length l and width w. Assume that the street has n evenly spaced mailboxes on each side of the street, that the mailboxes are directly across from one another, and that they are at the centre of each lot. Let dA and dB be the distance travelled along the first and second paths, respectively. Then dA = 2l + w − l/n and dB = nw + l. We find that dA = dB when l/n = w or when the width of the road is equal to the width of each lot. As long as w < l/n, the second path will be shorter. Curricular objective: linear equations, working with variables and parameters. Assumptions : the road is straight, mailboxes are equally spaced, mailboxes are directly across from one another, mailboxes are at the centre of each lot, there are an equal number of mailboxes on each side, the “best” route has the shortest distance. Variables : number of mailboxes, length of the street, width of the street, total distance travelled.

Cell Problem: Assume cells are cubes whose dimensions are approximately 1/5000 of an inch on a side. Assume a human is a box with dimensions 6′ × 6″ × 18″. Curricular objective: proportions, rates, estimation. Assumptions : cells are shaped like cubes, humans are shaped like boxes, cells are packed inside of humans. Variables : cell side length, human height, width, depth, number of cells.

Water Lilies : Since the number of water lilies doubles every day, on day N − 1 there are half as many lilies as on day N. Therefore, on day 29 there are half as many lilies as on day 30. Since the lake is covered on day 30, the lake was half covered on day 29. Curricular objective: exponential growth. Assumptions : each lily produces one new lily during the growth period. Variables : growth period, growth rate, final time.

Empire State Building: For an object moving at a constant rate, distance is speed multiplied by time: d = r × t. Estimate the height of the Empire State Building, the speed of the elevator, and solve for t. In order to use this model, one must implicitly assume that the elevator makes no stops and that its speed is constant. The latter is reasonable if r is taken to be the average velocity over the duration of the ascent. Curricular objective: rates, linear equations. Assumptions : elevator makes no stops, moves at constant speed. Variables : height of building, rate of elevator, time elapsed.

To understand how students handled the variables and assumptions they generated, I listed all variables and assumptions referenced by each participant on each task. The result was the set of variables and the set of assumptions identified on each task collectively by all participants. Note that some participants generated more than one model on a given task. I then tabulated the frequency that each variable and assumption was referenced across all participants: how many times a variable or assumption was identified, how many times it was prioritized for inclusion in a mathematical representation, and the number of times it appeared in a mathematical representation. If a variable or assumption was mathematized, it was assumed to have been prioritized. For example, if a participant included “height of the Empire State Building” in her representation but never stated it verbally, it was assumed to have been both identified and prioritized. Next, I calculated the following percentages from the analytic framework:

$$ \% \, identified = \frac{{\# \,{\text{times identified}}}}{\#\,{{\text{participants who worked on the task}}}} $$
$$ \%\,{\text{Prioritized}} = \frac{{\# \,{\text{times prioritized}}}}{{\#\,{\text{times identified}}}} $$
$$ \%\,{\text{Mathematized}} = \frac{{\#\,{\text{times mathematized}}}}{{\#\,{\text{times prioritized}}}} $$

6.4 Results

Data analysis led to two interrelated findings: (a) participants’ choices did not lead to the intended solutions and (b) their selection of relevant variables and assumptions reflected their desire to represent complexity (rather than to simplify). In elaborating these findings below I show how their episodic and encyclopaedic knowledge influenced their mathematical choices via examples of how their work diverged from the intended solutions .

No participants produced the intended solution for the Cell Problem or the Letter Carrier Problem. None produced the intended solution for the Water Lilies Problem on their first attempt. All identified important variables and assumptions for the Empire State Building Problem , but offered additional variables and assumptions which led to unintended solutions. Since the participants’ work did not match the intended solutions , there are two straightforward interpretations I will refute. First, the problems were too hard for the participants. Second, the participants failed to transfer their mathematical knowledge to a novel, real-world problem. Closer inspection of the data revealed that neither interpretation is accurate. Indeed, in every case the participants used well-known standard mathematical structure (e.g., linear equations, proportions, etc. Niss et al. 2007) even though their work was idiosyncratic and sometimes ad hoc. Thus the participants’ models were, in most cases, completely reasonable given the variables and assumptions they identified and prioritized.

Table 6.2 displays the number of assumptions and variables identified by the participants on each task and compares it to the number of assumptions and variables in the intended solution. On all problems, participants collectively identified more variables and assumptions (except for Letter Carrier ) than were in the intended solutions . This fact (i) implies that the participants knew enough about the task situations to gain entry to the problems (ii) demonstrates that participants had little difficulty in this stage of modelling (iii) suggests that they were engaged in the problems, and (iv) relied on real-world knowledge to help them analyse the situations. These four inferences together refute the interpretation that the problems were too hard.

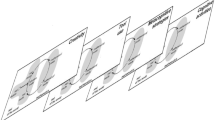
Table 6.2 Number of variables and assumptions collectively identified by participants, compared to number intended
Full size table

On the contrary, participants tried to include all variables and assumptions that could impact the selected dependent variable. For example, on the Letter Carrier Problem, 4/7 participants discussed various street layouts and mailbox arrangement and how each would impact the letter carrier’s path (see Fig. 6.2). One participant explicitly assumed that the letter carrier did not skip any houses (otherwise, to her, the second path would not make any sense at all). Another noted that mailboxes could be arranged directly across from one another (as in the intended solution) or they could be grouped together in a common area where all residents could retrieve their mail.

Fig. 6.2
figure 2

Different potential paths for the letter carrier sketched by an algebra student (Czocher and Moss 2017, p. 657)

Full size image

On the Empire State Building Problem , all participants identified the intended variables: speed of the elevator, height of the building, and time elapsed. However, they also identified additional factors affecting the time of ascent: acceleration, weight, the number of stops made, how long it takes for people to load and unload. Along with these went a variety of assumptions and observations such as whether or not floors below the observation deck were open to tourists or whether the rate of ascent would be constant. In this way, the students treated the tasks authentically, based on their episodic knowledge of streets and mailboxes and elevators.

On the Cell Problem, only one participant (an undergraduate) gave a ballpark estimate. Instead, participants were concerned about cell shapes and sizes varying over the body, rather than the shape or size of the body. They noted that bones and various organs were made up of different kinds of cells. Some mentioned that nerve cells could be a metre long whereas reproductive cells were much smaller. These concerns signal an unease in accepting that a set of measurements which vary can be replaced by the average of those measurements, which the intended solution expects.

These observations both support and challenge the finding of Schoenfeld (1982a, b) that his participants were concerned with finding “more legitimate” solutions. The participants in this study identified sources of variation based on the function of the cells (rather than on location) and desired their models to reflect those sources of variation. This does not necessarily constitute a “wild goose chase” or metacognitive failure. Rather than assume some dimension of variation could be eliminated (or rendered irrelevant altogether in order to simplify the problem), the participants were driven by a desire for the model to accurately and precisely capture their real-world knowledge of the task situations.

Similarly to other reports, participants identified variables and assumptions based on their episodic knowledge, their encyclopaedic knowledge (Stillman 2000), or through immediate relevancy to their lives (Manouchehri and Lewis 2017). This was evidenced by responses containing value statements or clarifying questions. For instance, responses included: (1) The letter carrier should take the simplest path. (2) Is there traffic? If so, the letter carrier should take the first path which is safer. (3) Does the letter carrier need to return to her vehicle? (4) Does the letter carrier have to visit every house? (5) What shape is the street? (6) What is the purpose of estimating all of the cells in the human body? It would make more sense to count T-Cells or heart muscle cells after a heart attack. (7) Should I count the non-human cells? (8) It makes more sense to time the elevator. (9) It depends on how big the lilies (lake) are.

Whereas considerations like: Does the size of the lake matter? get right to the heart of the curricular objectives of a modelling problem that uses exponential growth, the others might be interpreted as attempts to avoid developing a model altogether. Others have suggested writing tasks that avoid this tendency (see, for example, Lesh et al. 2000). However, I offer an alternative interpretation: the participants were not necessarily “avoiding” the problem, but offering a logical, well-reasoned response based on their personal knowledge of the world and the heuristic “what would this situation actually look like?” Individuals develop heuristics for quickly handling decision-making in real-life situations (Gigerenzer 2008), which may support them in identifying important variables and assumptions for mathematical modelling. The participants’ responses clarify the “rules” of the real-world situations described in the task statement and led sometimes to simplifying the situation to make it amenable to mathematical representation or at other times complicated it.

The majority of variables identified on a task were also mathematized in at least one participant’s representation (9/11 on the Letter Carrier Problem, 11/12 on the Cell Problem, 11/13 on the Water Lilies Problem, 9/11 on the Empire State Building Problem . This suggests participants’ difficulties lay in selecting the most important variables and assumptions in order to fit them to known mathematical concepts. For example, all participants who worked on the Cell Problem observed that the density or arrangement of cells varied over body parts, all of these acknowledged that the observation was important, but no one was able to mathematize the assumption. One undergraduate progressed so far as describing something like a weighted average for the different organs in the body, but abandoned this strategy before producing a mathematical representation. Similarly, on the Letter Carrier Problem, participants intended to include the shape of the street and variation of mailbox placement because both of these variables impact distance travelled. As a consequence, only 2/7 (29%) of the students were able to mathematize distance.

The majority of identified and prioritized variables did appear in at least one mathematical representation but this representation did not use the mathematics of the intended solution. For example, on the Letter Carrier Problem, two students focused on the arrangement of the mailboxes along the street because it would impact the total distance the letter carrier would travel. Their images of the street led to drawing a zig-zag path for the letter carrier to follow. Both created paths that would minimize distance between mailboxes, leading to mathematisation via the Pythagorean Theorem. These choices led to quadratic equations in two variables rather than the intended linear ones.

In the Empire State Building Problem , one undergraduate participant gave the following mathematical model:

$$ t = 2T(p) + h/v;\quad T(p) = {\text{enter/exit}}\;{\text{rate}} \times p + {\text{doors}} $$

where t was the total time, T(p) was the length of time it takes for people to enter (or exit), h was the height of the building, and v was the velocity of the elevator. He computed the length of time for people to exit as some per person rate times the number of people plus the length of time for the doors to open and close. The student transformed a problem about rate into a pair of affine linear equations depending on the number of people riding the elevator.

In the intended solutions , many of the variables and assumptions identified, prioritized, and mathematized by the participants were assumed to be unimportant, leading to simper models. However it is not necessary or even necessarily natural for students to seek these simpler models. At the very least, the participants’ choices led to mathematical concepts that were not the same as the curricular objectives of the tasks. And in these cases, the participants’ models might be seen as “incorrect” when compared to the intended solutions .

6.5 Interpretation and Discussion

In this study, participants tended to prioritize variables and assumptions in order to authentically reflect the complexity they perceived in the situations. They did so regardless of whether the variable or assumption could be mathematized, regardless of the magnitude of its impact, or even whether the resulting mathematical problem could be analysed with their on-hand mathematical tools. Thus, as in other studies (e.g. Czocher 2013; Ikeda and Stephens 1998; Manouchehri and Lewis 2017) participants struggled to prioritize those variables and assumptions that could be mathematized using their current mathematics knowledge, over those that could not.

Even though each participant had difficulty prioritizing variables he or she identified, most variables and assumptions identified appeared in at least one participant’s representation. Taken together, these observations refute the idea that participants were unable to transfer mathematical knowledge to a novel problem situation. Instead, the evidence highlights how students’ knowledge contributes to the contrast between student work and intended solutions in ways that parallel tensions which arise for those who wish to teach with modelling in the classroom.

In particular, participants prioritized variables and assumptions that would preserve precision. Each participant prioritized different variables and assumptions, which were amenable to different mathematical content or representations. It was therefore uncommon that two participants starting from differing sets of initial variables and assumptions produced the same model, let alone the model of the intended solution which was tied to curriculum content goals. On the surface it would seem that letting students freely and authentically engage in modelling, even on routine or simple word problems, is incompatible with meeting the curricular goals a teacher might use these tasks for. Moreover, managing a classroom full of distinct solutions seems daunting, a tension that has been reported before (e.g., Chan 2013; Tan and Ang 2013).

Concluding that student models are incorrect because they do not match the intended solutions or use curricular mathematics implicitly assumes that the intended solution is correct. It assumes that many of the variables and assumptions important to the participants should be neglected or assumed constant. But such assumptions cannot always be justified. For example, in real life the (average) speed of the Letter Carrier will be slower if she chose the second option or stops at more mailboxes. The many crossings require her to change direction more often and also to check whether she can safely cross the road. If there is a lot of traffic, she may not cross the road at all until she arrives at a pedestrian crossing. In the Empire State Building Problem , the door opening and closing speeds could be conceptualized as a constant that affects time to ascend the building but would not vary from trip to trip, unless there were more or fewer people entering and exiting. Yet the idea that only the potential distance travelled by the mail carrier or the elevator or the number of hours worked should be considered and that “all other things are equal” is an implicit assumption. These assumptions reveal the mathematical structures aligned with curricular content and representations and were not adopted unproblematically for the participants exactly because of their lived experiences, for example, waiting to cross the road safely.

Such choices simplify the problem situation in order to make it fit the target mathematics. However, student success in using mathematics to model real world situations is tied to their ability to see a correspondence between the behaviour of the system to be modelled and its potential mathematisation (Camacho-Machín and Guerrero-Ortiz 2015). Evidence presented here supports the claim that students desire that the mathematical model accurately reflects their lived experiences and empirical observations. This desire can create tension with the conventional simplifications suggested by the intended solutions . Conventional simplifying choices may seem arbitrary to students and contradict what they know to be true about the world. However, the preference for conventional assumptions that target curricular mathematics amounts to just that: preference. Thus intended solutions are correct insofar as they are privileged above other models.

Part of the tension that arises when using modelling as a vehicle to foster students’ engagement with mathematics content (Julie and Mudaly 2007) is between the intended solution and students’ ideas. When student work does not align with the intended solution, it is natural to interpret the student’s work as “incorrect.” Another common response is to disregard curricular tasks as avenues developing modelling skills. An actor-oriented perspective offers a middle ground. First, students do transfer mathematical and real-world knowledge to the novel situation described in the task situation (Lobato 2006). Second, the intended solution is not the correct model, it may simply be a convenient, conventional, or curricular one. From this perspective, it is possible to predict what variables and assumptions students might suggest when allowing them time and space to work authentically on such problems. The participants in this study selected variables and assumptions that would increase their models’ precision relative to their lived experiences with the task situations.

This interpretation shifts the locus of support to helping students prioritize those which can be modelled using either the mathematics they know or the intended mathematics. To meet the latter goal, it would be necessary to connect the student variables and assumptions to those in the intended solution. For example, making explicit that certain quantities adhere to conventions (e.g. assuming that elevator speed is constant), not because it is the “correct” assumption but because the assumption makes the problem amenable to a particular mathematical analysis which, in turn, provides insight into the problem. Other examples include variables like number of doublings in the Water Lilies Problem, which can be seen as a proxy for the intended variable time elapsed. Variables such as number of mailboxes, distance between mailboxes, variation in mailbox placement, and number of times the street was crossed can all be seen as proxies for length of the street.

6.6 Limitations, Future Directions and Recommendations

Greer (1997) asserted that “doing mathematics should be relatable to the experiential worlds of the pupils, and consistent with a sense-making disposition” (p. 306). The actor-oriented perspective offers a path toward Greer’s ideals by illuminating the rationality of the participants’ choices. The interview methodology allowed for close examination of participants’ responses but the small sample size and laboratory setting of this study raise questions about the situativity not only of the participants’ knowledge but also its analysis. That is, the findings were observable exactly because participants were free to identify, prioritize, and mathematize their own variables and assumptions without the imposition of the intended mathematics. Furthermore, the theory and methodology privilege student work and questions about what facilitator competencies might be necessary to bridge intended solutions to student thinking remain unanswered. Hypotheses are found already in the literature. For example, supporting student modelling processes will draw on skill sets like listening (Doerr 2006; Manouchehri and Lewis 2017) scaffolding (Schukajlow et al. 2015; Stender and Kaiser 2015), and attending to student validating and metacognition (Czocher 2014; Goos et al. 2002; Stillman and Galbraith 1998). The actor-oriented theory of transfer, and by extension a transactional view, applied to modelling, would be a useful perspective for exploring the viability of these conjectures because it views transfer as distributed across experiences, situations, and discourses among people (Danish et al. 2017; Jornet et al. 2016; Lobato 2012).

In conclusion, the issue is not that students fail to transfer (or suppress) their real world or mathematical knowledge or that tasks with intended solutions are too inauthentic to foster modelling skills. Students do engage sensibly in these problems and their willingness to engage in curricular tasks needs to be nurtured rather than discouraged. The path forward is to find ways to lead students to mathematics content that allows them to model the world as they see it, rather than constraining them to see the world as curricular mathematics allows. Part of learning modelling as a practice is learning the conventions about which variables or conditions can acceptably be ignored and under what conditions; but that is only part. Being explicit about the conventions and connecting the conventional decisions to the students’ natural ways of thinking may help the facilitator and the student develop a shared understanding of the real model, how it was chosen, and why. It might not be enough to show students that some considerations can be ignored (or variables replaced with constants) but rather there is a need to explore justifications for why this is so.