Abstract
We consider a new generalisation of the Dining Philosophers problem with a set of agents and a set of resource units which can be accessed by them according to a fixed graph of accessibility between agents and resources. Each agent needs to accumulate a certain (fixed for the agent) number of accessible resource units to accomplish its task, and once it is accomplished the agent releases all resources and starts accumulating them again. All this happens in succession of discrete ‘rounds’ and yields a concurrent game model of ‘dynamic resource allocation’. We use the Alternating time Temporal Logic (ATL) to specify important properties, such as goal achievability, fairness, deadlock, starvation, etc. These can be formally verified using the efficient model checking algorithm for ATL. However, the sizes of the resulting explicit concurrent game models are generally exponential both in the number of resources and the number of agents, which makes the ATL model checking procedure generally intractable on such models, especially when the number of resources is large. That is why we also develop an abstract representation of the dynamic resource allocation models and develop a symbolic version of the model checking procedure for ATL. That symbolic procedure reduces the time complexity of model checking to polynomial in the number of resources, though it can take a worst-case double exponential time in the number of agents.
\(^2\)V. Goranko—Visiting professorship.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
References
Alechina, N., Logan, B., Hoang Nga, N., Rakib, A.: Resource-bounded alternating-time temporal logic. In: Proceedings of the 9th International Conference on Autonomous Agents and Multiagent Systems: Volume 1, AAMAS 2010, vol. 1, pp. 481–488. International Foundation for Autonomous Agents and Multiagent Systems, Richland (2010)
Alechina, N., Logan, B., Hoang Nga, N., Raimondi, F.: Symbolic model checking for one-resource RB\(\pm \)ATL. In: Proceedings of the 24th International Conference on Artificial Intelligence, IJCAI 2015, pp. 1069–1075. AAAI Press (2015)
Alechina, N., Logan, B., Hoang Nga, N., Raimondi, F., Mostarda, L.: Symbolic model-checking for resource-bounded ATL. In: Proceedings of the 2015 International Conference on Autonomous Agents and Multiagent Systems, AAMAS 2015, pp. 1809–1810. International Foundation for Autonomous Agents and Multiagent Systems, Richland (2015)
Alur, R., Henzinger, T.A., Kupferman, O.: Alternating-time temporal logic. J. ACM 49(5), 672–713 (2002)
Bhargava, D., Vyas, S.: Agent based solution for dining philosophers problem. In: 2017 International Conference on Infocom Technologies and Unmanned Systems (Trends and Future Directions), ICTUS, pp. 563–567, December 2017
Chandy, K.M., Misra, J.: The drinking philosophers problem. ACM Trans. Program. Lang. Syst. 6(4), 632–646 (1984)
Chevaleyre, Y., et al.: Issues in multiagent resource allocation. Informatica 30, 3–31 (2006)
Choppella, V., Kasturi, V., Sanjeev, A.: Generalised dining philosophers as feedback control. CoRR abs/1805.02010 (2018)
Datta, A.K., Gradinariu, M., Raynal, M.: Stabilizing mobile philosophers. Inf. Process. Lett. 95(1), 299–306 (2005)
Demri, S., Goranko, V., Lange, M.: Temporal Logics in Computer Science. Cambridge Tracts in Theoretical Computer Science. Cambridge University Press, Cambridge (2016). http://www.cambridge.org/core_title/gb/434611
Dijkstra, E.W.: Hierarchical ordering of sequential processes. Acta Informatica 1(2), 115–138 (1971)
Herescu, O.M., Palamidessi, C.: On the generalized dining philosophers problem. In: Proceedings of the Twentieth Annual ACM Symposium on Principles of Distributed Computing, PODC 2001, pp. 81–89. ACM, New York (2001)
Hopcroft, J.E., Karp, R.M.: An n\({}^{\text{5/2 }}\) algorithm for maximum matchings in bipartite graphs. SIAM J. Comput. 2(4), 225–231 (1973)
Papatriantafilou, M.: On distributed resource handling: dining, drinking and mobile philosophers. In: Proceedings of the First International Conference on Principles of Distributed Systems, OPODIS, pp. 293–308 (1997)
Sidhu, D.P., Pollack, R.H.: A robust distributed solution to the generalized Dining Philosophers problem. In: 1984 IEEE First International Conference on Data Engineering, pp. 483–489, April 1984
Acknowledgements
The work of Valentin Goranko and Riccardo De Masellis was supported by a research grant 2015-04388 of the Swedish Research Council, which also partly funded a working visit of Nils Timm to Stockholm. Valentin Goranko was also partly supported by a visiting professorship grant by the University of Pretoria.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
A Appendix: Proof of Theorem 1
A Appendix: Proof of Theorem 1
The proof is by induction on \(\varphi \).
-
\(\varphi =g_{a} \). Then \([\![ \varphi ]\!]_{\mathfrak {G}} = \{{c: \mathsf {res} (c, a) = d (a)}\}\). The required formula is \(\alpha = \alpha _1\vee \ldots \vee \alpha _s\) where each \(\alpha _i\) is the conjunction of intervals for agents \(a' \,\not =\, a\) and the conjunction of intervals for a. The conjunction of intervals for \(a' \,\not =\, a\) is the same for every \(\alpha _i\), viz. \((a', R)[0, d (a')] \), for each \(a' \,\not =\, a\) and for each \(R \in \mathcal {R}\). The conjunction of intervals for a is different for each \(\alpha _i\), has the form \((a, R)[\ell ^{a}_{R}, \ell ^{a}_{R}] \) and is a solution of the constraint \(\sum _{R \in \mathcal {R}} \ell ^{a}_{R} = d (a)\).
-
 . Then \([\![ \varphi ]\!]_{\mathfrak {G}}\) is the set of configurations from which there exists a collective strategy \(\sigma _{A}\) for A such that for all \(\pi \in out (c, \sigma _{A})\), \(\mathfrak {G}, \pi [1] \,\models \, \psi \). We show that \(\textsc {pre}(\mathcal {G}, A, \alpha (\mathcal {G}, \psi ))\) satisfies the claim. We prove separately \([\![ \varphi ]\!]_{\mathfrak {G}} \,\supseteq \, \parallel \!\! \textsc {pre}(\mathcal {G}, A, \alpha (\mathcal {G}, \psi )) \!\!\parallel _{\mathfrak {G}}\) (soundness) and \([\![ \varphi ]\!]_{\mathfrak {G}} \,\subseteq \, \parallel \!\! \textsc {pre}(\mathcal {G}, A, \alpha (\mathcal {G}, \psi )) \!\!\parallel _{\mathfrak {G}}\) (completeness).
. Then \([\![ \varphi ]\!]_{\mathfrak {G}}\) is the set of configurations from which there exists a collective strategy \(\sigma _{A}\) for A such that for all \(\pi \in out (c, \sigma _{A})\), \(\mathfrak {G}, \pi [1] \,\models \, \psi \). We show that \(\textsc {pre}(\mathcal {G}, A, \alpha (\mathcal {G}, \psi ))\) satisfies the claim. We prove separately \([\![ \varphi ]\!]_{\mathfrak {G}} \,\supseteq \, \parallel \!\! \textsc {pre}(\mathcal {G}, A, \alpha (\mathcal {G}, \psi )) \!\!\parallel _{\mathfrak {G}}\) (soundness) and \([\![ \varphi ]\!]_{\mathfrak {G}} \,\subseteq \, \parallel \!\! \textsc {pre}(\mathcal {G}, A, \alpha (\mathcal {G}, \psi )) \!\!\parallel _{\mathfrak {G}}\) (completeness).
Soundness. We have to prove that for every \(c \,\in \, \parallel \!\! \textsc {pre}(\mathcal {G}, A, \alpha (\mathcal {G}, \psi )) \!\!\parallel _{\mathfrak {G}}\) there exists one step strategy to reach a state where \(\psi \) holds. By the inductive hypothesis, all (and only) configurations in \(\alpha (\mathfrak {G}, \psi )\) satisfy \(\psi \), thus it is enough to show that a one step strategy reaches \(\alpha (\mathfrak {G}, \psi )\). Let us then consider a generic \(c \,\in \, \parallel \!\! \textsc {pre}(\mathcal {G}, A, \alpha (\mathcal {G}, \psi )) \!\!\parallel _{\mathfrak {G}}\). If \(c \,\in \, \parallel \!\! \textsc {pre}(\mathcal {G}, A, \alpha (\mathcal {G}, \psi )) \!\!\parallel _{\mathfrak {G}}\) then, by the pre-image algorithm, there exists \(\beta \), \(\beta '\) and \(( ap , \overline{ ap }_{})\) such that:
-
\(c \,\in \, \parallel \!\! \beta \!\!\parallel _{\mathfrak {G}}\);
-
\(\beta \) is in the predecessor of \(\beta '\), thus \(\beta {\mathop {\rightarrow }\limits ^{{( ap , \overline{ ap }_{})}}} \beta '\) from soundness of step (2) in the pre-image computation;
-
there exists a one-step strategy \(\sigma _A\) from \(\beta \) which leads to \(\alpha (\mathcal {G}, \psi )\).
We have to prove that such a strategy satisfies Definition 11.
Let \(( ap , \overline{ ap }_{})\) be a generic action profile consistent with strategy \(\sigma _A\) such that \(\beta {\mathop {\rightarrow }\limits ^{{( ap , \overline{ ap }_{})}}} \beta ''\), with clearly \(\beta '' \,\in \, \textsc {expd}(\alpha (\mathcal {G}, \psi ))\). We show that for all \(c \,\in \, \parallel \!\! \beta \!\!\parallel _{\mathfrak {G}}\) there exists \( ap ' \,\in \, AP \) and there exists \(c ' \,\in \, Conf \) such that \(c {\mathop {\rightarrow }\limits ^{{ ap '}}} c '\), \(c ' \,\in \, \parallel \!\! \beta '' \!\!\parallel _{\mathfrak {G}}\) and the expansion of \( ap '\) is \(\overline{ ap }_{}\).
Constructively, we build \( ap '\) agent-wise from \(\overline{ ap }_{}\). For each \(a \in Agt \), its action in \(\overline{ ap }_{}\) can be one of the following:
-
(1)
\(\mathsf {idle}^{a} \);
-
(2)
(single release) \(\mathsf {rel}^{a}_{R} \);
-
(3)
(multiple release) \(\{{\mathsf {rel}^{a}_{R_1}, \ldots , \mathsf {rel}^{a}_{R_t}}\}\); or
-
(4)
\(\mathsf {req}^{a}_{R} \).
If (1) then the \( ap '(a)=\mathsf {idle}^{a} \). If (2) then \( ap '(a)=\mathsf {rel}^{a}_{r} \) for a random \(r \in R\) such that \(c (r) = a\). Notice that this is always possible, given that \(\beta {\mathop {\rightarrow }\limits ^{{( ap , \overline{ ap }_{})}}} \beta ''\), meaning that a does have the number of resources necessary to perform a release. If (3), then \( ap '(a)=\mathsf {rel}^{a}_{ all } \). This is always possible again from the same observations in (2). If (4), then it is not enough to pick a random available \(r \in R\) and set \( ap '(a)=\mathsf {req}^{a}_{r} \), as, depending on the requests actions performed by the other agents, a can own or not r in the next configuration. Thus, first the requested r must be such that \(c (r)= null \) (there exists one otherwise \(\beta {\mathop {\rightarrow }\limits ^{{( ap , \overline{ ap }_{})}}} \beta ''\) would not be a step) but also the request actions of all agents have to be considered together when building \( ap '\). It is, however, enough to look at the interval \((a,R)[\ell '^{a}_{R}, \ell '^{a}_{R}] \) in \(\beta ''\) in order to determine whether the request of a has been successful or not. If \(\ell '^{a}_{R} = \ell ^{a}_{R}\), then it was successful, and there is another agent \(a'\) performing a request for the same resource (this is guaranteed by how the intervals of \(\beta ''\) are computing from \(\beta \) by performing \(( ap , \overline{ ap }_{})\)). Otherwise, if \(\ell '^{a}_{R} = \ell ^{a}_{R}+1\), then the request by a of r has been successful and, when building \( ap '\) for the other agents, we have to be sure that no other agent requests r (again, this is always guaranteed by how the intervals of \(\beta ''\) are computing from \(\beta \) by performing \(( ap , \overline{ ap }_{})\)). Finally, we have to show that \(c ' \,\in \, \parallel \!\! \beta '' \!\!\parallel _{\mathfrak {G}}\). This is immediate, as the expansion of \( ap '\) is \(\overline{ ap }_{}\) and from the way intervals are updated when computing \(\beta {\mathop {\rightarrow }\limits ^{{( ap , \overline{ ap }_{})}}} \beta ''\).
Completeness. We have to prove that if \(c \in Conf \) and there exists a strategy \(\sigma _{A}\) which in one step reaches a configuration satisfying \(\psi \), then \(c \,\in \, \parallel \!\! \textsc {pre}(\mathcal {G}, A, \alpha (\mathfrak {G}, \psi )) \!\!\parallel _{\mathfrak {G}}\). If \(c \) satisfies the above, then \(\exists ap , c '.c {\mathop {\rightarrow }\limits ^{{ ap }}} c '\) with \( ap \in \sigma _{A}(c)\) and \(c ' \,\in \, [\![ \psi ]\!]_{\mathfrak {G}}\). By inductive hypothesis, \(c ' \,\in \, \parallel \!\! \alpha (\mathcal {G},\psi ) \!\!\parallel _{\mathfrak {G}}\), meaning that there exists \(\beta ' \in \alpha (\mathcal {G},\psi )\) and \(c ' \,\in \, \parallel \!\! \beta ' \!\!\parallel _{\mathfrak {G}}\). The pre-image algorithm tries all action profiles in \( AP \) that could lead to \(\beta '\), thus also \( ap \). We have to show that there exists \(\overline{ ap }_{k}\) such that \(\beta {\mathop {\rightarrow }\limits ^{{( ap , \overline{ ap }_{k})}}} \beta '\) and \(c \,\in \, \parallel \!\! \beta \!\!\parallel _{\mathfrak {G}}\). Constructively, the required \(\overline{ ap }_{k}\) is built by looking at configuration c, which tells us to which classes the resources of the agents performing the release-all actions belong. Since it exists, the algorithm finds it as it explores all possible \(\overline{ ap }_{k}\) for any \( ap \). Also, \(c \,\in \, \parallel \!\! \beta \!\!\parallel _{\mathfrak {G}}\) by inspecting how we modify the intervals when computing the predecessors. It remains to prove that \(\beta \) is controllable. This is straightforward, as the required controllable joint action for A in Definition 11 is easily obtained from \( ap \), which is a one-step strategy by hypothesis.
-
\(\varphi = \lnot \psi \). From \(\alpha (\mathcal {G}, \psi ) = \beta _1 \vee \ldots \beta _s\) we compute the negation \(\overline{\beta _i}\) of each \(\beta _i\), complementing its intervals. Such operation produces at most two intervals, thus each \(|\overline{\beta _i}|\) is at most \(2 \cdot |\beta _i|\). Then we produce the intersection of those \(\beta _i\) by simply “projecting” on intervals common to each \(\beta _i\).
-
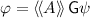 . Recursively, we start from \(\alpha (\mathcal {G}, \psi )\) and compute the conjunction with its pre-image until a fixpoint is reached, just like in the explicit model checking algorithm for ATL (cf. [4] or [10, Chap. 9]). Sound and completeness follows from the fixpoint characterisation of the
. Recursively, we start from \(\alpha (\mathcal {G}, \psi )\) and compute the conjunction with its pre-image until a fixpoint is reached, just like in the explicit model checking algorithm for ATL (cf. [4] or [10, Chap. 9]). Sound and completeness follows from the fixpoint characterisation of the  operator.
operator. -
\(\varphi = \langle \!\langle {A}\rangle \!\rangle _{_{\! }}\,{\psi _1 \mathsf {U}\psi _2}\). Similarly to the previous case, but each iteration computes the disjunction of \(\alpha (\mathcal {G}, \psi _2)\) with the conjunction of the pre-image of the expression obtained at the previous step with \(\alpha (\mathcal {G}, \psi _1)\), again just like in the explicit model checking algorithm for ATL. Soundness and completeness follow from the fixpoint characterisation of the operator \(\mathsf {U}\).
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
De Masellis, R., Goranko, V., Gruner, S., Timm, N. (2019). Generalising the Dining Philosophers Problem: Competitive Dynamic Resource Allocation in Multi-agent Systems. In: Slavkovik, M. (eds) Multi-Agent Systems. EUMAS 2018. Lecture Notes in Computer Science(), vol 11450. Springer, Cham. https://doi.org/10.1007/978-3-030-14174-5_3
Download citation
DOI: https://doi.org/10.1007/978-3-030-14174-5_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-14173-8
Online ISBN: 978-3-030-14174-5
eBook Packages: Computer ScienceComputer Science (R0)


 . Then
. Then 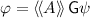 . Recursively, we start from
. Recursively, we start from  operator.
operator.