Compact Packings of the Plane with Three Sizes of Discs

Abstract

A compact packing is a set of non-overlapping discs where all the holes between discs are curvilinear triangles. There is only one compact packing by discs of radius 1. There are exactly 9 values of r which allow a compact packing with discs of radius 1 and r. It has been proven that at most 11462 pairs (r, s) allow a compact packing with discs of radius 1, r and s. We prove that there are exactly 164 such pairs.

The work of O. S was supported within frameworks of the state task for ICP RAS 0082-2014-0001 (state registration AAAA-A17-117040610310-6). The work of Th. F and A. H was supported by the Partenariat Hubert Curien (PHC) Gundishapur.

1 Introduction

A packing of the plane by discs is a set of interior-disjoint discs. Packings are of special interest to model the structure of materials, e.g., crystals or granular materials, and the goal in this context is to understand which typical or extremal properties have the packings. In 1964, Tóth coined the notion of compact packing [4]: this is a packing such that the graph which connects the center of mutually tangent discs is triangulated. Equivalently, a packing is compact when all its holes are curvilinear triangles.

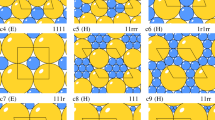
There is only one compact packing by one disc, called the hexagonal compact packing, where the disc centers are located on the triangular grid. In [9], it has been proven that there are exactly 9 values of r which allow a compact packing with discs of radius 1 and r (Fig. 1 – all already appeared in [4], except the fifth which later appeared in [11] and the second which was new at this time). Recently, it was proven in [12] that there are at most 11462 pairs (r, s) which allow a compact packing by discs of radii 1, r and s. The author provided several examples and suggested that a complete characterization of all the possible pairs is probably beyond the actual capacity of computers. Little is know for more discs, in particular it is still open whether there are always finitely many possible radii.

Fig. 1.

Compact packing with discs of radii 1 and $r<1$ for each of the 9 possible values of r. They are all periodic, with the parallelogram showing a fundamental domain. The top-right word over $\{1,r\}$ gives the sequence of radii of the discs around a small disc.

A classic problem in packing theory is to find the maximal density, defined by

$$ \delta {:}{=}\sup _{\text {packings}}\limsup _{k\rightarrow \infty }\frac{\text { covered area the }k\times k \text { square }}{k^2}. $$

For packings with only one disc, the maximal density has been proven in [3] to be $\delta _1{:}{=}\,\pi /\sqrt{12}\simeq 0.9069$, attained for the unique compact packing. For packings with discs of size 1 and r, the maximal density $\delta (r)$ is arbitrarily close to $\delta _1+(1-\delta _1)\delta _1\simeq 0.9913$ for r small enough, and it has been proven in [1] to be still equal to $\delta _1$ for $r\ge 0.7429$. An upper bound on $\delta (r)$ has been proven in [6] for any r, but the only exact results correspond to radii which allow a compact packing, namely those on Fig. 1, except the fifth and the last ones for which no proof has been given, see [7, 8, 10]. Compact packings thus seem to be good candidates to provably maximize the density. No result is known for more discs. This is our main motivation to study compact packings by three sizes of discs.

2 Results

Our main result is a complete characterization of the possible radii which allow a compact packing by three size of discs. We also found, for each case, a periodic compact packing. The characterization of the compact packings which maximize the density is still open, as well as the presumably harder issue of whether compact packings (for suitable radii) maximize the density among all the packings¹.

Fig. 2.

Distribution of the 164 pairs (r, s), with abscissa r and ordinate $\tfrac{s}{r}$. Pairs below the hyperbola are such that a small disc fits in the hole between three large discs. Voronoï cells aim to give an idea of how close are two pairs.

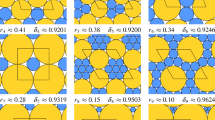
All the radii are algebraic and we have an explicit expression of their minimal polynomials, which we however do not give here because it would fill several rather uninteresting pages. Let us just mention that the mean algebraic degree is 6.08, with standard deviation 4.45 and maximal value 24. Instead, the following theorem states the number of possible pairs, Fig. 2 illustrates their distribution, and Fig. 3 shows some packings (the full list can be found in Appendix of [5]).

Theorem 1

There are exactly 164 pairs (r, s) which allow a compact packing by discs of radii 1, r and s, with $0<s<r<1$.

Fig. 3.

Some compact packings with three sizes of discs. Those on the first line are easily derived from compact packing with two sizes of discs. The other ones are more original. The top-left number refers to numbers on Fig. 2, and the two top-right words over $\{1,r,s\}$ give a possible sequence of radii of discs around, respectively, a disc of radius s and one of radius r (small and medium corona, see Sects. 3 and 4).

The examples given in [12] correspond on Fig. 2 to numbers 143, 145, 146, 144, 104 and 99. Number 107 also already appeared in [4] (p. 187). Number 51 (depicted on Fig. 3) can be seen on the floor in front of the library of Weggis, Switzerland (4 Luzernerstrasse). Other examples probably appear elsewhere. The challenge is to find them all.

This is rather simple in theory: as we shall see, we just need basic trigonometry and solving systems of polynomial equations. The challenge is computational: there are many cases to consider and the equations are very complicated. To get over the barrier encountered in [12], the main new ingredient we introduced are:

• use combinatorics to reduce the number of cases before computing;

• use resultants and interval arithmetic to solve systems of equations.

The rest of the paper is organized as follows. Sections 3 and 4 define small and medium coronas and show how to compute a list containing those which can appear in a compact packing. Section 5 explain how to associate with these coronas polynomial equations in the radii r and s. The three last sections are then devoted to solving these equations and finding the corresponding packings. We outline the theory in Sect. 6, review the main problems arising in practice in Sect. 7 and detail how we solved them in Sect. 8. The presentation is a bit sketchy due to space limitations, see [5] for full details.

3 Small Coronas

In a compact packing, the discs tangent to a given disc is called a corona. They form a circular sequence, ordered such that each disc is tangent to the next one. We code this sequence by the disc radii, i.e., a word over $\{\text {1},\text {r},\text {s}\}$ (see examples on Figs. 1 and 3). Since circular permutations or reversal of this word encode the same corona up to an isometry, we shall usually choose the lexicographically minimal coding. A corona is said to be small, medium or large depending whether it surrounds a small, medium or large disc. We shall also call x-disc a disc of radius x, and x-corona

An s-corona contains at most 6 small discs, and at most 5 discs if one of them is not small. There is thus finitely many different s-coronas. We shall bound as sharply as possible this number in order to reduce the complexity of the further exhaustive search. For this, let us define for $0<s<r<1$ and ${\varvec{k}}=(k_1,\ldots ,k_6)\in \mathbb {N}^6$ the function

$$ S_{{\varvec{k}}}(r,s){:}{=}\,k_1\widehat{1s1}+k_2\widehat{1sr}+k_3\widehat{1ss}+k_4\widehat{rsr}+k_5\widehat{rss}+k_6\widehat{sss},$$

where $\widehat{xyz}$ denotes, in the triangle which connects the centers of mutually tangent discs of radii x, y and z, the angle at the center of the disc of radius y. The function $S_{{\varvec{k}}}$ counts the angles to pass from disc to disc in an s-corona. To each s-corona corresponds a vector ${\varvec{k}}$, called its angle vector, such that $S_{{\varvec{k}}}(r,s)=2\pi$. For example, to the s-corona 1rsrs corresponds the angle vector (0, 1, 1, 0, 3, 0). We have to find the possible values ${\varvec{k}}$ for which the equation $S_{{\varvec{k}}}(r,s)=2\pi$ admits a solution $0<s<r<1$.

The angles which occur in $S_{{\varvec{k}}}(r,s)$ decrease with s, except $\widehat{sss}$, and increase with r. This yields the following inequalities, strict except for the s-corona ssssss:

$$ S_{{\varvec{k}}}(r,s)\le \lim _{r\rightarrow 1\atop s\rightarrow 0}S_{{\varvec{k}}}(r,s)=k_1\pi +k_2\pi +k_3\frac{\pi }{2}+k_4\pi +k_5\frac{\pi }{2}+k_6\frac{\pi }{3}, $$

$$ S_{{\varvec{k}}}(r,s)\ge \inf _r\lim _{s\rightarrow r}S_{{\varvec{k}}}(r,s)=\lim _{r\rightarrow 1\atop s\rightarrow 1}S_{{\varvec{k}}}(r,s)=k_1\frac{\pi }{3}+k_2\frac{\pi }{3}+k_3\frac{\pi }{3}+k_4\frac{\pi }{3}+k_5\frac{\pi }{3}+k_6\frac{\pi }{3}. $$

The existence of (r, s) such that $S_{{\varvec{k}}}(r,s)=2\pi$ thus yields the inequalities

$$ k_1+k_2+k_3+k_4+k_5+k_6< 6<3k_1+3k_2+\frac{3}{2}k_3+3k_4+\frac{3}{2}k_5+k_6, $$

except for the s-corona ssssss ($k_1=\ldots =k_5=0$ and $k_6=6$). An exhaustive search on computer yields 383 possible values for ${\varvec{k}}$. For each of them, one shall check that there indeed exists a coding over $\{1,r,s\}$ with this angle vector². This is also checked by computer and eventually yields 56 s-coronas, listed in Table 1.

Table 1. The 55 possible s-coronas, besides ssssss. Those on the first line have no 1-disc and those on the second line no r-disc. All the codings in a given column are identical up to the replacement $1\rightarrow r$ (this is the keypoint of Lemma 1).

4 Medium Coronas

Since s can be arbitrarily smaller than r, there can be infinitely many s-discs in an r-corona. Let us however see that this cannot happen in a compact packing.

Lemma 1

The ratio $\tfrac{s}{r}$ is uniformly bounded from below in compact packings with three sizes of discs.

Proof

Consider a compact packings with three sizes of discs. It contains an s-disc and not only s-discs, thus an s-corona other than ssssss. By replacing each 1 by r in this s-corona, Table 1 shows that we still get an s-corona. In this new corona, the ratio $\tfrac{s}{r}$ is smaller. Indeed, the 1-discs have been “deflated” in r-discs, so that the perimeter of the corona decreased, whence the size of the surrounded small disc too. But there is at most 10 possible ratios $\tfrac{s}{r}$ for an s-corona without large discs: they correspond to the values computed in [9] for compact packing with two sizes of discs (the smallest is $5-2\sqrt{6}\simeq 0.101$).

Table 2. Each s-corona whose 1-discs have been deflated in r-discs (first line) yields a lower bound $\alpha$ on $\tfrac{s}{r}$ in any compact packing which contains it (second line), and thus an upper bound on the number of possible r-coronas in this packing (third line).

This lemma ensures that the number of s-discs in an r-corona is uniformly bounded in compact packings. There is thus only finitely many different r-coronas in compact packings. To find them all, we proceed similarly as for s-coronas. We define for $0<s<r<1$ and ${\varvec{l}}=(l_1,\ldots ,l_6)\in \mathbb {N}^6$ the function

$$ M_{{\varvec{l}}}(r,s){:}{=}\,l_1\widehat{1r1}+l_2\widehat{1rr}+l_3\widehat{1rs}+l_4\widehat{rrr}+l_5\widehat{rrs}+l_6\widehat{srs}. $$

We have to find the possible values ${\varvec{l}}$ for which the equation $M_{{\varvec{l}}}(r,s)=2\pi$ admits a solution $0<s<r<1$. Actually, since the solution should correspond to an r-corona which occur in a packing, we can assume that it satisfies $\tfrac{s}{r}\ge \alpha$, where $\alpha$ is the lower bound on $\tfrac{s}{r}$ given by the s-coronas which occur in this packing. The angles which occur in $M_{{\varvec{l}}}(r,s)$ decrease with r (except $\widehat{rrr}$) and increase with s. This yields the following inequalities, strict except for the r-corona rrrrrr:

$$ M_{{\varvec{l}}}(r,s)\le \sup _r\lim _{s\rightarrow r} M_{{\varvec{l}}}(r,s)=l_1\pi +l_2\frac{\pi }{2}+l_3\frac{\pi }{2}+l_4\frac{\pi }{3}+l_5\frac{\pi }{3}+l_6\frac{\pi }{3}, $$

$$ M_{{\varvec{l}}}(r,s)\ge \inf _r\lim _{\tfrac{s}{r}\rightarrow \alpha }M_{{\varvec{l}}}(r,s)=l_1\frac{\pi }{3}+l_2\frac{\pi }{3}+l_3u_\alpha +l_4\frac{\pi }{3}+l_5u_\alpha +l_6v_\alpha , $$

where $\widehat{1rs}$ has been bounded from below by $\widehat{rrs}$ for any r, and the limits $u_\alpha$ and $v_\alpha$ of $\widehat{rrs}$ and $\widehat{srs}$ when $\tfrac{s}{r}\rightarrow \alpha$ are obtained via the cosine law:

$$ u_\alpha \;{:}{=}\arccos \left( \frac{1}{1+\alpha }\right) \quad \text {and}\quad v_\alpha \;{:}{=}\arccos \left( 1-\frac{2\alpha ^2}{(1+\alpha )^2}\right) . $$

The existence of (r, s) such that $M_{{\varvec{l}}}(r,s)=2\pi$ thus yields the inequalities

$$ l_1+l_2+l_4+\frac{3}{\pi }(l_3u_\alpha +l_5u_\alpha +l_6v_\alpha )< 6< 3l_1+\frac{3}{2}l_2+\frac{3}{2}l_3+l_4+l_5+l_6, $$

except for the r-corona rrrrrr ($l_1=\ldots =l_5=0$ and $l_6=6$). We also impose

$$ l_1+l_2+l_4+\frac{1}{2}(l_3+l_5)<6, $$

which tells that an r-corona (other than rrrrrr) contains at most 5 r- or 1-discs. An exhaustive search on computer, which also checks whether there indeed exists a coding for each possible ${\varvec{l}}$, eventually yields the possible r-coronas for each value of $\alpha$. Table 2 gives the numbers of such coronas.

Since any r-corona for some lower bound $\alpha$ also appears for a smaller $\alpha$, there are at most 1654 different r-coronas. Combining Tables 1 and 2 shows that there is at most 16805 pairs formed by an s-corona and an r-corona which can appear in the same compact packing with three sizes of discs.

5 Equations

We here describe an algorithm to associate with an s-corona with angle vector ${\varvec{k}}$ a polynomial equation in r and s whose solutions contain those of $S_{{\varvec{k}}}(r,s)=2\pi$.

Start from the equation $S_{{\varvec{k}}}(r,s)=2\pi$. Take the cosine of both sides and fully expand the left-hand side. Substract $\cos (2\pi )=1$ to both sides. This yields a polynomial equation in cosines and sines of the angles occuring in $S_{{\varvec{k}}}$.

The power of each sine can be decreased by 2 by using $\sin ^2 a=1-\cos ^2a$. Doing this as much as possible yields a polynomial where no sines is raised to a power greater than 1. The cosine law then allows to replace each cosine by a rational fraction in r and s. This yields a rational function in r, s and sines. Multiplying by the least common divisors of the denominators yields a polynomial in r, s and the sines which is equal to zero.

We shall now “remove” the sines one by one. Whenever the polynomial writes $A\sin a+B$, where A and B are polynomials without $\sin a$, we multiply by $A\sin a-B$ to get $A^2\sin ^2a-B^2=0$. We can then replace $\sin ^2a$ by $1-\cos ^2a$, use the cosine law to replace $\cos ^2a$ by a rational function in r and s, and multiply by the least common divisors of the denominators. By iterating this for each sine, we eventually get a polynomial equation in r and s. The final polynomial can however be quite large since each sine removal roughly doubles its degree.

The solutions (r, s) of $S_{{\varvec{k}}}(r,s)=2\pi$ are still solution of this polynomial equation, but each multiplication by $A\sin a-B$ could have added new solutions which shall eventually be ruled out (we shall come back to this later).

This algorithm has been implemented on computer. For example, it associates with the s-corona 11rs the polynomial equation

$$ r^2s^4 - 2r^2s^3 - 2rs^4 - 23r^2s^2 - 28rs^3 + s^4 - 24r^2s - 58rs^2 - 2s^3 + 16r^2 - 8rs + s^2. $$

The same algorithm also associates with each r-corona a polynomial equation.

We cannot write here all the equations. Let us just provide some statistics. The equations associated with the 55 s-coronas are computed on our laptop³ in less that 5 s and yield a 17Ko file. The mean degree of these polynomial equations is 6.71 (standard deviation 5.77), with maximum 28 for the s-corona 11rrs. The equations associated with the 1654 r-coronas are computed on our laptop in 2 h 21 min and yield a 35Mo file. The mean degree of these polynomial equations is 57.88 (standard deviation 50.16), with maximum 416 for the s-corona $\text {11rrs}^{12}$.

6 Computating Radii: The Theory

The path to compute the possible radii is now marked:

• 1. Compute the solutions (r, s) with $0<s<r<1$ of each system of two polynomial equations in r and s associated with a possible pair formed by an s-corona and an r-corona.

• 2. Use the computed values of r and s to compute the angles appearing in $S_{{\varvec{k}}}$ and $M_{{\varvec{l}}}$, as well as in the function defined for $0<s<r<1$ and ${\varvec{n}}\in \mathbb {N}^6$ by

  $$ L_{{\varvec{n}}}(r,s)\;{:}{=}\,n_1\widehat{111}+n_2\widehat{11r}+n_3\widehat{11s}+n_4\widehat{r1r}+n_5\widehat{r1s}+n_6\widehat{s1s}. $$

  Perform an exhaustive search for all the possible values ${\varvec{k}}$, ${\varvec{l}}$ and ${\varvec{n}}$ which satisfy the equations $S_{{\varvec{k}}}(r,s)=2\pi$, $M_{{\varvec{l}}}(r,s)=2\pi$ and $L_{{\varvec{n}}}(r,s)=2\pi$. This yields all the possible sets of s-, r- and 1-coronas.

• 3. Check the existence of a compact packing for each set of coronas.

Consider, for example, the pair s/r-coronas 1r1r/1r1r1s. The associated equations are respectively $rs + s^2 - r + s$ and $r^3 + r^2s - rs - s$. There is only one solution (r, s) with $0<s<r<1$, namely $r\simeq 0.751$ is a root of $X^4 - 4X^3 - 2X^2 + 2X + 1$ and $s\simeq 0.356$ is a root of $X^4 + 6X^3 + 2X - 1$. Searching for all the other coronas compatible with these values yields only large coronas, namely $\text {r}^3\text {sr}^3\text {s}$, $\text {r}^4\text {sr}^2\text {s}$ and $\text {r}^5\text {srs}$ (same angle vector). On then easily finds a periodic compact packing, namely the number 87 on Fig. 3.

7 Computating Radii: Problems

The above approach however suffers from a number of problems:

• 1. The example 1r1r/1r1r1s in the previous section has been chosen because it yields one of the most simple system to solve. The coronas 11rs/111srrss yield equations of degree 6 and 56 - close to the mean degree of equations associated with s- and r-coronas - and we need 22 min 44 s with SageMath [14] on our laptop to solve the system. For $\text {11rrs/11rrs}^{12}$, the equations have degree 28 and 416 and solving the system seems out or reach of our laptop⁴.

• 2. Algebraic values of r and s yield non-algebraic angles: how to perform exact computation to find all the compatible coronas and only them?

• 3. Not only systems can be highly complicated, but there are 16805 of them!

• 4. Checking the existence of a compact packing for a given set of coronas could be hard. This indeed amounts do decide whether a set of ten triangular tiles, namely the triangles between the centers of three mutually adjacent discs, does tile the plane. This is close to the domino problem, which is known to be undecidable [13].

The next section sketches how we got over this (full details can be found in [5]).

8 Computating Radii: The Practice

8.1 Solving Equations

We use the hidden variable method (see, e.g., Sect. 3.5 of [2] or Sect. 9.2.4 of [15]). Recall that the resultant of two univariate polynomials is a scalar which is equal to zero iff the two polynomials have a common root. Now, if P and Q are two polynomials of $\mathbb {Z}[r,s]$, we can see them as polynomials in r with coefficients in $\mathbb {Z}[s]$, i.e., we hide the variable s. Their resultant is thus a polynomial in s which has a root $s_0$ iff $P(r,s_0)$ and $Q(r,s_0)$ have a common root r. In other words, we can compute the second coordinates of the roots (r, s) of P and Q by computing the roots of an univariate polynomial (the above resultant). We can similarly compute the first coordinates by exchanging r and s. The cartesian product of these first and second coordinates then contains the roots (r, s) of P and Q.

We shall apply this to the two polynomial equations in r and s associated with each pair of s/r-coronas. The point is that resultants are easily computed (as determinants of Sylvester matrices), as well as the roots of an univariate polynomial (it amounts to find a proper interval for each root). Of course, the obtained cartesian product generally contains, besides the solutions, many “false pairs” (r, s) which have to be ruled out. Actually, even among the solutions there are also false pairs which must be ruled out: those introduced when we remove the sines to get a polynomial equation (Sect. 5). But too much is better than not enough: we shall now focus on finding the pairs which indeed allow coronas.

8.2 Finding Coronas

Assume two algebraic real numbers $0<s<r<1$ are given. We want to find all the values ${\varvec{k}}$, ${\varvec{l}}$ and ${\varvec{n}}$ which satisfy the equations $S_{{\varvec{k}}}(r,s)=2\pi$, $M_{{\varvec{l}}}(r,s)=2\pi$ and $L_{{\varvec{n}}}(r,s)=2\pi$. If they are no possible value for ${\varvec{k}}$, ${\varvec{l}}$ or ${\varvec{n}}$, then we rule out the pair (r, s).

We rely on interval arithmetic as much as possible. We compute intervals for r and s, then for the angles appearing in $S_{{\varvec{k}}}$, $M_{{\varvec{l}}}$, and $L_{{\varvec{n}}}$ via $\arccos$. We then compute the ${\varvec{k}}$, ${\varvec{l}}$ and ${\varvec{n}}$ such that the intervals $S_{{\varvec{k}}}(r,s)$, $M_{{\varvec{l}}}(r,s)$ and $L_{{\varvec{n}}}(r,s)$ contain $2\pi$. As we shall see, this actually suffices to rule out all the false pairs (a hint is that the remaining set is stable when the precision used for intervals is increased).

To check that the found coronas are indeed valid, we check the associated polynomial equations. We compute them as in Sect. 5, except that each time we multiply by $A\sin a-B$ to remove $\sin a$, we compute the interval for this expression and check that it does not contain zero. If it does⁵, we check exactly whether $A\sin a+B=0$ and rule out the case if it does not. We finally put the algebraic values of r and s in the polynomial equation to check it exactly⁶.

8.3 Reducing the Number of Cases

As seen in Sect. 4, there are 16805 pairs of s- and r-coronas, i.e., 16805 systems of polynomials equations to solve. Many of them are moreover too hard to solve. However, as we shall see, combinatorial arguments can be used to show that most of them do not allow compact packing, without even computing r and s. For this purpose, we distinguish three classes of compact packings:

• 1. those with no s- and r-discs in contact;

• 2. those with two different s-coronas (besides ssssss);

• 3. all the other ones.

The first class is very simple. There is an s-corona without r-disc which thus characterizes one of the 10 values of s for a compact packings with discs of radii 1 and s. Similarly, there is an r-corona without s-disc which yield 10 possibles values for r. With moreover $s<r$, this immediately yields $\left( {\begin{array}{c}10\\ 2\end{array}}\right) =45$ pairs (r, s).

The second class relies only on s-coronas. There are 55 of them, moreover associated with simpler equations than r-coronas. This yields $\left( {\begin{array}{c}55\\ 2\end{array}}\right) =1485$ systems. The hidden variable method gives 1573 pairs (r, s) where r and s are real algebraic numbers such that $0<s<r<1$. Only 37 of them admit coronas of all sizes⁷. All these computations required no more than a couple of minutes.

The last class is the main one. The fact that there is only one s-corona (besides ssssss) however yields a strong combinatorial constraint on the possible r-coronas. Since these compact packings contain an s-corona and a r-corona which intersect, i.e., the surrounded s- and r-discs are tangent, we can assume that the considered pair of s- and r-coronas intersect. Then, each pattern xsy in the coding of the r-corona force the pattern xry in the coding of the s-corona (the discs of radii x and y are those which are tangent to the centers of both coronas). This simple constraint reduces to only 803 the number of pairs of s- and r-coronas to be considered. Moreover, the remaining r-coronas are among the simplest ones⁸. The hidden variable method gives 62892 pairs (r, s) where r and s are real algebraic numbers such that $0<s<r<1$. Only 176 of them admit coronas of all sizes. All these computations required around 13 min⁹.

8.4 Finding Packings

The three above combinatorial classes now respectively contain 45, 37 and 176 pairs (r, s) which allow coronas of all sizes. It was a bit long but not too difficult to find, by hands, an example of a periodic compact packing with three size of discs for respectively 18, 1 and 145 of these pairs¹⁰. We then had to combinatorially prove that the other pairs do not allow any compact packing with three size of discs. Since $18+1+145=164$, Theorem 1 follows.

The 27 cases ruled out in the first combinatorial class were exactly those with no 1-corona containing both s- and r-discs. They do admit compact packings but not with all the three size of discs. All the cases in the second combinatorial class turned out to have no 1-corona containing an r-disc, and the only case which allows three sizes of discs is the one with an s-corona which contains both r- and 1-discs (namely 1srrs). In the last class, we proved that an s-corona 1rss, 11rss, 1rrss or 1srss in a compact packing actually implies another s-corona in this packing, which thus falls into the second combinatorial class. This ruled out 24 cases. The 7 remaining ones were ruled out one by one, each with a short combinatorial argument. They do not allow any compact packing.