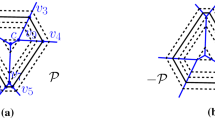Abstract
We propose a novel Voronoi Diagram based skeletonization algorithm that produces non-centered skeletons. The first strategy considers utilizing Elliptical Line Voronoi Diagrams with varied density based sampling of the polygonal shapes. The second strategy applies a weighting scheme on Elliptical Line Voronoi Diagrams and Line Voronoi Diagrams. The proposed skeletonization algorithm uses precomputed distance fields and basic element-wise operations, thus can be easily adapted for parallel execution. Non-centered Voronoi Skeletons give a representation that is more similar to real world skeletons and retain many of the desirable properties of skeletons.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Skeletonization plays an important role in the area of shape representation and description, since it decreases the dimensionality of the problem. By definition, a skeleton is a compact one-point wide representation of the shape that is associated with a locus of the points that are equidistant to two or more shape boundary points. This notion was originally introduced by Blum [1] as a medial axis transform (MAT). Skeletons provide useful properties for computer vision applications: invariance to translation, rotation and scaling; preservation of the topology of the shape; it can be computed for any 2D shape; incorporation of adjacency and neighborhood information; it is possible to completely reconstruct the original shape [13].
In order to represent the anatomical skeleton of an animal more closely, it is desirable to have a shape representation where the skeleton does not lie on the medial axis. In particular, MAT-based representation introduces wrong points to shape part connections (or joints) and results in deformations of rigid skeletal parts during articulated movement. This paper presents two approaches to obtain a non-centered skeleton. First, based on the properties of the Elliptical Line Voronoi Diagram we investigate the effect of the varied density based sampling of the polygonal shape approximation. Second, we propose a multiplicative weighting of shape boundary lines that enables modification of the medial axis position. Non-centered Voronoi skeletons fulfill all properties of skeletons except the reconstruction property. In the proposed algorithm, the shift of the medial axis towards the desired part of the shape is achieved by using varied density of the polygonal approximation of the shape and multiplicative weighting of shape boundary lines.
The remainder of the paper is organized as follows: Sect. 2 provides an overview of existing Voronoi Diagram types and presents a novel algorithm for computing a Generalized Voronoi Diagram using the Distance Transform. Section 3 discusses Voronoi Skeletons with an emphasis on Line Voronoi Skeletons, since dealing with polygonal shape approximations. Section 4 introduces Non-Centered Voronoi skeletons that can be obtained by (1) varied density-based sampling of the shape boundary and (2) weighting scheme for the distance maps. Section 5 concludes the paper.
2 Voronoi Diagram
The general idea behind the Voronoi Diagram (VD) is to associate each element in a set S with the closest element in a target set T (called sites) based on a distance metric \(d(s,t), s\in S, t \in T\). In other words, VD is a partition of the set S with regard to proximity of the elements to the target set. The Voronoi cell is the subset of S, where each element is closest to a single element in the target set. Points with identical proximity to two elements in the target set form Voronoi edges.
2.1 Point Voronoi Diagram
In classical VD, or Point Voronoi Diagram (PVD), a target set contains points in \(\mathbb {R}^2\), whereas S is the 2D plane. When the distance is Euclidean, the Voronoi edges are bisectors. PVD with 8 sites is illustrated in Fig. 1a.
2.2 Line Voronoi Diagram
In a Line Voronoi Diagram (LVD), sites in the target set T are line segments. In contrast to the Point Voronoi Diagrams (PVD), the Voronoi edges contain lines and parabolic arcs [12]. Voronoi cells might not be connected if the corresponding elements in the target set are crossing each other (see Fig. 1b). In classical LVD, distance between a point and a line segment is defined with the regard to the Hausdorff distance \(d_h (l, P ) = \inf \{\delta (P, L) | L \in l \}\).
2.3 Elliptical Line Voronoi Diagram
Gabdulkhakova and Kropatsch [3] proposed a different metric - Confocal Ellipse-based Distance (CED), \(d_e(P,l)\) - that defines a distance from the point P to the line segment l. As opposed to the Hausdorff distance, CED uses only the endpoints \(F_1, F_2\) of a line segment [4]:
where \(\delta \) denotes a Euclidean distance between two points.
CED is highly dependent on the length of the line segment. This enables longer line segments to have a greater influence on the Voronoi boundary and push the boundary away from them. This property is discussed in Sect. 4.1. Using the CED Gabdulkhakova et al. [4] introduced the Elliptical Line Voronoi Diagram (ELVD). This variation of the VD enables spatial control over the Voronoi edges without introducing weights.
Figure 2 shows this property. ELVD (black) has smaller regions associated with shorter line segments than the LVD (gray) using the Hausdorff distance.
2.4 Generalized Voronoi Diagrams from Distance Transform
Computational complexity of Generalized Voronoi Diagrams increases with the size of the target set. Especially explicit computations are difficult, since they rely on computing complex higher-order algebraic curves (see the green curve in Fig. 2b). In many cases an explicit computation [5, 7, 12, 14] of Voronoi edges is not necessary and algorithms [2, 6, 16, 17] have been proposed to implicitly calculate the boundaries based on grids.
Strzodka and Telea [15] introduced an approach to calculate Distance Transforms (DT) and Voronoi Skeletons on graphics hardware using different point distance functions. They propose a technique called Distance Splatting, where they go through every boundary point and then every image point and compare its distance to the minimum distance of the previous boundary points, iteratively building up the DT. They also store the closest site in a separate map by propagating it from a initialization on the boundary points. Additionally they provide implementation details on a GPU with a fixed graphics pipeline.
Since ELVD requires distances to a line segment, we propose an approach similar to the one from Strzodka and Telea [15], that uses arbitrary sites instead of boundary pixels and uses precomputed DT of these primitive sites. This allows for arbitrary distance measures and weighting schemes. Additionally, it is computationally efficient for point sites and line sites using CED.
The algorithm takes a list of distance maps \(L_D = \{dm_t \in \mathbb {R}^{N\times M}| t\in 0..T\}\) of T sites as input and an image resolution of N by M. Here, \(dm_t\) is the t-th distance map defining for each pixel the distance to the t-th site. It then loops through all sites building up a combined distance map DM and an ID-map IDM iteratively. Every pixel where \(DM-dm_t > 0\) the IDM is assigned t. Figure 3 shows the first iteration of this loop. In the end, the ID-map is used to create the Voronoi edges by comparing neighboring pixels. The algorithm can be found in Algorithm 1.

Distance Map Creation. For PVD and LVD the speed of distance map creation can be significantly increased. The distance maps are sampled from a bigger point distance map of size \(2N\times 2M\). Each pixel value represents the Euclidean distance to the center pixel. Therefore, it needs only one distance map creation, that can also be stored on the disk rather than being re-computed.
For ELVD the distance maps of the endpoints are summed up, then the distance between the two endpoints is subtracted. The above algorithm has to process a distance map \(dm_i\) only once, it can be generated on-the-fly by the single bigger point distance map.
Complexity and Error Estimation. Considering \(N\times M\) is the grid size and T is the number of sites (samples/line segments), sequential time complexity lies in \(O(T\cdot N\cdot M)\), leading to parallel complexity of O(T) on graphics hardware. For point sites and lines using CED the distance transform can be loaded from disc (or generated once), leading to linear time, otherwise, the time complexity of the distance transform times the number of sites must be taken into account. Memory complexity is \(O(N\cdot M)\), consisting of the \(N\cdot M\) maps DM, IDM and either another for on-the-fly generated distance maps, or one \(2N\times 2M\) map.
Since the algorithm considers only values on a grid, there is an accuracy error e. It is composed of the error of the distance transform \(e_d\) and the error of the boundary extraction \(e_b\). The distance transform error for the point distance described above is \(e_d = \frac{\sqrt{2}}{2}\) based on half the maximum distance between two pixel centers. The boundary extraction error is \(e_b = \sqrt{2}\), resulting from a maximum of one wrong pixel distance diagonally. This gives a combined error of \(e = \frac{3}{2}\sqrt{2}\). Additionally, the true Voronoi boundary after accounting for the distance transform error lies in the two pixel wide boundary found by the algorithm.
3 Voronoi Skeleton
A skeleton is a compact shape representation, which elements are equidistant from at least two points of the shape boundary. VD-based skeletonization is a continuous approach that preserves both geometrical and topological information of the shape. According to the definition, the boundaries of the Voronoi cells are equidistant to two or more elements in a target set. Ogniewicz and Ilg [10] use this property to obtain a Voronoi Skeleton (VS) of a shape by including all boundary pixels into the target set T. The resultant ridges are part of the skeleton that go through the edges connecting pixels along the boundary, but not through the pixels. Furthermore, they assign a residual value to each boundary between the two Voronoi cells that indicates its importance for the whole skeleton.
As can be seen throughout this paper, VD-based approaches construct the skeleton of the object (Endoskeleton), as well as the skeleton of the background (Exoskeleton) simultaneously.
3.1 Line Voronoi Skeletons
As VS edges by Ogniewicz and Ilg [10] lie between pixels their algorithm is extended to LVD with Voronoi edges passing through polygon points. The VD is computed on a polygonal shape using the DT approach described above.
After construction of the VD, each Voronoi edge between two cells must be evaluated for being a part of the skeleton. Lee [8] shows that all Voronoi edges that are not going through concave points are part of the skeleton. To avoid spurious branches (i.e. skeleton branches generated by noise) pruning is applied. In particular, densely sampled shapes have many spurious branches. Ogniewicz and Ilg propose four different residual values for each ridge that are based on the difference of the distance of the two adjacent points on the boundary and the distance through the shape. Ogniewicz [11] proves that their residual functions are monotonic and, thus, do not break topology. By using the midpoints of lines in the Line Voronoi Skeleton as adjacent points the same residual functions can be used. Mayya and Rajan [9] propose a similar procedure, but take only the number of intermediate object boundary segments into account. They show that topology is preserved by deleting only Voronoi ridges with no intermediate boundary segments in their adjacent sites.
Figure 4 shows the VD for a simplified horse shape and the Line Voronoi Skeleton. All three residuals are depicted with circular being purple, bicircular being green and chord being blue. The residuals follow the relation: circular \(\subseteq \) bicircular \(\subseteq \) chord.
4 Non-centered Skeletons
Using Euclidean distance as a distance measure has two advantages from the point of skeletonization: invariance to affine transformations and bending. The resultant skeleton is visually in the middle of the shape. For most cases the medial axis does not correspond to the physical skeleton of objects (e.g. animals, clothed objects). We introduce skeletons based on the medial axis using different distance measures to obtain a non-centered skeleton.
Definition 1
A non-centered skeleton of a 2D shape S is the medial axis of S given a different distance measure than a p-Norm. The medial axis using this distance must have the same topology as S.
4.1 Varied Density Based Sampling for Elliptic Voronoi Skeletons
It can be observed that the position of the VS produced by ELVD can be influenced by the length of the lines in the polygonal approximation of the shape. In our experiments we discovered that the influence gained solely by varied density based sampling of the shape is minor. Figure 6 gives three different approximations of the horse shape and the resulting skeletons.
In the following we study a special case, where the influence of varied density based sampling can be quantified. Let \(l=(F_1,F_2)\) be the long line segment with length 2f and (P, P) be the shortest possible line segment coinciding with the single point \(P \in \mathbb {R}^2\) (Fig. 5).
Let a, b, f be the parameters of the confocal ellipses that have foci at the end points of the line segment l with \(a^2 = b^2 + f^2\). Then, we know that the CED from the midpoint M to l is \(d_e(M,(F_1,F_2)) = 2(a-f)\). The distance between P and M is 2h and the normal distance of the point P from the line segment is \(d = h + b\). Given the requirement that \(d_e(M,(P,P)) = d_e(M,(F_1,F_2))\) we get \(h=a-f\).
Lemma 1
The ratio between the distance \(h = \delta (P,M)\) and the normal distance d of P to l ranges between 0.5 (the symmetric case \(f=0\)) to smaller values with increasing length of \(l=2f\) with ratio
Proof
The symmetric case would require \(b = h = d/2\) and \(b=a-f\). From the eccentricity formula \(a^2 = b^2 + f^2\) with f being the linear eccentricity (or focal length) we derive \(2 b f = 0\) which implies either
-
that \(b=0\), \(M \in l,\) \(a=f\), and \(h=0: P=M \in l\) or
-
that \(f=0,\) \(F_1=F_2\), \(a=b=h\): M is the midpoint between P and \(F_1\).
For all other cases \(f>0,b>0\) we assume that the values for f and d are known. From the equations given above it follows that \(a = d+f-b = \sqrt{b^2 + f^2}\). We solve for b, \(b=\frac{d}{2}\left( 1 + \frac{f}{d + f}\right) \) and, finally, with \(b = d - h\) get the ratio \(\frac{h}{d}\). \(\square \)
Strength of influence is not only determined by the length of the line segment, but also by the distance to the opposite point (line). In order to off-center the medial axis, it is unpractical to rely on varied density-based sampling alone - the difference in density has to be great to handle it in a reasonable image size.
4.2 Weighted Line Voronois
In order to have a greater shift of the non-centered skeleton from the medial axis, it is proposed to weight the distance maps. We use an adaptation of multiplicative weighting of lines [12] to move the medial axis closer to higher weighted lines by multiplying the weight instead of the reciprocal of the weight with the distance map. Figure 7 shows the horse shape with higher weights on its back for the ELVD- and LVD-based skeleton. It can be observed that the weighting on LVD has more influence than on ELVD. Figure 8 illustrates the difference between LVD and ELVD weighting.
For LVD the skeleton will move in one direction according to the weight, i.e. the Euclidean distance from line \(l_1\) to a point s on the skeleton ridge will be indirect proportional to the Euclidean distance from line \(l_2\) to S: \(\frac{d_h(l_1, s)}{d_h(l_2, s)} = \frac{w_2}{w_1}\), with \(w_1,w_2 \in \mathbb {R}\) being the weights of \(l_1\) and \(l_2\) respectively and \(d_h(l,p)\) being the Hausdorff distance between a line segment and a point.
For ELVD the task of estimating the skeleton position is harder. The distance is dependent on the focal length f and weighting is effecting the distance, as well as the elliptical parameter a.
For LVD and ELVD it is clear to see that no amount of weighting can push the medial axis outside of the object, because their values along the boundary lines are zero and can therefore never be closer to a different boundary segment.
4.3 Topology Preservation
In any of the skeletonization approaches presented above there exists the possibility of topology breakage, because the underlying VD may have cells that consist of multiple non-connected parts. This happens to skeletons that considered varied density based sampling, if line segment length proportions get too big. Analogically, for weighted skeletons it can happen, if weight proportions get too big. Figure 9 shows the problem. The gray areas belong to the same Voronoi cell, but are not connected and, hence, change topology in the medial axis.
Lemma 2
The medial axis obtained by weighted (E)LVD or ELVD with Varied Density Based Sampling of a convex object preserves connectivity.
Proof
This follows directly from the statement that the medial axis cannot be pushed outside the object. The influence region of a line can be behind another line, but since the object is convex, all additional regions are outside the object.
\(\square \)
Lemma 3
The medial axis of a concave object constructed by weighted LVD does not break topology under the following constraint: if two lines \(l_1,l_2\) in a concavity are weighted with \(w_1,w_2\) (\(w_1 > w_2\)), points in a distance greater than d times the distance from \(P_1\in l_1\) to \(P_2\in l_2\) in direction \(P_2\) to \(P_1\) from \(l_1\) must be closest to another line than \(l_2\) for all \(P_1 \in l_1\) and \(P_2 \in l_2\). The distance multiplier d is given as
Proof
Only considering two points \(P_1 \in l_1\) and \(P_2 \in l_2\), because the Hausdorff distance can be separated to a point level. Okabe et al. [12] show that multiplicative weighting results in Apollonius circles with two intersection points \(B_i, B_a\) on the line spanned by \(P_1,\) \(P_2\) (Fig. 10). \(B_i\) and \(B_a\) lie on the Voronoi edge of line \(l_1\). It follows, \(\frac{\delta (P_1,B_i)}{\delta (P_2,B_i)} = \frac{w_2}{w_1}\) and \(\frac{\delta (P_1,B_a)}{\delta (P_2,B_i)} = \frac{w_2}{w_1}\). The cross-ratio of the points \(A=P_2, B=P_1, C=B_i, D=B_a\) is 1 as a property of Apollonius circles. By setting \(\delta (B,C) = \frac{1}{w_1}\), \(\delta (A,C) = \frac{1}{w_2}\), \(\delta (B,D) = d\) and \(\delta (A,D) = \frac{1}{w_1} + \frac{1}{w_2} + d\) the cross-ratio equation (\(\frac{\delta (A,C)\delta (B,D)}{\delta (B,C)\delta (A,D)} = 1\)) can be solved for \(d\) resulting in (3). \(\square \)
As with weighting influence, deriving rules for topologically correct skeletonization using ELVD is hard and remains an open problem.
5 Conclusion and Future Work
This paper presents a novel algorithm for building the Generalized Voronoi Diagram based on Distance Transform and uses it to create Line Voronoi Skeletons. It further explores the possibilities to shift the skeleton from the center using (1) ELVD with varied density based sampling and (2) multiplicative weighting strategy for Elliptical Line Voronoi Diagrams and Line Voronoi Diagrams.
The experimental results prove the applicability of the proposed approach for the problem of skeletonization. Non-centered skeleton opens new possibilities in the area of shape representation and description. Possible directions are thin skeleton extraction by boundary following with the help of the combined distance map and learning weights and samples to obtain the medial axis following anatomical skeletons of various shapes.
References
Blum, H.: A transformation for extracting descriptors of shape. In: Models for the Perception of Speech and Visual Form (1967)
Boada, I., Coll, N., Madern, N., Antoni Sellares, J.: Approximations of 2D and 3D generalized voronoi diagrams. Int. J. Comput. Math. 85(7), 1003–1022 (2008)
Gabdulkhakova, A., Kropatsch, W.G.: Confocal ellipse-based distance and confocal elliptical field for polygonal shapes. In: Proceedings of the 24th International Conference on Pattern Recognition, ICPR (2018)
Gabdulkhakova, A., Langer, M., Langer, B.W., Kropatsch, W.G.: Line Voronoi diagrams using elliptical distances. In: Bai, X., Hancock, E.R., Ho, T.K., Wilson, R.C., Biggio, B., Robles-Kelly, A. (eds.) S+SSPR 2018. LNCS, vol. 11004, pp. 258–267. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-97785-0_25
Held, M.: Voronoi diagrams and offset curves of curvilinear polygons. Comput.-Aided Des. 30(4), 287–300 (1998)
Kalra, N., Ferguson, D., Stentz, A.: Incremental reconstruction of generalized voronoi diagrams on grids. Robot. Auton. Syst. 57(2), 123–128 (2009)
Klein, R., Langetepe, E., Nilforoushan, Z.: Abstract Voronoi diagrams revisited. Comput. Geom. 42(9), 885–902 (2009)
Lee, D.T.: Medial axis transformation of a planar shape. IEEE Trans. Pattern Anal. Mach. Intell. 4(4), 363–369 (1982)
Mayya, N., Rajan, V.: Voronoi diagrams of polygons: a framework for shape representation. J. Math. Imaging Vis. 6(4), 355–378 (1996)
Ogniewicz, R., Ilg, M.: Voronoi skeletons: theory and applications. In: Proceedings of 1992 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, CVPR 1992 (1992)
Ogniewicz, R.L.: Discrete Voronoi skeletons. Ph.D. thesis, ETH Zurich (1992)
Okabe, A., Boots, B., Sugihara, K., Chiu, S.N.: Spatial Tessellations: Concepts and Applications of Voronoi Diagrams. Wiley, Hoboken (2009)
Saha, P., Borgefors, G., Sanniti di Baja, G.: Skeletonization: Theory, Methods, and Applications (2017)
Setter, O., Sharir, M., Halperin, D.: Constructing two-dimensional Voronoi diagrams via divide-and-conquer of envelopes in space. In: Gavrilova, M.L., Tan, C.J.K., Anton, F. (eds.) Transactions on Computational Science IX. LNCS, vol. 6290, pp. 1–27. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-16007-3_1
Strzodka, R., Telea, A.: Generalized distance transforms and skeletons in graphics hardware. In: Proceedings of the Sixth Joint Eurographics-IEEE TCVG Conference on Visualization. Eurographics Association (2004)
Vleugels, J.M., Overmars, M.H.: Approximating generalized Voronoi diagrams in any dimension. Utrecht University (1995)
Yuan, Z., Rong, G., Guo, X., Wang, W.: Generalized Voronoi diagram computation on GPU. In: 2011 Eighth International Symposium on Voronoi Diagrams in Science and Engineering (ISVD) (2011)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Langer, M., Gabdulkhakova, A., Kropatsch, W.G. (2019). Non-centered Voronoi Skeletons. In: Couprie, M., Cousty, J., Kenmochi, Y., Mustafa, N. (eds) Discrete Geometry for Computer Imagery. DGCI 2019. Lecture Notes in Computer Science(), vol 11414. Springer, Cham. https://doi.org/10.1007/978-3-030-14085-4_28
Download citation
DOI: https://doi.org/10.1007/978-3-030-14085-4_28
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-14084-7
Online ISBN: 978-3-030-14085-4
eBook Packages: Computer ScienceComputer Science (R0)