A Spatial Convexity Descriptor for Object Enlacement

Abstract

In (Brunetti et al.: Extension of a one-dimensional convexity measure to two dimensions, LNCS 10256 (2017) 105–116) a spatial convexity descriptor is designed which provides a quantitative representation of an object by means of relative positions of its points. The descriptor uses so-called Quadrant-convexity and therefore, it is an immediate two-dimensional convexity descriptor. In this paper we extend the definition to spatial relations between objects and consider complex spatial relations like enlacement and interlacement. This approach permits to easily model these kinds of configurations as highlighted by the examples, and it allows us to define two interlacement descriptors which differ in the normalization. Experiments show a good behavior of them in the studied cases, and compare their performances.

This research was supported by the project “Integrated program for training new generation of scientists in the fields of computer science”, no EFOP-3.6.3-VEKOP-16-2017-0002. The project has been supported by the European Union and co-funded by the European Social Fund. Ministry of Human Capacities, Hungary grant 20391-3/2018/FEKUSTRAT is acknowledged.

1 Introduction

Shape representation is a current topic in digital image analysis, for example, for object recognition and classification issues. Suitable approaches for handling the problems consist in the design of new shape descriptors and measures for descriptors sensitive to distinguish the shapes but robust to noise. Some methods provide a unified approach that can be applied to determine a variety of shape measures, but more often they are specific to a single aspect of shape.

Over the years, measures for descriptors based on convexity have been developed. Area based measures form one popular category [6, 23, 25], while boundary-based ones [28] are also frequently used. Other methods use simplification of the contour [18] or a probabilistic approach [21, 22] to solve the problem. Recently, measures based on directional (line) convexity have been defined and investigated, independently, in [3, 26] and in [16, 17], to use the degree of directional convexity as a shape prior in image segmentation. These methods cannot be extended easily to a two-dimensional convexity measure. A different approach to this aim is to employ the concept of so-called Quadrant-convexity [8, 9] which is inherently two-dimensional. In this way, an extension of the directional convexity in [3] which uses quantitative information was introduced in [7], whereas in [1, 2] a different 2D convexity measure based on salient points [12, 13] was presented.

In this paper, we study more deeply the measure we derived the shape descriptors from, in [7]. The concepts on the basis of the measure definition have a counterpart in the framework of fuzzy sets for spatial relationships since the measure gives a quantitative representation of the object by means of relative positions of its points. Thus, the derived descriptors provide a model for studying the spatial relative position concepts in connection with unary relationships (to a reference object) and binary relationships (between two objects) [19].

Spatial relations have been studied in many disciplines (see Sect. 8 of [19] for a review of the related literature), and constitute an important part of the knowledge for image processing and understanding [4]. Two types of questions are raised when dealing with spatial relations: (1) given one reference object, define the region of space in which a relation to this reference is satisfied (to some degree); (2) given two objects (possibly fuzzy), assess the degree to which a relation is satisfied. Concerning the latter ones, they can be categorized into directional (relations like “to the left”), distance (relations like “far”), and topological. In particular, questions related to measuring complex spatial relations like enlacement, interlacement, and surrounding have been studied in [10, 11]. The term enlacement between F and G does indicate that object G is somehow between object F (the reference). Given a direction, a straight line parallel to the direction intersects the object in a one-dimensional finite slice (possibly empty), called longitudinal cut. Roughly speaking, the directional enlacement of G with regards to F along an oriented line is given by summing up the contributions of longitudinal cuts to count the number of triplet of points in $F\times G\times F$, as G is enlaced by F if their points alternate in this order [10]. If we consider the unary relationship, given the reference object F, the directional enlacement landscape of F along an oriented line consists in quantifying the region of space that is enlaced by F by longitudinal cuts. It is worth mentioning that objects can be imbricated each other only when the objects are concave, or constituted by multiple connected components, and indeed the use of some kind of convexity to deal with these spatial relationships has been already investigated also in [5]. Here we propose our Quadrant-convexity measure to tackle these issues directly in the two-dimensional space, i.e., to define a shape descriptor based on spatial relative positions of points which permits to define enlacement and interlacement between two objects. This approach is evaluated by suitable examples. In particular, we develop the idea to use our descriptor for enlacement landscape, i.e., taking the foreground as one object and the background as the other object. This permits to deal with the classification problem, and the experiments show a good performance in the studied cases.

In Sect. 2 we recall some information on Quadrant-convexity. In Sect. 3 we introduce the enlacement descriptor by normalizing the Quadrant-convexity measure. Then, in Sect. 4 we define the object enlacement and interlacement descriptors. Section 5 is for the experiments and Sect. 6 is for the conclusion.

2 Quadrant-Convexity

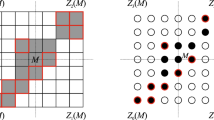
In the sequel, consider a two-dimensional object F to be represented by a non-empty lattice set, i.e. a finite subset of $\mathbb {Z}^2$, or equivalently, a function $f:\,\mathbb {Z}^2\rightarrow \{0,1\}$. Let $\mathcal {R}$ be the smallest rectangle containing F and suppose it is of size $m\times n$. We illustrate F as a union of white unit squares (foreground pixels), up to translations, and $\mathcal {R}\setminus F$ as a union of black unit squares (background pixels).

Each position (i, j) in the rectangle together with the horizontal and vertical directions determines the following four quadrants:

$$\begin{aligned} Z_0(i,j)&=\{ (l,k)\in \mathcal {R}:\; 0\le l\le i, \; 0\le k\le j\},\\ Z_1(i,j)&=\{ (l,k)\in \mathcal {R}:\; i\le l\le m-1, \; 0\le k\le j\},\\ Z_2(i,j)&=\{ (l,k)\in \mathcal {R}:\; i\le l\le m-1, \; j\le k\le n-1\},\\ Z_3(i,j)&=\{ (l,k)\in \mathcal {R}:\; 0\le l\le i, \; j\le k\le n-1\}. \end{aligned}$$

Let us denote the number of object points (foreground pixels) of F in $Z_p(i,j)$ by $n_p(i,j)$, for $p=0,\ldots ,3$, i.e.,

$$\begin{aligned} n_p(i,j)=card(Z_p(i,j)\cap F\}) \>\> (p=0,\ldots ,3). \end{aligned}$$

(1)

Definition 1

A lattice set F is Quadrant-convex (shortly, Q-convex) if for each (i, j) $(n_0(i,j)>0 \wedge n_1(i,j)>0 \wedge n_2(i,j)>0 \wedge n_3(i,j)>0)$ implies $(i,j)\in F$.

Fig. 1.

A Q-convex image (left) and a non Q-convex image (right). The four quadrants around the point (5, 5) are: $Z_0(5,5)$ left-bottom, $Z_1(5,5)$ right-bottom, $Z_2(5,5)$ right-top, $Z_3(5,5)$ left-top.

If F is not Q-convex, then there exists a position (i, j) violating the Q-convexity property, i.e. $n_p(i,j)>0$ for all $p=0,\ldots ,3$ and $(i,j)\notin F$. Figure 1 illustrates the definition of Q-convexity: the lattice set on the right is Q-concave (not Q-convex) because $(5,5)\notin F$ but $Z_p(5,5)$ contains object points, for all $p=0,1,2,3$. In the figure we have $n_0(5,5)=n_1(5,5)=n_2(5,5)=n_3(5,5)=24$. Let us notice that Definition 1 is based on the relative positions of the object points: the quantification of the object points in the quadrants with respect to the considered point gives rise to a quantitative representation of Q-concavity.

We define the Q-concavity measure of F as the sum of the contributions of non-Q-convexity for each point in $\mathcal {R}$. Formally,

$$\begin{aligned} \varphi _F(i,j)=n_0(i,j)n_1(i,j)n_2(i,j)n_3(i,j)(1-f(i,j)), \end{aligned}$$

(2)

where (i, j) is an arbitrary point of $\mathcal {R}$, and $f(i,j)=1$ if the point in position (i, j) belongs to the object, otherwise $f(i,j)=0$. Moreover,

$$\begin{aligned} \varphi _F=\varphi _F(F)=\sum _{(i,j)\in \mathcal {R}} \varphi _F(i,j). \end{aligned}$$

(3)

For example, for the image on the right of Fig. 1, we have $\varphi _F(5,5)=24\cdot 24\cdot 24\cdot 24\cdot 1=331776.$

Remark 1

If $f(i,j)=1$, then $\varphi _F(i,j)=0$. Moreover, if $f(i,j)=0$ and there exists $n_p(i,j)=0$, then $\varphi _F(i,j)=0$. Thus, F is Q-convex if and only if $\varphi _F=0$.

Remark 2

By definition, $\varphi$ is invariant by reflection and by point symmetry.

Remark 3

In [7] the authors showed that the Quadrant-concavity measure $\varphi$ extends the directional convexity in [3].

Remark 4

Previous definitions can be viewed in a slightly different way to provide a relationship to a reference object. Since, the latter one is the discrete version of the directional enlacement landscape of F along one oriented line, the Q-concavity measure extends fuzzy directional enlacement: The intersections of F with the four quadrants $Z_0,\;Z_1,\;Z_2,\;Z_3$ are an extension of the concept of longitudinal cut to two dimensions, and so relation (2) gives a quantification of the enlacement by the reference object F for the (landscape) point (i, j). Indeed, Q-convexity evaluates if a landscape point is among points of the reference object by looking at the presence of points of the reference object in each quadrant around the landscape point into consideration.

3 Obtaining Enlacement Descriptor by Normalization

In order to measure the degree of Q-concavity, or equivalently the degree of landscape enlacement for a given object F, we normalize $\varphi$ so that it ranges in [0, 1] (fuzzy enlacement landscape). We propose two possible normalizations gained by normalizing each contribution. A global one is obtained following [11]:

$$\begin{aligned} {\mathcal {E}}^{(1)}_F(i,j)=\frac{\varphi _F(i,j)}{\max _{(i',j')\in \mathcal {R}}\; \varphi _F(i',j')}. \end{aligned}$$

(4)

Second (local) one is based on [7]. There the authors proved

Proposition 1

Let $f(i,j)=0$, and $h_i^F$ and $v_j^F$ be the i-th row and j-th column sums. Then, $\varphi _F(i,j)\le ((card(F)+h_i^F+v_j^F)/4)^4$.

As a consequence we may normalize each contribution as

$$\begin{aligned} {\mathcal {E}}^{(2)}_F(i,j)=\frac{\varphi _F(i,j)}{((card(F)+h_i^F+v_j^F)/4)^4}. \end{aligned}$$

(5)

In order to obtain a normalization for the global enlacement for both (4) and (5), we sum up each single contribution and then we divide by the number of non-zero contributions.

Definition 2

For a given binary image F, its global enlacement landscape ${\mathcal {E}}^{(\cdot )}_F$ is defined by

$${\mathcal {E}}^{(\cdot )}_F=\sum _{(i,j)\in \bar{F}} \frac{ {\mathcal {E}}^{(\cdot )}_F(i,j)}{card(\bar{F})},$$

where $\bar{F}$ denotes the subset of (landscape) points in $\mathcal {R}\setminus F$ for which the contribution is not null.

Figure 2 illustrates the values of the descriptors for four images. The first image is Q-convex and thus the descriptor gives 0. The second image receives a greater value than the third one since the background region inside is deeper. In the fourth image part of the background is entirely closed into the object, thus this image receives a high value.

Fig. 2.

Example images with their enlacement values. In case of the last image a thin black frame is added just for visibility, it does not belong to the image.

Figure 3 shows the contribution of each pixel according to (4): the gray-scale levels correspond to the degrees of fuzzy enlacement of each pixel in the landscape. We can see that pixels inside the concavities have lighter colors (representing higher values) than pixels outside. Similar images can be given according to (5). Of course, in case of the first image of Fig. 2, the enlacement landscape is a completely black image. We point out that normalization plays a key role in Definition 2, as we will show in the experiments.

Fig. 3.

Enlacement landscapes of the last three images of Fig. 2.

4 Object Enlacement and Interlacement

In the previous sections we have defined a shape measure $\varphi _F$ based on the concept of Q-convexity which provides a quantitative measure for studying relationships to a reference object. Now, we modify it into a spatial relationship (a relationship between two objects). Let F and G be two objects. How much is G enlaced by F? The idea is to capture how many occurrences of points of G are somehow between points of F. This is obtained in a straightforward way, by restricting the points in $\mathcal {R}\setminus F$ taken into account to the points in G. Therefore,

$$\begin{aligned} \varphi _{FG}(i,j) = {\left\{ \begin{array}{ll} \varphi _F(i,j) &{} \quad \text {if } (i,j)\in G, \\ 0 &{} \quad \text {otherwise.} \end{array}\right. } \end{aligned}$$

(6)

Trivially note that if $G=\mathcal {R}\setminus F$, then $\varphi _{FG}(i,j)= \varphi _F(i,j)$. The enlacement descriptors of G by F are thus

$$\begin{aligned} {\mathcal {E}}^{(1)}_{FG}(i,j)=\frac{\varphi _{FG}(i,j)}{\max _{(i,j)\in G} \;\varphi _{FG}(i,j)}, \end{aligned}$$

(7)

and

$$\begin{aligned} {\mathcal {E}}^{(2)}_{FG}(i,j)=\frac{\varphi _{FG}(i,j)}{((card(F)+h_i^F+v_j^F)/4)^4}. \end{aligned}$$

(8)

For clarity, we observe that, by definition, $\varphi _{FG}(i,j)=0$ if $(i,j)\notin \bar{F}$, thus the maximum of $\varphi _{FG}(i,j)$ in G is equal to the maximum in $G\cap \bar{F}$. In order to obtain a normalization for the global enlacement, it is enough to get.

Definition 3

Let F and G be two objects. The enlacement of G by F is

$$ {\mathcal {E}}^{(\cdot )}_{FG}=\sum _{(i,j)\in G} \frac{ {\mathcal {E}}^{(\cdot )}_{FG}(i,j)}{card(G\cap \bar{F})}.$$

Remark 5

Let us notice that the definition of enlacement of two objects can be extended as follows:

$$ \frac{ \sum _{(i,j)\in \mathcal {R}} \min ({\mathcal {E}}^{(1)}_{FG}(i,j),g(i,j))}{\sum _{(i,j)\in \mathcal {R}} g(i,j)},$$

where g is the membership function representing G. If G is a fuzzy set, we may generalize the formula by substituting g with the membership function, and it corresponds to a satisfiability measure such as a normalized intersection [27].

Fig. 4.

Example images [10] with their interlacement values, where F and G is represented by white and gray pixels, respectively.

Of course, the enlacement of two objects is an asymmetric relation so that the enlacement of G by F and the enlacement of F by G provide different “views”. We may combine both by their harmonic mean to give a symmetric relation which is a description of mutual enlacement.

Definition 4

Let F and G be two objects. The interlacement of F and G is

$$\begin{aligned} {\mathcal {I}}^{(\cdot )}_{FG}= \frac{2{\mathcal {E}}^{(\cdot )}_{FG}{\mathcal {E}}^{(\cdot )}_{GF}}{{\mathcal {E}}^{(\cdot )}_{FG}+{\mathcal {E}}^{(\cdot )}_{GF}}, \end{aligned}$$

(9)

where ${\mathcal {E}}^{(\cdot )}_{FG}$ and ${\mathcal {E}}^{(\cdot )}_{GF}$ are the enlacement of G by F and the enlacement of F by G, respectively.

Figure 4 shows two example images with their interlacement values.

The measures can be efficiently implemented in linear time in the size of the image. By definition, $Z_0(l,k)\subseteq Z_0(i,j)$ if $l\le i$ and $k\le j$, and hence $n_0(l,k)\le n_0(i,j)$ with $l\le i$ and $k\le j$. Analogous relations hold for $Z_1,\;Z_2,\;Z_3$ and for $n_1,\; n_2,\;n_3$ accordingly. Exploiting this property, and proceeding line by line, we can count the number of points in F for $Z_p(i,j)$, for each (i, j) in linear time, and store them in a matrix for any $p=\{1,2,3,4\}$. Then, $\varphi (i,j)$ can be computed in constant time for any (i, j). Normalization is straightforward.

5 Experiments

We first conducted an experiment to investigate scale invariance on a variety of different shapes (Fig. 5) from [22]. After digitalizing the original 14 images on different scales ($32 \times 32, 64 \times 64, 128 \times 128, 256 \times 256, 512 \times 512$) we computed the two different interlacement values for each and compared them (being F the foreground and G the background). Table 1 shows the average of the measured interlacement differences over the 14 pairs of consecutive images. From the small values we can deduce that scaling has no significant impact on these measures, from the practical point of view. Obviously, in lower resolutions the smaller parts of the shapes may disappear, therefore the differences can be higher.

Fig. 5.

Variety of different shapes

Table 1. Average difference of interlacement values between consecutive image pairs

In the second and third experiments we used public datasets of fundus photographs of the retina for classification issues. We decided to compare our descriptor with its counterpart in [10] since they model a similar idea based on a quantitative concept of convexity. The main difference is that we provide a fully 2D approach, whereas the directional enlacement landscape in [10] is one-dimensional. The CHASEDB1 [15] dataset is composed of 20 binary images with centered optic disks, while the DRIVE [24] dataset contains 20 images where the optic disk is shifted from the center (Fig. 6).

Fig. 6.

Examples of the CHASEDB1 (left) and DRIVE datasets (right)

Following the strategy of [10] we gradually added different types of random noise to the images of size $1000\times 1000$ (which can be interpreted as increasingly strong segmentation errors). Gaussian and Speckle noise were added with 10 increasing variances $\sigma ^2\in [0,2]$, while salt & pepper noise was added with 10 increasing amounts in [0, 0.1]. Some example images are shown in Fig. 7. Then, we tried to classify the images into two classes (CHASEDB1 and DRIVE) based on their interlacement values (being F the object and G the background, again), by the 5 nearest neighbor classifier with inverse Euclidean distance (5NN). For the implementation we chose the WEKA Toolbox [14] and we used leave-one-out cross validation to evaluate accuracy. The results are presented in Table 2. In [10] the authors reported to reach an average accuracy of $97.75\%$, $99.25\%$, and $98.75\%$ for Speckle, Gaussian, and salt & pepper noise, respectively, on the same dataset with 5NN. In comparison, ${\mathcal {I}}^{(1)}_{FG}$ shows a worse performance. Fortunately, the way of normalization in (5) solves the problem, thus the results using ${\mathcal {I}}^{(2)}_{FG}$ are just slightly worse in case of Speckle and salt & pepper noise. This is especially promising, since our descriptor uses just two directions (four quadrants) being two-dimensional based whereas that of [10] uses 180 directions being one-dimensional based, and thus, it takes also more time to compute. Nevertheless, even a moderate amount of Gaussian noise distorts drastically the structures (see, again, Fig. 7), thus two-directional enlacement can no longer ensure a trustable classification.

Fig. 7.

Retina images with moderate (top row) and high (bottom row) amount of noise. Speckle, salt & pepper, and Gaussian noise, from left to right, respectively.

Table 2. 5NN classification accuracy (in percentage) of CHASEDB1 and DRIVE images for different types and levels of noise.

Fig. 8.

Examples of the HRF dataset (healthy case, glaucoma, diabetic retinopathy, from left to right, respectively)

Fig. 9.

Precision-recall curves obtained for classifying healthy and diseased cases of the HRF images. Green: ${\mathcal {I}}^{(1)}_{FG}$ Blue: ${\mathcal {I}}^{(2)}_{FG}$ Red: curve of [10] (Color figure online)

Finally, for a more complex classification problem, we used the High-Resolution Fundus (HRF) dataset [20], which is composed of 45 images of fundus: 15 healthy, 15 with glaucoma symptoms and 15 with diabetic retinopathy symptoms (Fig. 8). Using the same classifier as before we tried to separate the 15 healthy images from the 30 diseased cases. Figure 9 shows the precision-recall curves obtained for this classification problem by the two different interlacement descriptors. For comparison we present also the curve based on the interlacement descriptor introduced in [10]. The performance of ${\mathcal {I}}^{(1)}_{FG}$ seems to be worse, again, in this issue. On the other hand, we observe that descriptor ${\mathcal {I}}^{(2)}_{FG}$ performs as well as the one presented in [10] (or even slightly better). We stress again that our descriptor uses just two directions.

6 Conclusion

In this paper, we extended the Q-convexity measure of [7] to describe spatial relations between objects and consider complex spatial relations like enlacement and interlacement. We proposed two possible normalizations to obtain enlacement measures. The idea of the first one comes from [11], while the second one is based on our former work in [7]. As testified by the experiments, normalization plays a crucial role: the local normalization $\mathcal {E}^2$ performed generally better than the global normalization $\mathcal {E}^1$ in all the studied cases. In the experiments for classification issues, we developed the idea to assume the foreground being one object and the background being the other. This method is similar to the one in [10] so that the two methods aim at modelling the same idea. However, our method is based on a fully two-dimensional approach whereas the other is based on the one-dimensional directional enlacement. We believe that the two-dimensional approach is more powerful, and indeed in the experiments, just using two directions (so four quadrants), we reached comparable and even better results than that obtained by [10] employing many directions. This is the price to pay for the one-dimensional approach. Nevertheless, starting from the definition of Q-convexity, a further developement could consist in the employment of more directions. Another point is that the descriptors are not rotation invariant for rotations different from 90$^\circ$. A possibility is to preprocess the image by computing the principal axes and rotate the image before computing enlacement so that the principal axes will be aligned in the horizontal and vertical directions.