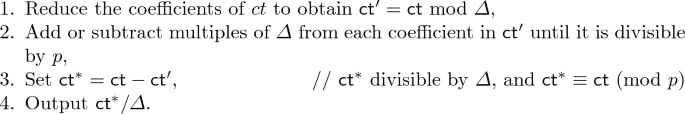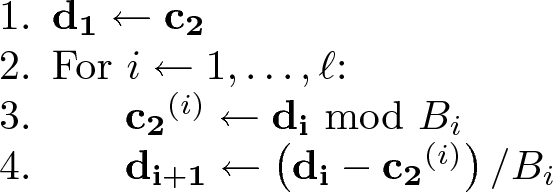A Comparison of the Homomorphic Encryption Libraries HElib, SEAL and FV-NFLlib

Abstract

Fully homomorphic encryption has considerably evolved during the past 10 years. In particular, the discovery of more efficient schemes has brought the computational complexity down to acceptable levels for some applications. Several implementations of these schemes have been publicly released, enabling researchers and practitioners to better understand the performance properties of the schemes. This improved understanding of the performance has led to the discovery of new potential applications of homomorphic encryption, fuelling further research on all fronts.

In this work, we provide a comparative benchmark of the leading homomorphic encryption libraries HElib, FV-NFLlib, and SEAL for large plaintext moduli of up to 2048 bits, and analyze their relative performance.

A Homomorphic Schemes and Libraries

In this section, we recall the variant of the Brakerski-Gentry-Vaikuntanathan (BGV) homomorphic encryption scheme [4], implemented in the software library HElib [11, 13]. This description is mostly taken from [10]. We also briefly describe the Fan-Vercauteren (FV) scheme [8], implemented in both SEAL [14] and FV-NFLlib.

1.1 A.1 A BGV Scheme Variant

The variant of the BGV scheme implemented in HElib is defined over polynomial rings of the form $R = \mathbb Z[x]/\varPhi _m(x)$ where m is a parameter and $\varPhi _m$ is the m-th cyclotomic polynomial. In order to make comparisons simpler we will consider that $m = 2*n$ with n a power of two, which implies that $\varPhi _m(x) = X^n + 1$. The plaintext space is usually the ring $R_p = R/pR$ for an integer p. A plaintext polynomial $\mathbf {a} \in R_p$ is encrypted as a vector over $R_q=R/qR$, where q is an odd public modulus. More specifically, BGV contains a chain of moduli of decreasing size $q_0>q_1>\cdots >q_L$ and freshly encrypted ciphertexts are defined modulo $q_0$. During homomorphic evaluation, we keep switching to smaller moduli after each multiplication until we get ciphertexts modulo $q_L$, which cannot be multiplied anymore. L is therefore an upper bound on the multiplicative depth of the circuit. We note $q_i$ to indicate that the current modulus we are working with may be any of $\{q_0,\ldots ,q_L\}$. We also define another set of primes whose product is noted $q'$. These are called the special primes and they are used to limit the error introduced in relinearization. Noise is drawn from a gaussian distribution $D_{\mathbb {Z}^{n},\sigma }$ with standard deviation $\sigma$ over the integer lattice $\mathbb {Z}^n$. Besides the usual input parameters for key generation used in lattice-based homomorphic schemes (degree n, deviation $\sigma$, plaintext modulus p, ciphertext modulus q), it is also possible to choose a relinearization parameter $\ell$ which enables different trade-offs between noise growth and computational costs. In practice, in HElib this parameter is always set to three.

• $\textsf {HElib.KeyGen}$:

  $\textsf {sk}$ :

  Sample a random secret key $\textsf {sk} := \mathbf {s} \leftarrow R_{q_0}$ with coefficients in $\{-1,0,1\}$, where exactly h of them are non-zero.

  $\textsf {pk}$ :

  Generate a public key $\textsf {pk} := (\mathbf {b},\mathbf {a}) \in R^2_{q_0}$, with $\mathbf {a} \leftarrow R_{q_0}$ drawn uniformly at random, and $\mathbf {b} := p\mathbf {e} - \mathbf {a}\cdot \mathbf {s}$, where $\mathbf {e} \leftarrow R_{q_0}$ follows $D_{\mathbb {Z}^{n},\sigma }$.

  $\textsf {rk}$ :

  Generate a relinearization key in $R^{2\times \ell }_{q_0\cdot q'}$. Split q in $\ell$ evenly-sized factors $B_1,\ldots ,B_\ell$. Define $\textsf {rk}_i := (\mathbf {a_i},\mathbf {b_i})^t \in R^{2}_{q_0 q'}$, with $\mathbf {a_i} \leftarrow R_{q_0 q'}$ drawn uniformly and $\mathbf {b_i} := \left( \prod _{j=0}^{i-1} B_j\right) \mathbf {s}^2 + p \mathbf {e_i} - \mathbf {a_i}\cdot \mathbf {s}$, where $\mathbf {e_i} \leftarrow R_{q_0 q'}$ follows $D_{\mathbb {Z}^{n},\sigma }$. Output $\textsf {rk} := (\textsf {rk}_1,\ldots ,\textsf {rk}_\ell )$.

• $\textsf {HElib.Encrypt}(\textsf {pk},\varvec{\mu })$: Generate a fresh ciphertext $\textsf {ct} \in R^2_{q_0}$ from a plaintext $\varvec{\mu } \in R_p$, encrypted using the public key $\textsf {pk} := (\mathbf {b},\mathbf {a}) \in R^2_{q_0}$. We have $\textsf {ct} := (\mathbf {c_0},\mathbf {c_1})$ with $\mathbf {c_0} := \mathbf {u}\cdot \mathbf {b} + p \mathbf {e_0} + \left[ q_0\varvec{\mu }\right] _p$ and $\mathbf {c_1} := \mathbf {u}\cdot \mathbf {a} + p \mathbf {e_1}$, where $\mathbf {u} \leftarrow R_{q_0}$ is drawn uniformly in $\{-1,0,1\}^n$ and $\mathbf {e_0},\mathbf {e_1}$ follow $D_{\mathbb {Z}^{n}, \sigma }$.

• $\textsf {HElib.Add}(\textsf {ct}_0,\textsf {ct}_1)$: Add two ciphertexts $\textsf {ct}_0 := (\mathbf {c_{00}},\mathbf {c_{01}}) \in R^2_{q_i}$ and $\textsf {ct}_1 := (\mathbf {c_{10}},\mathbf {c_{11}}) \in R^2_{q_i}$ into a ciphertext $\textsf {ct}_+ := (\mathbf {c_0},\mathbf {c_1}) \in R^2_{q_i}$, with $\mathbf {c_0} = \mathbf {c_{00}}+\mathbf {c_{10}}$ and $\mathbf {c_1} = \mathbf {c_{01}}+\mathbf {c_{11}}$.

• $\textsf {HElib.Mul}(\textsf {ct}_0,\textsf {ct}_1)$: Multiply two ciphertexts $\textsf {ct}_0 := (\mathbf {c_{00}},\mathbf {c_{01}}) \in R^2_{q_i}$ and $\textsf {ct}_1 := (\mathbf {c_{10}},\mathbf {c_{11}}) \in R^2_{q_i}$ into a ciphertext $\widetilde{\textsf {ct}}_\times := (\mathbf {c_0}, \mathbf {c_1}, \mathbf {c_2}) \in R^3_{q_i}$, with $\mathbf {c_0} = \left[ q^{-1}_i\right] _p\mathbf {c_{00}}\cdot \mathbf {c_{10}}$, $\mathbf {c_1} = \left[ q^{-1}_i\right] _p(\mathbf {c_{00}}\cdot \mathbf {c_{11}}+\mathbf {c_{01}}\cdot \mathbf {c_{10}})$ and $\mathbf {c_2} = \left[ q^{-1}_i\right] _p\mathbf {c_{01}}\cdot \mathbf {c_{11}}$.

• $\textsf {HElib.ModSwitch}(\textsf {ct},q)$: Remove primes from the current modulus to obtain a new target modulus q and scale the ciphertext $\textsf {ct}$ down by a factor of $\varDelta$ (equal to the current modulus divided by the target modulus) using the following optimized procedure described in [10]:

  

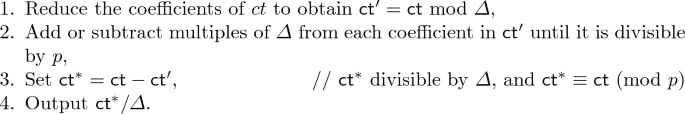
• $\textsf {HElib.Relin}(\textsf {rk},\widetilde{\textsf {ct}}_\times )$: Relinearize a ciphertext $\widetilde{\textsf {ct}}_\times := (\mathbf {c_0}, \mathbf {c_1}, \mathbf {c_2}) \in R^3_{q_i}$ into a ciphertext $\textsf {ct}_\times \in R^2_{q_i}$ using the relinearizing key $\textsf {rk} := W \in R^{2\times \ell }_{q_0 q'}$. First we break $\mathbf {c_2}$ into a collection of $\ell$ lower-norm polynomials $\mathbf {c_2}^{(i)}$:

  

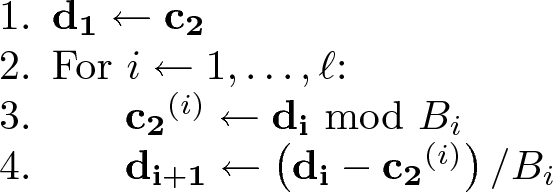
  We then reduce the relinearization key matrix modulo $q_iq'$, and add the small primes corresponding to $q_iq'$ to all the $\mathbf {c_2}^{(i)}$’s, then compute the ciphertext

  $$\begin{aligned} \overline{\textsf {ct}}_\times := \left( \mathbf {c_0} + \sum _{i=1}^\ell W_{i,0} \cdot \mathbf {c_2}^{(i)},\,\mathbf {c_1} + \sum _{i=1}^\ell W_{i,1} \cdot \mathbf {c_2}^{(i)}\right) \in R^2_{q_iq'} \end{aligned}$$

  Finally, using the modulus switching function defined above, we output $\textsf {ct}_\times := \textsf {HElib.ModSwitch}(\overline{\textsf {ct}}_\times , q_i) \in R^2_{q_i}$.

• $\textsf {HElib.Decrypt}(\textsf {sk},\textsf {ct})$: Decrypt a ciphertext $\textsf {ct} := (\mathbf {c_0},\mathbf {c_1}) \in R^2_{q_i}$ into a plaintext $\varvec{\mu } := \left[ \left[ q_i^{-1}\right] _p \left[ \mathbf {c_0} + \mathbf {c_1}\cdot \mathbf {s} \right] _{q_i} \right] _p \in R_p$.

1.2 A.2 Fan and Vercauteren’s Scheme

The Fan-Vercauteren (FV) scheme is closely related to BGV, but instead of modulus switching it uses the scale-invariant approach of Brakerski [3] to control noise growth, and encodes the plaintext in the high-order bits of the coefficients of the ciphertext polynomials, instead of the low-order bits.

It is possible to choose a relinearization parameter, noted in this case $\omega$. This value is a basis in which the relinearization key is decomposed and can be modified to tune performance. Two different distributions are used: $\chi _\mathsf {key}$ and $\chi _\mathsf {err}$. FV-NFLlib defines $\chi _\mathsf {key} = D_{\mathbb {Z}^n,\sigma _\mathsf {key}}$ and $\chi _\mathsf {err} = D_{\mathbb {Z}^n,\sigma _\mathsf {err}}$, for given $\sigma _\mathsf {err}$ and $\sigma _\mathsf {err}$. SEAL defines $\chi _{\mathsf {key}}$ as the uniform distribution over $\{-1,0,1\}$ and $\chi _\mathsf {err}$ as FV-NFLlib does.

• $\textsf {FV.KeyGen}$:

  • $\textsf {sk}$ Output $\textsf {sk} := \mathbf {s} \leftarrow \chi _{\mathsf {key}}$

  • $\textsf {pk}$ Let $\mathbf a \leftarrow R_q$ drawn uniformly and $\mathbf e \leftarrow \chi _{\mathsf {err}}$. Define $\textsf {pk} := ([-\mathbf a \cdot \mathbf s -\mathbf e ]_q, \mathbf a )$.

  • $\textsf {rk}$ Generate a relinearization key $\mathsf {rk} := (\mathsf {rk_1}, \ldots , \mathsf {rk_{\ell }})$ with $\ell = \lfloor \log _{\omega } (q) \rfloor + 1$ and $\mathsf {rk_i} := (\mathbf {s^2}\omega ^i - (\mathbf {a_i} \cdot \mathbf {s} +\mathbf {e_i}),\mathbf {a_i})$, with $\mathbf {a_i} \leftarrow R_{q}$ uniformly at random and $\mathbf {e_i} \leftarrow \chi _{\mathsf {err}}$.

• $\textsf {FV.Encrypt}(\textsf {pk},\mu )$: Generate a fresh ciphertext $\textsf {ct} \in R^2_{q}$ from a plaintext $\varvec{\mu } \in R_p$, encrypted using the public key $\textsf {pk} := (\mathbf {b},\mathbf {a}) \in R^2_{q}$. We have $\textsf {ct} := (\mathbf {c_0},\mathbf {c_1})$ with $\mathbf {c_0} := \mathbf {u}\cdot \mathbf {b} + \mathbf {e_0} + \varDelta [\mu ]_p$ and $\mathbf {c_1} := \mathbf {u}\cdot \mathbf {a} + \mathbf {e_1}$, where $\mathbf {u}$ follows $\chi _{\mathsf {key}}$ and $\mathbf {e_0},\mathbf {e_1}$ follow $\chi _{\mathsf {err}}$ and $\varDelta = q/p$.

• $\textsf {FV.Add}(\textsf {ct}_0,\textsf {ct}_1)$: Add two ciphertexts $\textsf {ct}_0 := (\mathbf {c_{00}},\mathbf {c_{01}}) \in R^2_{q}$ and $\textsf {ct}_1 := (\mathbf {c_{10}},\mathbf {c_{11}}) \in R^2_{q}$ into a ciphertext $\widetilde{\textsf {ct}}_{+} := (\mathbf {c_0}, \mathbf {c_1}) \in R^2_{q}$, with $\mathbf {c_0} = \mathbf {c_{00}}+\mathbf {c_{10}}$ and $\mathbf {c_1} = \mathbf {c_{01}} + \mathbf {c_{11}}$.

• $\textsf {FV.Mul}(\textsf {ct}_0,\textsf {ct}_1)$: Multiply two ciphertexts $\textsf {ct}_0 := (\mathbf {c_{00}},\mathbf {c_{01}}) \in R^2_{q}$ and $\textsf {ct}_1 := (\mathbf {c_{10}},\mathbf {c_{11}}) \in R^2_{q}$ into a ciphertext $\widetilde{\textsf {ct}}_\times := (\mathbf {c_0}, \mathbf {c_1}, \mathbf {c_2}) \in R^3_{q}$, with $\mathbf {c_0} = \lfloor p/q(\mathbf {c_{00}}\cdot \mathbf {c_{10}})\rceil$, $\mathbf {c_1} = \lfloor p/q(\mathbf {c_{00}}\cdot \mathbf {c_{11}}+\mathbf {c_{01}}\cdot \mathbf {c_{10}})\rceil )$ and $\mathbf {c_2} = \lfloor p/q(\mathbf {c_{01}}\cdot \mathbf {c_{11}})\rceil$.

• $\textsf {FV.Relin}(\textsf {rk},\widetilde{\textsf {ct}}_\times )$: Re-linearize a ciphertext $\widetilde{\textsf {ct}}_\times := (\mathbf {c_0}, \mathbf {c_1}, \mathbf {c_2}) \in R^3_{q}$ into a ciphertext $\textsf {ct}_\times \in R^2_{q}$. Noting the elements of the relinearization key $\mathsf {rk_i} = (\mathsf {rk_{i,0}}, \mathsf {rk_{i,1}}) \in R^2_{q}$, and $\mathbf {c_2}^{(i)}$ the decomposition of $\mathbf {c_2}$ in digits in base $\omega$, return

  $$\begin{aligned} \textsf {ct}_\times := \left( \mathbf {c_0} + \sum _{i=0}^\ell \mathsf {rk}_{i,1} \cdot \mathbf {c_2}^{(i)},\mathbf {c_1} + \sum _{i=1}^\ell \mathsf {rk_{i,1}} \cdot \mathbf {c_2}^{(i)}\right) \end{aligned}$$

• $\textsf {FV.Decrypt}(\textsf {sk},\textsf {ct})$: Decrypt a ciphertext $\textsf {ct} := (\mathbf {c_0},\mathbf {c_1}) \in R^2_{q}$ into a plaintext $\varvec{\mu } := [\lfloor p/q(\mathbf {c_0}+\mathbf {c_1}\cdot \mathbf {s})\rceil ]_p$

1.3 A.3 Homomorphic Operations

In the schemes presented, the plaintext space is $R_p$, and homomorphic additions correspond to additions over the ring $R_q$.⁵

In order to realize other operations (encryption, homomorphic multiplication, modulus switching, relinearization, decryption), we also need to compute multiplications over $R_q$ and, for some of these operations, to manipulate directly the coefficients of the polynomials in $R_q$.

Batching. Using the Chinese Remainder Theorem it is possible to encrypt a vector of elements of $\mathbb {Z}_p$ [7, 17, 18] so that homomorphic operations are applied component-wise between the plaintext vectors. This feature is called batching, and when used efficiently can massively improve the performance of homomorphic computations, e.g. by allowing thousands of instances of a function to be evaluated simultaneously on different inputs.

To understand how batching works, suppose the cyclotomic polynomial $\varPhi _m(x)$ factors modulo the plaintext modulus p into a product of irreducible factors $\varPhi _m(x) = \prod _{j=0}^{\ell -1} F_j(x)\pmod p$, then a plaintext polynomial $\mathbf {a}\in R_p$ can be viewed as encoding $\ell$ different small polynomials $a_j=a\bmod F_j$, and each constant coefficient of the $a_j$ can be set to an element of $\mathbb {Z}_p$.

Note that the factorization of the cyclotomic polynomial, $\varPhi _m(x) = \prod _{j=0 }^{\ell -1} F_j(x) \pmod p$, depends on m and p. If p is fixed for a given application, then the batching capacity will be different for each m depending on how $\varPhi _m(x)$ factors modulo p.

HElib gives complete freedom when choosing m but both FV-NFLlib and SEAL use optimized NTT transforms that require power-of-two cyclotomic polynomials. In practice this means that HElib is able, in some cases, to provide a better batching than FV-NFLlib and SEAL.

1.4 A.4 DoubleCRT Representation

In this section we recall the DoubleCRT representation used in HElib and NFLlib to represent elements of the cyclotomic ring $R_q$ (it is also used with $R_p$, but for conciseness we will focus on $R_q$). This representation is composed of two sub-representations, the Chinese remainder theorem (CRT) and the number theoretic transform (NTT).

CRT. We consider the CRT basis as a l-uple of co-prime numbers $(q_0,\ldots ,q_{l-1})$, we note $q = \prod _{i=0}^{l-1} p_i$. An integer $a \in \mathbb {Z}_q$ is represented in CRT as:

This representation is unique for all $a \in \mathbb {Z}_q$ by the Chinese Remainder Theorem.

NTT. Let q be an integer such that $\mathbb {Z}_q$ contains a primitive m-th root of unity $\zeta _i$. A polynomial $\mathbf {a} \in R_q$ is represented in NTT as:

DoubleCRT. To use at the same time the CRT representation for coefficients/values and the NTT representation, we need a CRT basis $(q_0,\ldots ,q_{l-1})$ such that every $q_i$ is chosen so that $\mathbb {Z}/q_i\mathbb {Z}$ contains a primitive m-th root of unity $\zeta _i$. A polynomial $\mathbf {a} \in R_q$ is represented in DoubleCRT as: