The Study of the Work Parameters of the Corn Harvester Cutter

Abstract

In this paper, the analytical method of multivariate variance is applied to study the function of the various performance factors of the straight-edge cylindrical cutter. Research results indicate that the main factor impacts the model type surface straight blade cylinder type chopped knife is the speed of the blade, and the application of regression analysis method establishes the regression equation of the blade of stem cutting speed and cutting length, cutting speed and stem throwing distance, speed and power consumption. This paper introduces how to choose chopped knife work parameters with the application of these regression equations.

1 Introduction

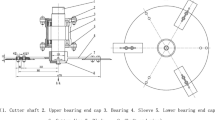
Chop model type surface straight blade cylinder type knife is according to the vertical roll type corn harvester pick ears designed the working characteristics of roller, it can simultaneously complete stem chopped recovery without setting up recycling equipment, if we use returning corn stalks as fertilizer, cutting length shorter as well, making green fodder as recycling corn stalks, and the stem cutting length should be in 30 mm advisable, because a cut stem is too long or too short are adverse to the digestion of the livestock [1,2,3]. Therefore, to control the cut length of the stalk, we need to find out the factors that affect the length of the stalk. If the stem is recycled as a feed, you will also know the rules of the cutting stem. We have to find out the factors that affect the distance of the stalk.

Based on the multivariate analysis of variance was carried out on the test data, found out the impacts like a cut stem length and stem toss distance are the main factors of chopped knife rotation speed, establish the equation of the stem cutting length and cutting knife rotating speed with the application of these regression equations. Applying the approximate function relation can provide the reference for research of corn harvester and users [4–5].

2 Experimental Conditions and Experimental Results

2.1 Definite Parameters

We have known the value of the blade radius(r) is 145 mm, the turning radius of the cutter(R) is 210 mm. The number of blade is 4, the spike roller speed - $n_{s} = 1000$ r/min, Hold the feed chain speed- .

2.2 Experimental Condition

The experiment was carried out on the laboratory bench, and the cutter was installed on the top of the picking part, which was driven separately by the adjustable-speed motor. Plants are fed to a roller which cut by sickle on the clamping. The stem from picking rolls back after discharge, cut by knife chop, and then was thrown. Test the power consumption [6].

2.3 Experimental and Experimental Results

The experimental scheme adopts orthogonal test method, take the orthogonal table ${\text{L}}_{16} (4^{5} )$ and arrange an experiment [7]. The factor A is the feeding speed, it has four levels A₁ = 1.5 m/s, A₂ = 1.7 m/s, A₃ = = 1.9 m/s, A₄ = 2.2 m/s. Factor B is the cutting speed, it is divided into four levels.

B₁ = 1800 r/min, B₂ = 1900 r/min, B₃ = 2000 r/min, B₄ = 2100 r/min. The purpose of this experiment is to look at the factor A, factor B, and the correlation of A with B. These factors will cause the influence of the three indexes for the length of the stem $y^{(1)}$, the distance of the stem $y^{(2)}$ and the power consumption $y^{(3)}$. Due to investigate whether the interaction between A and B is significant to the index, we have arranged three repeated trials under the same condition. The experimental and experimental results are listed in Table 1.

Table 1. Test plan and experimental results

3 Analysis of Variance of Experimental Results

From the data in Table 1, With the increase of feeding speed, the rotational speed of the cutter for increased power consumption is quite obvious. Without considering the influence of factor A and factor B power consumption therefore in the multivariate analysis of variance, we only consider factor A and B of binary indicators.

$y = (y^{(1)} ,y^{(2)} )^{\rm T}$ ($y^{(1)}$—The length of the stems, $y^{(2)}$—The throwing distance of stalks)

$y_{ijk}$ ($i = 1,2,3,4$, $j = 1,2,3,4$) –The test result of the i level of factor A ($i = 1,2,3,4$) and the j level of factor B. We make $\bar{y}_{ij \cdot } = \frac{1}{3}\mathop \varSigma \limits_{i = 1}^{4} \mathop \varSigma \limits_{j = 1}^{4} \mathop \varSigma \limits_{k = 1}^{3} y_{ijk}$, $\bar{y} = \frac{1}{3 \times 4 \times 4}\sum\limits_{i = 1}^{4} {\sum\limits_{j = 1}^{4} {\sum\limits_{k = 1}^{3} {y_{ijk} } } }$, $\bar{y}_{i \cdot \cdot } = \frac{1}{3 \times 4}\sum\limits_{j = 1}^{4} {\sum\limits_{k = 1}^{3} {y_{ijk} } }$ $\bar{y}_{ \cdot \cdot j} = \frac{1}{3 \times 4}\sum\limits_{i = 1}^{4} {\sum\limits_{k = 1}^{3} {y_{ijk} } }$

By analyzing the formula of variances, the dispersion matrix is obtained

• (1) Dispersion matrix-$Q:$

  $$ Q = \sum\limits_{i = 1}^{4} {\sum\limits_{j = 1}^{4} {\sum\limits_{k = 1}^{3} {(y_{ijk} - \bar{y})(y_{ijk} - \bar{y})^{\rm T} } } } = \left( {\begin{array}{*{20}c} {1785.42} & { - 81.06} \\ { - 18.06} & {11.51} \\ \end{array} } \right) $$

• (2) Group alienation matrix about factor A-$Q_{A} :$

  $$ Q_{A} = 3 \times 4\sum\limits_{i = 1}^{4} {(\bar{y}_{i \cdot \cdot } - \bar{y})(\bar{y}_{i \cdot \cdot } - \bar{y})^{\rm T} } = \left( {\begin{array}{*{20}c} {27.075} & { - 0.3} \\ { - 0.3} & {0.105} \\ \end{array} } \right) $$

• (3) Group alienation matrix about factor B-$Q_{B} :$

  $$ Q_{B} = 3 \times 4\sum\limits_{j = 1}^{4} {(\bar{y}_{ \cdot j \cdot } - \bar{y})(\bar{y}_{ \cdot j \cdot } - \bar{y})^{\rm T} } = \left( {\begin{array}{*{20}c} {1011.585} & { - 74.256} \\ { - 74.256} & {5.775} \\ \end{array} } \right) $$

• (4) Dispersion matrix of group-$Q_{R} :$

  $$ Q_{R} = \sum\limits_{i = 1}^{4} {\sum\limits_{j = 1}^{4} {\sum\limits_{k = 1}^{3} {(y_{ijk} - \bar{y}_{ij} )(y_{ijk} - \bar{y}_{ij} )^{\rm T} } } } = \left( {\begin{array}{*{20}c} {743.58} & { - 9.21} \\ { - 9.21} & {4.94} \\ \end{array} } \right) $$

• (5) Interaction with A and B of the difference matrix-$Q_{A \times B} :$

  $$ Q_{A \times B} = Q - Q_{A} - Q_{B} - Q_{R} = \left( {\begin{array}{*{20}c} {3.18} & {2.706} \\ {2.706} & {0.69} \\ \end{array} } \right) $$

Factor A, factor B, and A cross B have no significant effect on the indicators study, if so $\mathop y\nolimits_{ijk} \,{ \sim }\,N_{2} (\mu ,\Sigma ).$ $\mu (\mu_{1} ,\mu_{2} )^{\rm T}$ is the mean vector, $\Sigma = \left( {\begin{array}{*{20}c} {\sigma_{1}^{2} } & {\sigma_{1} \sigma_{2} \rho } \\ {\sigma_{1} \sigma_{2} \rho } & {\sigma_{2}^{2} } \\ \end{array} } \right)$ is the covariance matrix. We can get respectively distributions of the sum of the squares and the matrix,

$$ \begin{array}{*{20}c} {Q{ \sim }W_{2} (47,\Sigma );\,Q{}_{A}{ \sim }W_{2} (3,\Sigma );\,Q_{B} { \sim }W_{2} (3,\Sigma )} \\ {Q_{A \times B} { \sim }W_{2} (2,\Sigma );\,Q_{R} { \sim }W_{2} (32,\Sigma )\quad \quad \quad \quad \quad \quad \quad \quad \quad } \\ \end{array} $$

Whether Factor A, factor B and A cross B have significant impact on dual index. Test the above factors and we get the respectively distributions of statistics.

$$ \Lambda _{\text{A}} = \frac{{\left| {Q_{R} } \right|}}{{\left| {Q_{R} + Q_{\text{A}} } \right|}}\sim\Lambda (2,32,3) $$

$$ \Lambda _{\text{B}} = \frac{{\left| {Q_{R} } \right|}}{{\left| {Q_{R} + Q_{\text{B}} } \right|}}\sim\Lambda (2,32,3) $$

$$ \Lambda _{{{\text{A}} \times {\text{B}}}} = \frac{{\left| {Q_{R} } \right|}}{{\left| {Q_{R} + Q_{{{\text{A}} \times {\text{B}}}} } \right|}}\sim\Lambda (2,32,9) $$

Firstly, check the significance of factor A, $\Lambda _{\text{A}} = 0.94495$, make $\alpha = 0.05$ at a significance level.

We learn that $\Lambda _{0.01} (2,32,3) = 0.6569$ from the Table. For $\Lambda _{\text{A}} >\Lambda _{0.05} (2,32,3)$, So the influence of factor A on the binary index $y = (y^{(1)} ,y^{(2)} )^{\rm T}$ is not significant, The rate of feeding is not significantly affected by the length of the stalk and the distance of the cast.

Secondly, check the significance of factor B, $\Lambda _{\text{B}} = 0.30309$, make $\alpha = 0.01$ at a significant level. The critical value: $\Lambda _{0.01} (2,32,3) = 0.57061$. For $\Lambda _{\text{B}} <\Lambda _{0.01} (2,32,3)$, So the influence of factor B on the binary index $y = (y^{(1)} ,y^{(2)} )^{\rm T}$ is significant. The rate of feeding is significantly affected by the length of the stalk and the distance of the cast.

Finally, check the significance of the interaction of A cross B, $\Lambda _{{{\text{A}} \times {\text{B}}}} = 0.8662$, make $\alpha = 0.05$ at a significance level.

The critical value: $\mathop\Lambda \nolimits_{0.05} (2,32,9) = 0.41482$. For $\Lambda _{{{\text{A}} \times {\text{B}}}} >\Lambda (2,32,9)$, So the influence of the interaction of A cross B on the binary index $y = (y^{(1)} ,y^{(2)} )^{\rm T}$ is not significant, The rate of feeding is not significantly affected by the length of the stalk and the distance of the cast.

4 The Regression Equation of the Cutting Speed and the Length of the Stem, the Distance of the Stem and the Power Consumption

4.1 The Sorting of the Experimental Data

Multivariate analysis of variance shows that the main factor that influence the cut stem length, stem toss distance and power consumption is the speed of the blade. But the correlation of the feeding speed with stem cut length and toss distance can be neglected, and the cutting speed and feeding speed and power consumption has obvious relevance [8–9]. So we can take the knife speed of four different levels that matching with stem feeding speed of the collocation of four different levels as the cutting speed for different level 4 times in repeated trials, coupled with the test of each level 3 repetitions, is considered to be a four levels on cutting speed for 12 times [10]. Use $x$ for cutting speed, $y^{(1)}$ is the average of the test results in 12 repetitions, $y^{(2)}$ is the average of the toss distance of the test results of 12 repetitions, $y^{(3)}$ is the average of the test power consumption of the test results of 12 repetitions. Work up the data in Table 1 for the following Table 2.

Table 2. The relation of the cutting speed with $y^{(1)} ,y^{(2)} ,y^{(3)}$

4.2 The Regression Equation of the Length of the Stalk Section and the Cutting Speed

As the data in Table 2 shows, the length of the stem cut is decreasing as the cutting speed increasing. Therefore, there are two kinds of functional relations between the cutting speed and the length of the stem to be chosen.

$$ y^{(1)} = \beta_{0} + \beta_{1} x\quad \;(\beta_{1} < 0) $$

(1)

$$ y^{(1)} = ae^{ - bx} \quad \,(a > 0,b > 0) $$

(2)

But with the increase of stem cutting length are getting smaller, the cut stem length is not negative, so it is not reasonable to use the linear regression Eq. (1). Therefore we choose and the regression equation between $x$ with $y^{(1)}$ as the index regression model (2).

Estimate the two parameters of the regression Eq. (2).

First, take the natural log of both ends.

$$ { \ln }\,y^{(2)} = { \ln }\,a - bx $$

(3)

In the upper case, the (2) is converted into a linear regression model.

We set $Y = { \ln }\,y^{(2)} ,A = { \ln }\,a,B = - b$, so we get the linear regression model,

$$ Y = A + Bx $$

(4)

In the linear regression Eq. (4), the parameter A and the parameter B are estimated.

$$ \left\{ {\begin{array}{*{20}c} {B = \frac{{\sum\limits_{i = 1}^{n} {(Y_{i} - \bar{Y})(x_{i} - \bar{x})} }}{{\sum\limits_{i = 1}^{n} {(x_{i} - \bar{x})^{2} } }}} \\ {A = \bar{Y} - B\bar{x}} \\ \end{array} } \right. $$

(5)

Among the equations, $Y_{i} = { \ln }\,y_{i}^{(2)}$, $\bar{Y} = \frac{1}{n}\sum\limits_{i = 1}^{n} {Y_{i} }$, $\bar{x} = \frac{1}{n}\sum\limits_{i = 1}^{n} {x_{i} } .$

Take the data in Table 2 into type (5), we estimate $B = - 0.0011856$, $A = 5.77172$, then, $a = e^{A} = 321.089532$, $b = - B = 0.0011856$, And we get the regression equation of the cutting length $y^{(2)}$ and the cutting speed x.

$$ y^{(1)} = 321.089532\;e^{ - 0.0011856x} $$

(6)

4.3 The Regression Equation of the Throwing Distance and the Cutting Speed

In the beginning, by the data in Table 2 can be seen that with the increase in cutting speed. The distance of Stem began to increase, but when the cutting speed increased to 2100 RPM, toss distance began to decline. This reason is, with the increase of cutting speed, the stem get shorter and the quality lighter, so the throwing distance get smaller, Suppose that the original regression equation of toss distance with cutting speed is a quadratic function.

$$ y^{(2)} = \beta_{0} + \beta_{1} x + \beta_{2} x^{2} $$

(7)

Multiple linear regression analysis method can be used to estimate for the parameter estimates in type (7). Only need to make the type (7) $x_{1} = x$ $x_{2} = x{}^{2}$, at this moment, the type (7) is converted into a binary linear regression equation.

$$ y^{(2)} = \beta_{0} + \beta_{1} x_{1} + \beta_{2} \mathop x\nolimits_{2} $$

(8)

We estimated the $\beta_{0} = { - }41.0215$, $\beta_{1} = 0.048595$, $\beta_{2} = - 0.00001175$ by the parameters analysis of multivariate linear regression, and then the regression equation of the distance and the cutting speed of the stem is obtained.

$$ y^{(2)} = - 41.0215 + 0.048595x - 0.00001175x^{2} $$

(9)

4.4 The Regression Equation of Cutting Speed with Power Consumption

By the data in Table 2 can be seen, with the increase of cutting speed power, the power consumption is increasing, we can also find that power consumption has the obvious linear relationship with cutting speed [11], thus we have the regression equation of power consumption and the cutting speed of cutter

$$ y^{(3)} = \beta_{0} + \beta_{1} x $$

(10)

Estimate the parameters in the type (10) and evaluate the data in Table 2 into the formula (5), we have,

$$ y^{(3)} = - 8.297 + 0.00968x $$

(11)

4.5 The Precision Analysis of Each Regression Equation

The estimated values about the $\hat{y}_{i}^{(k)} (i = 1,2,3,4;k = 1,2,3)$ of the type (6), (9) and (11) are listed in Table 3. The estimated values of the regression equation are compared to the actual value

Table 3. Comparison of predicted and actual values

From the estimates in Table 3, the accuracy of each regression equation is higher, and the correlation index of each regression equation is calculated.

The correlation index is defined as

$$ R^{2} = 1 - \frac{{\sum\limits_{i = 1}^{n} {(y_{i} - \hat{y}_{i} )^{2} } }}{{\sum\limits_{i = 1}^{n} {(y_{i} - \bar{y})^{2} } }} $$

(12)

The value is more close to 1, the better the regression equation is, the value is more close to 0, the worse the regression equation is.

We conclude indexes of correlation in respectively regression equation are $R_{1}^{2} = 0.940\,R_{2}^{2} = 0.983\,R_{3}^{2} = 0.963$, thus the three regression equations are fitting well [12].

5 The Choice of the Chopping Knife Work Parameter

In the last section, we set up the regression equation of the cutting speed and the cutting length, toss distance and power consumption of the stem [13–14]. We are able to use the regression equation to forecast and control.

5.1 The Selection of the Cutting Length of the Stem

Regression Eq. (6) can be used to predict cutting length of stem,

For example, take knife speed = 1700, we get $y^{(1)} (1700) = 42.79(mm)$.

Take = 2050, we get $y^{(1)} (2050) = 28.25(mm)$.

Take = 2200, we get $y^{(1)} (2200) = 23.65$.

Using the regression Eq. (6). We only need to control the cutting speed if we control the cutting speed [15].

For example, if you want to control the value of cut stem length is $y^{(1)} = 30(mm)$, by making $y^{(1)} = 30$ in Eq. (6) and we can work out the result is 1900 r,

Take a cutting stem length as $y^{(1)} = 35(mm)$, we can work out the result is x = 1870.

5.2 The Choice of the Throwing Distance of the Stalks

The application regression Eq. (9) can be applied to predict the toss distance of the stem with the definite value [16].

For example, if you take the value of cutting speed is 1970, then we can predict the toss distance of the stem by type (9) is $y^{(2)} (1970) = 9.11(m)$, if you take the value is 2200, then we have the value of the distance is $y^{(2)} (2200) = 9(m)$.

5.3 Forecast Power Consumption

The regression Eq. (11) can be used to predict the power consumption when the cutting speed is determined.

For example, take the value of cutting speed is 1700, we get $y^{(3)} (1700) = 8.16$.

Take the value of cutting speed is 2200, we get $y^{(3)} (2200) = 13.$