Abstract
In this review paper I present two geometric constructions of distinguished nature, one is over the field of complex numbers \({\mathbb {C}}\) and the other one is over the two elements field \(\mathbb {F}_2\). Both constructions have been employed in the past 15 years to describe two quantum paradoxes or two resources of quantum information: entanglement of pure multipartite systems on one side and contextuality on the other. Both geometric constructions are linked to representation of semi-simple Lie groups/algebras. To emphasize this aspect one explains on one hand how well-known results in representation theory allows one to see all the classification of entanglement classes of various tripartite quantum systems (three qubits, three fermions, three bosonic qubits…) in a unified picture. On the other hand, one also shows how some weight diagrams of simple Lie groups are encapsulated in the geometry which deals with the commutation relations of the generalized N-Pauli group.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
- 2.
In quantum physics, the outcomes of a measurement are encoded in an hermitian operator, called an observable. The eigenvalues of the observable correspond to the possible outcomes of the measurement and the eigenvectors correspond to the possible projections of the state after measurement.
- 3.
Physically one may imagine that each part of the system is in a different location and experimentalists only apply local quantum transformations, i.e. some unitaries defined by local Hamiltonians.
- 4.
In this paper an algebraic variety will always be the zero locus of a collection of homogeneous polynomials.
- 5.
In the four-qubit case, the ring of SLOCC invariant polynomials is generated by four polynomials denoted by H, L, M and D in [57]. One way of defining the quotient map is to consider \(\Phi :\mathcal {H}\to {\mathbb {C}}^4\) defined by \(\Phi (\hat {x})=(H(\hat {x}),L(\hat {x}),N(\hat {x}),D(\hat {x}))\), see [37].
- 6.
The discriminant of the miniversal deformation of a singularity parametrizes all singular deformations of the singularity [3].
- 7.
The spin group Spin(2N) corresponds to the simply connected double cover of SO(2N) [27].
- 8.
A point-line incidence structure is called a generalized quadrangle of type (s, t), and denoted by GQ(s, t) iff it is an incidence structure such that every point is on t + 1 lines and every line contains s + 1 points such that if p∉L, ∃!q ∈ L such that p and q are collinear.
- 9.
Up to a transformation of coordinates, this is a set of points \(x\in \mathbb {P}^{2N-1}_2\) satisfying the standard equation x 1 x 2 + x 3 x 4 + ⋯ + x 2N−1 x 2N = 0.
- 10.
Up to a transformation of coordinates this is defined as points \(x\in \mathbb {P}^{2N-1}_2\) such that f(x 1, x 1) + x 2 x 3 + …x 2N−1 x 2N = 0.
References
E. Amselem, M. Rådmark, M. Bourennane, A. Cabello, State-independent quantum contextuality with single photons. Phys. Rev. Lett. 103(16), 160405 (2009)
A. Arkhipov, Extending and characterizing quantum magic games (2012). Preprint. arXiv:1209.3819
V.I. Arnold, Critical points of smooth functions, in Proceedings of ICM-74, vol. 1 (1974), pp. 19–40
V.I. Arnold, Singularity Theory, vol. 53 (Cambridge University Press, Cambridge, 1981)
A. Aspect, J. Dalibard, G. Roger, Experimental test of Bell’s inequalities using time-varying analyzers. Phys. Rev. Lett. 49(25), 1804 (1982)
M. Aulbach, Classification of entanglement in symmetric states. Int. J. Quantum Inf. 10(07), 1230004 (2012)
M. Aulbach, D. Markham, M. Murao, Geometric entanglement of symmetric states and the majorana representation, in TQC (2010), pp. 141–158
H. Bartosik, J. Klepp, C. Schmitzer, S. Sponar, A. Cabello, H. Rauch, Y. Hasegawa, Experimental test of quantum contextuality in neutron interferometry. Phys. Rev. Lett. 103(4), 040403 (2009)
J.S. Bell, On the problem of hidden variables in quantum mechanics. Rev. Mod. Phys. 38(3), 447 (1966)
C.H. Bennett, S. Popescu, D. Rohrlich, J.A. Smolin, A.V. Thapliyal, Exact and asymptotic measures of multipartite pure-state entanglement. Phys. Rev. A 63(1), 012307 (2000)
L. Borsten, D. Dahanayake, M.J. Duff, W. Rubens, H. Ebrahim, Freudenthal triple classification of three-qubit entanglement. Phys. Rev. A 80(3), 032326 (2009)
L. Borsten, D. Dahanayake, M.J. Duff, A. Marrani, W. Rubens, Four-qubit entanglement classification from string theory. Phys. Rev. Lett. 105(10), 100507 (2010)
L. Borsten, M.J. Duff, P. Lévay, The black-hole/qubit correspondence: an up-to-date review. Classical Quantum Gravity 29(22), 224008 (2012)
E. Briand, J.G. Luque, J.Y. Thibon, A complete set of covariants of the four qubit system. J. Phys. A Math. Gen. 36(38), 9915 (2003)
E. Briand, J.G. Luque, J.Y. Thibon, F. Verstraete, The moduli space of three-qutrit states. J. Math. Phys. 45(12), 4855–4867 (2004)
D.C. Brody, A.C.T. Gustavsson, L.P. Hughston, Entanglement of three-qubit geometry. J. Phys. Conf. Ser. 67, 012044 (2007)
J.L. Brylinski, Algebraic measures of entanglement, in Mathematics of Quantum Computation (Chapman and Hall/CRC, Boca Raton, 2002), pp. 3–23
A. Cabello, Experimentally testable state-independent quantum contextuality. Phys. Rev. Lett. 101(21), 210401 (2008)
A. Cabello, J. Estebaranz, G. García-Alcaine, Bell-Kochen-Specker theorem: a proof with 18 vectors. Phys. Lett. A 212(4), 183–187 (1996)
L. Chen, D.Ž. Djoković, M. Grassl, B. Zeng, Four-qubit pure states as fermionic states. Phys. Rev. A 88(5), 052309 (2013)
C. Chryssomalakos, E. Guzmán-González, E. Serrano-Ensástiga, Geometry of spin coherent states. J. Phys. A Math. Theor. 51(16), 165202 (2018)
O. Chterental, D.Ž. Djoković, Normal forms and tensor ranks of pure states of four qubits (2006). arXiv preprint quant-ph/0612184
R. Cleve, R. Mittal, Characterization of binary constraint system games. in International Colloquium on Automata, Languages, and Programming (Springer, Berlin, Heidelberg, 2014), pp. 320–331
M.J. Duff, S. Ferrara, E 7 and the tripartite entanglement of seven qubits. Phys. Rev. D 76(2), 025018 (2007)
W. Dür, G. Vidal, J.I. Cirac, Three qubits can be entangled in two inequivalent ways. Phys. Rev. A 62(6), 062314 (2000)
A. Einstein, B. Podolsky, N. Rosen, Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 47(10), 777 (1935)
W. Fulton, J. Harris, Representation Theory, vol. 129 (Springer Science & Business Media, Berlin, 1991)
I.M. Gelfand, M. Kapranov, A. Zelevinsky, Discriminants, Resultants, and Multidimensional Determinants (Springer Science and Business Media, Berlin, 2008)
J. Harris, Algebraic Geometry: A First Course, vol. 133 (Springer Science & Business Media, Berlin, 2013)
H. Havlicek, B. Odehnal, M. Saniga, Factor-group-generated polar spaces and (multi-) qudits. Symmetry Integr. Geom. Methods Appl. 5, 096 (2009)
H. Heydari, Geometrical structure of entangled states and the secant variety. Quantum Inf. Process. 7(1), 43–50 (2008)
F. Holweck, H. Jaffali, Three-qutrit entanglement and simple singularities. J. Phys. A Math. Theor. 49(46), 465301 (2016)
F. Holweck, P. Lévay, Classification of multipartite systems featuring only
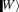 and
and  genuine entangled states. J. Phys. A Math. Theor. 49, 085201 (2016)
genuine entangled states. J. Phys. A Math. Theor. 49, 085201 (2016)F. Holweck, M. Saniga, Contextuality with a small number of observables. Int. J. Quantum Inf. 15(04), 1750026 (2017)
F. Holweck, J.G. Luque, J.Y. Thibon, Geometric descriptions of entangled states by auxiliary varieties. J. Math. Phys. 53(10), 102203 (2012)
F. Holweck, J.G. Luque, J.Y. Thibon, Entanglement of four qubit systems: a geometric atlas with polynomial compass I (the finite world). J. Math. Phys. 55(1), 012202 (2014)
F. Holweck, J.G. Luque, M. Planat, Singularity of type D4 arising from four-qubit systems. J. Phys. A Math. Theor. 47(13), 135301 (2014)
F. Holweck, M. Saniga, P. Lévay, A notable relation between N-qubit and 2N−1-qubit Pauli groups via binar LGr(N, 2N). Symmetry Integr. Geom. Methods Appl. 10, 041 (2014)
F. Holweck, H. Jaffali, I. Nounouh, Grover’s algorithm and the secant varieties. Quantum Inf. Process. 15(11), 4391–4413 (2016)
F. Holweck, J.G. Luque, J.Y. Thibon, Entanglement of four-qubit systems: a geometric atlas with polynomial compass II (the tame world). J. Math. Phys. 58(2), 022201 (2017)
M. Howard, J. Wallman, V. Veitch, J. Emerson, Contextuality supplies the “magic” for quantum computation. Nature 510(7505), 351–355 (2014)
V.G. Kac, V.L. Popov, E.B. Vinberg, Sur les groupes lineaires algebriques dont l’algebres des invariants est libres. CR Acad. Sci. Paris 283, 875–878 (1976)
G. Kirchmair, F. Zähringer, R. Gerritsma, M. Kleinmann, O. Gühne, A. Cabello, R. Blatt, C.F. Roos, State-independent experimental test of quantum contextuality. Nature 460(7254), 494–497 (2009)
S. Kochen, E.P. Specker, The problem of hidden variables in quantum mechanics, in The Logico-Algebraic Approach to Quantum Mechanics (Springer, Dordrecht, 1975), pp. 293–328
J.M. Landsberg, Tensors: Geometry and Applications (American Mathematical Society, Providence, 2012)
J.M. Landsberg, L. Manivel, The projective geometry of Freudenthal’s magic square. J. Algebra 239(2), 477–512 (2001)
J.M. Landsberg, L. Manivel, On the ideals of secant varieties of Segre varieties. Found. Comput. Math. 4(4), 397–422 (2004)
J.M. Landsberg, G. Ottaviani, Equations for secant varieties of Veronese and other varieties. Ann. Mat. Pura Appl. 192(4), 569–606 (2013)
C. Le Paige, Sur la théorie des formes binaires à plusieurs séries de variables. Bull. Acad. Roy. Sci. Belgique 2(3), 40–53 (1881)
P. Lévay, Strings, black holes, the tripartite entanglement of seven qubits, and the Fano plane. Phys. Rev. D 75(2), 024024 (2007)
P. Lévay, F. Holweck, Embedding qubits into fermionic Fock space: peculiarities of the four-qubit case. Phys. Rev. D 91(12), 125029 (2015)
P. Lévay, Z. Szabó, Mermin pentagrams arising from Veldkamp lines for three qubits. J. Phys. A Math. Theor. 50(9), 095201 (2017)
P. Lévay, P. Vrana, Three fermions with six single-particle states can be entangled in two inequivalent ways. Phys. Rev. A 78(2), 022329 (2008)
P. Lévay, M. Saniga, P. Vrana, P. Pracna, Black hole entropy and finite geometry. Phys. Rev. D 79(8), 084036 (2009)
P. Lévay, M. Planat, M. Saniga, Grassmannian connection between three-and four-qubit observables, Mermin’s contextuality and black holes. J. High Energy Phys. 2013(9), 37 (2013)
P. Lévay, F. Holweck, M. Saniga, Magic three-qubit Veldkamp line: a finite geometric underpinning for form theories of gravity and black hole entropy. Phys. Rev. D 96, 026018 (2017)
J.G. Luque, J.Y. Thibon, Polynomial invariants of four qubits. Phys. Rev. A 67(4), 042303 (2003)
J.G. Luque, J.Y. Thibon, Algebraic invariants of five qubits. J. Phys. A Math. Gen. 39(2), 371 (2005)
N.D. Mermin, Hidden variables and the two theorems of John Bell. Rev. Mod. Phys. 65(3), 803 (1993)
A. Miyake, Classification of multipartite entangled states by multidimensional determinants. Phys. Rev. A 67(1), 012108 (2003)
A. Miyake, F. Verstraete, Multipartite entanglement in 2×2×n quantum systems. Phys. Rev. A 69(1), 012101 (2004)
A. Miyake, M. Wadati, Multipartite entanglement and hyperdeterminants. Quantum Inf. Comput. 2(7), 540–555 (2002)
A.G. Nurmiev, Orbits and invariants of third-order matrices. Mat. Sb. 191(5), 101–108 (2000)
L. Oeding, Set-theoretic defining equations of the tangential variety of the Segre variety. J. Pure Appl. Algebra 215(6), 1516–1527 (2011)
P.G. Parfenov, Tensor products with finitely many orbits. Russ. Math. Surv. 53(3), 635–636 (1998)
M. Planat, M. Saniga, Five-qubit contextuality, noise-like distribution of distances between maximal bases and finite geometry. Phys. Lett. A 376(46), 3485–3490 (2012)
M. Planat, M. Saniga, F. Holweck, Distinguished three-qubit ‘magicity’ via automorphisms of the split Cayley hexagon. Quantum Inf. Process. 12(7), 2535–2549 (2013)
A. Peres, Two simple proofs of the Kochen-Specker theorem. J. Phys. A Math. Gen. 24(4), L175 (1991)
M. Saniga, M. Planat, Multiple Qubits as Symplectic Polar Spaces of Order Two. Advanced Studies in Theoretical Physics, vol. 1 (2007), pp. 1–4
M. Saniga, M. Planat, Finite geometry behind the Harvey-Chryssanthacopoulos four-qubit magic rectangle. Quantum Inf. Comput. 12(11–12), 1011–1016 (2012)
M. Saniga, M. Planat, P. Pracna, H. Havlicek, The Veldkamp space of two-qubits. Symmetry Integr. Geom. Methods Appl. 3, 075 (2007)
M. Saniga, H. Havlicek, F. Holweck, M. Planat, P. Pracna, Veldkamp-space aspects of a sequence of nested binary Segre varieties. Ann. Inst. Henri Poincaré D 2(3), 309–333 (2015)
M. Sanz, D. Braak, E. Solano, I.L. Egusquiza, Entanglement classification with algebraic geometry. J. Phys. A Math. Theor. 50(19), 195303 (2017)
G. Sárosi, P. Lévay, Entanglement in fermionic Fock space. J. Phys. A Math. Theor. 47(11), 115304 (2014)
A. Sawicki, V.V. Tsanov, A link between quantum entanglement, secant varieties and sphericity. J. Phys. A Math. Theor. 46(26), 265301 (2013)
A. Terracini, Sulle v k per cui la varieta degli s h(h + 1) seganti ha dimensione minore dell’ordinario. Rendiconti del Circolo Matematico di Palermo (1884–1940), 31(1), 392–396 (1911)
K. Thas, The geometry of generalized Pauli operators of N-qudit Hilbert space, and an application to MUBs. Europhys. Lett. 86(6), 60005 (2009)
F. Verstraete, J. Dehaene, B. De Moor, H. Verschelde, Four qubits can be entangled in nine different ways. Phys. Rev. A 65(5), 052112 (2002)
P. Vrana, P. Lévay, Special entangled quantum systems and the Freudenthal construction. J. Phys. A Math. Theor. 42(28), 285303 (2009)
P. Vrana, P. Lévay, The Veldkamp space of multiple qubits. J. Phys. A Math. Theor. 43(12), 125303 (2010)
M. Waegell, P.K. Aravind, Proofs of the Kochen-Specker theorem based on a system of three qubits. J. Phys. A Math. Theor. 45(40), 405301 (2012)
M. Waegell, P.K. Aravind, Proofs of the Kochen-Specker theorem based on the N-qubit Pauli group. Phys. Rev. A 88(1), 012102 (2013)
J. Weyman, A. Zelevinsky, Singularities of hyperdeterminants. Ann. Inst. Four. 46(3), 591–644 (1996)
F.L. Zak, Tangents and Secants of Algebraic Varieties. Translations of Mathematical Monographs, vol. 127 (American Mathematical Society, Providence, 1993)
Acknowledgements
The first part of this review paper was presented at the international workshop “Quantum Physics and Geometry” organized at Levico Terme in July 2017. I would like to thank the organizers for inviting me to present an overview on my research and to contribute to this UMI Lecture Notes. The research presented in this review has been done collectively; I would like to warmly thank my co-authors Jean-Gabriel Luque, Jean-Yves Thibon, Michel Planat, Metod Saniga, Péter Lévay and Hamza Jaffali for our rich collaboration over the past 6 years. This work was partially supported by the French “Investissements d’Avenir” program, project ISITE-BFC (contract ANR-15-IDEX-03).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Holweck, F. (2019). Geometric Constructions over \({\mathbb {C}}\) and \({\mathbb {F}}_2\) for Quantum Information. In: Ballico, E., Bernardi, A., Carusotto, I., Mazzucchi, S., Moretti, V. (eds) Quantum Physics and Geometry. Lecture Notes of the Unione Matematica Italiana, vol 25. Springer, Cham. https://doi.org/10.1007/978-3-030-06122-7_5
Download citation
DOI: https://doi.org/10.1007/978-3-030-06122-7_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-06121-0
Online ISBN: 978-3-030-06122-7
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


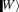 and
and  genuine entangled states. J. Phys. A Math. Theor. 49, 085201 (2016)
genuine entangled states. J. Phys. A Math. Theor. 49, 085201 (2016)