Preliminaries

Abstract

In this chapter we fix some conventions and recall the main definitions. The chapter may be used as a quick reference when reading the book. To learn background in metric geometry, the reader may consult the book of Dmitri Burago, Yuri Burago, and Sergei Ivanov [20].

In this chapter we fix some conventions and recall the main definitions. The chapter may be used as a quick reference when reading the book.

To learn background in metric geometry, the reader may consult the book of Dmitri Burago, Yuri Burago, and Sergei Ivanov [20].

1.1 Metric spaces

The distance between two points x and y in a metric space $\mathcal {X}$ will be denoted by $\vert x-y\vert _{}$ or $\vert x-y\vert _{\mathcal {X}}$. The latter notation is used if we need to emphasize that the distance is taken in the space ${\mathcal {X}}$.

The function

$$ \mathrm{{dist}}_{x}:y\mapsto \vert x-y\vert _{} $$

is called the distance function from x.

• The diameter of a metric space $\mathcal {X}$ is defined as

  $$ \mathop {\mathrm{diam}}\nolimits \mathcal {X}=\sup \left\{ \,{\vert x-y\vert _{\mathcal {X}}}\ {:}\ {x, y\in \mathcal {X}}\,\right\} . $$

• Given $R\in [0,\infty ]$ and $x\in \mathcal {X}$, the sets

  $$\begin{aligned} \mathrm {B}{}(x,R)&=\{y\in \mathcal {X}\mid \vert x-y\vert _{}<R\},\\ \overline{\mathrm {B}}{}[x, R]&=\{y\in \mathcal {X}\mid \vert x-y\vert _{}\leqslant R\} \end{aligned}$$

  are called, respectively, the open and the closed balls of radius R with center x. Again, if we need to emphasize that these balls are taken in the metric space $\mathcal {X}$, we write

  $$ \mathrm {B}{}(x,R)_{\mathcal {X}}\quad \text {and}\quad \overline{\mathrm {B}}{}[x, R]_{\mathcal {X}}. $$

A metric space $\mathcal {X}$ is called proper if all closed bounded sets in $\mathcal {X}$ are compact. This condition is equivalent to each of the following statements:

• 1. For some (and therefore any) point $p\in \mathcal {X}$ and any $R<\infty$, the closed ball $\overline{\mathrm {B}}{}[p, R]\subset \mathcal {X}$ is compact.

• 2. The function $\mathrm{{dist}}_{p}:\mathcal {X}\rightarrow \mathbb {R}$ is proper for some (and therefore any) point $p\in \mathcal {X}$; that is, for any compact set $K\subset \mathbb {R}$, its inverse image $\left\{ \,{x\in \mathcal {X}}\ {:}\ {\vert p-x\vert _{\mathcal {X}}\in K}\,\right\}$ is compact.

1.1.1.

Exercise. Let K be a compact metric space and

$$ f:K\rightarrow K $$

be a distance nondecreasing map. Prove that f is an isometry.

1.2 Constructions

Product space. Given two metric spaces $\mathcal {U}$ and $\mathcal {V}$, the product space $\mathcal {U}\times \mathcal {V}$ is defined as the set of all pairs (u, v) where $u\in \mathcal {U}$ and $v\in \mathcal {V}$ with the metric defined by formula

$$ \vert (u^1,v^1)-(u^2,v^2)\vert _{\mathcal {U}\times \mathcal {V}}= \sqrt{\vert u^1-u^2\vert _{\mathcal {U}}^2+\vert v^1-v^2\vert _{\mathcal {V}}^2}. $$

Cone. The cone $\mathcal {V}=\mathop {\mathrm{Cone}}\nolimits \mathcal {U}$ over a metric space $\mathcal {U}$ is defined as the metric space whose underlying set consists of equivalence classes in $[0,\infty )\times \mathcal {U}$ with the equivalence relation “$\sim$” given by $(0,p)\sim (0,q)$ for any points $p, q\in \mathcal {U}$, and whose metric is given by the cosine rule

$$ \vert (p,s)-(q, t)\vert _{\mathcal {V}} = \sqrt{s^2+t^2-2\cdot s\cdot t\cdot \cos \alpha }, $$

where $\alpha = \min \{\pi , \vert p-q\vert _{\mathcal {U}}\}$.

The point in the cone $\mathcal {V}$ formed by the equivalence class of $0\times \mathcal {U}$ is called the tip of the cone and is denoted by 0 or $0_{\mathcal {V}}$. The distance $\vert 0-v\vert _{\mathcal {V}}$ is called the norm of v and is denoted by |v| or $|v|_{\mathcal {V}}$.

Suspension. Thesuspension $\mathcal {V}=\mathop {\mathrm{Susp}}\nolimits \mathcal {U}$ over a metric space $\mathcal {U}$ is defined as the metric space whose underlying set consists of equivalence classes in $[0,\pi ]\times \mathcal {U}$ with the equivalence relation “$\sim$” given by $(0,p)\sim (0,q)$ and $(\pi ,p)\sim (\pi , q)$ for any points $p, q\in \mathcal {U}$, and whose metric is given by the spherical cosine rule

$$ \cos \vert (p,s)-(q, t)\vert _{\mathop {\mathrm{Susp}}\nolimits \mathcal {U}} = \cos s\cdot \cos t-\sin s\cdot \sin t\cdot \cos \alpha , $$

where $\alpha = \min \{\pi , \vert p-q\vert _{\mathcal {U}}\}$.

The points in $\mathcal {V}$ formed by the equivalence classes of $0\times \mathcal {U}$ and $\pi \times \mathcal {U}$ are called the north and the south poles of the suspension.

1.2.1.

Exercise. Let $\mathcal {U}$ be a metric space. Show that the spaces

$$ \mathbb {R}\times \mathop {\mathrm{Cone}}\nolimits \mathcal {U}\quad \text {and}\quad \mathop {\mathrm{Cone}}\nolimits [\mathop {\mathrm{Susp}}\nolimits \mathcal {U}] $$

are isometric.

1.3 Geodesics, triangles, and hinges

Geodesic. Let $\mathcal {X}$ be a metric space and $\mathbb {I}$ be a real interval. A globally isometric map $\upgamma :\mathbb {I}\rightarrow \mathcal {X}$ is called a geodesic¹; in other words, $\upgamma :\mathbb {I}\rightarrow \mathcal {X}$ is a geodesic if

$$ \vert \upgamma (s)-\upgamma (t)\vert _{\mathcal {X}}=|s-t| $$

for any pair $s, t\in \mathbb {I}$.

We say that $\upgamma :\mathbb {I}\rightarrow \mathcal {X}$ is a geodesic from point p to point q if $\mathbb {I}=[a, b]$ and $p=\upgamma (a)$, $q=\upgamma (b)$. In this case the image of $\upgamma$ is denoted by [pq] and with an abuse of notations we also call it a geodesic. Given a geodesic [pq], we can parametrize it by distance to p; this parametrization will be denoted by $\mathrm {geod}_{[p q]}(t)$.

We may write $[p q]_{\mathcal {X}}$ to emphasize that the geodesic [pq] is in the space ${\mathcal {X}}$. We also use the following shortcut notation:

$$\begin{aligned} \left] p q \right[&=[pq]\backslash \{p, q\},&\left] p q \right]&=[pq]\backslash \{p\},&\left[ p q \right[&=[pq]\backslash \{q\}. \end{aligned}$$

In general, a geodesic between p and q need not exist and if it exists, it need not be unique. However, once we write [pq] we mean that we have made a choice of geodesic.

A metric space is called geodesic if any pair of its points can be joined by a geodesic.

A geodesic path is a geodesic with constant-speed parametrization by [0, 1]. Given a geodesic [pq], we denote by $\mathrm {path}_{[pq]}$ the corresponding geodesic path; that is,

A curve $\upgamma :\mathbb {I}\rightarrow \mathcal {X}$ is called a local geodesic if for any $t\in \mathbb {I}$, there is a neighborhood U of t in $\mathbb {I}$ such that the restriction $\upgamma |_U$ is a geodesic. A constant-speed parametrization of a local geodesic by the unit interval [0, 1] is called a local geodesic path.

Triangle. For a triple of points $p,q, r\in \mathcal {X}$, a choice of a triple of geodesics ([qr], [rp], [pq]) will be called a triangle; we will use the short notation $[p q r]=([q r], [r p], [p q])$ .

Again, given a triple $p,q, r\in \mathcal {X}$ there may be no triangle [pqr] simply because one of the pairs of these points cannot be joined by a geodesic. Also, many different triangles with these vertices may exist, any of which can be denoted by [pqr]. However, if we write [pqr], it means that we have made a choice of such a triangle; that is, we have fixed a choice of the geodesics [qr], [rp], and [pq].

The value

$$ \vert p-q\vert _{}+\vert q-r\vert _{}+\vert r-p\vert _{} $$

will be called the perimeter of the triangle [pqr].

Hinge. Let $p,x, y\in \mathcal {X}$ be a triple of points such that p is distinct from x and y. A pair of geodesics ([px], [py]) will be called a hinge and will be denoted by $[p\,{}^{x}_{y}]=([p x],[p y])$ .

Convex set. A set A in a metric space $\mathcal {X}$ is called convex if for every two points $p, q\in A$, every geodesic [pq] in $\mathcal {X}$ lies in A.

A set $A\subset \mathcal {X}$ is called locally convex if every point $a\in A$ admits an open neighborhood $\Omega \ni a$ in $\mathcal {X}$ such that any geodesic lying in $\Omega$ and with ends in A lies completely in A.

Note that any open set is locally convex by definition.

1.4 Length spaces

A curve is defined as a continuous map from a real interval to a space. If the real interval is [0, 1], then the curve is called a path.

1.4.1.

Definition. Let $\mathcal {X}$ be a metric space and $\alpha : \mathbb {I}\rightarrow \mathcal {X}$ be a curve. We define the length of $\alpha$ as

Directly from the definition, it follows that if a path $\alpha :[0,1]\rightarrow \mathcal {X}$ connects two points x and y (that is, if $\alpha (0)=x$ and $\alpha (1)=y$), then

$$ \mathop {\mathrm{length}}\nolimits \alpha \geqslant \vert x-y\vert _{}. $$

Let A be a subset of a metric space $\mathcal {X}$. Given two points $x, y\in A$, consider the value

$$ \vert x-y\vert _{A}=\inf _{\alpha }\{\mathop {\mathrm{length}}\nolimits \alpha \}, $$

where the infimum is taken for all paths $\alpha$ from x to y in A.²

If $\vert x-y\vert _{A}$ takes finite value for each pair $x, y\in A$, then $\vert x-y\vert _{A}$ defines a metric on A; this metric will be called the induced length metric on A.

If for any $\upvarepsilon >0$ and any pair of points x and y in a metric space $\mathcal {X}$, there is a path $\alpha$ connecting x to y such that

$$ \mathop {\mathrm{length}}\nolimits \alpha < \vert x-y\vert _{}+\upvarepsilon , $$

then $\mathcal {X}$ is called a length space and the metric on $\mathcal {X}$ is called a length metric.

If $f:\tilde{\mathcal {X}}\rightarrow \mathcal {X}$ is a covering, then a length metric on $\mathcal {X}$ can be lifted to $\tilde{\mathcal {X}}$ by declaring

$$ \mathop {\mathrm{length}}\nolimits _{\tilde{\mathcal {X}}}\upgamma =\mathop {\mathrm{length}}\nolimits _{\mathcal {X}}(f\circ \upgamma ) $$

for any curve $\upgamma$ in $\tilde{\mathcal {X}}$. The space $\tilde{\mathcal {X}}$ with this metric is called the metric cover of $\mathcal {X}$.

Note that any geodesic space is a length space. As can be seen from the following example, the converse does not hold.

1.4.2.

Example. Let $\mathcal {X}$ be obtained by gluing a countable collection of disjoint intervals $\{\mathbb {I}_n\}$ of length $1+\tfrac{1}{n}$, where for each $\mathbb {I}_n$ the left end is glued to p and the right end to q. Then $\mathcal {X}$ carries a natural complete length metric with respect to which $\vert p-q\vert _{}=1$, but there is no geodesic connecting p to q.

1.4.3.

Exercise. Give an example of a complete length space for which no pair of distinct points can be joined by a geodesic.

Let $\mathcal {X}$ be a metric space and $x, y\in \mathcal {X}$.

• (i) A point $z\in \mathcal {X}$ is called amidpoint between x and y if

  $$ \vert x-z\vert _{}=\vert y-z\vert _{}=\tfrac{1}{2}\cdot \vert x-y\vert _{}. $$

• (ii) Assume $\upvarepsilon \geqslant 0$. A point $z\in \mathcal {X}$ is called an $\upvarepsilon$-midpoint between x and y if

  $$ \vert x-z\vert _{},\quad \vert y-z\vert _{}\leqslant \tfrac{1}{2}\cdot \vert x-y\vert _{}+\upvarepsilon . $$

Note that a 0-midpoint is the same as a midpoint.

1.4.4.

Lemma. Let $\mathcal {X}$ be a complete metric space.

• (a) Assume that for any pair of points $x, y\in \mathcal {X}$ and any $\upvarepsilon >0$ there is an $\upvarepsilon$-midpoint z. Then $\mathcal {X}$ is a length space.

• (b) Assume that for any pair of points $x, y\in \mathcal {X}$, there is a midpoint z. Then $\mathcal {X}$ is a geodesic space.

Proof.

We first prove (a). Let $x, y\in \mathcal {X}$ be a pair of points.

Set $\upvarepsilon _n=\frac{\upvarepsilon }{4^n}$, $\alpha (0)=x$ and $\alpha (1)=y$.

Let $\alpha (\tfrac{1}{2})$ be an $\upvarepsilon _1$-midpoint between $\alpha (0)$ and $\alpha (1)$. Further, let $\alpha (\frac{1}{4})$ and $\alpha (\frac{3}{4})$ be $\upvarepsilon _2$-midpoints between the pairs $(\alpha (0),\alpha (\tfrac{1}{2}))$ and $(\alpha (\tfrac{1}{2}),\alpha (1))$, respectively. Applying the above procedure recursively, on the n-th step we define $\alpha (\tfrac{k}{2^n})$, for every odd integer $k$ such that $0<\tfrac{k}{2^n}<1$, as an $\upvarepsilon _{n}$-midpoint between the already defined $\alpha (\tfrac{k-1}{2^n})$ and $\alpha (\tfrac{k+1}{2^n})$.

In this way we define $\alpha (t)$ for $t\in W$, where W denotes the set of dyadic rationals in [0, 1]. Since $\mathcal {X}$ is complete, the map $\alpha$ can be extended continuously to [0, 1]. Moreover,

Since $\upvarepsilon >0$ is arbitrary, we get (a).

To prove (b), one should repeat the same argument taking midpoints instead of $\upvarepsilon _n$-midpoints. In this case ➊ holds for $\upvarepsilon _n=\upvarepsilon =0$.$\square$

Since in a compact space a sequence of $\tfrac{1}{n}$-midpoints $z_n$ contains a convergent subsequence, Lemma 1.4.4 immediately implies

1.4.5.

Proposition. A proper length space is geodesic.

1.4.6.

Hopf–Rinow theorem. Any complete, locally compact length space is proper.

Proof.

Let $\mathcal {X}$ be a locally compact length space. Given $x\in \mathcal {X}$, denote by $\uprho (x)$ the supremum of all $R>0$ such that the closed ball $\overline{\mathrm {B}}{}[x, R]$ is compact. Since $\mathcal {X}$ is locally compact,

It is sufficient to show that $\uprho (x)=\infty$ for some (and therefore any) point $x\in \mathcal {X}$.

Assume the contrary; that is, $\uprho (x)<\infty$. We claim that

➌ $B=\overline{\mathrm {B}}{}[x,\uprho (x)]$ is compact for any x.

Indeed, $\mathcal {X}$ is a length space; therefore for any $\upvarepsilon >0$, the set $\overline{\mathrm {B}}{}[x,\uprho (x)-\upvarepsilon ]$ is a compact $\upvarepsilon$-net in B. Since B is closed and hence complete, it must be compact. $\triangle$

Next we claim that

➍ $|\uprho (x)-\uprho (y)|\leqslant \vert x-y\vert _{\mathcal {X}}$ for any $x, y \in \mathcal {X}$; in particular $\uprho :\mathcal {X}\rightarrow \mathbb {R}$ is a continuous function.

Indeed, assume the contrary; that is, $\uprho (x)+|x-y|<\uprho (y)$ for some $x, y\in \mathcal {X}$. Then $\overline{\mathrm {B}}{}[x,\uprho (x)+\upvarepsilon ]$ is a closed subset of $\overline{\mathrm {B}}{}[y,\uprho (y)]$ for some $\upvarepsilon >0$. Then compactness of $\overline{\mathrm {B}}{}[y,\uprho (y)]$ implies compactness of $\overline{\mathrm {B}}{}[x,\uprho (x)+\upvarepsilon ]$, a contradiction.$\triangle$

Set $\upvarepsilon =\min \left\{ \,{\uprho (y)}\ {:}\ {y\in B}\,\right\}$; the minimum is defined since B is compact. From ➋, we have $\upvarepsilon >0$.

Choose a finite $\tfrac{\upvarepsilon }{10}$-net $\{a_1,a_2,\ldots , a_n\}$ in B. The union W of the closed balls $\overline{\mathrm {B}}{}[a_i,\upvarepsilon ]$ is compact. Clearly $\overline{\mathrm {B}}{}[x,\uprho (x)+\frac{\upvarepsilon }{10}]\subset W$. Therefore $\overline{\mathrm {B}}{}[x,\uprho (x)+\frac{\upvarepsilon }{10}]$ is compact, a contradiction. $\square$

1.4.7.

Exercise. Construct a geodesic space that is locally compact, but whose completion is neither geodesic nor locally compact.

1.5 Model angles and triangles

Let $\mathcal {X}$ be a metric space and $p,q, r\in \mathcal {X}$. Let us define the model triangle $[{\tilde{p}}{\tilde{q}}{\tilde{r}}]$ (briefly, $[{\tilde{p}}{\tilde{q}}{\tilde{r}}]={\tilde{\triangle }}(p q r)_{\mathbb {E}^2}$ ) to be a triangle in the plane $\mathbb {E}^2$ with the same side lengths; that is,

$$ \vert \tilde{p}-\tilde{q}\vert _{}=\vert p-q\vert _{}, \quad \vert \tilde{q}-\tilde{r}\vert _{}=\vert q-r\vert _{}, \quad \vert \tilde{r}-\tilde{p}\vert _{}=\vert r-p\vert _{}. $$

In the same way we can define thehyperbolic and the spherical model triangles ${\tilde{\triangle }}(p q r)_{\mathbb {H}^2}$, ${\tilde{\triangle }}(p q r)_{\mathbb {S}^2}$ in the hyperbolic plane $\mathbb {H}^2$ and the unit sphere $\mathbb {S}^2$. In the latter case the model triangle is said to be defined if in addition

$$ \vert p-q\vert _{}+\vert q-r\vert _{}+\vert r-p\vert _{}< 2\cdot \pi . $$

In this case the model triangle again exists and is unique up to an isometry of $\mathbb {S}^2$.

If $[{\tilde{p}}{\tilde{q}}{\tilde{r}}]={\tilde{\triangle }}(p q r)_{\mathbb {E}^2}$ and $\vert p-q\vert _{},\vert p-r\vert _{}>0$, the angle measure of $[{\tilde{p}}{\tilde{q}}{\tilde{r}}]$ at $\tilde{p}$ will be called the model angle of the triple p, q, r and will be denoted by . In the same way we define and ; in the latter case we assume in addition that the model triangle ${\tilde{\triangle }}(p q r)_{\mathbb {S}^2}$ is defined.

We may use the notation if it is evident which of the model spaces $\mathbb {H}^2$, $\mathbb {E}^2$, or $\mathbb {S}^2$ is meant.

1.5.1.

Alexandrov’s lemma. Let p, x, y, z be distinct points in a metric space such that $z\in \left]x y\right[$. Then the following expressions for the Euclidean model angles have the same sign:

• (a) ,

• (b) .

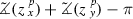Moreover,

with equality if and only if the expressions in (a) and (b) vanish.

The same holds for the hyperbolic and spherical model angles, but in the latter case one has to assume in addition that

$$ \vert p-z\vert _{}+\vert p-y\vert _{}+\vert x-y\vert _{}< 2\cdot \pi . $$

Proof.

Consider the model triangle $[{\tilde{x}}{\tilde{p}}{\tilde{z}}]={\tilde{\triangle }}(x p z)$. Take a point $\tilde{y}$ on the extension of $[\tilde{x}\tilde{z}]$ beyond $\tilde{z}$ so that $\vert \tilde{x}-\tilde{y}\vert _{}=\vert x-y\vert _{}$ (and therefore $\vert \tilde{x}-\tilde{z}\vert _{}=\vert x-z\vert _{}$).

Since increasing the opposite side in a plane triangle increases the corresponding angle, the following expressions have the same sign:

• (i) ,

• (ii) $\vert \tilde{p}-\tilde{y}\vert _{}-\vert p-y\vert _{}$,

• (iii) .

Since

and

the first statement follows.

For the second statement, construct a model triangle $[{\tilde{p}}{\tilde{z}}{\tilde{y}'}]={\tilde{\triangle }}(pzy)_{\mathbb {E}^2}$ on the opposite side of $[\tilde{p}\tilde{z}]$ from $[{\tilde{x}}{\tilde{p}}{\tilde{z}}]$. Note that

$$\begin{aligned} \vert \tilde{x}-\tilde{y}'\vert _{}&\leqslant \vert \tilde{x}-\tilde{z}\vert _{} + \vert \tilde{z}-\tilde{y}'\vert _{}=\\&=\vert x-z\vert _{}+\vert z-y\vert _{}=\\&=\vert x-y\vert _{}. \end{aligned}$$

Therefore

Equality holds if and only if $\vert \tilde{x}-\tilde{y}'\vert _{}=\vert x-y\vert _{}$, as required. $\square$

1.6 Angles and the first variation

Given a hinge $[p\,{}^{x}_{y}]$, we define its angle as the limit

where $\bar{x}\in \left]p x\right]$ and $\bar{y}\in \left]p y\right]$. (The angle $\measuredangle [p\,{}^{x}_{y}]$ is defined if the limit exists.)

The value under the limit can be calculated from the cosine law:

The following lemma implies that in ➊, one can use or instead of .

1.6.1.

Lemma. For any three points p, x, y in a metric space the following inequalities

hold whenever the left-hand side is defined.

Proof.

Note that

Therefore

The inequality ➋ follows since

$$\begin{aligned} 0&\leqslant \mathop {\mathrm{area}}\nolimits {\tilde{\triangle }}(pxy)_{\mathbb {H}^2}\leqslant \\&\leqslant \mathop {\mathrm{area}}\nolimits {\tilde{\triangle }}(pxy)_{\mathbb {S}^2}\leqslant \\&\leqslant \vert p-x\vert _{}\cdot \vert p-y\vert _{}.\\ \end{aligned}$$

$\square$

1.6.2.

Triangle inequality for angles. Let $[px^1]$, $[px^2]$, and $[px^3]$ be three geodesics in a metric space. If all the angles $\alpha ^{i j}=\measuredangle [p\,{}^{x^i}_{x^j}]$ are defined, then they satisfy the triangle inequality:

$$ \alpha ^{13}\leqslant \alpha ^{12}+\alpha ^{23}. $$

Proof.

Since $\alpha ^{13}\leqslant \pi$, we may assume that $\alpha ^{12}+\alpha ^{23}< \pi$.

Set $\upgamma ^i=\mathrm {geod}_{[px^i]}$. Given any $\upvarepsilon >0$, for all sufficiently small $t,\tau , s\in \mathbb {R}_+$ we have

$$\begin{aligned} \vert \upgamma ^1(t)-\upgamma ^3(\tau )\vert _{} \leqslant&\vert \upgamma ^1(t)-\upgamma ^2(s)\vert _{}+\vert \upgamma ^2(s)-\upgamma ^3(\tau )\vert _{}<\\ <&\sqrt{t^2+s^2-2\cdot t\cdot s\cdot \cos (\alpha ^{12}+\upvarepsilon )}\ + \\&+\sqrt{s^2+\tau ^2-2\cdot s\cdot \tau \cdot \cos (\alpha ^{23}+\upvarepsilon )}\leqslant \end{aligned}$$

Below we define $s(t,\tau )$ so that for $s=s(t,\tau )$, this chain of inequalities can be continued as follows:

$$ \leqslant \ \sqrt{t^2+\tau ^2-2\cdot t\cdot \tau \cdot \cos (\alpha ^{12}+\alpha ^{23}+2\cdot \upvarepsilon )}.\qquad \qquad \qquad \qquad \qquad \qquad \quad $$

Thus for any $\upvarepsilon >0$,

$$ \alpha ^{13}\leqslant \alpha ^{12}+\alpha ^{23}+2\cdot \upvarepsilon .\qquad \qquad \qquad \qquad \qquad \qquad \quad $$

Hence the result.

To define $s(t,\tau )$, consider three rays $\tilde{\upgamma }^1$, $\tilde{\upgamma }^2$, $\tilde{\upgamma }^3$ on a Euclidean plane starting at one point, such that $\measuredangle (\tilde{\upgamma }^1,\tilde{\upgamma }^2)\,=\,\alpha ^{12}+\upvarepsilon$, $\measuredangle (\tilde{\upgamma }^2,\tilde{\upgamma }^3)\,=\,\alpha ^{23}+\upvarepsilon$ and $\measuredangle (\tilde{\upgamma }^1,\tilde{\upgamma }^3)=\alpha ^{12}+\alpha ^{23}+2\cdot \upvarepsilon$. We parametrize each ray by the distance from the starting point. Given two positive numbers $t,\tau \in \mathbb {R}_+$, let $s=s(t,\tau )$ be the number such that $\tilde{\upgamma }^2(s)\in [\tilde{\upgamma }^1(t)\ \tilde{\upgamma }^3(\tau )]$. Clearly $s\leqslant \max \{t,\tau \}$, so $t,\tau , s$ may be taken sufficiently small.$\square$

1.6.3.

Exercise. Prove that the sum of adjacent angles is at least $\pi$.

More precisely, let $\mathcal {X}$ be a complete length space and $p,x,y, z\in \mathcal {X}$. If $p\in \left] x y \right[$, then

$$ \measuredangle [p\,{}^{x}_{z}]+\measuredangle [p\,{}^{y}_{z}]\geqslant \pi $$

whenever each angle on the left-hand side is defined.

1.6.4.

First variation inequality. Assume that for a hinge $[q\,{}^{p}_{x}]$ the angle $\alpha =\measuredangle [q\,{}^{p}_{x}]$ is defined. Then

$$ \vert p-\mathrm {geod}_{[qx]}(t)\vert _{} \leqslant \vert q-p\vert _{}-t\cdot \cos \alpha +o(t). $$

Proof.

Take a sufficiently small $\upvarepsilon >0$. For all sufficiently small $t>0$, we have

$$\begin{aligned} \vert \mathrm {geod}_{[qp]}(t/\upvarepsilon )-\mathrm {geod}_{[qx]}(t)\vert _{}&\leqslant \tfrac{t}{\upvarepsilon }\cdot \sqrt{1+\upvarepsilon ^2 -2\cdot \upvarepsilon \cdot \cos \alpha }+o(t)\leqslant \\&\leqslant \tfrac{t}{\upvarepsilon } -t\cdot \cos \alpha + t\cdot \upvarepsilon . \end{aligned}$$

Applying the triangle inequality, we get

$$\begin{aligned} \vert p-\mathrm {geod}_{[qx]}(t)\vert _{}&\leqslant \vert p-\mathrm {geod}_{[qp]}(t/\upvarepsilon )\vert _{}+\vert \mathrm {geod}_{[qp]}(t/\upvarepsilon )-\mathrm {geod}_{[qx]}(t)\vert _{} \leqslant \\&\leqslant \vert p-q\vert _{} -t\cdot \cos \alpha + t\cdot \upvarepsilon \end{aligned}$$

for any fixed $\upvarepsilon >0$ and all sufficiently small t. Hence the result. $\square$

1.7 Space of directions and tangent space

Let $\mathcal {X}$ be a metric space with defined angles for all hinges. Fix a point $p\in \mathcal {X}$.

Consider the set $\mathfrak {S}_p$ of all nontrivial geodesics that start at p. By 1.6.2, the triangle inequality holds for $\measuredangle$ on $\mathfrak {S}_p$, so $(\mathfrak {S}_p,\measuredangle )$ forms a pseudometric space; that is, $\measuredangle$ satisfies all the conditions of a metric on $\mathfrak {S}_p$, except that the angle between distinct geodesics might vanish.

The metric space corresponding to $(\mathfrak {S}_p,\measuredangle )$ is called the space of geodesic directions at p, denoted by $\Sigma '_p$ or $\Sigma '_p\mathcal {X}$. Elements of $\Sigma '_p$ are called geodesic directions at p. Each geodesic direction is formed by an equivalence class of geodesics in $\mathfrak {S}_p$ for the equivalence relation

$$ [px]\sim [py]\ \ \iff \ \ \measuredangle [p\,{}^{x}_{y}]=0. $$

The completion of $\Sigma '_p$ is called the space of directions at p and is denoted by $\Sigma _p$ or $\Sigma _p\mathcal {X}$. Elements of $\Sigma _p$ are called directions at p.

The Euclidean cone $\mathop {\mathrm{Cone}}\nolimits \Sigma _p$ over the space of directions $\Sigma _p$ is called the tangent space at p and is denoted by $\text {T}_p$ or $\text {T}_p\mathcal {X}$.

The tangent space $\text {T}_p$ could also be defined directly, without introducing the space of directions. To do so, consider the set $\mathfrak {T}_p$ of all geodesics with constant-speed parametrizations starting at p. Given $\alpha ,\upbeta \in \mathfrak {T}_p$, set

Since the angles in $\mathcal {X}$ are defined, ➊ defines a pseudometric on $\mathfrak {T}_p$.

The corresponding metric space admits a natural isometric identification with the cone $\text {T}'_p=\mathop {\mathrm{Cone}}\nolimits \Sigma '_p$. The elements of $\text {T}'_p$ are equivalence classes for the relation

$$ \alpha \sim \upbeta \ \ \iff \ \ \vert \alpha (t)-\upbeta (t)\vert _{\mathcal {X}}=o(t). $$

The completion of $\text {T}'_p$ is therefore naturally isometric to $\text {T}_p$.

Elements of $\text {T}_p$ will be called tangent vectors at p, regardless of the fact that $\text {T}_p$ is only a metric cone and need not be a vector space. Elements of $\text {T}'_p$ will be called geodesic tangent vectors at p.

1.8 Hausdorff convergence

It seems that Hausdorff convergence was first introduced by Felix Hausdorff in [42], and a couple of years later an equivalent definition was given by Wilhelm Blaschke in [16]. A refinement of this definition was introduced by Zdeněk Frolík in [35], and later rediscovered by Robert Wijsman in [68]. However, this refinement takes an intermediate place between the original Hausdorff convergence and closed convergence, also introduced by Hausdorff in [42]. For this reason we call it Hausdorff convergence instead of Hausdorff–Blascke–Frolík–Wijsman convergence.

Let $\mathcal {X}$ be a metric space and $A\subset \mathcal {X}$. We will denote by $\mathrm{{dist}}_{A}(x)$ the distance from A to a point x in $\mathcal {X}$; that is,

1.8.1.

Definition of Hausdorff convergence. Given a sequence of closed sets $(A_n)_{n=1}^\infty$ in a metric space $\mathcal {X}$, a closed set $A_\infty \subset \mathcal {X}$ is called the Hausdorff limit of $(A_n)_{n=1}^\infty$, briefly $A_n\rightarrow A_\infty$, if

$$ \mathrm{{dist}}_{A_n}(x)\rightarrow \mathrm{{dist}}_{A_\infty }(x)\ \ \text {as}\ \ n\rightarrow \infty $$

for every $x\in \mathcal {X}$.

In this case, the sequence of closed sets $(A_n)_{n=1}^\infty$ is said to converge in the sense of Hausdorff.

Example. Let $D_n$ be the disk in the coordinate plane with center (0, n) and radius n. Then $D_n$ converges to the upper half-plane as $n\rightarrow \infty$.

1.8.2.

Exercise. Let $A_n\rightarrow A_\infty$ as in Definition 1.8.1.

Show that $A_\infty$ is the set of all points p such that $p_n\rightarrow p$ for some sequence of points $p_n\in A_n$.

Does the converse hold? That is, suppose $(A_n)_{n=1}^\infty , A_\infty$ are closed sets such that $A_\infty$ is the set of all points p such that $p_n\rightarrow p$ for some sequence of points $p_n\in A_n$. Does this imply that $A_n\rightarrow A_\infty$?

1.8.3.

First selection theorem. Let $\mathcal {X}$ be a proper metric space and $(A_n)_{n=1}^\infty$ be a sequence of closed sets in $\mathcal {X}$. Assume that for some (and therefore any) point $x\in \mathcal {X}$, the sequence $\mathrm{{dist}}_{A_n}(x)$ is bounded. Then the sequence $(A_n)_{n=1}^\infty$ has a convergent subsequence in the sense of Hausdorff.

Proof.

Since X is proper, there is a countable dense set $\{x_1,x_2,\ldots \}$ in $\mathcal {X}$. Note that the sequence $d_n=\mathrm{{dist}}_{A_n}(x_k)$ is bounded for each $k$. Therefore, passing to a subsequence of $(A_n)_{n=1}^\infty$, we can assume that $\mathrm{{dist}}_{A_n}(x_k)$ converges as $n\rightarrow \infty$ for any fixed $k$.

Note that for each n, the function $\mathrm{{dist}}_{A_n}:\mathcal {X}\rightarrow \mathbb {R}$ is 1-Lipschitz and nonnegative. Therefore the sequence $\mathrm{{dist}}_{A_n}$ converges pointwise to a 1-Lipschitz nonnegative function $f:\mathcal {X}\rightarrow \mathbb {R}$.

Set $A_\infty =f^{-1}(0)$. Let us show that

$$ \mathrm{{dist}}_{A_\infty }(y)\leqslant f(y) $$

for any y.

Assume the contrary; that is,

$$ f(z)<R<\mathrm{{dist}}_{A_\infty }(z) $$

for some $z\in \mathcal {X}$ and $R>0$. Then for any sufficiently large n, there is a point $z_n\in A_n$ such that $\vert x-z_n\vert _{}\leqslant R$. Since $\mathcal {X}$ is proper, we can pass to a partial limit $z_\infty$ of $z_n$ as $n\rightarrow \infty$.

It is clear that $f(z_\infty )=0$; that is, $z_\infty \in A_\infty$. (Note that this implies that $A_\infty \ne \varnothing$). On the other hand,

$$\begin{aligned} \mathrm{{dist}}_{A_\infty }(y) \leqslant \vert z_\infty -y\vert _{} \leqslant R < \mathrm{{dist}}_{A_\infty }(y), \end{aligned}$$

a contradiction.

On the other hand, since f is 1-Lipschitz, $\mathrm{{dist}}_{A_\infty }(y)\geqslant f(y)$. Therefore

$$ \mathrm{{dist}}_{A_\infty }(y)= f(y) $$

for any $y\in \mathcal {X}$. Hence the result.$\square$

1.9 Gromov–Hausdorff convergence

1.9.1.

Definition. Let $\left\{ \,{\mathcal {X}_\alpha }\ {:}\ {\alpha \in \mathcal {A}}\,\right\}$ be a collection of metric spaces. A metric $\uprho$ on the disjoint union

$$ \varvec{X}=\bigsqcup _{\alpha \in \mathcal {A}} \mathcal {X}_\alpha $$

is called a compatible metric if the restriction of $\uprho$ to every $\mathcal {X}_\alpha$ coincides with the original metric on $\mathcal {X}_\alpha$.

1.9.2.

Definition. Let $\mathcal {X}_1,\mathcal {X}_2,\ldots$ and $\mathcal {X}_\infty$ be proper metric spaces and $\uprho$ be a compatible metric on their disjoint union $\varvec{X}$. Assume that $\mathcal {X}_n$ is an open set in $(\varvec{X},\uprho )$ for each $n\ne \infty$, and $\mathcal {X}_n\rightarrow \mathcal {X}_\infty$ in $(\varvec{X},\uprho )$ as $n\rightarrow \infty$ in the sense of Hausdorff (see Definition 1.8.1).

Then we say $\uprho$ defines a convergence³ in the sense of Gromov–Hausdorff , and write $\mathcal {X}_n\rightarrow \mathcal {X}_\infty$ or $\mathcal {X}_n\xrightarrow {\uprho } \mathcal {X}_\infty$. The space $\mathcal {X}_\infty$ is called the limit space of the sequence $(\mathcal {X}_n)$ along $\uprho$.

Usually Gromov–Hausdorff convergence is defined differently. We prefer this definition since it induces convergence for a sequence of points $x_n\in \mathcal {X}_n$ (Exercise 1.8.2), as well as weak convergence of measures $\mu _n$ on $\mathcal {X}_n$, and so on, corresponding to convergence in the ambient space $(\varvec{X},\uprho )$.

Once we write $\mathcal {X}_n\rightarrow \mathcal {X}_\infty$, we mean that we have made a choice of convergence. Note that for a fixed sequence of metric spaces $(\mathcal {X}_n)$, it might be possible to construct different Gromov–Hausdorff convergences, say $\mathcal {X}_n{\xrightarrow {\uprho }} \mathcal {X}_\infty$ and $\mathcal {X}_n\xrightarrow {\uprho '} \mathcal {X}_\infty '$, whose limit spaces $\mathcal {X}_\infty$ and $\mathcal {X}_\infty '$ need not be isometric to each other.

For example, for the constant sequence , there is a convergence with limit ; guess the metric $\uprho$ from the diagram.

                                       

For another metric $\uprho '$—also guess it from the diagram—the limit space $\mathcal {X}_\infty '$ is isometric to the real line.

1.9.3.

Second selection theorem. Let $\mathcal {X}_n$ be a sequence of proper metric spaces with marked points $x_n\in \mathcal {X}_n$. Assume that for any fixed $R,\upvarepsilon >0$, there is $N=N(R,\upvarepsilon )\in \mathbb {N}$ such that for each n the ball $\overline{\mathrm {B}}{}[x_n, R]_{\mathcal {X}_n}$ admits a finite $\upvarepsilon$-net with at most N points. Then there is a subsequence of $\mathcal {X}_n$ admitting a Gromov–Hausdorff convergence such that the sequence of marked points $x_n\in \mathcal {X}_n$ converges.

Proof.

From the main assumption in the theorem, in each space $\mathcal {X}_n$ there is a sequence of points $z_{i, n}\in \mathcal {X}_n$ such that the following condition holds for a fixed sequence of integers $M_1<M_2<\ldots$

• $\vert z_{i, n}-x_n\vert _{\mathcal {X}_n}\leqslant k+1$ if $i\leqslant M_k$,

• the points $z_{1,n},\ldots ,z_{M_k, n}$ form an $\tfrac{1}{k}$-net in $\overline{\mathrm {B}}{}[x_n, k]_{\mathcal {X}_n}$.

Passing to a subsequence, we can assume that the sequence

$$ \ell _n=\vert z_{i,n}-z_{j, n}\vert _{\mathcal {X}_n} $$

converges for any i and j.

Consider a countable set of points $\mathcal {W}=\{w_1,w_2,\ldots \}$ equipped with the pseudometric defined by

$$ \vert w_i-w_j\vert _{\mathcal {W}} = \lim _{n\rightarrow \infty }\vert z_{i,n}-z_{j, n}\vert _{\mathcal {X}_n}. $$

Let $\hat{\mathcal {W}}$ be the metric space corresponding to $\mathcal {W}$; that is, points in $\hat{\mathcal {W}}$ are equivalence classes in $\mathcal {W}$ for the relation $\sim$, where $w_i\sim w_j$ if and only if $\vert w_i-w_j\vert _{\mathcal {W}}=0$, and where

Denote by $\mathcal {X}_\infty$ the completion of $\hat{\mathcal {W}}$.

It remains to show that there is a Gromov–Hausdorff convergence $\mathcal {X}_n\rightarrow \mathcal {X}_\infty$ such that the sequence $x_n\in \mathcal {X}_n$ converges. To prove this, we need to construct a metric $\uprho$ on the disjoint union of

$$ \varvec{X}=\mathcal {X}_\infty \sqcup \mathcal {X}_1\sqcup \mathcal {X}_2\sqcup \ldots $$

satisfying definitions 1.9.1 and 1.9.2. The metric $\uprho$ can be constructed as the maximal compatible metric such that

$$ \uprho (z_{i,n}, w_i)\leqslant \tfrac{1}{m} $$

for any $n\geqslant N_m$ and $i<I_m$ for a suitable choice of two sequences $(I_m)$ and $(N_m)$ with $I_1=N_1=1$. $\square$

1.9.4.

Exercise. Let $\mathcal {X}_n$ be a sequence of metric spaces that admits two convergences $\mathcal {X}_n\xrightarrow {\uprho }\mathcal {X}_\infty$ and $\mathcal {X}_n\xrightarrow {\uprho '}\mathcal {X}_\infty '$.

• (a) If $\mathcal {X}_\infty$ is compact, then .

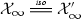• (b) If $\mathcal {X}_\infty$ is proper and there is a sequence of points $x_n\in \mathcal {X}_n$ that converges in both convergences, then .