Abstract
-
Adaptation planning and climate risk management are examples of decision processes made under climate uncertainty.
-
A variety of approaches exist for helping an analyst to evaluate alternatives over future unknown states of the world. However, climate uncertainty requires additional considerations, including how to use available climate information, such as climate change projections, to inform the decision process without overwhelming it.
-
Decision Scaling is specifically designed to support decisionmaking under climate uncertainty while it is general enough to address other uncertainties. The process is designed to make the best and most efficient use of uncertain but potentially useful climate change projections.
-
DS consists of three steps: Decision Framing, Climate Stress Test, and Estimating Climate-Informed Risks.
-
This is accomplished by using weather generator tools and systematic sampling algorithms to create an unbiased description of system response to plausible climate changes.
-
Climate information is incorporated as a sensitivity factor in the last stage of analysis for aiding the process of prioritizing risks or choosing among adaptation options through evaluation of probabilities of underperforming strategies and the need for adaptation.
-
An important benefit of using DS is the establishment of open lines of communication and trust among the analysts, decisionmakers, and representative stakeholders. This is achieved through frequent consultation and validation of models that will be used for the analysis.
You have full access to this open access chapter, Download chapter PDF
Similar content being viewed by others
1 Introduction
Decision Scaling (DS) originated in response to questions regarding the best approaches to process and use climate change projections for adaptation planning. At the time, and as continues to be the case, planners face an overwhelming number of choices of climate change projections, which vary in terms of climate model, downscaling approaches, emission scenarios, etc., and no clear guidance to navigate among them. DS uses a decision analytic framework and structured, physically based, multidimensional sensitivity analysis to first identify the priority climate-related concerns, reserving climate projections for use in latter stages of the analysis, to inform the level of concern for climate vulnerabilities that are identified. A formal probabilistic framework is used to characterize the information from climate projections in the spatial and temporal scales that maximize credibility.
The application of decision analysis techniques has evolved from an intent to identify an optimal decision to an intent to fully explore the consequences and trade-offs of alternative decisions, often to select a reduced set of best-performing or “non-inferior” decisions. Public resource problems consist of multiple objectives, often the goals of different groups or people or constituencies, and so are not reducible to a single numeraire. For public resource problems, there are important considerations:
-
1.
Multiple irresolvable preferences for the choice of a solution;
-
2.
Full exploration of the performance space over various uncertainties and in terms of multiple objectives;
-
3.
Multiple beliefs about the future, possibly conflicting information regarding relative likelihoods or simply indications of plausibility of different futures.
A planning approach for climate change must address each of these considerations. Methods for decisionmaking under uncertainty have long existed for exploring multiple objectives and irresolvable preferences among those objectives, including concepts such as preference dominance and Pareto optimality.
However, traditional methods do not address the issue of multiple beliefs about future states of the world. Typically, the scenarios used to explore the outcomes of different decisions include embedded beliefs that are not explicitly recognized. For example, the choice of a particular set of climate simulations, or downscaling approach, or emissions scenario, embeds the assumptions that those projections represent, and precludes other possible climate futures. Thus, the performance space of alternative decisions is affected and potentially biased by the choice of the climate futures considered, including those derived from climate models. Climate may change in a number of ways. There are two approaches in common practice: (1) the use of climate change projections from climate models (by far the most common) and (2) the use of climate narratives, such as used in a scenario planning approach.
Scenario planning typically uses a small number of narratives, representing internally consistent and mutually exclusive possible futures that are developed independently of climate projections or else informed by them (for example, considering the range of projections). For many planning exercises, this is probably adequate. But for natural resource systems or complex-coupled human-natural systems, such as a water resource system, a small set of narratives provides a limited view of potential climate change effects. Consequently, the resultant plans may be vulnerable to climate changes that could have been identified with a more comprehensive approach. (So, at best, scenario planning is able to deal with Level 3 uncertainties, but not Level 4 uncertainties.)
The most common approach to exploring climate futures is the use of climate change projections from general circulation model (GCM) simulations. Climate projections have the imprimatur of authority because they are used extensively by the climate science community to better understand the earth’s climate, the effect of anthropogenic emission of greenhouse gases and to inform key decisions regarding the regulation of these emissions. However, they may not be the best source of climate futures for use in adaptation planning. Most significantly, GCM projections are inefficient and biased samplers of possible future climate changes. They do not explore the full range of climate changes, but rather the “minimum range of the maximum uncertainty.” Projections typically have biases in terms of climate variability and extremes, which are sometimes the most important climate statistics in terms of impacts. Using climate projections as scenario generators requires processing steps that require many choices that can be controversial themselves. Many a climate change study becomes bogged down in the evaluation of alternative downscaling approaches and choices of which climate models to use. In the end, the results are dependent on these choices, and would be different if other choices were made, further confusing the results.
In practice, adaptation planners are often overwhelmed by the many choices involved in using climate projections for scenario analysis, including emissions scenarios, downscaling methods, model selection, and bias correction. In addition, with new sets of climate models, or new downscaling methods introduced every few years, practitioners feel compelled to redo the entire analysis to see if results have changed. Consequently, when using climate projections as the starting point, the analysis is never complete, and the planner will (and should) always wonder if the results would be different if a different set of projections were used.
DS reveals vulnerabilities to climate changes independent of climate projections, thus negating the time-consuming and expensive debates on the choices related to climate projection use. It does this through the application of a “climate stress test” algorithm, which generates physically realistic climate changes over the widest plausible range. It generates a comprehensive, unbiased estimation of climate effects on the system or decision of interest, without the assumptions and biases embedded in climate change projections from climate models. Climate information from projections or other information sources are used only in the final stages of analysis, to inform the vulnerabilities or differential performances that are identified in the climate stress test. In this way, climate information is used as a sensitivity factor. The understanding of climate change effects on a system only change if the system changes—the understanding is not dependent on the climate projections that happen to be used.
DS shares the general problem formulation and structure of decision analysis frameworks (c.f., Schlaifer and Raiffa 1961), with the formal structuring of decisions in terms of objectives, performance measures or “rewards,” unknown future states of the world, and alternative choices. It is designed to be incorporated into public decisionmaking processes, including with diverse sets of stakeholders holding different objectives and preferences for the matter at hand. It accommodates multi-objective analysis and multiple “beliefs” or viewpoints on the more likely future states of the world. This chapter explains the theoretical derivation of Decision Scaling, explains the process in detail, and summarizes a recent application to the challenge of assessing climate risks to the water supply system for Colorado Springs.
2 Technical Approach
2.1 Overview
DS was designed as a “fit-to-purpose” decision framework for the use of climate change information in climate risk management and adaptation planning. “Decision Scaling” (DS) is positioned as a method to use climate information to improve decisions made under climate uncertainty. DS inverts the usual order of forecast information used in decision analysis, focusing on understanding how decisions are sensitive to changing climate, and using that insight to tailor the climate information provided by GCMs to provide the most credible information to inform the decision. The approach is based on an implicit acceptance of the inherent uncertainty of future climate, and the difficulty of attempting to reduce that future uncertainty. Instead, the goal is to characterize the uncertainty in terms of its implications for decisions and identify the best decisions in view of this uncertainty.
DS consists of three steps (see also Sect. 1.5):
-
1.
Decision Framing
-
2.
Climate Stress Test
-
3.
Estimating Climate-Informed Risks.
The decision framing step is used to identify the mission objectives, and metrics for quantifying them, the uncertain factors that affect the decision, such as future climate, the models or functional relationships needed to represent the system being investigated, and if adaptations are being considered, any choices among adaptation alternatives. The climate stress test is a pragmatically designed multidimensional sensitivity analysis that reveals the fundamental sensitivity of the sector to climate changes, and/or, other uncertain factors. In doing so, it exposes the climate conditions that are problematic for the sector. The final step is to prepare climate information, such as downscaled climate projections, to assess the level of concern that one might assign to the problematic conditions. This can be accomplished using both informal approaches, such as “weight of evidence”, and formal approaches, such as probabilistic methods.
DS is expected to yield benefits in at least three ways. First, the process will provide a clear delineation of the climate risks that are problematic for a specific sector, and the climate changes by which a sector is not threatened. These results are independent of climate projections, and thus are not subject to the various choices and uncertainties associated with processing steps such as downscaling. They also do not require updating with every new generation of climate change projections. Second, the approach allows the characterization of climate change projections in terms relative to decisions and the revealed vulnerabilities. The effects of alternative methods for processing of climate change projections, including downscaling approaches (e.g., statistical vs. dynamic) and methods for estimating probability distributions of changes in climate variables, can be presented in terms of their implications regarding the response of the system or sector to climate changes. The information provided by the projections can inform judgments made relative to the level of concern associated with any revealed problematic climate conditions or vulnerabilities of a particular sector. Similarly, the information can be used to inform judgments made relative to adaptation. In this way, the DS approach does not reject the use of climate change information or projections, but rather is designed to use them in the most decision-relevant and helpful way. Third, the approach is designed to facilitate robust decisionmaking approaches, such as in the approaches described and applied in Parts I and II of the book. DS includes quantification of the robustness of alternative system configurations or other policies, and a clear indication of the expected risk reduction through alternative adaptations. This final benefit is not demonstrated explicitly here, although the results should provide a conceptual understanding of how this would be possible.
DS is based on traditional decision analytic approaches, in particular, the analysis technique known as pre-posterior analysis (Schlaifer and Raiffa 1961). Pre-posterior analysis involves identifying optimal decisions that you would make given new information (posterior to the new information) before you actually know what the new information will tell you (thus, “pre”–posterior). For example, a user may be interested in knowing the expected value of a forecast (say a weather forecast) before paying for it. One would have to account for the value of the improved decision that results from receiving the forecast. But since the forecast result is unknown prior to receiving it, one needs to evaluate the optimal decision for all possible future forecast results, and then account for the probability of receiving each of these forecasts. Application of this framework yields the expected value of perfect information (EVPI) and the expected value of including uncertainty (EVIU), which are two useful quantities for evaluating whether pursuing forecast information and considering uncertainties is worth the effort. EVPI is the difference in value when a decision is made with the uncertain outcome known and when a decision is made without considering a forecast. This serves as a check for whether to consider forecasts, since the value of decisions with actual operational forecasts cannot exceed this upper bound. EVIU is the value of a decision made taking account of the uncertain outcomes compared to the value of that decision when uncertainty is ignored. Again, it provides a check as to whether these more analytically demanding approaches are likely to be worth the effort.
While the classic decision analytic framework is typically used to evaluate information for decisionmaking prior to receiving it, it reveals insights about the decision that are more broadly useful. In particular, through a systematic exploration of all future states of the world, it produces a mapping of optimal decisions for each of these states. More critically, since the analysis assumes the forecast is not yet received, the mapping is created independent of the forecast or any expectations of future likelihoods. This creates a clear separation between our understanding of the decision at hand, and the estimates of probabilities of future states of the world.
DS exploits the advantages of this theoretical framework, using Monte Carlo stochastic sampling tools and currently available high-powered computers to create the mapping of the computed optimal decisions over the wide range of possible futures. The mapping is then used to identify the scenarios where one decision is favored over another and, in doing so, revealing what information would be most helpful in selecting one decision over another. It also can be used to identify and evaluate risks to an existing system or a planned system design.
DS provides several advantages for addressing uncertainties related to climate change. In typical climate change analyses, there are multiple sources of climate information available. These sources may be projections from general circulation models (GCMs) or regional circulation models (RCMs), stochastic models based on historical data, information drawn from paleoclimatological records, the historic observed record, or some combination of these sources. Often the views they offer for future climate vary widely and there is no clear guidance for choosing among them, because estimating their skill in future projections is difficult or impossible (Gleckler et al. 2008). Yet, because they vary, the results of any analysis are likely to be highly influenced by the choice of futures to consider. In addition, in a multi-stakeholder and multi-objective decisionmaking process, the stakeholders may hold strongly divergent beliefs about future climate. Consequently, an analysis that is driven by belief about future climate may not be responsive to some stakeholders, and the process for selecting the future scenarios to consider can become contentious and stall the process.
DS uses the mapping generated from a pre-posterior analysis framework to generate an understanding of optimal decisions prior to receiving “the forecast,” in this case, a particular set of climate futures. Since the mapping is independent of any set of futures, the selection of a set of futures to evaluate is no longer required. Instead of being a potential sticking point, alternative beliefs about the future can be used as a sensitivity factor. Indeed, the concept of “belief dominance” can be used to select the decisions that are best performing across the unknown probabilities of future climate. This results in a non-inferior set of decisions across beliefs, analogous to the more familiar preference dominance, which reveals the Pareto set of non-inferior solutions across preference weightings.
The key methodological challenge for applying this framework is the development of an approach for sampling the plausible range of climate changes. Known issues with climate projections, including their limited sampling of changes in extremes and variability, the debates regarding choices for processing the projections (e.g., “downscaling”), and the fact, as Stainforth et al. (2007) state that they sample “the minimum range of the maximum uncertainty,” preclude their utility for this purpose. Instead, a fit for purpose climate and weather sampler algorithm was created, allowing efficient and systematic sampling of plausible climate changes (Steinschneider and Brown 2013).Footnote 1
2.2 Step 1. Decision Framing
A premise of DS is that attributes of decisions have a significant and possibly critical effect on the utility of information produced to improve a given decision. In the context of climate change, this implies that the value of climate information and the best means of providing that information (in terms of both its attributes and the effort and expense to provide it) is best discovered by investigating vulnerabilities and decisions, rather than solely investigating the various ways of producing climate information. Therefore, the first step of the analysis is to frame decisions in terms of specific decision attributes and their context relative to climate change.
Following a traditional decision analytic framework, the process begins with gathering information on the decision at hand in a structured fashion, using four categories:
-
Choices (e.g., to adapt or not; plan A vs. plan B)
-
Uncertainties (e.g., future climate; future population)
-
Consequences (e.g., net benefits, damages)
-
Connections (e.g., system diagram, system model)
This is a general problem formulation framework common to many decision analytic frameworks; classic texts often use the alternative terminology “actions,” “states of the world,” “rewards,” and “models” (c.f., Winston and Goldberg 2004). In this book, the same framework is described as XPROW (X = exogenous uncertainties, P = policies, R = relationships, O = outcomes, W = weights) (see Fig. 1.2)Footnote 2. The framework described here is intended to be intuitive for a general participant. The articulation of choices should include not only the specific alternatives, but also characteristics of the decisions, such as the decision hierarchy (at what hierarchical levels are decisions made?) and the temporal nature of the decision (one shot, reversible, sequential, etc.). Uncertainties should include not only climate changes, but also other relevant external factors, which will vary based on the specific decision problem. Consequences should be quantifiable outcomes (also called performance measures) that are meaningful to the decisionmaker and other stakeholders. Ideally, they would represent the outcomes currently used to assess the performance of the system or activity. Finally, connections are the way in which decisions yield consequences, and the way by which uncertainties affect them. The connections between climate and consequences often exist in functional relationships between weather or climate and existing activities. In some cases, existing models quantify those functional relationships. In other cases, historical data may be used to characterize the relationships. In still other cases, such as for water supply, new models or model combinations that relate climate to the reliability of water serving a specific installation may be required.
The decision framing serves to organize what can often seem a nebulous discussion of information and desires into categories that fit directly into the analytical framework. That is, the decisionmaker faces choices that are to be evaluated in terms of their consequences that result from different realizations of the uncertainties. The consequences of choices are estimated based on our understanding of the connections between them, often represented by models or functions.
In many applications, the decision process will involve multiple stakeholders convening to incorporate multiple viewpoints on the objectives and important considerations for analysis. In public decisionmaking processes with many potentially affected people, it is essential to involve representatives of these groups, and understand their preferences and concerns. Otherwise, a decision may be optimal for a narrow set of planners but judged to be far from optimal by those affected by the decision. Trade-offs among objectives can be described and assessed in Step 3.
The results of the first stage of the analysis provide the inputs and information needed for the following stages. These include an articulation of alternative decisions, a list of key uncertainties to incorporate into the analysis, a list of the outcomes used to evaluate the consequences of different decisions, and the models or relationships used to represent the decision problem. The final key product of Step 1 is the establishment of open lines of communication and trust among the analysts, decisionmakers, and representative stakeholders. This is achieved through frequent consultation and validation of models that will be used for the analysis.
2.3 Step 2. Climate Stress Test
The climate stress test is the term given to the multidimensional sensitivity analysis that is used to reveal the effects of possible climate changes, and other uncertain factors, on the activity or system of interest. This step can be a more general stress test, since the sensitivity factors need not be climate-related. However, since climate requires special handling due to its distributed spatial and correlated temporal characteristics, this chapter focuses on the climate stress test. The approach is to parametrically vary climate variables in a representation of the system or activity, and infer from the results the response of the system to a wide range of climate changes. The representation of the system can range from a simple empirical relationship to sophisticated models or sequences of models. In most cases, a formal model of the natural, engineered, or socio-economic system is created that relates climate conditions to the outcomes identified in Step 1. The models are mathematical representations of physical, social, or economic processes that allow the analysts to systematically explore the potential effects of changes in climate on the system. The models might be complex or simple, depending on the attributes of the decision and the available resources for the analysis. The only requirement is that the representation includes some climate or weather inputs. Models are validated with available data to ensure that they appropriately represent the system of interest and the outcomes of interest in the terms the stakeholders utilize for decisionmaking. The climate stress test approach is quite general. In principle, any model that could be used for assessing climate change impacts via climate projections can be used for the climate stress test, and likely more.
The climate stress test represents advancement over traditional sensitivity analysis. In the past, single variable sensitivity analysis has been criticized because varying a single factor individually will fail to reveal sensitivities that are caused by the correlated behavior of multiple variables. For example, separately varying temperature and precipitation would not reveal problems that occur when both change together. However, varying multiple variables simultaneously requires preserving the physical relationships among these variables, if they are not independent, for the results to be physically meaningful. In the case of weather and climate variables, the challenge is maintaining spatial and temporal relationships in aspects such as precipitation, temperature, and wind. The answer to this challenge resides in stochastic weather generators, which are statistical models that are designed to produce stochastically generated weather time series and have been used in the past in crop modeling and hydrologic modeling to create alternative historical time series. They are used to investigate the effects of possible alternative realizations of weather and climate variability. These models can serve as the basis of climate stress testing.
The required attributes for a multipurpose climate stress testing algorithm include:
-
1.
Physical fidelity—the algorithm must preserve known physical relationships among climate variables.
-
2.
Spatial and temporal cogency—the algorithm must produce results that have a physically meaningful spatial and temporal scale (e.g., average annual temperature for a 30-year period over the spatial area of study). This allows the results to be linked to climate information, such as climate projections, which are always positioned in time and space.
-
3.
Modifiable—the climate conditions must be able to be changed in a controlled and predictable way, to allow exploration of climate changes.
-
4.
Representative variability—the representation of internal or “natural” variability, the unpredictable chaotic nature of weather time series, should be accurate to the degree possible. This is, especially, important because internal variability is typically dominant at the temporal and spatial scales of adaptation decisionmaking and risk assessment. For example, at the spatial scale of a water resources system and over a 30-year planning period, natural variability is likely to have a larger explanatory role in the conditions experienced than any trends in climate change.
A climate stress testing algorithm was designed with these desired qualities. It is fully described in Steinschneider and Brown (2013). As illustrated in that paper, the climate stress testing algorithm can create a wider range of climate changes than could have been derived from a typical downscaled, multi-model ensemble of projections. More important, in some cases, the algorithm can more efficiently (in terms of computational effort) sample a wide range of climate changes, due to its systematic approach. This is important when the model or models used to represent a specific system are expensive in terms of computation time (e.g., a model representing the California water supply system). Not all applications require such a sophisticated approach. Water supply systems require careful simulation because they are expected to provide water at very high reliability, and will only show sensitivity during critical periods, or rare events consisting of very dry conditions. In addition, they typically collect water from wide spatial areas, such as river basins, and the transport and storage of water defies a simple linear representation. As a result, the detailed representation of temporal and spatial variability is required to accurately assess these systems. Other systems (i.e., systems that have no spatial distribution) can be assessed using average conditions at a point location and do not require the full features of a climate stress testing algorithm.
The stress test provides the analyst and decisionmaker with a response function that relates a change in decision-relevant outcomes measuring performance to changes in the climate and socio-economic system, enabling the analyst to parse the space of future conditions into regions of “acceptable” and “unacceptable” performance (throughout this book, this process is termed Scenario Discovery (SD)). This functional relationship is extremely powerful in the decisionmaking process. For instance, it may indicate that the system is relatively insensitive to changes in climate or other stressors and further analysis is unnecessary. Alternatively, the stress test may reveal that the system is extremely sensitive to even a modest change in one component of the climate system or small amounts of population growth, suggesting that proactive measures may be needed sooner rather than later.
Although climate change is typically the focus of adaptation planning and climate risk assessment, other changing factors or uncertainties may be as important or even more so. The climate stress test incorporates these non-climate factors as well, in which case it is a more general type of stress test. The stress test uses stochastic sampling techniques to determine the system response and the performance of alternatives over the full range of uncertainties considered. The framework allows both simulation modeling and optimization modeling, and thus the response can be in terms of the system performance (simulation) or optimal decision (optimization) for each combination of factors considered.
Designing the climate stress test requires two additional considerations: the range of the factors to be sampled and the structure of the sampling algorithm. The goal of range setting on the uncertain factors is to sample all plausible values and not preclude unlikely but plausible outcomes. The range should be broad enough that there is no question that all plausible values are sampled. There should be little concern that implausible values might be sampled, since the goal of this step is to understand the response of the system, not to assess risks or vulnerabilities. If vulnerabilities are identified near the edge of the sampling range, they can be disregarded during Step 3. That is the appropriate time to make judgments on the plausibility of identified vulnerabilities.
The second consideration is the structure of the sampling algorithm and the preservation of correlations among uncertain factors, if necessary. The climate stress testing approach described earlier is specifically designed to preserve spatial and temporal patterns in weather and climate statistics. This is necessary in order to sample physically realistic values. Likewise, there may be a need to preserve correlations among other uncertain values. For example, the future demand for water may be an important uncertain factor in water supply planning that is to be sampled over a wide range of values. Depending on local conditions, water demand might be influenced by temperature and precipitation. Therefore, there may be a need to ensure that this relationship is preserved in the sampling technique—for example, by enforcing a positive correlation between water demand and temperature. While the procedures for doing so go beyond the scope of this chapter, there are several possible approaches, including parametric correlation functions and nonparametric (data-based) sampling techniques.
A water supply climate stress test provides an illustration of the approach. In the case of assessing vulnerabilities of a water system, a series of models is developed that can be used to identify the vulnerabilities of all components of the water resources system that serve the water demands of the installation. These models typically include the following three steps: (1) climate/weather generation, (2) hydrologic modeling, and (3) water resources system modeling (Fig. 12.1).
Stochastic weather generators can create new sequences of weather consistent with current or a changed climate that simultaneously exhibit different long-term mean conditions and alternative expressions of natural climate variability. The scenarios created by the weather generator are created independent of climate projections, allowing for a systematic exploration of future climates. The scenarios are designed to maintain physical attributes of weather and climate, such as spatial and temporal patterns and correlations. Furthermore, climate scenarios exhibiting the same mean climate changes can be stochastically generated many times to explore the effects of internal climate variability. In this way, the climate-weather generator (i.e., a weather generator linked to specific mean climate conditions) can be used to fully describe the response of the system to possible climate changes without making strong assumptions about how likely the particular climate changes are.
The climate information from the weather generator is fed into a hydrologic model. The hydrologic model translates changes in weather variables to hydrologic variables of interest (e.g., streamflow at inflow points to water infrastructure). The water resources model accepts hydrologic variables as inputs, as well as other driving variables (e.g., water demanded from domestic or agricultural users; environmental release requirements), simulates the infrastructure operation and conveyance plans that determine the flow of water through the engineered system, and calculates the variables that are of interest for policy and management (e.g., reservoir storage, water delivered to users, water released to the environment). This process is repeated a large number of times (total scenario runs may number in the thousands to fully sample climate and other changes), the performance of proposed plans is calculated, and the results are presented on a “climate response surface” that displays the climate changes that are problematic (Fig. 12.2). [In the rest of the book, this process is called Exploratory Modeling (EM).]
Figure 12.2 is an illustration of the results for a typical climate stress test. It shows a map of changes in climate (both precipitation and temperature) and the resulting impact. In this case, the area in red indicates that the impacts have exceeded an impact level, adaptation tipping point, or threshold beyond which adaptation would be required. Thus, the climate changes represented by the red area indicate the climate changes that would cause adaptation to be necessary. The way of determining threshold levels is not necessarily dependent on any specified threshold; thresholds are completely malleable and can be specified by the individual analyst for the question of interest.
The climate response surface is a two-dimensional visualization of the response of the system to climate change. In this case, the response variable is the reliability of water supply calculated for a 50-year simulation. The climate response surface summarizes the effects of climate change on the system, including changes in mean climate and the range of variability. In this case, the effects of mean climate changes were estimated with 13 stochastically generated weather time series of 50 years in length. The carefully designed sampling of mean climate changes and variability produces the best unbiased estimate of future system performance, and accounts for the internal variability of the climate system.
In a multidimensional uncertainty analysis, more than two dimensions may be needed to display all the effects of uncertain factors. There are a number of ways to display multidimensional results, including “parallel coordinate plots” and “tornado plots”. However, experience has shown that stakeholders are most receptive to two-dimensional visualizations, and these 2D figures can be created as slices of the multidimensional response surface for any two variables. The representation of the climate response surface is best determined through iteration with the stakeholder partners.
2.4 Step 3. Estimation of Climate-Informed Risks
The final step of DS is the characterization of risk associated with the problematic conditions for a given system. Here the term risk is used to denote the probability of occurrence of the problematic conditions. Up to this point, the analysis is free of the use of probabilities for particular scenarios. This allows exploration of the decision space that is not biased by prior probability assumptions that are weakly supported or not agreed, and that are thus deeply uncertain. At this step, the available sources of information regarding possible future outcomes is described quantitatively using a probabilistic framework. The information is then used as a sensitivity factor to inform final decisions. The use of a probabilistic framework facilitates accounting for the sampling characteristics of the source information, such as the sample size and the dependence among different sources. Ignoring sampling characteristics has been a common mistake in decisionmaking under uncertainty approaches to climate change uncertainty (e.g., the assumption that all projections are equally likely).
Because climate change projections are often commonly used and misused for long-term scenarios, the tailoring of climate information is described in detail here. The climate stress test is designed to create physically representative time series of weather variables at specific spatial scales that can match the source of climate information that is most credible. This enables the mapping of climate information from climate projections or other sources directly to the climate response surface, and thus to the decision. In the case of climate projections, the weather generator design can allow the projections to be used at the spatial and temporal scales where they have most skill (generally coarse scales, large areas (100’s of kilometers), and long averaging periods [e.g., 30 years]). Then inference on the relative likelihood of climate changes of interest can be made using the most credible scales of the climate projections.
Another way to increase the credibility of estimations of future climate changes is to create categories of interest and to estimate the likelihood of these categories, rather than the full probability distribution of outcomes. This approach has long been used in seasonal climate forecasts. Seasonal climate forecasts are forecasts made of the mean climate expected for an upcoming season, such as mean temperature and mean precipitation. The basis of these forecasts is typically deterministic or near-deterministic components of the climate system, which typically includes persistence of ocean temperatures and the resulting effects on atmospheric circulation. The El Niño/Southern Oscillation is the most well-known example. Given the amount of uncertainty associated with these forecasts, they are typically made as probabilities assigned to terciles of outcomes. For example, a typical forecast assigns probabilities to precipitation being Above Average, Near Average, or Below Average. This reflects the skill of the forecasts (no more precise forecasts can be made credibly) and the potential utility of the categories for stakeholders (it is useful to know whether precipitation may be above average).
The same approach can be used to improve the credibility of information about future climate change. Indeed, the DS approach enables the creation of categories that are directly relevant to the decision at hand, and also directly coordinated with the spatial and temporal scales at which climate information is most credible. Groves and Lempert (2007) describe the use of a cluster analysis approach to derive ex post socio-economic scenarios from the results of a sensitivity analysis. This approach can be employed with the results of a climate stress test, as described in Brown et al. (2012). This creates ex post categories of climate change, to which probabilities of occurrence can be assigned. The probabilities are conditional on the source (e.g., climate projections under a specific emissions scenario). The use of categories allows the information to be conveyed in terms that are meaningful for decisionmakers, and is a more credible prescription of a full probability distribution.
When the system is found to be sensitive to certain future scenarios, the process can be repeated and applied to evaluate possible adaptation strategies as well, by repeating the analysis for the new alternatives considered. The results of this analysis reveal how well each adaptation strategy can preserve system performance over a wide range of futures. Specifically, this analysis determines which adaptations can preserve outcomes above their thresholds across the range of future scenarios. The decision to accept a specific adaptation strategy then relies on an appraisal of the resilience of the original system and the alternatives considered. The climate risk analysis can be used to compare alternative plans or to evaluate the additional robustness that a specific planned adaptation might provide. Figure 12.3 is an illustration of how comparative analysis could be conducted using the results of the climate risk screening. The figure shows the probable fraction of futures for which the current system and the adapted system provide acceptable performance. In this case, the adapted system is more robust, as it performs acceptably over more of the future space. Note that these results are conditional on the assumed probability distribution, and in some cases it will be beneficial to use multiple distributions and compare across them. For example, see Moody and Brown (2013), where alternative adaptations are evaluated conditional on alternative future probability distributions of climate change, including those based on historical conditions and climate change projections from GCM.
This discussion has focused primarily on the particular treatment of climate information for informing decisions related to long-term plans that may be affected by climate change. In cases where climate change is not a key consideration, the analysis methods presented here are likely unnecessary. Other important aspects of formal decisionmaking processes are also not discussed here. These include the process of problem formulation, facilitating stakeholder discussions, and the enumeration of possible adaptation options. In addition, the selection of outcomes is an important component of decisionmaking. While the discussion here used robustness for illustrative purposes, the best or optimal performance for each alternative, the expected value of performance, and regrets are other useful means for evaluating performance. A rigorous analysis would use multiple outcomes to compare and evaluate alternatives.
3 Case Study: Assessing Climate Risks to the Water Supply for Colorado Springs, Colorado, USA
The Colorado Springs Utility (CSU) embarked on a long-term strategic planning process to create an Integrated Water Resource Plan (IWRP). The ultimate goal of this plan is to provide “reliable and sustainable water supply to customers in a cost-effective manner.” The overall planning process incorporates consideration of water supply and demand, water quality, infrastructure, and regulatory and financial issues. It includes activities such as stakeholder outreach, internal planning with Board leadership, and technical studies involving modeling and analysis. The planning time frame is defined as a future scenario described as “Build-Out,” meaning 50 or more years in the future when the city reaches a sustained equilibrium population. The planning process sought to answer these specific questions:
-
What is an acceptable level of risk in addressing future water demands?
-
What is an appropriate approach for CSU to follow in meeting regional water demands within the Pikes Peak region?
-
What role do different supply options contribute to achieving a balanced water supply portfolio?
-
How do we ensure a proper level of investment in CSU’s existing and future water system to maintain an acceptable level of risk?
As part of the planning process, CSU in collaboration with the University of Massachusetts and the National Center for Atmospheric Research, applied DS to investigate the effects of climate change on the reliability of their water supply deliveries. The analysis leveraged the planning processes that identified the key questions described above, as well as a cataloging of performance measures and possible investments. Much of this information was compiled through an earlier climate change study that incorporated aspects of Robust Decision Making. CSU maintain hydrologic models and water system models that were available for this analysis. This case study describes the application of DS to characterize the risk that climate change poses to the water supply reliability for Colorado Springs. Although the framework could be used to also evaluate alternative investments to address vulnerabilities, this was not part of the analysis.
In this case study, focus is given to a novel component of the analysis that relates to how we assess climate change uncertainty and integrate that evaluation with the vulnerability assessment to characterize climate-related risks to water supply. Specifically, we explore the processing of climate change projections, with particular attention to climate model similarity, and demonstrate how this issue can affect decisions related to adaptation measures taken by the water utilities.
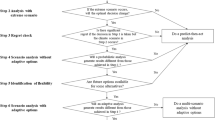
3.1 Step 1: Decision Framing
A key principle of the DS framework is tailoring the analysis to address the primary concerns of planners and decisionmakers. In this case, in order to provide useful information to inform municipality-level adaptations for water supply, it is critical to understand the water supply objectives of the municipality, identify quantitative outcome indicators that can measure those objectives, determine thresholds for those objectives that would indicate unacceptable water supply performance, determine the context and scale of a municipality’s water supply system, and identify the adaptation options available to the municipality. All of these components are necessary to adequately frame the future water supply risks facing a municipality, and the possible actions that can be taken to manage those risks.
In this case study, much of the decision framing had been established as part of the IWRP process. CSU established desired attributes for their strategy, including robustness to a wide variety of future conditions, economic sustainability (meaning that the strategy could be supported by available resources), reliability of water delivery services, and that the strategy was ultimately explainable and acceptable to customers and stakeholders. The analysis would look forward roughly 50 years (long term), and considered a “Build-Out” scenario as described above. It would also consider a wide range of possible investment options to meet its goals of reliable and sustainable water service. These included four different levels of demand management: multiple water reuse and non-potable water supply options, new agricultural transfers, construction of new reservoirs, and enlargement of existing reservoirs. An extended list of performance measures was also created for evaluation of current and future performance and for evaluation of the various options. For the purpose of this case study, reliability of water supply was used as an illustrative performance measure.
The spatial extent of the study included the entire water collection system (which extends to the continental divide in western Colorado) and the entire service area. The CSU water collection system serves an estimated 458,000 people, including the residents of Colorado Springs, the Ute Pass communities west of the city, and several military installations, including the United States Air Force Academy. Currently, the firm yield of potable and non-potable water for the system is about 187 million cubic meters per year, with potable deliveries at approximately 22 billion gallons per year. CSU estimates that they currently have enough water to meet the demand of their customers until approximately 2040, assuming average projections of population growth, per capita water demand changes, and the completion of planned infrastructure projects. These assumptions do not account for any changes in climate, however, and beyond 2040 additional water demands also become a substantial concern.
The CSU water collection system acquires its water from two primary sources—the Upper Colorado River Basin (Fig. 12.4a) and the Arkansas River Basin (Fig. 12.4b). The Upper Colorado River Basin is one of the most developed and complicated water systems in the world. Waters from the Colorado serve people in seven states and Mexico, and are allocated according to a complex set of compacts and water rights provisions. CSU holds one such water right, albeit a junior right, and acquires approximately 70% of its annual water supply through four transmountain diversions that divert water across the continental divide into storage reservoirs operated by CSU. In this way, the water supply security of the CSU is directly linked to the broader water supply risks facing the entire Colorado River Basin. The remaining 30% of the CSU water supply is derived from local runoff in the Arkansas River Basin that must also be shared with users downstream of Colorado Springs. In order to assess the climate-related risks to the CSU water supply, both the Upper Colorado and Arkansas systems need to be accounted for in the analysis. This presents a substantial challenge, which required significant modeling efforts and persistent collaboration and communication with the CSU engineering team, and composed a substantial portion of the ongoing CSU Integrated Water Resources Planning process.
3.2 Step 2: Climate Stress Test
The goal of the climate stress test is to identify the vulnerabilities of the CSU water delivery system to climate change. Step 2 starts with a vulnerability assessment. In this assessment, CSU system performance is systematically tested over a wide range of annual mean climate changes to determine under what conditions the system no longer performs adequately. The approach is illustrated in Fig. 12.5. This stress test is driven using a daily stochastic weather generator that creates new sequences of climate that simultaneously exhibit different long-term mean conditions and alternative expressions of natural climate variability. These weather sequences are passed through a series of hydrosystem models of the relevant river basins and infrastructure network to estimate how these changes in climate will translate into altered water availability for the customers of CSU, including the Air Force Academy. The results of the stress test are summarized in a climate response surface, which provides a visual depiction of changes in critical system outcomes due to changes in the climate parameters altered in the sensitivity analysis. The different components of the vulnerability assessment are detailed below.
-
Stochastic Climate Generator
This work utilizes a stochastic weather generator (Steinschneider and Brown 2013) to produce the climate time series over which to conduct the vulnerability analysis. The weather generator couples a Markov Chain and K-nearest neighbor (KNN) resampling scheme to generate appropriately correlated multisite daily weather variables (Apipattanavis et al. 2007), with a wavelet autoregressive modeling (WARM) framework to preserve low-frequency variability at the annual time scale (Kwon et al. 2007). A quantile mapping technique is used to post-process simulations of precipitation and impose various distributional shifts under possible climate changes; temperature is changed using simple additive factors. The parameters of the model can be systematically changed to produce new sequences of weather variables that exhibit a wide range of characteristics, enabling detailed climate sensitivity analyses. The scenarios created by the weather generator are independent of any climate projections, allowing for a wide range of possible future climates to be generated. Furthermore, climate scenarios exhibiting the same mean climate changes can be stochastically generated many times to explore the effects of internal climate variability. The preservation of internal climate variability is particularly important for the CSU system, because precipitation in the region exhibits substantial decadal fluctuations that can significantly influence system performance (Nowak et al. 2012; Wise et al. 2015). The stochastic model is designed to reproduce this low-frequency quasi-oscillatory behavior; many downscaled climate projections often fail in this regard (Johnson et al. 2011; Rocheta et al. 2014; Tallaksen and Stahl 2014).
The WARM component of the weather generator was fit to annual precipitation data over the Upper Colorado River Basin. These data were provided by CSU, and are derived from the DAYMET database (Thornton et al. 2014). The WARM model is used to simulate time series of annual precipitation averaged over the Upper Colorado Basin, with appropriate inter-annual and decadal variability. A Markov Chain and KNN approach is then used to resample the historic daily data to synthesize new daily time series, with the resampling conditioned on the annual WARM simulation. The data are resampled for both the Upper Colorado and Arkansas River Basins to ensure consistency between the synthesized climate data across both regions. In this way, the major modes of inter-annual and decadal variability are preserved in the simulations, as is the daily spatio-temporal structure of climate data across both the Upper Colorado and Arkansas River Basins.
-
CSU HydroSystems Models
The climate scenarios from the weather generator are used to drive hydrosystem models that simulate hydrologic response, water availability and demand, and infrastructure operations in the river basins that provide water to CSU. The output of the hydrosystem model simulations under each climate time series is used to create a functional link between water supply risk and a set of mean climate conditions. The CSU system requires two separate hydrosystem models, because water is sourced from both the Upper Colorado River Basin on the western side of the continental divide and the headwaters of the Arkansas River on the eastern side of the divide. These models are described in more detail below.
-
Upper Colorado River Basin Hydrosystems Model
The Water Evaluation and Planning System (WEAP) model (Yates et al. 2005) was used to simulate the hydrologic response, reservoir operations, withdrawals, and transmountain diversions of the Upper Colorado River Basin system. By necessity, the WEAP model simplifies the extreme complexity of the Upper Colorado system, yet still requires nearly 40 minutes per 59-year (period-of-record) run on a standard desktop computer (HP Z210 Workstation with a 3.40 GHz processor and 18.0 GB of RAM). The WEAP model approximates how the climate scenarios developed above translate into changes in water availability for users throughout the Colorado River system. Importantly, the WEAP model of the Upper Colorado simulates the availability of water for transfer across four transmountain diversion points that feed into the CSU system. Changes in these diversions substantially alter the water available for CSU and its customers.
-
Upper Arkansas River Basin Hydrosystems Model
The transmountain diversions estimated by the WEAP model are used to force a MODSIM-DSS model (Labadie et al. 2000) that represents the Eastern slope waterworks system operated by CSU. In addition to these diversions, the MODSIM model requires additional inflow data to a variety of nodes. But these inflows cannot be modeled as natural hydrologic response to meteorological forcings, because there are legal constraints on the inflows not accounted for by MODSIM. Therefore, historical years of inflow data, which implicitly account for legal constraints, are resampled from the historic record in all future simulations. To ensure that these flows are correctly correlated with the Western slope simulations from WEAP, the stochastic weather generator is used to produce synthetic weather simultaneously across both Western slope and Eastern slope regions. Natural streamflow response from the Eastern slope system under synthetic climate is estimated using the hydrologic model in WEAP calibrated to naturalized flows in the Arkansas River. A nearest-neighbor resampling scheme is then used to resample historic years based on a comparison between historical, naturalized Arkansas River streamflow, and modeled hydrology of the Arkansas River under synthetic climate. Inflow to all MODSIM nodes besides those associated with Western slope diversions are then bootstrapped for use in future simulations based on the resampled years. One major drawback of this approach is the simplicity of the WEAP hydrologic model used to simulate natural flow in the Arkansas River.
-
Climate and Demand Alterations Considered
The weather generator described above is used to generate day-by-day, 59-year (period-of-record length) climate sequences with different mean temperature and precipitation conditions that maintain the historic decadal variability in the observed data (McCabe et al. 2004, 2007). To impose various climate changes in simulated weather time series, multiplicative (additive) factors are used to adjust all daily precipitation (temperature) values over the simulation period, thus altering their mean annual values. Annual changes are most important for the long-term planning purposes of the CSU system, because the significant reservoir storage on both sides of the continental divide largely mitigates the impact of seasonal changes to runoff and snowmelt timing, consistent with classical reservoir operations theory (Hazen 1914; Barnett et al. 2005; Connell-Buck et al. 2011). This does not preclude the importance of other hydrologic characteristics for long-term planning, such as the effects of climate extremes on flood reduction capacity or water quality, but these issues are not addressed in this study. Annual changes to the precipitation mean were varied from −10% to +10% of the historic mean using increments of 5% (5 scenarios altogether), while temperature shifts were varied from approximately −1 to +4 °C using increments of 0.5 °C (10 scenarios). These changes were chosen to ensure the identification of climate changes that cause system failure. Each one of the 50 = 5 × 10 scenarios of climate change is simulated with the weather generator seven times to partially account for the effects of internal climate variability while balancing the computational burden of the modeling chain, leading to a total of 350 = 5 × 10 × 7 weather sequences.
The seven realizations of internal climate variability were selected in a collaborative process with the CSU engineering team as part of their Integrated Water Resources Planning process. The seven series were chosen among 10,000 original weather generator simulations to span the range of natural climate fluctuations that could influence the system. This selection proceeded in two steps. First, 40 simulations were selected from the original 10,000 to symmetrically span the empirical distribution of a precipitation-based drought outcome indicator preferred by the utility. Second, the subset of 40 simulations was run through the hydrosystem models (described above), and seven final simulations were chosen that spanned the empirical distribution of minimum total system reservoir storage across the 40 runs. Long-term climate changes were then imposed on these final seven climate simulations, and were used to force the hydrosystem models, producing a comprehensive vulnerability assessment that maps CSU system performance to long-term climate changes while also accounting for the effects of internal climate variability.
CSU considers two scenarios for water demands on their system. The first scenario is called the Status Quo. It reflects current water demands after accounting for the connection of several communities to the system’s supply that was to be completed by 2016. The second demand scenario, referred to as “Build-Out Conditions,” reflects a substantial increase in system demand. No date is associated with the water demands of the “Build-Out” scenario, but it is assumed that under current growth projections this level of demand will be reached around the year 2050. The stress test is repeated for both of these water demand scenarios to enable an assessment of the relative importance of climate and water demand changes on water resources vulnerability and risk.
3.3 Step 3. Estimation of Climate-Informed Risks
Over the past decade, the climate science community has proposed different techniques to develop probabilistic projections of climate change from ensemble climate model output. The most recent efforts (Groves et al. 2008; Manning et al. 2009; Hall et al. 2012; Christierson et al. 2012) for risk-based long-term planning have relied on climate probability density functions pdfs from perturbed physics ensembles (PPEs) (Murphy et al. 2004), a Bayesian treatment of multi-model ensembles (MMEs) (Tebaldi et al. 2005; Lopez et al. 2006; Smith et al. 2009; Tebaldi and Sanso 2009), or a combination thereof (Sexton et al. 2012). Of interest here, probabilities of change based on MMEs often assume each individual climate model in an MME serves as an independent representation of the Earth system. This assumption ignores the fact that many GCMs follow a common genealogy and supposes a greater effective number of data points than are actually available (Pennell and Reichler 2011). Following Masson and Knutti (2011) and Knutti et al. (2013), we consider models to share a common genealogy (or to be within the same family) if those models were developed at the same institution or if one is known to have borrowed a substantial amount of code from the other (e.g., the entire atmospheric model).
To address this issue, recent work has explored methods to optimally choose a subset of models to capture the information content of an ensemble (Evans et al. 2013) or to weight models based on the correlations in their error structure over a hindcast period (Bishop and Abramowitz 2013). This latter approach of independence-based weighting has recently shown promise in ensuring that observations and the ensemble of projections are more likely to be drawn from the same distribution, and consequently improve estimates of the ensemble mean and variance for climate variables of interest (Haughton et al. 2015). As noted in Haughton et al. (2015), improvements from independence-based weighting could provide substantial gains in projection accuracy and uncertainty quantification that may be relevant for informing adaptations to large climate changes.
For this case, we used an ensemble of projections from the Coupled Model Intercomparison Project Phase 5 (CMIP5) to develop probabilistic climate information, with and without an accounting of inter-model correlations for the river basins serving the CSU system, and use the pdfs to estimate mid-century climate-related risks to the water supply security of CSU. Climate change pdfs from both methods are coupled with the previously described vulnerability assessment of the CSU water resources system to estimate climate-related risks to water supply. The probability that climate change will lead to inadequate future performance is estimated by sampling 10,000 samples of ∆T and ∆P using the pdfs from above and counting the fraction of samples that coincide with climate changes in the vulnerability assessment with indoor water demand shortfalls (Moody and Brown 2013).
-
Vulnerability Assessment Results
There are many outcome indicators that can be used to assess the performance of the CSU system, but for the screening purposed in the Integrated Water Resources Planning process, CSU initially wanted to focus on two measures: (1) storage reliability and (2) supply reliability. Storage reliability reflects the frequency that total system storage drops below a critical threshold set by the utility, while supply reliability represents the percentage of time that indoor water demands are met in a simulation. At the most basic level, system performance is considered adequate for a particular climate sequence if indoor water demands are met for the entire simulation (i.e., 100% supply reliability), since any drop in supply reliability suggests that the tap runs dry for some customers, which is considered unacceptable. We note that indoor water demand is a representative rather than encompassing performance measure, but will be the outcome we focus on in this assessment.
We first present the results of the vulnerability assessment without any consideration of climate model output. Figure 12.6 shows the climate response surface of the CSU system to changes in mean precipitation and temperature under the Status Quo and Build-Out demand scenarios. The response surfaces, developed without the use of any projection-based data, show the mean precipitation and temperature conditions under which the utility can provide adequate water services, and those climate conditions under which the reliability of their service falls below an acceptable level. Here, we define unacceptable performance as an inability to meet indoor municipal water demands. For the Status Quo system, the response surface suggests that the system can effectively manage moderately increasing temperatures and declining precipitation, but large changes beyond +2.2 °C, coupled with declining precipitation, will cause the system to fail. For the Build-Out demand scenario, the current system cannot adequately deliver water even under baseline climate conditions (no changes in temperature and precipitation), let alone reduced precipitation or increased temperatures. These results highlight that the CSU system is at risk of water supply shortages simply due to the expected growth of water demands over the next several decades. These risks grow when the specter of climate change is considered, which is considered next.
-
Likelihood of Future Climate Changes
Regional mean annual temperature and accumulated precipitation for a baseline (1975–2004) and future (2040–2070) period averaged over the Upper Colorado and Arkansas River Basins are shown in Fig. 12.7a for the Representative Concentration Pathway (RCP) (Meinshausen et al. 2011) 8.5 scenario. Models that originate from the same institution or share large blocks of code are grouped into the families used in this analysis and denoted by the same color (Knutti et al. 2013). For example, the models within the NCAR family all use key elements of the CCSM/CESM model developed at NCAR. Likewise, the MPI and CMCC models are combined because they are based on the ECHAM6 and ECHAM5 atmospheric models, respectively. Being in the same family does not guarantee that regional climate characteristics of related models will cluster, but global clustering analyses (Masson and Knutti 2011; Knutti et al. 2013) suggest an increased likelihood of clustering even on small regional scales, a hypothesis which we test here.
a Scatterplot of mean temperature and precipitation over the Upper Colorado and Arkansas River Basin area from GCMs for a baseline (1975–2004) and future (2040–2070) period. The different models are colored according to their associated “families”, b Marginal probability density functions for mid-century temperature and precipitation change across the Upper Colorado and Arkansas regions developed with (red-dashed) and without (black solid) accounting for intra-family model correlations (Color figure online)
By visual inspection of Fig. 12.7a, there is nontrivial clustering in both temperature and precipitation among models belonging to the same family. A formal hierarchical clustering of the baseline and future climatology (not shown) confirms the tendency of models within the same family to cluster with respect to simulated regional precipitation and temperature averages. The degree to which clustering occurs within each family depends on the model family being considered (GISS and HadGEM cluster well, IPSL/CMCC less so). There is a tendency for models with very similar atmospheric structures to cluster, even if other components are different.
Probability models are fit to the climate model data with and without an accounting of the correlation among individual models within a family. The estimate of intra-family model correlation for both annual mean temperature and precipitation are statistically different from zero at the 0.05 significance level. Figure 12.7b shows pdfs of annual mean temperature and precipitation change with and without an accounting of within-family correlation. When inter-model correlations are included, an increase in variance is clear for both variables due to increased sampling uncertainty associated with a reduction in the effective number of data points. Beyond the increased variance of projected climate changes, high inter-model correlations also shift the mean climate change estimate, since entire families of models are no longer regarded as independent data points, allowing, for example, centers with only a single model to assume more weight in the calculation.
The pdfs of regional climate change can be used to determine the risk posed to the CSU water system. Figure 12.8 shows the climate response surface for the Colorado water utility under 2016 demand conditions presented previously, but with the bivariate pdfs of annual temperature and precipitation change with and without intra-family correlations superimposed. We do not show the Build-Out demand conditions because system performance is unacceptable under that scenario even without climate change. The degree to which the pdfs extend into the region of unacceptable system performance in Fig. 12.8 describes the risk that the water utility may face from climate change. Visually, it is clear that the tails of the pdf developed with an accounting of intra-family model correlations extend into the region of unacceptable system performance, while those of the pdf with an independence assumption do not. A climate robustness metric is used to summarize the risk by numerically integrating the pdf mass in the region of unacceptable performance. For the pdf that does not account for model correlation, essentially 0% of its mass falls into the region of unacceptable performance. When correlations are accounted for, the metric increases to 0.7%. While still small, this non-negligible probability (similar in magnitude to a 100-year event) is important because of the intolerable impact that such shortfalls would have on the local community. Any nontrivial probability that indoor water use will have to be forcibly curtailed would motivate the water utility to invest in measures to prevent such an outcome. Thus, there is an important increase in decision-relevant, climate-change-related risk facing the water utility when we alter our interpretation of the information content present in the model ensemble.
Climate response surface displaying the conditions of mean precipitation and temperature under which CSU can (blue) and cannot (red) provide reliable indoor drinking water. Bivariate pdfs of mean temperature and precipitation are superimposed on the response surface. The red pdf was developed with an accounting of intragroup model correlation, while the black pdf was not. Both pdfs are contoured at the same levels, with the final level equal to 1.5 × 103 (Color figure online)
4 Conclusions
DS leverages traditional decision analytic methods to create a decision analysis approach specifically designed for the treatment of climate change uncertainty, while also incorporating other uncertain and deeply uncertain factors. A distinctive attribute of the approach is the use of a climate stress-testing algorithm, or stochastic weather sampler, which produces an unbiased estimation of the response of the system of interest to climate change. This avoids the numerous difficulties that are introduced when climate projections from climate models are used to drive an analysis. Instead, the information from climate projections can be introduced after the climate response is understood, in order to provide an indication of whether problematic climate changes are more or less likely than non-problematic climate changes. The approach is effective for estimating climate risks and evaluating alternative adaptation strategies. It can be incorporated into typical collaborative stakeholder processes, such as described in Poff et al. (2015). DS has been applied in a number of cases around the world, including adaptation planning for the Great Lakes of North America (Moody and Brown 2012), evaluation of climate risks to US military installations (Steinschneider et al. 2015a, b), evaluation of water supply systems (Brown et al. 2012; Whateley et al. 2014), and evaluation of long-lived infrastructure investments (e.g., Ghile et al. 2014; Yang et al. 2014), among others. It also serves as the basis for a climate risk assessment process widely adopted at the World Bank (Ray and Brown 2015).
The process of DS is designed to generate insightful guidance from the often confusing and conflicting set of climate information available to decisionmakers. It generates information that is relevant and tailored to the key concerns and objectives at hand. The process bridges the gap in methodology between top-down and bottom-up approaches to climate change impact assessment. It uses the insights that emerge from a stakeholder-driven bottom-up analysis to improve the processing of GCM projections to produce climate information that improves decisions. The process is best applied to situations where the impacts of climate change can be quantified and where models exist or can be created to represent the impacted systems or decisions. Historical data are necessary. The process can be applied both in conjunction with large climate modeling efforts and where the analysis depends simply on globally available GCM projections. It is most effective when conducted with strong engagement and interaction with the decisionmakers and stakeholders of the planning effort. The transparent nature of the process attempts to make the analysis accessible to nontechnical participants, but having some participants with technical backgrounds is beneficial.
DS was one activity in the large set of activities that comprised the CSU IWRP development process. Through the approach, the climatic conditions that caused the system to not be able to meet their performance objectives were identified. Indeed, these conditions were identified in a way that preserves the findings from the usual uncertainty associated with projecting future climate conditions. In this case, it was found that the current system is very robust to climate changes when considering the current water demand. The problematic climate conditions were a precipitation reduction of greater than 20% from the long-term average when accompanied by a mean temperature increase of 3 °C or more. Such extreme changes were considered to have a low level of concern, as is discussed below. However, for the “Build-Out” scenario, which includes an increase in water demand, the climate conditions that cause vulnerability were much wider. In this case, the system is not able to meet their performance objectives unless precipitation increases substantially and mean temperatures do not increase more than 2 °C. This scenario was considered to have a much higher level of concern.
The level of concern associated with these vulnerability scenarios could be estimated from discussion with experts on Colorado climate change, derived from an ensemble of skillful climate projections, or (preferably) discussion with experts that are informed by skillful climate projections. In this case, careful attention was given to producing the most meaningful climate information available from an ensemble of climate projections. For example, the skill of the GCMs as indicated by past performance, and the fact that many GCMs are not truly independent, were accounted for in our estimation of probabilities from the ensemble. These probabilities are not intended to represent the known probabilities of future climate change for the region. Rather, they are a quantitative representation of the information contained in the ensemble of projections. In this case, the results show that the projections indicate a very low probability of the problematic scenario identified for current demand. On the other hand, they also indicate substantial probability for the problematic conditions identified for the future Build-Out demand.
What may be required are new tools that can effectively approximate and propagate the uncertainty at each stage of the modeling chain with greater efficiency to reduce the computational burden. This is an important avenue of future work to emerge from this research.
Notes
- 1.
For some applications, simpler methods could be used—for example, cases in which temporal and spatial patterns of weather and climate are not critical to preserve. In addition, tools such as Latin Hypercube Sampling and application of PRIM for scenario identification (e.g., Groves and Lempert 2007) have been productively applied.
- 2.
In RDM the same framework is described as XLRM (X = exogenous uncertainties, L = levers, R = relationships, and M = measures of performance (see Chap. 2)
References
Apipattanavis, S., Podesta, G., Rajagopalan, B., & Katz, R. W. (2007). A semiparametric multivariate and multisite weather generator. Water Resources Research, 43, W11401. https://doi.org/10.1029/2006WR005714.
Barnett, T. P., Adam, J.C., & Lettenmaier, D. P. (2005). Potential impacts of a warming climate on water availability in snow-dominated regions. Nature, 438, 303–309. https://doi.org/10.1038/nature04141.
Bishop, C., & Abramowitz, G. (2013) Climate model dependence and the replicate Earth paradigm. Climate Dynamics, 41(3–4), 885–900.
Brown, C., Ghile, Y., Laverty, M., & Li, K. (2012). Decision scaling: linking bottom-up vulnerability analysis with climate projections in the water sector. Water Resources Research, 48, W09537. https://doi.org/10.1029/2011wr011212.
Christierson, B. V., Vidal, J., & Wade, S. D. (2012). Using UKCP09 probabilistic climate information for UK water resource planning. Journal of Hydrology, 424, 48–67.
Connell-Buck, C. R., Medellin-Azuara, J., Lund, J. R., & Madani K. (2011). Adapting California’s water system to warm vs. dry climates. Climate Change, 109, 133–149.
Evans, J. P., Ji, F., Abramowitz, G., & Ekstrom, M. (2013). Optimally choosing small ensemble members to produce robust climate simulations. Environmental Research Letters, 8(4). https://doi.org/10.1088/1748-9326/8/4/044050.
Ghile, Y. B., Taner, M. U., Brown C. M., & Grijsen, J. G. (2014). Bottom-up climate risk assessment of infrastructure investment in the Niger River Basin. Climatic Change, 122(1–2), 97–111.
Gleckler, P. J., Taylor, K. E., & Doutriaux, C. (2008). Performance metrics for climate models. Journal Geophysical Research, 113, D06114.
Goddard, L., Aitchellouche, Y., Baethgen, W., Dettinger, M., Graham, R., Hayman, P., et al. (2010). Providing seasonal-to-interannual climate information for risk management and decision-making. Procedia Environmental Sciences, 1, 81–101.
Groves, D. G., & Lempert, R. J. (2007). A new analytic method for finding policy-relevant scenarios. Global Environmental Change, 17, 73–85.
Groves, D. G., Yates, D., & Tebaldi, C. (2008). Developing and applying uncertain global climate change projections for regional water management planning. Water Resources Research, 44.
Hall, J., et al. (2012). Towards risk-based water resources planning in England and Wales under a changing climate. Water and Environment Journal, 26, 118–129.
Haughton, N., Abramowitz, G., Pitman, A., & Phipps, S. J. (2015). Weighting climate model ensembles for mean and variance estimates, Climate Dynamics. https://doi.org/10.1007/s00382-015-2531-3.
Hazen, A. (1914). Storage to be provided in impounding reservoirs for municipal water supply. Transactions of the American Association of Civil Engineers, 77, 1539–1669.
Johnson, F., Westra, S., Sharma, A., Pitman, A. J. (2011). An assessment of GCM skills in simulating persistence across multiple scales. Journal of Climate, 24(14), 3609–3623.
Knutti, R., Furrer, R., Tebaldi, C., Cermak, J., & Meehl, G. A. (2010). Challenges in combining projections from multiple climate models. Journal of Climate, 23, 2739–2758.
Knutti, R., Masson, D., & Gettelman, A. (2013). Climate model genealogy: Generation CMIP5 and how we got there. Geophysical Research Letters, 40, 1194–1199.
Kwon, H.-H., Lall, U., & Khalil A. F. (2007). Stochastic simulation model for nonstationary time series using an autoregressive wavelet decomposition: Applications to rainfall and temperature. Water Resources Research, 43, W05407. https://doi.org/10.1029/2006WR005258.
Labadie, J., Baldo, M., & Larson, R. (2000). MODSIM: Decision support system for river basin management: Documentation and user manual. Ft. Collins, CO: Dept. of Civil Eng., Colo. State Univ.
Lopez, A., et al. (2006). Two approaches to quantifying uncertainty in global temperature changes. Journal of Climate, 19, 4785–4796.
Manning, L., Hall, J., Fowler, H., Kilsby, C., & Tebaldi, C. Using probabilistic climate change information from a multimodel ensemble for water resources assessment. Water Resources Research, 45.
Masson, D., & Knutti, R. (2011). Climate model genealogy. Geophysical Research Letters, 38.
McCabe, G. J., Betancourt, J. L., & Hidalgo, H. G. (2007). Associations of decadal to multidecadal sea-surface temperature variability with upper colorado river flow. JAWRA Journal of the American Water Resources Association, 43, 183–192. https://doi.org/10.1111/j.1752-1688.2007.00015.
McCabe, G. J., Palecki, M., & Betacourt, J. (2004). Pacific and Atlantic Ocean influences on multidecadal drought frequency in the United States. Proceedings of the National Academy of Sciences of the United States of America, 101(12), 4136–4141.
Meinshausen, M., et al. (2011). The RCP Greenhouse Gas Concentrations and their extensions from 1765 to 2300. Climatic Change, 109, 213–241.
Moody, P., & Brown, C. (2012). Modeling stakeholder-defined climate risk on the Upper Great Lakes. Water Resources Research, 48, W10524. https://doi.org/10.1029/2012WR012497.
Moody, P., & Brown, C. (2013). Robustness indicators for evaluation under climate change: Application to the upper Great Lakes. Water Resources Research, 49, 357. https://doi.org/10.1002/wrcr.20228.
Murphy, J. M., Sexton, D. M. H., Barnett, D. N., Jones, G. S., Webb, M. J., Collins, M., & Stainforth D. A. (2004, August). Quantification of modelling uncertainties in a large ensemble of climate change simulations. Nature, 430, 12.
Nowak, K., Hoerling, M., Rajagopalan, B., & Zagona, E. (2012). Colorado river basin hydroclimatic variability. Journal of Climate, 25, 4389–4403. http://dx.doi.org/10.1175/JCLI-D-11-00406.1
Pennell, C., & Reichler, T. (2011). On the effective number of climate models. Journal of Climate, 24, 2358–2367.
Poff, L., Brown, C., et al. (2015). Eco-engineering decision scaling for sustainable water management under future hydrologic uncertainty. Nature Climate Change, 6, 25. https://doi.org/10.1038/nclimate2765.
Ray, P., & Brown, C. (2015). Confronting climate uncertainty in water resources planning and project design—The decision tree framework (p. 128). Washington, DC.: World Bank Group Press.
Rocheta, E., Sugiyanto, M., Johnson, F., Evans, J., & Sharma, A. (2014). How well do general circulation models represent low-frequency rainfall variability? Water Resources Research, 50, 2108–2123.
Schlaifer, R., & Raiffa, H. (1961). Applied statistical decision theory (p. 356). Boston: Clinton Press Inc.
Sexton, D. M. H., Murphy, J. M., Collins, M., & Webb M. J. (2012). Multivariate probability projections using imperfect climate models part I: Outline of methodology. Climate Dynamics, 38 (11–12), 2513–2542.
Smith, R. L., Tebaldi, C., Nychka, D., & Mearns, L. O. (2009). Bayesian modeling of uncertainty in ensembles of climate models. Journal of the American Statistical Association, 104, 97–116.
Stainforth, D. A., et al. (2007). Issues in the interpretation of climate model ensembles to inform decisions. Philosophical Transactions of the Royal Society of London A, 365, 2163–2177.
Steinschneider, S., & Brown, C. (2013). A semiparametric multivariate, multi-site weather generator with low-frequency variability for use in climate risk assessments. Water Resources Research, 49, 7205.
Steinschneider, S., McCrary, R., Mearns, L., & Brown, C. (2015a). The effects of climate model similarity on probabilistic climate projections and the implications for local, risk-based adaptation planning. Geophysical Research Letters, 42, 5014–5022. https://doi.org/10.1002/2015GL064529.
Steinschneider, S., McCrary, R., Wi, S., Mulligan, K., Mearns, L. O., & Brown, C. (2015b). Expanded decision-scaling framework to select robust long-term water-system plans under hydroclimatic uncertainties. Journal of Water Resources Planning and Management, 141, 04015023.
Tallaksen, L. M., & Stahl K. (2014). Spatial and temporal patterns of large-scale droughts in Europe: Model dispersion and performance. Geophysical Research Letters, 41, 429–434. https://doi.org/10.1002/2013GL058573.
Tebaldi, C., & Sansó, B. (2009). Joint projections of temperature and precipitation change from multiple climate models: A hierarchical Bayesian approach. Journal of the Royal Statistical Society: Series A (Statistics in Society), 172, 83–106
Tebaldi, C., Smith, R. L., Nychka, D., & Mearns, L. O. (2005). Quantifying uncertainty in projections of regional climate change: A Bayesian approach to the analysis of multimodel ensembles. Journal of Climate, 18, 1524–1540.
Thornton, P. E., Thornton, M. M., Mayer, B. W., Wilhelmi, N., Wei, Y., Devarakonda, R., & Cook, R. B. (2014). Daymet: Daily surface weather data on a 1-km grid for North America, Version 2. ORNL DAAC, Oak Ridge, Tennessee, USA. Accessed July 07, 2013. http://dx.doi.org/10.3334/ORNLDAAC/1219
Whateley, S., Steinschneider, S., & Brown, C. (2014). A climate change range-based method for estimating robustness for water resources supply. Water Resources Research, 50, 8944. https://doi.org/10.1002/2014wr015956.
Winston, W. L., & Goldberg, J. B. (2004). Operations research: Applications and algorithms (Vol. 3). Belmont: Thomson Brooks/Cole.
Wise, E. K., Wrzesien, M. L., Dannenberg, M. P., & McGinnis, D. L. (2015). Cool-season precipitation patterns associated with teleconnection interactions in the United States. Journal of Applied Meteorology and Climatology, 54, 494–505. http://dx.doi.org/10.1175/JAMC-D-14-0040.1
Yang, Y.-C., Brown, C., Yu, W., Wescoat, J., & Ringler, C. (2014). Water governance and adaptation to climate change in the Indus River Basin. Journal of Hydrology, 519, 2527. https://doi.org/10.1016/j.jhydrol.2014.08.055.
Yates, D., Sieber, J., Purkey, D., & Huber-Lee, A. (2005). WEAP21—A demand-, priority-, and preference-driven water planning model: part 1: model characteristics. Water International, 30, 487–500.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2019 The Author(s)
About this chapter
Cite this chapter
Brown, C., Steinschneider, S., Ray, P., Wi, S., Basdekas, L., Yates, D. (2019). Decision Scaling (DS): Decision Support for Climate Change. In: Marchau, V., Walker, W., Bloemen, P., Popper, S. (eds) Decision Making under Deep Uncertainty. Springer, Cham. https://doi.org/10.1007/978-3-030-05252-2_12
Download citation
DOI: https://doi.org/10.1007/978-3-030-05252-2_12
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-05251-5
Online ISBN: 978-3-030-05252-2
eBook Packages: Business and ManagementBusiness and Management (R0)