Durrmeyer-Type Bernstein Operators Based on (p, q)-Integers with Two Variables

Abstract

The purpose of this study is to introduce the Durrmeyer-type Bernstein operators based on $\left ( p,q\right )$-integers with two variables. Then, we compute the error of approximation by using modulus of continuity and the degree of approximation by means of Lipschitz class. Finally, we obtain the numerical results in detail.

1 Introduction

Recently, one of the most interesting areas of research in approximation theory is the application of $\left ( p,q\right )$-calculus. Mursaleen et al. initiated the $\left ( p,q\right )$-type generalisation of linear positive operators, describing the $\left ( p,q\right )$-analogue of Bernstein operators [8] as:

$$\displaystyle \begin{aligned} B_{n,p,q}\left( f;x\right) {=}\frac{1}{p^{\frac{n\left( n-1\right) }{2}}} \sum_{k=0}^{n}\left[\begin{array}{c} n \\ k \end{array}\right]_{p,q}p^{\frac{k\left( k-1\right) }{2} }x^{k}\prod_{s=0}^{n-k-1}\left( p^{s}-q^{s}x\right) f\left( \frac{ \left[ k\right] _{p,q}}{p^{k-n}\left[ n\right] _{p,q}}\right) ,\ \ \ \ \end{aligned}$$

where $x\in \left [ 0,1\right ]$, 0 < q < p ≤ 1, the $\left ( p,q\right )$ -integers are given as [5]:

$$\displaystyle \begin{aligned} \left[ k\right] _{p,q}=\frac{p^{k}-q^{k}}{p-q}. \end{aligned}$$

For each $k\in \mathbb {N}_{0}$, the $\left ( p,q\right )$-factorial is represented by:

$$\displaystyle \begin{aligned} \left[ k\right] _{p,q}!=\left\{ \begin{array}{cc} \left[ k\right] _{p,q}\left[ k-1\right] _{p,q}\ldots\left[ 1\right] _{p,q}, & k=1,2,3,\ldots, \\ 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ , & k=0 \end{array} \right. \end{aligned}$$

and $\left ( p,q\right )$-binomial coefficients are defined as:

$$\displaystyle \begin{aligned} \left[\begin{array}{c} n \\ k \end{array}\right]_{p,q}=\frac{\left[ n\right] _{p,q}!}{\left[ n-k\right] _{p,q}!\left[ k\right] _{p,q}!} \end{aligned}$$

where n ≥ k ≥ 0.

Then, Sidharth and Agrawal [12] introduced the $\left (p,q\right )$-analogue of Bernstein–Schurer operators as:

$$\displaystyle \begin{aligned} \bar{B}_{n,s}\left( f;p,q;x\right) =\sum_{k=0}^{n+s}p^{\frac{k\left(k-1\right) }{2}-\frac{\left( n+s\right) \left( n+s-1\right) }{2}}\left[\begin{array}{c} n+s \\ k \end{array}\right]_{p,q}x^{k}\left( 1-x\right) _{p,q}^{n+s-k}f\left( p^{n-k}\frac{\left[ k\right] _{p,q}}{\left[ n\right] _{p,q}}\right) \end{aligned}$$

where $x\in \left [ 0,1+s\right ]$, $s\in \mathbb {N}_{0}$, 0 < q ≤ p < 1 and $n\in \mathbb {N}$.

Then, Gemikonakli and Vedi-Dilek constructed the Chlodowsky variant of Bernstein–Schurer operators based on $\left ( p,q\right )$-integers in [4] as:

$$\displaystyle \begin{aligned} \bar{C}_{n,s}\left( f;p,q;x\right) {=}\sum_{k=0}^{n+s}f\left( p^{n-k} \frac{\left[ k\right] _{p,q}}{\left[ n\right] _{p,q}}b_{n}\right) p^{\frac{ k\left( k-1\right) }{2}-\frac{\left( n+s-1\right) \left( n+s\right) }{2}} \left[\begin{array}{c} n+s \\ k \end{array}\right]_{p,q}\left( \frac{x}{b_{n}}\right) ^{k}\left( 1{-}x\right) _{p,q}^{n+s-k} \end{aligned}$$

where $x\in \left [ 0,b_{n}\right ]$, n, $s\in \mathbb {N}$, 0 < q < p ≤ 1 and $\left ( b_{n}\right )$ is the positive increasing sequence with b _n →∞ and $\frac {b_{n}}{n}\rightarrow 0$ as n →∞.

Over the past 2 years, there has been a considerable amount of research on the $\left ( p,q\right )$-analogue of Bernstein operators (see [1,2,3, 5,6,7, 9,10,11,12, 14]).

In 2016, Durrmeyer-type generalisation of (p, q)-Bernstein operators was defined by Sharma in [13] as:

$$\displaystyle \begin{aligned} D_{n}^{(p,q)}\left( f;x\right) =\left[ n+1\right] _{p,q}p^{-n^{2}}\sum \limits_{k=0}^{n}b_{n,k}^{\left( p,q\right) }\left( x\right) \left( \frac{q}{ p}\right) ^{-k}\int\limits_{0}^{1}b_{n,k}^{\left( p,q\right) }\left( qt\right) f\left( t\right) d_{p,q}t\,\text{,\quad }x\in \left[ 0,1 \right] \end{aligned}$$

where $b_{n,k}^{\left ( p,q\right ) }\left ( x\right ) =p^{k\left ( k-1\right ) /2} \left [\begin {array}{c} n+s \\ k \end {array}\right ]_{p,q}x^{k}\left ( 1-x\right ) _{p,q}^{n-k}$ and 0 < q < p ≤ 1 , $n\in \mathbb {N}$.

To giving the estimations, Sharma proved Lemmas 1 and 2, respectively:

Lemma 1

For s = 0, 1, 2, 3, …, we have

$$\displaystyle \begin{aligned} \int\limits_{0}^{1}b_{n,k}^{\left( p,q\right) }\left( qt\right) t^{s}d_{p,q}t=\left( \frac{q}{p}\right) ^{k}p^{-ks}p^{n(n+2s+1)/2}\frac{ \left[ n\right] _{p,q}!\left[ k+s\right] _{p,q}!}{\left[ k\right] _{p,q}! \left[ n+s+1\right] _{p,q}!}\mathit{\text{.}} \end{aligned}$$

Lemma 2

Let $D_{n}^{\left ( p,q\right ) }\left ( f;x\right )$ be given in Lemma 1 in [ 13 ]. Then,

• (i) $D_{n}^{\left ( p,q\right ) }\left ( 1;x\right ) =1,$

• (ii) $D_{n}^{\left ( p,q\right ) }\left ( t;x\right ) =\frac {1}{\left [ n+2 \right ] _{p,q}}\left ( p^{n}+q\left [ n\right ] _{p,q}x\right )$ ,

• (iii) $D_{n}^{\left ( p,q\right ) }\left ( t^{2};x\right )$ $=\frac {\left ( p+q\right ) p^{2n}+\left ( p+q\right ) ^{2}qp^{n-1}\left [ n\right ] _{p,q}x+q^{4} \left [ n\right ] _{p,q}\left [ n-1\right ] _{p,q}x^{2}}{\left [ n+2\right ] _{p,q} \left [ n+3\right ] _{p,q}}$.

Obtaining the proof of Lemmas 1 and 2, we need the following definition and corollary:

Definition 1

Let s,$t\in \mathbb {R}$ and for 0 < q < p ≤ 1, (p, q)-beta integral is defined by

$$\displaystyle \begin{aligned} \int\limits_{0}^{1}x^{t-1}\left( 1-qx\right) _{p,q}^{s-1}d_{p,q}x\text{.} \end{aligned}$$

Corollary 1

For 0 ≤ k ≤ n and 0 < q < p ≤ 1, we have relation between (p, q) -integers and q-integers:

$$\displaystyle \begin{aligned} \left[ n\right] _{p,q}=p^{n-1}\left[ n\right] _{q/p} \end{aligned}$$

and

$$\displaystyle \begin{aligned} \left[\begin{array}{c} n \\ k \end{array}\right]_{p,q}=p^{k\left( n-k\right) }\left[\begin{array}{c} n \\ k \end{array}\right]_{q/p}\mathit{\text{.}} \end{aligned}$$

This chapter is structured in the following way:

Section 2 introduces the Durrmeyer-type Bernstein operators based on $\left ( p,q\right )$-integers with two variables and investigates the moments of the operator. In Sect. 3, we obtain the order of convergence of the Durrmeyer-type Bernstein operators based on $\left ( p,q\right )$-integers with two variables by means of Lipschitz class functions and the full and partial modulus of continuities. Finally, in Sect. 4, numerical results to illustrate the contribution of the Durrmeyer-type Bernstein operators based on $\left ( p,q\right )$-integers with two variables are presented.

2 Construction of the Operators

In this section, we introduce Durrmeyer-type Bernstein operators based on $\left ( p,q\right )$-integers with two variables. Henceforth, let $I=\left [ 0,1\right ]$ and for I ² = I × I, let $C\left ( I^{2}\right )$ denote the space of all real-valued functions on I ² endowed with the norm $\left \Vert f\right \Vert _{I}=\sup \limits _{\left ( x,y\right ) \in I^{2}}\left \vert f\left ( x,y\right ) \right \vert$. Now, if $f\in C\left ( I^{2}\right )$ and 0 < q _1, q ₂ < p ₁, p ₂ ≤ 1, then we construct Durrmeyer-type Bernstein operators based on $\left ( p,q\right )$-integers with two variables by:

$$\displaystyle \begin{aligned} & D_{n,m}\left( f;\left( p_{1,}q_{1}\right) ,\left( p_{2},q_{2}\right) ;x,y\right) {} \\ & := \left[ n{+}1\right] _{p_{n},q_{n}}\left[ m+1\right] _{p_{m},q_{m}}p_{1}^{-n^{2}}p_{2}^{-m^{2}} \sum_{k=0}^{n} \sum_{l=0}^{m} \left( \frac{q_{1}}{p_{1}}\right) ^{-k}\left( \frac{q_{2}}{p_{2}}\right) ^{-l} \mathcal{R}_{n,k}(p_{1},q_{1};x) \notag \\ & \times \mathcal{R}_{m,l}(p_{2},q_{2};y) \int\limits_{0}^{1}\int\limits_{0}^{1}\mathcal{R} _{n,k}(p_{1},q_{1};qt)\mathcal{R}_{m,l}(p_{2},q_{2};qs)f\left( t,s\right) d_{p_{1,}q_{1}}td_{p_{2,}q_{2}}s , \notag \end{aligned} $$

(2.1)

where n, $m\,{\in }\, \mathbb {N}$, $\left ( x,y\right ) \in I^{2}$, and $\mathcal {R} _{n,k}(p_{1},q_{1};x)=p_{1}^{\frac {k\left ( k{-}1\right ) }{2}}{\left [\begin {array}{c} n \\ k \end {array}\right ]_{{p_{1},q_{1}}} x^{k}\left ( 1{-}x\right ) _{p_{1},q_{1}}^{n-k}}$.

Now, for giving our estimations we need that the following equalities hold for Eq. (2.1):

Lemma 3

Using the Lemma 2 , directly, we have

$$\displaystyle \begin{gathered} D_{n,m}\left( 1;\left( p_{1,}q_{1}\right) ,\left( p_{2},q_{2}\right) ;x,y\right) =1, \\ D_{n,m}\left( t;\left( p_{1,}q_{1}\right) ,\left( p_{2},q_{2}\right) ;x,y\right) =\frac{1}{\left[ n+2\right] _{p_{n},q_{n}}}\left( p_{n}^{n}+q_{n}\left[ n\right] _{p_{1},q_{1}}x\right) , \\ D_{n,m}\left( s;\left( p_{1,}q_{1}\right) ,\left( p_{2},q_{2}\right) ;x,y\right) =\frac{1}{\left[ m+2\right] _{p_{2},q_{2}}}\left( p_{2}^{m}+q_{2}\left[ m\right] _{p_{2},q_{2}}y\right) , \end{gathered} $$

$$\displaystyle \begin{gathered}D_{n,m}\left( t^{2};\left( p_{1,}q_{1}\right) ,\left( p_{2},q_{2}\right) ;x,y\right) \\ =\frac{\left( p_{1}+q_{1}\right) p_{1}^{2n}+\left( p_{1}+q_{1}\right) ^{2}q_{1}p_{1}^{n-1}\left[ n\right] _{p_{1},q_{1}}x+q_{1}^{4}\left[ n\right] _{p_{1},q_{1}}\left[ n-1\right] _{p_{1},q_{1}}x^{2}}{\left[ n+2\right] _{p_{1},q_{1}}\left[ n+3\right] _{p_{1},q_{1}}}, \end{gathered} $$

$$\displaystyle \begin{gathered}D_{n,m}\left( s^{2};\left( p_{1,}q_{1}\right) ,\left( p_{2},q_{2}\right) ;x,y\right) \\ =\frac{\left( p_{2}+q_{2}\right) p_{2}^{2m}+\left( p_{2}+q_{2}\right) ^{2}q_{2}p_{2}^{m-1}\left[ m\right] _{p_{2},q_{2}}y+q_{2}^{4}\left[ m\right] _{p,q}\left[ m-1\right] _{p,q}y^{2}}{\left[ m+2\right] _{p_{2},q_{2}}\left[ m+3\right] _{p_{2},q_{2}}} \end{gathered} $$

$$\displaystyle \begin{gathered}D_{n,m}\left( t^{2}+s^{2};\left( p_{1,}q_{1}\right) ,\left( p_{2},q_{2}\right) ;x,y\right) \\ =\frac{\left( p_{1}+q_{1}\right) p_{1}^{2n}+\left( p_{1}+q_{1}\right) ^{2}q_{1}p_{1}^{n-1}\left[ n\right] _{p_{1},q_{1}}x+q_{1}^{4}\left[ n\right] _{p_{1},q_{1}}\left[ n-1\right] _{p_{1},q_{1}}x^{2}}{\left[ n+2\right] _{p_{1},q_{1}}\left[ n+3\right] _{p_{1},q_{1}}} \\ +\frac{\left( p_{2}+q_{2}\right) p_{2}^{2m}+\left( p_{2}+q_{2}\right) ^{2}q_{2}p_{2}^{m-1}\left[ m\right] _{p_{2},q_{2}}y+q_{2}^{4}\left[ m\right] _{p,q}\left[ m-1\right] _{p,q}y^{2}}{\left[ m+2\right] _{p_{2},q_{2}}\left[ m+3\right] _{p_{2},q_{2}}}. \end{gathered} $$

Using the Korovkin’s theorem, we can obtain the following theorem.

Theorem 1

For all $f\in C\left ( I^{2}\right )$ and assuming that $q_{1}:\left ( q_{n}\right )$ , $q_{2}:\left ( q_{m}\right )$ ; $p_{1}:\left ( p_{n}\right )$ , $p_{2}:\left ( p_{m}\right )$ with 0 < q _n, q _m < p _n, p _m ≤ 1 such that q _n → 1 and q _m → 1 as n, m →∞, we get

$$\displaystyle \begin{aligned} \lim_{n,m\rightarrow \infty }\left\Vert D_{n,m}\left( f;\left( p_{n,}q_{n}\right) ,\left( p_{m},q_{m}\right) ;\cdot ,\cdot \right) -f\left( \cdot ,\cdot \right) \right\Vert _{I}=0\mathit{\text{.}} \end{aligned}$$

3 Order of Convergence

In this section, we compute the rate of convergence of the operators in terms of the modulus of continuity and then the degree of approximation in terms of Lipschitz-type space.

Let $f\in C\left ( I^{2}\right )$ and x, y ∈ I. Then, the definition of the modulus of continuity of f is given by:

$$\displaystyle \begin{aligned} \omega (f;\delta )=\max_{\substack{ \sqrt{\left( x_{1}-x_{2}\right) ^{2}+\left( y_{1}-y_{2}\right) ^{2}\leq \delta } \\ x,y\in C\left( I\right) }}\left\vert f\left( x_{1},y_{1}\right) -f\left( x_{2},y_{2}\right) \right\vert \text{.} {} \end{aligned} $$

(3.1)

It is known that for any δ > 0

$$\displaystyle \begin{aligned} \left\vert f\left( x_{1},y_{1}\right) -f\left( x_{2},y_{2}\right) \right\vert \leq \omega (f;\delta )\left( \frac{\sqrt{\left( x_{1}-x_{2}\right) ^{2}+\left( y_{1}-y_{2}\right) ^{2}}}{\delta }+1\right) \text{.} \end{aligned}$$

Theorem 2

For any $f\in C\left ( I^{2}\right )$ and let the following inequalities

$$\displaystyle \begin{gathered} \left\vert D_{n,m}\left( f;\left( p_{1,}q_{1}\right) ,\left( p_{2},q_{2}\right) ;x,y\right) -f(x,y)\right\vert \leq 2\left[ \omega ^{\left( 1\right) }\left( f;\delta _{n}\left( x\right) \right) +\omega ^{\left( 2\right) }\left( f;\delta _{m}\left( y\right) \right) \right] {} \end{gathered} $$

(3.2)

$$\displaystyle \begin{gathered} \left\vert D_{n,m}\left( f;\left( p_{1,}q_{1}\right) ,\left( p_{2},q_{2}\right) ;x,y\right) -f(x,y)\right\vert \leq 2\omega \left( f; \sqrt{\delta _{n}^{2}+\delta _{m}^{2}}\right) {} \end{gathered} $$

(3.3)

be satisfied where

$$\displaystyle \begin{aligned} \delta _{n}^{2}\left( x\right) :=\frac{\left( p_{1}+q_{1}\right) p_{1}^{2n}+\left( p_{1}+q_{1}\right) ^{2}q_{1}p_{1}^{n-1}\left[ n\right] _{p_{1},q_{1}}x+q_{1}^{4}\left[ n\right] _{p_{1},q_{1}}\left[ n-1\right] _{p_{1},q_{1}}x^{2}}{\left[ n+2\right] _{p_{1},q_{1}}\left[ n+3\right] _{p_{1},q_{1}}} {} \end{aligned} $$

(3.4)

and

$$\displaystyle \begin{aligned} \delta _{m}^{2}\left( y\right) :=\frac{\left( p_{2}+q_{2}\right) p_{2}^{2m}+\left( p_{2}+q_{2}\right) ^{2}q_{2}p_{2}^{m-1}\left[ m\right] _{p_{2},q_{2}}y+q_{2}^{4}\left[ m\right] _{p,q}\left[ m-1\right] _{p,q}y^{2} }{\left[ m+2\right] _{p_{2},q_{2}}\left[ m+3\right] _{p_{2},q_{2}}}. {} \end{aligned} $$

(3.5)

Proof

We directly have

$$\displaystyle \begin{aligned} & D_{n,m}\left( f;\left( p_{1,}q_{1}\right) ,\left( p_{2},q_{2}\right) ;x,y\right) -f(x,y) \\ & =\left[ n+1\right] _{p_{1},q_{1}}\left[ m+1\right] _{p_{2},q_{2}}p_{1}^{-n^{2}}p_{1}^{-m^{2}}\sum_{k=0}^{n}\sum_{l=0}^{m}\left( \frac{q_{1}}{p_{1}}\right) ^{-k}\left( \frac{q_{2}}{p_{2}}\right) ^{-l} \mathcal{R}_{n,k}(p_{1},q_{1};x)\mathcal{R}_{m,l}(p_{2},q_{2};y) \\ & \times \int\limits_{0}^{1}\int\limits_{0}^{1}\mathcal{R} _{n,k}(p_{1},q_{1};qt)\mathcal{R}_{m,l}(p_{2},q_{2};qs)\left[ f\left( t,s\right) -f\left( x,y\right) \right] d_{p_{1,}q_{1}}td_{p_{2,}q_{2}}s \\ & =\left[ n+1\right] _{p_{1},q_{1}}\left[ m+1\right] _{p_{2},q_{2}}p_{1}^{-n^{2}}p_{1}^{-m^{2}}\sum_{k=0}^{n}\sum_{l=0}^{m}\left( \frac{q_{1}}{p_{1}}\right) ^{-k}\left( \frac{q_{2}}{p_{2}}\right) ^{-l} \mathcal{R}_{n,k}(p_{1},q_{1};x)\mathcal{R}_{m,l}(p_{2},q_{2};y) \\ & \times \int\limits_{0}^{1}\int\limits_{0}^{1}\mathcal{R} _{n,k}(p_{1},q_{1};qt)\mathcal{R}_{m,l}(p_{2},q_{2};qs)\left[ f\left( t,s\right) -f\left( x,s\right) +f\left( x,s\right) -f\left( x,y\right) \right] d_{p_{1,}q_{1}}td_{p_{2,}q_{2}}s \end{aligned} $$

By linearity and positivity of the operators, we get

$$\displaystyle \begin{aligned} & \left\vert D_{n,m}\left( f;\left( p_{1,}q_{1}\right) ,\left( p_{2},q_{2}\right) ;x,y\right) -f(x,y)\right\vert \\ & \leq \left[ n+1\right] _{p_{1},q_{1}}\left[ m+1\right] _{p_{2},q_{2}}p_{1}^{-n^{2}}p_{2}^{-m^{2}}\sum_{k=0}^{n}\sum_{l=0}^{m}\left( \frac{q_{1}}{p_{1}}\right) ^{-k}\left( \frac{q_{2}}{p_{2}}\right) ^{-l} \mathcal{R}_{n,k}(p_{1},q_{1};x)\mathcal{R}_{m,l}(p_{2},q_{2};y) \\ & \times \int\limits_{0}^{1}\int\limits_{0}^{1}\mathcal{R} _{n,k}(p_{1},q_{1};qt)\mathcal{R}_{m,l}(p_{2},q_{2};qs)\left\vert f\left( t,s\right) -f\left( x,s\right) \right\vert d_{p_{1,}q_{1}}td_{p_{2,}q_{2}}s \end{aligned} $$

$$\displaystyle \begin{aligned}& +\left[ n+1\right] _{p_{1},q_{1}}\left[ m+1\right] _{p_{2},q_{2}}p_{1}^{-n^{2}}p_{2}^{-m^{2}}\sum_{k=0}^{n}\sum_{l=0}^{m}\left( \frac{q_{1}}{p_{1}}\right) ^{k}\left( \frac{q_{2}}{p_{2}}\right) ^{-l} \mathcal{R}_{n,k}(p_{1},q_{1};x)\mathcal{R}_{m,l}(p_{2},q_{2};y) \\ & \times \int\limits_{0}^{1}\int\limits_{0}^{1}\mathcal{R} _{n,k}(p_{1},q_{1};qt)\mathcal{R}_{m,l}(p_{2},q_{2};qs)\left\vert f\left( t,s\right) -f\left( x,y\right) \right\vert d_{p_{1,}q_{1}}td_{p_{2,}q_{2}}s \end{aligned} $$

$$\displaystyle \begin{aligned}& \leq \left[ n+1\right] _{p_{1},q_{1}}\left[ m+1\right] _{p_{2},q_{2}}p_{1}^{-n^{2}}p_{1}^{-m^{2}}\sum_{k=0}^{n}\sum_{l=0}^{m}\left( \frac{q_{1}}{p_{1}}\right) ^{-k}\left( \frac{q_{2}}{p_{2}}\right) ^{-l} \mathcal{R}_{n,k}(p_{1},q_{1};x)\mathcal{R}_{m,l}(p_{2},q_{2};y) \\ & \times \int\limits_{0}^{1}\int\limits_{0}^{1}\mathcal{R} _{n,k}(p_{1},q_{1};qt)\mathcal{R}_{m,l}(p_{2},q_{2};qs)\omega ^{\left( 1\right) }\left( f;\left\vert t-x\right\vert \right) d_{p_{1,}q_{1}}td_{p_{2,}q_{2}}s \\ & +\left[ n+1\right] _{p_{1},q_{1}}\left[ m+1\right] _{p_{2},q_{2}}p_{1}^{-n^{2}}p_{1}^{-m^{2}}\sum_{k=0}^{n}\sum_{l=0}^{m}\left( \frac{q_{1}}{p_{1}}\right) ^{-k}\left( \frac{q_{2}}{p_{2}}\right) ^{l} \mathcal{R}_{n,k}(p_{1},q_{1};x)\mathcal{R}_{m,l}(p_{2},q_{2};y) \\ & \times \int\limits_{0}^{1}\int\limits_{0}^{1}\mathcal{R} _{n,k}(p_{1},q_{1};qt)\mathcal{R}_{m,l}(p_{2},q_{2};qs)\omega ^{\left( 2\right) }\left( f;\left\vert s-y\right\vert \right) d_{p_{1,}q_{1}}td_{p_{2,}q_{2}}s \\ & =\varOmega _{1}\left( x,y\right) +\varOmega _{2}\left( x,y\right) . \end{aligned} $$

Using Lemma 1, we have

$$\displaystyle \begin{aligned} & \varOmega _{1}\left( x,y\right) \\ & =\left[ n+1\right] _{p_{1},q_{1}}\left[ m{+}1\right] _{p_{2},q_{2}}p_{1}^{-n^{2}}p_{1}^{-m^{2}}\sum_{k=0}^{n}\sum_{l=0}^{m}\left( \frac{q_{1}}{p_{1}}\right) ^{-k}\left( \frac{q_{2}}{p_{2}}\right) ^{-l} \mathcal{R}_{n,k}(p_{1},q_{1};x)\mathcal{R}_{m,l}(p_{2},q_{2};y) \end{aligned} $$

$$\displaystyle \begin{aligned}& \times \int\limits_{0}^{1}\int\limits_{0}^{1}\mathcal{R} _{n,k}(p_{1},q_{1};qt)\mathcal{R}_{m,l}(p_{2},q_{2};qs)\omega ^{\left( 1\right) }\left( f;\left\vert t-x\right\vert \right) d_{p_{1,}q_{1}}td_{p_{2,}q_{2}}s \\ & \leq \omega ^{\left( 1\right) }\left( f;\delta _{n}^{2}\left( x\right) \right) \\ & \times \left[ 1+\frac{\left[ n+1\right] _{p_{1},q_{1}}}{\delta _{n}^{2}\left( x\right) }p_{1}^{-n^{2}}\sum_{k=0}^{n}\left( \frac{q_{1}}{ p_{1}}\right) ^{k}\mathcal{R}_{n,k}(p_{1},q_{1};x)\int\limits_{0}^{1} \mathcal{R}_{n,k}(p_{1},q_{1};qt)\left( f;\left\vert t-x\right\vert \right) d_{p_{1,}q_{1}}t\right] . \end{aligned} $$

Using the Cauchy–Schwarz inequality, we get

$$\displaystyle \begin{aligned} \varOmega _{1}\left( x,y\right) \leq 2\omega ^{\left( 1\right) }\left( f;\delta _{n}^{2}\left( x\right) \right) {} \end{aligned} $$

(3.6)

where we chose $\delta _{n}^{2}$ $\left ( x\right )$ as in Eq. (3.4).

In the same way, we obtain

$$\displaystyle \begin{aligned} \varOmega _{2}\left( x,y\right) \leq 2\omega ^{\left( 2\right) }\left( f;\delta _{m}^{2}\left( y\right) \right) {} \end{aligned} $$

(3.7)

where $\delta _{m}^{2}\left ( y\right )$ is given in Eq. (3.5). Combining Eqs. (3.6) and (3.7), we get Eq. (3.2).

Now, by using linearity and the monotonicity of the operators, and taking into account Eq. (3.3), we have

$$\displaystyle \begin{aligned} & \left\vert D_{n,m}\left( f;\left( p_{1,}q_{1}\right) ,\left( p_{2},q_{2}\right) ;x,y\right) -f(x,y)\right\vert \\ & \leq \left[ n{+}1\right] _{p_{1},q_{1}}\left[ m+1\right] _{p_{2},q_{2}}p_{1}^{-n^{2}}p_{1}^{-m^{2}}\sum_{k=0}^{n}\sum_{l=0}^{m}\left( \frac{q_{1}}{p_{1}}\right) ^{-k}\left( \frac{q_{2}}{p_{2}}\right) ^{-l} \mathcal{R}_{n,k}(p_{1},q_{1};x)\mathcal{R}_{m,l}(p_{2},q_{2};y) \\ & \times \int\limits_{0}^{1}\int\limits_{0}^{1}\mathcal{R} _{n,k}(p_{1},q_{1};qt)\mathcal{R}_{m,l}(p_{2},q_{2};qs)\omega \left( f;\sqrt{ \left( t-x\right) ^{2}+\left( s-y\right) ^{2}}\right) d_{p_{1,}q_{1}}td_{p_{2,}q_{2}}s \\ & \leq \left[ n{+}1\right] _{p_{1},q_{1}}\left[ m+1\right] _{p_{2},q_{2}}p_{1}^{-n^{2}}p_{1}^{-m^{2}}\sum_{k=0}^{n}\sum_{l=0}^{m}\left( \frac{q_{1}}{p_{1}}\right) ^{-k}\left( \frac{q_{2}}{p_{2}}\right) ^{-l} \mathcal{R}_{n,k}(p_{1},q_{1};x)\mathcal{R}_{m,l}(p_{2},q_{2};y) \\ & \times \int\limits_{0}^{1}\int\limits_{0}^{1}\mathcal{R} _{n,k}(p_{1},q_{1};qt)\mathcal{R}_{m,l}(p_{2},q_{2};qs)\omega \left( f;\sqrt{ \left( t-x\right) ^{2}+\left( s-y\right) ^{2}}\right) d_{p_{1,}q_{1}}td_{p_{2,}q_{2}}s \end{aligned} $$

$$\displaystyle \begin{aligned} & \leq \left[ n+1\right] _{p_{1},q_{1}}\left[ m+1\right] _{p_{2},q_{2}}p_{1}^{-n^{2}}p_{1}^{-m^{2}}\sum_{k=0}^{n}\sum_{l=0}^{m}\left( \frac{q_{1}}{p_{1}}\right) ^{-k}\left( \frac{q_{2}}{p_{2}}\right) ^{-l} \mathcal{R}_{n,k}(p_{1},q_{1};x)\mathcal{R}_{m,l}(p_{2},q_{2};y) \\ & \times \int\limits_{0}^{1}\int\limits_{0}^{1}\mathcal{R} _{n,k}(p_{1},q_{1};qt)\mathcal{R}_{m,l}(p_{2},q_{2};qs)\left\vert f\left( t,s\right) -f\left( x,y\right) \right\vert d_{p_{1,}q_{1}}td_{p_{2,}q_{2}}s \\ & \leq 1+\frac{1}{\delta _{n}\left( x\right) }\left[ n+1\right] _{p_{1},q_{1}}\left[ m+1\right] _{p_{2},q_{2}}p_{1}^{-n^{2}}p_{1}^{-m^{2}} \sum_{k=0}^{n}\sum_{l=0}^{m}\left( \frac{q_{1}}{p_{1}}\right) ^{-k}\\ &\quad \times \left( \frac{q_{2}}{p_{2}}\right) ^{-l}\mathcal{R}_{n,k}(p_{1},q_{1};x)\mathcal{R} _{m,l}(p_{2},q_{2};y) \\ & \times \int\limits_{0}^{1}\int\limits_{0}^{1}\mathcal{R} _{n,k}(p_{1},q_{1};qt)\mathcal{R}_{m,l}(p_{2},q_{2};qs)\omega \left( f;\sqrt{ \left( t-x\right) ^{2}+\left( s-y\right) ^{2}}\right) d_{p_{1,}q_{1}}td_{p_{2,}q_{2}}s. \end{aligned} $$

Using Lemma 1 and Cauchy–Schwartz inequality, we have Eq. (3.3). □

Now, for 0 < μ ₁ ≤ 1 and 0 < μ ₂ ≤ 1, we give the Lipschitz class $Lip_{M}\left ( \mu _{1},\mu _{2}\right )$ for the bivariate case as follows:

$$\displaystyle \begin{aligned} \left\vert f\left( t,s\right) -f\left( x,y\right) \right\vert \leq M\left\vert t-x\right\vert ^{\mu _{1}}\left\vert s-y\right\vert ^{\mu _{2}} \end{aligned}$$

where $\left ( t,s\right ) ,\left ( x,y\right ) \in I^{2}$.

Theorem 3

Let $f\in Lip_{M}\left ( \mu _{1},\mu _{2}\right )$ and $\left ( q_{n},q_{m}\right ) \in \left ( 0,1\right )$ such that $\lim \limits _{n \rightarrow \infty }q_{n}=1$ and $\lim \limits _{m\rightarrow \infty }q_{m}=1$ . Then for all $\left ( x,y\right ) \in I^{2}\,$ , we get

$$\displaystyle \begin{aligned} \left\vert D_{n,m}\left( f;\left( p_{1,}q_{1}\right) ,\left( p_{2},q_{2}\right) ;x,y\right) -f(x,y)\right\vert \leq M\delta _{n}^{\mu _{1}/2}\left( x\right) \delta _{m}^{\mu _{2}/2}\left( y\right) \mathit{\text{,}} \end{aligned}$$

where $\delta _{n}\left ( x\right )$ and $\delta _{m}\left ( x\right )$ are defined as in Theorem 2.

Proof

Because $f\in Lip_{M}\left ( \mu _{1},\mu _{2}\right )$, we can write

$$\displaystyle \begin{aligned} & \left\vert D_{n,m}\left( f;\left( p_{n,}q_{n}\right) ,\left( p_{m},q_{m}\right) ;x,y\right) -f(x,y)\right\vert \\ & \leq D_{n,m}\left( \left\vert f\left( t,s\right) -f(x,y)\right\vert ;\left( p_{n,}q_{n}\right) ,\left( p_{m},q_{m}\right) ;x,y\right) \\ & \leq MD_{n,m}\left( \left\vert t-x\right\vert ^{\mu _{1}}\left\vert s-y\right\vert ^{\mu _{2}};\left( p_{n,}q_{n}\right) ,\left( p_{m},q_{m}\right) ;x,y\right) \\ & \leq MD_{n}\left( \left\vert t-x\right\vert ^{\mu _{1}};\left( p_{n,}q_{n}\right) ;x\right) D_{m}\left( \left\vert s-y\right\vert ^{\mu _{2}};\left( p_{m,}q_{m}\right) ;y\right) \text{.} \end{aligned} $$

Now, by the Hölder’s inequality with $\bar {p}=\dfrac {2}{\mu _{1}}$, $\bar {q}=\frac {2}{2-\mu _{1}}$ and $\bar {p}=\frac {2}{\mu _{2}}$, $\bar {q}= \frac {2}{2-\mu _{2}}$, respectively, we have

$$\displaystyle \begin{aligned} & \left\vert D_{n,m}\left( f;\left( p_{n,}q_{n}\right) ,\left( p_{m},q_{m}\right) ;x,y\right) -f(x,y)\right\vert \\ & \leq M\left\{ D_{n}\left( \left( t-x\right) ^{2};\left( p_{n,}q_{n}\right) ;x\right) \right\} ^{\mu _{1}}\left\{ D_{n}\left( 1;\left( p_{n,}q_{n}\right) ;x\right) \right\} ^{\frac{2-\mu _{1}}{2}} \\ & \times \left\{ D_{m}\left( \left( s-y\right) ^{2};\left( p_{m,}q_{m}\right) ;y\right) \right\} ^{\mu _{2}}\left\{ D_{m}\left( 1;\left( p_{m,}q_{m}\right) ;y\right) \right\} ^{\frac{2-\mu _{2}}{2}}\text{. } \end{aligned} $$

This completes the proof. □

4 Numerical Results

In order to show the effectiveness and accuracy of $D_{n,m}\left ( f;\left (p_{1,}q_{1}\right ) ,\left ( p_{2},q_{2}\right ) ;x,y\right )$ to f(x, y) with different values of parameters, numerical results are presented in this section. Sensitivity analysis is carried out to minimise the error of approximation of $D_{n,m}\left ( f;\left ( p_{1,}q_{1}\right ) ,\left ( p_{2},q_{2}\right ) ;x,y\right )$ to the function $f(x,y)=\cos \left (x^{2}+y^{2}\right )$ for minimum n and m values by taking into account different q ₁ and q ₂ values.

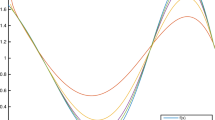
In Fig. 1, $D_{n,m}\left ( f;\left ( p_{1,}q_{1}\right ) ,\left ( p_{2},q_{2}\right ) ;x,y\right )$ results are given as a function of $f(x,y)=\cos \left (x^{2}+y^{2}\right )$ for different q ₁ and q ₂ values. Figure 2 demonstrates the convergence of $D_{n,m}\left ( f;\left ( p_{1,}q_{1}\right ) ,\left ( p_{2},q_{2}\right ) ;x,y\right )$ to f(x, y) but this time considering different n and m values, when q ₁ = q ₂ = 0.1 and p ₁ = p ₂ = 0.9.

Fig. 1

Convergence of $D_{n,m} \left ( f; \left ( p_{1,}q_{1} \right ) , \left (p_{2},q_{2} \right ) ;x,y \right )$ for different q ₁ and q ₂ values. (a) q ₁ = 0.2, q ₂ = 0.5, p ₁ = 0.9, p ₂ = 0.9. (b) q ₁ = 0.8, q ₂ = 0.8, p ₁ = 0.9, p ₂ = 0.9

Fig. 2

Convergence of $D_{n,m} \left ( f; \left ( p_{1,}q_{1} \right ) , \left (p_{2},q_{2} \right ) ;x,y \right )$ for different n and m values. (a) n = 20, m = 15. (b) n = 1, m = 1

In Fig. 2a, b, as n and m values are increased, the error of the approximation of $D_{n,m}\left ( f;\left ( p_{1,}q_{1}\right ) ,\left ( p_{2},q_{2}\right ) ;x,y\right )$ to f(x, y) is minimised given q ₁ = 0.2, q ₂ = 0.5 and p ₁ = 0.9, p ₂ = 0.9 values.

Table 1 Errors of approximation $D_{n,m} \left ( f; \left (p_{1,}q_{1} \right ) , \left ( p_{2},q_{2} \right ) ;x,y \right )$ to f(x, y)

Table 2 Errors of approximation $D_{n,m} \left ( f; \left (p_{1,}q_{1} \right ) , \left ( p_{2},q_{2} \right ) ;x,y \right )$ to f(x, y)

On the other hand, comparative results are given in Tables 1 and 2, for the errors of the approximation of $D_{n,m}\left ( f;\left (p_{1,}q_{1}\right ) ,\left ( p_{2},q_{2}\right ) ;x,y\right )$, considering each for different n, m values. However, using n = 20, m = 15 for $D_{n,m}\left ( f;\left ( p_{1,}q_{1}\right ) ,\left ( p_{2},q_{2}\right ) ;x,y\right )$ rather than n = 1, m = 1 gives better approximation results. Therefore, the effect of increasing n and m values further than n = 20 and m = 15 is less evident for x < 0.5 and y < 0.5 for the convergence of $D_{n,m}\left ( f;\left ( p_{1,}q_{1}\right ) ,\left ( p_{2},q_{2}\right ) ;x,y\right )$ to the function f(x, y).

On the other hand, it is required to increase the values of n and m further than n = 20 and m = 15 for x > 0.5 and y > 0.5 in order to have more accurate results.