Level Planarity: Transitivity vs. Even Crossings

Abstract

Recently, Fulek et al. [1,2,3] have presented Hanani-Tutte results for (radial) level planarity, i.e., a graph is (radial) level planar if it admits a (radial) level drawing where any two (independent) edges cross an even number of times. We show that the 2-Sat formulation of level planarity testing due to Randerath et al. [4] is equivalent to the strong Hanani-Tutte theorem for level planarity [3]. Further, we show that this relationship carries over to radial level planarity, which yields a novel polynomial-time algorithm for testing radial level planarity.

1 Introduction

Planarity of graphs is a fundamental concept for graph theory as a whole, and for graph drawing in particular. Naturally, variants of planarity tailored specifically to directed graphs have been explored. A planar drawing is upward planar if all edges are drawn as monotone curves in the upward direction. A special case are level planar drawings of level graphs, where the input graph $G=(V,E)$ comes with a level assignment $\ell :V \rightarrow \{1, 2, \ldots , k\}$ for some $k \in \mathbb N$ that satisfies $\ell (u) < \ell (v)$ for all $(u, v) \in E$. One then asks whether there is an upward planar drawing such that each vertex v is mapped to a point on the horizontal line $y = \ell (v)$ representing the level of v. There are also radial variants of these concepts, where edges are drawn as curves that are monotone in the outward direction in the sense that a curve and any circle centered at the origin intersect in at most one point. Radial level planarity is derived from level planarity by representing levels as concentric circles around the origin.

Despite the similarity, the variants with and without levels differ significantly in their complexity. Whereas testing upward planarity and radial planarity are NP-complete [5], level planarity and radial level planarity can be tested in polynomial time. In fact, linear-time algorithms are known for both problems [6, 7]. However, both algorithms are quite complicated, and subsequent research has led to slower but simpler algorithms for these problems [4, 8]. Recently also constrained variants of the level planarity problem have been considered [9, 10].

One of the simpler algorithms is the one by Randerath et al. [4]. It only considers proper level graphs, where each edge connects vertices on adjacent levels. This is not a restriction, because each level graph can be subdivided to make it proper, potentially at the cost of increasing its size by a factor of k. It is not hard to see that in this case a drawing is fully specified by the vertex ordering on each level. To represent this ordering, define a set of variables $\mathcal V = \{ uw \mid u, w \in V, u \ne w, \ell (u) = \ell (w) \}$. Randerath et al. observe that there is a trivial way of specifying the existence of a level-planar drawing by the following consistency (1), transitivity (2) and planarity constraints (3):

$$\begin{aligned}&\forall uw \ \in \mathcal V \ :\ uw \Leftrightarrow \lnot wu \end{aligned}$$

(1)

$$\begin{aligned}&\forall uw, wy \ \in \mathcal V \ :\ uw \wedge wy \Rightarrow uy \end{aligned}$$

(2)

$$\begin{aligned}&\forall uw, vx \ \in \mathcal V \text { with } (u, v), (w, x) \in E\text { independent} \ : \ uw \Leftrightarrow vx \end{aligned}$$

(3)

The surprising result due to Randerath et al. [4] is that the satisfiability of this system of constraints (and thus the existence of a level planar drawing) is equivalent to the satisfiability of a reduced constraint system obtained by omitting the transitivity constraints (2). That is, transitivity is irrelevant for the satisfiability. Note that a satisfying assignment of the reduced system is not necessarily transitive, rather Randerath et al. prove that a solution can be made transitive without invalidating the other constraints. Since the remaining conditions 1 and 3 can be easily expressed in terms of 2-Sat, which can be solved efficiently, this yields a polynomial-time algorithm for level planarity.

A very recent trend in planarity research are Hanani-Tutte style results. The (strong) Hanani-Tutte theorem [11, 12] states that a graph is planar if and only if it can be drawn so that any two independent edges (i.e., not sharing an endpoint) cross an even number of times. One may wonder for which other drawing styles such a statement is true. Pach and Tóth [13, 14] showed that the weak Hanani-Tutte theorem (which requires even crossings for all pairs of edges) holds for a special case of level planarity and asked whether the result holds in general. This was shown in the affirmative by Fulek et al. [3], who also established the strong version for level planarity. Most recently, both the weak and the strong Hanani-Tutte theorem have been established for radial level planarity [1, 2].

Contribution. We show that the result of Randerath et al. [4] from 2001 is equivalent to the strong Hanani-Tutte theorem for level planarity.

The key difference is that Randerath et al. consider proper level graphs, whereas Fulek et al. [3] work with graphs with only one vertex per level. For a graph G we define two graphs $G^\star$, $G^+$ that are equivalent to G with respect to level planarity. We show how to transform a Hanani-Tutte drawing of a graph $G^\star$ into a satisfying assignment for the constraint system of $G^+$ and vice versa. Since this transformation does not make use of the Hanani-Tutte theorem nor of the result by Randerath et al., this establishes the equivalence of the two results.

Moreover, we show that the transformation can be adapted also to the case of radial level planarity. This results in a novel polynomial-time algorithm for testing radial level planarity by testing satisfiability of a system of constraints that, much like the work of Randerath et al., is obtained from omitting all transitivity constraints from a constraint system that trivially models radial level planarity. Currently, we deduce the correctness of the new algorithm from the strong Hanani-Tutte theorem for radial level planarity [2]. However, also this transformation works both ways, and a new correctness proof of our algorithm in the style of the work of Randerath et al. [4] may pave the way for a simpler proof of the Hanani-Tutte theorem for radial level planarity. We leave this as future work. Omitted proofs, indicated by ($\star$), can be found in the full version [15].

2 Preliminaries

A level graph is a directed graph $G = (V, E)$ together with a level assignment $\ell : V \rightarrow \{1, 2, \ldots , k\}$ for some $k \in \mathbb N$ that satisfies $\ell (u) < \ell (v)$ for all $(u, v) \in E$. If $\ell (u) + 1 = \ell (v)~$ for all $(u, v) \in E$, the level graph G is proper. Two independent edges (u, v), (w, x) are critical if $\ell (u) \le \ell (x)$ and $\ell (v) \ge \ell (w)$. Note that any pair of independent edges that can cross in a level drawing of G is a pair of critical edges. Throughout this paper, we consider drawings that may be non-planar, but we assume at all times that no two distinct vertices are drawn at the exact same point, no edge passes through a vertex, and no three (or more) edges cross in a single point. If any two independent edges cross an even number of times in a drawing $\varGamma$ of G, it is called a Hanani-Tutte drawing of G.

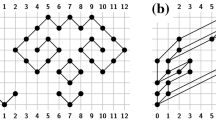
For any k-level graph G we now define a star form $G^\star$ so that every level of $G^\star$ consists of exactly one vertex. The construction is similar to the one used by Fulek et al. [3]. Let $n_i$ denote the number of vertices on level i for $1 \le i \le k$. Further, let $v_1, v_2, \ldots , v_{n_i}$ denote the vertices on level i. Subdivide every level i into $2n_i$ sublevels $1^i, 2^i, \ldots , (2n_i)^i$. For $1 \le j \le n_i$, replace vertex $v_j$ by two vertices $v_j'$, $v_j''$ with $\ell (v_j') = j^i$ and $\ell (v_j'') = n_i + j^i$ and connect them by an edge $(v_j', v_j'')$, referred to as the stretch edge $e(v_j)$. Connect all incoming edges of $v_j$ to $v_j'$ instead and connect all outgoing edges of $v_j$ to $v_j''$ instead. Let $e = (u, v)$ be an edge of G. Then let $e^\star$ denote the edge of $G^\star$ that connects the endpoint of e(u) with the starting point of e(v). See Fig. 1. Define $G^+$ as the graph obtained by subdividing the edges of $G^\star$ so that the graph becomes proper; again, see Fig. 1. Let (u, v), (w, x) be critical edges in $G^\star$. Define their limits in $G^+$ as $(u', v'), (w', x')$ where $u', v'$ are endpoints or subdivision vertices of (u, v), $w', x'$ are endpoints or subdivision vertices of (w, x) and it is $\ell (u') = \ell (w') = \max (\ell (u), \ell (w))$ and $\ell (v') = \ell (x') = \min (\ell (v), \ell (x))$.

Fig. 1.

A level graph G (a) modified to a graph $G^\star$ so as to have only one vertex per level (b) and its proper subdivision $G^+$ (c).

Lemma 1

($\star$). Let G be a level graph. Then

G is (radial) level pl. $\Leftrightarrow G^\star$ is (radial) level pl. $\Leftrightarrow G^+$ is (radial) level pl.

3 Level Planarity

Recall from the introduction that Randerath et al. formulated level planarity of a proper level graph G as a Boolean satisfiability problem $\mathcal S'(G)$ on the variables $\mathcal V = \{ uw \mid u \ne w, \ell (u) = \ell (w) \}$ and the clauses given by Eqs. (1)–(3).

It is readily observed that G is level planar if and only if $\mathcal S'(G)$ is satisfiable. Now let $\mathcal S(G)$ denote the Sat instance obtained by removing the transitivity clauses (2) from $\mathcal S'(G)$. Note that it is $(uw \Rightarrow \lnot wu) \equiv (\lnot uw \vee \lnot wu)$ and $(uw \Rightarrow vx) \equiv (\lnot uw \vee vx)$, i.e., $\mathcal S(G)$ is an instance of 2-Sat, which can be solved efficiently. The key claim of Randerath et al. is that $\mathcal S'(G)$ is satisfiable if and only if $\mathcal S(G)$ is satisfiable, i.e., dropping the transitivity clauses does not change the satisfiability of $\mathcal S'(G)$. In this section, we show that $\mathcal S(G)$ is satisfiable if and only if $G^\star$ has a Hanani-Tutte level drawing (Theorem 1). Of course, we do not use the equivalence of both statements to level planarity of G. Instead, we construct a satisfying truth assignment of $\mathcal S(G)$ directly from a given Hanani-Tutte level drawing (Lemma 3), and vice versa (Lemma 4). This directly implies the equivalence of the results of Randerath et al. and Fulek et al. (Theorem 1).

The common ground for our constructions is the constraint system $\mathcal S'(G^+)$, where a Hanani-Tutte drawing implies a variable assignment that does not necessarily satisfy the planarity constraints (3), though in a controlled way, whereas a satisfying assignment of $\mathcal S(G)$ induces an assignment for $\mathcal S'(G^+)$ that satisfies the planarity constraints but not the transitivity constraints (2). Thus, in a sense, our transformation trades planarity for transitivity and vice versa.

A (not necessarily planar) drawing $\varGamma$ of G induces a truth assignment $\varphi$ of $\mathcal V$ by defining for all $uw \in \mathcal V$ that $\varphi (uw)$ is true if and only if u lies to the left of w in $\varGamma$. Note that this truth assignment must satisfy the consistency clauses, but does not necessarily satisfy the planarity constraints. The following lemma describes a relationship between certain truth assignments of $\mathcal S(G)$ and crossings in $\varGamma$ that we use to prove Lemmas 3 and 4.

Lemma 2

Let (u, v), (w, x) be two critical edges of $G^\star$ and let $(u', v'), (w', x')$ be their limits in $G^+$. Further, let $\varGamma ^\star$ be a drawing of $G^\star$, let $\varGamma ^+$ be the drawing of $G^+$ induced by $\varGamma ^\star$ and let $\varphi ^+$ be the truth assignment of $\mathcal S(G^+)$ induced by $\varGamma ^+$. Then (u, v) and (w, x) intersect an even number of times in $\varGamma ^\star$ if and only if $\varphi ^+(u'w') = \varphi ^+(v'x')$.

Proof

We may assume without loss of generality that any two edges cross at most once between consecutive levels by introducing sublevels if necessary. Let X be a crossing between (u, v) and (w, x) in $G^\star$; see Fig. 2(a). Further, let $u_1, w_1$ and $u_2, w_2$ be the subdivision vertices of (u, v) and (w, x) on the levels directly below and above X in $G^\star$, respectively. It is $\varphi ^+(u_1w_1) = \lnot \varphi ^+(u_2w_2)$. In the reverse direction, $\varphi ^+(u_1w_1) = \lnot \varphi ^+(u_2w_2)$ implies that (u, v) and (w, x) cross between the levels $\ell (u_1)$ and $\ell (u_2)$. Due to the definition of limits, any crossing between (u, v) and (w, x) in $G^\star$ must occur between the levels $\ell (u') = \ell (w')$ and $\ell (v') = \ell (x')$. Therefore, it is $\varphi ^+(u'w') = \varphi ^+(v'x')$ if and only if (u, v) and (w, x) cross an even number of times.    $\square$

Fig. 2.

A Hanani-Tutte drawing (a) induces a truth assignment $\varphi ^+$that satisfies $\mathcal S(G^+)$ (b), the value where $\varphi ^+$ differs from $\psi ^+$ is highlighted in red. Using the subdivided stretch edges of $G^+$ (c), translate $\varphi ^+$ to a satisfying assignment $\varphi$ of $\mathcal S(G)$ (d). (Color figure online)

Lemma 3

Let G be a proper level graph and let $\varGamma ^\star$ be a Hanani-Tutte drawing of $G^\star$. Then $\mathcal S(G)$ is satisfiable.

Proof

Let $\varGamma ^+$ be the drawing of $G^+$ induced by $\varGamma ^\star$ and let $\psi ^+$ denote the truth assignment induced by $\varGamma ^+$. Note that $\psi ^+$ does not necessarily satisfy the crossing clauses. Define $\varphi ^+$ so that it satisfies all clauses of $\mathcal S(G^+)$ as follows.

Let $u'',w''$ be two vertices of $G^+$ with $\ell (u'')=\ell (w'')$. If one of them is a vertex in $G^\star$, then set $\varphi ^+(u'',w'')=\psi ^+(u'',w'')$. Otherwise $u''$, $w''$ are subdivision vertices of two edges $(u,v),(w,x)\in E(G^\star )$. If they are independent, then they are critical. In that case their limits $(u',v'),(w',x')$ are already assigned consistently by Lemma 2. Then set $\varphi ^+(u''w'') = \psi ^+(u'w')$. If (u, v), (w, x) are adjacent, then we have $u=w$ or $v=x$. In the first case, we set $\varphi ^+(u''w'') = \psi ^+(v'x')$. In the second case, we set $\varphi ^+(u''w'') = \psi ^+(u'w')$.

Thereby, we have for any critical pair of edges $(u'',v''),(w'',x'')\in E(G^+)$ that $\varphi ^+(u''w'')= \varphi ^+(v''x'')$ and clearly $\varphi ^+(u''w'')=\lnot \varphi ^+(w''u'')$. Hence, assignment $\varphi ^+$ satisfies $\mathcal S(G^+)$. See Fig. 2 for a drawing $\varGamma ^+$ (a) and the satisfying assignment of $\mathcal S(G^+)$ derived from it (b).

Proceed to construct a satisfying truth assignment $\varphi$ of $\mathcal S(G)$ as follows. Let u, w be two vertices of G with $\ell (u) = \ell (w)$. Then the stretch edges e(u), e(w) in $G^\star$ are critical by construction. Let $(u', u''), (w', w'')$ be their limits in $G^+$. Set $\varphi (uw) = \varphi ^+(u'w')$. Because $\varphi ^+$ is a satisfying assignment, all crossing clauses of $\mathcal S(G^+)$ are satisfied, which implies $\varphi ^+(u'w') = \varphi ^+(u''w'')$. The same is true for all subdivision vertices of e(u) and e(w) in $G^+$. Because $\varphi ^+$ also satisfies the consistency clauses of $\mathcal S(G^+)$, this means that $\varphi$ satisfies the consistency clauses of $\mathcal S(G)$. See Fig. 2 for how $\mathcal S(G^+)$ is translated from $G^+$ (c) to G (d). Note that the resulting assignment is not necessarily transitive, e.g., it could be $\varphi (uv) = \varphi (vw) = \lnot \varphi (uw)$.

Consider two edges (u, v), (w, x) in G with $\ell (u) = \ell (w)$. Because G is proper, we do not have to consider other pairs of edges. Let $(u', u''), (w', w'')$ be the limits of e(u), e(w) in $G^+$. Further, let $(v', v''), (x', x'')$ be the limits of e(v), e(x) in $G^+$. Because there are disjoint directed paths from $u'$ and $w'$ to $v'$ and $x'$ and $\varphi ^+$ is a satisfying assignment, it is $\varphi ^+(u'w') = \varphi ^+(v'x')$. Due to the construction of $\varphi$ described in the previous paragraph, this means that it is $\varphi (uw) = \varphi (vx)$. Therefore, $\varphi$ is a satisfying assignment of $\mathcal S(G)$.    $\square$

Lemma 4

Let G be a proper level graph together with a satisfying truth assignment $\varphi$ of $\mathcal S(G)$. Then there exists a Hanani-Tutte drawing $\varGamma ^\star$ of $G^\star$.

Proof

We construct a satisfying truth assignment $\varphi ^+$ of $\mathcal S(G^+)$ from $\varphi$ by essentially reversing the process described in the proof of Lemma 3. Proceed to construct a drawing $\varGamma ^+$ of $G^+$ from $\varphi ^+$ as follows. Recall that by construction, every level of $G^+$ consists of exactly one non-subdivision vertex. Let u denote the non-subdivision vertex of level i. Draw a subdivision vertex w on level i to the right of u if $\varphi ^+(uw)$ is true and to the left of u otherwise. The relative order of subdivision vertices on either side of u can be chosen arbitrarily. Let $\varGamma ^\star$ be the drawing of $G^\star$ induced by $\varGamma ^+$. To see that $\varGamma ^\star$ is a Hanani-Tutte drawing, consider two critical edges (u, v), (w, x) of $G^\star$. Let $(u', v'), (w', x')$ denote their limits in $G^+$. One vertex of $u'$ and $v'$ ($w'$ and $x'$) is a subdivision vertex and the other one is not. Lemma 2 gives $\varphi ^+(u'w') = \varphi ^+(v'x')$ and then by construction $u', w'$ and $v', x'$ are placed consistently on their respective levels. Moreover, Lemma 2 yields that (u, v) and (w, x) cross an even number of times in $G^\star$. Figure 3 illustrates the construction.    $\square$

Fig. 3.

A proper level graph G together with a satisfying variable assignment $\varphi$ (a) induces a drawing of $G^+$ (b), which induces a Hanani-Tutte drawing of $G^\star$ (c).

Theorem 1

Let G be a proper level graph. Then

$\mathcal S(G)$ is satisfiable $\Leftrightarrow G^\star$ has a Hanani-Tutte level drawing $\Leftrightarrow G$ is level planar.

4 Radial Level Planarity

In this section we present an analogous construction for radial level planarity. In contrast to level planarity, we now have to consider cyclic orders on the levels, and even those may still leave some freedom for drawing the edges between adjacent levels. In the following we first construct a constraint system of radial level planarity for a proper level graph G, which is inspired by the one of Randerath et al. Afterwards, we slightly modify the construction of $G^\star$. Finally, in analogy to the level planar case, we show that a satisfying assignment of our constraint system defines a satisfying assignment of the constraint system of $G^+$, and that this in turn corresponds to a Hanani-Tutte radial level drawing of $G^\star$.

A Constraint System for Radial Level Planarity. We start with a special case that bears a strong similarity with the level-planar case. Namely, assume that G is a proper level graph that contains a directed path $P = \alpha _1,\dots ,\alpha _k$ that has exactly one vertex $\alpha _i$ on each level i. We now express the cyclic ordering on each level as linear orders whose first vertex is $\alpha _i$. To this end, we introduce for each level the variables $\mathcal V_i = \{\alpha _i uv \mid u,v \in V_i \setminus \{\alpha _i\} \}$, where $\alpha _iuv\equiv \text {true}$ means $\alpha _i$, u, v are arranged clockwise on the circle representing level i. We further impose the following necessary and sufficient linear ordering constraints $\mathcal L_G(\alpha _i)$.

$$\begin{aligned}&\forall \text { distinct } \ u, v \ \in V \setminus \{\alpha _i\}\ : \ \alpha _iuv \ \Leftrightarrow \lnot \ \alpha _ivu \end{aligned}$$

(4)

$$\begin{aligned}&\forall \text { pairwise distinct } \ u, v, w \ \in V \setminus \{\alpha _i\}\ : \ \alpha _iuv \wedge \alpha _ivw \ \Rightarrow \lnot \ \alpha _iuw \end{aligned}$$

(5)

It remains to constrain the cyclic orderings of vertices on adjacent levels so that the edges between them can be drawn without crossings. For two adjacent levels i and $i+1$, let $\varepsilon _i = (\alpha _i,\alpha _{i+1})$ be the reference edge. Let $E_i$ be the set of edges (u, v) of G with $\ell (u) = i$ that are not adjacent to an endpoint of $\varepsilon _i$. Further $E_i^+ = \{(\alpha _i,v) \in E \setminus \{\varepsilon _i\} \}$ and $E_{i}^- = \{(u,\alpha _{i+1}) \in E \setminus \{\varepsilon _i\}\}$ denote the edges between levels i and $i+1$ adjacent to the reference edge $\varepsilon _i$.

In the context of the constraint formulation, we only consider drawings of the edges between levels i and $i+1$ where any pair of edges crosses at most once and, moreover, $\varepsilon _i$ is not crossed. Note that this can always be achieved, independently of the orderings chosen for levels i and $i+1$. Then, the cyclic orderings of the vertices on the levels i and $i+1$ determine the drawings of all edges in $E_i$. In particular, two edges (u, v), $(u',v') \in E_i$ do not intersect if and only if $\alpha _iuu' \Leftrightarrow \alpha _{i+1}vv'$; see Fig. 4(a). Therefore, we introduce constraint (6). For each edge $e\in E_i^+ \cup E_i^-$ it remains to decide whether it is embedded locally to the left or to the right of $\varepsilon _i$. We write $l(e)$ in the former case. Two edges $e\in E_i^-$, $f \in E_i^+$ do not cross if and only if $l(e) \Leftrightarrow \lnot l(f)$; see Fig. 4(b). This gives us constraint (7). It remains to forbid crossings between edges in $E_i$ and edges in $E_i^+ \cup E_i^-$. An edge $e = (\alpha _i,v'') \in E_i^+$ and an edge $(u',v') \in E_i$ do not cross if and only if $l(e) \Leftrightarrow \alpha _{i+1}v'v''$; see Fig. 4(c). Crossings with edges $(v,\alpha _{i+1}) \in E_i^-$ can be treated analogously. This yields constraints (8) and (9). We denote the planarity constraints (6)–(9) by $\mathcal P_G(\varepsilon _i)$, where $\varepsilon _i = (\alpha _i,\alpha _{i+1})$.

$$\begin{aligned}&\forall \text { independent } (u, v), (u', v') \in E_i \ :\ \alpha _iuu' \ \Leftrightarrow \alpha _{i+1}vv' \end{aligned}$$

(6)

$$\begin{aligned}&\forall e \in E_i^+, f \in E_i^- \ :\ l(e) \ \Leftrightarrow \lnot l(f) \end{aligned}$$

(7)

$$\begin{aligned}&\forall \text { independent } (\alpha _i,v'') \in E_i^+, (u,v) \in E_i \ :\ l(\alpha _i,v'') \ \Leftrightarrow \alpha _{i+1}vv'' \end{aligned}$$

(8)

$$\begin{aligned}&\forall \text { independent } (u'', \alpha _{i+1}) \in E_i^-, (u,v) \in E_i \ :\ l(u'',\alpha _{i+1}) \ \Leftrightarrow \alpha _{i}uu'' \end{aligned}$$

(9)

Fig. 4.

Illustration of the planarity constraints for radial planarity for the case of two edges in $E_i$ (a), constraint (6); the case of an edge in $e \in E_i^-$ and an edge $f \in E_i^+$ (b), constraint (7); and the case of an edge in $E_i$ and an edge $e \in E_i^+$ (c), constraint (8).

It is not difficult to see that the transformation between Hanani-Tutte drawings and solutions of the constraint system without the transitivity constraints (5) can be performed as in the previous section. The only difference is that one has to deal with edges that share an endpoint with a reference $\varepsilon _i$.

In general, however, such a path P from level 1 to level k does not necessarily exist. Instead, we use an arbitrary reference edge between any two consecutive levels. More formally, we call a pair of sets $A^+=\{\alpha _1^+,\dots , \alpha _k^+\}$, $A^-=\{\alpha _1^-,\dots , \alpha _k^-\}$ reference sets for G if we have $\alpha _1^-=\alpha _1^+$ and $\alpha _{k}^+=\alpha _k^-$ and for $1\le i \le k$ the reference vertices $\alpha _i^+$, $\alpha _i^-$ lie on level i and for $1\le i < k$ graph G contains the reference edge $\varepsilon _i=(\alpha _i^+,\alpha _{i+1}^-)$ unless there is no edge between level i and level $i+1$ at all. In that case, we can extend every radial drawing of G by the edge $(\alpha _i^+,\alpha _{i+1}^-)$ without creating new crossings. We may therefore assume that this case does not occur and we do so from now on.

To express radial level planarity, we express the cyclic orderings on each level twice, once with respect to the reference vertex $\alpha _i^+$ and once with respect to the reference vertex $\alpha _i^-$. To express planarity between adjacent levels, we use the planarity constraints with respect to the reference edge $\varepsilon _i$. It only remains to specify that, if $\alpha _i^+ \ne \alpha _i^-$, the linear ordering with respect to these reference vertices must be linearizations of the same cyclic ordering. This is expressed by the following cyclic ordering constraints $\mathcal C_G(\alpha _i^+, \alpha _i^-)$.

$$\begin{aligned}&\forall \text { distinct } u, \, v \in V_i \setminus \{\alpha _i^-, \alpha _i^+\}: \ (\alpha _i^-uv \Leftrightarrow \alpha _i^+uv) \ \Leftrightarrow (\alpha _i^-u\alpha _i^+ \Leftrightarrow \alpha _i^-v\alpha _i^+) \end{aligned}$$

(10)

$$\begin{aligned}&\forall \ \, v \in V_i \setminus \{\alpha _i^-, \alpha _i^+\}: \ \alpha _i^-v\alpha _i^+ \ \Leftrightarrow \alpha _i^+\alpha _i^-v \end{aligned}$$

(11)

The constraint set $\mathcal S'(G,A^+,A^-)$ consists of the linearization constraints $\mathcal L_G(\alpha _i^+)$ and $\mathcal L_G(\alpha _i^-)$ and the cyclic ordering constraints $\mathcal C_G(\alpha _i^+, \alpha _i^-)$ for $i = 1, 2, \ldots , k$ if $\alpha _i^+ \ne \alpha _i^-$, plus the planarity constraints $\mathcal P_G(\varepsilon _i)$ for $i = 1, 2, \ldots , k - 1$. This completes the definition of our constraint system.

Theorem 2

($\star$). Let G be a proper level graph with reference sets $A^+$, $A^-$. Then the constraint system $\mathcal S'(G,A^+,A^-)$ is satisfiable if and only if G is radial level planar. Moreover, the radial level planar drawings of G correspond bijectively to the satisfying assignments of $\mathcal S'(G,A^+,A^-)$.

Similar to Sect. 3, we now define a reduced constraints system $\mathcal S(G,A^+,A^-)$ obtained from $\mathcal S'(G, A^+, A^-)$ by dropping constraint (5). Observe that this reduced system can be represented as a system of linear equations over $\mathbb F_2$, which can be solved efficiently. Our main result is that $S(G,A^+,A^-)$ is satisfiable if and only if G is radial level planar.

Modified Star Form. We also slightly modify the splitting and perturbation operation in the construction of the star form $G^\star$ of G for each level i. This is necessary since we need a special treatment of the reference vertices $\alpha _i^+$ and $\alpha _i^-$ on each level i. Consider the level i containing the $n_i$ vertices $v_1,\dots ,v_{n_i}$. If $\alpha _i^+ \ne \alpha _i^-$, then we choose the numbering of the vertices such that $v_1 = \alpha _i^-$ and $v_{n_i} = \alpha _i^+$. We replace i by $2n_{i}-1$ levels $1^i,2^i,\dots ,(2n_i-1)^i$, which is one level less than previously. Similar to before, we replace each vertex $v_j$ by two vertices ${{\mathrm{bot}}}(v_j)$ and ${{\mathrm{top}}}(v_j)$ with $\ell ({{\mathrm{bot}}}(v_j)) = j^i$ and $\ell ({{\mathrm{top}}}(v_j)) = (n_i - 1 + j)^i$ and the corresponding stretch edge $({{\mathrm{bot}}}(v_j),{{\mathrm{top}}}(v_j))$; see Fig. 5(b). This ensures that the construction works as before, except that the middle level $m_i = j^{n_i}$ contains two vertices, namely $\alpha _i^{+}{}''$ and $\alpha _i^{-}{}'$.

Fig. 5.

Illustration of the modified construction of the stretch edges for $G^\star$ for the graph G in (a). The stretch edges for level $i+1$ where $\alpha _{i+1}^+ \ne \alpha _{i+1}^-$ (b) and for level i where $\alpha _i^+ = \alpha _i^-$ (c).

If, on the other hand, $\alpha _i^+ = \alpha _i^-$, then we choose $v_1 = \alpha _i^+$. But now we replace level i by $2n_i+1$ levels $1^i,\dots ,(2n_i+1)^i$. Replace $v_1$ by vertices ${{\mathrm{bot}}}(v_1),{{\mathrm{top}}}(v_1)$ with $\ell ({{\mathrm{bot}}}(v_1)) = 1^i$ and $\ell ({{\mathrm{top}}}(v_1)) = (2n_i+1)^j$. Replace all other $v_j$ with vertices ${{\mathrm{bot}}}(v_j),{{\mathrm{top}}}(v_j)$ with $\ell ({{\mathrm{bot}}}(v_j)) = j^i$ and $\ell ({{\mathrm{top}}}(v_j)) = (n_i+1+j)^i$. For all j, we add the stretch edge $({{\mathrm{bot}}}(v_j),{{\mathrm{top}}}(v_j))$ as before; see Fig. 5(c). This construction ensures that the stretch edge of $\alpha _i^+=\alpha _i^-$ starts in the first new level $1^i$ and ends in the last new level $(2n_i+1)^i$, and the middle level $m_i = {n_i+1}^j$ contains no vertex.

As before, we replace each original edge (u, v) of the input graph G by the edge $({{\mathrm{top}}}(u),{{\mathrm{bot}}}(v))$ connecting the upper endpoint of the stretch edge of u to the lower endpoint of the stretch edge of v. Observe that the construction preserves the properties that for each level i the middle level $m_i$ of the levels that replace i intersects all stretch edges of vertices on level i. Therefore, Lemma 1 also holds for this modified version of $G^\star$ and its proper subdivision $G^+$. For each vertex v of G we use $e(v) = ({{\mathrm{bot}}}(v),{{\mathrm{top}}}(v))$ to denote its stretch edge.

We define the function L that maps each level j of $G^\star$ or $G^+$ to the level i of G it replaces. For an edge e of $G^\star$ and a level i that intersects e, we denote by $e_i$ the subdivision vertex of e at level i in $G^+$. For two levels i and j that both intersect an edge e of $G^\star$, we denote by $e_i^j$ the path from $e_i$ to $e_j$ in $G^+$.

Constraint System and Assignment for $\varvec{G^+}$. We now choose reference sets $B^+$, $B^-$ for $G^+$ that are based on the reference sets $A^+$, $A^-$ for G. Consider a level j of $G^\star$ and let $i=L(j)$ be the corresponding level of G. For each level j, define two vertices $\beta _j^+$, $\beta _j^-$. If $\alpha _i^-=\alpha _i^+$, set $\beta _j^-=\beta _j^+=e(\alpha _i^-)_j$; see Fig. 6(b). Otherwise, the choice is based on whether j is the middle level $m=m_i$ of the levels $L^{-1}(i)$ that replace level i of G, or whether j lies above or below m. Choose $\beta _m^- = {{\mathrm{top}}}(\alpha _i^+)$ and $\beta _m^+ = {{\mathrm{bot}}}(\alpha _{i+1}^-)$. For $j<m$, choose $\beta _j^-=\beta _j^+=e(\alpha _i^-)_j$ and for $j>m$, choose $\beta _j^-=\beta _j^+ = e(\alpha _i^+)_j$; see Fig. 6(c).

Fig. 6.

Definition of $\beta ^+, \beta ^-$ in the assignment for $G^+$ for the same graph as in Fig. 5(a). Vertices $\beta ^+$ ($\beta ^-$) are drawn in green (red), or in blue if they coincide. (Color figure online)

We set $B^+$ to be the set containing all $\beta _j^+$ and likewise for $B^-$. Our next step is to construct from a satisfying assignment $\varphi$ of $\mathcal S(G,A^+,A^-)$ a corresponding satisfying assignment $\varphi ^+$ of $\mathcal S(G^+,B^+,B^-)$. The construction follows the approach from Lemma 4 and makes use of the fact that $G^+$ is essentially a stretched and perturbed version of G. Since the construction is straightforward but somewhat technical, we defer it to the full version [15].

Lemma 5

($\star$). If $\mathcal S(G,A^+,A^-)$ is satisfiable, then $\mathcal S(G^+,B^+,B^-)$ is satisfiable.

Constructing a Hanani-Tutte Drawing. We construct a radial drawing $\varGamma ^+$ of $G^+$, from which we obtain the drawing $\varGamma ^\star$ of $G^\star$ by smoothing the subdivision vertices. Afterwards we show that $\varGamma ^\star$ is a Hanani-Tutte drawing.

We construct $\varGamma ^+$ as follows. Consider a level j of $G^+$ and let $i=L(j)$ be the original level of G. First assume $j=m_i$ is the middle levels of the levels replacing level i of G. If $\beta _j^-=\beta _j^+$, then we place all vertices of $V_j(G^+)$ in arbitrary order. Otherwise, we place $\beta _j^-$ and $\beta _j^+$ arbitrarily on the circle representing the level $m_i$. We then place each vertex $v\in V_j(G^+)\setminus \{\beta _j^-,\beta _j^+\}$ such that $\beta _j^-,v,\beta _j^+$ are ordered clockwise if and only if $\varphi (\beta _j^-v\beta _j^+)$ is true (i.e., we place v on the correct side of $\beta _j^-$ and $\beta _j^+$ and arrange the vertices on both sides of $\beta _j^-$ and $\beta _j^+$ arbitrarily).

Next assume $j\ne m_i$. Then there is exactly one vertex $\xi \in V_j(G^+)\cap V(G^\star )$. If $\xi \in B^-$, then we place all vertices of $V_j(G^+)$ in arbitrary order on the circle representing the level j. Otherwise, we place $\beta _j^-$ and $\xi$ arbitrarily. We then place any vertex $v\in V_j(G^+)\setminus \{\beta _j^-,\xi \}$ such that $\beta _j^-,\xi ,v$ are ordered clockwise if and only if $\varphi ^+(\beta _j^-\xi v)$ is true. Again, we arrange the vertices on either side of $\beta _j^-$ and $\xi$ arbitrarily. We have now fixed the positions of all vertices and it remains to draw the edges.

Consider two consecutive levels j and $j+1$ of $G^+$. We draw the edges in $E_j(G^+)$ such that they do not cross the reference edges in $E(G^+)\cap (B^+\times B^-)$. We draw an edge $e=(\beta _j^+,x')\in E_j^+(G^+)$ such that it is locally left of $(\beta _j^+,\beta _j^-)$ if and only if $\varphi ^+(l(e))=\text {true}$. By reversing the subdivisions of the edges in $G^+$ we obtain $G^\star$ and along with that we obtain a drawing $\varGamma ^\star$ of $G^\star$ from $\varGamma ^+$.

Let a, b, c be curves or corresponding edges. Then we write ${{\mathrm{cr}}}(a,b)$ for the number of crossings between a, b and set ${{\mathrm{cr}}}(a,b,c)={{\mathrm{cr}}}(a,b)+{{\mathrm{cr}}}(a,c)+{{\mathrm{cr}}}(b,c)$. The following lemma is the radial equivalent to Lemma 2 and constitutes our main tool for showing that edges in our drawing cross evenly.

Lemma 6

($\star$). Let $C_1$ and $C_2$ be distinct concenctric circles and let a, b, c be radially monotone curves from $C_1$ to $C_2$ with pairwise distinct start- and endpoints that only intersect at discrete points. Then the start- and endpoints of a, b, c have the same order on $C_1$ and $C_2$ if and only if ${{\mathrm{cr}}}(a,b,c)\equiv 0 \mod 2$.

Lemma 7

The drawing $\varGamma ^\star$ is a Hanani-Tutte drawing of $G^\star$.

Proof

We show that each pair of independent edges of $G^\star$ crosses evenly in $\varGamma ^\star$. Of course it suffices to consider critical pairs of edges, since our drawing is radial by construction, and therefore non-critical independent edge pairs cannot cross.

Every edge $(\alpha _i^+,\alpha _{i+1}^-)$ is subdivided into edges of the form $(\beta _j^+,\beta _{j+1}^-)$ and therefore it is not crossed.

Let e, f be two independent edges in $E(G^\star )\setminus (A^+\times A^-)$ that are critical. Let a and b be the innermost and outermost level shared by e and f.

We seek to use Lemma 6 to analyze the parity of the crossings between e and f. To this end, we construct a curve $\gamma$ along the edges of the form $(\beta _j^+,\beta _{j+1}^-)$ as follows. For every level j we add a curve $c_j$ between $\beta _j^-$ and $\beta _j^+$ on the circle representing the level j (a point for $\beta _j^-=\beta _j^+$; chosen arbitrarily otherwise). The curve $\gamma$ is the union of these curves $c_j$ and the curves for the edges of the form $(\beta _j^+,\beta _{j+1}^-)$. Note that $\gamma$ spans from the innermost level 1 to the outermost level $(2n_k+1)^k$ with endpoints ${{\mathrm{bot}}}(\alpha _1^+)$ and ${{\mathrm{top}}}(\alpha _k^-)$.

For any edge $g\in G^\star$, we denote its curve in $\varGamma ^\star$ by c(g). For any radial monotone curve c we denote its subcurve between level i and level j by $c_i^j$ (using only one point on circle i and circle j each). We consider the three curves $g'=\gamma _a^b,e'=c(e)_a^b,f'=c(f)_a^b$. We now distinguish cases based on whether one of the edges e, f starts at the bottom end or ends at the top end of the reference edges on level a or b.

Case 1: We have $e_a,f_a\ne \beta _a^+$ and $e_b,f_b\ne \beta _b^-$. Note that ${{\mathrm{cr}}}(e,f,\gamma )={{\mathrm{cr}}}(e,f)+{{\mathrm{cr}}}(e,\gamma )+{{\mathrm{cr}}}(f,\gamma )$, and therefore ${{\mathrm{cr}}}(e,f) \equiv {{\mathrm{cr}}}(e,f,\gamma )+{{\mathrm{cr}}}(e,\gamma ) + {{\mathrm{cr}}}(f,\gamma ) \mod 2$.

By Lemma 6 we have that the orders of $e_a,f_a,\beta _a^+$ and $e_b,f_b,\beta _b^-$ differ if and only if ${{\mathrm{cr}}}(e,f,\gamma ) \equiv 1 \mod 2$. That is ${{\mathrm{cr}}}(e,f,\gamma ) \equiv 0 \mod 2$ if and only if $\varphi ^+(\beta _a^+,e_a,f_a) = \varphi ^+(\beta _b^-,e_b,f_b)$. We show that $\varphi ^+(\beta _a^+,e_a,f_a) = \varphi ^+(\beta _b^-,e_b,f_b)$ if and only if ${{\mathrm{cr}}}(e,\gamma )+{{\mathrm{cr}}}(f,\gamma )\equiv 0\mod 2$. In either case, ${{\mathrm{cr}}}(e,f)$ is even.

Let $a\le j\le b-1$. By construction we have for $\beta _j^-\ne \beta _j^+$ and any other vertex v on level j, that $\beta _j^-,v,\beta _j^+$ are placed clockwise if and only if $\varphi ^+(\beta _j^-,v,\beta _j^+)$ is true. Further, since $\varphi ^+$ satisfies $\mathcal C(\beta _j^+,\beta _j^-)$, we have for any other vertex u on level j that $\beta _j^-,u,v$ and $\beta _j^+,u,v$ have the same order if and only if $\beta _j^-,v,\beta _j^+$ and $\beta _j^-,u,\beta _j^+$ have the same order, i.e., if and only if u and v lie on the same side of $\beta _j^-$ and $\beta _j^+$. This however, is equivalent to ${{\mathrm{cr}}}(e,c_j)+{{\mathrm{cr}}}(f,c_j)\equiv 0\mod 2$.

Since $\varphi ^+$ satisfies $\mathcal P(\delta _j)$ where $\delta _j = (\beta _j^+,\beta _{j+1}^-)$, we have that $\varphi ^+(\beta _j^+,e_j,f_j)=\varphi ^+(\beta _{j+1}^-,e_{j+1},f_{j+1})$. We obtain, that $\varphi ^+(\beta _j^+,e_j,f_j)=\varphi ^+(\beta _{j+1}^-,e_{j+1},f_{j+1})$ unless $\varphi ^+(\beta _{j+1}^-,e_{j+1}f_{j+1})\ne \varphi ^+(\beta _{j+1}^+e_{j+1}f_{j+1})$ (which requires $\beta _{j+1}^-\ne \beta _{j+1}^+$). This is equivalent to ${{\mathrm{cr}}}(e,c_{j+1})+{{\mathrm{cr}}}(f,c_{j+1})\equiv 1\mod 2$. Hence, we have $\varphi ^+(\beta _a^+e_af_a)=\varphi ^+(\beta _b^+e_bf_b)$ if and only if $\sum _{j=a}^{b-1} {{\mathrm{cr}}}(c_j,e)+{{\mathrm{cr}}}(c_j,f)\equiv 0\mod 2$ (Note that $\beta _b^-=\beta _b^+$.). Since edges of the form $(\beta _j^+,\beta _{j+1}^-)$ are not crossed, this is equivalent to ${{\mathrm{cr}}}(\gamma ,e)+{{\mathrm{cr}}}(\gamma ,f) \equiv 0 \mod 2$. Which we aimed to show. By the above argument we therefore find that ${{\mathrm{cr}}}(e,f)$ is even.

Case 2. We do not have $e_a,f_a\ne \beta _a^+$ and $e_b,f_b\ne \beta _b^-$. For example, assume $e_a=\beta _a^+$; the other cases work analogously. We then have $\beta _a^+={{\mathrm{top}}}(\alpha _i^+)$. This means e originates from an edge in G. Since such edges do not cross middle levels, $g'$ is a subcurve of an original edge $\varepsilon _i$. Especially, we have only three vertices per level between a and b that correspond to $\gamma ,e,f$.

Let $H\subseteq G^+$ be the subgraph induced by the vertices of $(\varepsilon _i)_a^b$, $e_a^b$, $f_a^b$. Then $\varphi ^+$ satisfies all the constraints of $\mathcal S(H,V((\varepsilon _i)_a^b),V((\varepsilon _i)_a^b))$. However, each level of H contains only three vertices, and therefore the transitivity constraints are trivially satisfied, i.e., $\varphi ^+$ satisfies all the constraints of $\mathcal S'(H,V((\varepsilon _i)_a^b),V((\varepsilon _i)_a^b))$. Thus, by Theorem 2, a drawing $\varGamma _H$ of H according to $\varphi ^+$ is planar. I.e., we have ${{\mathrm{cr}}}_{\varGamma _H}((\varepsilon _i)_a^b,e_a^b,f_a^b) = 0$. Let $C_a,C_b$ be $\varepsilon$-close circles to levels a and b, respectively, that lie between levels a and b. With Lemma 6 we obtain that $\varepsilon _i,e,f$ intersect $C_a$ and $C_b$ in the same order.

Note that $\varGamma ^+$ is drawn according to $\varphi ^+$ in level a and in level b. We obtain that the curves for $\varepsilon _i,e,f$ intersect $C_a$ in the same order in $\varGamma ^+$ and in $\varGamma _H$. The same holds for $C_b$. Hence, the curves intersect $C_a$ and $C_b$ in the same order in $\varGamma ^+$. With Lemma 6 we have ${{\mathrm{cr}}}_{\varGamma ^+}((\varepsilon _i)_a^b,e_a^b,f_a^b) \equiv 0\mod 2$. Since $\gamma$ is a subcurve of $\varepsilon _i$ and thus not crossed in $\varGamma ^+$, this yields ${{\mathrm{cr}}}_{\varGamma ^+}(e_a^b,f_a^b) \equiv 0\mod 2$. Thus any two independent edges have an even number of crossings.    $\square$

As in the level planar case the converse also holds.

Lemma 8

($\star$). Let $G^\star$ be a level graph with reference sets $A^+$, $A^-$ for $G^+$. If $G^\star$ admits a Hanani-Tutte drawing, then there exists a satisfying assignment $\varphi$ of $\mathcal S(G^+,A^+,A^-)$.

Theorem 3

Let G be a proper level graph with reference sets $A^+$, $A^-$. Then

$\mathcal S(G, A^+, A^-) \text { is satisfiable} \Leftrightarrow G^\star \text { has a Hanani-Tutte radial level drawing}$

$\phantom {\mathcal S(G, A^+, A^-) \text { is satisfiable}} \Leftrightarrow G \text { is radial level planar.}$

5 Conclusion

We have established an equivalence of two results on level planarity that have so far been considered as independent. The novel connection has further led us to a new testing algorithm for radial level planarity. Can similar results be achieved for level planarity on a rolling cylinder or on a torus [16]?