Abstract
A Stick graph is an intersection graph of axis-aligned segments such that the left end-points of the horizontal segments and the bottom end-points of the vertical segments lie on a “ground line”, a line with slope \(-1\). It is an open question to decide in polynomial time whether a given bipartite graph G with bipartition \(A\cup B\) has a Stick representation where the vertices in A and B correspond to horizontal and vertical segments, respectively. We prove that G has a Stick representation if and only if there are orderings of A and B such that G’s bipartite adjacency matrix with rows A and columns B excludes three small ‘forbidden’ submatrices. This is similar to characterizations for other classes of bipartite intersection graphs.
We present an algorithm to test whether given orderings of A and B permit a Stick representation respecting those orderings, and to find such a representation if it exists. The algorithm runs in time linear in the size of the adjacency matrix. For the case when only the ordering of A is given, we present an \(O(|A|^3|B|^3)\)-time algorithm. When neither ordering is given, we present some partial results about graphs that are, or are not, Stick representable.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Let \(\mathcal {O}\) be a set of geometric objects in the Euclidean plane. The intersection graph of \(\mathcal {O}\) is a graph where each vertex corresponds to a distinct object in \(\mathcal {O}\), and two vertices are adjacent if and only if the corresponding objects intersect. Recognition of intersection graphs that arise from different types of geometric objects such as segments, rectangles, discs, intervals, etc., is a classic problem in combinatorial geometry. Some of these classes, such as interval graphs [2], can be recognized in polynomial-time, whereas many others are NP-hard [4, 25, 27]. There are many beautiful results that characterize intersection classes in terms of a vertex ordering without certain forbidden patterns, and recently, Hell et al. [20] unified many previous results by giving a general polynomial time recognition algorithm for all cases of small forbidden patterns.
In this paper we study a class of bipartite intersection graphs called Stick graphs. A Stick graph is an intersection graph of axis-aligned segments with the property that the left end-points of horizontal segments and the bottom end-points of vertical segments all lie on a ground line, \(\ell \), which we take, without loss of generality, to be a line of slope \(-1\). See Fig. 1(a)–(b). It is an open problem to recognize Stick graphs in polynomial time [8].
Stick graphs lie between two well-studied classes of bipartite intersection graphs. First of all, they are a subset of the grid intersection graphs (GIG) [19]—intersection graphs of horizontal and vertical segments in the plane—which are NP-complete to recognize [25]. When all the horizontal segments extend rightward to infinity and the vertical segments extend upward to infinity, we obtain the subclass of 2-directional orthogonal ray (2DOR) graphs (e.g., see Fig. 1(c)), which can be recognized in polynomial time [30]. It is easy to show that every 2DOR graph is a Stick graph—truncate each ray at a ground line placed above and to the right of every intersection point (and then flip the picture upside-down). Thus the class of Stick graphs lies strictly between these two classes.
What the two classes (GIG and 2DOR) have in common is a nice characterization in terms of vertex orderings. A bipartite graph G with vertex bipartition \(A \cup B\) can be represented as a bipartite adjacency matrix, M(G) with rows and columns corresponding to A and B, respectively, and a 1 in row i, column j, if (i, j) is an edge. Both GIG graphs and 2DOR graphs can be characterized as graphs G for which M(G) has a row and column ordering without certain ‘forbidden’ submatrices. (Details below.) Many other bipartite intersection graphs can be similarly characterized in terms of forbidden submatrices, see [24].
One of our main results is a similar characterization of Stick graphs. Specifically, we will prove that a bipartite graph G with vertex bipartition \(A \cup B\) has a Stick representation with vertices of A corresponding to horizontal segments and vertices of B corresponding to the vertical segments if and only if there is an ordering of A and an ordering of B such that M(G) has no submatrix of the following form, where \(*\) stands for either 0 or 1:

Although this characterization does not (yet) give us a polynomial time algorithm to recognize Stick graphs, it allows us to make some progress. Given a bipartite graph G with vertex bipartition \(A \cup B\), we want to know if G has a Stick representation with A and B corresponding to horizontal and vertical segments, respectively. It is easy to show that a solution to this problem is completely determined by a total ordering \(\sigma \) of the vertices of G corresponding to the order (from left to right) in which the segments touch the ground line. A natural way to tackle the recognition of Stick graphs is as a hierarchy of problems, each (possibly) more difficult than the next:
-
(i)
Fixed As and Bs: In this case an ordering, \(\sigma _a\), of the vertices in A and an ordering, \(\sigma _B\), of the vertices in B are given, and the output ordering \(\sigma \) must respect these given orderings. Because of our forbidden submatrix characterization, this problem can be solved in polynomial time.
-
(ii)
Fixed As: In this case only the ordering \(\sigma _A\) is given.
-
(iii)
General Stick graphs: In this case, neither \(\sigma _A\) nor \(\sigma _B\) is given, i.e., there is no restriction on the ordering of the vertices.
Our Results: We give an algorithm with run-time O(|A||B|) for problem (i). This is faster than naively looking for the forbidden submatrices. (And in fact, we use our algorithm to prove the forbidden submatrix characterization). Furthermore, the algorithm will find a Stick representation when one exists.
We give an algorithm for problem (ii) with run time \(O(|A|^3 |B|^3)\) that uses the forbidden submatrix characterization and reduces the problem to 2-Satisfiability. For problem (iii), recognizing Stick graphs, we give some conditions that ensure a graph is a Stick graph, and some conditions that ensure a graph is not a Stick graph.
Related Work: We now review the research related to the recognition of intersection graphs, in particular those that are bipartite.
Interval graphs, i.e., intersection graph of horizontal intervals on the real line, can be recognized in linear time [2, 13]. Bipartite interval graphs with a fixed bipartition are known as interval bigraphs (IBG) [14, 28], and can be recognized in polynomial time [28]. In contrast to the interval graphs, no linear-time recognition algorithm is known for IBG.
Many bipartite graph classes have been characterized in terms of forbidden submatrices of the graph’s bipartite adjacency matrix, and a rich body of research examines when the rows and columns of a matrix can be permuted to avoid forbidden submatrices [24]. For example, a graph G is chordal bipartite if and only if M(G) can be permuted to avoid the matrix \(\gamma _1\) in Fig. 2 [24], which led to a polynomial-time algorithm [26]. G is a bipartite permutation graph if and only if M(G) can be permuted to avoid \(\gamma _1, \gamma _2\), and \(\gamma _3\) [11].
A graph is a two-directional orthogonal ray (2DOR) graph if it admits an intersection representation of upward and rightward rays [30, 31]. A graph is a 2DOR graph if and only if its incidence matrix admits a permutation of its rows and columns that avoids \(\gamma _1\) and \(\gamma _2\) [30].
There is a linear-time algorithm to recognize 2DOR graphs [12, 30]. If there are 3 or 4 allowed directions for the rays, then the graphs are called 3DOR or 4DOR graphs, respectively. Felsner et al. [16] showed that if the direction (right, left, up, or down) for each vertex is given, then the existence of a 4DOR representation respecting the given directions can be decided in polynomial time. If the horizontal elements are segments and the vertical elements are rays, then the corresponding intersection graphs are called SegRay graphs [7,8,9, 23]. A graph G is a SegRay graph if and only if M(G) can be permuted to avoid \(\gamma _4\) [10].
The time-complexity questions for 3DOR, 4DOR and SegRay are all open.
The class of segment graphs contains the graphs that can be represented as intersections of segments (with arbitrary slopes and intersection angles). Every planar graph has a segment intersection representation [6]. Restricting to axis-aligned segments gives rise to grid intersection graphs (GIG) [25]. A bipartite graph is a GIG graph if and only if its incidence matrix admits a permutation of its rows and columns that avoids \(\gamma _5\) [19]. If all the segments must have the same length, then the graphs are known as unit grid intersection graphs (UGIG) [27]. The recognition problem is NP-complete for both GIG [25] and UGIG [27]. We note that 4DOR is a subset of UGIG but Stick is not [8].
Researchers have examined further restrictions on GIG. For example, the graphs that admit a GIG representation with the additional constraint that all the segments must intersect (or be “stabbed by”) a ground line form the stabbable grid intersection (StabGIG) graph class [8].
Another class of intersection graphs that restricts the objects on a ground line is defined in terms of hooks. A hook consists of a center point on the ground line together with an incident vertical segment and horizontal segment above the ground line. Hook graphs are intersection graphs of hooks [5, 21, 32], e.g., see Fig. 1(d). Hook graphs are also known as max point-tolerance graphs [5] and heterozygosity graphs [18]. The bipartite graphs that admit a Hook representation are called BipHook [8]. The complexities of recognizing the classes StabGIG, BipHook, and Stick are all open [8]. Chaplick et al. [8] examined the containment relations of these graph classes.
Grounded segment representations are a generalization of Stick representations, where the segments can have arbitrary slopes, e.g., see Fig. 1(e). Note that the segments are still restricted to lie on the same side of the ground line. Cardinal et al. [4] showed that the problem of deciding whether a graph admits a grounded segment representation is \(\exists \mathbb {R}\)-complete. We refer to [3, 4] for other related classes such as outersegment and outerstring graphs, and for the study of their containment relations.
The following table summarizes the time complexities of recognizing different classes of bipartite intersection graphs, where n and m are the sizes of the two vertex sets of the bipartition.
Graph class | Time complexity | Ref |
|---|---|---|
Chordal Bipartite Graphs | \(O((n+m)^2)\), or \(|E| \log (n+m)\) | |
Bipartite Permutation Graphs | O(nm)-time | [34] |
2-Directional Ray Graphs (2DOR) | O(nm)-time | |
3- or 4-Directional Ray Graphs (3DOR, 4DOR) | Open | |
4-DOR with given directions for vertices | f(n, m)-time\(^\mathrm{a}\) | [16] |
3-DOR with a given bipartition \((A\cup B)\), and an ordering for As, i.e., vertical rays | \(O((n+m)^2)\)-time | [16] |
Grid Intersection Graphs (GIG) | NP-complete | [25] |
Unit Grid Intersection Graphs (UGIG) | NP-complete | [27] |
Grounded Segment Intersection Graphs | \(\exists \mathbb {R}\)-complete | [4] |
StabGIG, SegRay, Hook, BipHook and Stick Graphs | Open |
2 Fixed As and Bs
In this section we study Stick representations of graphs with a fixed bipartition of the vertices and fixed vertex orderings for each vertex set. We call this problem Stick\(_{AB}\), defined formally as follows.

We first present an O(|A||B|)-time algorithm for Stick\(_{AB}\). A Stick representation is totally determined by the order \(\sigma \) of the segments’ intersection with the ground line (details in the proof of Lemma 1). Thus the idea of the algorithm is to impose some ordering constraints between the vertices of A and B based on some submatrices of the adjacency matrix of G. We show that the required Stick representation exists if and only if there exists a total order \(\sigma \) of \((A \cup B)\) that satisfies the constraints and preserves the given orderings \(\sigma _A\) and \(\sigma _B\). We now describe the details.
Assume that \(\sigma _A = (a_1,\ldots , a_n)\) and \(\sigma _B = (b_1,\ldots , b_m)\). Let M be the ordered bipartite adjacency matrix of A and B, i.e., M has rows \(a_1,\ldots ,a_n\) and columns \(b_1,\ldots ,b_m\), where the entry \(m_{i,p}\), i.e., the entry at the ith row and pth column, is 1 or 0 depending on whether \(a_i\) and \(b_p\) are adjacent or not, as illustrated in Fig. 3(a).
We start with the constraints \(a_{i-1} \prec a_i\), where \(2\le i\le n\), and \(b_{p-1} \prec b_p\), where \( 2\le p\le m\) to enforce the given orderings \(\sigma _A\) and \(\sigma _B\). We now add some more constraints, as follows.
-
\(C_1\): If an entry \(m_{i,p}\) is 1, then add the constraint \(a_i \prec b_p\), e.g., see the black edges in Fig. 3(b).
-
\(C_2\): If M contains an ordered submatrix
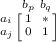 , then add the constraint \(b_p \prec a_j\). For example, see the gray edges in Fig. 3(b).
, then add the constraint \(b_p \prec a_j\). For example, see the gray edges in Fig. 3(b).
We now test whether the set of constraints is consistent. Consider a directed graph H with vertex set \((A \cup B)\), where each constraint corresponds to a directed edge (Fig. 3(b)). Then the set of constraints is consistent if and only if H is acyclic, and the following lemma claims that this occurs if and only if the graph admits a Stick representation.
Lemma 1
G admits a Stick representation respecting \(\sigma _A\) and \(\sigma _B\) if and only if H is acyclic, i.e., the constraints are consistent.
Proof
We first show that the constraints are necessary. Every constraint between two vertices of the same set is implied by \(\sigma _A\) or \(\sigma _B\). For Condition \(C_1\), observe that a horizontal segment \(a_i\) can intersect a vertical segment \(b_p\) only if \(a_i\) precedes \(b_p\), i.e., we must have \(a_i \prec b_p\). For Condition \(C_2\), we already have \(a_i\prec a_j, b_p\prec b_q, a_i\prec b_p, a_j\prec b_q\). If we assume that \(a_j\prec b_p\), then we have \(a_i \prec a_j\prec b_p \prec b_q\), and to reach the vertical segment \(b_q\), \(a_j\) would intersect \(b_p\). Since \(m_{j,p} = 0\), this intersection is forbidden. Figure 3(d) illustrates this scenario. Therefore, we must have the constraint \(b_p \prec a_j\). Since all the constraints are necessary, if G admits an intersection representation, then the set of constraints is consistent.
We now prove the converse. Suppose the set of constraints is consistent. Take a total order of \(A \cup B\) which is consistent with all the constraints, e.g., see Fig. 1(c). This is a “topological order” of H. Initiate the drawing of the corresponding orthogonal segments in this order on the ground line \(\ell \). This determines the y-coordinate of every \(a \in A\) and the x-coordinate of every \(b \in B\). For each vertex \(a\in A\), let \(\max _B(a)\) be the neighbor of a in G with the largest index. We extend the horizontal segment corresponding to a to the right until the x-coordinate of \(\max _B(a)\). Similarly, for each vertex \(b \in B\), let \(\min _A(b)\) be the neighbor of b in G with the minimum index. We extend the vertical segment corresponding to b upward until the y-coordinate of \(\min _A(b)\).
We must show that the resulting drawing does not contain any forbidden intersection. Suppose by contradiction that the segments of \(a_j\) and \(b_p\) intersect, but they are not adjacent in G, i.e., \(m_{j,p}=0\). We now have \(a_j \prec b_p\), and the entries \(b_q=\max _B(a_j)\) and \(a_i=\min _A(b_p)\) give the submatrix described in Condition \(C_2\), thus the constraint \(b_p \prec a_j\) applies, a contradiction. \(\square \)
An algorithm to solve Stick\(_{AB}\) follows immediately, and can be implemented in linear time in the size of the adjacency matrix M.
Theorem 1
There is an O(|A||B|)-time algorithm to decide the Stick\(_{AB}\) problem, and construct a Stick representation if one exists.
Proof
The algorithm was given above: We construct the directed graph H from the 0-1 matrix M and test if H is acyclic. This correctly decides Stick\(_{AB}\) by Lemma 1. Furthermore, if H is acyclic, then we can construct a Stick representation as specified in the proof of Lemma 1. Pseudocode for the algorithm is given in the full version [15].
The matrix M has size O(nm) where \(n=|A|\) and \(m=|B|\), and the graph H has \(n+m\) vertices and O(nm) edges. We can test acyclicity of a graph and find a topological ordering in linear time. Also, the construction of the Stick representation is clearly doable in linear time.
Thus we only need to give details on constructing H in time O(nm). We can construct the edges of H that correspond to \(\sigma _A\) and \(\sigma _B\) in time \(O(n+m)\). The edges arising from constraints \(C_1\) correspond to the 1’s in the matrix M, so we can construct them in O(nm) time. The edges arising from constraints \(C_2\) correspond to some of the 0’s in the matrix M. Specifically, a 0 in position \(m_{j,p}\) gives a \(C_2\) constraint \(b_p \prec a_j\) if and only if there is a 1 in row j to the right of the 0 and a 1 in column p above the 0. We can flag the 0’s that have a 1 to their right by scanning each row of M from right to left. Similarly, we can flag the 0’s that have a 1 above them by scanning each column of M from bottom to top. These scans take time O(nm). Finally, if a 0 in M has both flags, then we add the corresponding edge to H. The total time is O(nm). \(\square \)
Lemma 1 also yields a forbidden submatrix characterization for Stick\(_{AB}\).
Theorem 2
An instance of Stick\(_{AB}\) with graph \(G=(A \cup B, E)\) has a solution if and only if G’s ordered adjacency matrix M has no ordered submatrix of the following form:

Observe that \(P_2\) and \(P_3\) are special cases of \(P_1\) with \(p{=}q\) and \(j{=}k\), respectively.
Proof
We will use the graph H that we constructed above and used in Lemma 1. By Lemma 1, the theorem statement is equivalent to the statement that M has a submatrix \(P_1, P_2\) or \(P_3\) if and only if H has a directed cycle.
We first show that if the matrix M has one of the ordered submatrices \(P_1,P_2,P_3\) then H has a directed cycle. For \(P_1\), the cycle in H is \(a_k\prec b_p \) (by \(C_1\)), \(b_p\prec b_q\) (by \(\sigma _B\)), \(b_q\prec a_j\) (by \(C_2\)), \(a_j\prec a_k\) (by \(\sigma _A\)). For \(P_2\), the cycle is \(b_p\prec a_j \) (by \(C_2\)), \(a_j\prec a_k\) (by \(\sigma _A\)), \(a_k\prec b_p\) (by \(C_1\)). For \(P_3\), the cycle is \(b_q\prec a_j \) (by \(C_2\)), \(a_j\prec b_p\) (by \(C_1\)), \(b_p\prec b_q\) (by \(\sigma _B\)).
To prove the other direction, suppose that H has a directed cycle O. We will show that M has one of the submatrices \(P_1,P_2,P_3\). Let \(b_q\) be the rightmost vertex of O in \(\sigma _B\), and let \((b_q, z)\) be the outgoing edge of \(b_q\) in O. Since \(b_q\) is the rightmost vertex of O in \(\sigma _B\), z must be a vertex \(a_j\) of A. The constraint \(b_q\prec a_j\) can only be added by \(C_2\). Therefore, we must have the configuration  . The path can now continue from \(a_j\) following zero or more A vertices, but to complete the cycle, it eventually needs to reach a vertex \(b_p\) of B. Since \(b_q\) is the rightmost in \(\sigma _B\), \(b_p\) must appear either before \(b_q\) or coincide with \(b_q\). First suppose that \(b_p\not = b_q\). If the outgoing edge of \(a_j\) is \((a_j,b_p)\), then we obtain the configuration \(P_3\). Otherwise, the path visits several vertices of A and then visits \(b_p\), and we thus obtain the configuration \(P_1\).
. The path can now continue from \(a_j\) following zero or more A vertices, but to complete the cycle, it eventually needs to reach a vertex \(b_p\) of B. Since \(b_q\) is the rightmost in \(\sigma _B\), \(b_p\) must appear either before \(b_q\) or coincide with \(b_q\). First suppose that \(b_p\not = b_q\). If the outgoing edge of \(a_j\) is \((a_j,b_p)\), then we obtain the configuration \(P_3\). Otherwise, the path visits several vertices of A and then visits \(b_p\), and we thus obtain the configuration \(P_1\).
Suppose now that \(b_p = b_q\). In this case the outgoing edge of \(a_j\) cannot be \((a_j,b_p)\), because such an edge can only be added by \(C_1\), which would imply \(m_{j,p}=m_{j,q}=1\), violating the configuration above. If the path visits several vertices of A and then visits \(b_p(=b_q)\), then there must be a 1 in the qth column below the jth row. We thus obtain the configuration \(P_2\). \(\square \)
Bipartite Graphs Representable for All Orderings: The above forbidden submatrix characterization allows us to characterize the bipartite graphs \(G=(A\cup B,E)\) that have a Stick representation for every possible ordering of A and B. Observe that the forbidden submatrices \(P_2, P_3, P_1\) correspond, respectively, to the bipartite graphs shown in Fig. 4(a)–(c). We can construct \(2^2=4\) graphs from Fig. 4(a) based on whether each of the dotted edges is present or not. Similarly, we can construct \(2^2=4\) graphs from Fig. 4(b), and \(2^5=32\) graphs from Fig. 4(b). Let \(\mathcal {H}\) be the set that consists of these 40 graphs. From Theorem 2 we immediately obtain:
The forbidden subgraphs for Theorem 3. Dotted edges are optional.
Theorem 3
A bipartite graph \(G=(A\cup B,E)\) admits a Stick representation for every possible ordering of A and B if and only if G does not contain any graph of \(\mathcal H\).
3 Fixed As
In this section we study the Stick representation problem when the ordering of only the vertices in A is given. A formal description of the problem, which we call Stick\(_A\), is as follows.

We give a polynomial-time algorithm for Stick\(_A\). The idea is to use the forbidden submatrix characterization for Stick\(_{AB}\) (Theorem 2). We need an ordering of the B vertices that, together with the given ordering \(\sigma _A\), avoids the forbidden submatrices \(P_1,P_2,P_3\). We will express the conditions for the ordering of the B vertices as a 2-SAT formula, i.e., a CNF (conjunctive normal form) formula where each clause contains at most two literals. 2-SAT can be solved in polynomial time [1].
Theorem 4
There is an algorithm with run-time \(O(|A|^3|B|^3)\) to decide the Stick\(_A\) problem, and construct a Stick representation if one exists.
Proof
For each pair of vertices v, w of G, we create variables \(p_{v\prec w}\) and \(p_{w\prec v}\) (representing the ordering of segments v and w on the ground line). We will enforce \(p_{v\prec w} = \lnot p_{w\prec v}\) by adding clauses \((\lnot {p_{v\prec w}} \vee \lnot {p_{w\prec v}}) \wedge ({p_{v\prec w}} \vee {p_{w\prec v}})\). (One variable would suffice, but it is notationally easier to have both.) We first set the truth values of all the variables involving two vertices of A based on \(\sigma _A\). We then add a few other clauses based on \(P_1,P_2,P_3\), as follows.
For every \(b_p,b_q,b_r\) giving rise to \(P_1\), we add the clauses \((\lnot p_{{b_q\prec b_r}}\vee p_{b_q\prec b_p})\) and \((\lnot p_{{b_p\prec b_q}}\vee p_{b_r\prec b_q})\). The first clause means that if \(b_q\prec b_r\), then to avoid \(P_1\), we must have \(b_q\prec b_p\). Similarly, the second clause means if \(b_p\prec b_q\), then to avoid \(P_1\), we must have \(b_r\prec b_q\). These clauses ensure that if the SAT formula has a solution, then no configuration of the form \(P_1\) can arise.
For every \(b_p,b_q\) giving rise to \(P_2\), we set \(p_{b_q\prec b_p}\) to true. This would avoid any forbidden configuration of the form \(P_2\) in a solution of the 2-SAT formula.
Finally, for every \(b_p,b_q,b_r\) giving rise to \(P_3\), we add the clauses \((\lnot p_{{b_q\prec b_r}}\vee p_{b_q\prec b_p})\) and \((\lnot p_{{b_p\prec b_q}}\vee p_{b_r\prec b_q})\). Note that these clauses can be interpreted in the same way as for \(P_1\), i.e., if the 2-SAT formula has a solution, then no configuration of the form \(P_3\) can arise.
Let F be the resulting 2-SAT formula, which can be solved in linear time in the input size [1], i.e., \(O((|A| + |B|)^2)\) time. If F does not have a solution, then there does not exist any ordering of the Bs that avoids the forbidden patterns. Thus G does not admit the required Stick representation. If F has a solution, then there exists an ordering \(\sigma _B\) of Bs that together with \(\sigma _A\) avoids all the forbidden patterns. By Theorem 2, G admits the required Stick representation, and it can be constructed from \(\sigma _A\) and \(\sigma _B\) using Theorem 1.
Thus the time complexity of the algorithm is dominated by the time to construct the 2-SAT formula, which is \(O(|A|^3|B|^3)\). Pseudocode for the algorithm is given in the full version [15]. \(\square \)
Bipartite Graphs Representable for All A Orderings: We also considered the class of bipartite graphs \(G=(A \cup B, E)\) such that for every ordering of the vertices of A there exists a Stick representation. We will call this the Stick\(_{\forall A}\) class. Although we do not have a characterization of the Stick\(_{\forall A}\) class, we describe some positive and negative instances below in Remark 1 and Remark 2, with proofs in the full version [15].
Remark 1
Any bipartite graph \(G=(A\cup B,E)\) with at most three vertices in A belongs to the Stick\(_{\forall A}\) class.
Remark 2
A graph does not belong to Stick\(_{\forall A}\) if its bipartite adjacency matrix contains the submatrix  . (Here the columns are unordered.)
. (Here the columns are unordered.)
4 Stick Graphs
In this section we examine general Stick representations, i.e., we do not impose any constraints on the ordering of the vertices.

It is an open question to find a polynomial time algorithm for the above problem of recognizing Stick graphs.
We give some positive instances (Remarks 3–4) and some negative instances (Remark 5). The proofs of all but the first remark are included in the full version [15]. We need a few definitions to state the remarks, as follows.
A matrix has the simultaneous consecutive ones property if the rows and columns can be permuted so that the 1’s in each row and each column appear consecutively [29]. A one-sided drawing of a planar bipartite graph \(G=(A\cup B,E)\) is a planar straight-line drawing of G, where all vertices in A lie on the x-axis, and the vertices of B lie strictly above the x-axis [17].
Remark 3
Let \(G=(A\cup B, E)\) be a bipartite graph and let M be its adjacency matrix, where the rows and columns correspond to As and Bs, respectively. If M has the simultaneous consecutive ones property, then G admits a Stick representation, which can be computed in O(|A||B|) time.
Proof
One can determine whether M has the simultaneous consecutive ones property in O(|A||B|) time [29], and if so, then one can construct such a matrix \(M'\) within the same time complexity.
We now show how to construct the Stick representation from \(M'\). For each row (resp., column), we draw a horizontal (resp., vertical) segment starting from the rightmost (resp., topmost) 1 entry. We extend the horizontal segments to the left and vertical segments downward such that they touch a ground line \(\ell \).
Let the resulting drawing be D, which may contain many unnecessary crossings. However, for each unnecessary crossing, we can follow the segments involved in the crossings upward and rightward to find two distinct 1 entries. Since the matrix has the simultaneous ones property, the violated entries in each row (column) must lie consecutively at the left end of the row (bottom end of the column). Therefore, one can find a \((+x,-y)\)-monotone path P that separates the violated entries from the rest of the matrix.
Let \(b_1,b_2,\ldots ,b_k\) be the bend points creating \(90^\circ \) angles towards \(\ell \). To compute the required Stick representation, we remove these bends one after another, as follows. Consider the topmost bend point \(b_i\). Imagine a Cartesian coordinate system with origin at \(b_i\). Move the rows above \(b_i\) and columns to the right of \(b_i\) towards the upward and rightward directions, respectively. It is straightforward to observe that one now can construct a ground line \(\ell '\) through \(b_i\) such that the violated entries lie in the region below the path determined by \(b_{i+1},\ldots ,b_k\). \(\square \)
Remark 4
Let \(G=(A\cup B, E)\) be an n-vertex bipartite graph that admits a one-sided planar drawing. Then G is a Stick graph, and its Stick representation can be computed in \(O(n^2)\) time.
Remark 5
Let H be the graph obtained by deleting a perfect matching from a complete bipartite graph \(K_{4,4}\). Any graph \(G=(A \cup B, E)\) containing H as an induced subgraph does not admit a Stick representation. Since H is a planar graph, not all planar bipartite graphs are Stick graphs.
5 Open Problems
We conclude the paper with the following open problems.
Open Problem 1. What is the complexity of recognizing Stick graphs? Is the problem NP-complete? By Theorem 2 the problem is equivalent to ordering the rows and columns of a 0-1 matrix to exclude the 3 forbidden submatrices given in the Theorem statement. Note that these forbidden submatrices involve 5 or 6 rows and columns (vertices of the graph) so the results of Hell et al. [20], which apply to patterns of at most 4 vertices in a bipartite graph, do not provide a polynomial time algorithm.
One possible approach using 3-SAT is as follows. Given a bipartite graph \(G=(A\cup B, E)\), one can create a 3-SAT formula \(\varPhi \) such that \(\varPhi \) is satisfiable if and only if G admits a Stick representation, as follows. For each pair of vertices v, w of G, create variables \(p_{v\prec w}\) and \(p_{w\prec v}\) (representing the ordering of v and w on the ground line), and add clauses \((\lnot {p_{v\prec w}} \vee \lnot {p_{w\prec v}}) \wedge ({p_{v\prec w}} \vee {p_{w\prec v}})\) to enforce \(p_{v\prec w} = \lnot p_{w\prec v}\). Now express the conditions C1 and C2 from Sect. 2 as 3-SAT clauses.
-
\(\varPhi _1\): (Condition C1.) If \(m_{i,p}=1\), then set \(p_{a_i\prec b_p} = 1\).
-
\(\varPhi _2\): (Condition C2.) We must express the condition that if the ordered submatrix
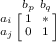 exists, then \(p_{b_p\prec a_j} =1\). Thus, if \(m_{i,p}=1, m_{j q}=1\) and \(m_{j,p}=0\), then we add the clause \((\lnot {p_{a_i\prec a_j}}\vee \lnot {p_{b_p\prec b_q}} \vee \lnot {p_{a_j\prec b_p}})\).
exists, then \(p_{b_p\prec a_j} =1\). Thus, if \(m_{i,p}=1, m_{j q}=1\) and \(m_{j,p}=0\), then we add the clause \((\lnot {p_{a_i\prec a_j}}\vee \lnot {p_{b_p\prec b_q}} \vee \lnot {p_{a_j\prec b_p}})\). -
\(\varPhi _3\): For each triple u, v, w of vertices, add the clause \((\lnot {p_{u\prec v}} \vee \lnot {p_{v\prec w}} \vee p_{u\prec w})\). Intuitively, these are transitivity constraints, which would ensure a total ordering on the ground line.
It is not difficult to show that the 3-SAT \(\varPhi \) is satisfiable if and only if G admits the required intersection representation. However, since \(\varPhi \) contains \(O(n^2)\) variables, using known SAT-solvers would not be faster than a naive algorithm that simply guesses the order of the segments along the ground line. Therefore, an interesting direction for future research would be to find a 3-SAT formulation with a linear number of variables.
Open Problem 2. Can we improve the time complexity of the recognition algorithm for graphs with fixed As?
References
Aspvall, B., Plass, M.F., Tarjan, R.E.: A linear-time algorithm for testing the truth of certain quantified Boolean formulas. Inf. Process. Lett. 8(3), 121–123 (1979)
Booth, K.S., Lueker, G.S.: Testing for the consecutive ones property, interval graphs, and graph planarity using PQ-tree algorithms. J. Comput. Syst. Sci. 13(3), 335–379 (1976)
Cabello, S., Jejcic, M.: Refining the hierarchies of classes of geometric intersection graphs. Electr. J. Comb. 24(1), 33 (2017)
Cardinal, J., Felsner, S., Miltzow, T., Tompkins, C., Vogtenhuber, B.: Intersection graphs of rays and grounded segments. In: Bodlaender, H.L., Woeginger, G.J. (eds.) WG 2017. LNCS, vol. 10520, pp. 153–166. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-68705-6_12
Catanzaro, D., et al.: Max point-tolerance graphs. Discrete Appl. Math. 216, 84–97 (2017)
Chalopin, J., Gonçalves, D.: Every planar graph is the intersection graph of segments in the plane. In: Proceedings of the Forty-First Annual ACM Symposium on Theory of Computing, pp. 631–638. ACM (2009)
Chan, T.M., Grant, E.: Exact algorithms and APX-hardness results for geometric packing and covering problems. Comput. Geom. 47(2, Part A), 112–124 (2014)
Chaplick, S., Felsner, S., Hoffmann, U., Wiechert, V.: Grid intersection graphs and order dimension. Order 35(2), 363–391 (2018)
Chaplick, S., Cohen, E., Morgenstern, G.: Stabbing polygonal chains with rays is hard to approximate. In: Canadian Conference on Computational Geometry (CCCG) (2013)
Chaplick, S., Hell, P., Otachi, Y., Saitoh, T., Uehara, R.: Intersection dimension of bipartite graphs. In: Gopal, T.V., Agrawal, M., Li, A., Cooper, S.B. (eds.) TAMC 2014. LNCS, vol. 8402, pp. 323–340. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-06089-7_23
Chen, L., Yesha, Y.: Efficient parallel algorithms for bipartite permutation graphs. Networks 23(1), 29–39 (1993)
Cogis, O.: On the Ferrers dimension of a digraph. Discrete Math. 38(1), 47–52 (1982)
Corneil, D.G., Olariu, S., Stewart, L.: The LBFS structure and recognition of interval graphs. SIAM J. Discrete Math. 23(4), 1905–1953 (2009)
Das, S., Sen, M., Roy, A.B., West, D.B.: Interval digraphs: an analogue of interval graphs. J. Graph Theory 13(2), 189–202 (1989)
De Luca, F., Hossain, M.I., Kobourov, S., Lubiw, A., Mondal, D.: Recognition and Drawing of Stick Graphs. arXiv preprint arXiv:1808.10005, August 2018
Felsner, S., Mertzios, G.B., Musta, I.: On the recognition of four-directional orthogonal ray graphs. In: Chatterjee, K., Sgall, J. (eds.) MFCS 2013. LNCS, vol. 8087, pp. 373–384. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40313-2_34
Fößmeier, U., Kaufmann, M.: Nice drawings for planar bipartite graphs. In: Bongiovanni, G., Bovet, D.P., Di Battista, G. (eds.) CIAC 1997. LNCS, vol. 1203, pp. 122–134. Springer, Heidelberg (1997). https://doi.org/10.1007/3-540-62592-5_66
Halldórsson, B.V., Aguiar, D., Tarpine, R., Istrail, S.: The clark phase-able sample size problem: long-range phasing and loss of heterozygosity in GWAS. In: Berger, B. (ed.) RECOMB 2010. LNCS, vol. 6044, pp. 158–173. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-12683-3_11
Hartman, I.B.A., Newman, I., Ziv, R.: On grid intersection graphs. Discrete Math. 87(1), 41–52 (1991)
Hell, P., Mohar, B., Rafiey, A.: Ordering without forbidden patterns. In: Schulz, A.S., Wagner, D. (eds.) ESA 2014. LNCS, pp. 554–565. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44777-2_46
Hixon, T.: Hook graphs and more: some contributions to geometric graph theory. Master’s thesis, Technische Universität Berlin (2013)
Hoffmann, U.: Intersection graphs and geometric objects in the plane. Master’s thesis, Technische Universität Berlin (2016)
Katz, M.J., Mitchell, J.S., Nir, Y.: Orthogonal segment stabbing. Comput. Geom. 30(2), 197–205 (2005)
Klinz, B., Rudolf, R., Woeginger, G.J.: Permuting matrices to avoid forbidden submatrices. Discrete Appl. Math. 1(60), 223–248 (1995)
Kratochvíl, J.: A special planar satisfiability problem and a consequence of its NP-completeness. Discrete Appl. Math. 52(3), 233–252 (1994)
Lubiw, A.: Doubly lexical orderings of matrices. SIAM J. Comput. 16(5), 854–879 (1987)
Mustaţă, I., Pergel, M.: Unit grid intersection graphs: Recognition and properties. arXiv preprint arXiv:1306.1855 (2013)
Müller, H.: Recognizing interval digraphs and interval bigraphs in polynomial time. Discrete Appl. Math. 78(1), 189–205 (1997)
Oswald, M., Reinelt, G.: The simultaneous consecutive ones problem. Theor. Comput. Sci. 410(21–23), 1986–1992 (2009)
Shrestha, A.M.S., Tayu, S., Ueno, S.: On orthogonal ray graphs. Discrete Appl. Math. 158(15), 1650–1659 (2010)
Soto, J.A., Telha, C.: Jump number of two-directional orthogonal ray graphs. In: Günlük, O., Woeginger, G.J. (eds.) IPCO 2011. LNCS, vol. 6655, pp. 389–403. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-20807-2_31
Soto, M., Caro, C.T.: p-Box: a new graph model. Discrete Math. Theor. Comput. Sci. 17(1), 169 (2015)
Spinrad, J.P.: Doubly lexical ordering of dense 0–1 matrices. Inf. Process. Lett. 45(5), 229–235 (1993)
Spinrad, J.P., Brandstädt, A., Stewart, L.: Bipartite permutation graphs. Discrete Appl. Math. 18(3), 279–292 (1987)
Acknowledgments
The research of A. Lubiw and D. Mondal is supported in part by the Natural Sciences and Engineering Research Council of Canada (NSERC). Also, this work is supported in part by NSF grants CCF-1423411 and CCF-1712119.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer Nature Switzerland AG
About this paper
Cite this paper
De Luca, F., Hossain, M.I., Kobourov, S., Lubiw, A., Mondal, D. (2018). Recognition and Drawing of Stick Graphs. In: Biedl, T., Kerren, A. (eds) Graph Drawing and Network Visualization. GD 2018. Lecture Notes in Computer Science(), vol 11282. Springer, Cham. https://doi.org/10.1007/978-3-030-04414-5_21
Download citation
DOI: https://doi.org/10.1007/978-3-030-04414-5_21
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-04413-8
Online ISBN: 978-3-030-04414-5
eBook Packages: Computer ScienceComputer Science (R0)







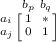 , then add the constraint
, then add the constraint 

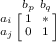 exists, then
exists, then