Abstract
Consider a random geometric graph over a random point process in  . Two points are connected by an edge if and only if their distance is bounded by a prescribed distance parameter. We show that projecting the graph onto a two dimensional plane is expected to yield a constant-factor crossing number (and rectilinear crossing number) approximation. We also show that the crossing number is positively correlated to the stress of the graph’s projection.
. Two points are connected by an edge if and only if their distance is bounded by a prescribed distance parameter. We show that projecting the graph onto a two dimensional plane is expected to yield a constant-factor crossing number (and rectilinear crossing number) approximation. We also show that the crossing number is positively correlated to the stress of the graph’s projection.
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
An undirected abstract graph \(G_0\) consists of vertices and edges connecting vertex pairs. An injection of \(G_0\) into  is an injective map from the vertices of \(G_0\) to
is an injective map from the vertices of \(G_0\) to  , and edges onto curves between their corresponding end points but not containing any other vertex point. For \(d\ge 3\), we may assume that distinct edges do not share any point (other than a common end point). For \(d=2\), we call the injection a drawing, and it may be necessary to have points where curves cross. A drawing is good if no pair of edges crosses more than once, nor meets tangentially, and no three edges share the same crossing point. Given a drawing D, we define its crossing number \(\mathrm{cr}(D)\) as the number points where edges cross. The crossing number \(\mathrm{cr}(G_0)\) of the graph itself is the smallest \(\mathrm{cr}(D)\) over all its good drawings D. We may restrict our attention to the rectilinear crossing number \({\overline{\mathrm{cr}}}(G_0)\), where edge curves are straight lines; note that \({\overline{\mathrm{cr}}}(G_0)\ge \mathrm{cr}(G_0)\).
, and edges onto curves between their corresponding end points but not containing any other vertex point. For \(d\ge 3\), we may assume that distinct edges do not share any point (other than a common end point). For \(d=2\), we call the injection a drawing, and it may be necessary to have points where curves cross. A drawing is good if no pair of edges crosses more than once, nor meets tangentially, and no three edges share the same crossing point. Given a drawing D, we define its crossing number \(\mathrm{cr}(D)\) as the number points where edges cross. The crossing number \(\mathrm{cr}(G_0)\) of the graph itself is the smallest \(\mathrm{cr}(D)\) over all its good drawings D. We may restrict our attention to the rectilinear crossing number \({\overline{\mathrm{cr}}}(G_0)\), where edge curves are straight lines; note that \({\overline{\mathrm{cr}}}(G_0)\ge \mathrm{cr}(G_0)\).
The crossing number and its variants have been studied for several decades, see, e.g., [30], but still many questions are widely open. We know the crossing numbers only for very few graph classes; already for \(\mathrm{cr}(K_n)\), i.e., on complete graphs with n vertices, we only have conjectures, and for \({\overline{\mathrm{cr}}}(K_n)\) not even them. Since deciding \(\mathrm{cr}(G_0)\) is NP-complete [15] (and \({\overline{\mathrm{cr}}}\) even  -complete [4]), several attempts for approximation algorithms have been undertaken. The problem does not allow a PTAS unless \(\mathrm {P}\,{=}\,\mathrm {NP}\) [6]. For general graphs, we currently do not know whether there is an \(\alpha \)-approximation for any constant \(\alpha \). However, we can achieve constant ratios for dense graphs [14] and for bounded pathwidth graphs [3]. Other strong algorithms deal with graphs of maximum bounded degree and achieve either slightly sublinear ratios [13], or constant ratios for further restrictions such as embeddability on low-genus surfaces [16,17,18] or a bounded number of graph elements to remove to obtain planarity [7, 9, 10, 12].
-complete [4]), several attempts for approximation algorithms have been undertaken. The problem does not allow a PTAS unless \(\mathrm {P}\,{=}\,\mathrm {NP}\) [6]. For general graphs, we currently do not know whether there is an \(\alpha \)-approximation for any constant \(\alpha \). However, we can achieve constant ratios for dense graphs [14] and for bounded pathwidth graphs [3]. Other strong algorithms deal with graphs of maximum bounded degree and achieve either slightly sublinear ratios [13], or constant ratios for further restrictions such as embeddability on low-genus surfaces [16,17,18] or a bounded number of graph elements to remove to obtain planarity [7, 9, 10, 12].
We will make use of the crossing lemma, originally due to [2, 25]Footnote 1: There are constantsFootnote 2 \(d\ge 4,c\ge \frac{1}{64}\) such that any abstract graph \(G_0\) on n vertices and \(m\ge dn\) edges has \(\mathrm{cr}(G_0)\ge c m^3/n^2\). In particular for (dense) graphs with \(m=\varTheta (n^2)\), this yields the asymptotically tight maximum of \(\varTheta (m^2)\) crossings.
Random Geometric Graphs (RGGs). We always consider a geometric graph G as input, i.e., an abstract graph \(G_0\) together with a straight-line injection into  , for some \(d\ge 2\); we identify the vertices with their points. For a 2-dimensional plane L, the postfix operator \(|_L\) denotes the projection onto L.
, for some \(d\ge 2\); we identify the vertices with their points. For a 2-dimensional plane L, the postfix operator \(|_L\) denotes the projection onto L.
Given a set of points V in  , the unit-ball graph (unit-disk graph if \(d=2\)) is the geometric graph using V as vertices that has an edge between two points iff balls of radius 1 centered at these points touch or overlap. Thus, points are adjacent iff their distance is \(\le 2\). In general, we may use arbitrary threshold distances \(\delta >0\). We are interested in random geometric graphs (RGGs), i.e., when using a Poisson point process to obtain V for the above graph class 2.
, the unit-ball graph (unit-disk graph if \(d=2\)) is the geometric graph using V as vertices that has an edge between two points iff balls of radius 1 centered at these points touch or overlap. Thus, points are adjacent iff their distance is \(\le 2\). In general, we may use arbitrary threshold distances \(\delta >0\). We are interested in random geometric graphs (RGGs), i.e., when using a Poisson point process to obtain V for the above graph class 2.
Stress. When drawing (in particular large) graphs with straight lines in practice, stress is a well-known and successful concept, see, e.g., [5, 20, 21]: let G be a geometric graph, \(d_0,d_1\) two distance functions on vertex pairs—(at least) the latter of which depends on an injection—and w weights. We have:
In a typical scenario, G is injected into  , \(d_0\) encodes the graph-theoretic distances (number of edges on the shortest path) or some given similarity matrix, and \(d_1\) is the Euclidean distance in
, \(d_0\) encodes the graph-theoretic distances (number of edges on the shortest path) or some given similarity matrix, and \(d_1\) is the Euclidean distance in  . Intuitively, in a drawing of 0 (or low) stress, the vertices’ geometric distances \(d_1\) are (nearly) identical to their “desired” distance according to \(d_0\). A typical weight function \(w(v_1,v_2):=d_0(v_1,v_2)^{-2}\) softens the effect of “bad” geometric injections for vertices that are far away from each other anyhow. It has been observed empirically that low-stress drawings tend to be visually pleasing and to have a low number of crossings, see, e.g., [8, 22]. While it may seem worthwhile to approximate the crossing number by minimizing a drawing’s stress, there is no sound mathematical basis for this approach.
. Intuitively, in a drawing of 0 (or low) stress, the vertices’ geometric distances \(d_1\) are (nearly) identical to their “desired” distance according to \(d_0\). A typical weight function \(w(v_1,v_2):=d_0(v_1,v_2)^{-2}\) softens the effect of “bad” geometric injections for vertices that are far away from each other anyhow. It has been observed empirically that low-stress drawings tend to be visually pleasing and to have a low number of crossings, see, e.g., [8, 22]. While it may seem worthwhile to approximate the crossing number by minimizing a drawing’s stress, there is no sound mathematical basis for this approach.
There are different ways to find (close to) minimal-stress drawings in 2D [5]. One way is multidimensional scaling, cf. [20], where we start with an injection of an abstract graph \(G_0\) into some high-dimensional space  and asking for a projection of it onto
and asking for a projection of it onto  with minimal stress. It should be understood that Euclidean distances in a unit-ball graph in
with minimal stress. It should be understood that Euclidean distances in a unit-ball graph in  by construction closely correspond to the graph-theoretic distances. In fact, for such graphs it seems reasonable to use the distances in
by construction closely correspond to the graph-theoretic distances. In fact, for such graphs it seems reasonable to use the distances in  as the given metrics \(d_0\), and seek an injection into
as the given metrics \(d_0\), and seek an injection into  —whose resulting distances form \(d_1\)—by means of projection.
—whose resulting distances form \(d_1\)—by means of projection.
Contribution. We consider RGGs for large t and investigate the mean, variance, and corresponding law of large numbers both for their rectilinear crossing number and their minimal stress when projecting them onto the plane. We also prove, for the first time, a positive correlation between these two measures.
While our technical proofs make heavy use of stochastic machinery (several details of which have to be deferred to the arXiv version [11]), the consequences are very algorithmic: We give a surprisingly simple algorithm that yields an expected constant approximation ratio for random geometric graphs even in the pure abstract setting. In fact, we can state the algorithm already now; the remainder of this paper deals with the proof of its properties and correctness:
Given a random geometric graph G in  (see below for details), we pick a random 2-dimensional plane L in
(see below for details), we pick a random 2-dimensional plane L in  to obtain a straight-line drawing \(G|_L\) that yields a crossing number approximation both for \({\overline{\mathrm{cr}}}(G_0)\) and for \(\mathrm{cr}(G_0)\).
to obtain a straight-line drawing \(G|_L\) that yields a crossing number approximation both for \({\overline{\mathrm{cr}}}(G_0)\) and for \(\mathrm{cr}(G_0)\).
Throughout this paper, we prefer to work within the setting of a Poisson point process because of the strong mathematical tools from the Malliavin calculus that are available in this case. It is straightforward to de-Poissonize our results: this yields asymptotically the same results—even with the same constants—for n uniform random points instead of a Poisson point process; we omit the details.
2 Notations and Tools from Stochastic Geometry
Let  be a convex set of volume \(\mathrm {vol}_d(W)=1\). Choose a Poisson distributed random variable n with parameter t, i.e.,
be a convex set of volume \(\mathrm {vol}_d(W)=1\). Choose a Poisson distributed random variable n with parameter t, i.e.,  . Next choose n points \(V=\{v_1, \dots , v_n\}\) independently in W according to the uniform distribution. Those points form a Poisson point process V in W of intensity t. A Poisson point process has several nice properties, e.g., for disjoint subsets \(A,B\subset W\), the sets \(V\cap A\) and \(V\cap B\) are independent (thus also their size is independent). Let \(V^k_{\ne }\), \(k\ge 1\), be the set of all ordered k-tuples over V with pairwise distinct elements. We will consider V as the vertex set of a geometric graph G for the distances parameter \((\delta _t)_{t>0}\) with edges \(E=\{ \{u,v\} \mid u,v\in V, u\ne v, \Vert u-v\Vert \le \delta _t \}\), i.e., we have an edge between two distinct points if and only if their distance is at most \(\delta _t\). Such random geometric graphs (RGG) have been extensively investigated, see, e.g., [27, 29], but nothing is known about the stress or crossing number of its underlying abstract graph \(G_0\).
. Next choose n points \(V=\{v_1, \dots , v_n\}\) independently in W according to the uniform distribution. Those points form a Poisson point process V in W of intensity t. A Poisson point process has several nice properties, e.g., for disjoint subsets \(A,B\subset W\), the sets \(V\cap A\) and \(V\cap B\) are independent (thus also their size is independent). Let \(V^k_{\ne }\), \(k\ge 1\), be the set of all ordered k-tuples over V with pairwise distinct elements. We will consider V as the vertex set of a geometric graph G for the distances parameter \((\delta _t)_{t>0}\) with edges \(E=\{ \{u,v\} \mid u,v\in V, u\ne v, \Vert u-v\Vert \le \delta _t \}\), i.e., we have an edge between two distinct points if and only if their distance is at most \(\delta _t\). Such random geometric graphs (RGG) have been extensively investigated, see, e.g., [27, 29], but nothing is known about the stress or crossing number of its underlying abstract graph \(G_0\).
A U-statistic \(U(k,f):=\sum _{\mathbf {v}\in V^k_{\ne }} f(\mathbf {v})\) is the sum over \(f(\mathbf {v})\) for all k-tuples \(\mathbf {v}\). Here, f is a measurable non-negative real-valued function, and \(f(\mathbf {v})\) only depends on \(\mathbf {v}\) and is independent of the rest of V. The number of edges in G is a U-statistic as  . Likewise, the stress of a geometric graph as well as the crossing number of a straight-line drawing is a U-statistic, using 2- and 4-tuples of V, respectively. The well-known multivariate Slivnyak-Mecke formula tells us how to compute the expectation
. Likewise, the stress of a geometric graph as well as the crossing number of a straight-line drawing is a U-statistic, using 2- and 4-tuples of V, respectively. The well-known multivariate Slivnyak-Mecke formula tells us how to compute the expectation  over all realizations of the Poisson process V; for U-statistics we have, see [31, Cor. 3.2.3]:
over all realizations of the Poisson process V; for U-statistics we have, see [31, Cor. 3.2.3]:

We already know  . Solving the above formula for the expected number of edges, we obtain
. Solving the above formula for the expected number of edges, we obtain

where \({\kappa }_d=\mathrm {vol}_d(B_d)\) is the volume of the unit ball \(B_d\) in  , and \(\mathrm {surf}(W)\) the surface area of W. For n and m, central limit theorems and concentration inequalities are well known as \(t \rightarrow \infty \), see, e.g., [27, 29].
, and \(\mathrm {surf}(W)\) the surface area of W. For n and m, central limit theorems and concentration inequalities are well known as \(t \rightarrow \infty \), see, e.g., [27, 29].
The expected degree  of a typical vertex v is approximately of order \(\kappa _d\, t\, \delta _t^d\) (this can be made precise using Palm distributions). This naturally leads to three different asymptotic regimes as introduced in Penrose’s book [27]:
of a typical vertex v is approximately of order \(\kappa _d\, t\, \delta _t^d\) (this can be made precise using Palm distributions). This naturally leads to three different asymptotic regimes as introduced in Penrose’s book [27]:
-
in the sparse regime we have \(\lim _{t\rightarrow \infty }t \, \delta _t^d=0\), thus
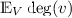 tends to zero;
tends to zero; -
in the thermodynamic regime we have \(\lim _{t\rightarrow \infty }t \, \delta _t^d=c >0 \), thus
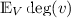 is asymptotically constant;
is asymptotically constant; -
in the dense regime we have \( \lim _{t\rightarrow \infty }t \, \delta _t^d=\infty \), thus
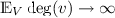 .
.
Observe that in standard graph theoretic terms, the thermodynamic regime leads to sparse graphs, i.e., via (3) we obtain  . Similarly, the dense regime—together with \(\delta _t \rightarrow c\)—leads to dense graphs, i.e.,
. Similarly, the dense regime—together with \(\delta _t \rightarrow c\)—leads to dense graphs, i.e.,  . Recall that to employ the crossing lemma, we want \(m \ge 4n\). Also, the lemma already shows that any good (straight-line) drawing of a dense graph \(G_0\) already gives a constant-factor approximation for \(\mathrm{cr}(G_0)\) (and \({\overline{\mathrm{cr}}}(G_0)\)). In the following we thus assume a constant \(0<c \le t\,\delta _t^{d}\) and \(\delta _t\rightarrow 0\), i.e., \(m=o(n^2)\).
. Recall that to employ the crossing lemma, we want \(m \ge 4n\). Also, the lemma already shows that any good (straight-line) drawing of a dense graph \(G_0\) already gives a constant-factor approximation for \(\mathrm{cr}(G_0)\) (and \({\overline{\mathrm{cr}}}(G_0)\)). In the following we thus assume a constant \(0<c \le t\,\delta _t^{d}\) and \(\delta _t\rightarrow 0\), i.e., \(m=o(n^2)\).
The Slivnyak-Mecke formula is a classical tool to compute expectations and will thus be used extensively throughout this paper. Yet, suitable tools to compute variances came up only recently. They emerged in connection with the development of the Malliavin calculus for Poisson point processes [23, 26]. An important operator for functions g(V) of Poisson point processes is the difference (also called add-one-cost) operator,
which considers the change in the function value when adding a single further point v. We know that there is a Poincaré inequality for Poisson functionals [23, 32], yielding the upper bound in (4) below. On the other hand, the isometry property of the Wiener-Itô chaos expansion [24] of an (square integrable) \(L^2\)-function g(V) leads to the lower bound in (4):

Often, in particular in the cases we are interested in in this paper, the bounds are sharp in the order of t and often even sharp in the occurring constant. This is due to the fact that the Wiener-Itô chaos expansion, the Poincaré inequality, and the lower bound are particularly well-behaved for Poisson U-statistics [28].
3 Rectilinear Crossing Number of an RGG
Let \({\mathcal L}\) be the set of all two-dimensional linear planes and \(L \in {\mathcal L}\) be a random plane chosen according to a (uniform) Haar probability measure on \({\mathcal L}\). The drawing \(G_L:= G|_L\) is the projection of G onto L. Let [u, v] denote the segment between vertex points \(u,v\in V\) if their distance is at most \(\delta _t\) and \(\emptyset \) otherwise. The rectilinear crossing number of \(G_L\) is a U-statistic of order 4:

Keep in mind that even for the best possible projection we only obtain \(\min _{L\in {\mathcal L}} {\overline{\mathrm{cr}}}(G|_L) \ge {\overline{\mathrm{cr}}}(G_0)\). To analyze  is more complicated than
is more complicated than  ; fortunately, we will not require it.
; fortunately, we will not require it.
3.1 The Expectation of the Rectilinear Crossing Numbers
For the expectation with respect to the underlying Poisson point process the Slivnyak-Mecke formula (2) gives

Let \(c_d\) be the constant given by the expectation of the event that two independent edges cross. In this paper’s arXiv version [11, Appendix A], we prove in Proposition 15 that \(c_d \le 2 \pi {\kappa }_d^2\), that \(\frac{I_W(v_1) }{\delta _t^{2d+2}} \) is bounded by \(c_d\) times the volume of the maximal \((d-2)\)-dimensional section of W, and that
where \(L^\perp \) is the \(d-2\) dimensional hyperplane perpendicular to L. Using the dominated convergence theorem of Lebesgue and Fubini’s theorem we obtain

Theorem 1
Let \( G_L\) be the projection of an RGG onto a two-dimensional plane L. Then, as \(t \rightarrow \infty \) and \(\delta _t \rightarrow 0\),

For unit-disk graphs, i.e., \(d=2\), the choice of L is unique and the projection superfluous. There the expected crossing number is asymptotically \( \frac{c_2}{8}\, t^4 \delta _t^{6} \) and thus of order \(\varTheta ( {m^3}/{n^2} )\) which is asymptotically optimal as witnessed by the crossing lemma. In general, the expectation is of order
The extra factor \(m/n^2\) can be understood as the probability that two vertices are connected via an edge, thus measures the “density” of the graph.
3.2 The Variance of the Rectilinear Crossing Numbers
By the variance inequalities (4) for functionals of Poisson point processes we are interested in the moments of the difference operator of the crossing numbers:


Plugging (7) into the Poincaré inequality (4) gives

Using calculations from integral geometry (see this paper’s arXiv version [11, Appendix B]), there is a constant \(0<c'_d\le 2 \pi {\kappa }_d c_d\) (given by the expectation of the event that two pairs of independent edges cross) such that

We use that \( t \delta _t^d \ge c>0\), assume \(d \ge 3\), and use Fubini’s theorem again.

On the other hand, (6) and the lower bound in (4) gives in our case

Thus our bounds have the correct order and, in the dense regime where \(t \delta _t^d \rightarrow \infty \), are even sharp. Using \(0<c'_d\le 2 \pi {\kappa }_d c_d\) we obtain:
Theorem 2
Let \( G_L\) be the projection of an RGG in  , \(d \ge 3\), onto a two-dimensional plane L. Then, as \(t \rightarrow \infty \) and \(\delta _t \rightarrow 0\),
, \(d \ge 3\), onto a two-dimensional plane L. Then, as \(t \rightarrow \infty \) and \(\delta _t \rightarrow 0\),

Theorems 1 and 2 show for the standard deviation

which is smaller than the expectation by a factor  . Or, equivalently, the coefficient of variation
. Or, equivalently, the coefficient of variation  is of order \(t^{- \frac{1}{2}}\). As \(t \rightarrow \infty \), our bounds on the expectation and variance together with Chebychev’s inequality lead to
is of order \(t^{- \frac{1}{2}}\). As \(t \rightarrow \infty \), our bounds on the expectation and variance together with Chebychev’s inequality lead to

Corollary 3
(Law of Large Numbers). For given L, the normalized random crossing number converges in probability (with respect to the Poisson point process V) as \(t \rightarrow \infty \),
Until now we fixed a plane L and computed the variance with respect to the random points V. Theorems 1 and 2 allow to compute the expectation and variance with respect to V and a randomly chosen plane L. For the expectation we obtain from Theorem 1 and by Fubini’s theorem

as \(t \rightarrow \infty \) and \(\delta _t \rightarrow 0\), where dL denotes integration with respect to the Haar measure on \({\mathcal L}\). For simplicity we assume in the following that \(\lim _{t \rightarrow \infty } (t \delta _t^d)^{-1}=0\). We use the variance decomposition  . By
. By

we obtain

Hölder’s inequality implies that the term in brackets is positive as long as \(I^{(2)}(W,L)\) is not a constant function.
3.3 The Rotation Invariant Case
If W is the ball B of unit volume and thus V is rotation invariant, then \(I^{(2)}(B,L)=I^{(2)}(B)\) is a constant function independent of L, and the leading term in (9) is vanishing. From (8) we see that in this case the expectation is independent of L.

For the variance this implies  , and hence
, and hence

In this case the variance  is of the order \(t^{-1}\)—and thus surprisingly significantly—smaller than in the general case.
is of the order \(t^{-1}\)—and thus surprisingly significantly—smaller than in the general case.
Theorem 4
Let \( G_L\) be the projection of an RGG in the ball  , \(d \ge 3\), onto a two-dimensional uniformly chosen random plane L. Then
, \(d \ge 3\), onto a two-dimensional uniformly chosen random plane L. Then

as \(t \rightarrow \infty \), \(\delta _t \rightarrow 0\) and \(t\delta _t^d \rightarrow \infty \).
Again, Chebychev’s inequality immediately yields a law of large numbers which states that with high probability the crossing number of \(G_L\) in a random direction is very close to \( \frac{1}{8} c_d \, t^4 \delta _t^{2d+2} I^{(2)}(B) \).
Corollary 5
(Law of Large Numbers). Let \( G_L\) be the projection of an RGG in  , \(d \ge 3\), onto a random two-dimensional plane L. Then the normalized random crossing number converges in probability (with respect to the Poisson point process V and to L), as \(t \rightarrow \infty \),
, \(d \ge 3\), onto a random two-dimensional plane L. Then the normalized random crossing number converges in probability (with respect to the Poisson point process V and to L), as \(t \rightarrow \infty \),
As known by the crossing lemma, the optimal crossing number is of order \(\frac{m^3}{n^2}\). In our setting this means that we are looking for the optimal direction of projection which leads to a crossing number of order \(t^4 \delta _t^{3d}\), much smaller than the expectation  . Chebychev’s inequality shows that if \(W=B\) it is difficult to find this optimal direction and to reach this order of magnitude; using \(\delta _t \rightarrow 0\) in the last step we have:
. Chebychev’s inequality shows that if \(W=B\) it is difficult to find this optimal direction and to reach this order of magnitude; using \(\delta _t \rightarrow 0\) in the last step we have:

Hence a computational naïve approach of minimizing the crossing numbers by just projecting onto a sample of random planes seems to be expensive. This suggests to combine the search for an optimal choice of the direction of projection with other quantities of the RGG. It is a long standing assumption in graph drawing that there is a connection between the crossing number and the stress of a graph. Therefore the next section is devoted to investigations concerning the stress of RGGs.
4 The Stress of an RGG
According to (1) we define the stress of \(G_L\) as
where \(w(v_1,v_2)\) a positive weight-function and \(d_0\) resp. \(d_L\) are the distances between \(v_1\) and \(v_2\), resp \(v_1|_L\) and \(v_2|_L\). As \({\overline{\mathrm{cr}}}(G)\), stress is a U-statistic, but now of order two. Using the Slivnyak-Mecke formula, it is immediate that

For the variance, the Poincaré inequality (4) implies

Hence the standard deviation of the stress is smaller than the expectation by a factor \(t^{- \frac{1}{2}}\) and thus the stress is concentrated around its mean. Again the computation of the lower bound for the variance in (4) is asymptotically sharp.

Theorem 6
Let \( G_L\) be the projection of an RGG in  , \(d \ge 3\), onto a two-dimensional plane L. Then
, \(d \ge 3\), onto a two-dimensional plane L. Then

The discussions from Sects. 3.2 and 3.3 lead to analogous results for the stress of the RGG. Using Chebychev’s inequality we could derive a law of large numbers. Taking expectations with respect to a uniform plane L we obtain:

Again, the term in brackets is only vanishing if \(W=B\). In this case

5 Correlation Between Crossing Number and Stress
It seems to be widely conjectured that the crossing number and the stress should be positively correlated. Yet it also seems that a rigorous proof is still missing. It is the aim of this section to provide the first proof of this conjecture, in the case where the graph is a random geometric graph.
Clearly, by the definition of \({\overline{\mathrm{cr}}}\) and \(\mathrm{stress}\) we have
for all v and all realizations of V. Such a functional F satisfying \(D_v (F) \ge 0\) is called increasing. The Harris-FKG inequality for Poisson point processes [23] links this fact to the correlation of \({\overline{\mathrm{cr}}}(G_L)\) and \(\mathrm{stress}(G,G_L)\).
Theorem 7
Because \(\mathrm{stress}\) and \({\overline{\mathrm{cr}}}\) are increasing we have

and thus the correlation is positive.
We immediately obtain that the covariance is positive and is of order at most

In [11, Appendix C] we use Mehler’s formula to prove a lower bound:

We combine this bound with (5), divide by the standard deviations from Theorems 2 and 6 and obtain the asymptotics for the correlation coefficient:
Theorem 8
Let \( G_L\) be the projection of an RGG in  , \(d \ge 3\), onto a two-dimensional plane L. Then
, \(d \ge 3\), onto a two-dimensional plane L. Then

It can be shown that this bound is even tight and asymptotically gives the correct correlation coefficient.
5.1 The Rotation Invariant Case
In principle the bounds for the covariance in the Poisson point process V given above can be used to compute covariance bounds in L and V when L is not fixed but random. For this we could use the covariance decomposition

Here we concentrate again on the case when \(W=B\) is the ball of unit volume and thus V is rotation invariant. Then  , and as an immediate consequence of Theorem 8 we obtain
, and as an immediate consequence of Theorem 8 we obtain
Corollary 9
Let \( G_L\) be the projection of an RGG in  , \(d \ge 3\), onto a two-dimensional random plane L. Then the correlation between the crossing number and the stress of the RGG is positive with
, \(d \ge 3\), onto a two-dimensional random plane L. Then the correlation between the crossing number and the stress of the RGG is positive with

In particular, the correlation does not vanish as \(t \rightarrow \infty \). This gives the first proof we are aware of, that there is a strict positive correlation between the crossing number and the stress of a graph. Hence, at least for RGGs, the method to optimize the stress to obtain good crossing numbers can be supported by rigorous mathematics.
6 Consequences and Conclusion
Apart from providing precise asymptotics for the crossing numbers of drawings of random geometric graphs, the main findings are the positive covariance and the non-vanishing correlation between the stress and the crossing number of the drawing of a random geometric graph. Of interest would be whether  for arbitrary graphs G. Yet there are simple examples of graphs G where this is wrong. Yet we could ask in a slightly weaker form whether at least
for arbitrary graphs G. Yet there are simple examples of graphs G where this is wrong. Yet we could ask in a slightly weaker form whether at least  but we have not been able to prove that.
but we have not been able to prove that.
We may coarsely summarize the gist of all the above findings algorithmically in the context of crossing number approximation, ignoring precise numeric terms that can be found above. We yield the first (expected) crossing number approximations for a rich class of randomized graphs:
Corollary 10
Let G be a random geometric graph in  (unit-disk graph) as defined above. With high probability, the number of crossings in its natural straight-line drawing is at most a constant factor away from \(\mathrm{cr}(G_0)\) and \({\overline{\mathrm{cr}}}(G_0)\).
(unit-disk graph) as defined above. With high probability, the number of crossings in its natural straight-line drawing is at most a constant factor away from \(\mathrm{cr}(G_0)\) and \({\overline{\mathrm{cr}}}(G_0)\).
Corollary 11
Let G be a random geometric graph in  (unit-ball graph) as defined above. We obtain a straight-line drawing D by projecting it onto a randomly chosen 2D plane. With high probability, the number of crossings in D is at most a factor \(\alpha \) away from \(\mathrm{cr}(G_0)\) and \({\overline{\mathrm{cr}}}(G_0)\). Thereby, \(\alpha \) is only dependent on the graph’s density.
(unit-ball graph) as defined above. We obtain a straight-line drawing D by projecting it onto a randomly chosen 2D plane. With high probability, the number of crossings in D is at most a factor \(\alpha \) away from \(\mathrm{cr}(G_0)\) and \({\overline{\mathrm{cr}}}(G_0)\). Thereby, \(\alpha \) is only dependent on the graph’s density.
Corollary 12
Let G be a random geometric graph and use its natural distances in  as input for stress minimization. The stress is positively correlated to the crossing number. Loosely speaking, a drawing of G with close to minimal stress is expected to yield a close to minimal number of crossings.
as input for stress minimization. The stress is positively correlated to the crossing number. Loosely speaking, a drawing of G with close to minimal stress is expected to yield a close to minimal number of crossings.
References
Aigner, M., Ziegler, G.M.: Proofs from THE BOOK, 4th edn. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-00856-6
Ajtai, M., Chvátal, V., Newborn, M., Szemerédi, E.: Crossing-free subgraphs. In: Theory and Practice of Combinatorics, North-Holland Mathematics Studies, North-Holland, vol. 60, pp. 9–12 (1982)
Biedl, T.C., Chimani, M., Derka, M., Mutzel, P.: Crossing number for graphs with bounded pathwidth. In: Proceedings of International Symposium on Algorithms and Computation (ISAAC) 2017, pp. 13:1–13:13. LIPIcs 92 (2017)
Bienstock, D.: Some provably hard crossing number problems. Discrete Comput. Geom. 6(5), 443–459 (1991)
Brandes, U., Pich, C.: An experimental study on distance-based graph drawing. In: Tollis, I.G., Patrignani, M. (eds.) GD 2008. LNCS, vol. 5417, pp. 218–229. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-00219-9_21
Cabello, S.: Hardness of approximation for crossing number. Discrete Comput. Geom. 49(2), 348–358 (2013)
Cabello, S., Mohar, B.: Crossing number and weighted crossing number of near-planar graphs. Algorithmica 60(3), 484–504 (2011). https://doi.org/10.1007/s00453-009-9357-5
Chimani, M., et al.: People prefer less stress and fewer crossings. In: Duncan, C., Symvonis, A. (eds.) Proceedings of International Symposium on Graph Drawing (GD) 2014. LNCS, vol. 8871, pp. 523–524. Springer, Heidelberg (2014)
Chimani, M., Hliněný, P.: Inserting multiple edges into a planar graph. In: Proceedings of International SYmposium on Computational Geometry (SoCG) 2016, pp. 30:1–30:15. LIPIcs 51 (2016)
Chimani, M., Hliněný, P., Mutzel, P.: Vertex insertion approximates the crossing number for apex graphs. Eur. J. Comb. 33, 326–335 (2012)
Chimani, M., Döring, H., Reitzner, M.: Crossing numbers and stress of random graphs. eprint arXiv:1808.07558v1 (2018)
Chimani, M., Hliněný, P.: A tighter insertion-based approximation of the crossing number. J. Comb. Optim. 33(4), 1183–1225 (2017)
Chuzhoy, J.: An algorithm for the graph crossing number problem. In: Proceedings of ACM Symposium on Theory of Computing (STOC) 2011, pp. 303–312. ACM (2011)
Fox, J., Pach, J., Suk, A.: Approximating the Rectilinear crossing number. In: Hu, Y., Nöllenburg, M. (eds.) GD 2016. LNCS, vol. 9801, pp. 413–426. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-50106-2_32
Garey, M.R., Johnson, D.S.: Crossing number is NP-complete. SIAM J. Algebr. Discrete Methods 4(3), 312–316 (1983)
Gitler, I., Hliněný, P., Leaño, J., Salazar, G.: The crossing number of a projective graph is quadratic in the face-width. Electron. J. Comb. 29, 219–233 (2007)
Hliněný, P., Chimani, M.: Approximating the crossing number of graphs embeddable in any orientable surface. In: Proceedings of ACM-SIAM Symposium on Discrete Algorithms (SODA) 2010, pp. 918–927 (2010)
Hliněný, P., Salazar, G.: Approximating the crossing number of toroidal graphs. In: Tokuyama, T. (ed.) ISAAC 2007. LNCS, vol. 4835, pp. 148–159. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-77120-3_15
de Klerk, E., Maharry, J., Pasechnik, D.V., Richter, R.B., Salazar, G.: Improved bounds for the crossing numbers of \(K_{m, n}\) and \(K_n\). SIAM J. Discrete Math. 20(1), 189–202 (2006)
Klimenta, M., Brandes, U.: Graph drawing by classical multidimensional scaling: new perspectives. In: Didimo, W., Patrignani, M. (eds.) GD 2012. LNCS, vol. 7704, pp. 55–66. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36763-2_6
Kobourov, S.G.: Force-directed drawing algorithms. In: Handbook of Graph Drawing and Visualization, pp. 383–408. CRC Press (2013)
Kobourov, S.G., Pupyrev, S., Saket, B.: Are crossings important for drawing large graphs? In: Duncan, C., Symvonis, A. (eds.) GD 2014. LNCS, vol. 8871, pp. 234–245. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-45803-7_20
Last, G., Penrose, M.: Fock space representation, chaos expansion and covariance, inequalities for general Poisson processes. Probab. Theory Relat. Fields 150, 663–690 (2011)
Last, G., Penrose, M.: Lectures on the Poisson Process. Cambridge University Press, Cambridge (2017)
Leighton, F.T.: Complexity Issues in VLSI: Optimal Layouts for the Shuffle-exchange Graph and Other Networks. MIT Press, Cambridge (1983)
Peccati, G., Reitzner, M. (eds.): Stochastic Analysis for Poisson Point Processes: Malliavin Calculus, Wiener-Itô Chaos Expansions and Stochastic Geometry. Bocconi & Springer Series, vol. 7. Springer, Switzerland (2016). https://doi.org/10.1007/978-3-319-05233-5. Bocconi University Press, Milan
Penrose, M.: Random Geometric Graphs (Oxford Studies in Probability). Oxford University Press, Oxford (2004)
Reitzner, M., Schulte, M.: Central limit theorems for U-statistics of poisson point processes. Ann. Probab. 41, 3879–3909 (2013)
Reitzner, M., Schulte, M., Thäle, C.: Limit theory for the Gilbert graph. Adv. Appl. Math. 88, 26–61 (2017)
Schaefer, M.: Crossing Numbers of Graphs. CRC-Press, Boca Raton (2017)
Schneider, R., Weil, W.: Stochastic and Integral Geometry. Probability and Its Applications. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78859-1
Wu, L.: A new modified logarithmic Sobolev inequality for Poisson point processes and several applications. Probab. Theory Relat. Fields 118, 427–438 (2000)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer Nature Switzerland AG
About this paper
Cite this paper
Chimani, M., Döring, H., Reitzner, M. (2018). Crossing Numbers and Stress of Random Graphs. In: Biedl, T., Kerren, A. (eds) Graph Drawing and Network Visualization. GD 2018. Lecture Notes in Computer Science(), vol 11282. Springer, Cham. https://doi.org/10.1007/978-3-030-04414-5_18
Download citation
DOI: https://doi.org/10.1007/978-3-030-04414-5_18
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-04413-8
Online ISBN: 978-3-030-04414-5
eBook Packages: Computer ScienceComputer Science (R0)


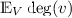 tends to zero;
tends to zero;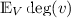 is asymptotically constant;
is asymptotically constant;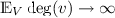 .
.