Abstract
The Species-Reaction Graph is a diagrammatic representation of a reaction network that closely resembles those commonly used to depict biochemical pathways. We shall see that a network’s Species-Reaction Graph often carries an extraordinary amount of far-from-obvious information about how the network might behave. In fact, the theorems in this chapter will tell us a great deal about behavior across the entire reaction network landscape, in particular about why dull, stable behavior is more prevalent than one might expect within a mathematical macrocosm so rife with nonlinearity.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
When we say that a component of the cycle intersection is a path, we mean that it is a sequence of one or more edges that connect a sequence of distinct vertices.
- 2.
The cycle consisting of the outer perimeter of cycles III and IV is odd.
- 3.
In particular there are such parameters when all species apart from J and G are in the feed stream.
- 4.
- 5.
Recall that the Species-Reaction Graph for the fully open CFSTR network, including feed reactions of the form
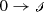 , is the same as the graph for (11.13).
, is the same as the graph for (11.13).
References
Banaji, M., Craciun, G.: Graph-theoretic approaches to injectivity and multiple equilibria in systems of interacting elements. Communications in Mathematical Sciences 7(4), 867–900 (2009)
Banaji, M., Craciun, G.: Graph-theoretic criteria for injectivity and unique equilibria in general chemical reaction systems. Advances in Applied Mathematics 44(2), 168–184 (2010)
Banaji, M., Donnell, P., Baigent, S.: P-matrix properties, injectivity, and stability in chemical reaction systems. SIAM Journal on Applied Mathematics 67(6), 1523 (2007)
Beretta, E.: Stability problems of chemical networks. In: Nonlinear Differential Equations: Invariance, Stability, and Bifurcation, pp. 11–27. Academic Press, Inc. (1981)
Beretta, E., Vetrano, F., Solimano, F., Lazzari, C.: Some results about nonlinear chemical systems represented by trees and cycles. Bulletin of Mathematical Biology 41(5), 641–664 (1979)
Chicone, C.: Ordinary Differential Equations with Applications, 2nd edn. Springer, New York (2006)
Craciun, G.: Systems of nonlinear differential equations deriving from complex chemical reaction networks. Ph.D. thesis, The Ohio State University (2002)
Craciun, G., Feinberg, M.: Multiple equilibria in complex chemical reaction networks. I. The injectivity property. SIAM Journal on Applied Mathematics 65(5), 1526–1546 (2005)
Craciun, G., Feinberg, M.: Multiple equilibria in complex chemical reaction networks: extensions to entrapped species models. IEE Proc. Syst. Biol 153(4), 179–186 (2006)
Craciun, G., Feinberg, M.: Multiple equilibria in complex chemical reaction networks. II. The species-reaction graph. SIAM Journal on Applied Mathematics 66(4), 1321–1338 (2006)
Craciun, G., Feinberg, M.: Multiple equilibria in complex chemical reaction networks: semi-open mass action systems. SIAM Journal on Applied Mathematics 70(6), 1859–1877 (2010)
Craciun, G., Tang, Y., Feinberg, M.: Understanding bistability in complex enzyme-driven reaction networks. Proceedings of the National Academy of Sciences 103(23), 8697–8702 (2006)
Delattre, P.: Evolution of Molecular Systems: Theoretical Foundations and Applications in Chemistry and Biology (in French). Maloine-Doin, Paris (1971)
Ellison, P., Ji, H., Knight, D., Feinberg, M.: The Chemical Reaction Network Toolbox, Version 2.3 (2014). Available at https://crnt.osu.edu
Greub, W.H.: Linear Algebra, 4th edn. Springer, New York (1981)
Hirsch, M.W., Smale, S., Devaney, R.L.: Differential Equations, Dynamical Systems, and an Introduction to Chaos, Third Edition. Academic Press (2012)
Hyver, C.: Valeurs propres des systèmes de transformation représentables par des graphes en arbres. Journal of Theoretical Biology 42(3), 397–409 (1973)
Hyver, C.: Stability of transformation systems representable by tree graphs: extension to structures of biological importance. Journal of Theoretical Biology 82(2), 187–204 (1980)
Joshi, B., Shiu, A.: Simplifying the Jacobian criterion for precluding multistationarity in chemical reaction networks. SIAM Journal on Applied Mathematics 72(3), 857–876 (2012)
Knight, D.: Reactor behavior and its relation to chemical reaction network structure. Ph.D. thesis, The Ohio State University (2015)
Knight, D., Shinar, G., Feinberg, M.: Sharper graph-theoretical conditions for the stabilization of complex reaction networks. Mathematical Biosciences 262(1), 10–27 (2015)
Lang, S.: Linear Algebra. Addison-Wesley, Reading, MA (1966)
Lee, E., Salic, A., Krüger, R., Heinrich, R., Kirschner, M.W.: The roles of APC and axin derived from experimental and theoretical analysis of the Wnt pathway. PLoS Biology 1(1), e10 (2003)
Rumschitzki, D.: On the theory of multiple steady states in isothermal CSTR’s. Ph.D. thesis, University of California, Berkeley [Work performed at the University of Rochester] (1983)
Rumschitzki, D., Feinberg, M.: Multiple steady states in complex isothermal CFSTRs II. Homogeneous reactors. Chemical Engineering Science 43(2), 329–337 (1988)
Schlosser, P.M.: A graphical determination of the possibility of multiple steady states in complex isothermal CFSTRs. Ph.D. thesis, University of Rochester (1988)
Schlosser, P.M., Feinberg, M.: A theory of multiple steady states in isothermal homogeneous CFSTRs with many reactions. Chemical Engineering Science 49(11), 1749–1767 (1994)
Shinar, G., Feinberg, M.: Concordant chemical reaction networks. Mathematical Biosciences 240(2), 92–113 (2012)
Shinar, G., Feinberg, M.: Concordant chemical reaction networks and the species-reaction graph. Mathematical Biosciences 241(1), 1–23 (2013)
Author information
Authors and Affiliations
Appendix 11.A Proof of Theorem 11.11.7
Appendix 11.A Proof of Theorem 11.11.7
Here we give a proof of Theorem 11.11.7 , which is repeated below as Theorem 11.A.1. The central idea of the proof is largely the one (“symmetrization”) used in earlier Knot Graph work, but the style is different.
Theorem 11.A.1 ( [20, 54, 112, 113])
Consider a mass action system \({\{\mathcal {S},\mathcal {C},\mathcal {R},k\}}\) with stoichiometric subspace S and species-formation-rate function \(f:{\mathbb {R}^{\mathcal {S}}} \to S\) . If the Knot Graph of the underlying network \({\{\mathcal {S},\mathcal {C},\mathcal {R}\}}\) has no cycles, then at each positive composition c ∗ (not necessarily an equilibrium), all eigenvalues of the derivative of the species-formation-rate function, df(c ∗) : S → S, are real and negative. Moreover, there exists for S a basis consisting of eigenvectors of df(c ∗). If c ∗ is an equilibrium, it is asymptotically stable.
Remark 11.A.2
Keep in mind that the base subnetwork of network \({\{\mathcal {S},\mathcal {C},\mathcal {R}\}}\) is presumed reversible. Keep in mind also the presumption that every reaction of the form  is accompanied by another reaction of the form
is accompanied by another reaction of the form  . If, in the mass action system of Theorem 11.A.1, there is a reaction of the form
. If, in the mass action system of Theorem 11.A.1, there is a reaction of the form  unaccompanied by a reaction of the form
unaccompanied by a reaction of the form  , we can still claim that all eigenvalues are real and nonpositive—see the proof—but an eigenvalue of 0 can occur. An example is provided by the simple network
, we can still claim that all eigenvalues are real and nonpositive—see the proof—but an eigenvalue of 0 can occur. An example is provided by the simple network
This network is degenerate, so for every choice of mass action rate constants, we will have singularity of df(c ∗) (and an eigenvalue of 0) at every positive composition.
By way of preparation for the proof of Theorem 11.A.1, we review some fundamental ideas of linear algebra. Suppose that V is a real vector space with a scalar product, denoted “◇”. A linear transformation T : V → V is symmetric relative to the scalar product ◇ if
Moreover, was say that T is negative-semi-definite relative to the scalar product ◇ if, for all v ∈ V ,
and negative-definite relative to that scalar product if equality holds only when v = 0.
Remark 11.A.3
Suppose that V is finite-dimensional. To establish the symmetry of a linear transformation T : V → V relative to a scalar product ◇, it is enough to test (11.A.2) against a basis for V . That is, if {v 1, v 2, …, v n} is a basis for V , then T is symmetric if and only if
The information contained in the following theorem is well known [98, 120].
Theorem 11.A.4 (Properties of a symmetric linear transformation)
Let V be a finite-dimensional real vector space and let T : V → V be a linear transformation. If there exists for V a scalar product “◇” with respect to which T is symmetric, then all roots of the characteristic polynomial of T are real. Moreover, there exists for V a basis that is orthonormal relative to ◇ and consists entirely of eigenvectors of T. If T is negative-semi-definite [negative-definite] relative to ◇, then all eigenvalues of T are nonpositive [negative].
Proof (Theorem 11.A.1)
To begin the proof of Theorem 11.A.1, we first note that, in the theorem statement, the derivative at c ∗ of the species-formation-rate function, df(c ∗) : S → S, is regarded as a map from the stoichiometric subspace into itself. For the purposes of the proof, it will be convenient to consider instead (temporarily) the extension of df(c ∗) to all of \({\mathbb {R}^{\mathcal {S}}}\), which we will denote by \(Df(c^*):{\mathbb {R}^{\mathcal {S}}} \to {\mathbb {R}^{\mathcal {S}}}\). This is just the linear map given by
For the mass action system \({\{\mathcal {S},\mathcal {C},\mathcal {R},k\}}\) of the theorem statement, the derivative Df(c ∗) takes the following form:
where, for each \({y \to y'} \in {\mathcal {R}}\),
and “∗” indicates the scalar product in \({\mathbb {R}^{\mathcal {S}}}\) defined by

We denote by \({\mathcal {B}}\) the subset of \({\mathcal {R}}\) consisting of reactions of the base subnetwork. Because the base subnetwork is presumed reversible, we can choose for each reversible reaction pair a “forward” reaction, and we denote by \({\mathcal {F}}\) the subset of \({\mathcal {B}}\) consisting of all forward reactions. With this in mind, we can rewrite (11.A.6) in the following way: For all \(\sigma \in {\mathbb {R}^{\mathcal {S}}}\)
Our aim will be to show that, when the Knot Graph is acyclic, it is possible to choose \(p \in {\mathbb {R}_+^{\mathcal {S}}}\) such that Df(c ∗) is symmetric relative to the scalar product “◇” defined by

In fact, we will show that we can choose p to get symmetry term by term in (11.A.9). That is, we will show that we can choose p such that, for all σ and σ′ in \({\mathbb {R}^{\mathcal {S}}}\), we have, for each \({y \to y'} \in {\mathcal {F}}\),
and, for each \({y \to y'} \in {\mathcal {R}} \setminus {\mathcal {B}}\),
It is easy to see that the requirement (11.A.12) for reactions not in the base subnetwork is satisfied trivially no matter how \(p \in {\mathbb {R}_+^{\mathcal {S}}}\) is chosen. Such reactions are either of the form  or
or  . In the first case, both sides of (11.A.12) reduce to zero. In the second case, both sides reduce to
. In the first case, both sides of (11.A.12) reduce to zero. In the second case, both sides reduce to

We turn, then, to consideration of reactions in the base subnetwork. To begin, we will choose \(p \in {\mathbb {R}_+^{\mathcal {S}}}\) to satisfy the requirement that when species  and
and  are in the same knot, then
are in the same knot, then  . (There will eventually be additional constraints on p.) When K is a knot, we denote by p
K the value of
. (There will eventually be additional constraints on p.) When K is a knot, we denote by p
K the value of  common to all
common to all  . Moreover, when y is a complex, we denote by p
y the value of
. Moreover, when y is a complex, we denote by p
y the value of  common to all
common to all  . (All members of supp y are in the same knot.)
. (All members of supp y are in the same knot.)
Now let y → y′ be a particular reaction in \({\mathcal {F}}\). In light of Remark 11.A.3 and because we can regard the species set \({\mathcal {S}}\) as a basis for \({\mathbb {R}^{\mathcal {S}}}\), the symmetry condition (11.A.11) will be satisfied if it is satisfied for all choices of  and
and  , where
, where  and
and  are distinct species.
are distinct species.
For the particular reaction \({y \to y'} \in {\mathcal {F}}\;\) under study, we consider various cases:
(i) Suppose that neither  nor
nor  is in supp y′. In this case (11.A.11) is satisfied, for both sides reduce to
is in supp y′. In this case (11.A.11) is satisfied, for both sides reduce to

(ii) Suppose that neither  nor
nor  is in supp y. Equation (11.A.11) is again satisfied, for both sides reduce to
is in supp y. Equation (11.A.11) is again satisfied, for both sides reduce to

(iii) Now suppose that  is in supp y and that
is in supp y and that  is in supp y′. In this case
is in supp y′. In this case  and
and  are in different knots, denoted K and K′. (Were the two species in the same knot, the Knot Graph would have a loop connecting the knot to itself, in contradiction to the hypothesis of Theorem 11.A.1.) Equation (11.A.11) reduces to
are in different knots, denoted K and K′. (Were the two species in the same knot, the Knot Graph would have a loop connecting the knot to itself, in contradiction to the hypothesis of Theorem 11.A.1.) Equation (11.A.11) reduces to

This last equation will be satisfied if we choose
There is precisely one equation of the form (11.A.16) for each edge in the Knot Graph. The question then becomes whether there is, for each knot K, a choice of p K > 0 such that the resulting system of equations is satisfied, regardless of the values of \(\{\eta _{{y \to y'}}\}_{{y \to y'} \in {\mathcal {B}}}\). Because the Knot Graph has no cycles, the answer is yes: The Knot Graph is a forest, so in each tree we can choose a leaf—that is, a knot K ∗ adjacent to precisely one edge—and then choose \(p_{K^*} = 1\). The assignments of p K for the remaining knots in the tree can be made by proceeding through the tree, applying (11.A.16) across each edge.
The resulting \(p \in {\mathbb {R}_+^{\mathcal {S}}}\) then gives the scalar product ◇ in \({\mathbb {R}^{\mathcal {S}}}\) with respect to which \(Df(c^*): {\mathbb {R}^{\mathcal {S}}} \to {\mathbb {R}^{\mathcal {S}}}\) is symmetric. Clearly, the stoichiometric subspace \(S \subset {\mathbb {R}^{\mathcal {S}}}\) inherits the scalar product ◇ from \({\mathbb {R}^{\mathcal {S}}}\), and, with respect to ◇, the restriction of Df(c ∗) to S—i.e., df(c ∗) : S → S—is also symmetric. From Theorem 11.A.4 it follows that all roots of the characteristic polynomial of df(c ∗) are real and that there exists for S a basis, orthonormal with respect to ◇, consisting entirely of eigenvectors of df(c ∗).
It remains to be shown that the eigenvalues of df(c ∗) are all negative. When the Species-Reaction Graph of the network \({\{\mathcal {S},\mathcal {C},\mathcal {R}\}}\) has no cycles, the negativity of the eigenvalues already follows from Theorem 11.5.1 and Corollary 10.7.3, provided that \({\{\mathcal {S},\mathcal {C},\mathcal {R}\}}\) is nondegenerate. Nevertheless, we are required to prove the negativity of the eigenvalues under the hypothesis of Theorem 11.11.7 (and the constraints imposed by Remark 11.11.1).
This we shall do by arguing that df(c ∗) is negative-definite relative to the scalar product ◇ just constructed. (See Theorem 11.A.4.) Thus, for σ ∈ S we consider the sign of
We will argue that the various individual terms in the two sums on the right side of (11.A.17) are all nonpositive with at least one negative so long as σ is not zero.
First consider a reaction \({y \to y'} \in {\mathcal {F}}\) with both y and y′ nonzero. In this case, supp y and supp y′ must reside in different knots K and K′. (Were they in the same knot, in the Knot Graph that knot would have a self-loop.) By virtue of the way ◇ and p were constructed, the term in (11.A.17) corresponding to y → y′ takes the form
The result is clearly nonpositive and is zero only when, for the particular \({y \to y'} \in {\mathcal {F}}\) under study, σ is orthogonal to the corresponding reaction vector relative to the ◇ scalar product.
We do not preclude the possibility that there are in \({\mathcal {F}}\) reactions of the form y → 0 (such as A + B → 0) or 0 → y (such as 0 → A + B). In such cases, it is not difficult to see that the corresponding terms in (11.A.17) reduce to, respectively,
Again, each is nonpositive and is zero only when σ is ◇-orthogonal to the reaction vector for the corresponding reaction, either y → 0 or 0 → y.
We turn now to terms in (11.A.17) that correspond to reactions that do not reside in the base subnetwork. These reactions are of the form  or
or  . In the first case, the corresponding term in (11.A.17) reduces to zero. In the second case, the term reduces to
. In the first case, the corresponding term in (11.A.17) reduces to zero. In the second case, the term reduces to

The result is again nonpositive and is zero only if  is zero or, stated differently, only if σ is ◇-orthogonal to the reaction vector (
is zero or, stated differently, only if σ is ◇-orthogonal to the reaction vector ( ) corresponding the reaction
) corresponding the reaction  .
.
In summary, then, we have established that the right side of (11.A.17) is negative and is zero precisely when σ ∈ S is ◇-orthogonal to all reaction vectors corresponding to reactions in the set
From the presumptions of Remark 11.11.1, it follows easily that
Thus, the right side of (11.A.17) is zero only when σ ∈ S is in the orthogonal complement of S (relative to ◇). This can happen only if σ = 0. We have established, then, that df(c ∗) : S → S is negative-definite relative to ◇, so all of its eigenvalues are negative.
When c ∗ is an equilibrium, it is asymptotically stable. This follows from the negativity of the eigenvalues associated with df(c ∗). [34, 104]. □
Remark 11.A.5
In Remark 11.11.1 we required that when, for a particular  , there is a reaction of the form
, there is a reaction of the form  , there is also one of the form
, there is also one of the form  . In fact, this requirement is stronger than it needed to be. It is enough that
. In fact, this requirement is stronger than it needed to be. It is enough that  , viewed as a vector of \({\mathbb {R}^{\mathcal {S}}}\), be a member of \({\mathrm {span} \,} \{y' - y : y \to y' \in {\mathcal {R}}^*\}\).
, viewed as a vector of \({\mathbb {R}^{\mathcal {S}}}\), be a member of \({\mathrm {span} \,} \{y' - y : y \to y' \in {\mathcal {R}}^*\}\).
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Feinberg, M. (2019). The Species-Reaction Graph. In: Foundations of Chemical Reaction Network Theory. Applied Mathematical Sciences, vol 202. Springer, Cham. https://doi.org/10.1007/978-3-030-03858-8_11
Download citation
DOI: https://doi.org/10.1007/978-3-030-03858-8_11
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-03857-1
Online ISBN: 978-3-030-03858-8
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


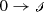 , is the same as the graph for (
, is the same as the graph for (