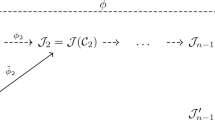Computing Supersingular Isogenies on Kummer Surfaces

Abstract

We apply Scholten’s construction to give explicit isogenies between the Weil restriction of supersingular Montgomery curves with full rational 2-torsion over $\mathbb {F}_{p^2}$ and corresponding abelian surfaces over $\mathbb {F}_{p}$. Subsequently, we show that isogeny-based public key cryptography can exploit the fast Kummer surface arithmetic that arises from the theory of theta functions. In particular, we show that chains of 2-isogenies between elliptic curves can instead be computed as chains of Richelot (2, 2)-isogenies between Kummer surfaces. This gives rise to new possibilities for efficient supersingular isogeny-based cryptography.

1 Introduction

Public key cryptography based on supersingular isogenies is gaining increased popularity due to its conjectured quantum-resistance. In November 2017, an actively secure key encapsulation mechanism called SIKE [22], which is based on Jao and De Feo’s supersingular isogeny Diffie-Hellman (SIDH) protocol [16, 23], was submitted to NIST in response to their call for quantum-resistant public key solutions [34]. When compared to other proposals of quantum-resistant key encapsulation mechanisms, SIKE currently offers an interesting bandwidth versus performance trade-off; its keys are appreciably smaller than its code- and lattice-based counterparts, but the times required for encapsulation and decapsulation are significantly higher. This performance drawback of supersingular isogeny-based cryptography is the main practical motivation for this paper.

This Work. 15 years ago, Scholten [31] showed that if E is an elliptic curve defined over a quadratic extension field L of a non-binary field K, and if its entire 2-torsion is L-rational, then a genus-2 curve C can be constructed over K such that its Jacobian $J_C$ is isogenous to the Weil restriction $\mathrm{Res}^{L}_K(E)$. Fortuitously, supersingular isogeny-based cryptography currently uses elliptic curves that precisely meet these requirements. In particular, state-of-the-art implementations (e.g., [14, 15]) of SIDH fix a large prime field $K=\mathbb {F}_{p}$ with $p=2^i3^j-1$ for $i>j>100$, construct $L=\mathbb {F}_{p^2}$, and work in the supersingular isogeny class of elliptic curves over $\mathbb {F}_{p^2}$ whose group structures are all isomorphic to $\mathbb {Z}_{p+1} \times \mathbb {Z}_{p+1}$. This necessarily means that all curves in the supersingular isogeny class have full rational 2-torsion, can be written in Montgomery form, and that for any such curve $E/\mathbb {F}_{p^2}$, Scholten’s construction can be used to write down the curve $C/\mathbb {F}_p$ whose Jacobian $J_C$ is isogenous to the Weil restriction of E with respect to $\mathbb {F}_{p^2}/\mathbb {F}_p$.

In Proposition 1 we use Scholten’s construction to write down a curve whose Jacobian is isogenous to the Weil restriction of any supersingular curve that satisfies the above requirements. Although the existence of this isogeny is guaranteed by his construction, Scholten does not provide the isogeny itself, and as is pointed out in [6, Sect. 2], the construction does not guarantee that this isogeny is efficiently computable. In our supersingular setting, however, we are able to derive simple explicit isogenies between the two varieties; these turn out to be dual (2, 2)-isogenies whose compositions are, by definition, the multiplication-by-2 morphism on the corresponding varieties.

The application of Scholten’s construction and the derivation of the explicit maps above allows us to study SIDH computations on abelian surfaces over $\mathbb {F}_p$, rather than on elliptic curves over $\mathbb {F}_{p^2}$. In particular, rather than using Vélu’s formulas [35] to compute secret $2^e$-isogenies as chains of 2- and/or 4-isogenies on elliptic curves over $\mathbb {F}_{p^2}$ [16], we show that the same secret isogenies can instead be computed as a chain of (2, 2)-isogenies on Jacobian varieties over $\mathbb {F}_p$. While computing isogenies on higher genus abelian varieties is, in general, much more complicated than Vélu’s formulas for elliptic curve isogenies, the special case of (2, 2)-isogenies between genus-2 Jacobians dates back to the works of Richelot [29, 30] from almost two centuries ago. Subsequently, the computation of Richelot isogenies is already well-documented in the literature (cf. [10, 33]), and this allows us to tailor the explicit formulas to our scenario of computing chains of (2, 2)-isogenies on supersingular Jacobians.

Crucial to the efficacy of this work is that we are able to compute (2, 2)-isogenies on the Kummer surfaces associated to supersingular Jacobians, rather than in the full Jacobian groups. This allows us to leverage the fast Kummer surface arithmetic arising from the classical theory of theta functions, which was first proposed for computational purposes by the Chudnovsky brothers [12], and which was brought to life in cryptography by Gaudry [19]. In his article [19, Remark 3.5], Gaudry points out that the fast (pseudo-)doublings on Kummer surfaces are the result of pushing points back and forth through a (2, 2)-isogenous variety, i.e., that the corresponding (2, 2)-isogenies split the multiplication-by-2 map on the associated Kummer surface. This observation plays a key role in deriving efficient isogenies on fast Kummer surfaces.

Related Work. This paper relies on the results of several authors:-

• The construction in Scholten’s unpublished manuscript [31] is at the heart of this work. It gives rise to Proposition 1 which paves the way for the rest of the paper.

• In 2014, Bernstein and Lange [6] revived Scholten’s work when they proposed using his construction in the context of (hyper)elliptic curve cryptography (H)ECC to convert keys back and forth between elliptic and hyperelliptic curves, in such a way so as to exploit advantageous properties of both settings. They were also the first to explicitly derive instances of the isogenies alluded to by Scholten, and to show that they can be efficient enough to be used in online cryptographic computations. The setting considered in [6] has the advantage of having a single elliptic-and-hyperelliptic curve pair that is fixed once-and-for-all (meaning the back-and-forth maps also remain fixed), while in our scenario we will need general-purpose maps that can handle any supersingular Montgomery curves efficiently at runtime. However, in the supersingular setting, we have the advantage that our Jacobians have a fixed embedding degree of $k=2$, and we can therefore exploit the existence of an efficiently computable trace map; this allows us to derive much simpler back-and-forth isogenies than those presented in [6].

• Renes and Smith [28] recently introduced qDSA: the quotient digital signature algorithm. In order to instantiate their scheme on fast Kummer surfaces, they deconstructed the pseudo-doubling map into the explicit (2, 2)-isogenies alluded to by Gaudry [19, Remark 3.5]; this deconstruction (depicted in [28, Fig. 1]) plays a key role in this paper. Indeed, it was their explicit treatment of the dual Kummer surface and subsequent illustration of simple (2, 2)-isogenies between fast Kummer surfaces that, in part, inspired the present work.

• Being able to study Kummer surface arithmetic as a viable alternative in the supersingular isogeny landscape is made easier by virtue of the fact that state-of-the-art SIDH implementations already work entirely in the Kummer variety, $E/ \{ \pm \}$, of a given supersingular elliptic curve E. In their article introducing SIDH, Jao and De Feo [23] showed that, in addition to its widely known application of computing scalar multiplications, fast Montgomery x-only style arithmetic [25] could also be used to push points through isogenies. In more recent work, Costello, Longa and Naehrig [14] exploited a similar optimisation when computing the isogenous curves in SIDH, observing that isogeny arithmetic is twist-agnostic in SIDH in a similar fashion to point arithmetic being twist-agnostic in Bernstein’s Curve25519 ECC software [3]. Subsequently, in the SIKE proposal [22], all elliptic curve points are only ever represented up to sign and all elliptic curves are only ever represented up to quadratic twist. Ultimately, this means that when we move to genus 2, we are able to work in the pre-existing SIDH infrastructure and replace abelian surfaces with Kummer surfaces and points on abelian surfaces with points on these Kummer surfaces.

• One significant hurdle to overcome in order to exploit fast isogenies on our Kummer surfaces it that the (2, 2)-isogeny that splits pseudo-doublings¹ corresponds to a special kernel, and in SIDH computations we need isogenies that work identically for general kernel elements, or at least identically for all of the kernel elements that can arise in a large-degree supersingular isogeny routine. This was achieved in the elliptic curve case by De Feo, Jao and Plût [16], who use an isomorphism to move the general Montgomery 2-torsion point $(\alpha ,0)$ with $\alpha \ne 0$ to the special 2-torsion point (0, 0). However, in our case, the kernels of Richelot isogenies are non-cyclic, and finding the isomorphism to move general kernels to special kernels is less obvious. Our overcoming this hurdle on Jacobians (see Sect. 4) is aided by the use of quadratic splittings introduced by Smith in his treatment of Richelot kernels [33, Chap. 8], and our overcoming this hurdle on fast Kummer surfaces (see Sect. 5) employs the technique of [16, Sect. 4.3.2], which uses higher order torsion points (lying above the kernel) to avoid square root computations.

Roadmap. Section 2 provides background and sets notation. Section 3 defines the abelian surfaces corresponding to supersingular Montgomery curves (by way of Proposition 1), and gives the back-and-forth maps between these two objects. Section 4 then studies (2, 2)-isogenies on supersingular abelian surfaces and, in particular, it shows how to replace even-power elliptic curve isogenies defined over $\mathbb {F}_{p^2}$ with chains of (2, 2)-isogenies inside full Jacobians defined over $\mathbb {F}_p$. This lays the foundations to move to Kummer surfaces in Sect. 5, where the (2, 2)-isogenies simplify and become much faster. Implications for isogeny-based cryptography are discussed in Sect. 6.

There are many constants, variables and formulas in this work, so the risk of typographical error is high. Thus, for readers wanting to verify or replicate this work, illustrative Magma source files can be found at

https://www.microsoft.com/en-us/download/details.aspx?id=57309.

Before going any further, we stress that this paper in no way changes the security picture of isogeny-based cryptography, and that using Kummer surfaces over $\mathbb {F}_p$ instead of elliptic curves over $\mathbb {F}_{p^2}$ can be viewed as a mere implementation choice. The efficient back-and-forth maps in Sect. 3 show that any conceivable hard problem that can be posed in one setting can be efficiently ported over to the other setting.

2 Preliminaries

This section gives the necessary background for the remainder of the paper. We start with a brief summary of some jargon for non-experts. An abelian variety is a general term for a projective algebraic variety that possesses an algebraic group law. When we quotient an abelian variety by the map that takes elements to their inverses, we get the associated Kummer variety. There are two examples that are relevant in this paper. An elliptic curve is an abelian variety of dimension 1, and its quotient by $\{\pm 1\}$ gives the associated Kummer line; if E is a short Weierstrass or Montgomery curve, then a geometric point $P \in E$ can be parameterised on the Kummer line $E/\{\pm 1\}$ by its x-coordinate, x(P), which is why it is often called the x-line. An abelian surface is an abelian variety of dimension 2, and all such instances in this work occur as Jacobian groups of genus-2 hyperelliptic curves; if C is a genus-2 curve and $J_C$ is its Jacobian, then the quotient $J_C/\{\pm 1\}$ is called a Kummer surface.

Supersingular Montgomery Curves. State-of-the-art SIDH implementations (cf. [14, 15]) currently employ large prime fields of the form $p=2^i3^j-1$ with $i>j>100$, so that, over $\mathbb {F}_{p^2}$, the supersingular isogeny class consists entirely of curves whose abelian group structure is isomorphic to $\mathbb {Z}_{p+1} \times \mathbb {Z}_{p+1}$. This necessarily means that all of the curves in the isogeny class have full $\mathbb {F}_{p^2}$-rational 2-torsion, and moreover, that they can be written in Montgomery form over $\mathbb {F}_{p^2}$ as $By^2=x^3+Ax^2+x$. Rather than parameterising Montgomery curves in this way, we will make an arbitrary choice of one of the two rational 2-torsion points $(\alpha ,0)$ with $\alpha \notin \{-1,0,1\}$ (the other is $(1/\alpha ,0)$), and from hereon will use $E_\alpha$ to denote the curve

$$\begin{aligned} E_\alpha /K :y^2=x (x-\alpha )(x-1/\alpha ), \end{aligned}$$

(1)

the j-invariant of which is

$$ j(E_\alpha ) = 256 \frac{(\alpha ^4-\alpha ^2+1)^3}{\alpha ^4(\alpha ^2-1)^2}. $$

Note that the j-invariant is the same for $E_\alpha$ as it is for the curve $\delta y^2=x (x-\alpha )(x-1/\alpha )$; this is because $\delta$ only helps fix the quadratic twist, i.e., only fixes the curve up to $\bar{K}$-isomorphism. As mentioned in Sect. 1, point and isogeny arithmetic is independent of $\delta$, so our curves need only be defined up to twist.

Throughout the paper we will often be making implicit use of the following result, which is essentially due to Auer and Top [1].

Lemma 1

If $E_\alpha /\mathbb {F}_{p^2} :y^2=x (x-\alpha )(x-1/\alpha )$ is supersingular, then $\alpha \in (\mathbb {F}_{p^2}^\times )^2$, and $\alpha ^2-1 \in (\mathbb {F}_{p^2}^\times )^8$.

Proof

The group structure of $E_\alpha$ implies that at least one of the three 2-torsion points (0, 0), $(\alpha ,0)$ and $(1/\alpha ,0)$ must be in $[2]E(\mathbb {F}_{p^2})$, so $\alpha \in (\mathbb {F}_{p^2}^\times )^2$ by [1, Lemma 2.1]. Thus, there exists $\epsilon \in \mathbb {F}_{p^2}$ such that $\epsilon ^2=-\alpha ^3$, and it follows that E is isomorphic over $\mathbb {F}_{p^2}$ to the curve $\tilde{E} :y^2=x(x-1)(x+\alpha ^2-1)$ via $(x,y) \mapsto (-\alpha x +1, \epsilon y)$. Applying [1, Proposition 3.1] yields that $\alpha ^2-1 \in (\mathbb {F}_{p^2}^\times )^8$.    $\square$

Abelian Surfaces. Over a field K of characteristic not 2, every genus-2 curve is birationally equivalent to a curve of the form $C:y^2=f(x)$, where $f(x) \in K[x]$ is of degree 6 and has no repeated factors. In this work we will only encounter such curves where f(x) splits completely in K[x], so we will often be writing them in the form

$$\begin{aligned} C/K :y^2=(x-z_1)(x-z_2)(x-z_3)(x-z_4)(x-z_5)(x-z_6), \end{aligned}$$

(2)

where $z_i \in K$ for $i \in \{1, \dots , 6\}$, and where we write $y^2$ instead of $\delta y^2$ for the same reason as for the elliptic curve case above.

Denote the difference $z_i-z_j$ by (ij). Following Igusa [21, p. 620], define the quantities

$$\begin{aligned} I_2&:= \sum (12)^2(34)^2(56)^2 ,\nonumber \\ I_4&:= \sum (12)^2(23)^2(31)^2(45)^2(56)^2(64)^2 ,\nonumber \\ I_6&:= \sum (12)^2(23)^2(31)^2(45)^2(56)^2(64)^2(14)^2(25)^2(36)^2 ,\nonumber \\ I_{10}&:= \prod (12)^2 , \end{aligned}$$

(3)

where the sums and product above run over all of the distinct expressions obtained by permuting the index set $\{1,\dots ,6\}$. The invariants $I_2$, $I_4$, $I_6$, and $I_{10}$ are called the Igusa-Clebsch invariants, and they play an analogous role to the j-invariant of an elliptic curve: two curves C and $C'$, with respective Igusa-Clebsch invariants $(I_2, I_4 , I_6 , I_{10})$ and $(I_2' , I_4' , I_6' , I_{10}')$, are isomorphic over $\bar{K}$ if and only if

$$ (I_2 :I_4 :I_6 :I_{10}) = (I_2' :I_4' :I_6' :I_{10}') \in \mathbb {P}(2,4,6,10)(\bar{K}), $$

i.e., if and only if there exists a $\lambda \in \bar{K}^\times$ such that

$$ (I_2' , I_4' , I_6' , I_{10}')=(\lambda ^2 I_2,\lambda ^4 I_4 ,\lambda ^6 I_6 , \lambda ^{10} I_{10}). $$

Observe that, as in the elliptic curve case, the invariants here are independent of $\delta$, i.e., are twist-independent. For $a,b,c,d \in K$ with $ad \ne bc$ and $e \in K^\times$, the map

$$\begin{aligned} \kappa _{(a , b , c , d)} :\quad C \rightarrow C', \quad (x,y) \mapsto \left( \frac{ax+b}{cx+d} \, , \, \frac{ey}{(cx+d)^3}\right) \end{aligned}$$

(4)

is a K-rational isomorphism to the curve $C'$. Up to isomorphism and quadratic twist, and by abuse of notation, we can write $C'$ as $C' :y^2=\prod _{i=1}^6(x-z_i')$, where $z_i' = (az_i+b)/(cz_i+d)$. Let $\{\ell _0, \ell _1, \ell _\infty , \ell _\lambda , \ell _\mu , \ell _\nu \}=\{z_1, \dots , z_6\}$ be some relabeling of the roots of the sextic in (2). Setting

$$ a=\ell _1-\ell _\infty , \quad b=\ell _0(\ell _\infty -\ell _1),\quad c=\ell _1-\ell _0, \quad \mathrm{and} \quad d=\ell _\infty (\ell _0-\ell _1) $$

in (4) yields a map $\kappa _{(a , b , c , d)} :C \rightarrow C_{\lambda ,\mu ,\nu }$, where

$$ C_{\lambda ,\mu ,\nu } :y^2=x(x-1)(x-\lambda )(x-\mu )(x-\nu ) $$

is the so-called Rosenhain form of C. Under $\kappa _{(a , b , c , d)}$, the points $(\ell _\lambda ,0)$, $(\ell _\mu ,0)$ and $(\ell _\nu ,0)$ on C are respectively sent to $(\lambda ,0)$, $(\mu ,0)$ and $(\nu ,0)$ on $C_{\lambda ,\mu ,\nu }$, while the points $(\ell _0,0)$, $(\ell _1,0)$ and $(\ell _\infty ,0)$ are respectively sent to (0, 0), (1, 0), and the point at infinity on $C_{\lambda ,\mu ,\nu }$. There are $6!=720$ possible relabelings of the six $z_i$, and as such there are 720 possible (ordered) triples $(\lambda ,\mu ,\nu )$ of Rosenhain invariants. In this work we can identify the Jacobian variety, $J_C$, of the curve C / K with the degree zero divisor class group of C, i.e., with $\mathrm{Pic}^0_K(C) = \mathrm{Div}^0_K(C)/\mathrm{Prin}_K(C)$ (cf. [18, Sect.  7.8]). In this way a point in the affine part of $J_C$ (see [18, p. 204]) is represented using the Mumford representation of the corresponding divisor $D \in \mathrm{Pic}^0_K(C)$; if D is reduced and non-zero, then the effective component of the support of D either contains 1 or 2 (not necessarily unique) $\bar{K}$-rational points on C. In the first (so-called degenerate) case, if $(x_1,y_1)$ is the only such point (and its multiplicity is 1) in the support of D, then $(x_1,y_1) \in C(K)$, and its Mumford representation is $(x-x_1,y_1) \in K[x] \times K[x]$. In the general case, when $(x_1,y_1)$ and $(x_2,y_2)$ with $x_1 \ne x_2$ are the two $\bar{K}$-rational points on C in $\mathrm{supp}(D)$, then the corresponding Mumford representation is

$$\begin{aligned} (x^2+u_1x+u_0, v_1x+v_0) \in K[x] \times K[x], \end{aligned}$$

where

$$\begin{aligned} u_1 = -x_1-x_2 \, , \quad u_0 = x_1x_2 \, , \quad v_1 = \frac{y_2-y_1}{x_2-x_1} \, , \quad \mathrm{and} \quad v_0 = \frac{y_1x_2-x_1y_2}{x_2-x_1}. \end{aligned}$$

(5)

Note that, in general, the Mumford representation of a point in $J_C(K)$ can always be written in $K[x] \times K[x]$, but this does not imply that the underlying points on $C(\bar{K})$ are K-rational.

If $(x^2+u_1 x+u_0 , v_1 x +v_0)$ is a generic point in $J_C$, then the map $\kappa _{(a , b , c , d)} :C \rightarrow C'$ in (4) induces a map between their Jacobians, where, for elements with $\ell _1 = c^2 u_0-cd u_1+d^2$ and $\ell _2=ad-bc$ such that $\ell _1\ell _2\ne 0$, we have $(x^2+u_1 x+u_0 , v_1 x +v_0) \mapsto (x^2+u_1' x+u_0' , v_1' x +v_0')$, with

$$\begin{aligned} u_1'&= \ell _1^{-1}\left( (ad+bc) u_1-2ac u_0-2bd\right) , \quad \quad \quad u_0' = \ell _1^{-1}\left( a^2 u_0-ab u_1+b^2\right) , \nonumber \\ v_0'&= -e (\ell _1^2 \ell _2)^{-1} \Big ( ac^2(u_0u_1v_1-u_1^2v_0+u_0v_0)-c(2ad+bc)(u_0v_1-u_1v_0)\nonumber \\&\quad \quad \quad \quad \quad \quad \quad \quad -d(ad+2bc)v_0+bd^2v_1\Big ),\\&\mathrm{and} \quad \quad v_1' = e (\ell _1^2 \ell _2)^{-1} \left( c^2(c u_1-3d)(u_0v_1-u_1v_0)+c v_0(c^2 u_0-3d^2)+d^3 v_1 \right) . \nonumber \end{aligned}$$

(6)

Weil Restriction of Scalars. The Weil restriction of scalars is the process of re-writing a system of equations over a finite extension L / K as a system of equations in more variables over K – we refer to [18, Sect. 5.7] for a more general discussion. In this work it can be considered as merely a formality to increase dimension so that speaking of isogenies makes sense. The Weil restriction of our one-dimensional varieties $E_\alpha /\mathbb {F}_{p^2}$ (with respect to the extension $\mathbb {F}_{p^2}=\mathbb {F}_p(i)$ with $i^2+1$) is the two-dimensional variety

$$\begin{aligned} W_\alpha :=\mathrm{Res}_{\mathbb {F}_p}^{\mathbb {F}_{p^2}}(E_\alpha ) = V\Big (W_0(x_0,x_1,y_0,y_1),W_1(x_0,x_1,y_0,y_1)\Big ), \end{aligned}$$

where

$$\begin{aligned} W_0&= (\alpha _0^2+\alpha _1^2)\left( \alpha _0(x_0^2-x_1^2)-2\alpha _1x_0x_1+\delta _0(y_0^2-y_1^2)-2y_0y_1\delta _1-x_0(x_0^2-3x_1^2+1)\right) \\&\quad \quad +\alpha _0(x_0^2-x_1^2)+2\alpha _1x_0x_1 \quad \quad \mathrm{and} \\ W_1&=(\alpha _0^2+\alpha _1^2)\left( \alpha _1(x_0^2-x_1^2)+2\alpha _0x_0x_1+\delta _1(y_0^2-y_1^2)+2y_0y_1\delta _0-x_1(3x_0^2-x_1^2+1)\right) \\&\quad \quad +\alpha _1(x_1^2-x_0^2)+2\alpha _0x_0x_1 \end{aligned}$$

are obtained by putting $x=x_0+x_1 \cdot i$, $y=y_0+y_1 \cdot i$ as well as $\alpha =\alpha _0+\alpha _1\cdot i$ and $\delta =\delta _0+\delta _1 \cdot i$ (with $x_0,x_1,y_0,y_1,\alpha _0,\alpha _1,\delta _0,\delta _1 \in \mathbb {F}_p$) into (1). In terms of dimension, it now makes sense to speak of isogenies between $W_\alpha$ and the two-dimensional abelian surfaces described in the next section.

We make the disclaimer that oftentimes we will speak loosely and refer to isogenies and maps between $E_\alpha$, intermediate curves, and abelian surfaces, but that from hereon it should be clear that, technically speaking, these maps are only well-defined when speaking of the corresponding Weil restrictions of these elliptic curves with respect to $\mathbb {F}_{p^2}/\mathbb {F}_p$.

Power-of-2 Elliptic Curve Isogenies in SIDH. Understanding how $2^e$-isogenies are computed in SIDH is key in understanding the directions we take in Sects. 4 and 5. Recall the three 2-torsion points on $E_\alpha$ as (0, 0), $(\alpha ,0)$ and $(1/\alpha ,0)$; in general, each of these corresponds to a different 2-isogeny emanating from $E_\alpha$. Following [16, Sect. 4.3.2] and [27, Sect. 4.2], when the kernel is generated by the special point (0, 0), applying Vélu’s formulas [35] to write down the isogeny allows us to (re)write the image curve in Montgomery form². However, when the kernel is generated by one of the other two points, direct application of Vélu’s formulas makes writing the image curve in Montgomery form much less obvious. This was achieved in [16, 27] by using an isomorphism to move these two kernel points to (0, 0) on an isomorphic curve (which differs depending whether the kernel is $\langle (\alpha ,0) \rangle$ or $\langle (1/\alpha ,0) \rangle$), prior to invoking Vélu.

In our case we follow an analogous path. From the work in [28], we have a very simple Kummer surface isogeny that corresponds to a special kernel $O$, and we use an isomorphism to move our two more general kernels, $\varUpsilon$ and $\tilde{\varUpsilon }$, prior to applying the isogeny (see Sects. 4 and 5 for the definitions of $O$, $\varUpsilon$ and $\tilde{\varUpsilon }$).

We point out that this analogue is not a coincidence, and is made concrete in Lemma 2. Moreover, just like in the elliptic curve case where (0, 0) cannot arise as the kernel of a repeated isogeny in SIDH (because it gives rise to the dual isogeny – see [16]), in our case it is $O$ that corresponds to the dual so our kernel will, with the possible exception of the very first (2, 2)-isogeny, only ever correspond to $\varUpsilon$ and $\tilde{\varUpsilon }$.

3 Abelian Surfaces Isogenous to Supersingular Montgomery Curves

This section links supersingular Montgomery curves defined over $\mathbb {F}_{p^2}$ with abelian surfaces defined over $\mathbb {F}_p$. We start with Proposition 1, which writes down the genus-2 curve $C_\alpha /\mathbb {F}_p$ arising from Scholten’s construction; its proof is postponed until after we have derived the back-and-forth (2, 2)-isogenies between the given Weil restriction and abelian surface. We point out that the exposition below is simplified by assuming³ $p \equiv 3 \bmod {4}$ so that $\mathbb {F}_{p^2} = \mathbb {F}_p(i)$ with $i^2+1=0$, but treating the complimentary or general case is analogous. The only impactful restriction made in addition to Scholten’s requirements is that of supersingularity. As mentioned in Sect. 1, this gives rise to simpler maps than those in [6] by way of the trace map, but several of our intermediate steps may still be useful beyond the supersingular scenario.

Proposition 1

Let $p \equiv 3 \bmod {4}$, let $\mathbb {F}_{p^2} = \mathbb {F}_p(i)$ with $i^2+1=0$, and let

$$\begin{aligned} E_\alpha /\mathbb {F}_{p^2} :y^2=x (x-\alpha )(x-1/\alpha ) \end{aligned}$$

be supersingular with $\alpha \not \in \mathbb {F}_p$. Write $\alpha = \alpha _0 + \alpha _1 \cdot i$ with $\alpha _0, \alpha _1 \in \mathbb {F}_p$. The Weil restriction of scalars of $E_\alpha (\mathbb {F}_{p^2})$ with respect to $\mathbb {F}_{p^2}/\mathbb {F}_p$ is (2, 2)-isogenous to the Jacobian, $J_{C_\alpha }$, of

$$\begin{aligned} C_\alpha /\mathbb {F}_{p} :y^2=f_1(x) f_2(x) f_3(x), \end{aligned}$$

(7)

where

$$\begin{aligned} f_1(x)&=x^2+\frac{2\alpha _0}{\alpha _1}\cdot x-1,\\ f_2(x)&= x^2-\frac{2\alpha _0}{\alpha _1}\cdot x-1, \quad \quad \quad and \\ f_3(x)&= x^2-\frac{2\alpha _0(\alpha _0^2+\alpha _1^2-1)}{\alpha _1(\alpha _0^2+\alpha _1^2+1)}\cdot x-1. \end{aligned}$$

Remark 1

(Singular quadratic splittings and split Jacobians). We immediately point out that the $f_i(x)$ in Proposition 1 are linearly dependent; namely, $f_3(x) = 1/(N+1) \cdot f_1(x) + N/(N+1) \cdot f_2(x)$, where $N=N_{\mathbb {F}_{p^2}/\mathbb {F}_p}(\alpha ) = \alpha _0^2+\alpha _1^2$. Oftentimes in the literature, this is referred to as the singular scenario, where the Jacobian of $C_\alpha$ is reducible, or split (e.g., [10, Theorem 14.1.1(ii)] and [33, Proposition 8.3.1]). However, we stress that those results do not necessarily imply that this splitting occurs over $\mathbb {F}_p$; Cassels and Flynn assume that they are working in the algebraic closure [10, p. 154] and Smith’s construction of the linear polynomials on [33, p. 119] also requires a field extension in the general case. Indeed, if all of the elliptic curves in our isogeny graph were (2, 2)-isogenous to a Jacobian that is split over $\mathbb {F}_p$, this would have serious implications on the quantum security of SIDH (see [11]). We conjecture that the Jacobian of $C_\alpha$ only splits over $\mathbb {F}_p$ when the j-invariant of $E_\alpha$ is itself defined over $\mathbb {F}_p$, and note that adhering to the constructions in [10] and [33] (over the algebraic closure) yields an isogeny between $J_{C_\alpha }(\mathbb {F}_{p^2})$ and $E^2_\alpha (\mathbb {F}_{p^2})$, which manifests $J_{C_\alpha }$ being supersingular [26, Theorem 4.2].

Fixing Roots of the Sextic. Following Lemma 1, let $\gamma , \beta \in \mathbb {F}_{p^2}$ be such that

$$\begin{aligned} \gamma ^2 = \alpha \quad \quad \mathrm{and} \quad \quad \beta ^2 = (\alpha ^2-1)/\alpha , \end{aligned}$$

(8)

and write $\beta = \beta _0+\beta _1 \cdot i$ and $\gamma =\gamma _0+\gamma _1 \cdot i$ for $\beta _0, \beta _1, \gamma _0, \gamma _1 \in \mathbb {F}_p$. The curve $C_\alpha /\mathbb {F}_p$ from Proposition 1 will henceforth be written as

$$\begin{aligned} C_\alpha /\mathbb {F}_{p} :y^2=(x-z_1)(x-z_2)(x-z_3)(x-z_4)(x-z_5)(x-z_6), \end{aligned}$$

where

$$\begin{aligned} z_1 :=\frac{\beta _0}{\beta _1} , \quad z_2 :=\frac{\gamma _0}{\gamma _1} , \quad z_3 :=-\frac{\gamma _0}{\gamma _1} , \quad z_4 :=-\frac{\beta _1}{\beta _0} , \quad z_5 :=-\frac{\gamma _1}{\gamma _0} , \quad z_6 := \frac{\gamma _1}{\gamma _0}, \end{aligned}$$

(9)

and where we note at once that

$$ z_3 = -z_2 \, , \quad z_4 = -1/z_1 \, , \quad z_5 = -1/z_2 \, , \quad \mathrm{and} \quad z_6 = 1/z_2. $$

Furthermore, observe that any combination of the choices of roots for $\gamma$ and $\beta$ in (8) gives rise to the same values of the $z_i$ in (9).

Mapping from ${\varvec{E}}_{\varvec{\alpha }}{} \mathbf{(}\mathbb {F}_{{\varvec{p}}^\mathbf{2}}{} \mathbf{)}$ to ${\varvec{J}}_{{{\varvec{C}}}_{\varvec{\alpha }}}{} \mathbf{(}\mathbb {F}_{{\varvec{p}}}{} \mathbf{)}$. The (2, 2)-isogeny from (the Weil restriction of) $E_\alpha (\mathbb {F}_{p^2})$ to the Jacobian $J_{C_\alpha }(\mathbb {F}_p)$ will be derived as the composition of maps between intermediate curves. We start by defining the curve

$$\begin{aligned} \tilde{E}_{\alpha }/\mathbb {F}_{p^2} \, :\, y^2=(x-r_1)(x-r_2)(x-r_3), \end{aligned}$$

with

$$\begin{aligned} r_1 := (\alpha -1/\alpha )^{p-1}, \quad \quad r_2:=\alpha ^{p-1}, \quad \quad \mathrm{and} \quad \quad r_3:=1/\alpha ^{p-1}. \end{aligned}$$

Fix $\hat{\beta }$ such that $\hat{\beta }^2=r_3-r_2$ (it is easy to see that $\hat{\beta }$ always exists over $\mathbb {F}_{p^2}$), and define an isomorphism between $E_\alpha$ and $\tilde{E}_\alpha$ as

$$\begin{aligned} \psi \, :&\, E_\alpha \rightarrow \tilde{E}_\alpha , \quad (x,y) \mapsto \left( (\hat{\beta }/\beta )^2 \cdot x + r_1 \, , \, (\hat{\beta }/\beta )^3 \cdot y \right) . \end{aligned}$$

Following [31, Lemma 2.1], define $\tilde{C}_\alpha /\mathbb {F}_{p^2}$ as the hyperelliptic curve

$$\begin{aligned} \tilde{C}_\alpha /\mathbb {F}_{p^2} :y^2= (x^2-r_1)(x^2-r_2)(x^2-r_3), \end{aligned}$$

where we have the map

$$\begin{aligned} \omega \, :\, \tilde{C}_\alpha \rightarrow \tilde{E}_{\alpha } , \quad (x,y) \mapsto (x^2,y). \end{aligned}$$

Observing that $r_1$, $r_2$ and $r_3$ are all square in $\mathbb {F}_{p^2}$, let W be the set of x-coordinates of the six Weierstrass points of $\tilde{C}_\alpha$. A key step in Scholten’s construction is to choose a map $\phi$ that, restricted to x-coordinates, leaves $\phi (W)$ invariant under the action of Galois. With $\mathbb {F}_{p^2}=\mathbb {F}_p(i)$, our choice is

$$\begin{aligned} \phi :&\tilde{C}_\alpha (\mathbb {F}_{p^2}) \rightarrow C_\alpha (\mathbb {F}_{p^2}), \\&(x,y) \mapsto \left( -i \cdot \frac{x-1}{x+1} \, , \, \frac{y}{w}\left( 1-\frac{x-1}{x+1}\right) ^3\right) , \end{aligned}$$

where $w:=r_3(1-r_1)(r_2-1)^2$ and $C_\alpha$ is the curve from Proposition 1. An important observation here is that $C_\alpha$ is defined over $\mathbb {F}_p$, while $\tilde{C}_\alpha$ is defined over $\mathbb {F}_{p^2}$, and the map $\phi$ is between the $\mathbb {F}_{p^2}$-rational points on these curves.

Composing the image of the pullback $\omega ^*$ (see [18, Definition 8.3.1]) with $\phi$ (which is extended linearly into $J_{C_\alpha }(\mathbb {F}_{p^2})$ via the Abel-Jacobi map as in (5)), induces the map

$$\begin{aligned} \rho :&\tilde{E}_{\alpha }(\mathbb {F}_{p^2}) \rightarrow J_{C_\alpha }(\mathbb {F}_{p^2}), \\&(\tilde{x},\tilde{y}) \mapsto (x^2+u_1x+u_0, v_1+v_0), \end{aligned}$$

where

$$\begin{aligned} u_1 = 2i \cdot \left( \frac{\tilde{x}+1}{\tilde{x}-1}\right) , \quad u_0 = -1 ,\quad v_1 = -4i \cdot \frac{\tilde{y}(\tilde{x}+3)}{w(\tilde{x}-1)^2}, \quad v_0 = \frac{4\tilde{y}}{w(\tilde{x}-1)}. \end{aligned}$$

Since $J_{C_\alpha }$ is defined over $\mathbb {F}_p$ and is supersingular with embedding degree $k=2$, we can use the trace map $\mathcal {T}$ to move elements from $J_{C_\alpha }(\mathbb {F}_{p^2})$ into $J_{C_\alpha }(\mathbb {F}_{p})$, i.e.,

$$\begin{aligned} \mathcal {T} :&\quad J_{C_\alpha }(\mathbb {F}_{p^2}) \rightarrow J_{C_\alpha }(\mathbb {F}_{p}), \\&\quad P \mapsto \sum _{\sigma \in \mathrm{Gal}(\mathbb {F}_{p^2}/\mathbb {F}_p)} \sigma (P), \end{aligned}$$

which for generic elements in $J_{C_\alpha }(\mathbb {F}_{p^2})$, becomes

$$\begin{aligned}&\mathcal {T} :(x^2+u_1x+u_0, v_1x+v_0) \mapsto (x^2+u_1x+u_0, v_1x+v_0) \oplus _J (x^2+u_1^p x+u_0^p, v_1^px+v_0^p), \end{aligned}$$

where $\oplus _J$ denotes the addition law in $J_{C_\alpha }(\mathbb {F}_{p^2})$, explicit formulas for which are in [20, Sect. 5].

Finally, we can now define the map from (the Weil restriction of) $E_\alpha (\mathbb {F}_{p^2})$ to $J_{C_\alpha }(\mathbb {F}_p)$ as

$$\begin{aligned} \eta :&E_\alpha (\mathbb {F}_{p^2}) \rightarrow J_{C_\alpha }(\mathbb {F}_p),\\&P \mapsto (\mathcal {T} \circ \rho \circ \psi )(P). \end{aligned}$$

Mapping from ${{\varvec{J}}}_{{\varvec{C}}_{\varvec{\alpha }}}{} \mathbf{(}\mathbb {F}_{{\varvec{p}}}{} \mathbf{)}$ to ${{\varvec{E}}}_{\varvec{\alpha }}{} \mathbf{(}\mathbb {F}_{{\varvec{p}}^\mathbf{2}}{} \mathbf{)}$. We start by writing down $\phi ^{-1}$, the inverse of $\phi$, as

$$\begin{aligned} \phi ^{-1} :&C_\alpha (\mathbb {F}_{p^2}) \rightarrow \tilde{C}_\alpha (\mathbb {F}_{p^2}), \\&(x,y) \mapsto \left( - \frac{x-i}{x+i} \, , \, -i \cdot \frac{yw}{(x+i)^3}\right) . \end{aligned}$$

Extending $\phi ^{-1}$ linearly to $\mathrm{Div}_{\overline{\mathbb {F}}_p}(C_\alpha )$ (and recalling our identification of $J_{C_\alpha }(K)$ and $\mathrm{Pic}^0_{K}(C_\alpha )$ – see Sect. 2) induces a map $\hat{\rho }$, defined for generic elements in the affine part of $J_{C_\alpha }(\mathbb {F}_p)$ as

$$\begin{aligned} \hat{\rho } :&J_{C_\alpha }(\mathbb {F}_{p}) \rightarrow \tilde{E}_{\alpha }(\mathbb {F}_{p^2}) \times \tilde{E}_{\alpha }(\mathbb {F}_{p^2}),\\&P \mapsto \left( (\omega \circ \phi ^{-1})(x_1,y_1)), (\omega \circ \phi ^{-1})(x_2,y_2)\right) , \end{aligned}$$

where the Mumford representation of $P \in J_{C_\alpha }(\mathbb {F}_p)$ is exactly as in (5), with $(x_1,y_1),(x_2,y_2) \in C_\alpha (\mathbb {F}_{p^2})$.

We can now define the full map from $J_{C_\alpha }(\mathbb {F}_p)$ to $E_\alpha (\mathbb {F}_{p^2})$ as

$$\begin{aligned} \hat{\eta } :&J_{C_\alpha }(\mathbb {F}_p) \rightarrow E_\alpha (\mathbb {F}_{p^2}) , \\&P \mapsto \left( \psi ^{-1} \circ \oplus _{\tilde{E}} \circ \hat{\rho } \right) (P), \end{aligned}$$

where $\oplus _{\tilde{E}} :\tilde{E}_{\alpha } \times \tilde{E}_{\alpha } \rightarrow \tilde{E}_{\alpha }$ is the addition law on $\tilde{E}_{\alpha }$, and the inverse of the isomorphism $\psi$ is

$$\begin{aligned} \psi ^{-1} \, :&\, \tilde{E}_\alpha \rightarrow E_\alpha , \quad (x,y) \mapsto \left( (\beta /\hat{\beta } )^2 \cdot (x - r_1) \, , \, (\beta /\hat{\beta })^3 \cdot y \right) . \end{aligned}$$

Kernels and Group Structures. Let $\mathcal {O}_{E_\alpha }$ be the point at infinity on $E_\alpha$. The kernel of the map $\eta :E_\alpha (\mathbb {F}_{p^2}) \rightarrow J_{C_\alpha }(\mathbb {F}_p)$ is

$$\begin{aligned} \mathrm{ker}(\eta ) = E_\alpha [2] = \left\{ \mathcal {O}_{E_\alpha } , (0,0), (\alpha ,0), (1/\alpha ,0) \right\} , \end{aligned}$$

which is isomorphic to $\mathbb {Z}_2 \times \mathbb {Z}_2$.

Let $\mathcal {O}_J$ be the identity in $J_{C_\alpha }$. The kernel of the map $\hat{\eta } :J_{C_\alpha }(\mathbb {F}_p) \rightarrow E_\alpha (\mathbb {F}_{p^2})$ is

$$\begin{aligned} \mathrm{ker}(\hat{\eta }) = \left\{ \mathcal {O}_{J} , \left( (x-z_1)(x-z_4), 0 \right) , \left( (x-z_3)(x-z_6), 0 \right) , \left( (x-z_2)(x-z_5), 0 \right) \right\} , \end{aligned}$$

a maximal 2-Weil isotropic subgroup of $J_{C_\alpha }[2]$, which is also isomorphic to $\mathbb {Z}_2 \times \mathbb {Z}_2$. It is readily verified that, up to isomorphism, we have $(\hat{\eta } \,\circ \, \eta ) = [2]_{E_\alpha }$, where $[2]_{E_\alpha }$ is the multiplication-by-2 map on $E_\alpha$. Similarly, up to isomorphism, we have $(\eta \,\circ \,\hat{\eta }) = [2]_{J}$, where $[2]_{J}$ is the multiplication-by-2 map on $J_{C_\alpha }$. Thus, $\eta$ and $\hat{\eta }$ are the (unique, up to isomorphism) dual isogenies of one another.

As abelian groups, we have

$$\begin{aligned} E_\alpha (\mathbb {F}_{p^2}) \cong \mathbb {Z}_{p+1} \times \mathbb {Z}_{p+1}, \end{aligned}$$

and

$$\begin{aligned} J_{C_\alpha }(\mathbb {F}_p) \cong \mathbb {Z}_{2} \times \mathbb {Z}_{2} \times \mathbb {Z}_{\frac{p+1}{2}} \times \mathbb {Z}_{\frac{p+1}{2}}. \end{aligned}$$

(10)

Proof

(of Proposition 1). This follows from [31]. $E_\alpha$ is isomorphic to $\tilde{E}_\alpha$ under $\psi$ (indeed, $\tilde{E}_\alpha$ is a monic version of the second curve in [31, Lemma 3.1], when $E_\alpha$ is the first). Thus, under $\omega :(x,y) \mapsto (x^2,y)$, $\tilde{E}_\alpha$ and $J_{C_\alpha }$ have the same L-polynomial and are therefore isogenous [31, Lemma 2.1]. It remains to show that $\eta$ is a (2, 2)-isogeny, which is an immediate consequence of $\mathrm{ker}(\omega ^*) \subseteq \tilde{E}_\alpha [2]$ [18, Exercise 10.5.2] and the definition of $\rho$.    $\square$

4 Richelot Isogenies on Supersingular Abelian Surfaces

This section studies Richelot (2, 2)-isogenies whose domain is the Jacobian, $J_{C_\alpha }$, of the curve $C_\alpha$ defined in Proposition 1. This lays the foundations for the following section, where we will study these isogenies as they are pushed down onto a corresponding Kummer surface $\mathcal {K}_{\alpha }=J_{C_\alpha }/\{\pm 1\}$. Readers should rest assured that, as is usual in the genus-2 landscape, the situation looks much more complicated on the full Jacobian (e.g., in (13)) than it does once we move to a well-specified Kummer surface.

In general, there are 15 Richelot isogenies emanating from $J_{C_\alpha }$, but we will be restricting our focus to the three that correspond to the 2-isogenies on $E_\alpha$.

Kernels of (2, 2)-Isogenies as Quadratic splittings. Recall the labeling of the roots $z_1,\dots , z_6 \in \mathbb {F}_p$ of the sextic $f(x) \in \mathbb {F}_{p}[x]$ in (9). As an abelian group, the 2-torsion of $J_{C_\alpha }$, $J_{C_\alpha }[2]$, is isomorphic to $(\mathbb {Z}/2\mathbb {Z})^4$; it consists of the zero element, $\mathcal {O}_J$, together with the 15 points whose Mumford representations are $((x-z_i)(x-z_j),0)$, where $i,j \in \{1,\dots 6\}$ and $i \ne j$. We will use $G_{i,j}$ to denote the quadratic polynomial $(x-z_i)(x-z_j) \in \mathbb {F}_{p}[x]$ and write $P_{i,j} \in J_{C_\alpha }[2]$ for the non-zero 2-torsion point whose Mumford representation is $P_{i,j} = (G_{i,j},0)$.

Following [33, Sect. 8.1], kernels of (2, 2)-isogenies are called (2, 2)-subgroups, and these correspond to the maximal 2-Weil isotropic subgroups of $J_{C_\alpha }[2]$. Smith [33, Sect. 8.2] formalises this connection by introducing quadratic splittings. In our case, a quadratic splitting is simply a choice of factorisation of the sextic polynomial f(x) in Proposition 1 into three quadratic factors in $\mathbb {F}_{p}[x]$; one such choice was already illustrated in (7). Henceforth, for any $\{i,j,k,l,m,n\} = \{1,2,3,4,5,6\}$, we use the notation $(G_{i,j},G_{k,l},G_{m,n}) \in \mathbb {F}_p[x]^3$ to denote the corresponding quadratic splitting of $f(x)=G_{i,j} \cdot G_{k,l} \cdot G_{m,n}$. There are 15 choices of splittings, and each corresponds to a unique (2, 2)-subgroup: the quadratic splitting $(G_{i,j},G_{k,l},G_{m,n})$ corresponds to the (2, 2)-subgroup of $J_{C_\alpha }[2]$ generated by any two of the three points in $\{P_{i,j},P_{k,l},P_{m,n}\}$ (the third point is the sum of the other two). In this way, we see that (2, 2)-subgroups are isomorphic to $(\mathbb {Z}/2\mathbb {Z})^2$.

(2, 2)-Subgroups Corresponding to the Montgomery 2-Torsion. Out of the 15 possible splittings described above, there are three splittings we are interested in; those where the subsequent (2, 2)-isogenies on $J_{C_\alpha }$ correspond to the three 2-isogenies on $E_\alpha$. We make these splittings concrete in the following lemma.

Lemma 2

Let $E_{\hat{\alpha }}/\mathbb {F}_{p^2}$, $E_{\alpha '}/\mathbb {F}_{p^2}$ and $E_{\alpha ''}/\mathbb {F}_{p^2}$ be three Montgomery curves that are respectively $\mathbb {F}_{p^2}$-isomorphic to $E_\alpha /\langle (0,0) \rangle$, $E_\alpha /\langle (\alpha ,0) \rangle$, and $E_\alpha /\langle (1/\alpha ,0) \rangle$, and let $C_{\hat{\alpha }}/\mathbb {F}_{p}$, $C_{\alpha '}/\mathbb {F}_{p}$ and $C_{\alpha ''}/\mathbb {F}_{p}$ be the corresponding hyperelliptic curves (as in Proposition 1). Furthermore, fix the three quadratic splittings $O$, $\varUpsilon$, and $\tilde{\varUpsilon }$, as

$$\begin{aligned} O&=(O_1, O_2, O_3) \, :=\quad (G_{2,3}, G_{5,6}, G_{1,4}),\\ \varUpsilon&=(\varUpsilon _1, \varUpsilon _2, \varUpsilon _3) \,\, \,\, :=\quad (G_{4,5}, G_{1,2}, G_{3,6}) , \quad \quad \quad and \\ \tilde{\varUpsilon }&=(\tilde{\varUpsilon }_1, \tilde{\varUpsilon }_2, \tilde{\varUpsilon }_3) \,\, \,\,:=\quad (G_{1,6}, G_{3,4}, G_{2,5}). \end{aligned}$$

Then, up to isomorphism, the image curves $C_{O}$, $C_{\varUpsilon }$ and $C_{\tilde{\varUpsilon }}$ of the Richelot (2, 2)-isogenies (with respective kernels corresponding to $O$, $\varUpsilon$ and $\tilde{\varUpsilon }$) are such that

$$\begin{aligned} C_{O} = C_{\hat{\alpha }}, \quad \quad \quad \mathrm{and} \quad \quad \quad \{C_{\varUpsilon }, C_{\tilde{\varUpsilon }}\} = \{ C_{\alpha '}, C_{\alpha ''}\}. \end{aligned}$$

Proof

Direct substitution of (9) gives

$$\begin{aligned} O_1= x^2-\frac{\gamma _0^2}{\gamma _1^2} , \quad \quad \quad O_2=x^2-\frac{\gamma _1^2}{\gamma _0^2}, \quad \quad \quad O_3=x^2+\left( \frac{\beta _1^2-\beta _0^2}{\beta _0\beta _1}\right) x-1, \end{aligned}$$

(11)

$$\begin{aligned} \varUpsilon _1=x^2+\left( \frac{\beta _1\gamma _0+\gamma _1\beta _0}{\beta _0\gamma _0}\right) x +\frac{\beta _1\gamma _1}{\beta _0\gamma _0} , \quad \varUpsilon _2=x^2-\left( \frac{\beta _0\gamma _1+\gamma _0\beta _1}{\beta _1\gamma _1}\right) x + \frac{\beta _0\gamma _0}{\beta _1\gamma _1} , \quad \varUpsilon _3=x^2+\left( \frac{\gamma _0^2-\gamma _1^2}{\gamma _0\gamma _1}\right) x-1, \end{aligned}$$

and

$$\begin{aligned} \tilde{\varUpsilon }_1= x^2-\left( \frac{\beta _0\gamma _0+\gamma _1\beta _1}{\beta _1\gamma _0}\right) x +\frac{\beta _0\gamma _1}{\beta _1\gamma _0} , \quad \tilde{\varUpsilon }_2= x^2+\left( \frac{\beta _0\gamma _0+\gamma _1\beta _1}{\beta _0\gamma _1}\right) x + \frac{\beta _1\gamma _0}{\beta _0\gamma _1} , \quad \tilde{\varUpsilon }_3= x^2+\left( \frac{\gamma _1^2-\gamma _0^2}{\gamma _0\gamma _1}\right) x-1. \end{aligned}$$

In each case, if the splitting is written as

$$ S=\left( x^2+g_{1,1}x+g_{1,0}, x^2+g_{2,1}x+g_{2,0},x^2+g_{3,1}x+g_{3,0}\right) , $$

then the curve with the corresponding (2, 2)-isogenous Jacobian (cf. [10, Sect. 9.2]) is isomorphic to

$$ C_S :y^2=h(x)=h_1(x)h_2(x)h_3(x), $$

where

$$\begin{aligned} h_1(x)&=(g_{1,1}-g_{2,1}) x^2 +2 \left( g_{1,0}-g_{2,0}\right) x + g_{1,0}g_{2,1}-g_{2,0}g_{1,1}, \nonumber \\ h_2(x)&= (g_{2,1}-g_{3,1}) x^2 +2 \left( g_{2,0}-g_{3,0}\right) x + g_{2,0}g_{3,1}-g_{3,0}g_{2,1}, \quad \quad \quad \mathrm{and} \nonumber \\ h_3(x)&= (g_{3,1}-g_{1,1}) x^2 +2 \left( g_{3,0}-g_{1,0}\right) x + g_{3,0}g_{1,1}-g_{1,0}g_{3,1}. \end{aligned}$$

(12)

Now, following Sect. 2, and using (8), we first write $\hat{\alpha }=(\alpha +1)/(1-\alpha )$, $\alpha ' =2\alpha (\alpha +\beta \gamma )-1$ and $\alpha ''=(2-\alpha ^2+2\beta \gamma \cdot i)/\alpha ^2$, and then write each of these constants in terms of its two $\mathbb {F}_p$ components (under the basis $\{1,i\}$ for $\mathbb {F}_{p^2}/\mathbb {F}_p$ as usual). We can then apply Proposition 1 to write down $C_{\hat{\alpha }}$, $C_{\alpha '}$ and $C_{\alpha ''}$. Using (3), lengthy but straightforward calculations show that the result follows from comparing the Igusa-Clebsch invariants of these three curves to those of the curves $C_{O}$, $C_{\varUpsilon }$ and $C_{\tilde{\varUpsilon }}$ obtained above.    $\square$

The explicit Richelot isogeny corresponding to ${{\varvec{O}}}$. Equation (12) writes down the curve whose Jacobian is (2, 2)-isogenous to that of a given genus-2 curve; here the prescribed kernel can be any (2, 2)-subgroup. To fully describe the isogeny, we also need to write down explicit formulas for pushing points in the domain Jacobian through the corresponding isogeny, which is the purpose of this subsection. However, we first note that we will only be needing explicit formulas for the special case when the kernel subgroup corresponds to a quadratic splitting of the form of $O$ in (11). To compute isogenies when the splitting is of the form of $\varUpsilon$ and/or $\tilde{\varUpsilon }$, we will be (pre)composing the isogeny described in this subsection with the isomorphisms (that transform these splittings into splittings of the form of $O$) in the next subsection. For reasons analogous to Montgomery 2-isogenies in the elliptic curve case (see Sect. 2), proceeding in this way makes life easier when we move down to the Kummer surface in Sect. 5.

Bost and Mestre [8] derive explicit (2, 2)-isogenies from Richelot correspondences [33, Definition 8.4.7]. In general, correspondences are divisors on the product $C \times C'$ of the two curves C and $C'$, and the theory of correspondences relates such divisors to homomorphisms between their Jacobians (see [33, Chap. 3]). In this paper we focus on the particular case of the Richelot correspondence

$$\begin{aligned} V_O:= V \begin{pmatrix} \, \, O_1(x_1)O_1'(x_2)+O_2(x_1)O_2'(x_2), \, \, \\ y_1y_2-O_1(x_1)O_1'(x_2)(x_1-x_2) \end{pmatrix} \end{aligned}$$

on $C_\alpha \times C_O$. With $O_1$ and $O_2$ as in (11), and with $O_1'$ and $O_2'$ as their derivatives, we get

$$\begin{aligned} V_O= V \begin{pmatrix} \, \, 4x_2(x_1^2-2\alpha _0^2/\alpha _1^2-1), \, \, \\ \alpha _1^2 y_1y_2+2x_2(4\alpha _0^2 +4\alpha _0\gamma _1^2+\alpha _1^2(1-x_1^2))(x_1-x_2) \end{pmatrix}. \end{aligned}$$

Following [33, Sect. 3.3], and viewing $V_O$ as a curve on $C_\alpha \times C_O$, we make use of the coverings

$$ \pi _1^{V_O} :\, \, V_O\rightarrow C_\alpha , \quad \left( (x_1,y_1),(x_2,y_2)\right) \mapsto (x_1,y_1) $$

and

$$ \pi _2^{V_O} :\, \, V_O\rightarrow C_O, \quad \left( (x_1,y_1),(x_2,y_2)\right) \mapsto (x_2,y_2), $$

and compose the pullback $\pi _1^{V_O*}$ with the pushforward $\pi _{2*}^{V_O}$ to obtain⁴ the induced isogeny

$$\begin{aligned} \varphi _{O} :\quad J_{C_\alpha }\rightarrow J_{C_O}, \end{aligned}$$

defined on general elements of $J_{C_\alpha }$ as

$$\begin{aligned} \varphi _{O} :\quad (x^2+u_1x+u_0,v_1 x +v_0) \mapsto (x^2+u_1'x+u_0',v_1' x +v_0'), \end{aligned}$$

(13)

where

$$\begin{aligned} u_1'&= - \frac{\alpha _1(u_1^2-1)(N+1)}{\alpha _0(N-1)}, \,\, u_0' = u_1^2 , \,\, v_0' = 2M\cdot \frac{u_1(\alpha _0(N-1)-u_1\alpha _1(N+1))}{v_1\alpha _1(N+1)} ,\\&\quad \quad \quad \quad \quad \quad \quad \mathrm{and} \\ v_1'&\!=\! 2M \cdot \frac{ (\alpha _1u_1(N+1))^2-(N^2-1)\alpha _1\alpha _0u_1-N(N+2\alpha _0+1)(N-2\alpha _0+1)) }{\alpha _0\alpha _1(N^2-1)v_1} , \end{aligned}$$

with $N=\alpha _0^2+\alpha _1^2$ and $M=(u_1^2-2\alpha _0/\alpha _1u_1-1)(u_1^2+2\alpha _0/\alpha _1u_1-1)$, and with

$$\begin{aligned} C_O:y^2= \epsilon _0 x \left( x^2-\epsilon _1 x-1\right) \left( x^2-\epsilon _2 x-1\right) , \end{aligned}$$

where $\epsilon _0=\frac{4\alpha _0(N-1)}{\alpha _1(N+1)}$, $\epsilon _1=\frac{2\alpha _0(N+1)+4N}{\alpha _1(N-1)}$ and $\epsilon _2=\frac{2\alpha _0(N+1)-4N}{\alpha _1(N-1)}$.

Isomorphisms of (2,2)-kernels. As mentioned in Sect. 2, we follow a similar path to that which was taken in the elliptic curve case and precompose the isogeny described above with isomorphisms that transform the (2, 2)-kernels $\varUpsilon$ and $\tilde{\varUpsilon }$ to be of the same form as $O$, but on an isomorphic curve.

Our situation is more complicated than the elliptic curve case because our kernels are non-cyclic, meaning that they cannot be defined using a single point in the Jacobian. But, in the scenario of chained (2, 2)-isogeny computations on supersingular abelian surfaces, we are able to overcome this and still use individual 2-torsion points $P_{i,j}$ to distinguish between the three kernel splittings $O$, $\varUpsilon$, and $\tilde{\varUpsilon }$. If n is the even integer $(p+1)/4$, and if $\mathcal {O}_J$ is the identity on $J_{C_\alpha }$, then $[n]J_{C_\alpha }$ is a (2, 2)-subgroup (see (10)), and in our case is always one of

$$[n]J_{C_\alpha }= \{ \mathcal {O}_J, \,\, (O_1,0), \,\, (\varUpsilon _1,0), \,\, (\tilde{\varUpsilon }_1,0)\},$$

or

$$[n]J_{C_\alpha }= \{ \mathcal {O}_J, \,\, (O_2,0) , \,\, (\varUpsilon _2,0), \,\, (\tilde{\varUpsilon }_2,0) \}.$$

In either case, if P is a point of exact order $2^\ell$ with $\ell >1$ in $J_{C_\alpha }$, then we see that $[2^{\ell -1}]P \ne \mathcal {O}_J$ reveals which of the three splittings $O$, $\varUpsilon$ or $\tilde{\varUpsilon }$, corresponds to our (2, 2)-kernel. Moreover, as discussed at the end of Sect. 2, in SIDH our kernel will always correspond to one of $\varUpsilon$ or $\tilde{\varUpsilon }$, since $O$ generates the dual of the previous isogeny.

Our task is now to define an isomorphism that moves the kernels $\varUpsilon$ and $\tilde{\varUpsilon }$ into a kernel of the same form as $O$, but on an isomorphic curve. For a given point $P = (x^2+u_1x+u_0,v_1x+v_0)$ in $J_{C_\alpha }$, we define

$$ \xi _P :\quad J_{C_\alpha }\rightarrow J_{C_\alpha '} $$

as the isomorphism of Jacobians corresponding to $\kappa _{a,b,c,d} :C_\alpha \rightarrow C_\alpha '$ from (4), with

$$\begin{aligned} d&= 1, \,\, \quad \quad c= -\frac{u_0-1+\sqrt{(u_0-1)^2+u_1^2}}{u_1}, \,\, \nonumber \\ b&= -\frac{\sqrt{-u_1(2c(u_0-1)-u_1)}}{u_1}, \quad \quad \mathrm{and} \quad a= - b\frac{2u_0+cu_1}{2c+u_1}. \end{aligned}$$

(14)

When $P=(x^2+u_1x+u_0, 0)$ is a 2-torsion point, the induced isomorphism of Jacobians in (6) simplifies significantly. Straightforward calculations reveal that, when P corresponds to the quadratic splitting $\varUpsilon$ (i.e., when $P \in \{\varUpsilon _1, \varUpsilon _2\}$), we have

$$\begin{aligned} \left\{ \,\, \xi _{(\varUpsilon _1,0)}((\varUpsilon _1,0)) \,\, , \,\, \xi _{(\varUpsilon _1,0)}((\varUpsilon _2,0)) \,\, \right\}&= \left\{ \,\, \xi _{(\varUpsilon _2,0)}((\varUpsilon _1,0)) \,\, ,\xi _{(\varUpsilon _2,0)}((\varUpsilon _2,0))\right\} \\&= \left\{ \,\, ((x^2-\gamma _0'^2/\gamma _1'^2),0) \,\, , \,\, ((x^2-\gamma _1'^2/\gamma _0'^2),0) \,\, \right\} , \end{aligned}$$

and

$$\begin{aligned} \xi _{(\varUpsilon _1,0)}((\varUpsilon _3,0))&= \xi _{(\varUpsilon _2,0)}((\varUpsilon _3,0)) = \left( x^2+\left( \frac{\beta _1'^2-\beta _0'^2}{\beta _0'\beta _1'}\right) x-1,0\right) , \end{aligned}$$

for some $\gamma _0', \gamma _1', \beta _0', \beta _1' \in \mathbb {F}_p$ such that $\beta '=\beta _0'+\beta _1' \cdot i \in \mathbb {F}_{p^2}$ and $\gamma ' = \gamma _0'+\gamma _1' \cdot i \in \mathbb {F}_{p^2}$ satisfy $\gamma '^2\beta '^2=\gamma '^4-1$, which comes from the relation in (8). Thus, the (2, 2)-subgroup corresponding to the splitting $\varUpsilon$ on $J_{C_\alpha }$ is isomorphic (via either $\xi _{(\varUpsilon _1,0)}$ or $\xi _{(\varUpsilon _2,0)}$) to the splitting

$$ O' = \Big (\,\, x^2-\gamma _0'^2/\gamma _1'^2 , \quad x^2-\gamma _1'^2/\gamma _0'^2 , \quad x^2+(\beta _1'^2-\beta _0'^2)/(\beta _0'\beta _1')x-1 \Big ) $$

on $J_{C_\alpha '}$.

Crucially, the analogous statements apply when the point P corresponds to the quadratic splitting $\tilde{\varUpsilon }$ (i.e., when $P \in \{\tilde{\varUpsilon }_1, \tilde{\varUpsilon }_2\}$), with the only difference being different values of $\gamma _0', \gamma _1', \beta _0', \beta _1' \in \mathbb {F}_p$ and a different (but still isomorphic) image curve $J_{C_\alpha '}$.

Finally, we fix

$$ \varphi _{P}:=(\varphi _{O} \circ \xi _P) $$

as the (2, 2)-isogeny of Jacobians whose kernel is the (2, 2)-subgroup corresponding to $\varUpsilon$ if $P \in \{(\varUpsilon _1,0), (\varUpsilon _2,0)\}$, or corresponding to $\tilde{\varUpsilon }$ if $P \in \{(\tilde{\varUpsilon }_1,0),(\tilde{\varUpsilon }_2,0)\}$. It is important to point out that $\varphi _{P}$ is computed in the same way regardless of whether P corresponds to $\varUpsilon$ or to $\tilde{\varUpsilon }$.

To summarise, we have so far derived all of the ingredients necessary to replace chained 2-isogenies on elliptic curves over $\mathbb {F}_{p^2}$ with chained (2, 2)-isogenies on Jacobians over $\mathbb {F}_p$. However, the combination of a relatively inefficient $\varphi _{P}$ and point doublings in the full Jacobian is what prompts us to now push this arithmetic down onto the corresponding fast Kummer surfaces.

Remark 2

It is not surprising that the isomorphism in (14) that transforms the (2, 2)-kernels $\varUpsilon$ and $\tilde{\varUpsilon }$ into a kernel of the form of $O$ (but on an isomorphic curve) seems to require square roots. Indeed, De Feo, Jao and Plût [16] encountered the same problem in their treatment of 2-isogenies between Montgomery curves, but noticed that the square roots were related to rational functions of torsion elements lying above their kernels, so were able to use these higher order points to avoid square roots and efficiently chain together 2-isogenies in the SIDH framework. We employ this same technique in the next section to avoid square roots during Kummer isogeny computations, and claim that (if there was any practical motivation to sort out these details) the square roots in (14) could also be circumvented by using points of order 4 lying above $P \in J_{C_\alpha }$. Indeed, the functions of $u_0$ and $u_1$ in (14) being squares in $\mathbb {F}_p$ is undoubtedly related to their being the output of a point doubling in $J_{C_\alpha }$. Finally, we point out that in the case of 2-isogenies on Montgomery elliptic curves, Renes [27, Sect. 4] recently removed the need for any higher order points, giving explicit formulas that depend only on the kernel element of order 2.

5 Richelot Isogenies on Supersingular Kummer Surfaces

The efficacy of this work relies on our being able to push $\varphi _P$ down onto specific choices of Kummer surfaces.

Supersingular Kummer Surfaces. Following the initial works of the Chudnovskys [12] and of Gaudry [19], a number of authors have exploited the fast Kummer surface arithmetic in the context of modern HECC (cf. [4, 5, 7]). We draw on the applicable techniques from that line of work in this paper, and in particular adopt the Chudnovskys’ [12] squared Kummer surface approach that was first exploited in high-speed HECC by Bernstein [4] and for fast factorisation by Cosset [13].

Choices of notations and parameterisations of Kummer surfaces have varied in the literature (see [28, Table 1]). We will aim to stick to that used in [28], but warn that our supersingular Kummer surfaces are special and will be defined as such. Kummer surfaces and their arithmetic are defined by fixing four fundamental theta constants, and the special squared Kummer surfaces used in this paper work entirely with their squares, denoted $\mu _1$, $\mu _2$, $\mu _3$ and $\mu _4$.

Following [7, Sect. 5.2], the $\mu _i$ can be computed from the Rosenhain form $C_{\lambda ,\mu ,\nu }$ of the associated genus-2 curve, as

$$\begin{aligned} \mu _4 = 1, \quad \quad \mu _3 = \sqrt{\frac{\lambda \mu }{\nu }} , \quad \quad \mu _2 = \sqrt{\frac{\mu (\mu -1)(\lambda -\nu )}{\nu (\nu -1)(\lambda -\mu )}} , \quad \quad \mu _1 = \mu _2\mu _3\frac{\nu }{\mu }. \end{aligned}$$

(15)

In the supersingular scenario, with the sextic form of genus-2 curves as in (9), we will fix the transformation to Rosenhain form that sends the point $(z_1,0)$ to (0, 0), the point $(z_2,0)$ to (1, 0), the point $(z_4,0)$ to the unique point at infinity, the point $(z_3,0)$ to $(\lambda ,0)$, the point $(z_6,0)$ to $(\mu ,0)$, and the point $(z_5,0)$ to $(\nu ,0)$. We achieve this by taking $a=z_2-z_4$, $b=-az_1$, $c=z_2-z_1$ and $d=-cz_4$, i.e.,

$$\begin{aligned}&\kappa _{(a,b,c,d)} :C_\alpha \rightarrow C_{\lambda ,\mu ,\nu }\\&(x,y) \mapsto \left( \,\, \left( \frac{\beta _0\gamma _0+\beta _1\gamma _1}{\gamma _0\beta _1-\gamma _1\beta _0}\right) \cdot \left( \frac{\beta _1 x-\beta _0}{\beta _0x+\beta _1}\right) \,\, , \,\, ey \cdot \left( \frac{\beta _0\beta _1\gamma _1}{(\beta _1\gamma _0-\beta _0\gamma _1)(\beta _0x+\beta _1)}\right) ^3 \,\, \right) , \end{aligned}$$

with $e^2 = ac(a-c)(a-\nu c)(a-\mu c)(a-\lambda c)$, and where

$$\begin{aligned} \lambda&:= -\frac{(\beta _0\gamma _1+\beta _1\gamma _0)(\beta _0\gamma _0+\beta _1\gamma _1)}{(\beta _0\gamma _0-\beta _1\gamma _1)(\beta _0\gamma _1-\beta _1\gamma _0)}, \quad \mu :=\frac{(\beta _0\gamma _0+\beta _1\gamma _1)(\beta _0\gamma _0-\beta _1\gamma _1)}{(\beta _0\gamma _1+\beta _1\gamma _0)(\beta _0\gamma _1-\beta _1\gamma _0)}, \quad \nu :=-\frac{(\beta _0\gamma _0+\beta _1\gamma _1)^2}{(\beta _0\gamma _1-\beta _1\gamma _0)^2}. \end{aligned}$$

Thus, we see that $\nu =\lambda \mu$, meaning that (15) simplifies to

$$\begin{aligned} \mu _4 := 1, \quad \quad \mu _3 := 1, \quad \quad \mu _2 := \left( \frac{\gamma _0^2-\gamma _1^2}{\gamma _0^2+\gamma _1^2}\right) /\sqrt{\lambda } , \quad \quad \mu _1 := \left( \frac{\gamma _0^2-\gamma _1^2}{\gamma _0^2+\gamma _1^2}\right) \cdot \sqrt{\lambda }. \end{aligned}$$

Previous works in the realm of high-speed HECC do not have $\mu _3=1$ in addition to $\mu _4=1$ (because the chances of finding a secure such Kummer surface over a given field are very small), which is why we stated above that our Kummer surfaces are special. One bonus of having $\mu _3=1$ is a simplified description of the Kummer surface, and for a fixed⁵ Kummer surface of this form, another is more efficient arithmetic for the pseudo-group operations.

Our special squared Kummer surface, $\mathcal {K}^\mathrm{Sqr}$, is defined as

$$\begin{aligned}&\quad \quad \quad \quad \quad \quad \mathcal {K}^\mathrm{Sqr} :\quad \quad \quad F \cdot X_1X_2X_3X_4 = \\&\left( X_1^2+X_2^2+X_3^3+X_4^2-G(X_1+X_2)(X_3+X_4)-H(X_1X_2+X_3X_4) \right) ^2, \end{aligned}$$

where

$$\begin{aligned} F&:= 4\mu _1\mu _2\frac{(\mu _1+\mu _2+2)^2(\mu _1+\mu _2-2)^2}{(\mu _1\mu _2-1)^2}, \quad G:=\mu _1+\mu _2, \quad \mathrm{and} \quad H:=\frac{\mu _1^2+\mu _2^2-2}{\mu _1\mu _2-1}. \end{aligned}$$

Elements on $\mathcal {K}^\mathrm{Sqr}$ are projective points $(X_1 :X_2 :X_3 :X_4) \in \mathbb {P}^3$ satisfying this equation, and the zero element is $\mathcal {O}_{\mathcal {K}}=(\mu _1 :\mu _2 :1 :1)$.

Let $\tau$ and $\tilde{\tau }$ be the roots of $x^2-Gx+1$ in $\mathbb {F}_p[x]$, and observe that $\tau \cdot \tilde{\tau }= 1$. On ${\mathcal {K}^\mathrm{Sqr}}$, the three (2, 2)-subgroups corresponding to those defined in Sect. 4 are

$$\begin{aligned} O&=(\mathcal {O}_{\mathcal {K}}, O_1 , O_2 , O_3 ) = \, \Big ( (\mu _1 :\mu _2 :1 :1), \, (1 :1 :\mu _1 :\mu _2), \, (1 :1 :\mu _2 :\mu _1), \, (\mu _2 :\mu _1 :1 :1) \Big ), \nonumber \\ \varUpsilon&=(\mathcal {O}_{\mathcal {K}}, \varUpsilon _1, \varUpsilon _2 , \varUpsilon _3 ) \, = \, \Big ( (\mu _1 :\mu _2 :1 :1), \, (1 :0 :0 :\tau ), \, (1 :0 :\tau :0), \, (\mu _1-\tau :\mu _2-\tau :0 :0) \Big ), \nonumber \\ \tilde{\varUpsilon }&=(\mathcal {O}_{\mathcal {K}}, \tilde{\varUpsilon }_1 , \tilde{\varUpsilon }_2 , \tilde{\varUpsilon }_3 ) \, = \, \Big ( (\mu _1 :\mu _2 :1 :1), \, (1 :0 :0 :\tilde{\tau }), \, (1 :0 :\tilde{\tau } :0), \, (\mu _1-\tilde{\tau } :\mu _2-\tilde{\tau } :0 :0) \Big ). \end{aligned}$$

(16)

Pseudo-doublings and ${\varvec{\varphi }}_{{\varvec{O}}}$ on ${\varvec{\mathcal {K}}}^\mathbf{Sqr}$. Our (2, 2)-isogenies and pseudo-doublings on $\mathcal {K}^\mathrm{Sqr}$ will be comprised of three sub-operations. Define $\mathcal {H} :\mathbb {P}^3 \rightarrow \mathbb {P}^3$ as the 4-way Hadamard transform in $\mathbb {P}^3$, i.e.,

$$\begin{aligned} \mathcal {H} :(\ell _1:\ell _2:\ell _3:\ell _4) \mapsto ( \ell _1+\ell _2+\ell _3+\ell _4 :\,\, \ell _1+\ell _2-\ell _3-\ell _4 :\,\, \ell _1-\ell _2+\ell _3-\ell _4 :\,\, \ell _1-\ell _2-\ell _3+\ell _4 ), \end{aligned}$$

together with the coordinate squaring operation $\mathcal {S} :\mathbb {P}^3 \rightarrow \mathbb {P}^3$, as

$$\begin{aligned} \mathcal {S} :\quad (\ell _1 :\ell _2 :\ell _3 :\ell _4) \mapsto (\ell _1^2 :\ell _2^2 :\ell _3^2 :\ell _4^2), \end{aligned}$$

and the coordinate scaling operation $\mathcal {C}_{(d_1:d_2:d_3 :d_4)}:\mathbb {P}^3 \rightarrow \mathbb {P}^3$, as

$$\begin{aligned} \mathcal {C}_{(d_1:d_2:d_3 :d_4)} :\quad (\ell _1 :\ell _2 :\ell _3 :\ell _4)&\mapsto (\ell _1/d_1 :\ell _2/d_2 :\ell _3/d_3 :\ell _4/d_4)\\&\quad =(\pi _1 \ell _1 :\pi _2 \ell _2 :\pi _3 \ell _3 :\pi _4 \ell _4), \end{aligned}$$

where $\pi _i = d_1d_2d_3d_4/d_i$ for $i \in \{1,2,3,4\}$. It follows that $\mathcal {H}$ requires at most 8 field additions, $\mathcal {S}$ requires at most 4 field squarings, and $\mathcal {C}_{(d_1:d_2:d_3 :d_4)}$ requires at most 10 field multiplications if the $\pi _i$ are not precomputed, and at most 4 field multiplications if they are.

Following [28, Sect. 4], define the dual squared Kummer surface as

$$\begin{aligned}&\quad \quad \quad \quad \quad \quad \hat{\mathcal {K}}^\mathrm{Sqr}_{O} :\quad \quad \quad \hat{F} \cdot X_1X_2X_3X_4 = \\&\left( X_1^2+X_2^2+X_3^3+X_4^2-\hat{G}(X_1+X_2)(X_3+X_4)-\hat{H}(X_1X_2+X_3X_4) \right) ^2, \end{aligned}$$

where

$$\begin{aligned} \hat{F}&:= 64\mu _1^2\mu _2^2\frac{(\mu _1+\mu _2+2)(\mu _1+\mu _2-2)}{(\mu _1\mu _2-1)^2(\mu _1-\mu _2)^2}, \quad \hat{G}:=2 \left( \frac{\mu _1+\mu _2}{\mu _1-\mu _2}\right) , \quad \mathrm{and} \quad \hat{H}:=2 \left( \frac{\mu _1\mu _2+1}{\mu _1\mu _2-1}\right) . \end{aligned}$$

In the previous section we derived formulas for computing $\varphi _O$ in the full Jacobian – see (13). The corresponding isogeny on the Kummer surface is defined (with abuse of notation) as

$$\begin{aligned} \varphi _O:&\quad \mathcal {K}^\mathrm{Sqr} \rightarrow \hat{\mathcal {K}}^\mathrm{Sqr}_O, \\&\quad P \mapsto \left( \mathcal {C}_{(\hat{\mu _1} :\hat{\mu _2} :\hat{\mu _3} :\hat{\mu _4} )} \circ \mathcal {S} \circ \mathcal {H}\right) (P), \end{aligned}$$

where $\hat{\mu _1} := (\mu _1+\mu _2+2)/2$, $\hat{\mu _2} := (\mu _1+\mu _2-2)/2$, and $\hat{\mu _3} := \hat{\mu }_4:= (\mu _1-\mu _2)/2$.

For the pseudo-doubling map, we compose $\varphi _O$ with its dual, $\hat{\varphi }_O:\hat{\mathcal {K}}^\mathrm{Sqr} \rightarrow \mathcal {K}^\mathrm{Sqr}$, which simply replaces $\mathcal {C}_{(\hat{\mu _1} :\hat{\mu _2} :\hat{\mu _3} :\hat{\mu _4} )}$ with $\mathcal {C}_{({\mu _1} :{\mu _2} :{\mu _3} :{\mu _4} )}$. The kernel of $\varphi _O$ is the (2, 2)-subgroup $O$ in (16), and the kernel of $\hat{\varphi }_O$ is the (2, 2)-subgroup consisting of $(\hat{\mu }_1 :\hat{\mu }_2 :\hat{\mu }_3 :\hat{\mu }_4)$, $(\hat{\mu }_2 :\hat{\mu }_1 :\hat{\mu }_4 :\hat{\mu }_3)$, $(\hat{\mu }_3 :\hat{\mu }_4 :\hat{\mu }_1 :\hat{\mu }_2 )$, and $(\hat{\mu }_4 :\hat{\mu }_3 :\hat{\mu }_2 :\hat{\mu }_1)$.

Isomorphisms and $\varvec{\varphi }_{{\varvec{P}}}$ on ${\varvec{\mathcal {K}}}^\mathbf{Sqr}$. We now turn to defining the (2, 2)-isogenies whose kernels are $\varUpsilon$ and $\tilde{\varUpsilon }$ in (16).

Observe that there is a subtle difference between our description $\varphi _O$ and $\hat{\varphi }_O$ above, and those described in the journey around the hexagon in [28, Fig. 1]. We define $\varphi _O$ as $\varphi _O= \left( \mathcal {C}_{(\hat{\mu _1} :\hat{\mu _2} :\hat{\mu _3} :\hat{\mu _4} )} \circ \mathcal {S} \circ \mathcal {H}\right)$, swapping the order of the scaling and squaring morphisms in [28, Fig. 1], which instead takes $\varphi _O= \left( \mathcal {S} \circ \mathcal {C}_{(\hat{\nu }_1 :\hat{\nu }_2 :\hat{\nu }_3 :\hat{\nu }_4)} \circ \mathcal {H}\right)$, where $\hat{\nu }_i^2 = \hat{\mu }_i$ for $i=1,2,3,4$ (this is analogous for $\hat{\varphi }_O$, but with $\nu _i^2=\mu _i$). In their intended application to HECC, this ordering makes no difference, since the (presumably $\mathbb {F}_p$-rational) $\nu _i$ and $\hat{\nu }_i$ are always fixed public parameters. In our case, however, all of the Kummer parameters change each time we compute an isogeny, and the ordering here turns out to be crucial; we will never be computing the $\nu _i$ or $\hat{\nu }_i$ (or, at least, not in time for their use in the pseudo-doublings that typically take place prior to the following isogeny computation in the SIDH framework).

Nevertheless, viewing the first two steps from $\mathcal {K}^\mathrm{Sqr}$ around the hexagon exactly as in [28, Fig. 1] aids our derivation of the isomorphisms. The first step is the Hadamard isomorphism, which moves us from $\mathcal {K}^\mathrm{Sqr}$ to $\mathcal {K}^\mathrm{Int}$, and the next step is the scaling isomorphism $\mathcal {C}_{(\hat{\nu }_1 :\hat{\nu }_2 :\hat{\nu }_3 :\hat{\nu }_4)}$, which takes us from $\mathcal {K}^\mathrm{Int}$ to $\hat{\mathcal {K}}^\mathrm{Can}_O$; here $\mathcal {K}^\mathrm{Int}$ is exactly as in [28] and $\hat{\mathcal {K}}^\mathrm{Can}_O$ corresponds to $\hat{\mathcal {K}}^\mathrm{Can}$ in [28]. Writing $O^\mathrm{Can}$ as the image of $O$ under $\mathcal {C}_O\circ \mathcal {H}$ with $\mathcal {C}_O:=\mathcal {C}_{(\hat{\nu }_1 :\hat{\nu }_2 :\hat{\nu }_3 :\hat{\nu }_4)}$, and similarly for $\varUpsilon$ and $\tilde{\varUpsilon }$, reveals that

$$\begin{aligned} O^\mathrm{Can}&= \, \Big ( (a : b : c : d), \, (a : -b : c : -d), \, (a : -b : -c : d), \, (a : b : -c : -d) \Big ), \nonumber \\ \varUpsilon ^\mathrm{Can}&= \, \Big ( (a : b : c : d), \, (d : c : b : a), \, (c : d : a : b), \, (b : a : d : c) \Big ), \, \, \mathrm{and} \nonumber \\ \tilde{\varUpsilon }^\mathrm{Can}&= \, \Big ( (a : b : c : d), \, (d : -c : -b : a), \, (c : -d : a : -b), \, (b : a : -d : -c) \Big ), \end{aligned}$$

(17)

where $(a : b : c : d) = (\hat{\nu }_1 :\hat{\nu }_2 :\hat{\nu }_3 :\hat{\nu }_4)$ is the neutral element on $\hat{\mathcal {K}}^\mathrm{Can}_O$. Note that $\hat{\mathcal {K}}^\mathrm{Can}$ is the Kummer surface used by Gaudry, which is why the points in (17) match up with those in [19, Sect.  3.4].

We now proceed analogously to the treatment in Sect. 4. When $\varUpsilon ^\mathrm{Can}$ is the intended (2, 2)-kernel, we seek an isomorphism that will transform $\varUpsilon ^\mathrm{Can}$ into a (2, 2)-subgroup whose four elements act like the four elements in $O^\mathrm{Can}$, but on an isomorphic surface. At the same time, this isomorphism should also transform the two subgroups in $\{O^\mathrm{Can},\tilde{\varUpsilon }^\mathrm{Can}\}$ into two subgroups whose elements act like those in the two subgroups in $\{\varUpsilon ^\mathrm{Can},\tilde{\varUpsilon }^\mathrm{Can}\}$, but on an isomorphic surface. Here the term ‘act’ refers to the action of translation by the 2-torsion elements of the corresponding Kummer surfaces. In the case of the 2-torsion on $\hat{\mathcal {K}}^\mathrm{Can}_O$, these actions (explained in [19, Sect. 3.4]) are extremely simple: for example, translating $(x :y :z :t) \in \hat{\mathcal {K}}^\mathrm{Can}_O$ by the element $(c : -d : a : -b)$ gives the point $(y :-x :t :-z)$.

We observe that when the (2, 2)-kernel is $\varUpsilon ^\mathrm{Can}$, its image under the Hadamard transform satisfies these constraints, but when the (2, 2)-kernel is $\tilde{\varUpsilon }^\mathrm{Can}$, we need to use a modified transform $\tilde{\mathcal {H}}: (x :y :z :t) \mapsto \mathcal {H}(-x :y :z :t)$. Looking closer, and using the relationship $\tau \tilde{\tau }=1$ in (16), we see that we can instead replace the scaling $\mathcal {C}_O$ with scalings $\mathcal {C}_{\varUpsilon }$ and $\mathcal {C}_{\tilde{\varUpsilon }}$ that depend on the subgroup at hand, and to follow both by the original Hadamard transform $\mathcal {H}$.

Importantly, the function for computing the constants for the coordinate scalings $\mathcal {C}_{\varUpsilon }$ and $\mathcal {C}_{\tilde{\varUpsilon }}$ is independent of which subgroup we are in; the values of the torsion elements are what changes the values of the scaling constants, which is crucial for obtaining a uniform isogeny algorithm. As alluded to above, to avoid the computation of square roots, the formulas for computing the scaling constants also take as input a point of order 4 on $\mathcal {K}^\mathrm{Sqr}$.

Let $Q \in \mathcal {K}^\mathrm{Sqr}$ be a point of order 4 such that $P=[2]Q \in \{\varUpsilon ,\tilde{\varUpsilon }\}$; writing $Q'=\mathcal {H}(Q) = (Q_1' :Q_2' :Q_3' :Q_4')$ and $P'=\mathcal {H}(P) = (P_1' :P_2' :P_3' :P_4')$, then the coordinate scaling is

$$ \mathcal {C}_{Q,P} :(X_1 :X_2 :X_3 :X_4) \mapsto (\pi _1 X_1 :\pi _2 X_2 :\pi _3 X_3 :\pi _4 X_4), $$

where

$$ \pi _1 = P_2' Q_4', \quad \quad \pi _2 = P_1' Q_4', \quad \quad \mathrm{and} \quad \quad \pi _3 = \pi _4 = P_2' Q_1', $$

when $P \in \{\varUpsilon _1,\tilde{\varUpsilon }_1\}$ (such that its last coordinate is non-zero), and where

$$ \pi _1 = P_2' Q_3', \quad \quad \pi _2 = P_1' Q_3', \quad \quad \mathrm{and} \quad \quad \pi _3 = \pi _4 = P_2' Q_1', $$

when $P \in \{\varUpsilon _2,\tilde{\varUpsilon }_2\}$ (such that its second to last coordinate is non-zero).

In our target application of chained (2, 2)-isogenies in the SIDH framework, the 2-torsion points that represent our (2, 2)-kernels are either always of the form of $\varUpsilon _1$ and $\tilde{\varUpsilon }_1$, or they are always of the form of $\varUpsilon _2$ and $\tilde{\varUpsilon }_2$. Thus, the function that computes the scaling constants can be determined at setup and fixed once-and-for-all in an implementation.

Let $\mathcal {G} \in \{\varUpsilon , \tilde{\varUpsilon }\}$ and let $P \in \mathcal {G}$ with $P = [2]Q$. We can now define the full (2, 2)-isogeny with (2, 2)-kernel $\mathcal {G}$ as

$$\begin{aligned} \varphi _P :&\quad \mathcal {K}^\mathrm{Sqr} \rightarrow \mathcal {K}^\mathrm{Sqr}/\mathcal {G} , \nonumber \\&\quad R \mapsto \left( \mathcal {S} \circ \mathcal {H} \circ \mathcal {C}_{Q,P} \circ \mathcal {H}\right) (R). \end{aligned}$$

(18)

Note that all four elements of the (2, 2)-kernel $\mathcal {G}$ map to the neutral element $(\mu _1' :\mu _2' :1 :1)$ on $\mathcal {K}^\mathrm{Sqr}/\mathcal {G}$.

In Fig. 1 we summarise the situation by making use of [28, Fig. 1]. The arrows in the middle comprise half of their hexagon; this corresponds to $\varphi _O$, whose kernel is the subgroup $O$. Note that our SIDH-style computations will never compute this isogeny, and that we will always be taking either the top or bottom path, depending on whether our (2, 2)-kernel is $\varUpsilon$ or $\tilde{\varUpsilon }$.

Fig. 1.

An illustration of the two (2, 2)-isogenies corresponding to the subgroups $\varUpsilon$ and $\tilde{\varUpsilon }$, based on the diagram in [28, Fig. 1]. Here $\mathcal {C}_{\varUpsilon }$ is used to denote $\mathcal {C}_{Q,P}$ when $P \in \varUpsilon$, and $\mathcal {C}_{\tilde{\varUpsilon }}$ is used to indicate $\mathcal {C}_{Q,P}$ when $P \in \tilde{\varUpsilon }$.

We point out that our use of the 4-torsion point Q above the 2-torsion point P means that we must modify the computational strategy to account for this; we refer to [16, Sect. 4.3.2], where this was done when 8-torsion points lying above 2-torsion kernel elements were incorporated into the computational strategies.

Operation Counts. Even though our Kummer surfaces are defined by the projective tuple $(\mu _1 :\mu _2 :1 :1)$, once we move into an SIDH computation (where we avoid inversions in the main loop), we cannot expect the surface constants to be normalised in this fashion, so in our context all multiplications by constants are counted as generic multiplications (the analogue in the elliptic curve case was treating the Montgomery coefficient in $\mathbb {P}^1$ – see [14]). In the HECC context, pseudo-doublings on fast Kummer surfaces incur 6 multiplications by curve constants, but this is because 2 of the constants were normalised; in our case, pseudo-doublings incur 4 multiplications during each of the scalings $\mathcal {D}_{({\mu _1} :{\mu _2} :{\mu _3} :{\mu _4} )}$ and $\mathcal {D}_{(\hat{\mu _1} :\hat{\mu _2} :\hat{\mu _3} :\hat{\mu _4} )}$. This brings the operation count for a pseudo-doubling to 8 multiplications, 8 squarings, and 16 additions, and the operation count for pushing a point through a (2, 2)-isogeny to 4 multiplications, 4 squarings, and 16 additions. Note that both of these counts are obtained by assuming that the inverted constants in the coordinate scalings have been precomputed during the computation of the (2, 2)-isogenous Kummer surface.

It therefore remains to tally the operations required to compute the isogenous Kummer surface constants. Firstly, we point out that an optimised implementation does not actually need to compute or use the constants F, G and H defining the surface, since these are not used directly in the pseudo-group law computations. The only constants needed are those in the two coordinate scalings that occur during pseudo-doublings; we obtain these by pushing any kernel point through the (2, 2)-isogeny to get the squared theta constants $(\mu _1' :\mu _2' :\mu _3' :\mu _4')$ that define the image surface, a further 6 multiplications to obtain a projective tuple equivalent to $(1/\mu _1' :1/\mu _2' :1/\mu _3' :1/\mu _4')$, and then 8 more additions and 6 more multiplications to compute a projective tuple whose coordinates are projectively equivalent to the inverses of the coordinates of $\mathcal {H}(\mu _1' :\mu _2' :\mu _3' :\mu _4')$. In total, the computation of the set of isogenous surface constants requires 19 multiplications, 4 squarings, and 28 additions. These counts are used in Table 1 in the next section.

6 Implications for Isogeny-Based Cryptography

We discuss potential implications and practical considerations of the Kummer surface approach in the realm of SIDH. The takeaway message is that this paper is a first step towards exploring the use of Kummer surfaces in isogeny-based cryptography, and that more work needs to be done to determine whether they will be utilised in real-world implementations. For example, it is possible that our approach to computing the isogeny $\varphi _P$ is sub-optimal, and that faster methods will be discovered, or that there are more specialised parameterisations of supersingular Kummer surfaces that provide even faster arithmetic.

Efficiency of (2,2)-Isogenies in SIDH. In Table 1, we compare (2, 2)-isogenies on Kummer surfaces with 2-isogenies on elliptic curves, by comparing the operation counts for isolated operations in both scenarios. On the elliptic curve side, the current state-of-the-art implementations actually use repeated 4-isogenies as they are slightly faster [14, 16, 27], so to take this into account we simply double the relevant operation counts for the (2, 2)-isogenies reported above (recall from Lemma 2 that our (2, 2)-isogenies correspond to 2-isogenies on the elliptic curves). Operation counts for the relevant 4-isogeny operations in the elliptic curve case are exactly as in the optimised version of the SIKE implementation [22], and for the relevant 2-isogeny operations are exactly as in [27, Table 1].

We use $\mathbf{M}$, $\mathbf{S}$ and $\mathbf{A}$ to denote multiplications, squarings and additions in $\mathbb {F}_{p^2}$, and use $\mathbf{m}$, $\mathbf{s}$ and $\mathbf{a}$ to denote the same respective operations in $\mathbb {F}_p$. It is common to approximate the former in terms of the latter by assuming Karatsuba-like routines for $\mathbb {F}_{p^2}$ operations, but this can be rather crude. To give a fairer comparison, we benchmarked these field operations directly using v3.0 of Microsoft’s SIDH library⁶: on a 3.4GHz Intel i7-6700 (Skylake) architecture, and over the 751-bit prime from [14], this benchmarking reported $\mathbf{M} = 1004$ cycles, $\mathbf{S} = 763$ cycles, and $\mathbf{A}=80$ cycles, while $\mathbf{m} = 349$ cycles and $\mathbf{a}=43$ cycles. The current library does not have a tailored squaring routine over $\mathbb {F}_p$, because the routines for $\mathbb {F}_{p^2}$ operations never call $\mathbb {F}_p$ squarings as a subroutine. Thus, we give two cycle count approximations for the Kummer case: one that assumes $\mathbf{s}=\mathbf{m}$ (i.e., that the $\mathbb {F}_p$ multiplication routine is called to compute squarings), and one that assumes $\mathbf{s}=0.8\mathbf{m}$, a common ratio used to approximate the speedup obtained by optimising tailored field squarings. We note that using cycle counts instead of Karatsuba approximations favours the elliptic curve setting over this work. For example, when using the above clock cycles as units, we have $\mathbf{M} < 3\mathbf{m}$, but a common approximation is that $\mathbf{M} \approx 3\mathbf{m}+5\mathbf{a} \gg 3 \mathbf{m}$.

Table 1. Field arithmetic required for the three main isolated operations on one side of the SIDH framework, comparing chained 2-isogenies on Montgomery curves over $\mathbb {F}_{p^2}$ (previous work) with chained Richelot isogenies on Kummer surfaces over $\mathbb {F}_p$ (this work). Further explanation in text.

The approximations in Table 1 suggest that the Kummer surface approach of computing Richelot isogenies over $\mathbb {F}_p$ will be competitive with the previous approaches that apply Vélu’s formulas to the x-line of Montgomery elliptic curves over $\mathbb {F}_{p^2}$. The main operations of interest are ‘quadrupling’ and ‘4-isog. point’, since these costs and their ratios are what determines the optimal strategy (see [16]), and they are computed many more times than the ‘4-isog. curve’ operation. Moreover, doubling the (2, 2)-isogeny operation counts is only accurate in the case of the point operations; in terms of the curve operations, we would not need to compute the full set of the surface constants of the intermediate curve in back-to-back (2, 2)-isogenies, so a more careful approach to computing the image curve in this case would likely lead to counts close to half of those in this row (on our side). One caveat worth mentioning is that the special Kummer surfaces in this work will also have a fast ladder for computing scalar multiplications, as well as a fast three-point ladder that is typically used before any isogenies are computed in the SIDH framework.

Of course, the only way to determine if the Kummer approach can outperform the elliptic curve approach is to present an optimised implementation of Kummer surface isogenies within the SIDH framework, e.g., one that factors in the cost ratios of pseudo-doublings and (2, 2)-isogenies to derive optimal strategies for the full SIDH isogeny computation – see [16, Sect. 4.2]. We leave such an implementation as future work (perhaps until the motivation is heightened by odd-power Kummer isogenies that can be used on the other side of the SIDH protocol, as we discuss below), but also mention that Kummer arithmetic is especially amenable to aggressive vectorised implementations (see [5]).

Utilising Kummer Surfaces in Practice. We discuss two potential options for taking advantage of Kummer surface arithmetic in the SIDH framework, and the practical considerations of each. The first option is that the public parameters and wire transmissions are as usual, i.e., using (points on) elliptic curves, but that Kummer arithmetic is internally preferred by at least one party. The second assumes that Kummer arithmetic is preferred everywhere, and that the SIDH framework is defined to facilitate this.

Option 1 – Kummer arithmetic in private. Suppose Alice wants to compute her secret isogenies on Kummer surfaces while engaging in an SIDH protocol that is specified entirely using elliptic curves. In terms of the public parameters, her easiest option would be to convert them (offline and once-and-for-all) into Kummer parameters by first using the map $\eta :E_\alpha \rightarrow J_{C_\alpha }$ in Sect. 3, and then applying the usual maps from $J_{C_\alpha }$ to $\mathcal {K}^\mathrm{Sqr}$. While this process seems complicated at a first glance, a closer inspection of these maps reveals that an optimised conversion in this direction would only require a few dozen field multiplications; the x-coordinates of three co-linear points on $E_\alpha$ (see [14, 22]) are all Alice needs to compute the corresponding Kummer surface and the three Kummer points required to kick-start her computations. Indeed, the only additional information she needs to convert Bob’s public key down to the Kummer domain is the initial 2-torsion point $(\alpha ,0)$ (assuming Bob sends her information for the curve coefficient instead), and this requires at most one square root in $\mathbb {F}_{p^2}$, which is not a deal-breaker.

In the other direction, after computing her public key or shared secret on $\mathcal {K}^\mathrm{Sqr}$, Alice needs to lift this information back up to $E_\alpha$ in order to comply with Bob. The maps lifting from $\mathcal {K}^\mathrm{Sqr}$ back up to $J_{C_{\lambda ,\mu ,\nu }}$ are naturally more complicated than their inverses [13, 19], but again the SIDH x-only framework simplifies the process significantly; we can recover the x-coordinate on $E_\alpha$ given only the values of $u_1$, $u_0$ and $v_0^2$ (corresponding to the Mumford coordinates of a point in $J_{C_\alpha }$), and we can lift up from $\mathcal {K}$ to these values without any square roots – see [19, Sect. 4.3].

In any case, equipped with the efficient maps in Sect. 3, we do not see any theoretical or practical obstacle preventing Alice from complying, should the efficiency of the Kummer warrant a small conversion overhead at either or both sides of the main isogeny computation.

Option 2 – Kummer arithmetic everywhere. If both sides of the SIDH protocol eventually warrant Kummer arithmetic (see below), then defining the public parameters to facilitate this is easy. The main issues we foresee involve maintaining the size of the public keys in the compressed setting.

Firstly, in the uncompressed scenario, transmitting elliptic curves and Kummer surfaces in the current framework has the same cost; Montgomery curves are specified up to twist with one element in $\mathbb {F}_{p^2}$, and our supersingular Kummer surfaces are completely specified by two elements of $\mathbb {F}_p$ ($\mu _1$ and $\mu _2$). Unambiguously specifying points on Montgomery curves amounts to sending one element of $\mathbb {F}_{p^2}$ and a sign bit; on the Kummer side, the elegant techniques in [28, Sect. 6] show that Kummer points can be specified by two elements of $\mathbb {F}_p$ and two sign bits, meaning we lose at most one bit per group element. Rather than sending any curve coefficients over the wire, recent works (including the SIKE proposal [22]) have instead specified public keys as three co-linear Montgomery x-coordinates, from which the underlying Montgomery curve can be recovered on the other side [14]. We have not yet investigated this analogue in the Kummer surface setting, but even if it does not work in a straightforward way, reverting back to the original form of public keys (from [16]) adds at most 4 bits to the public key sizes. To summarise, we would lose at most a few bits to specify uncompressed SIDH entirely using Kummer surfaces.

In terms of the shared secret, both parties would eventually arrive at a fast supersingular Kummer surface specified by $(\mu _1 :\mu _2 :1 :1)$. While we have yet to investigate convenient Kummer surface invariants that could act as the shared secret, we remark that emperical evidence seems to suggest that the approach of computing $\lambda$, $\mu$ and $\nu =\lambda \mu$ from (15) and normalising the Igusa-Clebsch invariants in $\mathbb {P}(2,4,6,10)(\mathbb {F}_p)$ makes the SIDH protocol commute. We leave further investigation into appropriate invariants as future work.

In terms of optimal compression of public keys, applying the techniques in [2] directly to the Kummer setting seems less straightforward, but again we cannot see any reason preventing this possibility⁷. This too needs further investigation, but we point out that as a fallback, we could of course always map the problem of compression back to the elliptic curve setting (moving back to the first option above), and specify the compressed public keys accordingly.

Of course, there are several other possibilities that lie somewhere between the two options above, e.g., where the two parties send information in such a way that the overall cost of the protocol is minimised.

Beyond (2,2)-Isogenies. The case for the Kummer approach in supersingular isogeny-based cryptography would be much stronger if it were able to be applied efficiently for both parties. There has been some explicit work done in the case of (3, 3)- and (5, 5)-isogenies (cf. [9, 17]), but those situations appear much more complicated than the case of Richelot isogenies, and we leave their investigation as future work. One hope in this direction is the possibility of pushing odd degree $\ell$-isogeny maps from the elliptic curve setting to the Kummer setting by way of the maps in Sect. 3. This was difficult in the case of 2-isogenies because the maps themselves are (2, 2)-isogenies (e.g., their kernel is the 2-torsion on $E_\alpha$), but in the case of odd degree isogenies there is nothing obvious preventing this approach.