Abstract
We consider a situation where multiple parties, owning data that have to be frequently updated, agree to share weighted sums of these data with some aggregator, but where they do not wish to reveal their individual data, and do not trust each other. We combine techniques from Private Stream Aggregation (PSA) and Functional Encryption (FE), to introduce a primitive we call Decentralized Multi-Client Functional Encryption (DMCFE), for which we give a practical instantiation for Inner Product functionalities. This primitive allows various senders to non-interactively generate ciphertexts which support inner-product evaluation, with functional decryption keys that can also be generated non-interactively, in a distributed way, among the senders. Interactions are required during the setup phase only. We prove adaptive security of our constructions, while allowing corruptions of the clients, in the random oracle model.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Functional Encryption (FE) [9, 15, 18, 28] is a new paradigm for encryption which extends the traditional “all-or-nothing” requirement of Public-Key Encryption in a much more flexible way. FE allows users to learn specific functions of the encrypted data: for any function f from a class \(\mathcal {F}\), a functional decryption key \(\mathsf {dk}_f\) can be computed such that, given any ciphertext c with underlying plaintext x, using \(\mathsf {dk}_f\), a user can efficiently compute f(x), but does not get any additional information about x. This is the most general form of encryption as it encompasses identity-based encryption, attribute-based encryption, broadcast encryption.
However, whereas the input can be large, like a high-dimensional vector, the basic definition of FE implies that the input data comes from only one party: all the coordinates of the vector are provided by one party, and all are encrypted at the same time. In many practical applications, the data are an aggregation of information that comes from different parties that may not trust each other.
A naive way to distribute the ciphertext generation would be to take an FE scheme and to have a trusted party handling the setup and the key generation phases, while the encryption procedure would be left to many clients to execute by Multi-Party Computation (MPC). This straw man construction has two obvious weaknesses:
-
1.
Generating any ciphertext requires potentially heavy interactions, with everybody simultaneously on line, and the full ciphertext has to be generated at once, with all the components being known at the same time;
-
2.
Some authority (the trusted third party) reserves the power to recover every client’s private data.
Multi-Client Functional Encryption [16, 20] addresses the former issue of independent generation of the ciphertext, and we introduce Decentralized Multi-Client Functional Encryption to address the latter, without any central authority nor master secret key.
Multi-Client Functional Encryption. In Multi-Client Functional Encryption (\(\textsf {MCFE}\)), as defined in [16, 20], the single input x to the encryption procedure is broken down into an input vector \((x_1,\ldots ,x_n)\) where the components are independent. An index i for each client and a (typically time-based) label \(\ell \) are used for every encryption: \((c_1 = \mathsf {Encrypt} (1,x_1,\ell ),\ldots ,c_n = \mathsf {Encrypt} (n,x_n,\ell ))\). Anyone owning a functional decryption key \(\mathsf {dk}_f\), for an n-ary function f and multiple ciphertexts for the same label \(\ell \), \(c_1 = \mathsf {Encrypt} (1,x_1,\ell ), \ldots , c_n = \mathsf {Encrypt} (n,x_n,\ell )\), can compute \(f(x_1, \ldots , x_n)\) but nothing else about the individual \(x_i\)’s. The combination of ciphertexts generated for different labels does not give a valid global ciphertext and the adversary learns nothing from it. \(\textsf {MCFE}\) is similar to the naive construction described above with MPC, except that ciphertext generation now simply takes one round, and each ciphertext \(c_i\) can also be generated independently for the others.
Decentralized Multi-Client Functional Encryption. Still, \(\textsf {MCFE}\) requires a trusted party to generate a master key \({\mathsf {msk}}\) and to distribute the encryption keys \({\mathsf {ek}_i}\) to the clients and the functional decryption keys \(\mathsf {dk}_f\) to the decryptors. In our scenario, however, the clients do not want to rely on any authority. We would thus be interested in a decentralized version of \(\textsf {MCFE}\), where no authority is involved, but the generation of functional decryption keys remains an efficient process under the control of the clients themselves. We introduce the notion of Decentralized Multi-Client Functional Encryption (\(\textsf {DMCFE}\)), in which the authority is removed and the clients work together to generate appropriate functional decryption keys. We stress that the authority is not simply distributed to a larger number of parties, but that the resulting protocol is indeed decentralized: each client has complete control over their individual data and the functional keys they authorize the generation of.
1.1 A Use Case
Consider a financial firm that wants to compute aggregates of several companies’ private data (profits, number of sales) so that it can better understand the dynamics of a sector. The companies may be willing to help the financial firm understand the sector as whole, or may be offered compensation for their help, but they don’t trust the financial firm or each other with their individual data. After setting up a \(\textsf {DMCFE}\), each company encrypts its private data with a time-stamp label under its private key. Together, they can give the financial firm a decryption aggregation key that only reveals a sum on the companies’ private data weighted by public information (employee count, market value) for a given time-stamp. New keys can retroactively decrypt aggregates on old data.
1.2 Related Work
In their more general form, FE and \(\textsf {MCFE}\) schemes have been introduced in [5, 6, 10, 16,17,18,19, 27, 30] but unfortunately, they all rely on non standard cryptographic assumptions (indistinguishability obfuscation, single-input FE for circuits, or multilinear maps). It is more important in practice, and it is an interesting challenge, to build FE for restricted (but concrete) classes of functions, satisfying standard security definitions, under well-understood assumptions.
Inner-Product Functional Encryption. In 2015, Abdalla, Bourse, De Caro, and Pointcheval [1] considered the question of building FE for inner-product functions. In their paper, they show that inner-product functional encryption (IP-FE) can be efficiently realized under standard assumptions like the Decisional Diffie-Hellman (\(\textsf {DDH}\)) and Learning-with-Errors (LWE) assumptions [26], but in a weak security model, named selective security. Later on, Agrawal, Libert and Stehlé [4] considered adaptive security for IP-FE and proposed constructions whose security is based on \(\textsf {DDH}\), LWE or Paillier’s Decisional Composite Residuosity (DCR) [25] assumptions.
Private Stream Aggregation (PSA). This notion, also referred to as Privacy-Preserving Aggregation of Time-Series Data, is an older primitive introduced by Shi et al. [29]. It is quite similar to our target \(\textsf {DMCFE}\) scheme, however PSA does not consider the possibility of adaptively generating different keys for different inner-product evaluations, but only enables the aggregator to compute the sum of the clients’ data for each time period. PSA also typically involves a Differential Privacy component, which has yet to be studied in the larger setting of \(\textsf {DMCFE}\). Further research on PSA has focused on achieving new properties or better efficiency [8, 11, 13, 21, 23, 24] but not on enabling new functionalities.
Multi-Input Functional Encryption. Goldwasser et al. [16] introduced the notion of Multi-Input Functional Encryption (MIFE) which breaks down a single input x into an input vector \((x_1,\ldots ,x_n)\) where the components are independent (as does \(\textsf {MCFE}\)), but for which there is no notion of ciphertext index or label: user i can enter \(x_i\) and encrypt it as \(c_i=\mathsf {Encrypt} (x_i)\). Anyone owning a functional decryption key \(\mathsf {dk}_f\), for an n-ary function f and multiple ciphertexts \(c_1 = \mathsf {Encrypt} (x_1), \ldots , c_n = \mathsf {Encrypt} (x_n)\), can compute \(f(x_1, \ldots , x_n)\) but nothing else about the individual \(x_i\)’s. Numerous applications of MIFE have been given in detail in [16].
As with \(\textsf {MCFE}\), general purpose MIFE schemes rely on indistinguishability obfuscation or multilinear maps, which we currently do not know how to instantiate under standard cryptographic assumptions. Extending IP-FE to the multi-input setting has proved technically challenging. [3] builds the first Multi-Input IP-FE, that is, each input slot encrypts a vector \(\varvec{x}_i \in \mathbb {Z}_p^m\) for some dimension m, each functional decryption key is associated with a vector \(\varvec{y}\), and decryption recovers \(\langle \varvec{x}, \varvec{y} \rangle \) where \(\varvec{x}:= (\varvec{x}_i \Vert \cdots \Vert \varvec{x}_n)\), \(\varvec{y}\in \mathbb {Z}_p^{n \cdot m}\), and n denotes the number of slots, which can be set up arbitrarily. They prove their construction secure under standard assumptions (\(\textsf {SXDH}\), and in fact, k-Lin for any \(k\ge 1\)) in bilinear groups. Concurrently, [22] build a two-input (i.e. \(n=2\)) FE using similar assumptions in bilinear groups. Very recently, [2, 12] gave a function-hiding multi-input FE for inner products, where the functional decryption keys do not reveal their underlying functions. [2] also gives a generic transformation from single to multi-input for IP-FE, which gives the first multi-input constructions whose security rely on \(\textsf {DDH}\), LWE, or DCR.
In multi-input FE, every ciphertext for every slot can be combined with any other ciphertext for any other slot, and used with functional decryption keys to decrypt an exponential number of values, as soon as there are more than one ciphertext per slot. This “mix-and-match” feature is crucial for some of the applications of MIFE, such as building Indistinguishability Obfuscation [16]. However, it also means the information leaked about the underlying plaintext is enormous, and in many applications, the security guarantees simply become void, especially when many functional decryption keys are queried. In the case of inner product, as soon as m well-chosen functional decryption keys are queried (i.e. for linearly independent vectors), the plaintexts are completely revealed. In the multi-client setting however, since only ciphertexts with the same label (think of it as a time-stamp, for instance) can be combined for decryption, information leakage of the plaintext is much reduced.
The fact that clients have more control over how much information is leaked about their data, and that we remove the need for a central authority in the case of \(\textsf {DMCFE}\), makes our schemes better suited for real-world use.
1.3 Multi-Client Functional Encryption
We remark that, as for \(\textsf {MIFE}\), private-key \(\textsf {MCFE}\) is more relevant than its public-key counterpart (this is explained in [16], or [3] in the context of IP-FE).
Essentially, in a public-key \(\textsf {MCFE}\), an encryption of unknown plaintext \(x_i\) (for some label \(\ell \)) can be used together with encryptions of arbitrarily chosen values \(x'_j\) for each slot \(j \in [n]\) (for the same label \(\ell \)) and a functional decryption key for some function f, to obtain the value \(f(x'_1,\cdots ,x'_{i_1},x_i,x'_{i+1},\cdots ,x'_n)\). Since the values \(x'_j\) for \(j \ne i\) are arbitrarily chosen, this reveals typically too much information on \(x_i\) for practical uses. In the case of inner product, that means that, from \({\mathsf {Enc}^{}}(i,x_i,\ell )\), \(\mathsf {dk}_{\varvec{y}}\), and the public key, one can efficiently extract the values \(x_i y_i + \sum _{j\ne i} x'_j y_j\) for chosen \(x'_j\), which exactly reveals the partial inner product \(x_i y_i\) (see [3] for more details on the limitations of public-key IP-FE in the multi-input setting).
Security is defined with an indistinguishability game, where the adversary has to distinguish between encryptions of chosen plaintexts \((x_i^0)_{i \in [n]}\) and \((x_i^1)_{i \in [n]}\). The inherent leakage of information about the plaintext given by functional decryption keys \(\mathsf {dk}_f\) is captured by a Finalize procedure in the security game, where the advantage is set to zero if the adversary performed a trivial attack, in the sense that correctness allows the adversary to distinguish encryptions of \((x_i^0)_{i \in [n]}\) from \((x_i^1)_{i \in [n]}\), simply because the underlying functions f of the decryption keys tell apart these plaintexts, i.e. \(f(x_1^0,\cdots ,x_n^0) \ne f(x_1^1,\cdots ,x_n^1)\).
In the public-key setting, in order to prevent the adversary from a trivial win, one should make the restriction that the adversary is only allowed to ask functional decryption keys \(\mathsf {dk}_f\) for functions f that satisfy \(f(x^0_1,\cdot ,\ldots ,\cdot ) = f(x^1_1,\cdot ,\ldots ,\cdot )\), \(f(\cdot ,x^0_2, \ldots ,\cdot ) = f(\cdot ,x^1_2, \ldots ,\cdot )\), ..., \(f(\cdot ,\cdot ,\ldots ,x^0_n) = f(\cdot ,\cdot ,\ldots ,x^1_n)\). Again, this would essentially exclude any function. A private-key encryption solves this issue, and is still well-suited for practical applications.
In this paper, we will thus consider this private-key setting which naturally fits the \(\textsf {MCFE}\) (and \(\textsf {DMCFE}\)) model as each component in the plaintext is separately provided by a different client. In such a case, the corruption of some clients is an important issue, since several of them could collude to learn information about other clients’ inputs. More precisely, we propose such an \(\textsf {MCFE}\) for Inner-Product functions in Sect. 4, that is secure even against adaptive corruptions of the senders.
1.4 Decentralized Multi-Client Functional Encryption
While it allows independent generation of the ciphertexts, \(\textsf {MCFE}\) (like MIFE) still assumes the existence of a trusted third-party who runs the \(\mathsf {SetUp} \) algorithm and distributes the functional decryption keys. This third-party, if malicious or corrupted, can easily undermine any client’s privacy. We are thus interested in building a scheme in which such a third-party is entirely taken out of the equation.
We thus introduce the notion of Decentralized Multi-Client Functional Encryption (\(\textsf {DMCFE}\)), in which the setup phase and the generation of functional decryption keys are decentralized among the same clients as the ones that generate the ciphertexts. We are interested in minimizing interactions during those operations. While one can do it, in a generic way, using MPC, our target is at least a non-interactive generation of the functional decryption keys, that we achieve in Sect. 5, again for Inner-Product functions. The one-time setup phase might remain interactive, but this has to be done once only.
1.5 Technical Overview
We briefly showcase the techniques that allow us to build efficient \(\textsf {MCFE}\) and \(\textsf {DMCFE}\) schemes. The schemes we introduce later enjoy adaptive security (aka full security), where encryption queries are made adaptively by the adversary against the security game, but for the sake of clarity, we will here give an informal description of a selectively-secure scheme from the \(\textsf {DDH}\) assumption, where queries are made beforehand. Namely, the standard security notion for FE is indistinguishability-based, where the adversary has access to a Left-or-Right oracle, that on input \((m_0,m_1)\) either always encrypts \(m_0\) or always encrypts \(m_1\). While for the adaptive security, the adversary can query this oracle adaptively, in the selective setting, all queries are made at the beginning, before seeing the public parameters.
We first design a secret-key \(\textsf {MCFE}\) scheme building up from the public-key FE scheme introduced by Abdalla et al. [1] (itself a selectively-secure scheme) where we replace the global randomness with a hash function (modeled as a random oracle for the security analysis), in order to make the generation of the ciphertexts independent for each client. The comparison is illustrated in Fig. 1. Note that for the final decryption to be possible, one needs the function evaluation \(\gamma \) to be small enough, within this discrete logarithm setting. This is one limitation, which is still reasonable for real-world applications that use concrete numbers, that are not of cryptographic size.
Comparison of the Inner-Product FE scheme from Abdalla et al. [1] and a similar \(\textsf {MCFE}\) obtained by introducing a hash function \(\mathcal {H}\).
If we write \(c_0 = g^r\) in the single input case and \(c_0 = \mathcal {H}(\ell )\) in the Multi-Client case, we have \(c_i = g^{x_i}{c_0}^{s_i}\) for \(i\in [n]\) in both cases. In the public-key scheme from [1], \(s_i\) was private, and only \(v_i = g^{s_i}\) was known to the encryptor. Since we are now dealing with private encryption, the encryptor can use \(s_i\). Correctness then follows from
We further define this \(\textsf {MCFE}\) scheme and prove it selectively secure under the \(\textsf {DDH}\) assumption in Appendix B.
We can easily decentralize the above protocol using standard MPC techniques, but as we mentioned, our main goal is to minimize interactions during the \(\mathsf {DKeyGen} \) protocol. This simple protocol can illustrate our main insight: we need to provide the aggregator with the decryption key \(\langle \varvec{s}, \varvec{y} \rangle \). Since the \(s_i\)’s are owned individually by the clients, we are interested in a protocol that would let them send shares from which the decryptor would recover an agreed upon Inner Product on their individual inputs. This sounds like a job for \(\textsf {MCFE}\).
More precisely, sending \(\widetilde{\mathsf {Encrypt}}(s_i)\) under some other key \(t_i\) would not solve our problem, because we would still need to provide \(\langle \varvec{t}, \varvec{y} \rangle \) to enable decryption, so we send \(\widetilde{\mathsf {Encrypt}}(y_is_i)\) under \(t_i\). Now we only need to compute one decryption key: the key for the inner product with vector \(\varvec{1}= (1,\ldots ,1)\), namely \(\sum _i t_i\).
There is one final caveat. The result of the inner product evaluation requires a final discrete logarithm computation, and we are no longer operating on real-world data, but on random elements from \(\mathbb {Z}_p\). Any attempt to recover the discrete logarithm is hopeless, and we are stuck with \(g^{\langle \varvec{s}, \varvec{y} \rangle }\). We work around this issue by using pairings, which effectively enable us to decrypt using only \(g^{\langle \varvec{s}, \varvec{y} \rangle }\). The standard \(\textsf {SXDH}\) assumption on pairing groups states that the \(\textsf {DDH}\) assumption holds in both groups, so introducing pairings doesn’t compromise the security of our scheme. Our fully-secure \(\textsf {DMCFE}\) from pairings, that inherits from this approach, is described in Sect. 5.
1.6 Contributions
Practical constructions of functional encryption for specific classes of functions is of high interest. In this paper, we focus on \(\textsf {MCFE}\) and \(\textsf {DMCFE}\) for Inner Product.
We present the first solutions for Inner-Product Functional Encryption in the Multi-Client and Decentralized Multi-Client settings:
-
1.
Efficiency: the proposed schemes are highly practical as their efficiency is comparable to that of the \(\textsf {DDH}\)-based IP-FE scheme from [4]. A value \(x_i\) is encrypted as a unique group element \(C_i\). The setup phase, key generation and decryption all take time linear in the number of participants, and encryption takes time linear in its input.
-
2.
Security under a standard assumption: our schemes are all adaptively secure under either the classical \(\textsf {DDH}\) assumption or the standard \(\textsf {SXDH}\) assumption.
-
3.
Security against adaptive corruptions: In addition, we successfully address corruptions of clients, even adaptive ones in the \(\textsf {MCFE}\) setting, exploring what Goldwasser et al. [16] highlighted as an “interesting direction”.
-
4.
Non interactivity: The \(\textsf {DMCFE}\) scheme we present in Sect. 5 has a key generation protocol that does not require interactions.
Refer to Fig. 2 for a comparison of the different schemes mentioned here. We leave open the problems of considering LWE-based or Paillier-based constructions and of extending this work beyond inner-product functions.
2 Definitions and Security Models
This section is devoted to defining \(\textsf {MCFE}\) and \(\textsf {DMCFE}\) and the security models that are appropriate for those primitives, in the indistinguishability setting.
2.1 Multi-Client Functional Encryption
An \(\textsf {MCFE}\) scheme encrypts vectors of data from several senders and allows the controlled computation of functions on these heterogeneous data. We now define a private-key \(\textsf {MCFE}\) as in [16, 20]:
Definition 1
(Multi-Client Functional Encryption). A multi-client functional encryption on \(\mathcal {M}\) over a set of n senders is defined by four algorithms:
-
\(\mathsf {SetUp} (\lambda )\): Takes as input the security parameter \(\lambda \), and outputs the public parameters \({\mathsf {mpk}}\), the master secret key \({\mathsf {msk}}\) and the n encryption keys \({\mathsf {ek}_i}\);
-
\({\mathsf {Encrypt} (\mathsf {ek}_i, x_i,\ell )}\): Takes as input a user encryption key \({\mathsf {ek}_i}\), a value \(x_i\) to encrypt, and a label \(\ell \), and outputs the ciphertext \(C_{\ell ,i}\);
-
\({\mathsf {DKeyGen} (\mathsf {msk}, f)}\): Takes as input the master secret key \({\mathsf {msk}}\) and a function \(f:\mathcal {M}^n\rightarrow \mathcal {R}\), and outputs a functional decryption key \(\mathsf {dk}_f\);
-
\(\mathsf {Decrypt} (\mathsf {dk}_f, \ell , \varvec{C})\): Takes as input a functional decryption key \(\mathsf {dk}_f\), a label \(\ell \), and an n-vector ciphertext \(\varvec{C}\), and outputs \(f(\varvec{x})\), if \(\varvec{C}\) is a valid encryption of \(\varvec{x}= (x_i)_i\in \mathcal {M}^n\) for the label \(\ell \), or \(\perp \) otherwise.
We make the assumption that \({\mathsf {mpk}}\) is included in \({\mathsf {msk}}\) and in all the encryption keys \({\mathsf {ek}_i}\) as well as the functional decryption keys \(\mathsf {dk}_f\). The correctness property states that, given \({(\mathsf {mpk},\mathsf {msk},(\mathsf {ek}_i)_i)\leftarrow \mathsf {SetUp} (\lambda )}\), for any label \(\ell \), any function \(f:\mathcal {M}^n\rightarrow \mathcal {R}\), and any vector \(\varvec{x}= (x_{i})_i\in \mathcal {M}^n\), if \({C_{\ell ,i}\leftarrow \mathsf {Encrypt} (\mathsf {ek}_i, x_{i},\ell )}\), for \(i \in \{1,\ldots ,n\}\), and \({\mathsf {dk}_f\leftarrow \mathsf {DKeyGen} (\mathsf {msk},f)}\), then \(\mathsf {Decrypt} (\mathsf {dk}_f, \ell , \varvec{C}_\ell = (C_{\ell ,i})_i) = f(\varvec{x}= (x_{i})_i)\).
The security model is quite similar to the one defined for FE, but as noted in [16, 20], one has to consider corruptions, since the senders do not trust each other, and they can collude and give their secret keys to the adversary who will play on their behalf.
Definition 2
(IND-Security Game for MCFE). Let us consider an \(\textsf {MCFE}\) scheme over a set of n senders. No adversary \(\mathcal {A}\) should be able to win the following security game against a challenger \(\mathcal {C}\):
-
Initialization: the challenger \(\mathcal {C}\) runs the setup algorithm \({(\mathsf {mpk},\mathsf {msk},(\mathsf {ek}_i)_i)\leftarrow \mathsf {SetUp} (\lambda )}\) and chooses a random bit \(b{\mathop {\leftarrow }\limits ^{{}_\$}}\{0,1\}\). It provides \({\mathsf {mpk}}\) to the adversary \(\mathcal {A}\);
-
Encryption queries \(\mathsf {QEncrypt} (i, x^0, x^1,\ell )\): \(\mathcal {A}\) has unlimited and adaptive access to a Left-or-Right encryption oracle, and receives the ciphertext \(C_{\ell ,i}\) generated by \({\mathsf {Encrypt} (\mathsf {ek}_i, x^b,\ell )}\). We note that any further query for the same pair \((\ell ,i)\) will later be ignored;
-
Functional decryption key queries \(\mathsf {QDKeyGen} (f)\): \(\mathcal {A}\) has unlimited and adaptive access to the \({\mathsf {DKeyGen} (\mathsf {msk},f)}\) algorithm for any input function f of its choice. It is given back the functional decryption key \(\mathsf {dk}_f\);
-
Corruption queries \(\mathsf {QCorrupt} (i)\): \(\mathcal {A}\) can make an unlimited number of adaptive corruption queries on input index i, to get the encryption key \({\mathsf {ek}_i}\) of any sender i of its choice;
-
Finalize: \(\mathcal {A}\) provides its guess \(b'\) on the bit b, and this procedure outputs the result \(\beta \) of the security game, according to the analysis given below.
The output \(\beta \) of the game depends on some conditions, where \(\mathcal {CS}\) is the set of corrupted senders (the set of indexes i input to \(\mathsf {QCorrupt} \) during the whole game), and \(\mathcal {HS}\) the set of honest (non-corrupted) senders. We set the output to \(\beta \leftarrow b'\), unless one of the three cases below is true, in which case we set \(\beta {\mathop {\leftarrow }\limits ^{{}_\$}}\{0,1\}\):
-
1.
some \(\mathsf {QEncrypt} (i,x^0_i,x^1_i,\ell )\)-query has been asked for an index \(i\in \mathcal {CS}\) with \(x^0_i \ne x^1_i\);
-
2.
for some label \(\ell \), an encryption-query \(\mathsf {QEncrypt} (i,x^0_i,x^1_i,\ell )\) has been asked for some \(i\in \mathcal {HS}\), but encryption-queries \(\mathsf {QEncrypt} (j,x^0_j,x^1_j,\ell )\) have not all been asked for all \(j\in \mathcal {HS}\);
-
3.
for some label \(\ell \) and for some function f asked to \(\mathsf {QDKeyGen} \), there exists a pair of vectors \((\varvec{x}^0 = (x^0_i)_i,\varvec{x}^1 = (x^1_i)_i)\) such that \(f(\varvec{x}^0) \ne f(\varvec{x}^1)\), when
-
\(x^0_i = x^1_i\), for all \(i\in \mathcal {CS}\);
-
\(\mathsf {QEncrypt} (i,x^0_i,x^1_i,\ell )\)-queries have been asked for all \(i\in \mathcal {HS}\).
-
We say this \(\textsf {MCFE}\) is \(\texttt {IND} \)-secure if for any adversary \(\mathcal {A}\), \(\mathsf {Adv}^{\texttt {IND}}(\mathcal {A}) = |P[\beta = 1 | b = 1] - P[\beta = 1 | b = 0]|\) is negligible.
Informally, this is the usual Left-or-Right indistinguishability [7], but where the adversary should not be able to get ciphertexts or functional decryption keys that trivially help distinguish the encrypted vectors:
-
1.
since the encryption might be deterministic, if we allow Left-or-Right encryption queries even for corrupted encryption keys, these queries should be on identical messages: with the encryption key, the adversary could simply re-encrypt and compare in case of deterministic encryption;
-
2.
intuitively, if some input is missing, no function evaluation can be done by the adversary, so we enforce the adversary to ask \(\mathsf {QEncrypt} \)-queries for all the non-corrupted keys (since the adversary can generate any ciphertext itself for the corrupted components) as soon as one label is used;
-
3.
for any functional decryption key, all the possible evaluations should not trivially allow the adversary to distinguish the ciphertexts generated through \(\mathsf {QEncrypt} \)-queries (on honest components).
In all these cases, the guess of the adversary is not considered (a random bit \(\beta \) is output). Otherwise, this is a legitimate attack, and the guess \(b'\) of the adversary is output. We stress that we bar the adversary from querying several ciphertexts under the same pair \((\ell ,i)\). In real life, it is of course the responsibility of the senders not to encrypt under the same label twice (as explained in the introduction, the labels are typically time-stamps, only used once).
Remark 3
While the third constraint aims at preventing the adversary from trivially winning by guessing the bit b from the evaluation of a functional decryption, the two first might look artificial, but they are required for our proof to go through with our constructions:
-
with a probabilistic encryption scheme, one could hope to remove the first one, but up to now, we only have deterministic constructions, which is quite classical in the private-key setting (such as symmetric encryption);
-
depending on the scheme, an encryption on an “inactive” component (a component that has no impact on the value of a function f, for instance the ith ciphertext in the case of \(f_{\varvec{y}}:\varvec{x}\rightarrow \langle \varvec{x}, \varvec{y} \rangle \) when \(y_i = 0\)) might not be needed for a complete evaluation, as is the case in our schemes (see Sect. 4). Moreover, our keys are homomorphic: from \(\mathsf {dk}_{f_{\varvec{y}}}\) and \(\mathsf {dk}_{f_{\varvec{y}'}}\), one can easily obtain \(\mathsf {dk}_{f_{\varvec{y}+\varvec{y}'}}\). Rather than defining the inactivity of components of functions in the span of those queried, we simply require that ciphertexts be obtained for every component for a given label (either through an explicit query to \(\mathsf {QEncrypt} \) or thanks to the encryption key obtained from \(\mathsf {QCorrupt} \)), which is consistent with the use-case we outlined in Sect. 1.1. One could also enforce, by construction, all the queries to be asked and otherwise guarantee that no information is leaked about the plaintexts, which is not the case of our schemes.
Weaker Notions. One may define weaker variants of indistinguishability, where some queries can only be sent before the initialization phase:
-
Selective Security (
 ): the encryption queries (\(\mathsf {QEncrypt} \)) are sent before the initialization;
): the encryption queries (\(\mathsf {QEncrypt} \)) are sent before the initialization; -
Static Security (
 ): the corruption queries (\(\mathsf {QCorrupt} \)) are sent before the initialization.
): the corruption queries (\(\mathsf {QCorrupt} \)) are sent before the initialization.
2.2 Decentralized Multi-Client Functional Encryption
In \(\textsf {MCFE}\), an authority owns a master secret key \({\mathsf {msk}}\) to generate the functional decryption keys. We would like to avoid such a powerful authority, and make the scheme totally decentralized among the owners of the data (the senders). We thus define \(\textsf {DMCFE}\), for Decentralized Multi-Client Functional Encryption. In this context, there are n senders \((\mathcal {S}_i)_{i}\), for \(i=1,\ldots ,n\), who will play the role of both the encrypting players and the functional decryption key generators, for a functional decryptor \(\mathcal {FD}\). Of course, the senders do not trust each other and they want to control the functional decryption keys that will be generated. There may be several functional decryptors, but since they could collude and combine all the functional decryption keys, in the description below, and in the security model, we will consider only one functional decryptor \(\mathcal {FD}\). As already noticed, we could simply use the definition of \(\textsf {MCFE}\) [16, 20], where the setup and the functional decryption key algorithms are replaced by MPC protocols among the clients. But this could lead to a quite interactive process. We thus focus on efficient one-round key generation protocols \(\mathsf {DKeyGen} \) that can be split in a first step \(\mathsf {DKeyGenShare} \) that generates partial keys and the combining algorithm \(\mathsf {DKeyComb} \) that combines partial keys into the functional decryption key.
Definition 4
(Decentralized Multi-Client Functional Encryption). A decentralized multi-client functional encryption on \(\mathcal {M}\) between a set of n senders \((\mathcal {S}_i)_{i}\), for \(i=1,\ldots ,n\), and a functional decrypter \(\mathcal {FD}\) is defined by the setup protocol and four algorithms:
-
\(\mathsf {SetUp} (\lambda )\): This is a protocol between the senders \((\mathcal {S}_i)_i\) that eventually generate their own secret keys \({\mathsf {sk}_i}\) and encryption keys \({\mathsf {ek}_i}\), as well as the public parameters \({\mathsf {mpk}}\);
-
\({\mathsf {Encrypt} (\mathsf {ek}_i, x_i,\ell )}\): Takes as input a user encryption key \({\mathsf {ek}_i}\), a value \(x_i\) to encrypt, and a label \(\ell \), and outputs the ciphertext \(C_{\ell ,i}\);
-
\({\mathsf {DKeyGenShare} (\mathsf {sk}_i,\ell _f)}\): Takes as input a user secret key \({\mathsf {sk}_i}\) and a label \(\ell _f\), and outputs the partial functional decryption key \(\mathsf {dk}_{f,i}\) for a function \(f:\mathcal {M}^n\rightarrow \mathcal {R}\) that is described in \(\ell _f\);
-
\(\mathsf {DKeyComb} ((\mathsf {dk}_{f,i})_i,\ell _f)\): Takes as input the partial functional decryption keys and eventually outputs the functional decryption key \(\mathsf {dk}_f\);
-
\(\mathsf {Decrypt} (\mathsf {dk}_f, \ell , \varvec{C})\): Takes as input a functional decryption key \(\mathsf {dk}_f\), a label \(\ell \), and an n-vector ciphertext \(\varvec{C}\), and outputs \(f(\varvec{x})\), if \(\varvec{C}\) is a valid encryption of \(\varvec{x}= (x_i)_i\in \mathcal {M}^n\) for the label \(\ell \), or \(\perp \) otherwise;
We make the assumption that \({\mathsf {mpk}}\) is included in all the secret and encryption keys, as well as the (partial) functional decryption keys. Similarly, the function f might be included in the (partial) functional decryption keys. The correctness property states that, given \({(\mathsf {mpk},(\mathsf {sk}_i)_i,(\mathsf {ek}_i)_i)\leftarrow \mathsf {SetUp} (\lambda )}\), for any label \(\ell \), any function \(f:\mathcal {M}^n\rightarrow \mathcal {R}\), and any vector \(\varvec{x}= (x_{i})_i\in \mathcal {M}^n\), if \({C_{\ell ,i}\leftarrow \mathsf {Encrypt} (\mathsf {ek}_i, x_{i},\ell )}\), for \(i \in \{1,\ldots ,n\}\), and \(\mathsf {dk}_f\leftarrow \mathsf {DKeyComb} ((\mathsf {DKeyGenShare} (\mathsf {sk}_i,\ell _f))_i,\ell _f)\), then we have \(\mathsf {Decrypt} (\mathsf {dk}_f, \ell , \varvec{C}_\ell = (C_{\ell ,i})_i) = f(\varvec{x}= (x_{i})_i)\).
The security model is quite similar to the one defined above for \(\textsf {MCFE}\), except that for the \(\mathsf {DKeyGen} \) protocol, the adversary has access to transcripts of the communications and can make some senders play maliciously. Corrupt-queries additionally reveal the secret keys \({\mathsf {sk}_i}\).
Definition 5
(IND-Security Game for DMCFE ). Let us consider a \(\textsf {DMCFE}\) scheme between a set of n senders. No adversary \(\mathcal {A}\) should be able to win the following security game against a challenger \(\mathcal {C}\):
-
Initialization: the challenger \(\mathcal {C}\) runs the setup protocol \({(\mathsf {mpk},(\mathsf {sk}_i)_i,(\mathsf {ek}_i)_i)\leftarrow \mathsf {SetUp} (\lambda )}\) and chooses a random bit \(b{\mathop {\leftarrow }\limits ^{{}_\$}}\{0,1\}\). It provides \({\mathsf {mpk}}\) to the adversary \(\mathcal {A}\);
-
Encryption queries \(\mathsf {QEncrypt} (i, x^0, x^1,\ell )\): \(\mathcal {A}\) has unlimited and adaptive access to a Left-or-Right encryption oracle, and receives the ciphertext \(C_{\ell ,i}\) generated by \({\mathsf {Encrypt} (\mathsf {ek}_i, x^b,\ell )}\). We note that any further query for the same pair \((\ell ,i)\) will later be ignored;
-
Functional decryption key queries \(\mathsf {QDKeyGen} (i,f)\): \(\mathcal {A}\) has unlimited and adaptive access to the (non-corrupted) senders running the \({\mathsf {DKeyGenShare} (\mathsf {sk}_i,f)}\) algorithm for any input function f of its choice. It is given back the partial functional decryption key \(\mathsf {dk}_{f,i}\);
-
Corruptions queries \(\mathsf {QCorrupt} (i)\): \(\mathcal {A}\) can make an unlimited number of adaptive corruption queries on input index i, to get the secret and encryption keys \({(\mathsf {sk}_i,\mathsf {ek}_i)}\) of any sender i of its choice.
-
Finalize: \(\mathcal {A}\) provides its guess \(b'\) on the bit b, and this procedure outputs the result \(\beta \) of the security game, according to the analysis given below.
The output \(\beta \) of the game depends on some conditions, where \(\mathcal {CS}\) is the set of corrupted senders (the set of indexes i input to \(\mathsf {QCorrupt} \) during the whole game), and \(\mathcal {HS}\) the set of honest (non-corrupted) senders. We set the output to \(\beta \leftarrow b'\), unless one of the three cases below is true, in which case we set \(\beta {\mathop {\leftarrow }\limits ^{{}_\$}}\{0,1\}\):
-
1.
some \(\mathsf {QEncrypt} (i,x^0_i,x^1_i,\ell )\)-query has been asked for an index \(i\in \mathcal {CS}\) with \(x^0_i \ne x^1_i\);
-
2.
for some label \(\ell \), an encryption-query \(\mathsf {QEncrypt} (i,x^0_i,x^1_i,\ell )\) has been asked for some \(i\in \mathcal {HS}\), but encryption-queries \(\mathsf {QEncrypt} (j,x^0_j,x^1_j,\ell )\) have not all been asked for all \(j\in \mathcal {HS}\);
-
3.
for some label \(\ell \) and for some function f asked to \(\mathsf {QDKeyGen} \) for all \(i\in \mathcal {HS}\), there exists a pair of vectors \((\varvec{x}^0 = (x^0_i)_i,\varvec{x}^1 = (x^1_i)_i)\) such that \(f(\varvec{x}^0) \ne f(\varvec{x}^1)\), when
-
\(x^0_i = x^1_i\), for all \(i\in \mathcal {CS}\);
-
\(\mathsf {QEncrypt} (i,x^0_i,x^1_i,\ell )\)-queries have been asked for all \(i\in \mathcal {HS}\).
-
We say this \(\textsf {DMCFE}\) is \(\texttt {IND} \)-secure if for any adversary \(\mathcal {A}\), \(\mathsf {Adv}^{\texttt {IND}}(\mathcal {A}) = |P[\beta = 1 | b = 1] - P[\beta = 1 | b = 0]|\) is negligible.
We define  (selective) and
(selective) and  (static) security for \(\textsf {DMCFE}\) as we did for \(\textsf {MCFE}\).
(static) security for \(\textsf {DMCFE}\) as we did for \(\textsf {MCFE}\).
3 Notations and Assumptions
3.1 Groups
Prime Order Group. We use a prime-order group generator \(\mathsf {GGen}\), a probabilistic polynomial time (PPT) algorithm that on input the security parameter \(1^\lambda \) returns a description \(\mathcal {G}=(\mathbb {G},p,P)\) of an additive cyclic group \(\mathbb {G}\) of order p for a \(2\lambda \)-bit prime p, whose generator is P.
We use implicit representation of group elements as introduced in [14]. For \(a \in \mathbb {Z}_p\), define \([a] = a P \in \mathbb {G}\) as the implicit representation of a in \(\mathbb {G}\). More generally, for a matrix \(\mathbf {A} = (a_{ij}) \in \mathbb {Z}_p^{n\times m}\) we define \([\mathbf {A}]\) as the implicit representation of \(\mathbf {A}\) in \(\mathbb {G}\):
We will always use this implicit notation of elements in \(\mathbb {G}\), i.e., we let \([a] \in \mathbb {G}\) be an element in \(\mathbb {G}\). Note that from a random \([a] \in \mathbb {G}\) it is generally hard to compute the value a (discrete logarithm problem in \(\mathbb {G}\)). Obviously, given \([a],[b] \in \mathbb {G}\) and a scalar \(x \in \mathbb {Z}_p\), one can efficiently compute \([ax] \in \mathbb {G}\) and \([a+b] = [a]+[b] \in \mathbb {G}\).
Pairing Group. We also use a pairing group generator \(\mathsf {PGGen}\), a PPT algorithm that on input \(1^\lambda \) returns a description \(\mathcal {PG}=(\mathbb {G}_1,\mathbb {G}_2,p,P_1,P_2,e)\) of asymmetric pairing groups where \(\mathbb {G}_1\), \(\mathbb {G}_2\), \(\mathbb {G}_T\) are additive cyclic groups of order p for a \(2 \lambda \)-bit prime p, \(P_1\) and \(P_2\) are generators of \(\mathbb {G}_1\) and \(\mathbb {G}_2\), respectively, and \(e: \mathbb {G}_1 \times \mathbb {G}_2 \rightarrow \mathbb {G}_T\) is an efficiently computable (non-degenerate) bilinear map. Define \(P_T := e(P_1, P_2)\), which is a generator of \(\mathbb {G}_T\). We again use implicit representation of group elements. For \(s \in \{1, 2, T\}\) and \(a \in \mathbb {Z}_p\), define \([a]_s = a P_s \in \mathbb {G}_s\) as the implicit representation of a in \(G_s\). Given \([a]_1\), \([a]_2\), one can efficiently compute \([ab]_T\) using the pairing e. For two matrices \(\mathbf {A}\), \(\mathbf {B}\) with matching dimensions define \(e([\mathbf {A}]_1, [\mathbf {B}]_2 ) := [\mathbf {A} \mathbf {B}]_T \in \mathbb {G}_T\).
Compatibility. Our construction from Sect. 4 uses a prime-order group, while the one from Sect. 5 uses pairing groups. Since the latter use the former as a building block, we must use groups that are compatible with each other. Notice that one can generate a prime-order group either with \(\mathcal {G}:=(\mathbb {G},p,P) {\mathop {\leftarrow }\limits ^{{}_\$}}\mathsf {GGen}(1^\lambda )\), but also using \(\mathcal {PG}:=(\mathbb {G}_1,\mathbb {G}_2,p,P_1,P_2,e) {\mathop {\leftarrow }\limits ^{{}_\$}}\mathsf {PGGen}(1^\lambda )\), and setting \(\mathbb {G}:= \mathbb {G}_1\). This is possible here because we use asymmetric pairings and rely on the \(\textsf {SXDH}\) assumption in the pairing group, which is \(\textsf {DDH}\) in \(\mathbb {G}_1\) and \(\mathbb {G}_2\). More details on computational assumptions follow.
3.2 Computational Assumptions
Definition 6
(Decisional Diffie-Hellman Assumption). The Decisional Diffie-Hellman Assumption states that, in a prime-order group \(\mathcal {G}{\mathop {\leftarrow }\limits ^{{}_\$}}\mathsf {GGen}(1^\lambda )\), no PPT adversary can distinguish between the two following distributions with non-negligible advantage:

Equivalently, this assumption states it is hard to distinguish, knowing [a], a random element from the span of \([\varvec{a}]\) for  , from a random element in \(\mathbb {G}^2\):
, from a random element in \(\mathbb {G}^2\):  .
.
Definition 7
(Symmetric eXternal Diffie-Hellman Assumption). The Symmetric eXternal Diffie-Hellman (\(\textsf {SXDH}\)) Assumption states that, in a pairing group \(\mathcal {PG}{\mathop {\leftarrow }\limits ^{{}_\$}}\mathsf {PGGen}(1^\lambda )\), the \(\textsf {DDH}\) assumption holds in both \(\mathbb {G}_1\) and \(\mathbb {G}_2\).
4 A Fully-Secure MCFE for Inner Product
After the first construction drafted in the introduction, from the Abdalla et al. [1] selectively-secure FE, we propose another construction of \(\textsf {MCFE} \) for inner product adapted from the Agrawal et al. [4] scheme. We also provide the full security analysis under the \(\textsf {DDH}\) assumption, since the security proof of our \(\textsf {DMCFE}\) construction will rely on it.
Overview of the Construction. This construction is an extension of the previous one proposed in the introduction: we first extended the scheme from Abdalla et al. [1] in the multi-client setting with a hash function. Because of the selective security of the underlying scheme, our first proposal was just selectively secure too. We now adapt the Agrawal et al. [4] scheme, in the same manner. This construction and its proof of adaptive security are for the sake of clarity, since the proof of our next \(\textsf {DMCFE}\) will be made clearer when reducing to this one.
4.1 Description
We use a prime-order group, and the bracket notation, as defined in Sect. 3.1.
-
\(\mathsf {SetUp} (\lambda )\): Takes as input the security parameter, and generates prime-order group \(\mathcal {G}:=(\mathbb {G},p,P) {\mathop {\leftarrow }\limits ^{{}_\$}}\mathsf {GGen}(1^\lambda )\), and \(\mathcal {H}\) a full-domain hash function onto \(\mathbb {G}^2\). It also generates the encryption keys \(\varvec{s}_i{\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}^2_p\), for \(i=1,\ldots ,n\). The public parameters \({\mathsf {mpk}}\) consist of \((\mathbb {G},p,g,\mathcal {H})\), while the encryption keys are \({\mathsf {ek}_i = \varvec{s}_i}\) for \(i=1,\ldots ,n\), and the master secret key is \({\mathsf {msk}= ((\mathsf {ek}_i)_i)}\), (in addition to \({\mathsf {mpk}}\), which is omitted);
-
\({\mathsf {Encrypt} (\mathsf {ek}_i,x_i,\ell )}\): Takes as input the value \(x_i\) to encrypt, under the key \({\mathsf {ek}_i = \varvec{s}_i}\) and the label \(\ell \). It computes \([\varvec{u}_\ell ] := \mathcal {H}(\ell ) \in \mathbb {G}^2\), and outputs the ciphertext \([c_i] = [\varvec{u}_\ell ^\top \varvec{s}_i +x_i] \in \mathbb {G}\);
-
\({\mathsf {DKeyGen} (\mathsf {msk}, \varvec{y})}\): Takes as input \({\mathsf {msk}= (\varvec{s}_i)_i}\) and an inner-product function defined by \(\varvec{y}\) as \(f_{\varvec{y}}(\varvec{x}) = \langle \varvec{x}, \varvec{y} \rangle \), and outputs the functional decryption key \(\mathsf {dk}_{\varvec{y}} = \left( \varvec{y},\sum _{i} \varvec{s}_i \cdot y_i \right) \in \mathbb {Z}_p^n \times \mathbb {Z}_p^2\);
-
\(\mathsf {Decrypt} (\mathsf {dk}_{\varvec{y}}, \ell , ([c_i])_{i \in [n]})\): Takes as input a functional decryption key \(\mathsf {dk}_{\varvec{y}} = (\varvec{y},\varvec{d})\), a label \(\ell \), and ciphertexts. It computes \([\varvec{u}_\ell ] := \mathcal {H}(\ell )\), \([\alpha ] = \sum _i [c_i] \cdot y_i - [\varvec{u}^\top _\ell ] \cdot \varvec{d}\), and eventually solves the discrete logarithm to extract and return \(\alpha \).
Note that, as for [4], the result \(\alpha \) must be polynomially bounded to efficiently compute the discrete logarithm in the last decryption step: let \(\varvec{x}, \varvec{y}\in \mathbb {Z}_p^n\), we have:
4.2 Security Analysis
Theorem 8
(IND -Security). The above \(\textsf {MCFE}\) protocol (see Sect. 4.1) is IND-secure under the \(\textsf {DDH}\) assumption, in the random oracle model. More precisely, we have
for any adversary \(\mathcal {A}\), running within time t, where Q is the number of (direct and indirect—asked by \(\mathsf {QEncrypt} \)-queries—) queries to \(\mathcal {H}\) (modeled as a random oracle), and \(t_\mathbb {G}\) is the time for an exponentiation in \(\mathbb {G}\).
We stress that this Theorem supports both adaptive encryption queries and adaptive corruptions.
Proof Technique. To obtain adaptive security, we use a technique that consists of first proving perfect security in the selective variant of the involved games, then, using a guessing (a.k.a. complexity leveraging) argument, which incurs an exponential security loss, we obtain the same security guarantees in the adaptive games. Since the security in the selective game is perfect (the advantage of any adversary is exactly zero), the exponential security loss is multiplied by a zero term, and the overall adaptive security is preserved. This technique has been used before in [31] in the context of Attribute-Based Encryption, or more recently, in [2, 3] in the context of multi-input IP-FE. We defer to [31, Remark 1] and [3, Remark 5] for more details on this proof technique.
Games for the proof of Theorem 8. Here, \(\mathsf {RF}\), \(\mathsf {RF}'\), \(\mathsf {RF}''\) are random functions onto \(\mathbb {G}^2\), \(\mathbb {Z}_p\), and \(\mathbb {Z}_p^*\), respectively, that are computed on the fly. In each procedure, the components inside a solid (dotted, gray) frame are only present in the games marked by a solid (dotted, gray) frame. The Finalize procedure is defined as in Definition 2.
Proof
We proceed using hybrid games, described in Fig. 3. Let \(\mathcal {A}\) be a PPT adversary. For any game \(G_{\mathsf {index}}\), we denote by \(\mathsf {Adv}_{\mathsf {index}} := |\Pr [G_{\mathsf {index}}(\mathcal {A})|b=1]-\Pr [G_{\mathsf {index}}(\mathcal {A})|b=0]|\), where the probability is taken over the random coins of \(G_{\mathsf {index}}\) and \(\mathcal {A}\). Also, by event \(G_{\mathsf {index}}(\mathcal {A})\), or just \(G_{\mathsf {index}}\) when there is no ambiguity, we mean that the Finalize procedure in game \(G_{\mathsf {index}}\) (defined as in Definition 2) returns \(\beta = 1\) from the adversary’s answer \(b'\) when interacting with \(\mathcal {A}\).
-
Game \(G_0\): This is the IND-security game as given in Definition 2. Note that the hash function \(\mathcal {H}\) is modeled as a random oracle \(\mathsf {RO}\) onto \(\mathbb {G}^2\). This is essentially used to generate \([\varvec{u}_\ell ] = \mathcal {H}(\ell )\).
-
Game \(G_1\): We simulate the answers to any new \(\mathsf {RO}\)-query by a truly random pair in \(\mathbb {G}^2\), on the fly. The simulation remains perfect, and so \(\mathsf {Adv}_0 = \mathsf {Adv}_1\).
-
Game \(G_2\): We simulate the answers to any new \(\mathsf {RO}\)-query by a truly random pair in the span of \([\varvec{a}]\) for
 , with \(a {\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}_p\). This uses the Multi-\(\textsf {DDH}\) assumption, which tightly reduces to the \(\textsf {DDH}\) assumption using the random-self reducibility (see Lemma 10, in Appendix A): \(\mathsf {Adv}_1 - \mathsf {Adv}_2 \le \mathsf {Adv}_\mathbb {G}^\textsf {ddh} (t + 4 Q\times t_\mathbb {G})\), where Q is the number of \(\mathsf {RO}\)-queries and \(t_\mathbb {G}\) the time for an exponentiation.
, with \(a {\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}_p\). This uses the Multi-\(\textsf {DDH}\) assumption, which tightly reduces to the \(\textsf {DDH}\) assumption using the random-self reducibility (see Lemma 10, in Appendix A): \(\mathsf {Adv}_1 - \mathsf {Adv}_2 \le \mathsf {Adv}_\mathbb {G}^\textsf {ddh} (t + 4 Q\times t_\mathbb {G})\), where Q is the number of \(\mathsf {RO}\)-queries and \(t_\mathbb {G}\) the time for an exponentiation. -
Game \(G_3\): We simulate any \(\mathsf {QEncrypt} \) query as the encryption of \(x_i^0\) instead of \(x_i^b\) and go back for the answers to any new \(\mathsf {RO}\) query by a truly random pair in \(\mathbb {G}^2\).
While it is clear that in this last game the advantage of any adversary is exactly 0 since b does not appear anywhere, the gap between \(G_2\) and \(G_3\) will be proven using a hybrid technique on the \(\mathsf {RO}\)-queries. We thus index the following games by q, where \(q=1,\ldots , Q\). Note that only distinct \(\mathsf {RO}\)-queries are counted, since a second similar query is answered as the first one. We detail this proof because the technique is important.
Games \(G^\star _{3.q.2}\) and \(G^\star _{3.q.3}\), with \(q \in [Q]\), for the proof of Theorem 8. Here, \(\mathsf {RF}\), \(\mathsf {RF}'\) are random functions onto \(\mathbb {G}^2\), and \(\mathbb {Z}_p\), respectively, that are computed on the fly. In each procedure, the components inside a solid (gray) frame are only present in the games marked by a solid (gray) frame.
-
\(G_{3.1.1}\): This is exactly game \(G_2\). Thus, \(\mathsf {Adv}_2= \mathsf {Adv}_{3.1.1}\).
-
\(G_{3.q.1} \rightsquigarrow G_{3.q.2}\): We first change the distribution of the output of the q-th \(\mathsf {RO}\)-query, from uniformly random in the span of \([\varvec{a}]\) to uniformly random over \(\mathbb {G}^2\), using the DDH assumption. Then, we use the basis
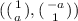 of \(\mathbb {Z}_p^2\), to write a uniformly random vector over \(\mathbb {Z}_p^2\) as \(u_1 \cdot \varvec{a} + u_2 \cdot \varvec{a}^{\bot }\), where \(u_1, u_2 {\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}_p\). Finally, we switch to \(u_1 \cdot \varvec{a} + u_2 \cdot \varvec{a}^{\bot }\) where \(u_1 {\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}_p\), and \(u_2 {\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}_p^*\), which only changes the adversary view by a statistical distance of \(1{\slash }p\): \(\mathsf {Adv}_{3.q.1} - \mathsf {Adv}_{3.q.2} \le \mathsf {Adv}_\mathbb {G}^\textsf {ddh} (t) + 1/p\). The last step with \(u_2 \in \mathbb {Z}_p^*\) will be important to guarantee that \(\varvec{u}_\ell ^\top \varvec{a}^{\bot }\ne 0\).
of \(\mathbb {Z}_p^2\), to write a uniformly random vector over \(\mathbb {Z}_p^2\) as \(u_1 \cdot \varvec{a} + u_2 \cdot \varvec{a}^{\bot }\), where \(u_1, u_2 {\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}_p\). Finally, we switch to \(u_1 \cdot \varvec{a} + u_2 \cdot \varvec{a}^{\bot }\) where \(u_1 {\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}_p\), and \(u_2 {\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}_p^*\), which only changes the adversary view by a statistical distance of \(1{\slash }p\): \(\mathsf {Adv}_{3.q.1} - \mathsf {Adv}_{3.q.2} \le \mathsf {Adv}_\mathbb {G}^\textsf {ddh} (t) + 1/p\). The last step with \(u_2 \in \mathbb {Z}_p^*\) will be important to guarantee that \(\varvec{u}_\ell ^\top \varvec{a}^{\bot }\ne 0\). -
\(G_{3.q.2} \rightsquigarrow G_{3.q.3}\): We now change the generation of the ciphertext \([c_i] := [\varvec{u}_\ell ^\top ] \cdot \varvec{s}_i + [x^b_i]\) by \([c_i] := [\varvec{u}_\ell ^\top ] \cdot \varvec{s}_i + [x^0_i]\), where \([\varvec{u}_\ell ]\) corresponds to the q-th \(\mathsf {RO}\)-query. We then prove this does not change the adversary’s view.
Note that if the output of the q-th \(\mathsf {RO}\)-query is not used by \(\mathsf {QEncrypt} \)-queries, then the games \(G_{3.q.2}\) and \(G_{3.q.3}\) are identical. But we can show this is true too when there are \(\mathsf {RO}\)-queries that are really involved in \(\mathsf {QEncrypt} \)-queries, and show that \(\mathsf {Adv}_{3.q.2} = \mathsf {Adv}_{3.q.3}\) in that case too, in two steps. In Step 1, we show that there exists a PPT adversary \(\mathcal {B}^\star \) such that \(\mathsf {Adv}_{3.q.t} = (p^2+1)^n \cdot \mathsf {Adv}^\star _{3.q.t}(\mathcal {B}^\star )\), for \(t=2,3\), where the games \(G^\star _{3.q.2}\) and \(G^\star _{3.q.3}\) are selective variants of games \(G_{3.q.2}\) and \(G_{3.q.3}\) respectively (see Fig. 4), where \(\mathsf {QCorrupt} \) queries are asked before the initialization phase. In Step 2, we show that for all PPT adversaries \(\mathcal {B}^\star \), we have \(\mathsf {Adv}^\star _{3.q.2}(\mathcal {B}^\star ) = \mathsf {Adv}^\star _{3.q.3}(\mathcal {B}^\star )\). This will conclude the two steps.
Step 1. We build a PPT adversary \(\mathcal {B}^\star \) playing against \(G^\star _{3.q.t}\) for \(t=2,3\), such that \(\mathsf {Adv}_{3.q.t} = (p^2+1)^n \cdot \mathsf {Adv}^\star _{3.q.t}(\mathcal {B}^\star )\).
Adversary \(\mathcal {B}^\star \) first guesses for all \(i \in [n]\), \(z_i {\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}_p^2\cup \{\bot \}\), which it sends to its selective game \(G^\star _{3.q.t}\). That is, each guess \(z_i\) is either a pair of values \((x_i^{0},x_i^{1})\) queried to \(\mathsf {QEncrypt} \), or \(\bot \), which means no query to \(\mathsf {QEncrypt} \). Then, it simulates \(\mathcal {A}\)’s view using its own oracles. When \(\mathcal {B}^\star \) guesses successfully (call E that event), it simulates \(\mathcal {A}\)’s view exactly as in \(G_{3.q.t}\). If the guess was not successful, then \(\mathcal {B}^\star \) stops the simulation and outputs a random bit \(\beta \). Since event E happens with probability \((p^2+1)^{-n}\) and is independent of the view of adversary \(\mathcal {A}\): \(\mathsf {Adv}^{\star }_{3.q.t}(\mathcal {B}^\star )\) is equal to
$$\begin{aligned}&\Big |\Pr [G^\star _{3.q.t}|b=0,E] \cdot \Pr [E] + \frac{\Pr [\lnot E]}{2} - \Pr [G^\star _{3.q.t}|b=1,E] \cdot \Pr [E] - \frac{\Pr [\lnot E]}{2}\Big |\\&=\Pr [E] \cdot |\Pr [G^\star _{3.q.t}|b=0,E]- \Pr [G^\star _{3.q.t}|b=1,E]| =(p^2+1)^{-n} \cdot \mathsf {Adv}_{3.q.t}. \end{aligned}$$Step 2. We assume the values \((z_i)_{i \in [n]}\) sent by \(\mathcal {B}^\star \) are consistent, that is, they don’t make the game end and return a random bit, and Finalize on \(b'\) does not return a random bit independent of \(b'\) (call \(E'\) this event).
We show that games \(G^\star _{3.q.2}\) and \(G^\star _{3.q.3}\) are identically distributed, conditioned on \(E'\). To prove it, we use the fact that the two following distributions are identical, for any choice of \(\gamma \):
$$\left( \varvec{s}_{i}\right) _{i \in [n], z_i = (x_i^{0},x_i^{1})} \text{ and } \left( \varvec{s}_{i} + \varvec{a}^{\bot }\cdot \gamma (x_i^{b} - x_i^{0})\right) _{i \in [n], z_i = (x_i^{0},x_i^{1})},$$where
 and \(\varvec{s}_{i} {\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}_p^2\), for all \(i=1,\ldots ,n\). This is true since the \(\varvec{s}_{i}\) are independent of the \(z_i\) (note that this is true because we are in a selective setting, while this would not necessarily be true with adaptive \(\mathsf {QEncrypt} \)-queries). Thus, we can re-write \(\varvec{s}_{i}\) into \(\varvec{s}_{i} + \varvec{a}^{\bot }\cdot \gamma (x_i^{b} - x_i^{0})\) without changing the distribution of the game.
and \(\varvec{s}_{i} {\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}_p^2\), for all \(i=1,\ldots ,n\). This is true since the \(\varvec{s}_{i}\) are independent of the \(z_i\) (note that this is true because we are in a selective setting, while this would not necessarily be true with adaptive \(\mathsf {QEncrypt} \)-queries). Thus, we can re-write \(\varvec{s}_{i}\) into \(\varvec{s}_{i} + \varvec{a}^{\bot }\cdot \gamma (x_i^{b} - x_i^{0})\) without changing the distribution of the game.We now take a look at where the extra terms \(\varvec{a}^{\bot }\cdot \gamma (x_i^{b} - x_i^{0})\) actually appear in the adversary’s view:
-
They do not appear in the output of \(\mathsf {QCorrupt} \), because we assume event \(E'\) holds, which implies that if \(z_i \ne \bot \), then i is not queried to \(\mathsf {QCorrupt} \) or \(x_i^{1} = x_i^{0}\).
-
They might appear in \(\mathsf {QDKeyGen} (\varvec{y})\) as

But the gray term equals \(\mathbf {0}\) by the constraints for \(E'\) in Definition 2: for all \(i\in \mathcal {HS}\), \(z_i \ne \bot \); if \(i\in \mathcal {CS}\) and \(z_i \ne \bot \), \(x_i^{1} = x_i^{0}\); and \(f(\varvec{x}^0) = f(\varvec{x}^1)\), hence \(\sum _{i: z_i = (x_i^{0},x_i^{1})} y_i (x_i^{b} - x_i^{0})=0\).
-
Eventually, they appear in the output of the \(\mathsf {QEncrypt} \)-queries which use \([\varvec{u}_\ell ]\) computed on the q-th \(\mathsf {RO}\)-query, since for all others, the vector \([\varvec{u}_\ell ]\) lies in the span of \([\varvec{a}]\), and \(\varvec{a}^\top \varvec{a}^{\bot }=0\). We thus have \([c_i] := [\varvec{u}_\ell ^\top ] \cdot \varvec{s}_{i} + (x_i^{b} - x_i^{0}) \gamma [\varvec{u}_\ell ^\top ] \varvec{a}^{\bot }+ [x_i^{b}]\). Since \(\varvec{u}_\ell ^\top \varvec{a}^{\bot }\ne 0\), we can choose \(\gamma = -1/\varvec{u}_\ell ^\top \varvec{a}^{\bot }\bmod p\), and then \([c_i] = [\varvec{u}_\ell ^\top ] \cdot \varvec{s}_i + [x_i^{0}]\), which is the encryption of \(x_i^0\). We stress that \(\gamma \) is independent of the index i, and so this simultaneously converts all the encryptions of \(x_i^b\) into encryptions of \(x_i^0\). Finally, reverting these statistically perfect changes, we obtain that \([c_i]\) is identically distributed to \([\varvec{u}_\ell ^\top ] \cdot \varvec{s}_{i} + [x_i^{0}]\), as in game \(G^\star _{3.q.3}\).
Thus, when event \(E'\) happens, the games are identically distributed. When \(\lnot E\) happens, the games both return \(\beta {\mathop {\leftarrow }\limits ^{{}_\$}}\{0,1\}\): \(\mathsf {Adv}^\star _{3.q.2}(\mathcal {B}^\star )=\mathsf {Adv}^\star _{3.q.3}(\mathcal {B}^\star )\). As a conclusion, we get \(\mathsf {Adv}_{3.q.2} = \mathsf {Adv}_{3.q.3}\).
-
\(G_{3.q.3} \rightsquigarrow G_{3.q+1.1}\): This transition is the reverse of \(G_{3.q.1} \rightsquigarrow G_{3.q.2}\), namely, we use the \(\textsf {DDH}\) assumption to switch back the distribution of \([\varvec{u}_\ell ]\) computed on the q-th \(\mathsf {RO}\)-query from uniformly random over \(\mathbb {G}^2\) (conditioned on the fact that \(\varvec{u}_\ell ^\top \varvec{a}^{\bot }\ne 0\)) to uniformly random in the span of \([\varvec{a}]\): \(\mathsf {Adv}_{3.q.3} - \mathsf {Adv}_{3.q+1.1} \le \mathsf {Adv}_\mathbb {G}^\textsf {ddh} (t) + 1/p\).
As a conclusion, since \(G_{3.Q+1.1} = G_{3}\), we have \(\mathsf {Adv}_{2} - \mathsf {Adv}_{3} \le 2Q (\mathsf {Adv}_\mathbb {G}^\textsf {ddh} (t) + 1/p)\). In addition, \(\mathsf {Adv}_{3} = 0\), which concludes the proof.
5 A Statically-Secure DMCFE for Inner Product
Overview of the Scheme. Our construction of \(\textsf {MCFE}\) for inner product uses functional decryption keys \(\mathsf {dk}_{\varvec{y}} = (\varvec{y},\langle \varvec{s}, \varvec{y} \rangle ) = (\varvec{y},\varvec{d})\), where \(\varvec{d} = \langle \varvec{s}, \varvec{y} \rangle = \sum _i s_i y_i = \langle \varvec{t}, \varvec{1} \rangle \), with \(t_i = s_i y_i\), for \(i=1,\ldots ,n\), and \(\varvec{1}= (1,\ldots ,1)\). Hence, one can split \({\mathsf {msk}= \varvec{s}}\) into \({\mathsf {msk}_i = s_i}\), define \({T(\mathsf {msk}_i,\varvec{y}) = t_i = s_i y_i}\) and \(F(\varvec{t}) = \langle \varvec{t}, \varvec{1} \rangle \). We could thus wish to use the above generic construction from the introduction with our \(\textsf {MCFE}\) for inner product, that is self-enabling, to describe a \(\textsf {DMCFE}\) for inner product. However, this is not straightforward as our \(\textsf {MCFE}\) only allows small results for the function evaluations, since a discrete logarithm has to be computed. While, for real-life applications, it might be reasonable to assume the plaintexts and any evaluations on them are small enough, it is impossible to recover such a large scalar as \(\varvec{d} = \langle \varvec{s}, \varvec{y} \rangle \), which comes up when we use our scheme to encrypt encryption keys.
Nevertheless, following this idea we can overcome the concern above with pairings: One can only recover \([\varvec{d}]\), but using a pairing \(e:\mathbb {G}_1\times \mathbb {G}_2\rightarrow \mathbb {G}_T\), one can use our \(\textsf {MCFE}\) in both \(\mathbb {G}_1\) and \(\mathbb {G}_2\). This allows us to compute the functional decryption in \(\mathbb {G}_T\), to get \([{\langle \varvec{x}, \varvec{y} \rangle }]_T\), which is decryptable as \(\langle \varvec{x}, \varvec{y} \rangle \) is small enough.
5.1 Construction
Let us describe the new construction, using an asymmetric pairing group, as in Sect. 3.1.
-
\(\mathsf {SetUp} (\lambda )\): Generates \(\mathcal {PG}:=(\mathbb {G}_1,\mathbb {G}_2,p,P_1,P_2,e) {\mathop {\leftarrow }\limits ^{{}_\$}}\mathsf {PGGen}(1^\lambda )\). Samples two full-domain hash functions \(\mathcal {H}_1\) and \(\mathcal {H}_2\) onto \(\mathbb {G}^2_1\) and \(\mathbb {G}^2_2\) respectively. Each sender \(\mathcal {S}_i\) generates \(\varvec{s}_i {\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}^2_p\) for all \(i \in [n]\), and interactively generates \(\mathbf {T}_i {\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}_p^{2 \times 2}\) such that \(\sum _{i \in [n]} \mathbf {T}_i = \mathbf {0}\). One then sets \({\mathsf {mpk}\leftarrow (\mathcal {PG},\mathcal {H}_1,\mathcal {H}_2)}\), and for \(i=1,\ldots ,n\), \({\mathsf {ek}_i=\varvec{s}_i}\), \({\mathsf {sk}_i=(\varvec{s}_i,\mathbf {T}_i)}\);
-
\({\mathsf {Encrypt} (\mathsf {ek}_i,x_i,\ell )}\): Takes as input the value \(x_i\) to encrypt, under the key \({\mathsf {ek}_i = \varvec{s}_i}\) and the label \(\ell \). It computes \([\varvec{u}_\ell ]_1 := \mathcal {H}_1(\ell ) \in \mathbb {G}_1^2\), and outputs the ciphertext \([c_i]_1 = [\varvec{u}_\ell ^\top \varvec{s}_i +x_i]_1 \in \mathbb {G}_1\);
-
\({\mathsf {DKeyGenShare} (\mathsf {sk}_i,\varvec{y})}\): on input \(\varvec{y}\in \mathbb {Z}_p^n\) that defines the function \(f_{\varvec{y}}(\varvec{x}) = \langle \varvec{x}, \varvec{y} \rangle \), and the secret key \({\mathsf {sk}_i=(\varvec{s}_i,\mathbf {T}_i)}\), it computes \([\varvec{v}_{\varvec{y}}]_2 := \mathcal {H}_2(\varvec{y}) \in \mathbb {G}_2^2\), \([\varvec{d}_i]_2 := [y_i \cdot \varvec{s}_i + \mathbf {T}_i \varvec{v}_{\varvec{y}}]_2\), and returns the partial decryption key as \(\mathsf {dk}_{\varvec{y},i} := ([\varvec{d}_i]_2)\).
-
\(\mathsf {DKeyComb} ((\mathsf {dk}_{\varvec{y},i})_{i \in [n]}, \varvec{y})\): the partial decryption keys \(\left( \mathsf {dk}_{\varvec{y},i} = ([\varvec{d}_i]_2)\right) _{i \in [n]}\), lead to \(\mathsf {dk}_{\varvec{y}} := (\varvec{y}, [\varvec{d}]_2)\), where \([\varvec{d}]_2 = \sum _{i \in [n]} [\varvec{d}_i]_2\);
-
\(\mathsf {Decrypt} (\mathsf {dk}_{\varvec{y}}, \ell , ([c_i]_1)_{i \in [n]})\): on input the decryption key \(\mathsf {dk}_{\varvec{y}} = [\varvec{d}]_2\), the label \(\ell \), and ciphertexts \(([c_i]_1)_{i \in [n]}\), it computes \([\alpha ]_T := \sum _{i \in [n]} e([c_i]_1,[y_i]_2) - e([\varvec{u}_\ell ]_1^\top ,[\varvec{d}]_2)\), and eventually solve the discrete logarithm in basis \([1]_T\) to extract and return \(\alpha \).
Correctness: Let \(\varvec{x}, \varvec{y}\in \mathbb {Z}_p^n\), we have:
Thus:
5.2 Security Analysis
Theorem 9
(sta-IND -Security). The above \(\textsf {DMCFE}\) protocol (see Sect. 5.1) is sta-IND secure under the \(\textsf {SXDH}\) assumption, in the random oracle model. Namely, for any PTT adversary \(\mathcal {A}\), there exist PPT adversaries \(\mathcal {B}_1\) and \(\mathcal {B}_2\) such that:
where \(Q_1\) and \(Q_2\) are the number of (direct and indirect) queries to \(\mathcal {H}_1\) and \(\mathcal {H}_2\) respectively (modeled as random oracles). The former being asked by \(\mathsf {QEncrypt} \)-queries and the latter being asked by \(\mathsf {QDKeyGen} \)-queries.
We stress that this Theorem supports adaptive encryption queries, but static corruptions only.
Proof
We proceed using hybrid games, described in Fig. 5, with similar notations as in the previous proof.
-
Game \(G_0\): This is the sta-IND-security game as given in Definition 5, but with the set \(\mathcal {CS}\) of corrupted senders known from the beginning. Note that the hash functions \(\mathcal {H}_1\) and \(\mathcal {H}_2\) are modeled as random oracles. The former is used to generate \([\varvec{u}_\ell ]_1 := \mathcal {H}_1(\ell ) \in \mathbb {G}_1^2\) and the latter \([\varvec{v}_{\varvec{y}}]_2 := \mathcal {H}_2(\varvec{y}) \in \mathbb {G}_2^2\).
-
Game \(G_1\): We replace the hash function \(\mathcal {H}_2\) by a random oracle \(\mathsf {RO}_2\) that generates random pairs from \(\mathbb {G}_2^2\) on the fly. In addition, for any \(\mathsf {QDKeyGen} \)-query on a corrupted index \(i\in \mathcal {CS}\), one generates the partial functional decryption key by itself, without explicitly querying \(\mathsf {QDKeyGen} \). Hence, we can assume that \(\mathcal {A}\) does not query \(\mathsf {QCorrupt} \) and \(\mathsf {QDKeyGen} \) on the same indices \(i \in [n]\). The simulation remains perfect, and so \(\mathsf {Adv}_0 = \mathsf {Adv}_1\).
-
Game \(G_2\): Now, the outputs of \(\mathsf {RO}_2\) are uniformly random in the span of \([\varvec{b}]_2\) for
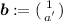 , with \(a' {\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}_p\). As in the previous proof, we have \(\mathsf {Adv}_1 - \mathsf {Adv}_2 \le \mathsf {Adv}_{\mathbb {G}_2}^\textsf {ddh} (t + 4 Q_2 \times t_{\mathbb {G}_2})\), where \(Q_2\) is the number of \(\mathsf {RO}_2\)-queries and \(t_{\mathbb {G}_2}\) the time for an exponentiation.
, with \(a' {\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}_p\). As in the previous proof, we have \(\mathsf {Adv}_1 - \mathsf {Adv}_2 \le \mathsf {Adv}_{\mathbb {G}_2}^\textsf {ddh} (t + 4 Q_2 \times t_{\mathbb {G}_2})\), where \(Q_2\) is the number of \(\mathsf {RO}_2\)-queries and \(t_{\mathbb {G}_2}\) the time for an exponentiation. -
Game \(G_3\): We replace all the partial key decryption answers by \(\mathsf {dk}_{\varvec{y},i} := [y_i \cdot \varvec{s}_i + \varvec{w}_i \cdot (\varvec{b}^{\bot })^\top \varvec{v}_{\varvec{y}} + \mathbf {T}_i \varvec{v}_{\varvec{y}}]_2\), for new \(\varvec{w}_i {\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}_p^2\), such that \(\sum _i \varvec{w}_i = \mathbf {0}\), for each \(\varvec{y}\). We show below that \(\mathsf {Adv}_2 = \mathsf {Adv}_3\).
-
Game \(G_4\): We switch back the distribution of all the vectors \([\varvec{v}_{\varvec{y}}]_2\) output by \(\mathsf {RO}_2\), from uniformly random in the span of \([\varvec{b}]_2\), to uniformly random over \(\mathbb {G}_2^2\), thus back to \(\mathcal {H}_2(\varvec{y})\). This transition is reverse to the two first transitions of this proof: \(\mathsf {Adv}_3 - \mathsf {Adv}_4 \le \mathsf {Adv}_{\mathbb {G}_2}^\textsf {ddh} (t + 4 Q_2 \times t_{\mathbb {G}_2})\).
In order to prove the gap between \(G_2\) and \(G_3\), we do a new hybrid proof:
Games for the proof of Theorem 9. Here, \(\mathsf {RF}\), \(\mathsf {RF}'\) are random functions onto \(\mathbb {G}_2^2\) and \(\mathbb {Z}_p\), respectively, that are computed on the fly. The \(\mathsf {RF}_i\) are random functions conditioned on the fact that \(\sum _{i \in [n]} \mathsf {RF}_i\) is the zero function. In each procedure, the components inside a solid (dotted, gray) frame are only present in the games marked by a solid (dotted, gray) frame. The Finalize procedure is defined as in Definition 5
-
Game \(G_{3.1.1}\): This is exactly game \(G_2\). Thus, \(\mathsf {Adv}_2= \mathsf {Adv}_{3.1.1}\).
-
\(G_{3.q.1} \rightsquigarrow G_{3.q.2}\): As in the previous proof, we first change the distribution of the output of the q-th \(\mathsf {RO}_2\)-query, from uniformly random in the span of \([\varvec{b}]\) to uniformly random over \(\mathbb {G}^2\), using the DDH assumption. Then, we use the basis
 of \(\mathbb {Z}_p^2\), to write a uniformly random vector over \(\mathbb {Z}_p^2\) as \(v_1 \cdot \varvec{b} + v_2 \cdot \varvec{b}^{\bot }\), where \(v_1, v_2 {\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}_p\). Finally, we switch to \(v_1 \cdot \varvec{b} + v_2 \cdot \varvec{b}^{\bot }\) where \(v_1 {\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}_p\), and \(v_2 {\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}_p^*\), which only changes the adversary view by a statistical distance of \(1{\slash }p\): \(\mathsf {Adv}_{3.q.1} - \mathsf {Adv}_{3.q.2} \le \mathsf {Adv}_\mathbb {G}^\textsf {ddh} (t) + 1/p\). The last step with \(v_2 \in \mathbb {Z}_p^*\) will be important to guarantee that \(\varvec{v}_{\varvec{y}}^\top \varvec{b}^{\bot }\ne 0\).
of \(\mathbb {Z}_p^2\), to write a uniformly random vector over \(\mathbb {Z}_p^2\) as \(v_1 \cdot \varvec{b} + v_2 \cdot \varvec{b}^{\bot }\), where \(v_1, v_2 {\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}_p\). Finally, we switch to \(v_1 \cdot \varvec{b} + v_2 \cdot \varvec{b}^{\bot }\) where \(v_1 {\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}_p\), and \(v_2 {\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}_p^*\), which only changes the adversary view by a statistical distance of \(1{\slash }p\): \(\mathsf {Adv}_{3.q.1} - \mathsf {Adv}_{3.q.2} \le \mathsf {Adv}_\mathbb {G}^\textsf {ddh} (t) + 1/p\). The last step with \(v_2 \in \mathbb {Z}_p^*\) will be important to guarantee that \(\varvec{v}_{\varvec{y}}^\top \varvec{b}^{\bot }\ne 0\). -
\(G_{3.q.2} \rightsquigarrow G_{3.q.3}\): We now change the simulation of \(\mathsf {dk}_{\varvec{y},i}\) from \(\mathsf {dk}_{\varvec{y},i} = [y_i\cdot \varvec{s}_i +\mathbf {T}_i \varvec{v}_{\varvec{y}}]_2\) to \(\mathsf {dk}_{\varvec{y},i} = [y_i\cdot \varvec{s}_i + \mathsf {RF}_i(\varvec{y}) +\mathbf {T}_i \varvec{v}_{\varvec{y}}]_2\), with some \(\mathsf {RF}_i\) functions onto \(\mathbb {Z}_p^2\) such that \(\sum _i \mathsf {RF}_i(\varvec{y}) = 0\) for any input \(\varvec{y}\). We prove \(\mathsf {Adv}_{3.q.2} = \mathsf {Adv}_{3.q.3}\). To this aim, we use the fact that the two following distributions are identical, for any choice of \(\varvec{w}_i {\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}_p^2\), such that \(\sum _i \varvec{w}_i = \mathbf {0}\):
$$(\mathbf {T}_i)_{i \in \mathcal {HS}} \text{ and } (\mathbf {T}_i + \varvec{w}_i (\varvec{b}^{\bot })^\top )_{i \in \mathcal {HS}},$$where for all \(i \in [n]\), \(\mathbf {T}_i {\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}_p^{2 \times 2}\) such that \(\sum _i \mathbf {T}_i = \mathbf {0}\), and
 . The extra terms \((\varvec{w}_i (\varvec{b}^{\bot })^\top )_{i \in \mathcal {HS}}\) only appear in the output of the queries to \(\mathsf {QDKeyGen} \) which use the vector \([\varvec{v}_{\varvec{y}}]_2\) computed on the q-th \(\mathsf {RO}_2\)-query (if there are such queries), because for all other queries, \([\varvec{v}_{\varvec{y}}]_2\) lies in the span of \([\varvec{b}]_2\), and \(\varvec{b}^\top \varvec{b}^{\bot }=0\). We thus have \(\mathsf {dk}_{\varvec{y},i} := [y_i \cdot \varvec{s}_i + \varvec{w}_i \cdot (\varvec{b}^{\bot })^\top \varvec{v}_{\varvec{y}} + \mathbf {T}_i \varvec{v}_{\varvec{y}}]_2\). Since \(\varvec{v}_{\varvec{y}}\) is such that \(\varvec{v}_{\varvec{y}}^\top \varvec{b}^{\bot }\ne 0\), \((\varvec{b}^{\bot })^\top \varvec{v}_{\varvec{y}} \ne 0\). In that case, the vectors \(\varvec{w}_i \cdot (\varvec{b}^{\bot })^\top \varvec{v}_{\varvec{y}}\) are uniformly random over \(\mathbb {Z}_p^2\) such that \(\sum _i \varvec{w}_i \cdot (\varvec{b}^{\bot })^\top \varvec{v}_{\varvec{y}} = \mathbf {0}\), which is as in \(G_{3.q.3}\), by setting \(\mathsf {RF}_i(\varvec{y}) := \varvec{w}_i \cdot (\varvec{b}^{\bot })^\top \varvec{v}_{\varvec{y}}\).
. The extra terms \((\varvec{w}_i (\varvec{b}^{\bot })^\top )_{i \in \mathcal {HS}}\) only appear in the output of the queries to \(\mathsf {QDKeyGen} \) which use the vector \([\varvec{v}_{\varvec{y}}]_2\) computed on the q-th \(\mathsf {RO}_2\)-query (if there are such queries), because for all other queries, \([\varvec{v}_{\varvec{y}}]_2\) lies in the span of \([\varvec{b}]_2\), and \(\varvec{b}^\top \varvec{b}^{\bot }=0\). We thus have \(\mathsf {dk}_{\varvec{y},i} := [y_i \cdot \varvec{s}_i + \varvec{w}_i \cdot (\varvec{b}^{\bot })^\top \varvec{v}_{\varvec{y}} + \mathbf {T}_i \varvec{v}_{\varvec{y}}]_2\). Since \(\varvec{v}_{\varvec{y}}\) is such that \(\varvec{v}_{\varvec{y}}^\top \varvec{b}^{\bot }\ne 0\), \((\varvec{b}^{\bot })^\top \varvec{v}_{\varvec{y}} \ne 0\). In that case, the vectors \(\varvec{w}_i \cdot (\varvec{b}^{\bot })^\top \varvec{v}_{\varvec{y}}\) are uniformly random over \(\mathbb {Z}_p^2\) such that \(\sum _i \varvec{w}_i \cdot (\varvec{b}^{\bot })^\top \varvec{v}_{\varvec{y}} = \mathbf {0}\), which is as in \(G_{3.q.3}\), by setting \(\mathsf {RF}_i(\varvec{y}) := \varvec{w}_i \cdot (\varvec{b}^{\bot })^\top \varvec{v}_{\varvec{y}}\). -
\(G_{3.q.3} \rightsquigarrow G_{3.q+1.1}\): This transition is the reverse of \(G_{3.q.1} \rightsquigarrow G_{3.q.2}\), namely, we use the \(\textsf {DDH}\) assumption to switch back the distribution of \([\varvec{v}_{\varvec{y}}]_2\) to uniformly random in the span of \([\varvec{b}]_2\): \(\mathsf {Adv}_{3.q.3} - \mathsf {Adv}_{3.q+1.1} \le \mathsf {Adv}_{\mathbb {G}_2}^\textsf {ddh} (t) + 1/p\).
Then one can note that \(G_{3.Q_2+1.1} = G_3\), but also that in Game \(G_4\), all the \(\mathsf {dk}_{\varvec{y},i}\) output by \(\mathsf {QDKeyGen} \) can be computed only knowing \(\sum _{i \in [n]} \varvec{s}_i \cdot y_i\), which is exactly the functional decryption key \(\mathsf {dk}_{\varvec{y}}\) from our \(\textsf {MCFE}\) in Sect. 4.1. This follows from the fact that the values \(\mathsf {RF}_i(\varvec{y})\) perfectly mask the vectors \(\varvec{s}_i \cdot y_i\), up to revealing \(\sum _{i \in [n]} \varvec{s}_i \cdot y_i\) (as the \(\mathsf {RF}_i\) must sum up to the zero function). Thus, we can reduce to the IND-security of the \(\textsf {MCFE}\) from Sect. 4.1 (or even sta-IND-security) by designing an adversary \(\mathcal {B}\) against the \(\textsf {MCFE}\) from Sect. 4.1: Adversary \(\mathcal {B}\) first samples \(\mathbf {T}_i {\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}_p^{2 \times 2}\) for all \(i \in [n]\), such that \(\sum _{i \in [n]} \mathbf {T}_i = \mathbf {0}\). It sends \(\mathcal {CS}\) given by \(\mathcal {A}\) (set of static corruptions), then it receives \({\mathsf {mpk}}\) from the \(\textsf {MCFE} \) security game, as well as the secret keys \(\varvec{s}_i\) for \(i\in \mathcal {CS}\). It forwards \({\mathsf {mpk}}\) as well as \((\varvec{s}_i, \mathbf {T}_i)\) for \(i\in \mathcal {CS}\) to \(\mathcal {A}\). Then
-
\(\mathcal {B}\) answers oracle calls to \(\mathsf {RO}_1\), \(\mathsf {RO}_2\) and \(\mathsf {QEncrypt} \) from \(\mathcal {A}\) using its own oracles.
-
To answer \(\mathsf {QDKeyGen} (i,\varvec{y})\): if i is the last non-corrupted index for \(\varvec{y}\), \(\mathcal {B}\) queries its own \(\mathsf {QDKeyGen} \) oracle on \(\varvec{y}\), to get \(\mathsf {dk}_{\varvec{y}} := \sum _i \varvec{s}_i \cdot y_i \in \mathbb {Z}^2_p\), computes \([\varvec{v}_{\varvec{y}}]_2 := \mathcal {H}_2(\varvec{y})\), and returns \(\mathsf {dk}_{\varvec{y},i} := [\mathsf {dk}_{\varvec{y}} + \mathsf {RF}_i(\varvec{y}) + \mathbf {T}_i \varvec{v}_{\varvec{y}}]_2\) to \(\mathcal {A}\). Otherwise, it computes \([\varvec{v}_{\varvec{y}}]_2 := \mathcal {H}_2(\varvec{y})\), and returns \(\mathsf {dk}_{\varvec{y},i} := [\mathsf {RF}_i(\varvec{y}) + \mathbf {T}_i \varvec{v}_{\varvec{y}}]_2\) to \(\mathcal {A}\). The random functions \(\mathsf {RF}_i\) are computed on the fly, such that their sum is the zero function.
We stress that this last simulation requires to know \(\mathcal {CS}\) and \(\mathcal {HS}\), hence static corruptions only. From this reduction, one gets
where \(Q_1\) denotes the number of calls to \(\mathsf {RO}_1\), \(t_{\mathbb {G}_1}\) denotes the time to compute an exponentiation in \(\mathbb {G}_1\). This concludes the proof.
6 Conclusion
Multi-Client Functional Encryption and Decentralized Cryptosystems are invaluable tools for many emerging applications such as cloud services or big data. These applications often involve many parties who contribute their data to enable the extraction of knowledge, while protecting their individual privacy with minimal trust in the other parties, including any central authority. We make an important step towards combining the desired functionalities and properties by introducing the notion of Decentralized Multi-Client Functional Encryption. It opens some interesting directions:
-
For inner-product, in the \(\textsf {DDH}\)-based setting with ElGamal-like encryption, we have a strong restriction on the plaintexts, since the inner-product has to be small, in order to allow complete decryption of the scalar evaluation. It is an interesting problem to consider whether the LWE-based and DCR-based schemes can address this issue.
-
Getting all the desired properties, namely efficiency, new functionalities and the strongest security level, is a challenging problem. One of the main challenges is to construct an efficient, non-interactive \(\textsf {DMCFE}\) which is fully secure (adaptive encryptions and adaptive corruptions), for a larger class of functions than that of inner-product functions. The security analyses of our concrete constructions heavily rely on the linear properties of inner-product functions, however, the global methodology of the constructions themselves is not restricted to the inner-product setting. Therefore, new constructions could follow it.
References
Abdalla, M., Bourse, F., De Caro, A., Pointcheval, D.: Simple functional encryption schemes for inner products. In: Katz, J. (ed.) PKC 2015. LNCS, vol. 9020, pp. 733–751. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46447-2_33
Abdalla, M., Catalano, D., Fiore, D., Gay, R., Ursu, B.: Multi-input functional encryption for inner products: function-hiding realizations and constructions without pairings. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018, part I. LNCS, vol. 10991, pp. 597–627. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96884-1_20
Abdalla, M., Gay, R., Raykova, M., Wee, H.: Multi-input inner-product functional encryption from pairings. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017, part I. LNCS, vol. 10210, pp. 601–626. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56620-7_21
Agrawal, S., Libert, B., Stehlé, D.: Fully secure functional encryption for inner products, from standard assumptions. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016, part III. LNCS, vol. 9816, pp. 333–362. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53015-3_12
Ananth, P., Brakerski, Z., Segev, G., Vaikuntanathan, V.: From selective to adaptive security in functional encryption. In: Gennaro, R., Robshaw, M.J.B. (eds.) CRYPTO 2015, part II. LNCS, vol. 9216, pp. 657–677. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48000-7_32
Badrinarayanan, S., Goyal, V., Jain, A., Sahai, A.: Verifiable functional encryption. In: Cheon, J.H., Takagi, T. (eds.) ASIACRYPT 2016, part II. LNCS, vol. 10032, pp. 557–587. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53890-6_19
Bellare, M., Desai, A., Jokipii, E., Rogaway, P.: A concrete security treatment of symmetric encryption. In: 38th FOCS, pp. 394–403. IEEE Computer Society Press, October 1997
Benhamouda, F., Joye, M., Libert, B.: A new framework for privacy-preserving aggregation of time-series data. ACM Trans. Inf. Syst. Secur. 18(3), 10:1–10:21 (2016)
Boneh, D., Sahai, A., Waters, B.: Functional encryption: definitions and challenges. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 253–273. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19571-6_16
Brakerski, Z., Komargodski, I., Segev, G.: Multi-input functional encryption in the private-key setting: stronger security from weaker assumptions. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016, part II. LNCS, vol. 9666, pp. 852–880. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49896-5_30
Chan, T.-H.H., Shi, E., Song, D.: Privacy-preserving stream aggregation with fault tolerance. In: Keromytis, A.D. (ed.) FC 2012. LNCS, vol. 7397, pp. 200–214. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32946-3_15
Datta, P., Okamoto, T., Tomida, J.: Full-hiding (unbounded) multi-input inner product functional encryption from the k-linear assumption. In: Abdalla, M., Dahab, R. (eds.) PKC 2018, part II. LNCS, vol. 10770, pp. 245–277. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-76581-5_9
Emura, K.: Privacy-preserving aggregation of time-series data with public verifiability from simple assumptions. In: Pieprzyk, J., Suriadi, S. (eds.) ACISP 2017. LNCS, vol. 10343, pp. 193–213. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-59870-3_11
Escala, A., Herold, G., Kiltz, E., Ràfols, C., Villar, J.: An algebraic framework for diffie-hellman assumptions. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013, part II. LNCS, vol. 8043, pp. 129–147. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40084-1_8
Garg, S., Gentry, C., Halevi, S., Raykova, M., Sahai, A., Waters, B.: Candidate indistinguishability obfuscation and functional encryption for all circuits. In: 54th FOCS, pp. 40–49. IEEE Computer Society Press, October 2013
Goldwasser, S., et al.: Multi-input functional encryption. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 578–602. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-55220-5_32
Goldwasser, S., Kalai, Y.T., Popa, R.A., Vaikuntanathan, V., Zeldovich, N.: How to run turing machines on encrypted data. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013, part II. LNCS, vol. 8043, pp. 536–553. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40084-1_30
Goldwasser, S., Kalai, Y.T., Popa, R.A., Vaikuntanathan, V., Zeldovich, N.: Reusable garbled circuits and succinct functional encryption. In: Boneh, D., Roughgarden, T., Feigenbaum, J. (eds.) 45th ACM STOC, pp. 555–564. ACM Press, June 2013
Gorbunov, S., Vaikuntanathan, V., Wee, H.: Functional encryption with bounded collusions via multi-party computation. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 162–179. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_11
Gordon, S.D., Katz, J., Liu, F.H., Shi, E., Zhou, H.S.: Multi-input functional encryption. Cryptology ePrint Archive, Report 2013/774 (2013). http://eprint.iacr.org/2013/774
Joye, M., Libert, B.: A scalable scheme for privacy-preserving aggregation of time-series data. In: Sadeghi, A.-R. (ed.) FC 2013. LNCS, vol. 7859, pp. 111–125. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-39884-1_10
Lee, K., Lee, D.H.: Two-input functional encryption for inner products from bilinear maps. IACR Cryptology ePrint Archive 2016, 432 (2016). http://eprint.iacr.org/2016/432
Li, Q., Cao, G.: Efficient and privacy-preserving data aggregation in mobile sensing. In: ICNP 2012, pp. 1–10. IEEE Computer Society (2012)
Li, Q., Cao, G.: Efficient privacy-preserving stream aggregation in mobile sensing with low aggregation error. In: De Cristofaro, E., Wright, M. (eds.) PETS 2013. LNCS, vol. 7981, pp. 60–81. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-39077-7_4
Paillier, P.: Public-key cryptosystems based on composite degree residuosity classes. In: Stern, J. (ed.) EUROCRYPT 1999. LNCS, vol. 1592, pp. 223–238. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-48910-X_16
Regev, O.: On lattices, learning with errors, random linear codes, and cryptography. In: Gabow, H.N., Fagin, R. (eds.) 37th ACM STOC, pp. 84–93. ACM Press, May 2005
Sahai, A., Seyalioglu, H.: Worry-free encryption: functional encryption with public keys. In: Al-Shaer, E., Keromytis, A.D., Shmatikov, V. (eds.) ACM CCS 2010, pp. 463–472. ACM Press, October 2010
Sahai, A., Waters, B.R.: Fuzzy identity-based encryption. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 457–473. Springer, Heidelberg (2005). https://doi.org/10.1007/11426639_27
Shi, E., Chan, T.H.H., Rieffel, E.G., Chow, R., Song, D.: Privacy-preserving aggregation of time-series data. In: NDSS 2011. The Internet Society, February 2011
Waters, B.: A punctured programming approach to adaptively secure functional encryption. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015, part II. LNCS, vol. 9216, pp. 678–697. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48000-7_33
Wee, H.: Dual system encryption via predicate encodings. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 616–637. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54242-8_26
Acknowledgments
This work was supported in part by the European Community’s Seventh Framework Programme (FP7/2007-2013 Grant Agreement no. 339563 – CryptoCloud), the European Community’s Horizon 2020 Project FENTEC (Grant Agreement no. 780108), the Google PhD fellowship, the ANR ALAMBIC (ANR16-CE39-0006) and the French FUI ANBLIC Project.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
A Multi DDH Assumption
Theorem 10
For any distinguisher \(\mathcal {A}\) running within time t, the best advantage \(\mathcal {A}\) can get in distinguishing

is bounded by \(\mathsf {Adv}^\textsf {ddh} (t + 4 m\times t_\mathbb {G})\), where \(t_\mathbb {G}\) is the time for an exponentiation in \(\mathbb {G}\).
Proof
One can first note that the best advantage one can get, within time t, between

is bounded by \(\mathsf {Adv}^\textsf {ddh} (t)\). This is actually the \(\textsf {DDH}\) assumption. One can note that \(\mathcal {D}_m\) and \(\mathcal {D}'_m\) can be rewritten as

Since, from (X, Y, Z), the m tuples require 4 additional exponentiations per index j, one get the expected bound.
B A Selectively-Secure MCFE
1.1 B.1 Description
In this section, we formally present the selectively secure \(\textsf {MCFE} \) scheme for inner product we described in Sect. 1. It is inspired by Abdalla et al.’s scheme [1]:
-
\(\mathsf {SetUp} (\lambda )\): Takes as input the security parameter, and generates a group \(\mathbb {G}\) of prime order \(p \approx 2^\lambda \), \(g \in \mathbb {G}\) a generator, and \(\mathcal {H}\) a full-domain hash function onto \(\mathbb {G}\). It also generates the encryption keys \(s_i{\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}_p\), for \(i=1,\ldots ,n\), and sets \(\varvec{s}= (s_i)_i\). The public parameters \({\mathsf {mpk}}\) consist of \((\mathbb {G},p,g,\mathcal {H})\), while the master secret key is \({\mathsf {msk}=\varvec{s}}\) and the encryption keys are \({\mathsf {ek}_i = s_i}\) for \(i=1,\ldots ,n\) (in addition to \({\mathsf {mpk}}\), which is omitted);
-
\({\mathsf {Encrypt} (\mathsf {ek}_i,x_i,\ell )}\): Takes as input the value \(x_i\) to encrypt, under the key \({\mathsf {ek}_i = s_i}\) and the label \(\ell \). It computes \([u_\ell ] := \mathcal {H}(\ell ) \in \mathbb {G}\), and outputs the ciphertext \([c_i] = [u_\ell s_i + x_i] \in \mathbb {G}\);
-
\({\mathsf {DKeyGen} (\mathsf {msk}, \varvec{y})}\): Takes as input \({\mathsf {msk}= (s_i)_i}\) and an inner-product function defined by \(\varvec{y}\) as \(f_{\varvec{y}}(\varvec{x}) = \langle \varvec{x}, \varvec{y} \rangle \), and outputs the functional decryption key \(\mathsf {dk}_{\varvec{y}} = \left( \varvec{y},\sum _{i} s_i y_i \right) \in \mathbb {Z}_p^n \times \mathbb {Z}_p\);
-
\(\mathsf {Decrypt} (\mathsf {dk}_{\varvec{y}}, \ell , ([c_i])_{i \in [n]})\): Takes as input a decryption key \(\mathsf {dk}_{\varvec{y}} = (\varvec{y}, d)\), a label \(\ell \). It computes \([u_\ell ] := \mathcal {H}(\ell )\), \([\alpha ] = \sum _i y_i \cdot [c_i] - d \cdot [u_\ell ]\), and eventually solves the discrete logarithm to extract and return \(\alpha \).
As for Abdalla et al.’s scheme [1], the result \(\alpha \) should not be too large to allow the final discrete logarithm computation.
Correctness: if the scalar dk in the decryption functional key \(\mathsf {dk}_{\varvec{y}}=(\varvec{y},dk)\) is indeed \(dk = \langle \varvec{s}, \varvec{y} \rangle \), then
1.2 B.2 Selective Security
Like Abdalla et al.’s original scheme [1], our protocol can only be proven secure in the weaker security model, where the adversary has to commit in advance to all of the pairs of messages for the Left-or-Right encryption oracle (\(\mathsf {QEncrypt} \)-queries). However, it can adaptively ask for functional decryption keys (\(\mathsf {QDKeyGen} \)-queries) and encryption keys (\(\mathsf {QCorrupt} \)-queries). Concretely, the challenger is provided (plaintext,label) pairs: \((x_{j,i}^b,\ell _j)_{b \in \{0,1\},i\in [n], j \in [Q]}\), where Q is the number of query to \(\mathsf {QEncrypt} (i,\cdot ,\cdot )\), each one for a different label \(\ell _j\) (note that in the security model, we assume each slots are queried the same number of time, on different labels). The challenge ciphertexts \({C_{i,j} = \mathsf {Encrypt} (\mathsf {ek}_i, x_{j,i}^b,\ell _j)}\), for the random bit b, are returned to the adversary.
Note that the adversary committing to challenge ciphertexts also limits its ability to corrupt users during the game: it must corrupt clients for which it didn’t ask a ciphertext and cannot corrupt any client from which it asked a ciphertext for \(x_{j,i}^0\ne x_{j,i}^1\).
1.3 B.3 Security Analysis
Theorem 11
(sel-IND Security). The \(\textsf {MCFE}\) protocol described above (see Appendix B.1) is sel-IND secure under the \(\textsf {DDH}\) assumption, in the random oracle model. More precisely, we have
for any adversary \(\mathcal {A}\), running within time t, where Q is the number of encryption queries per slot.
Games \(G_0\), \(G_1\), \((G_{2.})_{q \in [Q+1]}\), for the proof of Theorem 11. Here, \(\mathsf {RF}\) is a random function onto \(\mathbb {G}\), that is computed on the fly. Note that \(\mathsf {QEncrypt} \) is only used as a subroutine of the initialization of the game and is not accessible to the adversary. In each procedure, the components inside a solid frame are only present in the games marked by a solid frame.
Proof
We proceed using hybrid games, described in Fig. 6, with the same notations as in the previous proofs.
-
Game \(G_0\): This is the
 security game as given in Definition 2 (see the paragraph about weaker models), with all the encryption queries being sent first: they are stored in \(z_{j,i}=(x_{j,i}^0,x_{j,i}^1)\), for \(j\in [Q]\) and \(i\in [n]\), where j is for the j-th \(\mathcal {H}\)-query that specifies the label \(\ell _j\) and i is for the index of the sender. If the query is not asked, we have \(z_{j,i} = \bot \). Note that the hash function \(\mathcal {H}\) is modeled as a random oracle \(\mathsf {RO}\) onto \(\mathbb {G}\). This is used to generate \([u_\ell ] = \mathcal {H}(\ell )\).
security game as given in Definition 2 (see the paragraph about weaker models), with all the encryption queries being sent first: they are stored in \(z_{j,i}=(x_{j,i}^0,x_{j,i}^1)\), for \(j\in [Q]\) and \(i\in [n]\), where j is for the j-th \(\mathcal {H}\)-query that specifies the label \(\ell _j\) and i is for the index of the sender. If the query is not asked, we have \(z_{j,i} = \bot \). Note that the hash function \(\mathcal {H}\) is modeled as a random oracle \(\mathsf {RO}\) onto \(\mathbb {G}\). This is used to generate \([u_\ell ] = \mathcal {H}(\ell )\). -
Game \(G_1\): We simulate the answers to any new \(\mathsf {RO}\) query by computing a truly random element of \(\mathbb {G}\), on the fly. The simulation remains perfect, so \(\mathsf {Adv}_0 = \mathsf {Adv}_1\).
-
Game \(G_2\): We simulate every encryption as the encryption of \(x_i^0\) instead of \(x_i^b\).
While it is clear that in this last game the advantage of any adversary is exactly 0 since b does not appear anywhere, the gap between \(G_1\) and \(G_2\) will be proven using an hybrid argument on the \(\mathsf {RO}\)-queries. We thus index the following games by q, where \(q=1,\ldots , Q\). Note that only distinct \(\mathsf {RO}\)-queries are counted, since a second similar query is answered as the first one.
-
\(G_{2.1}\): This is exactly game \(G_1\). Thus, \(\mathsf {Adv}_1= \mathsf {Adv}_{2.1}\).
-
\(G_{2.q} \rightsquigarrow G_{2.q+1}\): We change the generation of the ciphertexts from \([c_{q,i}] := [u_{\ell _q}s_i + x_{q,i}^{b}]\) to \([c_{q,i}] := [u_{\ell _q}s_i + x_{q,i}^{0}]\). We proceed in three steps:
Step 1. We use the fact that the two following distributions are identical, for any choice of \(\gamma \):
$$\left( s_{i}\right) _{i \in [n], z_{q,i} = (x_{q,i}^{0},x_{q,i}^{b})} \text{ and } \left( s_{i} + \gamma (x_{q,i}^{0} - x_{q,i}^{b}) \right) _{i \in [n], z_{q,i} = (x_{q,i}^{0},x_{q,i}^{1})},$$where \(s_{i} {\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}_p\), for all \(i\in [n]\). This is true since the \(s_{i}\) are independent of the \(z_{q,i}\) (we are in a selective setting, so the \(s_i\)’s are generated after the \(z_{q,i}\)’s have been chosen). Thus, we can re-write \(s_{i}\) into \(s_{i} + \gamma (x_{q,i}^{0} - x_{q,i}^{b})\) without changing the distribution of the game.
Note that when Finalize does not output a random bit \(\beta {\mathop {\leftarrow }\limits ^{{}_\$}}\{0,1\}\) independent of the guess \(b'\), \(\gamma \) does not appear in the outputs of \(\mathsf {QCorrupt} (i)\), since it must be that \(x_i^0=x_i^1\) or \(z_{q,i}=\bot \), and it does not appear in the output of \(\mathsf {QDKeyGen} (\varvec{y})\) either, since
 , where the gray term equals zero by Definition 1. The fact that \(\gamma \) does not appear in the outputs of these oracles will be crucial for step 2, which applies \(\textsf {DDH}\) on \([\gamma ]\).
, where the gray term equals zero by Definition 1. The fact that \(\gamma \) does not appear in the outputs of these oracles will be crucial for step 2, which applies \(\textsf {DDH}\) on \([\gamma ]\).Step 2. We use the \(\textsf {DDH}\) assumption to replace the \([u_{\ell _q}\gamma ]\) that appear in the output of the q-th query to \(\mathsf {QEncrypt} \) queries with \([r_{\ell _q} + 1]\) with \(r_{\ell _q} {\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}_p\). This is possible since the rest of the adversary view can be generated only from \([\gamma ]\) and \([r_{\ell _q}+1]\). This increases the adversary’s advantage by no more than \(\mathsf {Adv}_\mathbb {G}^\textsf {ddh} (t)\). We now have:
$$\begin{aligned}{}[c_{q,i}] :=&[u_{\ell _q}s_i + (x_{q,i}^{0} - x_{q,i}^{b}) (r_{\ell _q} + 1) + x_{q,i}^{b}] \\ =&[u_{\ell _q}s_i + r_{\ell _q}(x_{q,i}^{0} - x_{q,i}^{b}) + x_{q,i}^{0} - x_{q,i}^{b} + x_{q,i}^{b}] \\ =&[u_{\ell _q}s_i + r_{\ell _q}(x_{q,i}^{0} - x_{q,i}^{b}) + x_{q,i}^{0}]. \end{aligned}$$Step 3. We switch \([r_{\ell _q}]\) in the output of the q-query to \(\mathsf {QEncrypt} \) back to \([u_{\ell _q} \gamma ]\), using the \(\textsf {DDH}\) assumption again. This is possible since the adversary’s view is simulatable solely from \([\gamma ]\), \([u_{\ell _q}]\), and \([r_{\ell _q}]\). We finally undo the distribution change on the \(\varvec{s}_i\), which brings us to \(G_{2.q+1}\).
As a conclusion, since \(G_{2.Q+1} = G_{2}\), we have \(\mathsf {Adv}_{1} - \mathsf {Adv}_{2} \le 2Q\cdot \mathsf {Adv}_\mathbb {G}^\textsf {ddh} (t)\). In addition, \(\mathsf {Adv}_{2} = 0\), which concludes the proof.
Rights and permissions
Copyright information
© 2018 International Association for Cryptologic Research
About this paper
Cite this paper
Chotard, J., Dufour Sans, E., Gay, R., Phan, D.H., Pointcheval, D. (2018). Decentralized Multi-Client Functional Encryption for Inner Product. In: Peyrin, T., Galbraith, S. (eds) Advances in Cryptology – ASIACRYPT 2018. ASIACRYPT 2018. Lecture Notes in Computer Science(), vol 11273. Springer, Cham. https://doi.org/10.1007/978-3-030-03329-3_24
Download citation
DOI: https://doi.org/10.1007/978-3-030-03329-3_24
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-03328-6
Online ISBN: 978-3-030-03329-3
eBook Packages: Computer ScienceComputer Science (R0)







 ): the encryption queries (
): the encryption queries ( ): the corruption queries (
): the corruption queries (
 , with
, with 
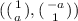 of
of  and
and 
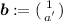 , with
, with 
 of
of  . The extra terms
. The extra terms 
 security game as given in Definition
security game as given in Definition  , where the gray term equals zero by Definition
, where the gray term equals zero by Definition 