Pseudo-Dynamic Approach to Analyse the Effect of Soil Amplification in the Calculation of Seismic Active Earth Pressure Distribution Behind the Inclined Retaining Wall for Inclined c-ϕ Soil Backfill

Abstract

In the current practice for the design of a retaining wall in the earthquake-prone regions, the study of seismic earth pressure is essential for the soil life-support system. Regarding the design of retaining walls in the earthquake-prone region, pseudo-static and pseudo-dynamic approaches are widely used for c-ϕ soil backfill without taking the effect of soil amplification. Soil amplification is very important and necessary factor to calculate the seismic active earth pressure analyzing the retaining walls. It should not be ignored in the design in the earthquake-prone regions. In this paper, a detailed formulation has been reported to calculate the seismic active earth pressure distribution along with the calculations of seismic active thrust for the inclined retaining wall. The retaining wall supports the inclined c-ϕ soil backfill. A parametric study is conducted to study the effect of various parameters like c-ϕ values of soil backfill, wall friction, soil amplification, horizontal and vertical seismic coefficients and the effect of time and phase difference in the shear waves and the primary waves. The results obtained for seismic earth pressure distribution is clearly showing the non-linear behavior behind the inclined retaining wall, which is the need for the design of retaining wall in earthquake-prone regions. The negative value of seismic active earth pressure distribution up to a normalized depth of wall is showing the zone of tension crack for the case of cohesive soil backfill.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

During the design of retaining wall in the earthquake prone regions, the critical study of seismic earth pressure is very crucial. To study the seismic active earth pressure, various researchers have been analyzed the retaining walls using the pseudo-static method. Using the pseudo-static method, the pioneer work for determining seismic earth pressure for the design of retaining walls had been reported by Okabe (1926) and Mononobe and Matsuo (1929) and then known as Mononobe and Okabe method. The time dependent effect during the earthquake loading was completely missing in the pseudo-static method. In pseudo-static method, magnitude and phase of seismic accelerations were also taken uniform throughout the soil backfill.

For analyzing the real seismic problems during the design of retaining walls, Steedman and Zeng (1990) had proposed the pseudo-dynamic approach considering the finite shear waves in the backfiill. Pseudo-dynamic method had been used to overcome the deficiencies of pseudo-static method. Choudhury and Nimbalkar (2005 and 2006) had extended that pseudo-dynamic approach for determining the seismic passive and seismic active earth pressure behind vertical retaining wall. Nimbalkar and Choudhury (2008) introduced the soil amplification effect in the pseudo-dynamic approach to determine the seismic active earth pressure coefficients and seismic active earth pressure distribution for vertical retaining wall. Ghosh (2008) had extended the study of Nimbalkar and Choudhury (2008) for the inclined retaining wall. Gupta and Sawant (2018) studied the effect of soil amplification on the dynamic response of retaining wall having cohesionless backfill. Both wall and backfill are having nonzero inclination with vertical and horizontal. Using the pseudo-dynamic approach considering c-ϕ soil backfill, Ghosh and Sharma (2010) had reported the effect of tension crack in the top portion of the backfill. The tension crack was determined by the Rankine’s analysis of active earth pressure for c-ϕ soil backfill under static case, which was the limitation of this study. Shao-jun et al. (2012) extended the study of Ghosh and Sharma (2010) to investigate the effect of tension crack under seismic loading in the top portion of the backfill, without considering the effect of soil modification factor.

In the present work, a detailed formulation incorporating the soil amplification effect has been reported to compute the seismic active earth pressure distribution. The retaining wall is inclined supporting the inclined c-ϕ soil backfill.

2 Detailed Formulation

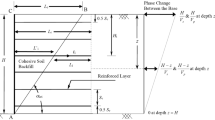
The rigid inclined retaining wall AB of height H inclined at an angle θ with vertical and wall friction angle δ as shown in Fig. 1. It is retaining soil backfill of cohesion c and soil friction angle ϕ, having unit weight γ inclined at an angle i with horizontal. Effect of propagation of both shear waves and the primary waves is also considered along with the effect of soil amplification. Linear variation in input ground acceleration along depth is taken for showing the effect of soil amplification, within the soil media due to the seismic loading. Amplitude of horizontal and vertical seismic acceleration of base of the retaining wall assumed as a_h = k_h g and a_v = k_v g. The primary and shear wave velocities, V_s and V_p are assumed to propagate within the soil media due to the earthquake.

Fig. 1.

Forces acting on retaining wall in active state

The horizontal and vertical seismic acceleration at the top has been assumed, higher than the value of horizontal and vertical seismic acceleration at the base. In the present work, horizontal and vertical seismic acceleration at the top of the retaining wall is taken as k_h(z=0) = f_a.k_h(z=H) and k_v(z=0) = f_a.k_v(z=H), where f_a is the soil amplification factor. The present analysis induces a period of lateral shaking T = 2π/ω, where ω is the angular frequency.

A failure wedge ABE is assumed, which makes an angle α with horizontal. W is the weight of failure wedge. The horizontal and vertical inertia forces are Q_h(t) and Q_v(t). C is the total cohesive force and C_a is the total soil-wall adhesion force. Soil-wall adhesion factor is taken as a_f which defines a_f = (C_a/C) = (c_a/c), where c_a is the soil-wall adhesion.

From Fig. (1), the mass of the strip of thickness dz at depth z can be obtained as:

$$ m(z) = \frac{\gamma }{g}m\left( \alpha \right)\left( {H - z} \right)dz $$

(1a)

where,

$$ m\left( \alpha \right) = \frac{{\left( {1 + \tan \alpha \,\tan \theta } \right)\;\sin \alpha \;\cos \left( {\theta - i} \right)}}{{\tan \alpha \;\sin \left( {\alpha - i} \right)\;\cos \theta }} $$

(1b)

The weight of the failure wedge can be obtained as:

$$ W = \frac{1}{2}\gamma H^{2} m\left( \alpha \right) $$

(2)

At any depth z below the top of the wall, the horizontal and the vertical acceleration can be expressed as:

$$ a_{h} \left( {z,t} \right) = \left\{ {1 + \frac{H - z}{H}\left( {f_{a} - 1} \right)} \right\}k_{h} \;g\;\sin \omega \left( {t - \frac{H - z}{{V_{S} }}} \right) $$

(3a)

$$ a_{v} \left( {z,t} \right) = \left\{ {1 + \frac{H - z}{H}\left( {f_{a} - 1} \right)} \right\}k_{v} \;g\;\sin \omega \left( {t - \frac{H - z}{{V_{P} }}} \right) $$

(3b)

The total horizontal inertia force Q_h(t) acting in the failure wedge is given by:

$$ Q_{h} \left( t \right) = \int\limits_{0}^{H} {m(z)\;} a_{h} \left( {z,t} \right) = \gamma \;k_{h} \;m\left( \alpha \right)\;\left( {I_{1} + I_{2} } \right) $$

(4)

where,

$$ I_{1} = \frac{\lambda }{{4\pi^{2} }}\left[ {2\pi H\,\cos \omega \zeta + \lambda \left( {\sin \omega \zeta - \sin \omega t} \right)} \right] $$

(5a)

$$ I_{2} = \frac{{\left( {f_{a} - 1} \right)\lambda }}{{4\pi^{3} H}}\left\{ {2\pi H\left( {\pi H\,\cos \omega \zeta + \lambda \,\sin \omega \zeta } \right) + \lambda^{2} \left( {\cos \omega t - \cos \omega \zeta } \right)} \right\} $$

(5b)

The total horizontal inertia force Q_h(t) can be rewritten as:

$$ Q_{h} \left( t \right) = \frac{{\lambda \gamma k_{h} m\left( \alpha \right)}}{{4\pi^{2} }}\left[ {\left\{ {\begin{array}{*{20}l} {2\pi H\,\cos \omega \zeta } \hfill \\ { + \lambda \left( {\sin \omega \zeta - \sin \omega t} \right)} \hfill \\ \end{array} } \right\} + \frac{{\left( {f_{a} - 1} \right)}}{\pi H}\left\{ \begin{aligned} 2\pi H\left( \begin{aligned} \pi H\,\cos \omega \zeta \hfill \\ + \lambda \,\sin \omega \zeta \hfill \\ \end{aligned} \right) \hfill \\ + \lambda^{2} \left( {\cos \omega t - \cos \omega \zeta } \right) \hfill \\ \end{aligned} \right\}} \right] $$

(6)

Using the same procedure for calculating the total vertical inertia force Q_v(t) acting in the failure wedge is given by:

$$ Q_{v} \left( t \right) = \frac{{\eta \gamma k_{v} m\left( \alpha \right)}}{{4\pi^{2} }}\left[ {\left\{ {\begin{array}{*{20}l} {2\pi H\,\cos \omega \psi } \hfill \\ { + \eta \left( {\sin \omega \psi - \sin \omega t} \right)} \hfill \\ \end{array} } \right\} + \frac{{\left( {f_{a} - 1} \right)}}{\pi H}\left\{ \begin{aligned} 2\pi H\left( \begin{aligned} \pi H\,\cos \omega \psi \hfill \\ + \eta \,\sin \omega \psi \hfill \\ \end{aligned} \right) \hfill \\ + \eta^{2} \left( {\cos \omega t - \cos \omega \psi } \right) \hfill \\ \end{aligned} \right\}} \right] $$

(7)

where,

$$ \lambda = TV_{S} ;\eta = TV_{P} ;\zeta = \left( {t - \frac{H}{{V_{S} }}} \right)\text{and} \;\psi = \left( {t - \frac{H}{{V_{P} }}} \right) $$

Resolving the forces in the horizontal and vertical direction on the failure wedge, the total active thrust P_ae(t) can be obtained as:

$$ P_{ae} \left( t \right) = \left[ {\begin{array}{*{20}l} {\left\{ {\frac{{\left\{ {W - Q_{v} \left( t \right)} \right\}\sin \left( {\alpha - \phi } \right) + Q_{h} \left( t \right)\cos \left( {\alpha - \phi } \right)}}{{\cos \left( {\delta + \theta - \alpha + \phi } \right)}}} \right\}} \hfill \\ { - \left\{ {\frac{{cH\left\{ {\cos \left( {\theta - i} \right)\cos \phi - a_{f} \sin \left( {\theta - \alpha + \phi } \right)\sin \left( {\alpha - i} \right)} \right\}}}{{\sin \left( {\alpha - i} \right)\cos \theta \,\cos \left( {\delta + \theta - \alpha + \phi } \right)}}} \right\}} \hfill \\ \end{array} } \right] $$

(8)

Using Eq. (8), the seismic active earth pressure coefficient, K_ae(t) can be obtained as:

$$ K_{ae} \left( t \right) = \left[ {\begin{array}{*{20}l} {\left\{ {\frac{{2\left\{ {W - Q_{v} \left( t \right)} \right\}\sin \left( {\alpha - \phi } \right) + 2Q_{h} \left( t \right)\cos \left( {\alpha - \phi } \right)}}{{\gamma H^{2} \cos \left( {\delta + \theta - \alpha + \phi } \right)}}} \right\}} \hfill \\ { - \frac{2c}{\gamma H}\left\{ {\frac{{\left\{ {\cos \left( {\theta - i} \right)\cos \phi - a_{f} \sin \left( {\theta - \alpha + \phi } \right)\sin \left( {\alpha - i} \right)} \right\}}}{{\sin \left( {\alpha - i} \right)\cos \theta \,\cos \left( {\delta + \theta - \alpha + \phi } \right)}}} \right\}} \hfill \\ \end{array} } \right] $$

(9)

Substituting the values of W, Q_h(t) and Q_v(t) in Eq. (9), an expression for K_ae(t) can be derived. On optimizing Eq. (9) with respect to their two variables α and t/T, it can be obtain the maximum value of K_ae(t).

On taking the partial derivative of P_ae(t) with respect to z, seismic active earth pressure distribution behind the retaining wall can be determined and expressed as:

$$ p_{ae} \left( {z,t} \right) = \frac{{\partial P_{ae} \left( {z,t} \right)}}{\partial z} = \left\{ {D_{1} + D_{2} + D_{3} + D_{4} + D_{5} + D_{6} } \right\} $$

(10)

where,

$$ D_{1} = m\left( \alpha \right)\frac{{\gamma \;z\;\sin \left( {\alpha - \phi } \right)}}{{\cos \left( {\delta + \theta - \alpha + \phi } \right)}} $$

(11a)

$$ D_{2} = m\left( \alpha \right)\frac{{k_{h} \;\gamma \;z\;\cos \left( {\alpha - \phi } \right)}}{{\cos \left( {\delta + \theta - \alpha + \phi } \right)}}\sin \theta_{\lambda z} $$

(11b)

$$ D_{4} = - m\left( \alpha \right)\frac{{k_{v} \;\gamma \;z\;\sin \left( {\alpha - \phi } \right)}}{{\cos \left( {\delta + \theta - \alpha + \phi } \right)}}\sin \theta_{\eta z} $$

(11c)

$$ D_{3} = \left[ {\begin{array}{*{20}l} {\left\{ {m\left( \alpha \right)\frac{{k_{h} \;\gamma \;\left( {f_{a} - 1} \right)\cos \left( {\alpha - \phi } \right)}}{{\cos \left( {\delta + \theta - \alpha + \phi } \right)}}\frac{\lambda }{2\pi }} \right\}} \hfill \\ {\left\{ { - \cos \theta_{\lambda z} - \frac{\lambda }{\pi z}\sin \theta_{\lambda z} + \frac{{\lambda^{2} }}{{2\pi^{2} z^{2} }}\left\{ {\cos \theta_{\lambda z} - \cos \theta_{t} } \right\} + \frac{2\pi z}{\lambda }\sin \theta_{\lambda z} } \right\}} \hfill \\ \end{array} } \right] $$

(11d)

$$ D_{5} = - \left[ {\begin{array}{*{20}l} {\left\{ {m\left( \alpha \right)\frac{{k_{v} \;\gamma \;\left( {f_{a} - 1} \right)\sin \left( {\alpha - \phi } \right)}}{{\tan \alpha \,\cos \left( {\delta + \theta - \alpha + \phi } \right)}}\frac{\eta }{2\pi }} \right\}} \hfill \\ {\left\{ { - \cos \theta_{\eta z} - \frac{\eta }{\pi z}\sin \theta_{\eta z} + \frac{{\eta^{2} }}{{2\pi^{2} z^{2} }}\left\{ {\cos \theta_{\eta z} - \cos \theta_{t} } \right\} + \frac{2\pi z}{\eta }\sin \theta_{\eta z} } \right\}} \hfill \\ \end{array} } \right] $$

(11e)

$$ D_{6} = - \frac{{c\left\{ {\cos \left( {\theta - i} \right)\cos \phi - a_{f} \sin \left( {\theta - \alpha + \phi } \right)\sin \left( {\alpha - i} \right)} \right\}}}{{\sin \left( {\alpha - i} \right)\cos \theta \,\cos \left( {\delta + \theta - \alpha + \phi } \right)}} $$

(11f)

$$ \theta_{\lambda z} = 2\pi \left( {\frac{t}{T} - \frac{z}{\lambda }} \right)\;\text{and} \;\theta_{\eta z} = 2\pi \left( {\frac{t}{T} - \frac{z}{\eta }} \right) $$

(11g)

By optimizing Eq. (9) with respect to α and t/T, optimized values of α and t/T are obtained. Using these two optimized values, terms D₁, D₂, D₃, D₄, D₅ and D₆ are evaluated. On putting D₁, D₂, D₃, D₄, D₅ and D₆ in Eq. (10), it provides a general expression of seismic active earth pressure distribution behind the inclined wall considering inclined c-ϕ soil backfill.

3 Results and Discussion

Seismic active earth pressure distribution is presented in the non-dimensional (p_ae/γH) using Eq. (10). In the present study, a parametric study has been done to quantify the value of p_ae/γH along the normalized depth of the retaining wall. Variation of parameters considered are stated in Table 1.

Table 1. Variation of parameters considered in the present study

3.1 Effect of f_a on p_ae/γH

Figures 2, 3, 4 and 5 are showing the variation of p_ae/γH along the normalized depth (z/H) for the soil amplification factor (f_a) varying from 1.0 to 1.8. On increasing the value of f_a from 1.0 to 1.8, it can be clearly observed that the value of p_ae/γH increases significantly. From the Figs. 2, 3, 4 and 5 for the higher value of f_a (for z/H ≥ 0.5), the effect of f_a is significantly decreases for the case of c-ϕ soil backfill. From Figs. 2, 3, 4 and 5, it can be also observed that the value of p_ae/γH increases considerably faster when f_a increases from 1.4 to 1.8 as compare to f_a increases from 1.0 to 1.4 for four cases (c = 0 and a_f = 0.0; c = 10 kPa and a_f = 0.0; c = 10 kPa and a_f = 1.0; c = 20 kPa and a_f = 1.0). For example, at z/H = 0.8 (for c = 0 and a_f = 0.0), p_ae/γH increases about 11% when f_a increases from 1.0 to 1.4 and 14% when f_a increases from 1.4 to 1.8 (for i = 0°) and about 20.3% and 34.7% respectively for i = 10°. The same is increases about 10.1% and 11.9% (for i = 0°) and about 15.5% and 20.6% (for i = 10°) for c = 10 kPa and a_f = 0.0. The value of p_ae/γH is increases about 11.3% and 13.3% (for i = 0°) and about 16.7% and 21.8% (for i = 10°) for c = 10 kPa and a_f = 1.0; which shows a little bit effect of soil-wall adhesion. On increasing the value of c as 20 kPa keeping a_f = 1.0; p_ae/γH is increases about 11.8% and 13.3% (for i = 0°) and about 15.3% and 18.1% (for i = 10°). The negative value of p_ae/γH in all cases is showing the zone of tension crack due to the cohesive soil backfill. For i = 10°, on increasing the value of f_a as 1.0, 1.2, 1.4, 1.6 and 1.8, the value of depth of tension crack increases respectively as 1.01 m, 1.095 m, 1.215 m, 1.385 m and 1.595 m (for c = 10 kPa and a_f = 1.0). For the same case, the depth of tension crack increases as 1.736 m, 1.781 m, 1.842 m, 1.919 m and 2.017 m (for c = 20 kPa and a_f = 1.0).

Fig. 2.

(p_ae/γ H) with (z/H) for different values of f_a (for c = 0, a_f = 0.0)

Fig. 3.

(p_ae/γ H) with (z/H) for different values of f_a (for c = 10 kPa, a_f = 0.0)

Fig. 4.

(p_ae/γ H) with (z/H) for different values of f_a (for c = 10 kPa, a_f = 1.0)

Fig. 5.

(p_ae/γ H) with (z/H) for different values of f_a (for c = 20 kPa, a_f = 1.0)

3.2 Effect of k_h and k_v on p_ae/γH

The variation of p_ae/γH along the normalized depth (z/H) for different values of k_h, varying from 0.0 to 0.3 is shown in Fig. 6. The effect of k_v on the value of p_ae/γH is also shown in Fig. 7. Effect of soil amplification is also taken in the variation of p_ae/γH for both k_h and k_v. It can be noticed from Fig. 6, that the value of p_ae/γH increases continuously, when the value of k_h increases from 0.0 to 0.3 (for z/H > 0.3). The same trend can be noticed when the value of k_v increases from 0.0k_h to 0.75k_h for k_h = 0.3 (for z/H > 0.4). On increasing the values of k_h, the behavior of p_ae/γH changes from linear to non-linear. The considerable increase of p_ae/γH can be also observed when k_h increases from 0.2 to 0.3 and k_v increases from 0.50k_h to 0.75k_h (for c = 10 kPa and a_f = 1.0; f_a = 1.4; i = 10°). For example, for z/H = 0.8, p_ae/γH increases about 68.3% when k_h increases from 0.0 to 0.2 and 81.3% when k_h increases from 0.2 to 0.3. For the same case p_ae/γH increases about 13.9% (k_v increases from 0.0k_h to 0.50k_h) and 21.1% (k_v increases from 0.50k_h to 0.75k_h). On increasing the value of k_h as 0.0, 0.1, 0.2 and 0.3, the value of depth of tension crack increases respectively as 0.86 m, 0.91 m, 1.215 m and 2.410 m for c = 10 kPa and a_f = 1.0 (for i = 10°). For the same case with the values of k_v as 0.0 k_h, 0.25k_h, 0.50k_h and 0.75k_h; the depth of tension crack increases as 1.771 m, 2.054 m, 2.412 m and 2.916 m.

Fig. 6.

(p_ae/γ H) with (z/H) for different values of k_h (for c = 10 kPa, a_f = 1.0)

Fig. 7.

(p_ae/γ H) with (z/H) for different values of k_v (for c = 10 kPa, a_f = 1.0)

3.3 Effect of θ on p_ae/γH

The effect of wall inclination θ on p_ae/γH along z/H is shown in Fig. 8 for θ from −30°, −15°, 0°, 15° and 30° (for c = 10 kPa and a_f = 1.0; f_a = 1.2; i = 10°). As the wall moves from negative inclination to the positive inclination, the value of p_ae/γH increases more, for θ more than 0°. For example, for z/H = 0.8, p_ae/γH increases about 79.8%, and 125.2% when θ increases from −30° to 0° and 0° to 30°. On increasing the value of θ from −30°, −15°, 0°, 15° and 30°, the value of depth of tension crack increases respectively as 4.37 m, 3.00 m, 2.13 m, 1.52 m and 1.10 m for c = 10 kPa and a_f = 1.0 (for i = 10°).

Fig. 8.

(p_ae/γ H) with (z/H) for different values of θ (for c = 10 kPa, a_f = 1.0)

3.4 Effect of ϕ on p_ae/γH

The effect of soil friction angle ϕ on the value of p_ae/γH along the normalized depth (z/H) is shown in Fig. 9 for ϕ increases from 25° to 50° (for c = 10 kPa and a_f = 1.0; f_a = 1.2; i = 10°). The value of p_ae/γH decreases more, when ϕ increases from 30° to 40°. For example, for z/H = 0.8, p_ae/γH decreases about 12.5%, 18.8% and 15.4% when ϕ increases from 25° to 30°, 30° to 40° and 40° to 50°. On increasing the value of ϕ as 25°, 30°, 40° and 50°, the value of depth of tension crack decreases respectively as 1.27 m, 1.10 m, 0.94 m and 0.79 m for c = 10 kPa and a_f = 1.0 (for i = 10°).

Fig. 9.

(p_ae/γ H) with (z/H) for different values of ϕ (for c = 10 kPa, a_f = 1.0)

4 Comparision of Results

The depth of tension crack obtained in the present study have been compared with the values reported by Ghosh and Sharma (2010) and Shao-jun et al. (2012) for a set of parameters (θ = 10°, δ = ϕ/2, a_f = 0.5, k_h = 0.2 and k_v = 0.1) which is shown in Table 2. The values of the depth of tension crack obtained from the present analysis are lower than those obtained by Ghosh and Sharma (2010) and Shao-jun et al. (2012) for the same set of parameters. The difference in the values is quite significant for the higher values of cohesion of soil backfill.

Table 2. Comparison of depth of tension crack obtained from present study with earlier analytical works (for θ = 10°, δ = ϕ/2, a_f = 0.5, k_h = 0.2 and k_v = 0.1)

5 Conclusions

The detailed formulation is reported for calculating the seismic earth pressure distribution behind the inclined retaining wall. These formulations are obtained for the inclined cohesive soil backfill including the effect of soil amplification. From the equation of seismic earth pressure distribution, it can be clearly observed the non-linear behavior behind the inclined retaining wall in the pseudo-dynamic analysis, which shows the actual behavior of retaining wall under seismic condition. The negative value of the seismic active earth pressure distribution shows the zone of tension cracks developed for the case of c-ϕ soil backfill under seismic condition. The main conclusions drawn from the present study are as follows:

• 1. Non-dimensional value of seismic active earth pressure distribution increases when soil amplification factor increases for increasing depth. The effect is more significant for soil amplification factor more than 1.4. For the case inclined retaining wall for the cohesionless soil backfill the non-linear behavior is more, which reduces for the case of cohesive soil backfill.

• 2. On increasing the values of horizontal seismic coefficient, non-dimensional seismic active earth pressure distribution increases substantially for the horizontal seismic coefficient value more than 0.1. Non-linear behavior is also increases for the higher value of horizontal seismic coefficient.

• 3. On increasing the wall inclination for its negative to positive values, non-dimensional seismic active earth pressure distribution increases very fast for the positive values of the wall inclination.

• 4. Non-dimensional value of seismic active earth pressure distribution decreases when soil friction angle increases for increasing depth. For soil friction angle more than 25° and less than 40°, the effect is more.

• 5. The depth of tension crack increases when soil amplification factor increases for increasing depth for the case of cohesive soil backfill. The depth of tension crack also increases, when the angle of shearing resistance increases.

• 6. The depth of tension crack is high for the negative value of the wall inclination, which decreases for the positive value of the wall inclination.