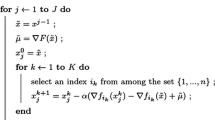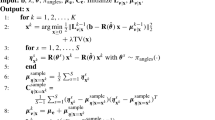Super-Resolution and Sparse View CT Reconstruction

Abstract

We present a flexible framework for robust computed tomography (CT) reconstruction with a specific emphasis on recovering thin 1D and 2D manifolds embedded in 3D volumes. To reconstruct such structures at resolutions below the Nyquist limit of the CT image sensor, we devise a new 3D structure tensor prior, which can be incorporated as a regularizer into more traditional proximal optimization methods for CT reconstruction. As a second, smaller contribution, we also show that when using such a proximal reconstruction framework, it is beneficial to employ the Simultaneous Algebraic Reconstruction Technique (SART) instead of the commonly used Conjugate Gradient (CG) method in the solution of the data term proximal operator. We show empirically that CG often does not converge to the global optimum for tomography problem even though the underlying problem is convex. We demonstrate that using SART provides better reconstruction results in sparse-view settings using fewer projection images. We provide extensive experimental results for both contributions on both simulated and real data. Moreover, our code will also be made publicly available.

Mohamed Aly—Now at iRobot Corp.

1 Introduction

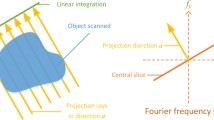
X-ray tomography is a popular imaging technique used for reconstructing volumetric properties for a large range of objects [1]. For example, it is used for industrial inspection, luggage inspection, research and development in mechanical engineering and material sciences, biomedical diagnosis and treatment, and it serves as an input to many computer vision algorithms, including methods for automatic segmentation, detection, and recognition. As with all imaging methods, an important goal in CT is to maximize the amount of information about a target while minimizing the number of measurements, and therefore reducing the acquisition time, memory consumption, and (in the case of CT) radiation dose. This general desire comes in two variants: (a) reducing the number of projections needed for a detailed 3D reconstruction, and (b) resolving fine structures, ideally beyond the Nyquist limit of the individual projection images. In this paper, we tackle both problems in a proximal operator framework respectively with a new solver for the data term, and a new regularizer for volumes with thin sheets and tube-like structures.

Fig. 1.

Five datasets with thin 2D (a-c) and 1D (d-e) structures embedded in 3D volumes. Top row: scanned objects. Middle row: representative projection images. Bottom row: rendering results of volumes reconstructed by our method.

State of the art robust CT reconstruction usually employs iterative methods [1, 2] and poses the problem as an optimization problem of the form

$$\begin{aligned} \min _{x}\underbrace{f(x)}_{\text {data fidelity}}+\underbrace{g(Mx)}_{\text {regularizer}}, \end{aligned}$$

(1)

where $x\in \mathbb {R}^{n}$ is the unknown 3D reconstruction volume, $f(\cdot )$ is the data fidelity term that measures how well the volume fits the measured input projections, and is usually of the form $f(x)=\left\| Ax-{b}\right\| _2^2$, where A describes the projection geometry, and ${b}$ represents the observed projection images. g(Mx) is the regularizer consisting of a loss function g(.) and a linear operator M that transforms the volume x into a sparse domain (e.g. for Total Variation, $g(.)=\Vert .\Vert _1$ and M is the volume gradient operator). Problem (1) is a general model, and can incorporate many noise models, e.g. Poisson [3, 4] or Gaussian noise [5]; and regularizers, e.g. $\ell _{1}$ [6] or Total Variation (TV) [7]. Such optimization problems are commonly solved with proximal algorithms [8,9,10], which allow the decomposition of (1) into independent proximal operators, one for the linear least squares data term, and one for the non-linear regularizer.

The regularizer can be used to enforce specific prior information about the reconstructed volume. Our major contribution is to show that enforcing sparsity on the eigenvalues of the 3D structure tensor allows for super-resolved reconstruction of thin structures such as thin sheets or tubes, see for example Fig. 1. The intuition is that the 3D structure tensor should have two zero eigenvalues on a 2D manifold embedded into a 3D volume, since the volume will only vary along the normal direction. Likewise, for curves embedded in 3D, one of the eigenvalues is expected to be zero.

The linear least squares problem in the data term requires a matrix-free solver in order to control memory consumption, and Conjugate Gradients is frequently used for this purpose [11, 12]. In this work we show that using the Simultaneous Algebraic Reconstruction Technique (SART, [13, 14]) for this problem yields better results, especially in reconstructions from a sparse numbers of projections. While SART has historically played an important role in solving the unregularized CT problem [15, 16], we demonstrate how to use it for solving the data term proximal operator, which to our knowledge has not been done before.

We provide the following contributions:

• 1. We introduce a 3D structure tensor prior into tomographic reconstruction problems, derive its proximal operator, and show its effectiveness in reconstructing specific structural features.

• 2. We show how to use SART for solving the proximal operator for the data term, and demonstrate improvements in sparse-view reconstructions.

• 3. We validate the efficacy of our algorithm and show superior reconstruction quality compared to existing popular methods and software packages.

2 Related Work

X-ray tomography reconstruction has received extensive attention since the first practical medical CT device was invented in the early 1970s by Hounsfield. There are two general approaches for tomography reconstruction: transform-based methods and iterative methods [1, 2]. Transform-based methods rely on the Radon transform and its inverse, introduced in 1917. The most widely used 3D cone beam reconstruction method is the filtered backprojection algorithm introduced by Feldkamp, Davis, and Kress and known as FDK [17]. Transform methods are usually viewed as much faster than iterative methods, and have therefore been the method of choice for X-ray scanner manufacturers [18].

Iterative methods on the other hand use algebraic techniques to solve the reconstruction problem. They generally model the problem as a linear system and solve it using established numerical linear algebraic methods [2]. One challenge for using iterative methods in computed tomography is the memory consumption of the system matrix. This limits the range of available algorithms to matrix-free solvers, in which the data fidelity term is represented procedurally instead of explicitly. The Algebraic Reconstruction Technique (ART) and its many variants are among the best known iterative reconstruction algorithms [13, 14, 19,20,21,22]. They use variations of the projection method of Kaczmarz, have modest memory requirements, and have been shown to yield better reconstruction results than transform-based methods. They are matrix free, and work without having to explicitly store the system matrix.

The importance of priors for state-of-the-art CT reconstruction cannot be overstated, especially for sparse-view and super-resolution reconstruction. In this setting, the number of pixels in the projection image is significantly lower than the number of voxels in the volume to be reconstructed, so the system $Ax=b$ is under-determined, and the un-regularized least squares problem is ill-posed. Regularizers (priors) are needed to restrict the solution space to a single point, but also the choice of solver can influence which solution within the null space of $A^TA$ is preferred.

Proximal algorithms have been widely used in many problems in machine learning and signal processing [8, 9, 23, 24]. In particular, they have also been used in tomography reconstruction. For example, [11] used the Alternating Direction Method of Multipliers (ADMM) [8] with a Total Variation prior, where the data term was optimized using Conjugate Gradient (CG) [25]. [6] discussed using the Chambolle-Pock algorithm [26] for tomography reconstruction with different priors. [27] used ADMM with Preconditioned Conjugate Gradients [25] for optimizing the weighted least squares data term. [28] used Linearized ADMM [9] (also known as Inexact Split Uzawa [29]) with Ordered Subset-based methods [30] for optimizing the data term and FISTA [31] for optimizing the prior term. However, none of these methods used SART as their data term solver within a proximal framework. In this article, we demonstrate several advantages of using SART over CG for this subproblem, including most notably an improved reconstruction quality.

Recently, some methods based on deep learning have been developed for CT reconstruction problems [32,33,34,35]. While some promising initial results have been demonstrated, current versions are strongly data dependent, e.g. with respect the noise level in the input. We also note that many applications of CT require a fairly conservative behavior of the reconstruction algorithm, i.e. algorithms should not “invent” structures. We are not aware of deep learning approaches that can make such guarantees, while regularizers for optimization-based approaches (including the structure tensor prior in this work) can easily be designed to favor the “simplest” reconstruction that satisfies the observed measurements.

There are currently a number of open source software packages for tomography reconstruction. SNARK09 [36] is one of the oldest. It has several algorithms implemented for 2D reconstruction, but very little support for 3D reconstruction. The Reconstruction ToolKit (RTK) [12] is a high performance C++ toolkit focusing on 3D cone beam reconstruction that is based on the image processing package Insight ToolKit (ITK). It includes implementations of several algorithms, including FDK, SART, and an ADMM TV-regularized solver with CG [11]. The ASTRA toolbox [37] is a Matlab-based GPU-accelerated toolbox for tomography reconstruction. It includes implementations of several algorithms, including SART, SIRT, FDK, FBP, among others. However, neither of these packages uses SART for the data term, or supports structure tensor regularization. We demonstrate that the combination of these two methods results in marked improvements for the reconstruction of thin features.

3 Review of Proximal Methods

With the CT reconstruction problem expressed as an optimization problem (1), we turn to the question of finding appropriate solvers. Like several recent approaches, we rely on proximal algorithms [8], namely the first-order primal-dual algorithm proposed by Chambolle and Pock [26] (henceforth referred to as the CP algorithm). Proximal algorithms are able to solve complex optimization problems by splitting them into several smaller and easier sub-problems, that are solved independently, and then combined to find a solution to the original problem.

These simple sub-problems take the form of proximal operators [8]:

$$\begin{aligned} {{\mathrm{\mathbf {prox}}}}_{\zeta h}(u) \triangleq \mathop {\text {argmin}}_x h(x) + \frac{1}{2\zeta } \Vert x-u \Vert _2^2, \end{aligned}$$

(2)

where $u\in \mathbb {R}^n$ is the input to the function and $\zeta \in \mathbb {R}$ is a weighting parameter. For the CP algorithm to work, we need to determine and implement two proximal operators: The proximal operator for the data term: ${{\mathrm{\mathbf {prox}}}}_{\tau f}(u)$, and the proximal operator for the convex conjugate [38] function $g^{*}(\cdot )$ of $g(\cdot )$ defined as: ${{\mathrm{\mathbf {prox}}}}_{\mu g^{*}}(u)$. By using different regularization functions $g(\cdot )$ and matrices M, we can plug in different priors based on different models of what the reconstructed volume should look like.

4 Method

4.1 Motivation and Overview

The main components of our proximal framework are the regularization term and the data term.

Regularization Term. Our framework can easily incorporate different regularizers that have been used before in tomography reconstruction, e.g. Anisotropic Total Variation (ATV), Isotropic Total Variation (ITV), and Sum of Absolute Differences (SAD). Please see the supplement for more details on these. In addition, in Sect. 4.2, we propose a new 3D structure tensor prior to better handle thin structures.

Data Term. The proximal operator for the data term ${{\mathrm{\mathbf {prox}}}}_{\tau f}(u)$ has traditionally been solved using Conjugate Gradient (CG) [27]. In particular, it can be cast as a least squares problem, and solved using CGLS [39]. However, we find that CG does not in general converge to the global optimum for the tomography data term proximal operator, although it is a convex problem (see supplemental material and [40] for experiments with two different implementations of CG as well as the tomography system itself). These problems can be traced back to two factors, that are both related to the size of the linear system in computed tomography problems:

• CG in general is known to have issues with large systems [41, 42]. Then, it requires a good preconditioner for large and sparse systems. For tomography, preconditioning is usually not an option, since it is infeasible to store the system matrix A, and CG is instead used in a matrix-free fashion. In fact support for matrix-free operation is one of the primary motivators for using CG in this context, but it limits the choice of preconditioner to e.g. Jacobi preconditioning, which is not very effective for tomography matrices.

• As another consequence of needing to operate in matrix free mode, the matrices themselves are laden with numerical noise. Specifically, solving the least squares problem with a system matrix $\mathbf{A}^T\mathbf{A}$ requires the procedural implementation of two operations: $\mathbf{A}\cdot \mathbf{x}$ (projection) and $\mathbf{A}^T\cdot \mathbf{y}$ (backprojection), where $\mathbf{x}$ is a volume and $\mathbf{y}$ is the set of projection images. Because of slight numerical discrepancies between the implementations of these two procedural operators, the resulting matrices are not generally exact transposes of each other. CG does tend to be more sensitive to this issue than other solvers.

4.2 Structure Tensor Prior (STP)

The structure tensor [43] $S_{K}(x_{i})\in \mathbb {S}_{+}^{3}$ for a 3D volume at voxel i is a $3\times 3$ positive semi-definite matrix that captures the local structure around a voxel, and is defined as:

$$\begin{aligned} \begin{aligned} S_{K}(x_{i}) =&\sum _{j\in \mathcal {N}(q_{i})}K(q_{j}-q_{i})\left( \nabla x_{j}\nabla x_{j}^{T}\right) , \end{aligned} \end{aligned}$$

(3)

where $q_{i}=[i_{1},i_{2},i_{3}]^{T}\in \mathbb {R}^{3}$ is the coordinate vector of voxel i, $K(q_{j}-q_{i}):\mathbb {R}^{3}\rightarrow \mathbb {R}$ is a 3D rotationally-symmetric smoothing kernel that down-weights the contributions of voxel j in the set $\mathcal {N}(q_{i})$ of the l neighbors of the voxel i and $\nabla x_{j}\in \mathbb {R}^{3}$ is the local gradient at voxel j. So we can regard the structure tensor as a weighted average of the outer product of the local gradients at the neighborhood of the voxel.

The STP regularizer was introduced by [44, 45]. It includes the standard TV as a special case, when the smoothing kernel is a Dirac delta i.e. it is a local structure tensor at each voxel [45]. Intuitively, the STP tries to estimate the volume such that its structure tensor is low rank, by minimizing the deviation of voxel values in the region around it. We will introduce the STP and develop its solver by extending it from the case of images in [44, 45] to 3D volumes and by employing more efficient proximal algorithms for its computation.

The STP at a voxel i is defined as the $\ell _{p}$ norm of the square roots of the eigenvalues of the structure tensor $S_{K}(x_{i})$ defined in Eq. (3). Let $\varLambda \left( S_{K}(x_{i})\right) \in \mathbb {R}^{3}$ be the vector of eigenvalues of $S_{K}(x_{i})$:

$$\begin{aligned} STP_{p}(x_{i})=\Vert \sqrt{\varLambda \left( S_{K}(x_{i})\right) }\Vert _{p} \end{aligned}$$

(4)

To represent the STP in a form that fits Eq. (1), we define the “patch-based Jacobian” [45] as a linear map $J_{K}:\mathbb {R}^{n}\rightarrow \mathbb {R}^{nl\times 3}$ between the space of volumes and a set of weighted gradients that are computed from the l-neighborhood of each of the n voxels. We can write the patch-based Jacobian at voxel i as $J_{K}(x_{i})\in \mathbb {R}^{l\times 3}$ by stacking the weighted local gradients side-by-side:

$$\begin{aligned} J_{K}(x_{i})=\left[ \begin{array}{ccc} \kappa _{j_{1}}\nabla x_{j_{1}}&\cdots&\kappa _{j_{l}}\nabla x_{j_{l}}\end{array}\right] ^{T}\in \mathbb {R}^{l\times 3}, \end{aligned}$$

(5)

where $\{j_{1},\ldots ,j_{l}\}=\mathcal {N}(q_{i})$ denotes the indices of the neighbors of voxel i (including i itself), and $\kappa _{j_{k}}=\sqrt{K(q_{i}-q_{j_{k}})}$. The patch-based Jacobian for the whole volume $J_{K}x\in \mathbb {R}^{nl\times 3}$ is now formed by stacking “local" components $J_{K}(x_{i})$ on top of each other. Using this linear operator $J_{K}$, Eq. (3) can be rewritten as follows:

$$\begin{aligned} S_{K}(x_{i})=J_{K}(x_{i})^{T}J_{K}(x_{i}), \end{aligned}$$

(6)

which means that the singular values of $J_{K}(x_{i})$ are actually equal to the square root of the eigenvalues of $S_{K}(x_{i})$ in Eq. (4).

Thus we get the definition of $STP_{p}$ as

$$\begin{aligned} STP_{p}(x)=\sum _{i=1}^{n}\Vert J_{K}(x_{i})\Vert _{\mathcal {S}_{p}}, \end{aligned}$$

(7)

where $\Vert \cdot \Vert _{\mathcal {S}_{p}}$ is the Schatten $p-$norm. In our experiments, we set $p=1$ which is equivalent to the nuclear norm.

We can write this regularizer in a more compact compound norm $STP_{p}(x)=\Vert J_{K}x\Vert _{1,p}$ where the mixed norm $\ell _{1}-S_{p}$ or (1, p)-norm is defined for a matrix $J=J_{K}x\in \mathbb {R}^{nl\times 3}$ as follows:

$$\begin{aligned} \Vert J\Vert _{1,p}=\Vert J_{K}x\Vert _{1,p}=\sum _{i=1}^{n}\Vert J_{i}\Vert _{\mathcal {S}_{p}}, \end{aligned}$$

(8)

where $J_{i}\in \mathbb {R}^{l\times 3}$ represents the patch-based Jacobian at some voxel i. With q satisfying $\frac{1}{p} + \frac{1}{q} = 1$, the mixed norm $(\infty ,q)$ is the dual norm of the mixed norm (1, p). We can rewrite the Eq. (8) as in [46]:

$$\begin{aligned} {\Vert J\Vert _{1,p}= \max _{H\in \mathcal {B}_{\infty ,q}} \langle H,J\rangle _{\mathbb {R}^{nl\times 3}} = \max _{H\in \mathcal {B}_{\infty ,q}} \sum _{i} tr(H_{i}^{T} J_{i})} \end{aligned}$$

(9)

where $\mathcal {B}_{\infty ,q}$ is the $(\infty ,q)$ unit-norm ball.

Now, we define the regularizer function $g(\cdot )$ as:

$$\begin{aligned} g(J_K x) = \lambda \Vert J \Vert _{1,p} = \max _{H\in \lambda \mathcal {B}_{\infty ,q}} \langle H,J\rangle _{\mathbb {R}^{nl\times 3}} \end{aligned}$$

(10)

where: $\lambda \mathcal {B}_{\infty ,q}$ refers to the $(\infty ,q)$-norm ball with a radius of $\lambda$. Thus, the optimization problem in Eq. (1) can be rewritten as follows:

$$\begin{aligned} {\min _{x} \left[ \Vert Ax-b\Vert _{2}^{2} + \max _{H\in \lambda \mathcal {B}_{\infty ,q}} \langle H,J\rangle _{\mathbb {R}^{nl\times 3}} \right] } \end{aligned}$$

(11)

where $H,J\in \mathbb {R}^{nl\times 3}$. This formulation is equivalent to:

$$\begin{aligned} {\min _{x} \max _{H} \left[ \Vert Ax-b\Vert _{2}^{2} + \langle H,J\rangle _{\mathbb {R}^{nl\times 3}} - \imath _{\mathcal {\lambda B}_{\infty ,q}}(H) \right] } \end{aligned}$$

(12)

where: $\imath _{\mathcal {\lambda B}_{\infty ,q}}(H)$ is the indicator function of the ball $\mathcal {\lambda B}_{\infty ,q}$. Otherwise the convex conjugate of the STP regularizer $g(\cdot )$ is defined by:

$$\begin{aligned} { g^*(H) = \max _{J\in \mathbb {R}^{nl\times 3}} \langle H,J\rangle - g(J),} \end{aligned}$$

(13)

From Eqs. (12) and (13), we deduce that $g^*(\cdot )$ is equal to the indicator function $\imath _{\mathcal {\lambda B}_{\infty ,q}(\cdot )}$. Thus, the proximal operator of $g^*(\cdot )$ is the projection on the convex ball $\mathcal {\lambda B}_{\infty ,q}$:

$$\begin{aligned} {{\mathrm{\mathbf {prox}}}}_{\eta g^{*}}(H)=\Pi _{\mathcal {\lambda B}_{\infty ,q}}\left( H\right) , \end{aligned}$$

(14)

In our case $p=1$ and $q=\infty$, so that the projection is simply performed by soft thresholding the singular values of each component of H.

Algorithm 1 outlines the overall steps to solve the tomography problem with the STP prior as defined in Eq. (1), where f(x) is the data term and g(Mx) is the STP regularizer. Detailed derivations of the structure tensor prior are provided in the supplement.

4.3 SART For The Data Term

We now show how to use the SART algorithm to solve the data term proximal operator $\text {prox}_{\lambda f}(u)$. In particular, we want to solve:

$$\begin{aligned} \text {prox}_{\lambda f}(u)=\mathop {\text {argmin}}_{x}\Vert Ax-{b}\Vert _{2}^{2}+\frac{1}{2\lambda }\Vert x-u\Vert _{2}^{2}. \end{aligned}$$

(15)

Recall that SART solves a minimum norm problem. By introducing new variables: $y = \sqrt{2\lambda }(b - Ax)$ and $z = x-u$, and after further manipulations, it can be shown that solving the optimization problem in Eq. (15) is equivalent to solving:

$$\begin{aligned} {\min }_{y,z}&\left\| \left[ \begin{array}{c} y\\ z \end{array}\right] \right\| _{2}^{2} \quad {\text {subject to:}}&\left[ \begin{array}{cc} I&\sqrt{2\lambda }A\end{array}\right] \left[ \begin{array}{c} y\\ z \end{array}\right] =\sqrt{2\lambda }\left( {b}-Au\right) , \end{aligned}$$

(16)

which can be written as:

$$\begin{aligned} {\min }_{\tilde{x}}&\left\| \tilde{x}\right\| _{2}^{2} \quad {\text {subject to:}}&\tilde{A}\tilde{x}={\tilde{b}}, \end{aligned}$$

(17)

where $\tilde{x}\in \mathbb {R}^{m+n}$, $\tilde{A}\in \mathbb {R}^{m\times m+n}$, and ${\tilde{b}}\in \mathbb {R}^{m}$. This is now an under-determined linear system, and can be solved using SART.

Algorithm 2 summarizes the steps for the modified SART to solve the proximal operator.

5 Experiments

The experiments were run on a machine with two Intel Xeon E5-2697 processors (56 cores overall) and 128 GB of RAM. We present two kinds of experiments:

• 1. focusing on sparse view reconstruction using the 3D Shepp-Logan phantom and the scans of the rose in Fig. 1(c).

• 2. focusing on super resolution using a simulated 3D Fresnel zone plate, scans of the artificial rose, the plumeria flower, and the toothbrush((a), (b), and (d) in Fig. 1, respectively).

5.1 Sparse-View Reconstruction

We first validate our choice of SART as the solver for the data term in Eq. (1). We run experiments comparing SART head-to-head with Conjugate Gradient (CG) in a sparse-view setting, using the TV regularizer in both cases. In particular, we show the reconstruction quality, measured in PSNR and SSIM, as a function of the number of projections available. We use the implementation provided in RTK and compare to our framework using the SART proximal operator solver. The size of the 3D Shepp-Logan volume is $300 \times 300 \times 300$ with voxel size of $1 \times 1 \times 1$ mm, while the volume size of the rose is $436\times 300 \times 365$ with voxel size of $0.3 \times 0.3 \times 0.3$ mm.

Fig. 2.

A sample slice with different number of projections from a 3D Shepp-Logan (a) and scanned rose (b). The PSNR and SSIM values are shown at the top of each image. For each data, we compare PCG-TV (top) with our proposed PSART-TV method (bottom). For Shepp-Logan data, 90, 60, 45, and 30 projections as input. For the real scanned rose, 90, 60, 45 were used projections as input. (Color figure online)

As Fig. 2 shows, SART as a solver for the data term provides better quality than CG, which is expected given the known limitations of CG, whereby it is prone to overfitting the projection noise in the data, which becomes even more pronounced when the number of projections is smaller. For more details on the experimental parameters and extensive experimental results, we refer readers to the supplemental material.

5.2 Super Resolution Experiments

Now we run experiments to compare the new regularizer in a super-resolution setting. We chose the following algorithms for our comparison:

• PSART-STP: this is our complete framework using the Structure Tensor prior.

• PSART-SAD: this is our framework with the previously used SAD (Sum of Absolute Differences) prior [40]. It was shown before [47] that SAD performs better than TV, and so we chose it as the best alternative prior to compare to STP.

Fig. 3.

2D slice from the reconstructed 3D Fresnel zone plate (top) and its Sobel filtered visualization (bottom). The green ring in each image represents the smallest feature we can extract according to the Nyquist limit. PSNR and SSIM of slice images (top) from (a) to (e): FDK (17.5978, 0.9354), SART (19.5440, 0.9582), PCG-TV (22.0659, 0.9756), PSART-SAD (22.6293, 0.9781), PSART-STP (24.8331, 0.9864), Reference volume. The display window is [0, 0.8]. For Sobel filtered images, smoother features in the superresolution frequencies for the PSART results indicate a better suitability for post-processing tasks such as segmentation. (Color figure online)

We compare results from our framework to state-of-the-art algorithms and comparable implementations in RTK, namely:

• Cone Beam Filtered Back Projection (FDK) [17], as the FDK algorithm is still the most commonly used method in practical CT scanners [18].

• Plain SART with no priors (SART).

• ADMM with ATV prior (PCG-TV) using Conjugate Gradient (CG) [11].

The initial volume for all methods is set to 0. For choosing the hyper parameters in all the algorithms, we experiment with a range of values and pick the ones with the best performance.

First, we use a synthetic volume dataset to demonstrate the super-resolution capabilities of the PSART framework. Specifically, we show a cone-beam tomographic reconstruction of a 3D version of the Fresnel zone “plate” (a 2D cross-section is shown in Fig. 3(f)). After adding Gaussian noise with standard deviation $\sigma =2$, the projection images are downsampled with the scale factor as 6.4 using bicubic interpolation, which are the input for our experiments. We run the SART algorithm with 180 projections with the original size until convergence (15 iterations), and considered the resulting reconstruction the reference volume for numerical comparisons. More details for the parameters can be found in the supplement.

Fig. 4.

RMSE of the reconstructed volume as a function of iteration (left) and running time (right) for the various methods.

Fig. 5.

a-f: Representative slice visualization in the sagittal plane for the volume and its closeup view for the artificial flower data reconstructed by FDK, SART, PCG-TV, PSART-SAD, PSART-STP, and the reference volume, respectively.

Figure 3 (top) shows a visual comparison of the different reconstruction methods, together with the obtained PSNR and SSIM values. As can be seen, the PSART framework, with SART as a solver for the data fidelity term outperforms the other state-of-the-art methods, even when used in combination with the SAD regularizer. The use of the STP provides an additional quality boost. In particular, we note the improved reconstruction quality for frequencies above the Nyquist limit for the 2D pixel sampling rate (green circle).

These results are further confirmed in Fig. 3 (bottom). Since tomographic reconstruction is often just the first step in an image analysis pipeline, we tested how robust and reliable the super-resolution information is for further processing such as image segmentation. As a stand-in for more sophisticated segmentation methods, we applied a 3D variant of the Sobel filter [48] to extract the boundaries between the rings. Smoother results from the Sobel filter indicate that it will be easier to trace thin structures through the volume in a segmentation process. We can again see that PSART generates significant super-resolution information, with PSART-STP performing best.

Figure 4 shows the evolution of the RMSE plotted against the iteration and running time during the zone plate volume reconstruction for each method. The PSART methods (PSART-SAD and PSART-STP) converge faster than PCG-TV in terms of running time, and PSART-STP converges slower than PSART-SAD but finds a solution with lower RMSE.

We ran another round of experiments on real datasets that were scanned using a Nikon X ray CT, namely artificial flowers, a plumeria flower, and a toothbrush. These objects have the structural features we are interested in modeling i.e. thin sheets and thin tubes.

Fig. 6.

Representative slice visualization in the axial plane for (f): the reference volume and (a)-(e): the volumes reconstructed by FDK, SART, PCG-TV, PSART-SAD, and PSART-STP, respectively. From top to bottom: volume visualization, its edge detection, and the closeup views.

The reconstructed volume size for artificial rose is $415\times 314\times 393$. 120 original-size projection images are used as input for PSART-STP and the best reconstructed result is used as the reference volume for our comparison. Figure 5 shows reconstruction results from different methods in the sagittal plane, and the edge detection results from applying Sobel filter are provided in the supplementary material. We can see clearly that our PSART-SAD and PSART-STP achieve better performance than existing methods. Figure 6 shows the results in the axial plane. The reconstructed volume size for the plumeria is $406\times 259\times 336$. Figure 7 (a) shows the comparison to the state-of-the-art PCG-TV method. For better visualization and comparisons, we generated a reference volume by running the PSART-STP method with 360 original images as input until convergence.The reconstructed volume size for the toothbrush is $690\times 668\times 776$. Figure 7 (b) shows the comparison between PCG-TV and the proposed PSART-STP. Again, compared to PCG-TV, our method achieves shaper results.

Fig. 7.

Reconstruction results for the real flower (a) and toothbrush (b) in the sagittal, axial, and coronal planes, respectively.

In summary, for both simulated and real scanned data, our PSART reconstructions (PSART-SAD and PSART-STP) consistently give better results than the equivalent PCG-TV. PSART-SAD works better than PCG-TV, confirming earlier results about the SAD regularizer [40, 47]. Our PSART-STP method produces the best results in terms of both quantitative (PSNR and SSIM) and qualitative comparisons (visualization of volume and edge detection filter), allowing for super-resolved reconstruction of thin structures shown in Fig. 1.

6 Conclusions and Future Work

We have presented a flexible proximal framework for robust 3D cone beam reconstruction of super-resolved thin features. Our two main contributions are (a) introduction of the 3D structure tensor as a regularizer for the tomographic reconstruction problem, and (b) the use of SART for the data-fidelity subproblem in the proximal framework. We have experimentally demonstrated that the 3D structure tensor prior is best suited for reconstructing specific structural features such as thin sheets and filaments, and that using SART provides better reconstructions than other solvers, especially in the case of under-determined tomographic reconstruction from a small number of projections.

We have experimentally compared our framework with the popular RTK open-source software toolkit, both on real and simulated datasets, using different state-of-the-art priors. We showed the robustness of our algorithms in terms of reconstruction quality.

In the future, we plan to extend our framework by adding a GPU version providing a higher level of parallelism.