Simultaneous 3D Reconstruction for Water Surface and Underwater Scene

Abstract

This paper presents the first approach for simultaneously recovering the 3D shape of both the wavy water surface and the moving underwater scene. A portable camera array system is constructed, which captures the scene from multiple viewpoints above the water. The correspondences across these cameras are estimated using an optical flow method and are used to infer the shape of the water surface and the underwater scene. We assume that there is only one refraction occurring at the water interface. Under this assumption, two estimates of the water surface normals should agree: one from Snell’s law of light refraction and another from local surface structure. The experimental results using both synthetic and real data demonstrate the effectiveness of the presented approach.

1 Introduction

Consider the imaging scenario of viewing an underwater scene through a water surface. Due to light refraction at the water surface, conventional land-based 3D reconstruction techniques are not directly applicable to recovering the underwater scene. The problem becomes even more challenging when the water surface is wavy and hence constantly changes the light refraction paths. Nevertheless, fishing birds are capable of hunting submerged fish while flying over the water, which suggests that it is possible to estimate the depth for underwater objects in the presence of the water surface.

In this paper, we present a new method to mimic a fishing bird’s underwater depth perception capability. This problem is challenging for several reasons. Firstly, the captured images of the underwater scene are distorted due to light refraction through the water. Under the traditional triangulation-based scheme for 3D reconstruction, tracing the poly-linear light path requires the 3D geometry of the water surface. Unfortunately, reconstructing a 3D fluid surface is an even harder problem because of its transparent characteristic [23]. Secondly, the water interface is dynamic and the underwater scene may be moving as well. Hence, real-time data capture is required.

In addition to the biological motivation [19] (e.g. the above example of fishing birds), the problems of reconstructing underwater scene and of reconstructing water surface both have attracted much attention due to applications in computer graphics [14], oceanography [17] and remote sensing [38]. These two problems are usually tackled separately in computer vision. On the one hand, most previous works reconstruct the underwater scene by assuming the interface between the scene and the imaging sensor is flat [4, 7, 12]. On the other hand, existing methods for recovering dynamic water surfaces typically assume that the underwater scene is a known flat pattern, for which a checkerboard is commonly used [10, 24]. Recently, Zhang et al. [44] make the first attempt to solve the two problems simultaneously using depth from defocus. Nevertheless, their approach assumes that the underwater scene is stationary and an image of the underwater scene with a flat water surface is available. Because of the assumptions of the flat water surface or the flat underwater scene, none of the above mentioned methods can be directly applied to solving the problem of jointly recovering the wavy water surface and the natural underwater dynamic scene. Indeed, the lack of any existing solution to the above problem forms the motivation of our work.

In this paper, we propose to employ multiple viewpoints to tackle such a problem. In particular, we construct a portable camera array to capture the images of the underwater scene distorted by the wavy water surface. Our physical setup does not require any precise positioning and thus is easy to use. Following the conventional multi-view reconstruction framework for on-land objects, we first estimate the correspondences across different views. Then, based on the inter-view correspondences, we impose a normal consistency constraint across all camera views. Suppose that the light is refracted only once while passing through the water surface. We present a refraction-based optimization scheme that works in a frame-by-frame¹ fashion, enabling us to handle the dynamic nature of both the water surface and the underwater scene. More specifically, our approach is able to return the 3D positions and the normals of a dynamic water surface, and the 3D points of a moving underwater scene simultaneously. Encouraging experimental results on both synthetic and real data are obtained.

2 Related Work

Fluid Surface Reconstruction. Reconstructing dynamic 3D fluid surface is a difficult problem because most fluids are transparent and exhibit a view-dependent appearance. Therefore, traditional Lambertian-based shape recovery methods do not work. In the literature, the problem is usually solved by placing a known flat pattern beneath the fluid surface. Single camera [17, 26] or multiple cameras [10, 24, 30] are used to capture the distorted versions of the flat pattern. 3D reconstruction is then performed by analyzing the differences between the captured images and the original pattern. Besides, several methods [39, 43, 45], rather than using a flat board, propose to utilize active illumination for fluid shape acquisition. Precisely positioned devices are usually required in these methods, such as Bokode [43] and light field probes [39]. In contrast, our capturing system uses cameras only and thus is easy to build. More importantly, all of the above methods focus on the fluid surface only, whereas the proposed approach can recover the underwater scene as well.

Underwater Scene Reconstruction. Many works recover the 3D underwater scene by assuming the water surface is flat and static. For example, several land-based 3D reconstruction models, including stereo [12], structure-from-motion [7, 32], photometric stereo [27], have been extended for this task, which is typically achieved by explicitly accounting for light refraction at the flat interface in their methods. The location of the flat water surface is measured beforehand by calibration [12] or parameterization [32]. Asano et al. [4] use the water absorption property to recover depths of underwater objects. However, the light rays are assumed to be perpendicular to the flat water surface. In contrast, in our new approach, the water surface can be wavy and is estimated along with the underwater scene.

There are existing methods targeting at obtaining the 3D structure of underwater objects under a wavy surface. Alterman et al. [3] present a stochastic method for stereo triangulation through wavy water. However, their method can produce only a likelihood function of the object’s 3D location. The dynamic water surface is also not estimated. More recently, Zhang et al. [44] treat such a task in monocular view and recover both the water surface and the underwater scene using a co-analysis of refractive distortion and defocus. As mentioned in Sect. 1, their method is limited in practical use. Firstly, to recover the shape of an underwater scene, an undistorted image captured through a flat water surface is required. However, such an image is very hard to obtain in real life, if not impossible. Secondly, the image plane of their camera has to be parallel with the flat water surface in their implementation, which is impractical to achieve. In contrast, our camera array-based setup can be positioned casually and is easy to implement. Thirdly, for the water surface, their method can return the normal information of each surface point only. The final shape is then obtained using surface integration, which is known to be prone to error in the absence of accurate boundary conditions. In comparison, our approach bypasses surface integration by jointly estimating the 3D positions and the normals of the water surface. Besides, the methods in [3] and [44] assume a still underwater scene, while both the water surface and the underwater scene can be dynamic in this paper. Hence, our proposed approach is applicable to a more general scenario.

Our work is also related to other studies on light refraction, e.g. environment matting [8, 29], image restoration under refractive distortion [11, 37], shape recovery of transparent objects [16, 21, 28, 36, 40] and gas flows [18, 41], and underwater camera calibration [2, 33, 42].

3 Multi-view Acquisition Setup

As shown in Fig. 1(a), to capture the underwater scene, we build a small-scale, $3\times 3$ camera array (highlighted in the red box) placed above the water surface. The cameras are synchronized and capture video sequences. For clarity, in the following, we refer to the central camera in the array as the reference view, and the other cameras as the side views. Similar to the traditional multi-view triangulation-based framework for land-based 3D reconstruction, the 3D shapes of both the water surface and the underwater scene are represented in the reference view. Notice that an additional camera, referred to as the evaluation camera, is also used to capture the underwater scene at a novel view, which is for accuracy assessment in our real experiments and is presented in detail in Sect. 5.2.

Fig. 1.

Acquisition setup using a camera array (a) and the corresponding imaging model illustrated in 2D (b). The evaluation camera in (a) is for accuracy evaluation only and is not used for 3D shape recovery.

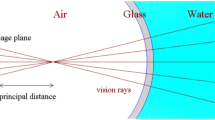
Figure 1(b) further illustrates the imaging model in 2D. We set Camera 1 as the reference camera and Camera $k\in \mathrm {\Pi }$ as the side cameras, where $\mathrm {\Pi }$ is $\{2,3,\cdots \}$. For each pixel $(x_i^1,y_i^1)$ in Camera 1, the corresponding camera ray $\mathbf {e}_i^1$ gets refracted at the water surface point $\mathbf {S}_i$. Then the refracted ray $\mathbf {r}_i^1$ intersects with the underwater scene at point $\mathbf {P}_i$. The underwater scene point $\mathbf {P}_i$ is also observed by the side cameras through the same water surface but at different interface locations.

Our approach builds upon the correspondences across multiple views. Specifically, we compute the optical flow field between the reference camera and each of the side cameras. Take side Camera 2 for example, for each pixel $(x_i^1,y_i^1)$ of Camera 1, we estimate the corresponding projection $(x_i^2,y_i^2)$ of $\mathbf {P}_i$ in Camera 2, by applying the variational optical flow estimation method [6]. Suppose that the intrinsic and extrinsic parameters of the camera array are calibrated beforehand and fixed during capturing, we can easily compute the corresponding camera ray $\mathbf {e}_i^2$ of ray $\mathbf {e}_i^1$. The same procedure of finding correspondences applies to the other side views and each single frame is processed analogously.

After the above step, we obtain a sequence of the inter-view correspondences of the underwater scene. Below, we present a new reconstruction approach that solves the following problem: Given the dense correspondences of camera rays {$\mathbf {e}^1\Leftrightarrow \mathbf {e}^k, k\in \mathrm {\Pi }$} of each frame, how to recover the point set $\mathbf {P}$ of the underwater scene, as well as the depths and the normals of the dynamic water surface?

4 Multi-view Reconstruction Approach

We tackle the problem using an optimization-based scheme that imposes a normal consistency constraint. Several prior works [24, 30] have used such a constraint for water surface reconstruction. Here we show that, based on the similar form of normal consistency, we can simultaneously reconstruct dynamic water and underwater surfaces using multi-view data captured from a camera array. The key insight is that, at each water surface point, the normal estimated using its neighboring points should agree with the normal obtained based on the law of light refraction.

4.1 Normal Consistency at Reference View

As mentioned in Sect. 3, we represent the water surface by a depth map $\mathbf {D}$ and the underwater scene by a 3D point set $\mathbf {P}$, both in the reference view. In particular, as shown in Fig. 1(b), for each pixel in Camera 1, we have four unknowns: the depth $\mathbf {D}_i$ of point $\mathbf {S}_i$ and the 3D coordinates of point $\mathbf {P}_i$.

Given the camera ray $\mathbf {e}_i^1$, we can compute the 3D coordinates of $\mathbf {S}_i$ when a depth hypothesis $\mathbf {D}_i$ is assumed. At the same time, connecting the hypothesized point $\mathbf {P}_i$ and point $\mathbf {S}_i$ gives us the refracted ray direction $\mathbf {r}_i^1$. Then, the normal of $\mathbf {S}_i$ can be computed based on Snell’s law, which is called the Snell normal in this paper and denoted by $\mathbf {a}_i^1$. Here superscript 1 in $\mathbf {a}_i^1$ indicates that $\mathbf {a}_i^1$ is estimated using ray $\mathbf {e}_i^1$ of Camera 1. Consider the normal $\mathbf {a}_i^1$, the camera ray $\mathbf {e}_i^1$ and the refracted ray $\mathbf {r}_i^1$ are co-planar as stated in Snell’s law. Hence, we can express $\mathbf {a}_i^1$ as a linear combination of $\mathbf {e}_i^1$ and $\mathbf {r}_i^1$, i.e.  $\mathbf {a}_i^1=\varPsi (\eta _a\mathbf {e}_i^1-\eta _f\mathbf {r}_i^1)$, where $\eta _a$ and $\eta _f$ are the refractive index of air and fluid, respectively. We fix $\eta _a=1$ and $\eta _f=1.33$ in our experiments. $\varPsi ()$ is a function defining the operation of vector normalization.

On the other hand, the normal of a 3D point can be obtained by analyzing the structure of its nearby points [31]. Specifically, suppose that the water surface is spatially smooth, at each point $\mathbf {S}_i$, we fit a local polynomial surface from its neighborhood and then estimate its normal based on the fitted surface. In practice, for a 3D point (x, y, z), we assume its z component can be represented by a quadratic function of the other two components:

$$\begin{aligned} z(x,y)=w_1x^2+w_2y^2+w_3xy+w_4x+w_5y+w_6, \end{aligned}$$

(1)

where $w_1,w_2\dots ,w_6$ are unknown parameters. Stacking all quadratic equations of the set $\mathcal {N}_i$ of the neighboring points of $\mathbf {S}_i$ yields:

$$\begin{aligned} \small \mathbf {A}(\mathcal {N}_i)\mathbf {w}(\mathcal {N}_i)=\mathbf {z}(\mathcal {N}_i) \Leftrightarrow \begin{bmatrix} x_1^2&y_1^2&x_1y_1&x_1&y_1&1\\&\cdots \\ x_m^2&y_m^2&x_my_m&x_m&y_m&1\\&\cdots \\ \end{bmatrix}\times \begin{bmatrix} w_1\\ w_2\\ :\\ w_6 \end{bmatrix}= \begin{bmatrix} z_1\\ :\\ z_m\\ : \end{bmatrix}, \end{aligned}$$

(2)

where $\mathbf {A}(\mathcal {N}_i)$ is a $\vert \mathcal {N}_i\vert \times 6$ matrix calculated from $\mathcal {N}_i$, and $\vert \mathcal {N}_i\vert$ the size of $\mathcal {N}_i$. $\mathbf {z}(\mathcal {N}_i)$ is a $\vert \mathcal {N}_i\vert$ dimensional vector. After getting the parameter vector $\mathbf {w}(\mathcal {N}_i)$, the normal of point (x, y, z) in this quadratic surface is estimated as the normalized cross product of two vectors: $[1,0,\frac{\partial }{\partial x}z(x,y)]$ and $[0,1,\frac{\partial }{\partial y}z(x,y)]$. Plugging in the 3D coordinates of $\mathbf {S}_i$, we obtain its normal $\mathbf {b}_i^1$, which is referred to as the Quadratic normal in this paper.

So far, given the camera ray set $\mathbf {e}^1$ of Camera 1, we obtain two types of normals at each water surface point, which should be consistent if the hypothesized depth $\mathbf {D}$ and point set $\mathbf {P}$ are correct. We thus define the normal consistency error as:

$$\begin{aligned} E_i^1(\mathbf {D},\mathbf {P},\mathbf {e}_i^1)=\Vert \mathbf {a}_i^1-\mathbf {b}_i^1\Vert _2^2 \end{aligned}$$

(3)

at ray $\mathbf {e}_i^1$. Next, we show how to measure the normal consistency term at the side views using their camera ray sets $\{\mathbf {e}^k,k\in \mathrm {\Pi }\}$, the point set $\mathbf {S}$ estimated from the depth hypothesis $\mathbf {D}$, and the hypothesized point set $\mathbf {P}$.

4.2 Normal Consistency at Side Views

We take side Camera 2 for illustration and the other side views are analyzed in a similar fashion. As shown in Fig. 1(b), point $\mathbf {P}_i$ is observed by Camera 2 through the water surface point $\mathbf {T}_i$. Similarly, we have the Snell normal $\mathbf {a}_i^2$ and the Quadratic normal $\mathbf {b}_i^2$ at $\mathbf {T}_i$.

To compute the Snell normal $\mathbf {a}_i^2$ via Snell’s law, the camera ray $\mathbf {e}_i^2$ and the refracted ray $\mathbf {r}_i^2$ are required. $\mathbf {e}_i^2$ is acquired beforehand in Sect. 3. Considering the point hypothesis $\mathbf {P}_i$ is given, $\mathbf {r}_i^2$ can be obtained if the location of $\mathbf {T}_i$ is known. Hence, the problem of estimating normal $\mathbf {a}_i^2$ is reduced to the problem of locating the first-order intersection between ray $\mathbf {e}_i^2$ and the water surface point set $\mathbf {S}$. A similar problem has been studied in ray tracing [1]. In practice, we first generate a triangular mesh for $\mathbf {S}$ by creating a Delaunay triangulation of 2D pixels of Camera 1. We then apply the Bounding Volume Hierarchy-based ray tracing algorithm [20] to locate the triangle that $\mathbf {e}_i^2$ intersects. Using the neighboring points of that intersecting triangle, we fit a local quadratic surface as described in Sect.  4.1, and the final 3D coordinates of $\mathbf {T}_i$ is obtained by the standard ray-polynomial intersection procedure. Meanwhile, the fitted quadratic surface gives us the Quadratic normal $\mathbf {b}_i^2$ of point $\mathbf {T}_i$.

In summary, given each ray $\mathbf {e}_i^k$ of each side Camera k, we obtain two normals $\mathbf {a}_i^k$ and $\mathbf {b}_i^k$. The congruity between them results in the normal consistency error:

$$\begin{aligned} E_i^k(\mathbf {D},\mathbf {P},\mathbf {e}_i^k)=\Vert \mathbf {a}_i^k-\mathbf {b}_i^k\Vert _2^2,~k\in \mathrm {\Pi }. \end{aligned}$$

(4)

4.3 Solution Method

Here we first discuss the feasibility of recovering both the water surface and the underwater scene using normal consistency at multiple views. Combining the error terms Eq. (3) at the reference view and Eq. (4) at the side views, we have:

$$\begin{aligned} E_i^k(\mathbf {D},\mathbf {P},\mathbf {e}_i^k)=0,~\text {for each}~i\in \mathrm {\Omega }~\text {and}~k\in \mathrm {\Phi }, \end{aligned}$$

(5)

where $\mathrm {\Omega }$ is the set of all pixels of Camera 1, and $\mathrm {\Phi }=\{1\}\cup \mathrm {\Pi }$ the set of camera indices. Let $\bar{\mathtt {i}}=\vert \mathrm {\Omega }\vert$ and $\bar{\mathtt {k}}=\vert \mathrm {\Phi }\vert$ be the size of $\mathrm {\Omega }$ and $\mathrm {\Phi }$, respectively. Assume that each camera ray $\mathbf {e}_i^1$ can find a valid correspondence in all side views, we get a total of $\bar{\mathtt {i}}\times \bar{\mathtt {k}}$ equations. Additionally, recall that we have 4 unknowns at each pixel of Camera 1, so we have $\bar{\mathtt {i}}\times 4$ unknowns. Hence, to make the problem solvable, we should have $\bar{\mathtt {i}}\times \bar{\mathtt {k}}\ge \bar{\mathtt {i}}\times 4$, which means that at least 4 cameras are required. In reality, some camera rays (e.g. those at corner pixels) of the reference view cannot locate a reliable correspondence in all side views because of occlusion or of the field of view. We essentially need more than four cameras.

Directly solving Eq. (5) is impractical due to the complex operations involved in computing the Snell and Quadratic normals. Therefore, we cast the reconstruction problem as minimizing the following objective function:

$$\begin{aligned} \min _{\mathbf {D},\mathbf {P}} \sum _{i\in \mathrm {\Omega }}\sum _{k\in \mathrm {\Phi }}E_i^k(\mathbf {D},\mathbf {P},\mathbf {e}_i^k)+\lambda \sum _{i\in \mathrm {\Omega }}F_i(\mathbf {D},\mathbf {e}_i^1), \end{aligned}$$

(6)

where the first term enforces the proposed normal consistency constraint. The second term ensures the spatial smoothness of the water surface. In particular, we set

$$\begin{aligned} F_i(\mathbf {D},\mathbf {e}_i^1)=\Vert \mathbf {A}(\mathcal {N}_i)\mathbf {w}(\mathcal {N}_i)-\mathbf {z}(\mathcal {N}_i)\Vert _2^2, \end{aligned}$$

(7)

which measures the local quadratic surface fitting error using the neighborhood $\mathcal {N}_i$ of the water surface point $\mathbf {S}_i$. Adding such a polynomial regularization term helps to increase the robustness of our multi-view formulation, as demonstrated in our experiments in Sect. 5.1. Please also note that this smoothness term is only defined w.r.t Camera 1 since we represent our 3D shape in that view. $\lambda$ is a parameter balancing the two terms.

Fig. 2.

Discontinuity of underwater scene points. As indicated by the purple arrow, the red points are interlaced with the green points, although the red and green rays are each emitted from contiguous pixels. (Color figure online)

While it may be tempting to enforce the spatial smoothness of underwater surface points $\mathbf {P}$ computed for different pixels as well, it is not imposed in our approach for the following reason. As shown in Fig. 2, when the light paths are refracted at the water surface, the neighborhood relationship among underwater scene points can be different from the neighborhood relationship among observed pixels in Camera 1. Hence, we cannot simply enforce that the 3D underwater surface points computed for adjacent camera rays are also adjacent.

Optimization. Computing the normal consistency errors in Eq. (6) involves some non-invertible operations such as vector normalization, making the analytic derivatives difficult to derive. To handle such a problem, we use the L-BFGS method [47] with numerical differentiation for optimization. However, calculating numerical derivatives is computationally expensive especially for a large-scale problem. We elaborately optimize our implementation by sharing common intermediate variables in derivative computation at different pixels. In addition, solving Eq. (6) is unfortunately a non-convex problem; hence, there is a chance of getting trapped by local minima. Here we adopt a coarse-to-fine optimization procedure commonly used in refractive surface reconstruction [28, 30, 34]. Specifically, we first downsample the correspondences acquired in Sect. 3 to 1 / 8 of the original resolution. We then use the results under the coarse resolution to initialize the optimization at the final scale.

Notice that the input of Eq. (6) is the multi-view data of a single time instance. Although it is possible to process all frames in a sequence simultaneously by concatenating them into Eq. (6), a large system with high computational complexity will be produced accordingly. In contrast, we process each frame independently and initialize the current frame using the results of the last one. Such a single-shot method effectively reduces the computational cost in terms of running time and memory consumption and, more importantly, can handle moving underwater scenes.

It is also noteworthy that, even when the underwater scene is strictly static, our recovered point set $\mathbf {P}$ could be different for different frames. This is because each point $\mathbf {P}_i$ can be interpreted as the intersection between the refracted ray $\mathbf {r}_i^1$ and the underwater scene, as shown in Fig. 1(b). When the water surface is flowing, because $\mathbf {S}_i$ relocates, the refracted ray direction is altered, and thus the intersection $\mathbf {P}_i$ is changed. Our frame-by-frame formulation naturally handles such a varying representation of point set $\mathbf {P}$.

5 Experiments

The proposed approach is tested on both synthetic and real-captured data. Here we provide some implementation details. While computing the Quadratic normals at both the reference and side views, we set the neighborhood size to $5\times 5$. The parameter $\lambda$ is fixed at 2 units in the synthetic data and 0.1 mm in the real experiments. During the coarse-to-fine optimization of Eq. (6), the maximum number of L-BFGS iterations at the coarse scale is fixed to 2000 and 200 for synthetic data and real scenes, respectively, and is set to 20 at the full resolution in both cases. The linear least squares system Eq. (2) is solved via normal equations using Eigen [15]. As the Snell and Quadratic normal computations at different pixels are independent, we implement our algorithm in C++, with parallelizable steps optimized using OpenMP [9], on an 8-core PC with 3.2GHz Intel Core i7 CPU and 32GB RAM.

5.1 Synthetic Data

We use the ray tracing method [20] to generate synthetic data for evaluation. In particular, two scenes are simulated: a static Stanford Bunny observed through a sinusoidal wave: $z(x,y,t)=2+0.1\cos (\pi (t+50)\sqrt{(x-1)^2+(y-0.5)^2}/80)$, and a moving Stanford Dragon seen through a different water surface: $z(x,y,t)=2-0.1\cos (\pi (t+60)\sqrt{(x+0.05)^2+(y+0.05)^2}/75)$. The Dragon object moves along a line with a uniform speed of 0.01 units per frame. Because of the different sizes of the two objects, we place the Bunny and Dragon objects on top of a flat backdrop positioned at $z=3.5$ and $z=3.8$, respectively. The synthetic scenes are captured using a $3\times 3$ camera array. The reference camera is placed at the origin and the baseline between adjacent cameras in the array system is set to 0.3 and 0.2 for the Bunny and Dragon scene, respectively.

Table 1. Reconstruction errors of the synthetic Bunny scene and the Dragon scene. Here, for each scene, we list the average errors by considering all frames.

We start with quantitatively evaluating the proposed approach. Since our approach can return the depths and the normals of the water surface, and the 3D point set of the underwater scene, we employ the following measures for accuracy assessment: the root mean square error (RMSE) between the ground truth (GT) depths and the estimated depths $\mathbf {D}$, the mean angular difference (MAD) between the GT normals and the recovered Snell normals $\mathbf {a}^1$, the MAD between the true normals and the computed Quadratic normals $\mathbf {b}^1$, and the mean Euclidean distance (MED) between the reconstructed point set $\mathbf {P}$ of the underwater scene and the GT one. Table 1 shows our reconstruction accuracy by averaging over all frames. It is noteworthy that the average MAD of the Snell normals and that of the Quadratic normals are quite similar for both scenes, which coincides with our normal consistency constraint.

Fig. 3.

Visual comparisons with GT on two example frames of the Bunny scene (left two columns) and the Dragon scene (right two columns). In each subfigure, we show the GT and our result in the top and bottom row, respectively. (a) shows the GT water surface depth and the estimated one. (b) shows the GT water surface colored with the GT normal map, and the computed one colored with the Quadratic normals. The Snell normals are not shown here because they are similar to the Quadratic normals. (c) shows the GT point set of the underwater scene and the recovered one, where each point is colored with its z-axis coordinate. The red boxes highlight an obvious different region of the underwater point clouds of two different frames; see text for details. (Color figure online)

Fig. 4.

Different error measures as a function of the balancing parameter $\lambda$.

Fig. 5.

Different error measures as a function of the number of cameras used.

Figure 3 visually shows the reconstruction results of several example frames. The complete sequences can be found in the supplementary materials [35]. Compared to the GT, our approach accurately recovers both the dynamic water surfaces and the underwater scenes. We can also observe that, while the underwater scene in the Bunny case is statically positioned in the simulation, different point clouds are obtained at different frames (see the red boxes in Fig. 3(c)), echoing our varying representation $\mathbf {P}$ of underwater points. Besides, with the frame-by-frame reconstruction scheme, our approach successfully captures the movement of the underwater Dragon object. In short, accurate results are obtained for the two scenes generated using different water fluctuations, different underwater objects (static or moving), and data acquisition settings, which demonstrate the robustness of our approach.

We then adjust the weight $\lambda$ in Eq. (6) to validate the effect of the polynomial smoothness term Eq. (7). Here we use the Dragon scene for illustration. As shown in Fig. 4, when $\lambda =0$, the method depends on the normal consistency prior only. Explicitly applying a smoothness term with a proper setting $\lambda =2$ performs favorably against other choices w.r.t. all error metrics. Figure 5 further shows our reconstruction accuracy under different number of cameras used. Using a larger number of cameras gives a higher accuracy.

5.2 Real Data

To capture real scenes from multiple viewpoints, we build a camera array system as shown in Fig. 1(a). Ten PointGrey Flea2 cameras are mounted on three metal frames to observe the bottom of a glass tank containing water. The cameras are connected to a PC via two PCI-E Firewire adapters, which enables us to use the software provided by PointGrey for synchronization. We use 9 cameras highlighted by the red box in Fig. 1(a) for multi-view 3D reconstruction, whereas the 10th camera, i.e. the evaluation camera, is used for accuracy evaluation only. We calibrate the intrinsic and extrinsic parameters of the cameras using a checkerboard [46]. The baseline between adjacent cameras is about 75mm and the distance between the camera array and the bottom of the tank is about 55cm. All the cameras capture video at 30 fps with a resolution of $516\times 388$. Flat textured backdrops are glued to the bottom of the tank, which is for facilitating optical flow estimation.

Fig. 6.

Reconstruction results of four example frames of our captured scenes. In each subfigure, we show the captured image of the reference camera (top), the point cloud of the water surface colored with the Quadratic normals (middle), the point cloud of the underwater scene colored with the z-axis coordinates (bottom). Note that the motion blur (green box) in the captured image may affect the reconstruction result (red box). (Color figure online)

In order to verify our approach on real data, we first capture a simple scene: a flat textured plane placed at the bottom of the tank, which is referred to as Scene 1. The water surface is perturbed by continuously dripping water drops near one corner of the pattern. As shown in Fig. 6(a), our approach not only faithfully recovers the quarter-annular ripples propagated from the corner with the dripping water, but also accurately returns the 3D underwater plane without any prior knowledge of the flat structure. For accuracy assessment, we also fit a plane for the reconstructed underwater point set of each frame using RANSAC [13]. The MED between the reconstructed points and the fitted plane is 0.44mm by averaging over all frames. It is noteworthy that no post-processing steps like smoothing are performed here.

Two non-flat underwater scenes are then used to test our approach: (i) a toy tiger that is moved by strong water turbulence, and (ii) a moving hand in a textured glove. We refer to the two scenes as Scene 2 and Scene 3, respectively. In both cases, to generate water waves, we randomly disturb the water surface at one end of the tank. Figure 6(b and c) shows several example results on Scene 2 and Scene 3, and the full videos can be found in the supplemental materials. Our approach successfully recovers the 3D shapes of the tiger object and the moving hand, as well as the fast evolving water surfaces.

Fig. 7.

View synthesis on two example frames (top and bottom) of Scene 3. From left to right, it shows the images captured using the evaluation camera, the synthesized images and the absolute difference maps between them. The effects of specular reflection (red box) and motion blur (green box) can be observed in the captured images. These effects cannot be synthesized, leading to higher differences in the corresponding areas. (Color figure online)

Novel View Synthesis. Since obtaining GT shapes in our problem is difficult, we leverage the application of novel view synthesis to examine reconstruction quality. In particular, as shown in Fig. 1(a), we observe the scene at an additional calibrated view, i.e. the evaluation camera. At each frame, given the 3D point set of the underwater scene, we project each scene point to the image plane of the evaluation camera through the recovered water surface. Here such a forward projection is non-linear because of the light bending at the water surface, which is implemented by an iterative projection method similar to [5, 22, 25]; see the supplementary materials for the detailed algorithm. Then, the final synthesized image at the evaluation camera is obtained using bilinear interpolation. Figure 7 shows that the synthesized images and the captured ones look quite similar, which validates the accuracy of our approach. Take Scene 2 and Scene 3 for example, the average peak signal-to-noise ratio by comparing the synthesized images to the captured images is 30dB and 31dB, respectively.

Running Time. For our real-captured data, each scene contains 100 frames and each frame has 119,808 water surface points and 119,808 underwater scene points. It takes about 5.5 h to process each whole sequence, as shown in Table 2.

Table 2. Average running time of the three real scenes.

6 Conclusions

This paper presents a novel approach for a 3D reconstruction problem: recovering underwater scenes through dynamic water surfaces. Our approach exploits multiple viewpoints by constructing a portable camera array. After acquiring the correspondences across different views, the unknown water surface and underwater scene can be estimated through minimizing an objective function under a normal consistency constraint. Our approach is validated using both synthetic and real data. To our best knowledge, this is the first approach that can handle both dynamic water surfaces and dynamic underwater scenes, whereas the previous work [44] uses a single view and cannot handle moving underwater scenes.

Our approach works under several assumptions that are also commonly used in state-of-the-art works in shape from refraction. Firstly, we assume that the medium (i.e. water in our case) is transparent and homogeneous, and thus light is refracted exactly once from water to air. Secondly, the water surface is assumed to be locally smooth, so that the Quadratic normal of each surface point can be reliably estimated based on the local neighborhood. Thirdly, the underwater scene is assumed to be textured so that the optical flow field across views can be accurately estimated. The above assumptions may be violated in real-world scenarios. For example, water phenomena like bubbles, breaking waves, light scattering, may lead to multiple light bending events along a given light path. The observed motion blur and specular reflection in Fig. 7 can affect the accuracy of correspondence matching and the subsequent reconstruction, as highlighted by the red box in Fig. 6(c).

Although promising reconstruction performance is demonstrated in this paper, our approach is just a preliminary attempt to solving such a challenging problem. The obtained results are not perfect, especially at the boundary regions of the surfaces, as shown in Fig. 6. That is because those regions are covered by fewer views compared to other regions. To cope with this issue, we plan to build a larger camera array or use a light-field camera for video capture. In addition, occlusion is a known limitation in a multi-view setup because correspondence matching in occluded areas is not reliable. We plan to accommodate occlusion in our model in the near future.

Finally, our work is inspired by fishing birds’ ability of locating underwater fish. Our solution requires 4 or more cameras, whereas a fishing bird uses only two eyes. It would be interesting to further explore additional constraints or cues that the birds use to make this possible. Our hypotheses include that the birds have prior knowledge on the size of the fish and estimate only a rough depth of the fish [3]. Whether the depth of underwater scene can be estimated under these additional assumptions is worthy for further investigation.