Abstract
The integral theorems of vector analysis build a relation between differentiation and integration and reduce often the ‘dimension of integration’ \(\bullet \) the area and geometrical center of planar figures (theorem of Green), \(\bullet \) the flux through a surface or volume (theorem of Gauß), \(\bullet \) or the circulation within a (curved) surface (theorem of Stokes).
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Author information
Authors and Affiliations
Corresponding author
Appendices
Exercises
Area Calculation by the Theorem of Green
-
37.
A closed curve is given by
$$\begin{aligned} \varvec{\Psi } = \begin{pmatrix} \cos ^3 t,&\sin ^3 t \end{pmatrix}^\top \qquad t\in [0,2\pi ]. \end{aligned}$$Determine the arc length of the boundary and the enclosed area.
-
38.
Calculate the area enclosed by the curve \(x^3+y^3-3xy = 0\) in the first quadrant.
-
39.
Given the implicit curve
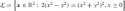 . Determine the enclosed area
. Determine the enclosed area-
(a)
in a rational parametrization with \(y = x\cdot t\),
-
(b)
and by introducing polar coordinates.
-
(a)
-
40.
Calculate the area enclosed by the curve \(\rho (\phi ) = \cos (n\phi )\) in polar coordinates for \(n\in \mathbb {N}\).
-
41.
Calculate the geometrical center of the domain

-
(a)
by the standard surface integrals
$$\begin{aligned} \bar{x} = \frac{1}{A}\int \int x \mathrm {d}x\mathrm {d}y, \qquad \bar{y} = \frac{1}{A}\int \int y \mathrm {d}x \mathrm {d}y, \end{aligned}$$ -
(b)
and by application of Green’s theorem.
-
(a)
-
42.
Determine the geometrical center of the domain
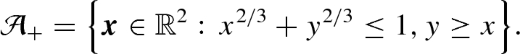
-
43.
Figure out the area which is enclosed by the implicit curve
$$\begin{aligned} (x^2+y^2)^2-2(x^2+y^2)-1 = 0. \end{aligned}$$ -
44.
A pedal curve \(\varvec{P}_{\varvec{\Psi },\varvec{E}}(t)\) is a planar figure which is defined by the orthogonal intersection of
-
the tangent vectors of the curve \(\varvec{\Psi }(t)\)
-
and the family of straight lines passing the pedal point \(\varvec{E}\).
-
(a)
Derive a parametrization of all pedal curves of the parabola \(x = 0.5y^2\) with an arbitrary pedal point.
-
(b)
Evaluate the area of the closed loop for the pedal point \(\varvec{E} = \begin{pmatrix} -\frac{3}{2},&0\end{pmatrix}^\top \).
-
Flux Through Volume and Surface
-
45.
Determine the surface integral for the vector field
$$\varvec{F} = \frac{1}{\sqrt{x^2+y^2}}\begin{pmatrix} x-yz\cdot \arccos \, z\\ y+xz\cdot \arccos \, z\\ \ln |x^2+y^2|\end{pmatrix}$$through the ‘mathematical cylindrical’
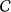 with \(x = 2\phi \sin \phi \), \(y = 2\phi \cos \phi \) for \(\phi \in [0,4\pi ]\) and \(0\le z\le 1\).
with \(x = 2\phi \sin \phi \), \(y = 2\phi \cos \phi \) for \(\phi \in [0,4\pi ]\) and \(0\le z\le 1\). -
46.
Evaluate surface and volume integral of the theorem of Gauß for the flux of the vector field \(\varvec{F} = -x\,\hat{\varvec{i}}+ y\,\hat{\varvec{j}}+ 6z\,\hat{\varvec{k}}\) through the torus \(\mathcal {T}\). The surface of the torus is given by
$$\begin{aligned} x&= (4+\cos u)\sin w\\ y&= (4+\cos u)\cos w\qquad u, w\in [0,2\pi ]\\ z&= \sin u. \end{aligned}$$ -
47.
Evaluate the surface integral of the vector field
$$\begin{aligned} \varvec{G}(r,\vartheta ,\lambda )&= \ln \left( 1+\sqrt{1-\cos ^2 \vartheta }\right) \,\hat{\varvec{h}}_r + \tan ^4\lambda \varvec{h}_\lambda +\arctan \vartheta \,\hat{\varvec{h}}_\vartheta \end{aligned}$$given in spherical coordinates through the upper semi-sphere
$$\Sigma _{+} = \Big \{\varvec{x}\in \mathbb {R}^3:\, x^2+y^2+z^2 = 4, z\ge 0\Big \}.$$ -
48.
Evaluate the flux of the vector field \(\varvec{G}(\rho ,\phi , z) = 2\rho \,\hat{\varvec{h}}_\rho + z\,\hat{\varvec{h}}_\phi + \frac{8}{3}z^2\,\hat{\varvec{h}}_z \) through the common volume \(\mathcal {V}\) of the cylinder \(\mathcal {Z} = \Big \{\varvec{x}\in \mathbb {R}^3:\,\left( y-\frac{1}{2}\right) ^2+x^2 \le \frac{1}{4}\Big \}\) and the semisphere \(\Sigma _+ = \Big \{\varvec{x}\in \mathbb {R}^3:\, x^2+y^2+z^2\le 1,\, z\ge 0\Big \}\).
For parametrization, consider the plane z \(=\) 0 and express the non-centered circle in polar coordinates.
-
49.
Given a regular tetraeder \(\mathcal {T}\) with the corner points \(\{\varvec{A},\varvec{B},\varvec{C},\varvec{D}\}\), where
-
all triangles are equilateral with the sides \(\ell = \sqrt{3}\),
-
the triangle \(\Delta \varvec{ABC}\) lies in the plane \(z=0\),
-
the point \(\varvec{A}\) has the coordinates \(\begin{pmatrix} 1,&0,&0 \end{pmatrix}^\top \),
-
and the point \(\varvec{D}\) is on the positive z-axis.
-
(a)
Determine the coordinates of \(\{\varvec{B},\varvec{C},\varvec{D}\}\).
-
(b)
Move the whole tetraeder – without rotations – along the \(x-\)axis, so that in the shifted tetraeder \(\mathcal {T}_s\) the x-component of \(\varvec{C}_s\) is zero, while the y- and z-coordinates remain unchanged.
-
(c)
Determine the flux through the tetraeder \(\mathcal {T}_s\) for the vector field
$$\begin{aligned}\varvec{F} = \begin{pmatrix}-y,&x,&\sqrt{3}\text {e}^{-z} \end{pmatrix}^\top . \end{aligned}$$In case of surface integrals, the 4 faces can be solved together by an adequate parametrization of the triangles. Consider the orientation of the normal vectors.
-
-
50.
Move the area enclosed by the boundary curve \(\varvec{\Psi } = \begin{pmatrix} \cos ^3 t,&\sin ^3 t,&0 \end{pmatrix}^\top \) without rotations along the vector \(\varvec{v} = \begin{pmatrix} 1,&1,&1 \end{pmatrix}^\top \) to create a solid mathematical cylinder \(\mathcal {M}_C\) with the height \(z_{\max } = 2\). Determine the flux of the vector field
$$\begin{aligned} \varvec{F} = \begin{pmatrix} 2y^2-\text {e}^{z^2},&y\frac{1}{(z+2)\ln |z+2| },&\sin (\text {e}^{x^2-y})-x \end{pmatrix}^\top \end{aligned}$$through the volume \(\mathcal {M}_C\).
-
51.
Given the vector field \(\varvec{G}(\rho ,\phi , z) = \frac{25}{4}\rho ^3\,\hat{\varvec{h}}_\rho +\frac{25}{3}z^3\,\hat{\varvec{h}}_z\) in cylindrical coordinates, the plane \(\mathcal {E}: z = \frac{x}{7}+\frac{24}{35\sqrt{2}}\) and the cone \(\mathcal {C} = \Big \{\varvec{x}\in \mathbb {R}^3: x^2+y^2 = z^2\Big \}\).
-
(a)
Determine the curl and the divergence of the vector field \(\varvec{G}\) and use the result to figure out the circulation within the ellipse defined by the intersection of the plane \(\mathcal {E}\) and the cone \(\mathcal {C}\).
-
(b)
Calculate the flux through the smaller Dandelin sphere \(\mathcal {D}_1\), which is tangential to the cone and the plane.
The radius can be found in the plane y \(=\) 0 by the incircle formula \(R= \frac{2A}{u}\) with the area A and the perimeter u of the corresponding triangle.
-
(a)
-
52.
Calculate the flux through the area \(\mathcal {O}_p = \left\{ \varvec{x}\in \mathbb {R}^3\!\!:\!z = \frac{1}{3} \sqrt{9-x^2-y^2}, |y|\le 1\right\} \) with the vector field
$$\begin{aligned} \varvec{G}(\alpha ,\beta ,\gamma ) = \sinh \alpha \,\hat{\varvec{h}}_\beta + \cos \beta \,\hat{\varvec{h}}_\gamma \end{aligned}$$given in oblate spheroidal coordinates
$$\begin{aligned} x&=\sqrt{8}\cosh \alpha \cos \beta \cos \gamma \\ y&=\sqrt{8}\cosh \alpha \cos \beta \sin \gamma \\ z&= \sqrt{8} \sinh \alpha \sin \beta . \end{aligned}$$Consider, that the surface is a partial coordinate surface of the system.
-
53.
Given the vector field \(\varvec{G} = (\alpha ^2+\beta ^2)\cos \gamma \,\hat{\varvec{h}}_\alpha +\frac{1}{(\alpha ^2+\beta ^2)}\,\hat{\varvec{h}}_\beta \) in parabolic coordinates
$$\begin{aligned} x = \alpha \beta \cos \gamma , \qquad y = \alpha \beta \sin \gamma , \qquad z = \frac{\alpha ^2-\beta ^2}{2}. \end{aligned}$$Evaluate the flux through the parabolic surface
$$\mathcal {P} : \Big \{\varvec{x} \in \mathbb {R}^3:\, x^2+y^2-1 = 2z, -0.5\le z\le 4 \Big \}$$-
(a)
in parabolic coordinates,
-
(b)
and verify the result via cylindrical coordinates.
-
(a)
-
54.
Evaluate the flux of the vector field \(\varvec{F} = (2x+y)\,\hat{\varvec{i}} - (4y-x)\,\hat{\varvec{j}}+ (2z-16)\,\hat{\varvec{k}}\) through the surface \(\tilde{\mathcal {C}}\), which is defined by the rotation of the curve \(\varvec{\Psi } = \begin{pmatrix} 3+\cos (z\cos \root 3 \of {z}),&{} 0,&{} z\\ \end{pmatrix}^\top \) for \(0\le z\le 6\) around the z-axis with the angle \(\phi \in [0,2\pi ]\). Consider the theorem of Gauß.
Circulation Within a Surface
-
55.
Verify Stokes’ theorem by evaluating line integrals and surface integral for the vector field \(\varvec{F} = \begin{pmatrix} (1-2z)\text {e}^{x},&xy,&xz^2\end{pmatrix}^\top \) and the surface
$$\mathcal {S} = \Big \{\varvec{x} \in \mathbb {R}^3:\, y = 4-z^2, 0 \le x\le 1, y \ge 0 \Big \}.$$ -
56.
Verify Stokes’ theorem by evaluating line and surface integrals in cylindrical coordinates for the vector field \(\varvec{G}(\rho ,\phi , z) = -\rho \cos \phi \,\hat{\varvec{h}}_\rho + \rho z \,\hat{\varvec{h}}_z \) and the surface
$$\mathcal {V}_{+} = \Big \{\varvec{x}\in \mathbb {R}^3:\, \Vert x\Vert = 1, z\ge 0, \bigg (y-\frac{1}{2}\bigg )^2+x^2 \le \frac{1}{4}\Big \}.$$ -
57.
Calculate the circulation of the vector field \(\varvec{G} = \rho ^3\cos ^2\phi \,\hat{\varvec{h}}_\phi +z^4 \,\hat{\varvec{h}}_z\) through the surface \(z = xy\)
-
(a)
in the domain \(x^2+y^2\le 1\),
-
(b)
and in the domain \(|x|+|y|\le 1\).
-
(a)
-
58.
Given the vector field \(\varvec{G} = \cos (\lambda +\vartheta )\Big (\,\hat{\varvec{h}}_r+\,\hat{\varvec{h}}_\vartheta +\,\hat{\varvec{h}}_\lambda \Big )\). Determine the circulation within the spherical triangle on the unit sphere \(\Sigma : \Big \{\varvec{x}\in \mathbb {R}^3:\, \Vert \varvec{x}\Vert = 1\Big \}\) with the corner points \(\varvec{A} = \begin{pmatrix} 1,&0,&0 \end{pmatrix}^\top \), \(\varvec{B} = \begin{pmatrix} 0,&1,&0 \end{pmatrix}^\top \), \(\varvec{C} = \begin{pmatrix} 0,&0,&1 \end{pmatrix}^\top \). What is the result for the planar triangle with the same corner points?
-
59.
Evaluate the circulation of the vector field \(\varvec{F} = \begin{pmatrix} 2z,&x^2,&\ln \Big | (x-2)^2+4(y+1)^2 \Big |\end{pmatrix}^\top \) within the parabolic partial area
$$\mathcal {P}:\Big \{\varvec{x}\in \mathbb {R}^3:\, x^2+y^2-z = 0, (x-2)^2+4(y+1)^2 \le 1\Big \}.$$ -
60.
Given an arbitrary planar surface \(\mathcal {S}_\mathcal {E}\) in the plane \(\mathcal {E}: y+4x -2z = 0\). Find a non-conservative vector field \(\varvec{F}\) so that the circulation for all figures \(\mathcal {S}_\mathcal {E}\) is zero. The solution is not unique.
-
61.
Evaluate the circulation of the vector field \(\varvec{G}(\alpha ,\beta ,\gamma ) =\alpha ^2\cos \gamma \,\hat{\varvec{h}}_\alpha + \,\hat{\varvec{h_\beta }}\) given in cardioid coordinates
$$\begin{aligned} x&= \frac{\alpha \beta }{(\alpha ^2+\beta ^2)^2}\cos \gamma \\ y&= \frac{\alpha \beta }{(\alpha ^2+\beta ^2)^2}\sin \gamma \\ z&= \frac{\alpha ^2-\beta ^2}{2(\alpha ^2+\beta ^2)^2} \end{aligned}$$through the partial coordinate surfaces with \(\gamma \in [0,\pi ]\) and \(\alpha = \mathop {\mathrm {const.}}\nolimits \) and \(\beta = \mathop {\mathrm {const.}}\nolimits \), respectively.
Solutions
4.37. Enclosed Area of \(\varvec{\Psi } = \left( \cos ^3 t, \sin ^3 t\right) \)
We calculate the tangent vector \(\varvec{T}\) and simplify the inner product by trigonometric identities
For the arc length, we must consider the modulus
We re-write the integrand of Green’s theorem
Hence, we obtain the enclosed area by
-
The planar figure \(\varvec{\Psi } = \begin{pmatrix} \cos ^3 t,&\sin ^3 t\end{pmatrix}^\top \) is known as
 but also as cubocycloid, or paracycle.
but also as cubocycloid, or paracycle. -
In a geometrical definition, the astroid is created by tracing a marked point on a circle, which is rolling inside a fixed circle. Therefore, the curves belongs to the family of

-
The algebraic equation of the curve is \(x^{2/3}+y^{2/3} = 1\). Therefore, the curve belongs to the family of

-
Due to the symmetry, it is also possible to integrate only in the first quadrant (Fig. 4.1).
4.38. Area Enclosed by \(x^3+y^3-3xy = 0\)
Obviously, the origin \(\varvec{0}\) is a point of the curve. Hence, we try to parametrize by a family of straight lines, e.g. with \(y = x\cdot t\)
For this kind of parametrization, we can avoid computing y and \(\dot{y}\)
The curve is closed in the origin, if we consider the interval \(t\in [0,\infty [\).
Hence, we calculate the area by Green’s theorem:

-
The figure \(x^3+y^2-3xy = 0\) – in particular its closed part – is known as
 and the relevant part of the curve is visualized in Fig.
4.2.
and the relevant part of the curve is visualized in Fig.
4.2. -
In exercise 28, the x- and y-components are exchanged. Due to its symmetry, the result is the same curve (after the parametrization \(x = y\cdot t\)).
-
The parametrization by \(y =xt\) or \(x=yt\) might work for curves which contain the origin \(\varvec{0}\). In the area calculation by Green’s theorem, the calculation of \(\{x,\dot{x}\}\) or \(\{y,\dot{y}\}\) can be avoided in this case.
4.39. Area Enclosed by the Curve \(2(x^2-y^2) = (x^2+y^2)^2\)
Rational Parametrization
The point \(\varvec{0}\) fulfills the equation of the curve. Hence, we try again a parametrization by \(y = x\cdot t\):
For the integrand, we consider the simplification
which avoids the calculation of y and \(\dot{y}\).
The curve is closed in the domain \(x\ge 0\) for the interval \(t\in [-1,1]\). Therefore, we calculate the area by
Polar Representation
First we re-write the integrand of Green’s theorem in polar coordinates for an arbitrary curve:
Then we insert polar coordinates into the equation
and recognize the representation of the lemniscate of Bernoulli (exercise 5b ) (Fig. 4.3).
The curve is lying in the domain \(x\ge 0\) for the interval \(\phi \in \left[ -\frac{\pi }{4},\frac{\pi }{4}\right] \) with the enclosed area
Due to symmetry reasons, the complete lemniscate encloses the doubled area \(A_{lemniscate}=2\).
-
In polar coordinates, the theorem of Green reduces to the
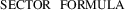
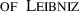 : $$\begin{aligned} A&= \frac{1}{2}\int \limits _{\phi _0}^{\phi _1} \rho ^2\mathrm {d}\phi . \end{aligned}$$
: $$\begin{aligned} A&= \frac{1}{2}\int \limits _{\phi _0}^{\phi _1} \rho ^2\mathrm {d}\phi . \end{aligned}$$This formula holds for closed curves which are either passing the origin or going around the origin. In particular it holds for ‘sectors’, which are defined by one curved line \(\rho (\phi )\) and two straight lines intersecting in the origin (cf. Fig. 4.4).
4.40. Area Enclosed by \(\rho = \cos n \phi \)
First we have to find the interval of \(\phi \), so that the curve
is closed. For each choice of \(n\in \mathbb {N}\) the closed figure will have a blossom-like shape with different widths of the petals (cf. Fig. 4.5). We assume \(\phi _0=0\) as the starting point with the coordinates \(\varvec{\Psi }(0) = \begin{pmatrix}1,&0\end{pmatrix}^\top \). The curve will be closed when this point is reached again, which is equivalent to \(\phi = k\pi \) with \(k\in \mathbb {N}\).
-
For an even number n, we find \(x = \cos (n\cdot k\pi ) \cos (k\pi ) =+\cos (k\pi ) \) which leads to an upper limit \(\phi _e = 2\pi \).
-
For an odd number n, we find \(x = \cos (n\cdot k\pi ) \cos (k\pi ) =-\cos (k\pi ) \) which leads to an upper limit \(\phi _e = \pi \).
According to the sector formula of Leibniz, the area is calculated by
4.41. Geometrical Center of the Loop: \(3x^2+y^3-y^2 = 0\)
Different parametrizations of this curve have been discussed already in exercise 6. The question here considers only the area of the upper part with \(y \ge 0\) (cf. Fig. 4.6).
a. ‘Standard Integrals’
In case of a double integral, we use the parametrization in x(y):
The enclosed area is given by

Due to symmetry considerations, the x-coordinate of the geometrical center is zero:
For the y-component, we use the integral recursion (4.8) and consider for the first term \(\Big [\sin ^n t \cos t\Big ]_0^{\pi /2} = 0\). This leads to the coordinate:

b. Theorem of Green
For this question we have to recall the fact that the formula
is only the most popular form of Green’s theorem. The original formula
enables other applications then the calculation of enclosed areas.
When we compare the right hand side with the geometrical center
we conclude \(F_1 = 0\) and \(F_2 = 0.5x^2\). By inserting into the line integral we obtain
We use the parametrization \(x = y t\) with the integrand
In addition, we know \(y = 1-3t^2\) and so we get the area
For the geometrical center we calculate
In an analogous way, we conclude \(F_1 = -\frac{y^2}{2}\) and \(F_2 = 0\) for the y-component:
4.42. Geometrical Center
For the parametrization, we identify the domain as part of the astroid of exercise 37.
When we remove the parts below the line \(x=y\), we obtain the interval \(t\in \left[ \frac{\pi }{4},\frac{5\pi }{4}\right] \) for the boundary part \(\partial B_1\). In addition we consider the straight line \(y = x\) in the interval \(y\in \left[ -2^{3/2}, 2^{3/2}\right] \) as boundary \(\partial B_2\):
In a similar way, we could calculate the y-coordinate of the geometric center:
but we can also argue with the symmetry:
The complete astroid is symmetric w.r.t. the axes \(x=0\), \(y=0\) and \(x = y\) and \(x = -y\). After removing the part below the line \(x = y\), the remaining figure is still symmetric w.r.t. to the line \(y = -x\). Therefore, we get the relation \(\bar{y} = - \bar{x}\) for the geometrical center (Fig. 4.7).
4.43. Area Enclosed by \((x^2+y^2)^2-2(x^2+y^2)-1 = 0\)
The formula contains only terms like \(x^2+y^2 =: \rho ^2\). Therefore, we introduce polar coordinates
By adding zero we obtain
In other words, we figure out that the curve consists of concentric circles with the two radii
The first solution describes a circle with the radius \(\rho _1 = \sqrt{1+\sqrt{2}}\) and the enclosed area \(A =\rho _1^2 \pi = \left( 1+\sqrt{2}\right) \pi \).
The second solution might be an artifact as the squared radius \(\rho ^2_2 = 1-\sqrt{2}\) should not be negative. In previous examples, it was possible to interpret a negative radius as the reflected curve. We insert the radius \(\rho _2 = \sqrt{|1-\sqrt{2}|} = \sqrt{\sqrt{2}-1}\) into the equation and obtain
Hence, the second solution turns out to be an algebraic artifact and the only real solution is the circle with the radius \(\rho = \sqrt{1+\sqrt{2}}\).
-
In this question, we could avoid the theorem of Green due to known properties of the circle.
-
The existence of \((x^2+y^2)\)-terms is often an indication for polar/cylindrical coordinates.
-
The formal result of a negative radius can be a real solution (exercise 4) or an algebraic artifact.
4.44. Pedal Curve of a Parabola
a. Parametrization
The parabola \(x = 0.5y^2\) can be represented by
with the tangent vector \(\varvec{T} = \begin{pmatrix} t,&1\end{pmatrix}^\top \). The tangent line through an arbitrary point of the parabola is given by
In a similar way, we set up the straight line through the pedal point \(\varvec{E}(x_0,y_0)\) with unknown coordinates
where the orthogonality is already ensured by \(\begin{pmatrix} t,&1\end{pmatrix}\begin{pmatrix} -1,&t\end{pmatrix}^\top = 0\).
We intersect the two lines \(\mathcal {G}\) and \(\mathcal {H}\)
and eliminate p and q:
We obtain the pedal curve of the parabola by inserting q into the equation of \(\mathcal {H}\):
Three different pedal curves are shown in Fig. 4.8. The curve with the solid black line is the one where we want to calculate the enclosed area.
b. Area
We insert the values \(y_0 = 0\) and \(x_0 = -\frac{3}{2}\) into the general expression:
For the area we use the theorem of Green and find after some simplifications the integrand
By polynomial long division, we split into the ‘integer’ and ‘fractional’ part and apply partial fraction decomposition
Due to symmetry, the curve is closing somewhere on the x-axis, which is equivalent to the condition \(t(t^2-3) = 0\), i.e. \(t = \pm \sqrt{3}\) or \(t = 0\). Now we consider, that the path of integration must be anti-clockwise enclosing the area. Hence, the integration interval starts at \(t=\sqrt{3}\):
4.45. Mathematical Cylinder
First we parametrize the cylindrical surface \( \mathcal {C}^E(\phi , z)=\begin{pmatrix}2\phi \sin \phi ,&2\phi \cos \phi ,&z\end{pmatrix}^\top \) in Fig. 4.9 with the normal vector
Then we evaluate the vector field \(\varvec{F}\) on the surface and introduce the abbreviation \(\alpha _z = \arccos \, z\)
and multiply with the normal vector
The flux is then calculated by the surface integral

-
A mathematical cylinder is defined by a planar curve \(\varvec{\Psi }\) and its translation \(\varvec{\Psi }_{\varvec{v}}\) in an arbitrary direction \(\varvec{v}\) outside the plane. The straight lines between \(\varvec{\Psi }\) and \(\varvec{\Psi }_{\varvec{v}}\) form the surface of the cylinder. The curve \(\varvec{\Psi }\) is not necessarily closed. If the curve is closed, then also the whole body is sometimes called a cylinder in the mathematical sense.
4.46. Flux of the Vector Field \(\varvec{F} = \left( -x,\quad y,\quad 6z\right) ^\top \) Through a Torus
a. Surface Integral
First we calculate the normal vector of the torus surface:
Then we evaluate the vector field at the location of the surface and multiply with the normal vector
We obtain the flux by the surface integral
b. Volume Integral
The divergence \(\mathop {\mathrm {div}}\nolimits \varvec{F} = 6\) is independent of the position, which makes the problem equivalent to determining the volume of the torus in Fig. 4.10. It is possible, to work with cylindrical coordinates, but we want to practice the volume integral with the Jacobian determinant here as well.
For a volume integral, a third parameter \(\xi \in [0,1]\) has to be introduced:
The volume element \(\mathrm {d}\varvec{V} = |\underline{\mathbf {J}}| \,\mathrm {d}w \, \mathrm {d}\xi \,\mathrm {d}w \) requires the Jacobian determinant
The flux is then calculated by the volume integral
4.47. Flux Through a Semisphere in Spherical Coordinates
-
The normal vector \(\varvec{N}\) of a sphere around the origin is proportional to the radial vector \(\,\hat{\varvec{h}}_r\) with \(\varvec{N} = r^2\sin \vartheta \,\hat{\varvec{h}}_r\).
-
In case of surface integral over a (partial) spherical surface around the origin, the field components \(\,\hat{\varvec{h}}_\lambda \) and \(\,\hat{\varvec{h}}_{\vartheta }\) cannot contribute due to orthogonality of the frame vectors.
We multiply the vector field with the normal vector of the sphere
The flux is calculated by the surface integral
4.48. Flux of the Vector Field \(\varvec{G}(\rho ,\phi , z) = 2\rho \,\hat{\varvec{h}}_\rho + z\,\hat{\varvec{h}}_\phi + \frac{8}{3}z^2\,\hat{\varvec{h}}_z\) Through Vivani’s Figure
The divergence of the field \(\varvec{G}(\rho ,\phi , z) = 2\rho \,\hat{\varvec{h}}_\rho + z\,\hat{\varvec{h}}_\phi + \frac{8}{3}z^2\,\hat{\varvec{h}}_z \) is
which is depending only on the z-coordinate. Hence, a volume integral within the upper Vivani’s figure (cf. Fig. 4.11) might be easier to evaluate. We express the shifted cylinder in polar coordinates. In the xy-plane we find
Therefore, the circle is represented in polar coordinates by \(\rho = \sin \phi \) with \(\phi \in [0,\pi ]\). The maximum z-component of the volume integral is obviously \(z = \sqrt{1-\rho ^2}\):
-
In case of volume integrals there are two fundamental ‘options’:
-
Adapt the volume element \(\mathrm {d}\varvec{V}\) by the Jacobian determinant to the body and obtain simple integration limits (e.g. exercise 46b).
-
Use standard volume elements of cylindrical, spherical or Cartesian coordinates and adapt the integration limits (e.g. exercise 48 and 51 ).
4.49. Flux Through a Tetraeder
a. Determine the Corner Coordinates
Based on the given conditions, we have to determine the corner points of the tetraeder. For \(\varvec{D}\) we use the known distance to \(\varvec{A}\) and obtain \(\varvec{D} = \begin{pmatrix} 0,&0,&\sqrt{2} \end{pmatrix}^\top \).
For \(\varvec{B},\varvec{C}\) we rotate the location \(\varvec{A}\) around the z-axis by the angle \(\phi =\pm \frac{2\pi }{3}\):
b. Translation of Coordinates
A translation by the vector \(\varvec{v} = \begin{pmatrix} \frac{1}{2},&0,&0 \end{pmatrix}^\top \) leads to the new coordinates:
c. Flux Through the Tetraeder
If we want to solve the problem by surface integrals, then we have to calculate the flux through four faces of the tetraeder. Therefore, we consider the parametrization of an arbitrary triangle \(\Delta (\varvec{P}_2,\varvec{P}_1,\varvec{P}_3)\) in space
with \(0\le u\le 1-w\) and \(0\le w\le 1\) and also the direction of the normal vectors.
This will lead – after simplifications – to the double integral
Alternative Solution by the Principle of Cavalieri
The calculation via four faces and the double integral is time consuming. A smarter method is a ‘one-dimensional volume integral’. The divergence
is only dependent on z. Therefore, we can apply the principle of Cavalieri for the integration
where A(z) is the area while cutting the volume at height z.
With the intercept theorem or some drawings, we find
The flux is calculated by a one-dimensional integration over z:
4.50. Mathematical Cylinder
A closer inspection of the divergence
shows that the principle of Cavalieri could be applied again and we don’t need a complete parametrization of body visualized in Fig. 4.12. The area was determined already in exercise 37 with \(A(z) = \frac{3\pi }{8}\). The maximum height is given by the question and so we obtain the flux
4.51. Dandelin Sphere: Flux and Circulation
a. Divergence, Curl and Circulation
We insert the vector field into the formula of the divergence
and the curl
The curl of the vector field is the null vector. Hence, the circulation within the ellipse – or any other surface – is also zero.
b. Flux Through Dandelin Sphere
This question has the remarkable property, that we can integrate the flux without knowing the exact parametrization like radius or center coordinates.
Cylinder Coordinates with Unknown Radius
Due to symmetry, the center of the sphere is somewhere on the z-axis with the coordinates \(\varvec{Z} = \begin{pmatrix} 0,&0,&z_0 \end{pmatrix}^\top \). We assume a radius of R, introduce the abbreviation \(\sigma = \sqrt{R^2-\rho ^2}\) and solve the problem in cylindrical coordinates:
Geometry
Now, we figure out the geometry of the problem (cf. Figs. 4.13 and 4.14). In the plane \(y=0\), we draw a triangle with \(\varvec{C}' = \begin{pmatrix} 0,&0 \end{pmatrix}^\top \), \( \varvec{A}' = \begin{pmatrix} \frac{4}{5\sqrt{2}},&\frac{4}{5\sqrt{2}} \end{pmatrix}^\top \) and \( \varvec{B}' = \begin{pmatrix} \frac{-3}{5\sqrt{2}},&\frac{3}{5\sqrt{2}} \end{pmatrix}^\top \) representing the cone and the plane.
The lattices have the dimensions \(b=|\varvec{C'A'}| = \frac{4}{5}\), \(a = |\varvec{C'B'}|= \frac{3}{5}\) and \(c = |\varvec{A'B'}| =1\). Hence we calculate the perimeter \(u = \frac{12}{5}\) and the area \(A =\frac{6}{25} \), which leads to the radius \(R = \frac{2A}{u} = \frac{1}{5}\). For the z-component of the center we obtain \(z_{0} = \sqrt{2} R = \frac{\sqrt{2}}{5}\).
After returning to the 3D space, we determine the center \(\varvec{Z} = \begin{pmatrix} 0,&0,&\frac{\sqrt{2}}{5} \end{pmatrix}^\top \) and the radius \(R = \frac{1}{5}\). Hence, we insert the geometry to the flux integral and obtain
c. Spherical Coordinates
As an alternative, we could solve the integration in spherical coordinates. We want to integrate a sphere centered around the origin \(\varvec{0}\) for simplicity. Therefore, we ‘translate’ the divergence of the vector field in the opposite direction
We determine the flux by integration:
4.52. Oblate Spheroidal Coordinates
The surface \(\mathcal {O}_p =\left\{ \varvec{x}\in \mathbb {R}^3:\, z = \frac{1}{3} \sqrt{9-x^2-y^2}, |y|\le 1\right\} \) is a partial area of an ellipsoid (cf. Fig. 4.15). We re-formulate
and find the semi-major axis \(a=3\) and the semi-minor axis \(b=1\).
The oblate spheroidal coordinates represent also ellipsoid surfaces for all constant pairs \(\{p,\alpha \}\). Our calculation will be very simple, if we find a value of \(\alpha \) so that the surface \(\mathcal {O}_P\) is a coordinate surface.
We solve
and obtain \(\alpha = {\mathop {\text {artanh}}}\, \frac{1}{3}\) for the correct ratio between the axis. In the remaining step, we prove that \(p = \sqrt{8}\) is the correct scaling:

Hence, we conclude that in the oblate spheroidal coordinate system, the parameter \(p = \sqrt{8}\) and the coordinate \(\alpha = {\mathop {\text {artanh}}}\, \frac{1}{3}\) represent the ellipsoidal surface with the equation
The normal vector of the ellipsoid (with \(\alpha = \mathop {\mathrm {const.}}\nolimits \)) points in the same direction as \(\,\hat{\varvec{h}}_\alpha \). Therefore, the product with the vector field \(\varvec{G}(\alpha ,\beta ,\gamma ) = \sinh \alpha \,\hat{\varvec{h}}_\beta + \cos \beta \,\hat{\varvec{h}}_\gamma \) will vanish:
The given vector field provides a zero flux through every partial area on the ellipsoid \(\mathcal {O} =\left\{ \varvec{x}\in \mathbb {R}^3:\, \frac{x^2+y^2}{9}+z^2 = 1\right\} \).
-
A coordinate surface is given by a fixed value \(q_i = \mathop {\mathrm {const.}}\nolimits \) (for \(i = \{1,2,3\}\)) in the system
$$\begin{aligned} x&= x(q_1,q_2,q_3)\\ y&= y(q_1,q_2,q_3)\\ z&= z(q_1,q_2,q_3). \end{aligned}$$ -
For every orthogonal coordinate system, the normal vector of a coordinate surface (\(q_i = \mathop {\mathrm {const.}}\nolimits \)) is parallel to the corresponding frame vector \(\,\hat{\varvec{h}}_{q_i}\). Assuming \(q_i = \beta \), the normal vector is found by the non-normalized frame vectors:
$$\begin{aligned} \varvec{N} = \varvec{h}_\alpha \times \varvec{h}_\gamma =\pm \Vert \varvec{h}_\alpha \Vert \cdot \Vert \varvec{h}_\gamma \Vert \cdot \,\hat{\varvec{h}}_\beta . \end{aligned}$$The positive and negative signs are introduced here, to consider the right-handed orientation of the ‘frame vectors’ \(\Big \{\,\hat{\varvec{h}}_\alpha ,\,\hat{\varvec{h}}_\beta ,\,\hat{\varvec{h}}_\gamma \Big \}\).
4.53. Flux Through a Paraboloid
a. Parabolic Coordinates
The surface
fulfills the equation \(x^2+y^2-1 = \alpha ^2-1 = 2z\). This is equivalent to the coordinate surface \(\beta \equiv 1\) with \(u = \alpha \) and \(w = \gamma \) in parabolic coordinates. In other words, the paraboloid in Fig. 4.16 is a coordinate surface of the applied coordinate system.
We use the ‘frame vectors’ of exercise 14 and obtain the normal vector
where the minus sign is a consequence of the right-handed coordinate system.
We evaluate the vector field on the surface and multiply with the normal vector
The flux of the vector field is calculated by the surface integral
b. Cylindrical Coordinates
For the solution in cylindrical coordinates, we have to re-write the vector field similar to exercise 20. We identify \(\phi \equiv \gamma \) and solve for the ‘frame vectors’:
By multiplication, we obtain
with \(\alpha = \rho \), \(\beta = 1\) and \(z = 0.5(\alpha ^2-1)\). This choice has the consequence, that we evaluate the vector field already on the given paraboloid
while the general expression in cylindrical coordinates might be more demanding. The normal vector in cylindrical coordinates is
We evaluate the vector field on the surface and multiply with the normal vector:
Hence, we obtain the again flux
-
This exercise demonstrates the benefit of the ‘optimal’ coordinate system. For known ‘frame vectors’ and coordinate surfaces, the calculation of the normal vector is performed in one line only.
4.54. ‘Theorem of Gauß’ for Surface Integrals
The surface \(\tilde{\mathcal {C}}\) is defined by a rotation of a one-dimensional function, which enables a parametrization in cylindrical coordinates with a variable radius \(\rho (z)\). Nevertheless, the integrals might not be handy.
To apply the theorem of Gauß, we calculate the divergence \(\mathop {\mathrm {div}}\nolimits \varvec{F} = 2-4+2 = 0\). Therefore, every closed volume will have a total flux of zero through its total surface.
The rotational surface \(\tilde{\mathcal {C}}\) is not closed, but open on both ends (Fig. 4.17). We add the missing partial areas and calculate the flux through them. For simplicity we choose circles in the plane \(z= 0\) and \(z=6\). The normal vector of these circles is \(\varvec{N} = \rho (\pm \,\hat{\varvec{k}})\) with the radius \(\rho \) depending on the height.
For the ‘bottom’ of the surface \(\tilde{\mathcal {C}}\) we find \(\rho = 3\) and the flux
In a similar way we calculate for the ‘top’ of \(\tilde{\mathcal {C}}\)
The flux through the rotational surface \(\tilde{\mathcal {C}}\) is
4.55. Verification of Stokes’ Theorem for the Parabolic Cylinder \(\mathcal {S} = \{{\varvec{x}}\in \mathbb {R}^3: y = 4-z^2, 0 \le x\le 1, y\ge 0\}\)
a. Circulation via the Surface Integral
We introduce the obvious parametrization \(\mathcal {S} = \begin{pmatrix} x,&4-z^2,&z \end{pmatrix}^\top \) with \(x\in [0,1]\) and \(z\in [-2,2]\) for the surface, which is visualized in Fig. 4.18. Then we calculate the normal vector
The curl of the vector field is
Hence, we obtain the circulation
-
By interchanging the parameters – here x and y – the opposite direction of the normal vector is used. Without further condition (e.g. ‘pointing away from ...’), also the negative answers are correct in Stokes’ theorem.
b. Circulation via the Line Integral
For the line integral, we split the boundary into four parts.
We start with the boundary \(\varvec{\Psi }_1: \begin{pmatrix} t,&0,&2 \end{pmatrix}^\top \) with \(t\in [0,1]\) and obtain
The next path is then given by \(\varvec{\Psi }_2 : \begin{pmatrix} 1 ,&4-t^2,&-t \end{pmatrix}^\top \) and \(\, t\in [-2,2]\) with the integral
Considering the orientation, we continue with the curve \(\varvec{\Psi }_3: \begin{pmatrix} 1-t,&0,&-2 \end{pmatrix}^\top \) and with \(\, t\in [0,1]\)
For the last boundary, we find the curve \(\varvec{\Psi }_4 : \begin{pmatrix} 0,&4-t^2,&t \end{pmatrix}^\top \) with \(t\in [-2,2]\):
The total circulation is the sum
-
In case of line integrals, it might be necessary to split the path and to consider the orientation. The path should enclose the area anti-clockwise.
4.56. Circulation of the Field \(\varvec{G}(\rho ,\phi , z) = -\rho \cos \phi \,\hat{\varvec{h}}_\rho + \rho z \,\hat{\varvec{h}}_z\) in Cylindrical Coordinates
The boundary of the surface is again part of Vivani’s curve of exercise 29. We have already determined its tangent vectors:
We evaluate the vector field along the two curves (with \(\rho = \sin \phi \) and \(z = |\cos \phi |\)) and multiply with the tangent vectors
The modulus of the z-component has no effect on the integrand and we can integrate in one step:
a. Surface Integral
To parametrize the surface in Fig. 4.19, we have to vary the radius in the interval \(\rho \in [0,\sin \phi ]\)
The corresponding normal vector can be expressed in cylindrical coordinates
We determine the curl of the vector field
and insert into the surface integral
4.57. Circulation Within the Hyperbolic Surface \(z=xy\) for the Vector Field \(\varvec{G} = \rho ^3\cos ^2\phi \,\hat{\varvec{h}}_\phi +z^4 \,\hat{\varvec{h}}_z\)
a. In the Domain \(x^2+y^2\le 1\)
In the domain \(x^2+y^2\le 1\) the surface is ‘circular pattern’ in space (Fig. 4.20, left). Hence, we find – in cylindrical coordinates – the boundary
with the tangent vector
We evaluate the vector field along the curve and multiply with the tangent vector
The circulation is calculated by the line integral
b. In the Domain \(|x|+|y| \le 1\)
This figure is a pattern within a square domain (Fig. 4.20, right). It is possible, but not recommended, to solve the question in cylindrical coordinates. The radius can be found by \(\rho = \frac{1}{|\cos \phi |+|\sin \phi |}\) according to exercise 3. We prefer to re-write into Cartesian coordinates. For the vector field, we obtain
with the corresponding curl
The normal vector of the surface \(\mathcal {H}(x, y) =\begin{pmatrix} x,&y,&xy \end{pmatrix}^\top \) is easy to find
which leads to the circulation
4.58. Circulation of \(\varvec{G} = \cos (\lambda +\vartheta )(\,\hat{\varvec{h}}_r+\,\hat{\varvec{h}}_\vartheta +\,\hat{\varvec{h}}_\lambda )\) Within a Spherical Triangle
We choose the surface integral with the normal vector \(\varvec{N} =\sin \vartheta \,\hat{\varvec{h}}_r\) of the unit sphere. Due to later multiplication with the normal vector, we have to derive only the \(\varvec{h}_r\)-component of the curl:
We evaluate the circulation within the spherical triangle by the surface integral
The vector field depends on the angles but not on the distance to the origin. The planar triangle is described by the same angles as the spherical one. Therefore, the circulation within the planar triangle must be the same \(\Omega _{\Delta \varvec{ABC}} = -3\).
4.59. Circulation within a Parabolic Partial Area
The domain \((x-2)^2+4(y+1)^2 = 1\) describes an ellipse in the plane \(z=0\) with the center \((2,-1)\). The semi-major axis \(a=1\) and the semi-minor axis \(b = \frac{1}{2}\) are oriented parallel to the coordinate axes (cf. Fig. 4.21). Its projection on the paraboloid \(z=x^2+y^2\) has the boundary
We evaluate the vector field along the curve and multiply with its tangent vector
Hence, we obtain the circulation
within the parabolic partial area.
4.60. No Circulation for Planar Figures
Based on the Stokes’ theorem we conclude that the circulation will vanish when the product of normal vector and curl is zero for every figure. The normal vector of the plane \(y+4x -2z = 0\) is \( \varvec{N} = \begin{pmatrix} 4,&1,&-2 \end{pmatrix}^\top \). Hence, we have to determine a vector field whose curl is orthogonal to \(\varvec{N}\).
This problem is under-determined and we can use different methods to find an arbitrary solution. The methods and the results will differ in complexity. To keep the calculation simple, we assume a vector field with linear components
and calculate the corresponding curl
Due to the curl operator, every linear or non-linear function \(g_1(x)\) is eliminated for the first component, and in a similar way also functions of \(g_2(y)\) and \(g_3(z)\) for the second and third components, respectively. For the other variables we make an ansatz of a (linear) vector field
The inner product
still contains six degrees of freedom.
We normalize by one value \(a_{ik}\) and set some others to zero to derive a possible solution:
-
For \(a_{21} = 1\) and \(a_{12}=a_{23}=a_{13}=0\) we obtain \(a_{31} = 4a_{32}-2\) and the field
$$\begin{aligned} \varvec{F}_{1} = \begin{pmatrix} 0,&x,&(4a_{32}-2)x+a_{32}y \end{pmatrix}^\top \end{aligned}$$ -
For \(a_{21}=1\) and \(a_{23} = a_{31} = a_{12} = 0\) we obtain \(a_{13} = 2-4a_{32}\)
$$\begin{aligned} \varvec{F}_2 = \begin{pmatrix} (2-4a_{32})z,&x,&a_{32}y\end{pmatrix}^\top . \end{aligned}$$ -
Further solutions \(\varvec{F}_j\) are found by cyclic permutation or setting other components to zero.
After deriving a set of independent vectors \(\varvec{F}_j\), also the linear combinations solve the problem:
We want to point out once more that many solutions exist for a question in this general form without further conditions.
4.61. Circulation of the Field \(\varvec{G} =\alpha ^2\cos \gamma \,\hat{\varvec{h}}_\alpha + \,\hat{\varvec{h}}_\beta \) in Cardioid Coordinates
We use the ‘frame vectors’ of exercise 15 to calculate the curl of the vector field by the formal determinant
Coordinate Surface of \(\alpha = \mathop {\mathrm {const.}}\nolimits \)
In this coordinate system, the coordinate surfaces for constant \(\alpha \) or \(\beta \) form rotational cardioids. Three examples are shown in Fig. 4.22. Hence, we find the normal vector via:
The inner product
is zero and also the circulation:
Coordinate Surface of \(\beta = \mathop {\mathrm {const.}}\nolimits \)
In an analogous way, we calculate
with the inner product
and the circulation:
Although the vector field is non-conservative, we found two families of surfaces with vanishing circulation:
-
All partial areas on the surface \(\alpha = \mathop {\mathrm {const.}}\nolimits \) have zero circulation, because of the orthogonality between the surface’s normal vector and the curl of the vector field.
-
On the surface \(\beta = \mathop {\mathrm {const.}}\nolimits \), the circulation vanishes due to symmetry of \(\sin \gamma \) for the interval \(\gamma \in [0,\pi ]\).
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Antoni, M. (2019). Integral Theorems of Vector Analysis. In: Calculus with Curvilinear Coordinates. Springer, Cham. https://doi.org/10.1007/978-3-030-00416-3_4
Download citation
DOI: https://doi.org/10.1007/978-3-030-00416-3_4
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-00415-6
Online ISBN: 978-3-030-00416-3
eBook Packages: EngineeringEngineering (R0)


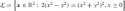 . Determine the enclosed area
. Determine the enclosed area
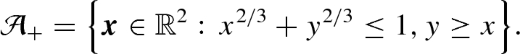
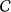 with
with 
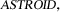 but also as cubocycloid, or paracycle.
but also as cubocycloid, or paracycle.


 and the relevant part of the curve is visualized in Fig.
and the relevant part of the curve is visualized in Fig.

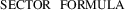
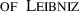 :
: 

















