Abstract
Many engineers might face some of the following questions:
-
What is the shortest flight connection between two airports?
-
Is the new roller coaster longer than the previous one?
-
How long will a new road be in a mountainous area?
-
When will the space probe reach the planet Mars?
-
How much material is required for a cable transport system or a suspension bridge?
These questions can be traced back to the problem of calculating the arc length of a curve, which is presented in this chapter.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Author information
Authors and Affiliations
Corresponding author
Appendices
Exercises
Curves in the Plane
-
1.
Calculate the arc length of the curve
$$\begin{aligned} \varvec{\Psi }(t)&= \left( \ln \sqrt{1+t^2}, \quad \arctan t\right) ^\top \qquad \text {for } 0\le t \le 2. \end{aligned}$$ -
2.
Determine the arc length of the closed curve
$$\begin{aligned} \varvec{\Psi }(t) = \begin{pmatrix} 5\cos t - 2\cos \frac{5t}{2},&5\sin t -2\sin \frac{5t}{2} \end{pmatrix}^\top . \end{aligned}$$The curve contains multiple points, which must be considered for finding the interval length.
-
3.
Calculate the arc length of the curve, which is given in polar coordinates with the radius
$$\begin{aligned} \rho (\phi ) = \frac{1}{|\cos \phi |+|\sin \phi |}\qquad \text {for } \phi \in [0,2\pi ]. \end{aligned}$$ -
4.
Use polar coordinates to parametrize the closed curve, which is given in the implicit form
$$\begin{aligned} (2x+x^2+y^2)^2 = 4(x^2+y^2) \end{aligned}$$and determine the arc length s.
-
5.
Given two points \(\varvec{B}_1 = \begin{pmatrix} 1,&0 \end{pmatrix}^\top \) and \(\varvec{B}_2 =\begin{pmatrix} -1,&0 \end{pmatrix}^\top \) in the xy-plane. The curve \(\mathcal {C}\) consist in all points \(\varvec{X} = \begin{pmatrix} x,&y \end{pmatrix}^\top \), where the product of the Euclidean distances \(\overline{\varvec{X}\varvec{B}}_1\cdot \overline{\varvec{X}\varvec{B}}_2 = c\) is constant.
-
(a)
Find a parametric representation of the curve for \(c\in \mathbb {R}^+\) by introducing polar coordinates. Use the addition theorem of cosine for simplification.
-
(b)
Consider now the case \(c=1\) and express the tangent vector \(\varvec{T}\) in terms of normalized polar coordinates \(\{\,\hat{\varvec{h}}_r,\,\hat{\varvec{h}}_\phi \}\) and simplify the term \(\sqrt{\varvec{T}^\top \varvec{T}}\) without calculating the arc length.
-
(a)
-
6.
Given the implicit curve
$$\begin{aligned} 3x^2+|y|^3-y^2 = 0. \end{aligned}$$Find three different parametrizations and calculate for each of them the arc length.
Arc Length in Cartesian, Spherical and Cylindrical Coordinates
-
7.
Verify, that the curve
$$\begin{aligned} \varvec{\Psi }(t) = \begin{pmatrix} \sin t,&\frac{\sin ^2 t}{2},&\frac{1}{2}(t-\sin t\cos t) \end{pmatrix}^\top \end{aligned}$$is already parametrized w.r.t. its arc length.
-
8.
Given the curve
$$\begin{aligned} \varvec{\Psi }(t) = t\,\hat{\varvec{h}}_\rho +\,\hat{\varvec{h}}_\phi + (t^2+1)\,\hat{\varvec{h}}_z \quad \quad t \in \mathbb {R}_0^+ \end{aligned}$$in cylindrical coordinates with \(\rho = \sqrt{t^2+1}\) and \(\phi = t-\arctan t+\frac{\pi }{2}\).
-
(a)
Determine the arc length s.
-
(b)
Verify, that the curve is lying on the paraboloid \(x^2+y^2-z = 0\).
-
(c)
Re-write the curve in Cartesian representation with the arc length s as parameter.
-
(a)
-
9.
Investigate the curve
$$\begin{aligned} \varvec{\Psi }(t) = \begin{pmatrix} 2t^3-2t ,&4t^2,&t^3+t \end{pmatrix}^\top \quad \quad t\in \mathbb {R}^{+}_0. \end{aligned}$$-
(a)
Express the tangent vector \(\varvec{T}\) in spherical coordinates in terms of normalized ‘frame vectors’ \(\,\hat{\varvec{h}}_{q_i}\).
-
(b)
Verify, that all points of the curve are lying on a quadric surface \(\mathcal {Q}\) and determine its type and coefficients. The general form of a quadric is given by
$$\begin{aligned} \mathcal {Q}: \sum _{i=1}^{3}\sum _{k=1}^{3}a_{ik}x_ix_k + 2\sum _{i=1}^{3}b_{i}x_i + c = 0\quad \quad (x = x_1, y = x_2, z = x_3). \end{aligned}$$Conclusions based on previous results/geometry are strongly recommended!
-
(a)
-
10.
Verify, that for every chosen parameter \(a\in [-1,1]\) the Villarceau curves
$$\begin{aligned} \varvec{\Psi }_a = \begin{pmatrix} ra+Ra\cos t+\sqrt{R^2-r^2}\sqrt{1-a^2} \sin t \\ r\sqrt{1-a^2}+R\sqrt{1-a^2}\cos t-\sqrt{R^2-r^2}a \sin t \\ r\sin t \end{pmatrix},\qquad t\in [0,2\pi ] \end{aligned}$$consist in circles on a torus \((x^2+y^2+z^2+R^2-r^2)^2 -4R^2(x^2+y^2) = 0\) with \(R>r\).
-
11.
Given the curve
$$\begin{aligned} \varvec{\Psi } = \begin{pmatrix} 3\sin t + \sin 3t\\ 3\cos t+\cos 3t\\ \sqrt{12} \sin t \end{pmatrix}. \end{aligned}$$-
(a)
Calculate the arc length for \(t\in [0,2\pi ]\).
-
(b)
Prove, that the curve has a constant distance to the origin \(\varvec{0}\).
-
(c)
Express the tangent vector via the formula \(\varvec{T} = \sum \limits _{i=1}^{3}\dot{q}_i\Vert \varvec{h}_{q_i}\Vert \,\hat{\varvec{h}}_{q_i}\) in spherical coordinates and simplify the expressions. Explicit determination of the ‘frame vectors’ \(\,\hat{\varvec{h}}_{q_i}\) is not necessary here.
-
(a)
-
12.
A curve is called a ‘loxodrome’ \(\varvec{\ell }_\mathcal {S}(t)\) of the surface \(\mathcal {S}\), if the intersection angles between the curve and the (orthogonal) parameter lines are constant. Derive a representation of a loxodrome on the unit sphere, which is parametrized w.r.t. longitude and co-latitude, and determine the arc length s.
Arc Length in Alternative and Modified Coordinate Systems
-
13.
Given the curve \(\varvec{\Psi } =(10\sin t)\,\hat{\varvec{h}}_\rho +8\cos t \,\hat{\varvec{h}}_z \) with \(\phi = \frac{3t}{5}\) in cylindrical coordinates.
-
(a)
Calculate the tangent vector \(\varvec{T}\) and the arc length s without using Cartesian expressions.
-
(b)
Determine the coordinates \(\{\alpha (t),\beta (t),\gamma (t)\}\) and the (positive) scaling parameter p for this curve in (modified) oblate spheroidal coordinates
$$\begin{aligned} x&=p\cosh \alpha \sin \beta \sin \gamma \\ y&=p\cosh \alpha \sin \beta \cos \gamma \\ z&= p \sinh \alpha \cos \beta \end{aligned}$$and express the tangent vector \(\varvec{T}\) in terms of non-normalized ‘frame vectors’ without calculating \(\varvec{h}_{q_i}\) explicitly. All points of the curve are on the surface \(\alpha = \mathop {\mathrm {const.}}\nolimits \)
-
(a)
-
14.
Calculate the arc length of the curve
$$\begin{aligned} \varvec{\Psi } = \left( \frac{2t}{\sqrt{1+t^2}}+t^2\right) \,\hat{\varvec{h}}_\alpha +\left( \frac{2t^2}{\sqrt{1+t^2}}-1\right) \,\hat{\varvec{h}}_\beta \end{aligned}$$with \( \beta = 1\), \( \alpha = t\) and \( \gamma = \frac{\pi }{2}-t\) given in parabolic coordinates:
$$\begin{aligned} x = \alpha \beta \cos \gamma ,\qquad y = \alpha \beta \sin \gamma ,\qquad z = \frac{\alpha ^2-\beta ^2}{2}. \end{aligned}$$ -
15.
The relationship between Cartesian coordinates and a set of curvilinear coordinates \((\alpha ,\beta ,\gamma )\) is given by
$$\begin{aligned} x&= \frac{\alpha \beta }{(\alpha ^2+\beta ^2)^2}\cos \gamma \\ y&= \frac{\alpha \beta }{(\alpha ^2+\beta ^2)^2}\sin \gamma \\ z&= \frac{\alpha ^2-\beta ^2}{2(\alpha ^2+\beta ^2)^2}. \end{aligned}$$-
(a)
Determine the tangent vector \(\varvec{T}\) and the arc length s of the ‘meridian’ with \(\alpha = \mathop {\mathrm {const.}}\nolimits \) and \(\gamma = \mathop {\mathrm {const.}}\nolimits \) for \(\beta = [0,B]\).
-
(b)
Verify that these meridians are cardioid curves which fulfill the equation \(x^2+y^2+z^2 = c \left( \sqrt{x^2+y^2+z^2}+z\right) \) and determine c.
-
(a)
-
16.
The curve is given by the coordinates \(\alpha = 0\), \(\beta = t\) and \(\gamma = t\) in the coordinate system
$$\begin{aligned}x&= {\sqrt{2}}^\alpha \Big (\sin \beta -\cos \beta \Big )\frac{1}{\cosh \gamma } \\ y&= {\sqrt{2}}^\alpha \Big (\cos \beta +\sin \beta \Big )\frac{1}{\cosh \gamma } \\ z&= {\sqrt{2}}^{\alpha +1}\tanh \gamma .\end{aligned}$$-
(a)
Derive/note down all normalized ‘frame vectors’ of this system.
-
(b)
Calculate the arc length s.
-
(a)
Solutions
1.1. Arc Length of \(\varvec{\Psi }(t) = \left( \ln \sqrt{1+t^2}, \quad \arctan t\right) ^\top \)
We differentiate the curve to obtain the tangent vector and its inner product:
Based on the inner product we calculate the arc length:
1.2. Closed Curve: \(\varvec{\Psi }(t) = \left( 5\cos t - 2\cos \frac{5t}{2},\right. \left. 5\sin t -2\sin \frac{5t}{2}\right) ^{\top }\)
First, we have to determine the length of the interval so that the curve is closed. We assume \(t_0=0\) as the starting point with the coordinates \(\varvec{\Psi }(0) = \begin{pmatrix}3,&0\end{pmatrix}^\top \). The curve will be closed when this point is reached again.
Taking the square of the radius, we can reformulate the condition:
The curve can only be closed for \(t = \frac{4\pi }{3}k\), where k is an integer number. We try the first multiples and find the curve to be closed for \(k = 3\), which is equivalent to \(t = 4\pi \).
To ensure that it is not a multiple point on the curve, we calculate the tangent vector
with \(\varvec{T}(0) = \varvec{T}(4\pi ) = \begin{pmatrix} 0,&0 \end{pmatrix}^\top \). Since both the coordinates and the tangential vector are identical in this point, the curve is closed for the interval \(t\in [0,4\pi ]\), which can be seen also from Fig. 1.2.
For the arc length we simplify the inner product:
and use the trigonometric identity \(\sqrt{1-\cos \phi } = \left| \sqrt{2}\sin \frac{\phi }{2}\right| \) for the arc length:
-
In particular for an arc length containing sine and cosine expressions, one must keep in mind: \(\sqrt{f(t)^2} = |f(t)|\not = f(t)\).
-
In case of expected multiple points, the tangent vector in start and end point must be checked.
-
The zero vector as tangential vector indicates that the parametrization has a non-regular point (here: at t= 0), and the curve might have a cusp at this location.
1.3. Arc Length of \(\rho (\phi ) = \frac{1}{|\cos \phi |+|\sin \phi |}\) in Polar Coordinates
Instead of investigating four cases due to modulus, we prove the symmetry:
If a point \(\varvec{P} = \begin{pmatrix} x,&y \end{pmatrix}^\top \) is on the curve, then the points \(\varvec{P}^* = \begin{pmatrix} \pm x,&\pm y \end{pmatrix}^\top \) are on the curve as well. Therefore, we can calculate the arc length in the first quadrant with \(\tau \in \left[ 0,\frac{\pi }{2}\right] \) and multiply the result by 4. In addition, we use the trigonometric identity \({\cos x+\sin x} = {\sqrt{2} \sin \left( x+\frac{\pi }{4}\right) }\) and find the arc length:
-
The curve is a square in polar coordinates with the corner points \(\left\{ \begin{pmatrix} \pm 1,&0 \end{pmatrix}^\top ,\begin{pmatrix} 0,&\pm 1 \end{pmatrix}^\top \right\} \) , which is shown in Fig. 1.3. Hence, Cartesian coordinates would be better suited for this problem. The solution demonstrates that the arc length can be calculated in any coordinate system, but with different amount of effort.
-
Integration of triangles and squares in polar coordinates has a practical application for boundary elements. In this method, the (gravitational) potential is modeled by single layers on the planar surface elements, and the integrals become singular for points on the element. One could overcome the singularity in some cases by introducing polar coordinates in the integrals.
-
Recognizing (and proving) symmetry reduces the calculation effort. Ignoring symmetries would lead to
$$\begin{aligned} \rho '(\phi ) = \cos \phi \sin \phi \frac{\frac{1}{|\cos \phi |}-\frac{1}{|\sin \phi |}}{(|\cos \phi | + |\sin \phi |)^2 } \end{aligned}$$and four cases in the integration.
1.4. Length of the Implicit Curve \( (2x+x^2+y^2)^2 = 4(x^2+y^2)\)
We insert polar coordinates into the equation to find the radius
Both solutions lead to a curve which fulfills the implicit equation. We simplify the integrand
and calculate the two arc lengths:
-
A radius is usually assumed to be positive in polar coordinates. If negative values are obtained by calculations, then this solution should be investigated carefully. It can be either a artifact (e.g. exercise 43) or a real solution. In the later case it might be better to replace the word ‘radius’ by a neutral expression like ‘curve parameter’.
-
The two curves are known as
 and they are visualized in Fig.
1.4 together. In the geometrical definition, these curves are created by tracing a marked point on a circle, which is rolling around a fixed circle of the same radius. Therefore, the curves belong to the family of
and they are visualized in Fig.
1.4 together. In the geometrical definition, these curves are created by tracing a marked point on a circle, which is rolling around a fixed circle of the same radius. Therefore, the curves belong to the family of 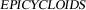 .
. -
In polar coordinates, we obtain two curves with different radii. There might be other parameterizations which describe only one curve with the total arc length \(s = 32\).
1.5. Different Parametrizations of \(3x^2+|y|^3-y^2 = 0\)
All terms occur either in squared form or with the modulus, i.e. the curve is symmetric w.r.t x- and y-axis, which can be seen also in Fig. 1.5. Therefore, we can determine the arc length only in the first quadrant and multiply the result by 4. In this concept, we can ignore the modulus for the following.
a. Parametrization in the Variable \(\varvec{y}\)
We use y as a variable and solve the equation
The derivative is then found by
with the arc length
In this particular case, the integration is performed and evaluated with Mathematica.
b. Rational Parametrization by \(\varvec{x= y\cdot t}\)
The origin \(\varvec{0} = \begin{pmatrix} 0,&0 \end{pmatrix}^\top \) is lying on the curve. Hence, we can try a rational parametrization \(x = y\cdot t\)
In the first quadrant, the coordinates \(\{x, y\}\) are both positive and so we find the interval \(t\in \Big [0,\frac{1}{\sqrt{3}}\Big ]\) and the arc length
c. Rational Parametrization by \(\varvec{y= x\cdot t}\)
A second rational parametrization is found by \(y= x\cdot t \)
with the inner product
and the arc length
Below we sketch some more parametric representations without calculations:
-
1.
A rational parametrization is possible for every rational point of the curve, in particular for \(\begin{pmatrix} 0,&0 \end{pmatrix}^\top \), \(\begin{pmatrix} 0,&\pm 1 \end{pmatrix}^\top \) and \(\begin{pmatrix} \pm \frac{2}{9},&{}\pm \frac{2}{9} \\ \end{pmatrix}^\top \).
-
2.
By introducing polar coordinates we obtain
$$\begin{aligned} 3\rho ^2\cos ^2\phi +\rho ^3|\sin \phi |^3-\rho ^2\sin ^2\phi = 0\\ \Rightarrow \rho (\phi )=\frac{1}{|\sin \phi |^3}\Big (\sin ^2\phi - 3\cos ^2\phi \Big )= \frac{4\sin ^2\phi -3}{\sin ^3\phi }. \end{aligned}$$ -
3.
We can also solve the algebraic equation of order 3 in a closed form:
$$\begin{aligned} y(x) = \frac{1}{3}\left( \frac{\root 3 \of {-81x^2+9\sqrt{81x^4-4x^2}+2}}{\root 3 \of {2}}+\frac{\root 3 \of {2}}{\root 3 \of {-81x^2+9\sqrt{81x^4-4x^2}+2}}+1\right) . \end{aligned}$$
-
A curve might have different parametric representations and the calculation effort for arc length (or line integral, area, geometrical center...) can differ significantly.
-
It should be pointed out that not every implicit curve has a parametric representation.
-
The idea of the rational parametrization exploits the relationship between a (common) curve point with rational coordinates and a family of straight lines passing through the common point and the other points of the curve. This parametrization often leads to simpler integrals than a polar representation.
1.6. Constant Product of Euclidean Distances
a. Parametrization in Polar Coordinates
We insert polar coordinates into the constant product condition of the Euclidean distances to the points \(\varvec{B}_1 = \begin{pmatrix} 1,&0 \end{pmatrix}^\top \) and \(\varvec{B}_2 =\begin{pmatrix} -1,&0 \end{pmatrix}^\top \) and get a equation for the radius \(\rho \):
By using the trigonometric identity \((-\cos 2\phi ) = (-2\cos ^2\phi +1)\), we get
The squared radius is determined from the quadratic equation in the variable \(\rho ^2\):
b. Tangent Vector for \(\varvec{c=1}\)
In the case \(c=1\), we can eliminate the inner root (for \(\cos 2\phi \ge 0\))
and obtain with the formula (1.19) the tangent vector
The parametrization is valid for \(\cos 2\phi \ge 0\), which leads to 3 intervals \(\left[ 0,\frac{\pi }{4}\right] ,\) \(\left[ \frac{3\pi }{4},\frac{5\pi }{4}\right] ,\) and \(\left[ \frac{7\pi }{4}, 2\pi \right] \) for the curve parameter \(\phi \).
-
The curves are known as
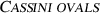 in the general case for
\(c \in \mathbb {R}\)
and four of the curves are visualized in Fig. 1.6.
in the general case for
\(c \in \mathbb {R}\)
and four of the curves are visualized in Fig. 1.6. -
For \(c=1 \) we get the
 . Its arc length leads to the elliptic integral of Gauß: \(s = 4\sqrt{2}\int \limits _{0}^{1} \frac{\mathrm {d}t}{\sqrt{1-t^4}} =2\sqrt{2}\varpi \).
. Its arc length leads to the elliptic integral of Gauß: \(s = 4\sqrt{2}\int \limits _{0}^{1} \frac{\mathrm {d}t}{\sqrt{1-t^4}} =2\sqrt{2}\varpi \).
1.7. Parametrization of a Curve w.r.t. its Arc Length: \(\varvec{\Psi }(t) = \left( \sin t,\quad \frac{\sin ^2 t}{2},\quad \frac{1}{2}(t-\sin t\cos t)\right) ^\top \)
A curve is parametrized w.r.t. its arc length, if the norm of the tangent vector \(\Vert \varvec{T}\Vert \) is equal to one for all points on the curve:

-
The parametrization w.r.t. the arc length leads to easier expressions for further quantities in differential geometry like the curvature of a curve. In vector analysis, the re-parametrization is usually not performed.
1.8. Curve on a Paraboloid: \(\varvec{\Psi }(t) = t\,\hat{\varvec{h}}_\rho +\,\hat{\varvec{h}}_\phi + (t^2+1)\,\hat{\varvec{h}}_z\)
a. Arc Length
We calculate the derivatives of the coordinates
and the tangent vector
Hence, we obtain the arc length
b. On a Paraboloid
-
To prove, whether a curve is lying on a certain surface, we have to insert its components into the surface equation and achieve a true expression.
In this case, we obtain
so that all points are lying on the paraboloid (cf. Fig. 1.7).
c. Re-write w.r.t. Arc Length
For the parametrization w.r.t. the arc length, we invert the relation \(s = \frac{\sqrt{5}}{2}t^2\) and insert \(t = \sqrt{\frac{2s}{\sqrt{5}}}\) into the original curve:
1.9. Curve \(\varvec{\Psi }(t) = \left( 2t^3-2t ,\quad 4t^2,\quad (t^3+t) \right) ^\top \) Lying on a Quadric
a. Spherical Coordinates
The relation between the spherical and the Cartesian coordinate system provide us:
The longitude might by expressed by \(\arctan \)-function as well, the \({\mathop {\text {arccot}}}\)-function is chosen here to avoid the problem for \(t = \pm 1\).
The derivatives of the coordinates are given by
which leads to the tangent vector
in spherical coordinates.
b. Quadric
The quadric form
has at a first glance up to 13 unknowns \(\{a_{ik},b_k, c\}\). From linear algebra it is known that the matrix \(\underline{\mathbf {A}} = [a_{ik}]\) is symmetric, which reduces the problems to 10 unknowns.
Now we have a closer look on the geometry:
-
We find \(c=0\) as the point \(\varvec{0} = \begin{pmatrix} 0,&0,&0 \end{pmatrix}^\top \) is lying on the curve.
-
The curve is on a circular cone because of the constant co-latitude for all points:
-
There are no mixed terms \((a_{ik})_{i\not = k}\) due to circular symmetry.
-
In circular cones we get also \(a_{11} = a_{22}\).
-
The curve is centered around the origin and so there are no translation terms: \(b_i=0\) for \(i=1,2,3\).
-
The combination of these facts leads to the reduced quadric form:
with only two unknowns. We insert one point of the curve e.g. \(\varvec{\Psi }(1) = \begin{pmatrix}0,&4,&2\end{pmatrix}^\top \), to find a relation between \(a_{11}\) and \(a_{33}\):
As a last check, we insert now the parameter form of the curve, to make sure, that all points are on the cone:

-
The study of quadratic form or quadric is usually performed in courses on linear algebra. The type is determined by the sign of the eigenvalues. Via translation, rotation, and re-scaling the so-called normal form of the quadric form is achieved.
-
Prominent examples of the quadratic form in 3D space are spheres, ellipsoids, cones, cylinder, paraboloids and hyperboloids.
1.10. Villarceau Circles
The investigation of the Villarceau circles is carried out in the following steps:
-
1.
We verify that all points are lying on a torus with the given equation.
-
2.
We prove that all points are lying on a sphere by calculating the curvature.
-
3.
We prove that the curve is planar.
Lying on a Torus
With the abbreviations \(\sigma : =\sqrt{R^2-r^2}\) and \(\tau = \sqrt{1-a^2}\) we first calculate the term \(\rho ^{2}=x^2+y^2\), which occurs twice in the torus equation:
In the first sum, we add the term \((z^2+R^2-r^2)\)
and insert the result into the torus equation:

As this equation is fulfilled for all parameter t and every choice of a, every point of these curves is lying on a torus (Fig. 1.8).
Radius of the Circle
To verify, that a curve is lying on a sphere, we can either consider the equation
with the unknown center \(\varvec{M} = \begin{pmatrix} m_x,&m_y,&m_z \end{pmatrix}^\top \) and the radius r, or we demonstrate that the curvature
is constant and positive. In the latter method, we don’t have to determine the center.
The cross product of first and second derivatives of the curve delivers
which leads to the curvature
The curve has a positive constant curvature, so all the points are lying on a sphere with radius \(\frac{1}{\kappa } = R\).
Lying in a Plane
Finally we prove that all points are lying in a plane, which is depending on the parameter a.
We select three points on the curve, and use their vectors to span up the plane \(\mathcal {E}\). For simplicity we choose points where either sine or cosine-terms vanish:
These points are used to find the normal vector of the plane
which leads to the plane equation
Now we want to ensure that all points are in the plane which is spanned by these 3 vectors. Hence we insert the curve components into the plane equation:

The curve is on a sphere and a plane, hence, the points are lying on a circle.
1.11. Curve on a Sphere: \(\varvec{\Psi } = \left( 3\sin t + \sin 3t,\quad 3\cos t+\cos 3t,\quad \sqrt{12} \sin t\right) ^\top \)
a. Arc Length
We calculate the tangent vector and simplify the inner product by trigonometric identities:
For the arc length, we must consider the modulus
b. Distance to the Origin
The distance to the origin is equivalent to the radius in spherical coordinates:
All points of the curve are lying on a sphere around the origin \(\varvec{0}\) with the radius \(r = \sqrt{16}=4\) (cf. Fig. 1.9).
c. Tangent Vector in Spherical Coordinates
The tangent vector in spherical coordinates is given by formula (1.15). In the previous step, we found already \(r = 4\) and \(\dot{r} = 0\). We calculate the co-latitude \(\vartheta \) by
and consider \(\sin \vartheta = \sqrt{1-\cos ^2\vartheta } = \sqrt{1- \frac{{3} \sin ^2 t}{4}}\).
For the longitude, we differentiate the expression \(\lambda = \arctan \frac{y}{x}\) in general:
It might be necessary to add \(\pm \pi \) to the longitude for the correct quadrant, but this will not affect the derivative \(\dot{\lambda }\). We insert the components of the curve \(\varvec{\Psi }\) into the last formula
and obtain the tangent vector
1.12. Loxodrome on the Sphere
The angle \(\psi (t)\) between two curves \(\varvec{\Psi }_1(t)\) and \(\varvec{\Psi }_1(t)\) is determined by the inner product of the normalized tangent vectors
In the following, we present the calculation in spherical and Cartesian coordinates to highlight again the advantage of using adequate coordinates. (Even more adequate is the introduction of cylindrical coordinates, to find the loxodrome curves of all rotational surfaces.)
Every curve on a unit sphere can be re-written in the form
with differentiable functions \(\lambda (t)\) and \(\vartheta (t)\). The condition of a loxodrome provides a relation between these two functions. Hence, we choose one of them to be the parameter of the curve, e.g. \(\vartheta (t) := t\).
We obtain the tangent vector
The parameter line \(\lambda = t\) of constant co-latitude \( \vartheta = \vartheta _0\) is a circle
with the tangent vector
We calculate the inner product
The intersection angle is constant for
which provides the relation
using the substitution of Weierstraß (\(u = \tan \frac{t}{2}\)) for the integration. Hence, we obtain the expression
with \(\frac{c}{\sqrt{c^2+1}} = \cos \psi \) for the spherical loxodrome. The arc length can be read from the previous nominator
-
A loxodrome on the sphere is visualized in Fig. 1.10 and by straight lines in the Mercator projection.
-
There are other parametric representations due to different reasons:
-
other spherical coordinates, e.g. latitude instead of co-latitude,
-
alternative solution of the integral \(\int \frac{1}{\sin t}\mathrm {d}t\),
-
or by using the longitude \(\lambda := t\) as curve parameter.
1.13. Arc Length of \(\varvec{\Psi } =(10\sin t)\,\hat{\varvec{h}}_\rho +8\cos t \,\hat{\varvec{h}}_z \)
a. Arc Length
Based on the expression in cylindrical coordinates, we can identify:
We determine the tangent vector
and the arc length
b. Oblate Spheroidal Coordinates
We have to compare the Cartesian expression (based on the cylindrical system) and the oblate spherical coordinates:
Based on the (squared) polar distance
we find the coordinates \(\gamma = \frac{\pi }{2}-\frac{3t}{5}\) and \(\beta = t\). The last conditions \(p\cosh \alpha = 10\) and \(p\sinh \alpha = 8\) are fulfilled by
The values \(\alpha \) and p are constant for this curve. Hence, all points are lying complety on the ellipsoid (cf. Fig. 1.11), which is defined by these parameters.
The tangent vector in terms of non-normalized ‘frame vectors’ is
-
\({}\)
The coordinate surface for fixed values of \(\{p, \alpha \}\) is a rotational ellipsoid :
$$\begin{aligned} \frac{x^2+y^2}{p^2 \cosh ^2 \alpha }+\frac{z^2}{p^2 \sinh ^2 \alpha } = \sin ^2\beta +\cos ^2\beta = 1. \end{aligned}$$The value of \(\alpha \) is responsible for the ratio between semi-major and semi-minor axes, while p provides an up- or downscaling of the complete figure. In a similar way, constant values of\(\{p, \beta \}\) lead to one-sheeted hyperboloids
$$\begin{aligned} \frac{x^2+y^2}{p^2 \sin ^2 \beta }-\frac{z^2}{p^2 \cos ^2 \beta } = \cosh ^2\alpha -\sinh ^2\alpha = 1. \end{aligned}$$ -
Compared to other textbooks, the sine- and cosine terms are interchanged, which doesn’t affect the principle.
1.14. Arc Length in Parabolic Coordinates
‘Frame Vectors’ of Parabolic Coordinates
We differentiate the relationship between Cartesian and parabolic coordinates to obtain the ‘frame vectors’ \(\,\hat{\varvec{h}}_{q_i}\):

Based on the expression \( \beta = 1\), \( \alpha = t\) and \( \gamma = \frac{\pi }{2}-t\) for the curve, we obtain the tangent vector
and the corresponding arc length

-
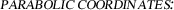
The coordinate surfaces consist of two pairs of
 , which are rotated around the z-axis, and the half planes with constant value of \(\gamma \). For a constant value of \(\beta \), the surface$$\begin{aligned} 2z = \frac{x^2+y^2}{\beta ^2}-\beta ^2 \end{aligned}$$
, which are rotated around the z-axis, and the half planes with constant value of \(\gamma \). For a constant value of \(\beta \), the surface$$\begin{aligned} 2z = \frac{x^2+y^2}{\beta ^2}-\beta ^2 \end{aligned}$$describes a confocal paraboloid that open upwards. For a constant value of \(\alpha \), the surface
$$\begin{aligned} 2z = -\frac{x^2+y^2}{\alpha ^2}+\alpha ^2 \end{aligned}$$describes a confocal paraboloid that open downwards (cf. Fig. 1.12).
1.15. Meridian of Cardioid Coordinates
a. Arc Length of the Meridian
Tangential Vectors of the Frame
We differentiate the fractions separately w.r.t. the coordinate \(\alpha \):
The derivatives w.r.t. the coordinate \(\beta \) are recognizable the same, apart from a minus sign.
For the ‘frame vectors’ we get
Arc Length
The meridian in \(\beta \)-direction is the curve with a constant value of \(\alpha \) and \(\gamma \) which leads to the tangent vector
For the corresponding arc length, we find

b. Cardioid
We calculate the terms
of the cardioid equation:
which leads to the conclusion \(c = \frac{1}{4\alpha ^2}\).
-
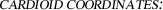
The coordinate surfaces consist of two pairs of cardioids, which are rotated around the z-axis, and the half planes with constant value of \(\gamma \). For a constant value of \(\alpha \), the surface
$$\begin{aligned} (x^2+y^2+z^2) = \frac{1}{4\alpha ^2}\left( \sqrt{x^2+y^2+z^2}+z\right) \end{aligned}$$describes a
 intersecting the positive
z-axis. For a constant value of \(\beta \), the surface$$\begin{aligned} (x^2+y^2+z^2) = \frac{1}{4\beta ^2}\left( \sqrt{x^2+y^2+z^2}-z\right) \end{aligned}$$
intersecting the positive
z-axis. For a constant value of \(\beta \), the surface$$\begin{aligned} (x^2+y^2+z^2) = \frac{1}{4\beta ^2}\left( \sqrt{x^2+y^2+z^2}-z\right) \end{aligned}$$describes a cardioid intersecting the negative z-axis (cf. Fig. 1.13).
1.16. Curve on a Sphere
a. ‘Frame Vectors’ of Modified Spherical Coordinates
We differentiate the relationship between Cartesian and the new curvilinear coordinates to obtain the ‘frame vectors’ \(\,\hat{\varvec{h}}_{q_i}\):
b. Arc Length
Based on the expression \(\alpha = 0\), \(\beta = t\) and \(\gamma = t\) for the curve, we calculate the tangent vector
and the corresponding arc length
-
The result of \(x^2+y^2+z^2 = \left( \sqrt{2}^{\alpha }\right) ^2 \Big (\frac{(2\sin ^2\beta +2\cos ^2\beta )}{\cosh ^2 \gamma }+2\tanh ^2\gamma \Big ) = 2^{\alpha +1}\) is independent of the coordinates \(\{\gamma ,\beta \}\). Hence, we have a spherical surface for constant values of \(\alpha \). In other words, it is a modified spherical system, where \(\alpha \) is responsible for the distance to the origin and \(\beta \) for the ‘longitude’
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Antoni, M. (2019). Arc Length and Tangent Vector. In: Calculus with Curvilinear Coordinates. Springer, Cham. https://doi.org/10.1007/978-3-030-00416-3_1
Download citation
DOI: https://doi.org/10.1007/978-3-030-00416-3_1
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-00415-6
Online ISBN: 978-3-030-00416-3
eBook Packages: EngineeringEngineering (R0)




 and they are visualized in Fig.
and they are visualized in Fig.
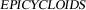 .
.


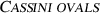 in the general case for
in the general case for
 . Its arc length leads to the elliptic integral of Gauß:
. Its arc length leads to the elliptic integral of Gauß: 





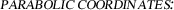
 , which are rotated around the z-axis, and the half planes with constant value of
, which are rotated around the z-axis, and the half planes with constant value of 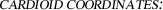
 intersecting the positive
z-axis. For a constant value of
intersecting the positive
z-axis. For a constant value of 